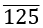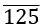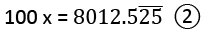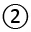महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download
परिचय
- एक प्रणाली सिद्धांतों या प्रक्रियाओं का एक सेट है जिसके अनुसार कुछ किया जाता है।
- संख्या प्रणाली सिद्धांतों का एक सेट है जिसके अनुसार संख्याएँ प्रस्तुत की जाती हैं और उन पर विभिन्न अंकगणितीय क्रियाएँ जैसे कि जोड़ना, घटाना, गुणा आदि लागू की जाती हैं। यह विभिन्न अंकों और प्रतीकों के उपयोग के लिए मूल नियमों को निर्धारित करता है।
- जब भी हम सिद्धांतों को बदलते हैं, हमें संख्या प्रणाली का एक नया सेट प्राप्त होता है। इसके परिणामस्वरूप विभिन्न प्रकार की संख्या प्रणालियाँ उत्पन्न होती हैं।
- संख्या प्रणालियों के कुछ उदाहरण हैं:
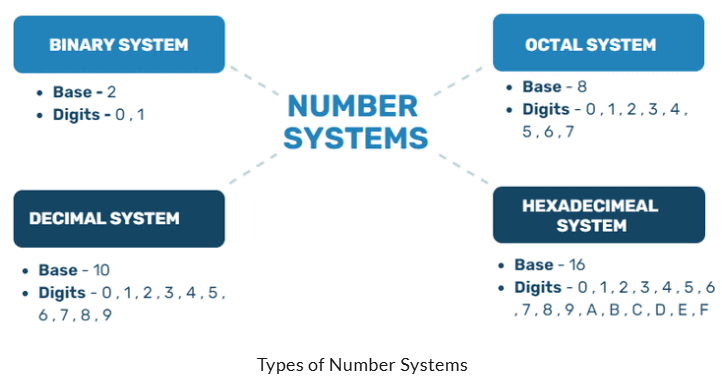
- (i) आधार को उन अंकों की संख्या के रूप में परिभाषित किया गया है जो हम संख्याओं को प्रस्तुत करने के लिए उपयोग करते हैं।
- (ii) अंक वे उपकरण हैं जिनका उपयोग संख्याओं को प्रस्तुत करने के लिए किया जाता है।
हम अगले अध्यायों में विभिन्न संख्या प्रणालियों और उनके आधारों के बारे में बात करेंगे। दुनिया भर में उपयोग की जाने वाली मानक संख्या प्रणाली दशमलव संख्या प्रणाली है। दशमलव संख्या प्रणाली का आधार "10" है क्योंकि यह सभी संख्याओं को प्रस्तुत करने के लिए 10 अंक (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) का उपयोग करती है।
मुख्य मान और स्थान मान
- मुख्य मान: किसी विशेष अंक का मान स्वयं अंकों का मुख्य मान कहा जाता है। दशमलव संख्या प्रणाली में, हम 10 अंकों का उपयोग करते हैं, जैसा कि ऊपर उल्लेखित है। जहाँ भी उपयोग किया जाता है, मुख्य मान वही रहता है।
उदाहरण: 568 और 1285 तथा 58738 में 5 का मुख्य मान 5 है। - स्थान मान: किसी संख्या का स्थान मान उस स्थान पर निर्भर करता है जहाँ यह स्थित है। दशमलव संख्या प्रणाली में विभिन्न स्थानों और उनके संबंधित गुणकों की सूची नीचे दी गई है। हम सबसे बाएँ से शुरू करेंगे और दाएँ स्थान के अनुसार आगे बढ़ेंगे।
उदाहरण: संख्या 786543 के लिए।
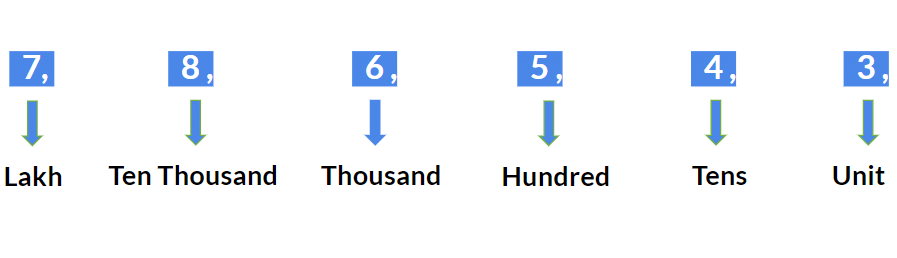

- किसी विशेष संख्या प्रणाली में एक अंक का स्थान मान उस अंक के मुख्य मान को उसके संबंधित स्थान से गुणा करके परिभाषित किया जाता है। दशमलव प्रणाली में, स्थान का मान ऊपर दी गई तालिका के अनुसार होगा।
उदाहरण: 568 में 5 का स्थान मान 500 है और 1285 में 5 का स्थान मान 5 है और 58738 में 5 का स्थान मान 50000 है।
इस अध्याय में हम संख्याओं, उनके गुणों और उनके वर्गीकरण के बारे में बात करेंगे। जैसा कि पहले चर्चा की गई थी, ये सभी गुण केवल दशमलव संख्या प्रणाली तक सीमित रहेंगे क्योंकि यही सभी पूछे गए प्रश्नों का आधार है। इस अध्याय में चर्चा किए गए सिद्धांत आपके किसी भी प्रवेश परीक्षा को पास करने के लिए गणित की आवश्यकताओं की सामान्य समझ की ओर आपका पहला कदम होंगे। जैसे-जैसे हम आगे बढ़ेंगे, आप महसूस करेंगे कि आपने पहले से ही इन सिद्धांतों में से अधिकांश को स्कूल में सीखा है।
संख्याओं के प्रकार
1. प्राकृतिक संख्या
गणित का मुख्य अनुप्रयोग गणना करना है। यहीं से संख्याओं की पहली श्रेणी आती है, अर्थात् प्राकृतिक संख्याएँ या सामान्यतः जिन्हें गणना करने की संख्याएँ कहा जाता है।
प्राकृतिक संख्याओं की विशेषताएँ
- ये पूर्ण संख्याएँ हैं, अर्थात् भिन्न/दशमलव शामिल नहीं हैं।
- शून्य शामिल नहीं है।
- ऋणात्मक संख्याएँ शामिल नहीं हैं।
- इन्हें "N" द्वारा दर्शाया जाता है।
- N = {1, 2, 3, 4, 5.........अनंत}
2. पूर्ण संख्याएँ
प्राकृतिक संख्याएँ और 0 मिलकर संख्याओं का एक समूह बनाते हैं जिसे पूर्ण संख्याएँ कहा जाता है। चूंकि '0' किसी चीज़ की अनुपस्थिति का प्रतिनिधित्व करता है और इसका उपयोग गणना के लिए नहीं किया जाता है, इसलिए इन्हें गणना की संख्याएँ नहीं कहा जाता।
पूर्ण संख्याओं की विशेषताएँ
- ये पूर्ण संख्याएँ हैं, अर्थात् भिन्न/दशमलव शामिल नहीं हैं।
- शून्य शामिल है।
- ऋणात्मक संख्याएँ शामिल नहीं हैं।
- इन्हें "W" द्वारा दर्शाया जाता है।
- W = {0, 1, 2, 3, 4, 5.........अनंत}।

3. पूर्णांक
शून्य से कम की संख्याएँ ऋणात्मक चिह्न के साथ दर्शाई जाती हैं और इन्हें ऋणात्मक संख्याएँ कहा जाता है। पूर्ण संख्याएँ, साथ ही प्राकृतिक संख्याओं के ऋणात्मक, संख्याओं के एक समूह को बनाते हैं जिसे पूर्णांक कहा जाता है।
पूर्णांकों की विशेषताएँ
- ये पूर्ण संख्याएँ हैं, अर्थात् भिन्न/दशमलव शामिल नहीं हैं।
- शून्य शामिल है।
- ऋणात्मक संख्याएँ शामिल हैं।
- इन्हें "I" द्वारा दर्शाया जाता है।
- I = {-अनंत.......-3, -2, -1, 0, 1, 2, 3 ......... अनंत}।
4. भिन्न
शब्द 'भिन्न' लैटिन 'fractus' से लिया गया है जिसका अर्थ है “टूटा हुआ”। भिन्न एक सम्पूर्ण का भाग दर्शाती है। जब हम एक सम्पूर्ण को टुकड़ों में बाँटते हैं, तो प्रत्येक भाग सम्पूर्ण का एक भिन्न होता है।
उदाहरण: 1/2, 3/5, 2/7, 10/21
एक भिन्न में दो भाग होते हैं। रेखा के ऊपर का संख्या को संख्यक कहा जाता है। रेखा के नीचे का संख्या को हरण कहा जाता है।
भिन्नों के प्रकार
भिन्नों को सामान्यतः प्रतिनिधित्व के आधार पर दो प्रकारों में वर्गीकृत किया जाता है:
(i) साधारण भिन्न
उदाहरण: 30/7
(ii) मिश्रित भिन्न
उदाहरण: 4(2/7)
5. दशमलव संख्याएँ
ये भिन्नों के प्रतिनिधित्व का एक रूप हैं। हम हरण के मान को एकता, अर्थात् "1" के रूप में बनाते हैं। ये दोनों, नकारात्मक और सकारात्मक हो सकते हैं।
उदाहरण: 2.5, 1.25, 1.3333 ......., 2.666....., 2.8284.....
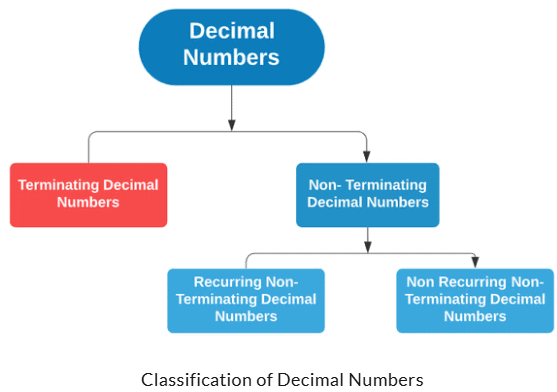
दशमलव संख्याओं के प्रकार
दशमलव संख्याएँ मुख्यतः दो श्रेणियों में वर्गीकृत की जाती हैं:
- समापन दशमलव संख्याएँ - ये दशमलव संख्याएँ निश्चित अंत वाली होती हैं।
उदाहरण: 2.5, 1.25 - असमापन दशमलव संख्याएँ - ये दशमलव संख्याएँ बिना निश्चित अंत वाली होती हैं।
उदाहरण: 1.3333 ......., 2.666....., 2.8284.....
असमापन दशमलव संख्याएँ आगे दो श्रेणियों में विभाजित की जाती हैं:
(i) पुनरावर्ती असमापन दशमलव संख्याएँ: ये असमापन दशमलव संख्याएँ होती हैं जिनमें दशमलव के बाद के अंक बार-बार दोहराते हैं।
(ii) गैर-पुनरावर्ती असमापन दशमलव संख्याएँ: ये असमापन दशमलव संख्याएँ होती हैं जिनमें दशमलव के बाद के अंक दोहराते नहीं हैं बल्कि एक पूरी तरह से यादृच्छिक पैटर्न में होते हैं। ये असंगत संख्याएँ हैं, जिन पर हम इसी अध्याय में आगे चर्चा करेंगे।
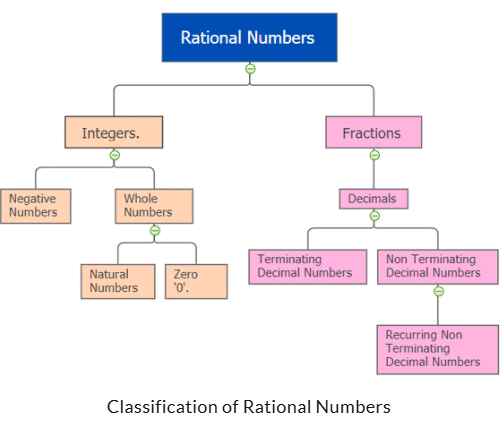
6. परिमेय संख्याएँ
वे सभी संख्याएँ जो p/q के रूप में प्रदर्शित की जा सकती हैं जहाँ p और q पूर्णांक हैं और q ≠ 0 है, उन्हें परिमेय संख्याएँ कहा जाता है। सभी पूर्णांक, भिन्न, समापन दशमलव संख्याएँ और असमापन पुनरावर्ती दशमलव संख्याएँ परिमेय संख्याओं की श्रेणी में आती हैं।
7. अव्यक्त संख्याएँ
वे सभी संख्याएँ जो अव्यक्त होती हैं, उन्हें अव्यक्त संख्याएँ कहा जाता है। गैर-प्रतिपादक, गैर-समाप्ति दशमलव संख्याएँ अव्यक्त संख्याएँ होती हैं। प्राकृतिक संख्याओं की वर्गमूल, घनमूल आदि अव्यक्त संख्याएँ होती हैं।
उदाहरण: √3 = 1.7320.... , √8 = 2.8284 ......, 3√4 = 1.5874 .......
समाप्ति दशमलव संख्या को p/q रूप में परिवर्तित करना:
उदाहरण: 80.125 को p/q रूप में परिवर्तित करें
- देखें कि दशमलव के बाद कितने अंक हैं, इस मामले में 3।
- दशमलव को हटाएँ और प्राप्त संख्या को उतने ही 10 से विभाजित करें जितने अंक आपने पहले चरण में गिनें।
⇒ 80.125 = 80125/1000 = 641/8
गैर-समाप्ति आवर्ती दशमलव संख्या को p/q रूप में परिवर्तित करना:
उदाहरण: 80.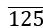 को p/q रूप में परिवर्तित करें।
को p/q रूप में परिवर्तित करें।
- मान लीजिए संख्या x
⇒ x = 80 है।- गिनें कि उसके बाद कितने अंक दशमलव हैं, इस स्थिति में 3।
- इस स्थिति में दोनों पक्षों के दहाई से गुणा करें, अर्थात 1000 से।
⇒ 1000x = 80125.- घटाएँ
⇒ 999x = 80045 ⇒ x = 80045
/ 999
उदाहरण: 80. 1 को p / q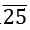 रूप में परिवर्तित करें ।
रूप में परिवर्तित करें ।
7922.4
- माना 80.1
= x
- दोनों पक्षों को 100 से गुणा करें
⇒- घटाएँ
⇒ 99x =
हमने ऊपर दिए गए उदाहरणों में जो प्रक्रिया अपनाई है, वह बहुत समय लेने वाली है। हमें एक ऐसा तरीका चाहिए जो इसी प्रक्रिया को बहुत कम समय में कर सके। इसके लिए हमारे पास एक सूत्र है जिससे आप एक ही कदम में उत्तर प्राप्त कर सकते हैं।
हर समाप्त होने वाली आवर्ती दशमलव संख्या के 3 भाग होते हैं:
(उदाहरण लेते हुए: (i) दशमलव से पहले के अंक (80)। (ii) दशमलव के बाद बार के साथ अंकों की संख्या (2)। (iii) दशमलव के बाद बार के बिना अंकों की संख्या (1)।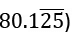
सामान्य रूप: सभी अंकों को दशमलव के बिना एक बार लिखा गया - बार के बिना के सभी अंकों को एक बार लिखा गया / जितने 9 हैं, उतने बार के साथ अंकों की संख्या के बाद दशमलव के बाद जितने 0 हैं, उतने बार के बिना अंकों की संख्या।
उदाहरण: 80. को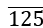 p/q रूप में परिवर्तित करें।
p/q रूप में परिवर्तित करें।
- सभी अंकों को एक बार लिखा गया = 80125
- बार के बिना के सभी अंकों को एक बार लिखा गया = 80
- दशमलव के बाद बार के साथ अंकों की संख्या = 3
- दशमलव के बाद बार के बिना अंकों की संख्या = 0
- सामान्य रूप = (80125 - 80) / 999 = 80045 / 999
उदाहरण: 80.1 को 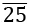 p/q रूप में परिवर्तित करें।
p/q रूप में परिवर्तित करें।
- सभी अंकों को एक बार लिखा गया = 80125
- बार के बिना के सभी अंकों को एक बार लिखा गया = 801
- दशमलव के बाद बार के साथ अंकों की संख्या = 2
- दशमलव के बाद बार के बिना अंकों की संख्या = 1
- सामान्य रूप = (80125 - 801) / 990 = 79324 / 990
8. वास्तविक संख्याएँ
- राशि संख्याएँ और अव्यवस्थित संख्याएँ मिलकर वास्तविक संख्याएँ बनाती हैं। परिभाषा के अनुसार, सभी संख्याएँ जिन्हें संख्या रेखा पर दर्शाया जा सकता है, उन्हें वास्तविक संख्याएँ कहा जाता है।
- अब तक चर्चा की गई सभी श्रेणियाँ वास्तविक संख्याओं के सेट में आती हैं, जिसमें अव्यवस्थित संख्याएँ भी शामिल हैं। इन्हें भी संख्या रेखाओं पर दर्शाया जा सकता है।
9. काल्पनिक संख्याएँ
- काल्पनिक संख्याएँ वे संख्याएँ हैं जो वास्तव में किसी संख्या प्रणाली में मौजूद नहीं होतीं, लेकिन गणनाओं के लिए इनकी उपस्थिति मान ली जाती है।
- इन्हें संख्या रेखाओं पर प्रदर्शित नहीं किया जा सकता। इन्हें जटिल संख्याएँ भी कहा जाता है।
उदाहरण: √−3, √−16, 4√−8
नोट: जटिल संख्याओं का अध्ययन अभिलाषा परीक्षण के दृष्टिकोण से महत्वपूर्ण नहीं है। इसलिए, हम इस विषय को आगे नहीं बढ़ाएंगे।
10. विषम और सम संख्याएँ
- सम संख्याएँ वे होतीं हैं जो 2 से विभाज्य होतीं हैं। ये संख्याएँ होतीं हैं जिनका इकाई अंक 2, 4, 6, 8 या 0 होता है। सम संख्याओं का सामान्य अभिव्यक्ति 2n है, जहाँ n एक पूर्ण संख्या है।
- विषम संख्याएँ वे होतीं हैं जो 2 से विभाज्य नहीं होतीं। ये संख्याएँ होतीं हैं जिनका इकाई अंक 1, 3, 5, 7 या 9 होता है। विषम संख्याओं का सामान्य अभिव्यक्ति 2n + 1 है, जहाँ n एक पूर्ण संख्या है।
पूर्ण संख्याओं पर कुछ क्रियाएँ:
(i) विषम ± विषम = सम
(ii) सम ± सम = सम
(iii) विषम ± सम = विषम
(iv) सम ± सम ± सम ........... n पद = सम
(v) विषम ± विषम ± विषम .............. n पद = सम यदि n सम है, विषम यदि n विषम है
(vi) विषम × विषम = विषम
(vii) सम × विषम = सम
(viii) सम × सम = सम
(ix) सम × सम × सम ....... n पद = सम
(x) विषम × विषम × विषम ....... n पद = विषम
(xi) (सम)n = सम
(xii) (विषम)n = विषम
11. प्रमुख और समाकलित संख्याएँ
(a) प्रमुख संख्याएँ: प्रमुख होना प्राकृतिक संख्याओं की एक विशेषता है। वे सभी संख्याएँ जो केवल 2 संख्याओं से विभाज्य होती हैं, अर्थात् स्वयं और एकता "1"।
उदाहरण: 2, 3, 5, 7, 11 आदि।
(b) समाकलित संख्याएँ: वे संख्याएँ हैं जो 2 से अधिक संख्याओं से विभाज्य होती हैं, अर्थात् स्वयं, एकता "1" और कम से कम एक अन्य।
उदाहरण: 4, 6, 8, 9, 10 आदि।
1 न तो प्रमुख है और न ही समाकलित।

➢ प्रमुख संख्याओं की विशेषता
- सभी प्रमुख संख्याएँ जो 3 से बड़ी हैं, वे 6n ± 1 के रूप में होती हैं, लेकिन 6n ± 1 के रूप में सभी संख्याएँ प्रमुख नहीं होतीं।
- यह विशेषता यह दर्शाती है कि जब 3 से बड़ी प्रमुख संख्याएँ 6 से विभाजित की जाती हैं, तो वे 1 या 5 का शेष छोड़ती हैं।
12. सह-प्रमुख संख्याएँ
- यह एक जोड़ी या दो से अधिक प्राकृतिक संख्याओं की विशेषता है।
- दो संख्याएँ सह-प्रमुख कहलाती हैं यदि केवल एक संख्या जो दोनों संख्याओं को पूरी तरह से विभाजित कर सकती है, वह 1 है।
- 1 के अलावा कोई भी संख्या दी गई संख्याओं के जोड़े को विभाजित नहीं कर सकती।
- ये संख्याएँ स्वयं प्रमुख या समाकलित हो सकती हैं। 1 सभी प्राकृतिक संख्याओं के साथ सह-प्रमुख है, सिवाय 1 के।
उदाहरण: (3, 7); (4, 15); (3, 10) आदि। - यदि उनके HCF (सर्वाधिक समान भाजक) की मान 1 है, तो संख्याओं का एक समूह सह-प्रमुख कहलाता है। हम अगले अध्यायों में HCF के बारे में जानेंगे।
उदाहरण: (3, 7, 11); (4, 15, 10); (3, 10, 8) आदि।
|
142 videos|172 docs|185 tests
|
FAQs on महत्वपूर्ण अवधारणाएँ: संख्या प्रणाली - Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA
| 1. मुख्य मान और स्थान मान में क्या अंतर है? |  |
| 2. संख्याओं के प्रकार क्या-क्या होते हैं? |  |
| 3. संख्या प्रणाली क्या है और इसके कितने प्रकार होते हैं? |  |
| 4. क्या संख्याएँ केवल सकारात्मक होती हैं? |  |
| 5. मुख्य मान और स्थान मान का उपयोग कहाँ किया जाता है? |  |