Damping in Second-Order Systems | Control Systems - Electrical Engineering (EE) PDF Download
Introduction to Damping in Second-Order Systems
In control systems, a second-order system is a dynamic system described by a second-order differential equation. These systems are common in modeling mechanical, electrical, or other physical setups. A key feature of these systems is damping, which shows how oscillations in the system's response fade over time after a disturbance. Damping depends on the damping ratio (zeta), a number that decides if the system oscillates, decays smoothly, or settles without oscillation. Understanding damping is essential for designing stable and efficient control systems, as it affects response speed, overshoot, and settling time.

Damping Ratio and Its Importance
The damping ratio (zeta) measures how much damping a second-order system has. It’s the ratio of actual damping to critical damping, where critical damping is the point at which the system returns to steady state as fast as possible without oscillating. For a typical second-order system with the transfer function G(s) = 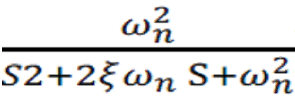
zeta controls the response:
- zeta < 1: Underdamped (oscillatory response).
- zeta = 1: Critically damped (fastest non-oscillatory response).
- zeta > 1: Overdamped (slow, non-oscillatory response). The damping ratio is key to adjusting the system for the performance you want.
Types of Damping Responses
The damping ratio value splits the system’s response into different types:
- Underdamped (0 < zeta < 1): The system oscillates, and these oscillations shrink over time. A lower zeta means more oscillation and overshoot.
- Critically Damped (zeta = 1): The system gets back to steady state as fast as possible without oscillating, great for quick settling needs.
- Overdamped (zeta > 1): The response is slow and doesn’t oscillate, taking longer to settle, good when overshoot must be avoided. You can see these differences in the system’s step response.
How Damping Affects Performance
Damping changes important aspects of a second-order system’s performance:
- Overshoot: In underdamped systems, more oscillations mean bigger overshoot, which can be bad for precise control.
- Settling Time: Critically damped systems settle quickest, while overdamped ones take longer because of too much damping.
- Stability: Too little damping (low zeta) can cause constant oscillations, while too much damping keeps things stable but slows them down. Engineers tweak zeta to find a balance, depending on uses like suspension systems or electronic filters.
Real-World Uses of Damping
Damping matters a lot in practical control systems:
- In mechanical systems (like car suspensions), damping stops too much bouncing.
- In electrical circuits (like RLC circuits), it manages resonance and signal fade.
- In robotics and automation, good damping ensures smooth, steady movement. By studying the damping ratio, engineers can predict and improve how systems work for safety, efficiency, and performance.
Natural Frequency and Damping Interaction
The natural frequency (omega_n) of a second-order system works closely with damping. It’s the frequency at which the system would oscillate if there were no damping (zeta = 0). When damping is added, it reduces the actual oscillation frequency in underdamped systems, called the damped frequency (omega_d), where omega_d = omega_n * sqrt(1 - zeta^2). A higher natural frequency with low damping leads to faster oscillations, while higher damping slows everything down. This interaction helps engineers set both zeta and omega_n for the right response.
Design Considerations for Damping
When designing a control system, damping isn’t just about picking a zeta value—it’s about the bigger picture. Engineers must consider trade-offs: too little damping might make a system unstable or too bouncy, while too much damping could make it slow and unresponsive. For example, in a car suspension, you want enough damping to avoid bouncing but not so much that the ride feels stiff. Designers also use tools like root locus or frequency response to see how damping affects the system and adjust components (like resistors or springs) to hit the target zeta.
Conclusion
Damping in second-order systems is a vital factor that controls how a system reacts to inputs or disturbances. The damping ratio defines whether the response is underdamped, critically damped, or overdamped, and it shapes things like overshoot, settling time, and stability. It also interacts with the natural frequency and requires careful design choices to meet performance goals. By choosing the right damping ratio and understanding its effects, engineers can customize a system’s behavior for specific needs, making damping a core part of control system design and analysis. Knowing and adjusting damping helps systems work well in all kinds of applications.
|
53 videos|107 docs|40 tests
|
FAQs on Damping in Second-Order Systems - Control Systems - Electrical Engineering (EE)
| 1. What is the damping ratio and why is it important in second-order systems? |  |
| 2. What are the different types of damping responses in second-order systems? |  |
| 3. How does damping affect the performance of a second-order system? |  |
| 4. What are some real-world applications of damping in engineering and technology? |  |
| 5. How do natural frequency and damping interact in second-order systems? |  |





















