Gears | Mechanical Engineering SSC JE (Technical) PDF Download
INTRODUCTION
- Gears
- The efficiency of gear drives is very high even up to 99% in case of spur gears.
- Spur gears are used only when shafts are parallel, spur gears impose radial loads on the shafts
- In Helical gear, the magnitude of helix angle of pinion and gear is same, however the hand of helix is opposite. Helical gears impose radial and thrust loads on shaft.
- A double helical gears with a small groove between two helix is called herringbone gears. There is no thrust load on shaft herringbone gears are used only for parallel shafts.
- Bevel gears have the shape of truncated cone, used for shafts which are at right angles to each other. Bevel gear impose radial and thrust load on shaft.
- Worm gears are used for shafts, the axes of which do not intersect and are perpendicular to each other. The worm imposes high thrust load, while worm wheel imposes high radial load on the shafts. It is characterized by high speed reduction ratio used in material handling equipment.
- When the axes of two shafts are neither perpendicular nor intersecting spiral helical gears are employed.
Fundamental Law of Gearing
- The common normal to the tooth profile at the point of contact should always pass through a fixed point, called pitch point; in order to obtain a constant velocity ratio.
is the velocity of point C when it is considered on gear 1, while CB is velocity of point C, when it is considered on gear 2 CA perpendicular to O1C and
perpendicular to O2C.
Figure 7-2 shows two mating gear teeth, in which
- Tooth profile 1 drives tooth profile 2 by acting at the instantaneous contact point K.
- N1N2 is the common normal of the two profiles.
- N1 is the foot of the perpendicular from O1 to N1N2
- N2 is the foot of the perpendicular from O2 to N1N2.
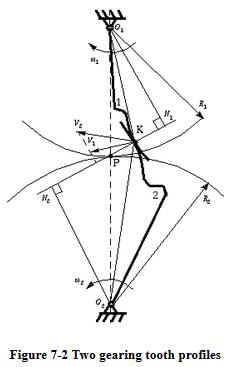
Although the two profiles have different velocities V1 and V2 at point K, their velocities along N1N2 are equal in both magnitude and direction. Otherwise the two tooth profiles would separate from each other. Therefore, we have
 (7-1)
(7-1)
or
 (7-2)
(7-2)
We notice that the intersection of the tangency N1N2 and the line of center O1O2 is point P, and
 (7-3)
(7-3)
Thus, the relationship between the angular velocities of the driving gear to the driven gear, or velocity ratio, of a pair of mating teeth is
 (7-4)
(7-4)
Point P is very important to the velocity ratio, and it is called the pitch point. Pitch point divides the line between the line of centers and its position decides the velocity ratio of the two teeth. The above expression is the fundamental law of gear-tooth action.
- Only involute and cycloidal curves satisfy this fundamental law of gearing.
- In case of cycloid curves, the pitch point is fixed but the inclination a varies.
- The module (m) is defined as the inverse of diametral pitch.
- Diametral pitch
- Circular pitch
- Centre distance between two gears
- Diametral pitch
- Standard system of Gears
- There are two system for the shape of gear tooth depending upon pressure angle. 14.5° and 20° involute system. The 20° pressure angle system has the following advantage.
- It reduces the risk of undercutting.
- The tooth is stronger with higher load carrying capacity.
- It has greater length of contact.
- It gives larger radius of curvature.
The main advantage of 14.5° pressure angle system is its quietness of operations.
- In the design of gears, the number of teeth are decided from speed reduction and the module is calculated from strength and wear consideration.
- There are two system for the shape of gear tooth depending upon pressure angle. 14.5° and 20° involute system. The 20° pressure angle system has the following advantage.
Force Analysis
- According to fundamental law of gearing, this resultant force PN always acts along the pressure line.
- The tangential component (Pt) is a useful load because it determines the magnitude of torque and consequently the power, which is transmitted.
- The radial component (Pr) is a separating force which is always directed towards the centre of gear.
- As the point of contacts moves, the magnitude of resultant force PN changes.
- Minimum Number of Teeth : on pinion to avoid interference.
- Tmin can be further reduced by giving a slight radius to the tip of tooth.
- For 20° full depth involute tooth system, it is always sefe to assume the No. of teeth on the pinion as 18 to 20.
- If the face width is too large; there is a possibility of concentration of load at one end of gear tooth due to misalignment, elastic deformation and warping gear tooth. optimum range of face width is 8m < b < 12 m
Lewis Equation
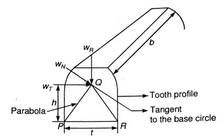
The first equation used for bending stress was the Lewis equation. This is derived by treating the tooth as a simple cantilever and with tooth contact occuring at the tip as shown below:
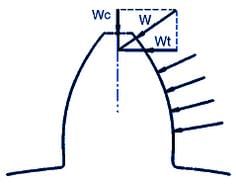
Only the tangent component(Wt) is considered. It is also assumed that only one pair of teeth is in contact. Stress concentrations at the tooth root fillet are ignored. It can be shown that the maximum bending stress occurs at the tangent points on the parabola shown above. Use of the standard equation for bending stress(σ=Mc/I) leads to:

The value of Y independent of the size of tooth and depend only on No. of teeth on gear and system of teeth.
Maximum tangential force Pt called beam strength and replaced by Sb.
known as Lewis equation.
- In design when same material is used for pinion and gear, the product ( sb × Y) decides weaker between pinion and gear the lewis form factor (Y) is always less for pinion than gear, for same material pinion is always weaker than gear.
- Effective load on Gear Tooth
Since torque developed by source and required by driven machine varies during working cycle. It is balanced by flywheel. In gear design maximum force is the criterion. This is accounted by means of a service factor.
- Service factor
- The dynamic force is induced due to the following factors :
- Inaccuracies of tooth profile
- Errors in tooth spacing
- Misalignment between bearings
- Elasticity of parts
- Inertia of rotating mass.
Due to inability in calculation of dynamic load a velocity factor (Cv) developed,
d — diameter of gear (in mm)
Effective load
where, Pd is the dynamic load
|
5 videos|103 docs|59 tests
|
FAQs on Gears - Mechanical Engineering SSC JE (Technical)
| 1. What is Gears SSC? |  |
| 2. What kind of exams does Gears SSC cover? |  |
| 3. How can I access the exam preparation materials provided by Gears SSC? |  |
| 4. Are the study materials provided by Gears SSC effective for exam preparation? |  |
| 5. Can Gears SSC help me with exam-specific strategies and tips? |  |