Calendar | Quantitative Techniques for CLAT PDF Download
| Table of contents |

|
| What is Calendar? |

|
| Concept of an Odd Day |

|
| Decoded day of the week |

|
| Evaluation of Leap Year |

|
| Evaluation of Odd Days of a Century |

|
What is Calendar?
A calendar is a chart or a series of pages that displays the days, weeks, and months of a specific year, or provides particular seasonal information.
Below is the list of topics covered under the Calendar section:
- Basic structure of a calendar and the concept of odd days.
- Decoding the days of the week.
- Determining a leap year.
- Calculating odd days in a century.
- Type 1 Problems: Identifying the day of the week when a reference day is given.
- Type 2 Problems: Identifying the day of the week when no reference day is given.
- Type 3 Problems: Finding months with matching calendars.
Basic Structure of a Calendar
- Ordinary Year: A year with 365 days is termed as an ordinary year.Examples: 1879, 2009, 2019, etc.
- Leap Year: A year with 366 days is termed as a leap year.
Examples: 2012, 2016, 2020, etc. - When 365 is divided by 7, the quotient is 52, and the remainder is 1. This means an ordinary year consists of 52 weeks and one extra day, which is referred to as an “odd day” in calendar-related topics.
- A leap year, with 366 days, gives a quotient of 52 and a remainder of 2 when divided by 7. This indicates that a leap year comprises 52 weeks and two extra days, both referred to as “odd days”.
Thus, an ordinary year has one odd day, while a leap year has two odd days.
Concept of an Odd Day
Number of Odd Days in a Month
January has 31 days, regardless of whether it is an ordinary year or a leap year. Dividing 31 by 7 gives a remainder of 3, indicating that January has 3 odd days. In general, any month with 31 days has 3 odd days, while any month with 30 days has 2 odd days.
The exception occurs with February. In an ordinary year, February has 28 days, and dividing 28 by 7 gives a remainder of 0. Therefore, February in an ordinary year has 0 odd days, while in a leap year, February has 29 days, giving 1 odd day.
The table below summarizes the number of odd days for each month in a calendar year: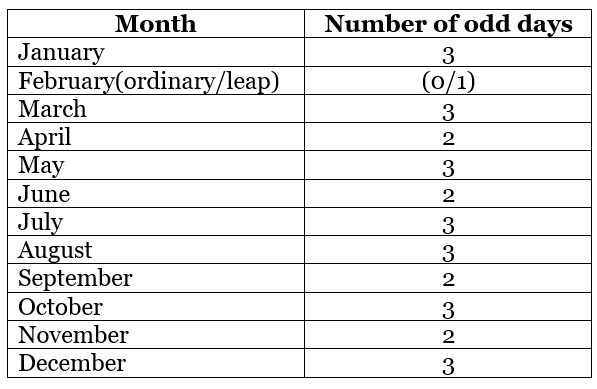 Table 1: Number of Odd Days in Each Month
Table 1: Number of Odd Days in Each Month
Decoded day of the week
Days of the Week and Their Codes
The week begins with Monday, with Saturday and Sunday collectively referred to as the weekend. To simplify calculations and save time during exams, the days of the week are assigned specific codes: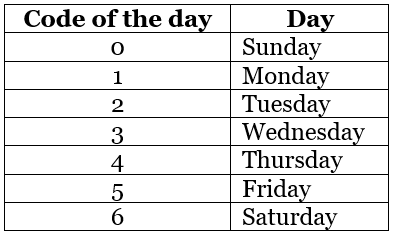 Table 2: Codes for Days of the Week
Table 2: Codes for Days of the Week
This coding system helps decode the results obtained during problem-solving in calendar-related topics. If the final calculated value is 10, dividing 10 by 7 (since there are 7 days in a week) gives a remainder of 3. Using the table, the remainder 3 corresponds to Wednesday as the correct answer.
Example: Today is Monday. What day will it be after 61 days?
(a) Tuesday
(b) Wednesday
(c) Thursday
(d) Saturday
Ans: Days of the week repeat every 7 days. After 63 days, it will again be Monday. Therefore, after 61 days, the day will be Saturday.
Evaluation of Leap Year
Understanding Leap Years
A leap year typically occurs every four years; however, there are cases where the interval between two leap years extends to 8 years instead of the usual 4.
Examples:
- The year 1896 was a leap year, but the next leap year was 1904, as 1900 was not a leap year.
- To identify leap years quickly, any year that is completely divisible by 4 (with no remainder) is considered a leap year.
- Years like 1888, 2012, and 2016 are leap years as they are divisible by 4, whereas years like 2009 and 2019 are not, making them ordinary years.
Exception for Century Years: For a century year to be a leap year, it must be divisible by 400, not just by 4.
- The year 700 is divisible by 4 but not by 400, so it is not a leap year.
Leap Years: Years like 400, 800, and 1200 are leap years as they are divisible by 400.
Not Leap Years: Years like 300, 700, and 1000 are not leap years as they are not divisible by 400.
Evaluation of Odd Days of a Century
This concept helps students in answering the question of calendars in less than 30 seconds. The question looks unsolvable, but the application of these concepts makes it easier to solve it in a quicker way.
Observe the question:
Q: What day of the week was year 100 A.D December 31st?
This might look like a difficult and big problem. But it’s definitely not.
Ans: Let’s consider the first 100 years i.e. Year 1.A.D to year 100 A.D
Dividing the first 100 by 4 we get that first 100 years had 76 ordinary years and 24 ordinary years. (The quotient when 100 is divided by 4 gives 25 but the year 100 itself is not a leap year as it is not divisible by 400 hence 24 is considered instead of 25)
Step 1: 100 years = 76 ordinary years + 24 leap years
We know that an ordinary year has 1 odd day and a leap year has 2 odd days. Hence, 76 ordinary years will have 76 odd days and 24 leap years will 24*2 = 48 odd days. Adding both the results we get 76+48 = 124 odd days in total.
Step 2: 100 years = (76 x 1 + 24 x 2) odd days = 124 odd days.
Dividing the total odd days 124 by 7 gives the quotient as 17 and a remainder as 5. This indicates that 124 days had 17 weeks and 5 odd days.
Step 3: 100 years = (17 weeks + days) 5 odd days.
A number of odd days in 100 years = 5.
Now decoding the number to the days of the week from the table gives the result that the number 5 stands for Friday.
Hence, the last day (December 31st) of the year 100 A.D was Friday.
Extension of the logic
- Similarly, one can find the last day of the other century years by extending the same logic.
- If 100 years had 5 odd days, then logically 200 years should have 10 odd days. Since 10 is greater than 7, the division of 10 by 7 gives the remainder 3. Hence, the 200 years had 3 odd days, which means the last day of the year 200 was Wednesday.
- Number of odd days in 200 years = (5 x 2) = 10 = (7+3) = 3 odd days.
- If 100 years had 5 odd days and 200 years 10 odd days logically 300 years should have 15 odd days. The division of 15 by 7 indicates it has 1 odd day from the remainder which indicates it is Monday. Hence, the last day of the year 300 was Monday.
- Number of odd days in 300 years = (5 x 3) = 15 = (14+1) = 1 odd day.
- Logically, 400 years should have 20 odd days since 400th year is a leap year as it is divisible by 400. This year will have 20+1 = 21 odd days, which when divided by 7 gives the zero (0) as remainder. Hence, 400 years had 0 odd day and that was Sunday.
The logical approach for the next few years is shown in the table given below: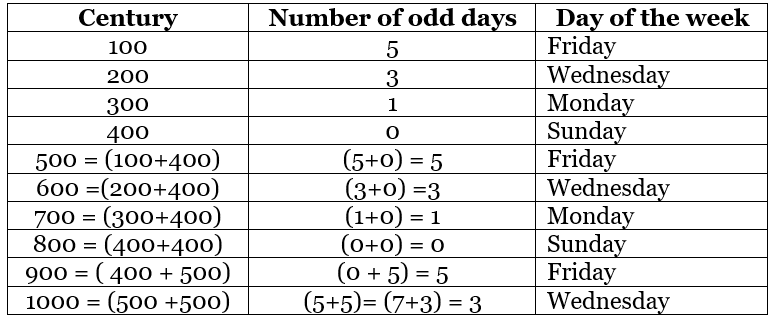
Observations from the table:
- The cycle of a number of days repeats after every four centuries and also hence the days at which it ends. The order will always be Friday, Wednesday Monday and Sunday.
- A century will always end on either Friday, Wednesday, Monday or Sunday (Decoded values of these days are 5, 3, 1, and 0 respectively).
- A century will never end on Tuesday, Thursday and Saturday (Decoded values of these days are 2, 4, and 6 respectively).
Type 1 Problems: Finding the day when another day is given
In this section, one has to find out the day of the week of a given date using the day of the week information on the reference date.
Q: If 17th march 2008 was Monday, what was 1st April 2012?
Ans: The total number of odd days from 17th March 2008 to 17th March 2012.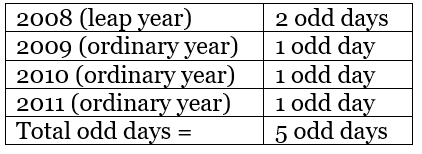 Since 17th march 2008 was Monday and 17th march 2012 is 5 days more than Monday. Then adding 5 odd days to Monday, we get Saturday. Hence 17th march to April 1st we have 15 days. Saturday+15=Sunday. Adding 15 days or (15 = 14+1) to Saturday, we get the answer as Sunday.
Since 17th march 2008 was Monday and 17th march 2012 is 5 days more than Monday. Then adding 5 odd days to Monday, we get Saturday. Hence 17th march to April 1st we have 15 days. Saturday+15=Sunday. Adding 15 days or (15 = 14+1) to Saturday, we get the answer as Sunday.
Q: If today is Sunday, what will be the day on 7777th day?
Ans: If today is Sunday, then the 7th day from today will be Sunday. Similarly, the 14th day, 21st day or 70th day or 700th day or 7000th day or 7777th day will be Sunday. Hence, the answer is Sunday.
Type 2 Problems: Find the day when another day is not given
In this section, one has to find out the day of the week of a given date. There will no reference date or day has given here. One can make use of the concept of an odd day to find the answer.
Q: What day of the week was 15th August 1947?
Ans: The date August 15th 1947 can be divided as follows for easy calculation:
1600 years + 300 years+ 46 years (1901 to 1946) + Jan 1st to august 15th (of 1947)
Note:- Do not write 47 years in the third section, it would indicate 47th year in that century is over.
1600 years + 300 years+ 46 years (1901 to 1946) + Jan 1st to august 15th (of 1947)
Now let’s find out the total number of odd days in each section:
Section 1:
1600 is a multiple of 400 years. 400 years have 0 odd days hence 1600 years should have 0 odd days.
Section 2:
The second section 30 years will have 1 odd day. Kindly refer to “evaluation of odd days in a century” topic for clarification.
Section 3:
This section has 46 years from 1901 to 1946, we know that an ordinary year has one odd day and a leap year has 2 odd days.
Let’s first calculate the total number of leap years from 1901 to 1946.
Division of 46 by 4 gives the quotient as 11, which indicates that from 1901 to 1946 we have 11 leap years. If there are 11 leap years among 46 years then remaining 35 years should be ordinary years. Hence, 35 ordinary years will have 35 odd days and 11 leap years will have 11*2 = 22 years.
The total number of odd days in 46 years will be 35+22 = 57 odd days. The division of 57 by 7 given the remainder as 1.This indicates from 1901 to 1946 there is only one odd day.
Section 4:
It has months from January to August 15th. We have already calculated the total number of odd days in each month in the odd day’s section.
Since 1947 is not a leap year February had zero odd days.
Check the table below for a better understanding of the number of odd days in a month:
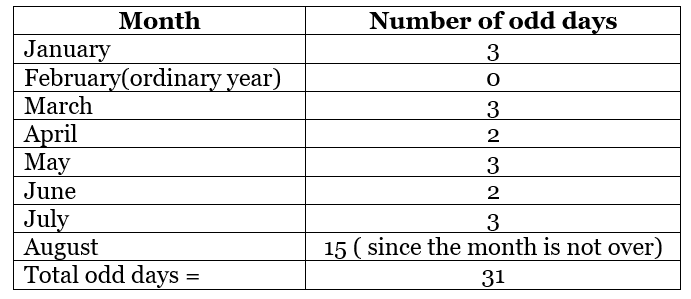
The total number of odd days is 31 which when divided by 7 gives the remainder 3. Hence, the total number of odd days in the year 1947 from January 1st to August 15th is 3.
Adding the total number of odd days of each section: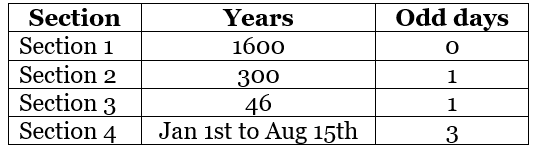 The total number of odd days = 0+1+1+3 = 5 = Friday. Hence, August 15th 1947 was Friday.
The total number of odd days = 0+1+1+3 = 5 = Friday. Hence, August 15th 1947 was Friday.
Type 3 Problems: Matching the Calendar
Q: Which year in the future will have the same calendar exactly as 2009?
(a) 2010
(b) 2013
(c) 2015
(d) 2017
Ans: If the total number of odd days between any years is zero or it’s a multiple of seven. Then, those two years will have the same calendar.
The total number of odd days is listed below: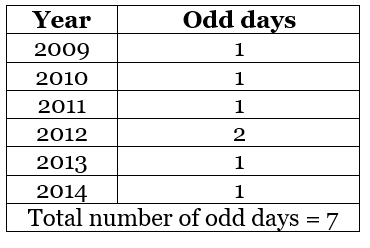 Hence, 2015 will have the same calendar as 2009. Option C is the correct answer.
Hence, 2015 will have the same calendar as 2009. Option C is the correct answer.
|
57 videos|108 docs|73 tests
|
FAQs on Calendar - Quantitative Techniques for CLAT
| 1. What is a calendar and why is it important? |  |
| 2. What is the concept of an odd day in a calendar? |  |
| 3. How can I decode the day of the week for any given date? |  |
| 4. How is a leap year evaluated, and what are its rules? |  |
| 5. How do you calculate the odd days of a century? |  |

















