Reflection of Light | Science Class 10 PDF Download
| Table of contents |

|
| What is Reflection of Light? |

|
| Basic Terminologies |

|
| Laws of Reflection |

|
| Types of Reflection of Light |

|
| Solved Examples |

|
What is Reflection of Light?
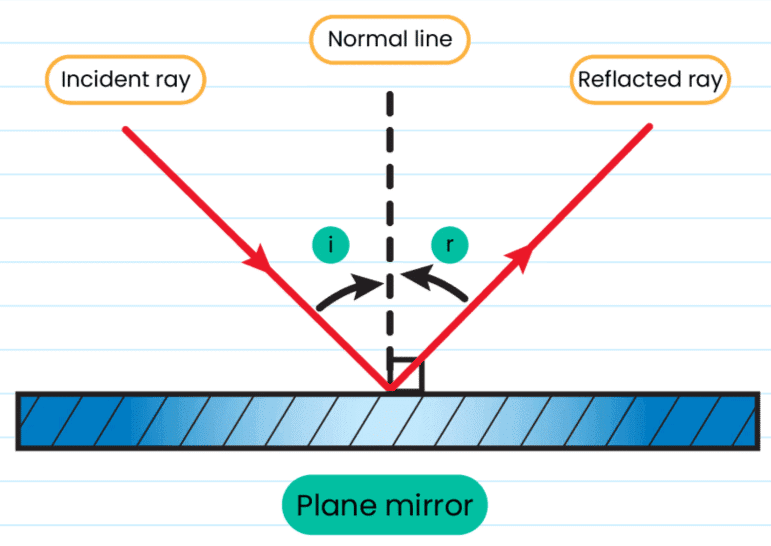
When a ray of light approaches a smooth polished surface and the light ray bounces back, it is called the reflection of light.
- The incident light ray which lands upon the surface is said to be reflected off the surface. The ray that bounces back is called the reflected ray.
- If a perpendicular were to be drawn on a reflecting surface, it would be called normal. The figure below shows the reflection of an incident beam on a plane mirror.
- Here, the angle of incidence and angle of reflection are with respect to normal and the reflective surface.
Basic Terminologies
- Ray of Light: A straight line that shows the direction moment of light is called a ray of light.
- Beam of Light: A bunch of light rays or bundle of rays at a point is called a beam of light.

- Reflection of Light: When rays of light fall on any object and return back in the same medium from the surface is called reflection of light. Due to reflection of light, we can see all the nature.
- Incident Ray: The ray of light that falls on a polished surface (or a mirror) is called the incident ray of light.
- Reflected Ray: The ray of light which gets reflected from a polished surface (or a mirror) is called the reflected ray of light.
- Normal: The normal is a line at a right angle to the reflecting surface.
Laws of Reflection
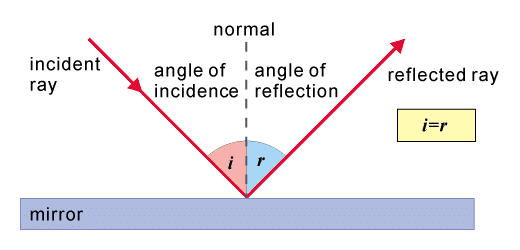
The laws of reflection determine the reflection of incident light rays on reflecting surfaces, like mirrors, smooth metal surfaces and clear water. The law of reflection states that:- Law 1: The incident ray, the reflected ray and the normal to the surface at the point of incidence all lie in the same plane.
- Law 2: The angle of incidence (i) is always equal to the angle of reflection (∠r) i.e. ∠i = ∠r
Types of Reflection of Light
Different types of reflection of light are briefly discussed below:
- Regular reflection is also known as specular reflection
- Irregular (Diffused) reflection
- Multiple reflection
Regular Reflection
- When parallel light rays fall on a smooth plane surface like a mirror, all rays of light are reflected parallel along a definite direction. Then this kind of reflection is called regular reflection.
- Specular Reflection refers to a clear and sharp reflection, like the ones you get in a mirror. A mirror is made of glass which is coated with a uniform layer of a highly reflective material such as powder.
- This reflective surface reflects almost all the light incident on it uniformly. There is not much variation in the angles of reflections between various points. This means that the haziness and the blurring are almost entirely eliminated.
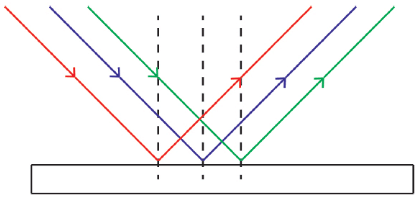 Regular Reflection
Regular Reflection
 |
Download the notes
Reflection of Light
|
Download as PDF |
Irregular (Diffused) Reflection
- When parallel light rays fall on a rough surface all the rays of light are reflected in all possible (different) directions this is called diffused or irregular reflection.
- Reflective surface other than mirrors, in general, has a very rough finish. This may be due to wear and tear such as scratches and dents or dirt on the surface.
- Sometimes even the material of which the surface is made of matters. All this leads to a loss of both the brightness and the quality of the reflection.
- In the case of such rough surfaces, the angle of reflection when compared between points is completely haphazard. For rough surfaces, the rays incident at slightly different points on the surface is reflected in completely different directions.
- This type of reflection is called diffused reflection and is what enables us to see non-shiny objects.
Irregular Reflection
Multiple Reflection
- A single image is formed when an object is placed in front of a mirror.
What happens if we use two mirrors?
- Since reflective surfaces such as mirrors are very good at preserving the intensity of light in a reflection, a single source of light can be reflected multiple times. This multiple reflection is possible until the intensity of light becomes low until the point that we cannot see.
- This means that we can have almost infinite multiple reflections. We can also see an image at every individual reflection. This means that each image is the result of an image or an image of an image.
- The number of images we see is dependent largely on the angle between the two mirrors. We see that as we go on decreasing the angle between the mirrors, the number of images goes on increasing.
- And when the angle becomes zero, i.e., when the mirrors become parallel to each other, the number of images becomes infinite. This effect can be easily observed when your barber uses another smaller mirror to show you the back of your head.
- When this happens, not only do you see the back of your head, you also see innumerable images of yourself. The variation of the number of images of an object placed between two mirrors with the angle between the mirrors can be described by a simple formula:
Solved Examples
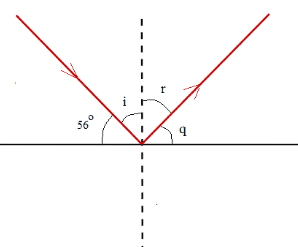
Example 1: A light ray strikes a reflective plane surface at an angle of 56° with the surface.
a) Find the angle of incidence.
b) Find the angle of reflection.
c) Find the angle made by the reflected ray and the surface.
d) Find the angle made by the incident and reflected rays.
We use the diagram shown below to answer the questions.
a) angle of incidence: ∠i = 90 - 56 = 34°
b) angle of reflection ∠r = i = 34 ° (by the law of reflection)
c) ∠q = 90 - ∠r = 90 - 34 = 56°
d) ∠i + ∠r = 34 + 34 = 68°
Example 2: A ray of light is reflected by two parallel mirrors (1) and (2) at points A and B. The ray makes an angle of 25° with the axis of the two mirrors.
a) What is the angle of reflection at the point of incidence A?
b) What is the angle of reflection at the point of incidence B?
c) If the distance between the two mirrors is d = 4 cm and the length L of the two mirror system is 3 meters, approximately how many reflections take place between the two mirrors?
d) In a real system, at each reflection, there are losses of the light energy travelling between the two mirrors. If L and d are fixed, what can be done to decrease the number of reflections on the mirrors and hence, the energy lost by reflection?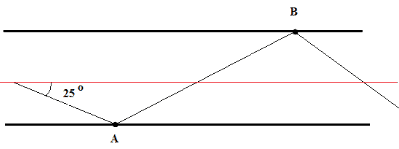
Let's use the diagram shown below to answer the questions. n1 and n2 are normal to the reflecting mirrors and are therefore perpendicular to the axis of the two mirror system.
a) ∠i = 90° - 25° = 65°
or
25° + 90° + ∠i = 180°
115° + ∠i = 180°
∠i = 180° - 115°
Therefore, ∠i = 65°b) The two mirrors are parallel and AB intersects both of them, hence angle r and i' are alternate interior and therefore equal in size.
Also ∠r = ∠i (law of reflection).
Hence ∠i' = ∠r = ∠i = 65°c) If the distance between the two mirrors is = 4 cm, AC can be calculated as follows
tan(75°) = AC / d = AC / 4AC = 4 tan(75°) = 15 cm
The number of reflections N that will take place between the two mirrors may be approximated as follows.
N = L / AC = 3 m / 15 cm = 20 cm
d) Let the angle made by the light ray and the axis of the two mirror system be α instead of 25 °.
The angle of incidence ∠i = 90 - α = ∠r = ∠i'tan(i') = tan( 90 - α) = cot (α) = AC / d
AC = d cot(α)Number of reflections = N = L / AC = L / d cot(α)
If L and d are fixed, the only way to decrease N is to increase cot(α) and hence decrease α.
Example 3: A light ray at an angle of incidence i first strikes mirror (1) at point A, then mirror (2) at point B and then mirror (1) again at point C. The two mirrors make an angle α. Express the angles of incidence at point B and point C in terms of the angle of incidence i and angle α?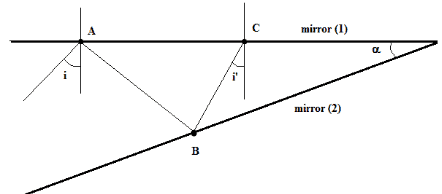
We first complete the given diagram drawing the various rays at points of incidence. The diagram is shown below.
Let AD and CE be the normals to mirror (1) at A and C respectively.
∠r = ∠i (law of reflection)In triangle OAD, we can write
∠α + 90 + ∠r' = 180 °
Simplify to get: ∠r' = 90 - αIn triangle ADB, we have
∠r + ∠r' + ∠r" = 180 °
∠r" = 180 - ∠r' - ∠rSubstitute r' by 90 - α and r by i in r" to obtain
∠r" = 90 + ∠α - ∠i
The angle of incidence at B is given by
90 - ∠r" = 90 - (90 + ∠α - ∠i) = ∠i - ∠αIn triangle CBE, we have
∠CBE = ∠r" (incident ray and reflected ray make angles with surface of reflection of equal size)
In triangle OCB, we have
∠α + 90 + ∠i' + ∠CBE = 180 °
Substitute ∠CBE by ∠r"
α + 90 + i' + r" = 180 °
Substitute r" by 90 + ∠α - i to obtain
∠α + 90 + ∠i' + 90 + ∠α - i = 180 °
Simplify to obtain the angle of incidence i' at C
∠i' = i - 2 α
At each reflection, the angle of incidence decreases by an amount equal to the size of angle α.
Example 4: Find angle α made by the system of the two mirrors shown in the figure below so that the incident ray at A and the reflected ray at B are parallel.
We first complete the given diagram with the angles of incidence and reflection as shown below and also labeling the incident and reflected rays.
For the incident ray at A and the reflected ray at B to be parallel, angles i + r and i' + r' have to be supplementary.(geometry: parallel lines cut by a transversal).Hence
∠i + ∠r + ∠i'+ ∠r' = 180 °
by law of reflection : ∠r = ∠i and ∠r' = ∠i'Substitute to obtain
∠i + ∠i + ∠i' + ∠i' = 180 °
∠i + ∠i' = 90In triangle AOB, we have
∠α + (90 - r) + (90 - i') = 180 °
∠α = ∠r + ∠i' = ∠i + ∠i' = 90 °If ∠α = 90 °, the incident ray at A and the reflected ray at B are parallel.
|
80 videos|512 docs|74 tests
|
FAQs on Reflection of Light - Science Class 10
| 1. What is the definition of reflection of light? |  |
| 2. What are the basic terminologies associated with reflection of light? |  |
| 3. What are the laws of reflection? |  |
| 4. What are the different types of reflection of light? |  |
| 5. Can you provide a simple example of reflection of light in everyday life? |  |