Number Systems | Analog and Digital Electronics - Electrical Engineering (EE) PDF Download
| Table of contents |

|
| Number Systems |

|
| The System Radix |

|
| The Radix Point. |

|
| Exponents |

|
| Floating Point Notation |

|
| Normalised Form |

|
| Electronic storage of numbers. |

|
| Alphanumeric Codes |

|
| Types of Alphanumeric Code. |

|
Number Systems
Most number systems follow a common pattern for writing down the value of a number:
A fixed number of values can be written with a single numerical character, then a new column is used to count how many times the highest value in the counting system has been reached. The number of numerical values the system uses is called the base of the system. For example, the decimal system has 10 numerical characters and so has a base of 10:
0 1 2 3 4 5 6 7 8 9
For writing numbers greater than 9 a second column is added to the left, and this column has 10 times the value of the column immediately to its right.
Because number systems commonly used in digital electronics have different base values to the decimal system, they look less familiar, but work in essentially the same way.
Decimal, (base 10)
Decimal has ten values 0 to 9. If larger values than 9 are needed, extra columns are added to the left. Each column value is ten times the value of the column to its right. For example the decimal value twenty-two is written 22 (2 tens + 2 ones).
Binary, (base 2)
Binary has only two values 0 and 1. If larger values than 1 are needed, extra columns are added to the left. Each column value is now twice the value of the column to its right. For example the decimal value three is written 11 in binary (1 two + 1 one).
Octal, (base 8)
Octal has eight values 0 to 7. If larger values than 7 are needed, extra columns are added to the left. Each column value is now 8 times the value of the column to its right. For example the decimal value twenty-seven is written 33 in octal (3 eights + 3 ones).
Hexadecimal, (base 16)
Hexadecimal has sixteen values 0 to 15, but to keep all these values in a single column, the 16 values (0 to 15) are written as 0 to F, using the letters A to F to represent numbers 10 to 15, so avoiding the use of a second column. Again, if higher values than 15 (F in hexadecimal) are needed, extra columns to the left are used. Each column value is sixteen times that of the column to its right. For example the decimal value sixty-eight is written as 44 in hexadecimal (4 sixteens + 4 ones).
Each of these different number systems works in the same way, it is just that each system has a different base, and the column values in each system increase by multiples of the base number as columns are added to the left.
Because this module describes several different number systems, it is important to know which system is being described. Therefore if there is some doubt which system a number is in, the base of the system, written as a subscript immediately after the value, is used to identify the number system.
For example:
1010 represents the decimal value ten. (1 ten + 0 units)
102 represents the binary value two. (1 two + 0 units)
108 represents the octal value eight. (1 eight + 0 units)
1016 represents the hexadecimal value sixteen. (1 sixteen + 0 units)
The System Radix
The base of a system, more properly called the RADIX, is the number of different values that can be expressed using a single digit. Therefore the decimal system has a radix of 10, the octal system has a radix of 8, hexadecimal is radix 16, and binary radix 2 .
The range of number values in different number systems is shown in Table 1.1.2, Notice that because the hexadecimal system must express 16 values using only one column, it uses the letters A B C D E & F to represent the numbers 10 to 15.
The Radix Point.
When writing a number, the digits used give its value, but the number is ‘scaled’ by its RADIX POINT.
For example, 456.210 is ten times bigger than 45.6210 although the digits are the same.
Notice also that when using multiple number systems, the term ‘RADIX point’ instead of ‘DECIMAL point’ is used. When using decimal numbers, a decimal point is used, but if a different system is used, it would be wrong to call the point a decimal point, it would need to be called "Binary point" or "Octal point" etc. The simplest way around this is to refer to the point in any system (which will of course have its value labelled with its radix) as the RADIX POINT.
Exponents
A decimal number such as 456.210 can be considered as the sum of the values of its individual digits, where each digit has a value dependent on its position within the number (the value of the column):
= 456.210
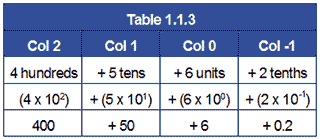
Each digit in the number is multiplied by the system radix raised to a power depending on its position relative to the radix point. This is called the EXPONENT. The digit immediately to the left of the radix point has the exponent 0 applied to its radix, and for each place to the left, the exponent increases by one. The first place to the right of the radix point has the exponent -1 and so on, positive exponents to the left of the radix point and negative exponents to the right.
This method of writing numbers is widely used in electronics with decimal numbers, but can be used with any number system. Only the radix is different.
Hexadecimal exponents 98.216 = (9 x 161) + (8 x 160) + (2 x 16-1)
Octal exponents 56.28 = (5 x 81) + (6 x 80) + (2 x 8-1)
Binary Exponents 10.12 = (1 x 21) + (0 x 20) + (1 x 2-1)
When using your calculator for the above examples you may find that it does not like radix points in anything other than decimal mode. This is common with many electronic calculators.
Floating Point Notation
If electronic calculators cannot use radix points other than in decimal, this could be a problem. Fortunately for every problem there is a solution. The radix exponent can also be used to eliminate the radix point, without altering the value of the number. In the example below, see how the value remains the same while the radix point moves. It is all done by changing the radix exponent.
102.610 = 102.6 x 100 = 10.26 x 101 = 1.026 x 102 = .1026 x 103
The radix point is moved one place to the left by increasing the exponent by one.
It is also possible to move the radix point to the right by decreasing the exponent. In this way the radix point can be positioned wherever it is required, in any number system, simply by changing the exponent. This is called FLOATING POINT NOTATION and it is how calculators handle decimal points in calculations.
Normalised Form
By putting the radix point at the front of the number, and keeping it there by changing the exponent, calculations become easier to do electronically, in any radix.
Electronic storage of numbers.
A number written (or stored) in this way, with the radix point at the left of the most significant digit is said to be in NORMALISED FORM. For example .110112 x 23 is the normalised form of the binary number 110.112. Because numbers in electronic systems are stored as binary digits, and a binary digit can only be 1 or 0, it is not possible to store the radix point within the number. Therefore the number is stored in its normalised form and the exponent is stored separately. The exponent is then reused to restore the radix point to its correct position when the number is displayed.
In electronics systems a single binary digit is called a bit (short for Binary DigIT), but as using a single digit would seriously limit the maths that could be performed, binary bits are normally used in groups.
4 bits = 1 nibble
8 bits = 1 byte
Multiple bytes, such as 16 bits, 32 bits, 64 bits are usually called ‘words’, e.g. a 32 bit word. The length of the word depends on how many bits can be physically handled or stored by the system at one time.
4 Bit Binary Representation
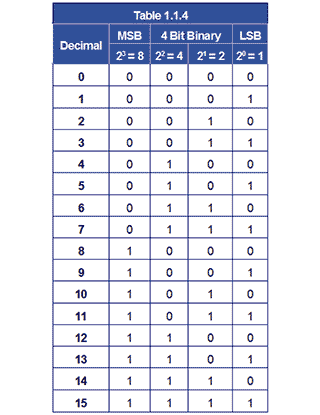
When a number is stored in an electronic system, it is stored in a memory location having a fixed number of binary bits. Some of these memory locations are used for general storage whilst others, having some special function, are called registers. Wherever a number is stored, it will be held in some form of binary, and must always have a set number of bits. Therefore a decimal number such as 13, which can be expressed in four binary bits as 11012 becomes 000011012 when stored in an eight-bit register. This is achieved by adding four NON SIGNIFICANT ZEROS to the left of the most significant ‘1’ digit.
Using this system, a binary register that is n bits wide can hold 2n values.
Therefore an 8 bit register can hold 28 values = 256 values (0 to 255)
A 4 bit register can hold 24 values = 16 values (0 to 15)
Alphanumeric Codes
Earlier computers were used only for the purpose of calculations i.e. they were only used as a calculating device. But now computers are not just used for numeric representations, they are also used to represent Information such as names, addresses, item descriptions etc. Such information is represented using letters and symbols. computer is a digital system and can only deal with l's and 0’s. So to deal with letters and symbols they use alphanumeric codes.
Alphanumeric codes, also called character codes, are binary codes used to represent alphanumeric data. The codes write alphanumeric data, including letters of the alphabet, numbers, mathematical symbols and punctuation marks, in a form that is understandable and process able by a computer. Using these codes, we can interface input-output devices such as keyboards, monitors, printers etc. with computer.
Several coding techniques have been invented that represent alphanumeric information as a series of l's and O's. The earliest better-known alphanumeric codes were the Morse code used in telegraph and 12-bit Hollerith code used when punch cards were used as a medium of inputting and outputting data. As the punched cards have completely vanished with the evolution of new mediums, the Hollerith code was rendered obsolete. Now the ASCII and EBCDIC codes are the two most widely used alphanumeric codes. The ASCII Code is very popular code used in all personal computers and workstations whereas the EBCDIC code is mainly alphanumeric code, the UNICODE, has evolved to overcome the limitation of limited character encoding as in case of ASCII and EBCDIC code.
Types of Alphanumeric Code.
MORSE CODE
The Morse code, invented in 1837 by Samuel F.B. Morse, was the first alphanumeric code used in telecommunication. It uses a standardized sequence of short and long elements to represent letters, numerals and special characters of a given message. The short and long elements can be formed by sounds, marks, pulses, on off keying and are commonly known as dots and dashes. For example : The letter 'A' is formed by a dot followed by a dash. The digit 5 is formed by 5 dots in succession. The International Morse code treats a dash equal to three dots. To see the details of Morse code table you can refer the Internet search engines.
Due to variable length of Morse code characters, the morse code could not adapt to automated circuits. In most electronic communication, the Baudot code and ASCII code are used.
Morse code has limited applications. It is used in communication using telegraph lines, radio circuits. Pilots and air traffic controllers also use them to transmit their identity and other information.
BAUDOT CODE
The Baudot code was another popular alphanumeric code used in early 1860's. It was invented by the French engineer Emile Baudot in 1870. It is a 5-unit code (i.e. it uses five elements to represent an alphabet). Moreover, unlike the Morse code, all the symbols all of equal duration. This allowed telegraph transmission of the Roman alphabet and punctuation and control signals.
HOLLERITH CODE
In 1896, Herman Hollerith formed a company called the Tabulating Machine Company. This company developed a line of machines that used punched cards for tabulation. After a number of mergers, this company was formed into the IBM, Inc. We often refer to the punched-cards used in computer systems as Hollerith cards and the 12-bit code used on a punched-card is called the Hollerith code.
A Hollerith string is a sequence of l2-bit characters; they are encoded as two ASCII characters, containing 6 bits each. The first character contains punches 12,0,2,4,6,8 and the second character contains punches 11, 1,3,5, 7, 9. Interleaving the two characters gives the original 12 bits. To make the characters printable on ASCII terminals, bit 7 is always set to 0 and bit 6 is said to the complement of bit 5. These two bits are ignored when reading Hollerith cards.
Today, as punched cards are mostly obsolete and replaced with other storage medias so the Hollerith code is rendered obsolete.
American Standard-Code for information Interchange (ASCII)
The American Standard-Code for Information Interchange (ASCII) pronounced "as-kee" is a 7-bit code based on the ordering of the English alphabets. The ASCII codes are used to represent alphanumeric data in computer input/output.
Historically, ASCII developed from telegraphic codes. It was first published as a standard in 1967. It was subsequently updated and many versions of it were launched with the most recent update in 1986. Since it is a seven-bit code, it can almost represent 128 characters. These include 95 printable characters including 26 upper-case letters (A to Z), 26 lowercase letters (a to z), 10 numerals (0 to 9) and 33 special characters such as mathematical symbols, space character etc. It also defines codes for 33 non-printing obsolete characters except for carriage return and/or line feed. The below table lists the 7 bit ASCII code containing the 95 printable characters.
The format of ASCII code for each character is X6' ·Xs, X4, X3, X2, Xl' X0 where each X is 0’ or 1. For instance, letter D is coded as .1000100. For making reading easier, we leave space as follows: 1000100.
Similarly, from the above table, we see that letter 'A' has X6 X5X4 of 100 and X3 X2 Xl Xo of 0001 (A). Similarly, the digit '9' has X6 X5 X4 values of 011 and X3 X2 Xl X0 of 1001 so the ASCII-7 code for digit 9 is 0111001.
More examples are:
The ASCll-7 code for 'd' is 1100100 as seen from the table 3.4.
The ASCll-7 code for '+' is 0101011 as seen from the table 3.4.
An eight-bit version of the ASCII code, known as US ASCII-8 or ASCII-8, has also been developed. Since it uses 8-bits, so this version of ASCII can represent a maximum of 256 characters.
The table below lists some ASCII-8 codes.
When the ASCII -7 codes was introduced, many computers dealt with eight -bit groups (or bytes) as the smallest unit of information. This eight bit code was commonly used as parity bit for detection of error on communication lines. Machines that did not use the parity bit typically set the eighth bit to O. In that case, the ASCII code format would be X7 X6 X5 X4 X3 X2 Xl X0' In case of ASCII-7 code, if this representation is chosen to represent characters then X7 would always be zero. So, the eight-bit ASCII-7 code for 'A’ would be 01000001 and for 4' would be 00101011.
Example 1: With an ASCII-7 keyboard, each keystroke produces the ASCII equivalent of the designated character. Suppose that you type PRINT X. What is the output of an ASCII-7 keyboard?
Solution: The sequence is as follows:
The ASCII-7 equivalent of P = 101 0000
The ASCII-7 equivalent of R = 101 0010
The ASCII-7 equivalent of I = 1001010
The ASCII-7 equivalent of N = 100 1110
The ASCII-7 equivalent of T = 1-010100
The ASCII-7 equivalent of space = 010 0000
The ASCII-7 equivalent of X = 101 1000
So the output produced is 1010000101001010010101001110101010001000001011000. The output in hexadecimal equivalent is 50 52 49 4E 54 30 58
Example2: A computer sends a message to another computer using an odd-parity bit. Here is the message in ASCII-8 Code.
1011 0001
1011 0101
1010 0101
1010 0101
1010 1110
What do these numbers mean?
Solution
On translating, the 8-bit numbers into their equivalent ASCII-8 code we get the word 1011 0001 (Q), 10110101 (U), 10100101 (E), 1010 0101 (E), 1010 1110 (N)
So, on translation we get QUEEN as the output.
Extended Binary Coded Decimal Interchange Code (EBCDIC)
The Extended Binary Coded Decimal Interchange Code (EBCDIC) pronounced as "ebi-si disk" is another frequently used code by computers for transferring alphanumeric data. It is 8-bit code in which the numerals (0-9) are represented by the 8421 BCD code preceded by 1111. Since it is a 8-bit code, it can almost represent 23 (= 256) different characters which include both lowercase and uppercase letters in addition to various other symbols and commands.
EBCDIC was designed by IBM corp. so it is basically used by several IBM· models. In this code, we do not use a straight binary sequence for representing characters, as was in the case of ASCII code. Since it is a 8-bit code, so it can be easily grouped into groups of 4 so as to represent in arm of hexadecimal digits. By using the hexadecimal number system notation, the amount of digits used to represent various characters and special characters using EBCDIC code is reduced in volume of one is to four. Thus 8-bit binary code could be reduced to 2 hexadecimal digits which are easier to decode if we want to view the internal representation in memory. The above table lists the EBCDIC code for certain characters.
Read the above table as you read the graph. Suppose you want to search for EBCDIC code for letter 'A’. To that case, the value of X3 X2 Xl X0 bits is 0001 and value X7 X6 X5 X4 bits is 1100.
Therefore, EBCDIC code for letter 'A’ is 11000001(A). Similarly, the EBCDIC code for 'B' is 11000010(B).
The EBCDIC code '=' is 01111110
The EBCDIC code for '$' is 0101 1011
UNICODE
The ASCII and EBCDIC encodings and their variants that we have studied suffer from some limitations.
1. These encodings do not have a sufficient number of characters to be able to encode alphanumeric data of all forms, scripts and languages. As a result, they do not permit multilingual computer processing.
2. These encoding suffer from incompatibility. For example: code 7A (in hex) represents the lowercase letter 'Z' in ASCII code and the semicolon sign ';' in EBCDIC code.
To overcome these limitations, UNICODE also known as universal code was developed jointly by the Unicode Consortium and the International Organization for Standardization (ISO). The Unicode is a 16-bit code so it can represent 65536 different characters. It is the most complete character encoding scheme that allows text of all forms and languages to be encoded for use by computers. In addition to multilingual support, it also supports a comprehensive set of mathematical and technical symbols, greatly simplifying any scientific information interchange.
UNICODE has a number of uses
1. It is increasingly being used for internal processing and storage of text. Window NT and its descendents, Java environment, Mac OS all follow Unicode as the sole internal character encoding.
2. All World Wide Web consortium recommendations have used Unicode as their document character set since HTML 4.0.
3. It partially addresses the new line problem that occurs when trying to read a text file on different platforms. It defines a large number of characters that can be recognized as line terminators.
Unicode is currently being adopted by top computer industry leaders like Microsoft, Apple, Oracle, Sun, SAP and many more in their products.
|
135 videos|167 docs|71 tests
|
FAQs on Number Systems - Analog and Digital Electronics - Electrical Engineering (EE)
| 1. What are number systems? |  |
| 2. What are the most commonly used number systems? |  |
| 3. How does the decimal number system work? |  |
| 4. What is the binary number system? |  |
| 5. How is the hexadecimal number system used? |  |





















