All Exams >
JEE >
Weekly Tests for JEE Preparation >
All Questions
All questions of September Week 4 for JEE Exam
Material is said to be ductile if- a)a large amount of plastic deformation takes place between the elastic limit and the fracture point
- b)fracture occurs soon after the elastic limit is passed
- c)material cross section is not significantly reduced at failure
- d)material breaks suddenly at little elongation
Correct answer is option 'A'. Can you explain this answer?
Material is said to be ductile if
a)
a large amount of plastic deformation takes place between the elastic limit and the fracture point
b)
fracture occurs soon after the elastic limit is passed
c)
material cross section is not significantly reduced at failure
d)
material breaks suddenly at little elongation
|
Nandini Iyer answered |
A ductile material is one that can withstand a large amount of plastic deformation between the elastic limit and the fracture point.
A material that breaks suddenly when elongated or fracture occurs in it soon after the elastic limit is crossed is called a brittle material.
A ductile material that exhibits extra elongation or deformation and does not fracture is also referred as superplastic material.
A material that breaks suddenly when elongated or fracture occurs in it soon after the elastic limit is crossed is called a brittle material.
A ductile material that exhibits extra elongation or deformation and does not fracture is also referred as superplastic material.
A 200-kg load is hung on a wire with a length of 4.00 m, a cross-sectional area of 0.200 × 10−4 m2, and a Young’s modulus of 8.00 × 1010N/ m2. What is its increase in length?- a)4.80 mm
- b)4.90 mm
- c)4.80 mm2.4.90 mm
- d)80 mm2.4.90 mm3.
Correct answer is option 'C'. Can you explain this answer?
A 200-kg load is hung on a wire with a length of 4.00 m, a cross-sectional area of 0.200 × 10−4 m2, and a Young’s modulus of 8.00 × 1010N/ m2. What is its increase in length?
a)
4.80 mm
b)
4.90 mm
c)
4.80 mm2.4.90 mm
d)
80 mm2.4.90 mm3.
|
Jyoti Sengupta answered |
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?- a)0.065 mm
- b)0.055 mm
- c)0.045 mm
- d)0.075 mm
Correct answer is option 'C'. Can you explain this answer?
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire had the same length but twice the diameter?
a)
0.065 mm
b)
0.055 mm
c)
0.045 mm
d)
0.075 mm
|
Pritam Kapoor answered |
Given:
- The flood lamp stretches the wire by 0.18 mm
- The stress is proportional to the strain
To find:
- How much would it have stretched if the wire had the same length but twice the diameter
Let's begin by understanding the given information.
Stress is defined as the force per unit area and is denoted by the symbol σ (sigma). Mathematically, stress is given by:
σ = F / A
where F is the force applied and A is the area over which the force is applied.
Strain is defined as the change in length per unit length and is denoted by the symbol ε (epsilon). Mathematically, strain is given by:
ε = ΔL / L
where ΔL is the change in length and L is the original length.
From the given information, we know that the stress is proportional to the strain. This can be expressed mathematically as:
σ ∝ ε
or
σ = kε
where k is a constant of proportionality.
Now, let's apply this information to the problem at hand.
When the flood lamp is hung from the wire, it exerts a force on the wire which causes it to stretch. Let's assume that the original diameter of the wire is d and the original length is L.
From the given information, we know that the stress is proportional to the strain. Therefore, we can write:
σ = kε
where σ is the stress, k is a constant of proportionality, and ε is the strain.
The stress can be calculated using the formula:
σ = F / A
where F is the force applied and A is the cross-sectional area of the wire.
The force applied is the weight of the flood lamp, which can be calculated using the formula:
F = mg
where m is the mass of the flood lamp and g is the acceleration due to gravity.
The cross-sectional area of the wire can be calculated using the formula:
A = πd^2 / 4
where d is the diameter of the wire.
Therefore, we can write:
σ = (mg) / (πd^2 / 4)
The strain can be calculated using the formula:
ε = ΔL / L
where ΔL is the change in length and L is the original length.
From the given information, we know that the flood lamp stretches the wire by 0.18 mm. Therefore, we can write:
ε = 0.18 / L
Now, let's combine the equations for stress and strain:
σ = kε
σ = (mg) / (πd^2 / 4)
ε = 0.18 / L
Substituting the values of σ and ε, we get:
(mg) / (πd^2 / 4) = k (0.18 / L)
Simplifying, we get:
k = (mgL) / (0.18πd^2)
Now, let's use this value of k to calculate the change in length when the diameter of the wire is doubled.
When the diameter of the wire is doubled, the cross-sectional area of the wire becomes 4 times the original area. Therefore, the new diameter is 2d and the new cross-sectional area is:
A' = π(2d)^2 / 4 = 4πd^2
Using the same formula for stress,
- The flood lamp stretches the wire by 0.18 mm
- The stress is proportional to the strain
To find:
- How much would it have stretched if the wire had the same length but twice the diameter
Let's begin by understanding the given information.
Stress is defined as the force per unit area and is denoted by the symbol σ (sigma). Mathematically, stress is given by:
σ = F / A
where F is the force applied and A is the area over which the force is applied.
Strain is defined as the change in length per unit length and is denoted by the symbol ε (epsilon). Mathematically, strain is given by:
ε = ΔL / L
where ΔL is the change in length and L is the original length.
From the given information, we know that the stress is proportional to the strain. This can be expressed mathematically as:
σ ∝ ε
or
σ = kε
where k is a constant of proportionality.
Now, let's apply this information to the problem at hand.
When the flood lamp is hung from the wire, it exerts a force on the wire which causes it to stretch. Let's assume that the original diameter of the wire is d and the original length is L.
From the given information, we know that the stress is proportional to the strain. Therefore, we can write:
σ = kε
where σ is the stress, k is a constant of proportionality, and ε is the strain.
The stress can be calculated using the formula:
σ = F / A
where F is the force applied and A is the cross-sectional area of the wire.
The force applied is the weight of the flood lamp, which can be calculated using the formula:
F = mg
where m is the mass of the flood lamp and g is the acceleration due to gravity.
The cross-sectional area of the wire can be calculated using the formula:
A = πd^2 / 4
where d is the diameter of the wire.
Therefore, we can write:
σ = (mg) / (πd^2 / 4)
The strain can be calculated using the formula:
ε = ΔL / L
where ΔL is the change in length and L is the original length.
From the given information, we know that the flood lamp stretches the wire by 0.18 mm. Therefore, we can write:
ε = 0.18 / L
Now, let's combine the equations for stress and strain:
σ = kε
σ = (mg) / (πd^2 / 4)
ε = 0.18 / L
Substituting the values of σ and ε, we get:
(mg) / (πd^2 / 4) = k (0.18 / L)
Simplifying, we get:
k = (mgL) / (0.18πd^2)
Now, let's use this value of k to calculate the change in length when the diameter of the wire is doubled.
When the diameter of the wire is doubled, the cross-sectional area of the wire becomes 4 times the original area. Therefore, the new diameter is 2d and the new cross-sectional area is:
A' = π(2d)^2 / 4 = 4πd^2
Using the same formula for stress,
A steel wire of length 4.7 m and cross-sectional area 3.0 × 10−5 m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4.0 × 10−5 m2 under a given load. What is the ratio of the Young’s modulus of steel to that of copper?- a)1.2
- b)1.6
- c)1.8
- d)2.0
Correct answer is option 'C'. Can you explain this answer?
A steel wire of length 4.7 m and cross-sectional area 3.0 × 10−5 m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4.0 × 10−5 m2 under a given load. What is the ratio of the Young’s modulus of steel to that of copper?
a)
1.2
b)
1.6
c)
1.8
d)
2.0
|
Krishna Iyer answered |
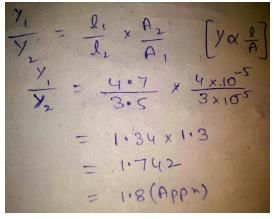
For HF, pKa = 3.45. What is the pH of an aqueous buffer solution that is 0.1M HF (aq) and 0.300 M KF (aq)?
a)11.03b)2.97c)10.07d)3.93 Correct answer is option 'D'. Can you explain this answer?
|
Suresh Iyer answered |
Given, pKa = 3.45
Concentration of HF = 0.1 M, concentration of KF = 0.300 M
For acidic buffer;
pH = pKa + log [salt of weak acid]/[weak acid]
= 3.45 + log0.3/0.1
= 3.45 + 0.48
= 3.93
Concentration of HF = 0.1 M, concentration of KF = 0.300 M
For acidic buffer;
pH = pKa + log [salt of weak acid]/[weak acid]
= 3.45 + log0.3/0.1
= 3.45 + 0.48
= 3.93
What diameter should a 10-m-long steel wire have if we do not want it to stretch more than 0.5 cm under a tension of 940 N? Take Young's modulus of steel as 20 × 1010 Pa- a)3.2 mm
- b)3.0 mm
- c)3.4 mm
- d)3.6 mm
Correct answer is option 'C'. Can you explain this answer?
What diameter should a 10-m-long steel wire have if we do not want it to stretch more than 0.5 cm under a tension of 940 N? Take Young's modulus of steel as 20 × 1010 Pa
a)
3.2 mm
b)
3.0 mm
c)
3.4 mm
d)
3.6 mm
|
|
Rajesh Gupta answered |
Y=F x l/A x Δ l
Δ l=0.5cm=0.5x10-2m, l=10M, F=940N
Y=20x1010pa
20x1010=940x10/πr2x0.5x10-10
πr2=94x100/5x10-3x2x1011=94x102/10x108
r2=94/π x 10-7 =2.99 x 10-6
r2 ≅3x10-6
r=1.13x10-10 m
diameter=2r=3.6mm
Δ l=0.5cm=0.5x10-2m, l=10M, F=940N
Y=20x1010pa
20x1010=940x10/πr2x0.5x10-10
πr2=94x100/5x10-3x2x1011=94x102/10x108
r2=94/π x 10-7 =2.99 x 10-6
r2 ≅3x10-6
r=1.13x10-10 m
diameter=2r=3.6mm
With reference to figure the elastic zone is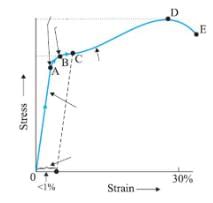
- a)BC
- b)CD
- c)AB
- d)OA
Correct answer is option 'D'. Can you explain this answer?
With reference to figure the elastic zone is
a)
BC
b)
CD
c)
AB
d)
OA
|
Hansa Sharma answered |
Hooke’s law: a law stating that the strain in a solid is proportional to the applied stress within the elastic limit of that solid.
In the OA line Hooke’s law is valid because stress is directly proportional to strain.
In the OA line Hooke’s law is valid because stress is directly proportional to strain.
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire were twice as long?- a)0.36 mm
- b)0.34 mm
- c)0.38 mm
- d)0.40 mm
Correct answer is option 'A'. Can you explain this answer?
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched if the wire were twice as long?
a)
0.36 mm
b)
0.34 mm
c)
0.38 mm
d)
0.40 mm
|
|
Rajesh Gupta answered |
F/A = e/L
F/A = 0.18/l ( let the length be l)
F/A = x/2l
0.18/L = x/2l
0.18×2l = xl
0.36l = xl
x = 0.36
F/A = 0.18/l ( let the length be l)
F/A = x/2l
0.18/L = x/2l
0.18×2l = xl
0.36l = xl
x = 0.36
The S.I unit of stress is- a)Watt
- b)Joule
- c)Pascal
- d)Newton
Correct answer is option 'C'. Can you explain this answer?
The S.I unit of stress is
a)
Watt
b)
Joule
c)
Pascal
d)
Newton
|
|
Krishna Iyer answered |
Stress has its own SI unit called the Pascal. 1 Pascal (Pa) is equal to 1 N/m2. In imperial units stress is measured in pound force per square inch which is often shortened to "psi". The dimension of stress is same as that of pressure.
Consider KA, the potassium salt of a weak acid, HA. If a sample of KA is dissolved in water, with no other substances added, which of the following statements is true (approximately)?- a)[H3O+] = [OH-]
- b)[HA] = [K+]
- c)[HA] = [OH-]
- d)[H3O+] = [A-]
Correct answer is option 'C'. Can you explain this answer?
Consider KA, the potassium salt of a weak acid, HA. If a sample of KA is dissolved in water, with no other substances added, which of the following statements is true (approximately)?
a)
[H3O+] = [OH-]
b)
[HA] = [K+]
c)
[HA] = [OH-]
d)
[H3O+] = [A-]
|
|
Suresh Iyer answered |
The correct answer is option C
[HA] = [OH–]
The reaction is: A– + H2O ⇌ HA + OH–
[HA] = [OH–]
The reaction is: A– + H2O ⇌ HA + OH–
Elasticity is the property of a body, by virtue of which- a)it remains in original size and shape when the force is applied
- b)it changes size and shape when the force is applied and stays in that shape when applied force is removed
- c)it tends to regain its original size and shape when the applied force is removed
- d)it is distorted or stretches without the application of force
Correct answer is option 'C'. Can you explain this answer?
Elasticity is the property of a body, by virtue of which
a)
it remains in original size and shape when the force is applied
b)
it changes size and shape when the force is applied and stays in that shape when applied force is removed
c)
it tends to regain its original size and shape when the applied force is removed
d)
it is distorted or stretches without the application of force
|
Lavanya Menon answered |
Explanation:When external force is applied on the solid bodies, the solid bodies get deformed. The atoms or molecules are displaced from their equilibrium positions causing a change in the interatomic ( or intermolicular ) distances. When the deforming foce is removed, the interatomic forces tend to drive them back to their original postions. Thus the body regains its original shape and size.
Compute the fractional change in volume of a glass slab, when subjected to a hydraulic pressure of 10 atm. Bulk modulus of glass 37 GPa.- a)0.0027
- b)0.0030
- c)0.0024
- d)0.0022
Correct answer is option 'A'. Can you explain this answer?
Compute the fractional change in volume of a glass slab, when subjected to a hydraulic pressure of 10 atm. Bulk modulus of glass 37 GPa.
a)
0.0027
b)
0.0030
c)
0.0024
d)
0.0022
|
|
Pranavi Kulkarni answered |
Given data:
Bulk modulus of glass = 37 GPa
Hydraulic pressure = 10 atm
Formula used:
Bulk modulus of elasticity (K) = (pressure * volume)/(volume change)
Calculation:
Let initial volume of the glass slab be V₀ and let the change in volume be ΔV.
Bulk modulus of elasticity (K) = (pressure * volume)/(volume change)
⇒ K = (10 atm * V₀)/(ΔV)
⇒ ΔV/V₀ = (10 atm * V₀)/K
⇒ ΔV/V₀ = (10 atm * V₀)/(37 × 10⁹ N/m²)
⇒ ΔV/V₀ = 2.7 × 10⁻⁶
Hence, the fractional change in volume of a glass slab, when subjected to a hydraulic pressure of 10 atm, is 0.0027. Therefore, option A is the correct answer.
Bulk modulus of glass = 37 GPa
Hydraulic pressure = 10 atm
Formula used:
Bulk modulus of elasticity (K) = (pressure * volume)/(volume change)
Calculation:
Let initial volume of the glass slab be V₀ and let the change in volume be ΔV.
Bulk modulus of elasticity (K) = (pressure * volume)/(volume change)
⇒ K = (10 atm * V₀)/(ΔV)
⇒ ΔV/V₀ = (10 atm * V₀)/K
⇒ ΔV/V₀ = (10 atm * V₀)/(37 × 10⁹ N/m²)
⇒ ΔV/V₀ = 2.7 × 10⁻⁶
Hence, the fractional change in volume of a glass slab, when subjected to a hydraulic pressure of 10 atm, is 0.0027. Therefore, option A is the correct answer.
According to Hooke’s law- a)For small deformations the stress and strain are inversely proportional to each other
- b)For small deformations the stress is proportional to square of strain
- c)For large deformations the stress and strain are proportional to each other
- d)For small deformations the stress and strain are proportional to each other
Correct answer is option 'D'. Can you explain this answer?
According to Hooke’s law
a)
For small deformations the stress and strain are inversely proportional to each other
b)
For small deformations the stress is proportional to square of strain
c)
For large deformations the stress and strain are proportional to each other
d)
For small deformations the stress and strain are proportional to each other
|
|
Krishna Iyer answered |
Hook’s Law states that for small deformations the stress and strain are proportional to each other.
Role of NH4Cl in qualitative analysis of third group cations- a)to provide basic medium
- b)to provide acidic medium
- c)to increase the degree of dissociation of NH4OH
- d)to suppress the degree of dissociation of NH4OH
Correct answer is option 'D'. Can you explain this answer?
Role of NH4Cl in qualitative analysis of third group cations
a)
to provide basic medium
b)
to provide acidic medium
c)
to increase the degree of dissociation of NH4OH
d)
to suppress the degree of dissociation of NH4OH
|
|
Raghav Bansal answered |
The correct answer is option D
Common ion effect is observed when a solution of weak electrolyte is mixed with a solution of strong electrolyte, which provides an ion common to that provided by weak electrolyte.
The NH4OH is a weak base and it does not ionise completely. Thus, due to presence of common ion NH4+ in NH4Cl, it suppresses the ionisation of weak base NH4OH in order to decrease the OH- concentration so that higher group cations will not get precipitated.
Thus the pair NH4OH+NH4Cl shows a common ion effect.
Ammonium chloride suppresses the ionization of ammonium hydroxide
.
Common ion effect is observed when a solution of weak electrolyte is mixed with a solution of strong electrolyte, which provides an ion common to that provided by weak electrolyte.
The NH4OH is a weak base and it does not ionise completely. Thus, due to presence of common ion NH4+ in NH4Cl, it suppresses the ionisation of weak base NH4OH in order to decrease the OH- concentration so that higher group cations will not get precipitated.
Thus the pair NH4OH+NH4Cl shows a common ion effect.
Ammonium chloride suppresses the ionization of ammonium hydroxide
.
We eat a variety of foods still pH of our blood does not change every time. The reason is- a)Strong bases in the blood donot let pH change
- b)Stomach wall is resistant
- c)There are buffers in the blood which resist pH change
- d)Strong acids in the blood donot let pH change
Correct answer is option 'C'. Can you explain this answer?
We eat a variety of foods still pH of our blood does not change every time. The reason is
a)
Strong bases in the blood donot let pH change
b)
Stomach wall is resistant
c)
There are buffers in the blood which resist pH change
d)
Strong acids in the blood donot let pH change
|
Pooja Shah answered |
The correct answer is option C
pH of blood remains constant because of the buffer system present in the blood. Acid-base buffers confer resistance to a change in the pH of a solution when hydrogen ions (protons) or hydroxide ions are added or removed. An acid-base buffer typically consists of a weak acid, and its conjugate base (salt).It used to neutralized the extra added protons or OH- in blood.The buffer for maintaining acid-base balance in the blood is the carbonic-acid-bicarbonate buffer.So pH of blood remains even after eating spicy food.
pH of blood remains constant because of the buffer system present in the blood. Acid-base buffers confer resistance to a change in the pH of a solution when hydrogen ions (protons) or hydroxide ions are added or removed. An acid-base buffer typically consists of a weak acid, and its conjugate base (salt).It used to neutralized the extra added protons or OH- in blood.The buffer for maintaining acid-base balance in the blood is the carbonic-acid-bicarbonate buffer.So pH of blood remains even after eating spicy food.
If the line 2x – y + λ = 0 is a diameter of the circle x2+y2+6x−6y+5 = 0 then λ =- a)6
- b)9
- c)3
- d)12
Correct answer is option 'B'. Can you explain this answer?
If the line 2x – y + λ = 0 is a diameter of the circle x2+y2+6x−6y+5 = 0 then λ =
a)
6
b)
9
c)
3
d)
12
|
|
Rajesh Gupta answered |
x2 + y2 + 6x − 6y + 5 = 0
Center O = (-3, 3)
radius r = √{(-3)2 + (3)2 - 5}
= √{9 + 9 - 5}
= √13
Since diameter of the circle passes through the center of the circle.
So (-3, 3) satisfies the equation 2x – y + λ = 0
=> -3*2 - 3 + λ = 0
=> -6 - 3 + λ = 0
=> -9 + λ = 0
=> λ = 9
Center O = (-3, 3)
radius r = √{(-3)2 + (3)2 - 5}
= √{9 + 9 - 5}
= √13
Since diameter of the circle passes through the center of the circle.
So (-3, 3) satisfies the equation 2x – y + λ = 0
=> -3*2 - 3 + λ = 0
=> -6 - 3 + λ = 0
=> -9 + λ = 0
=> λ = 9
Two strips of metal are riveted together at their ends by four rivets, each of diameter 6.0 mm. What is the maximum tension that can be exerted by the riveted strip if the shearing stress on the rivet is not to exceed 6.9 × 107Pa? Assume that each rivet is to carry one quarter of the load.- a)749 kN
- b)856 kN
- c)652 N
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
Two strips of metal are riveted together at their ends by four rivets, each of diameter 6.0 mm. What is the maximum tension that can be exerted by the riveted strip if the shearing stress on the rivet is not to exceed 6.9 × 107Pa? Assume that each rivet is to carry one quarter of the load.
a)
749 kN
b)
856 kN
c)
652 N
d)
None of these
|
|
Sanchita Mukherjee answered |
If the value of the solubility product for AgBr is 4.0 x 10-12 at 25°C, calculate the solubility of AgBr(s) in water.- a)2.5 x 10-13
- b)2.5 x 10-6
- c)2 x 10-6
- d)5.0 x10-7
Correct answer is option 'C'. Can you explain this answer?
If the value of the solubility product for AgBr is 4.0 x 10-12 at 25°C, calculate the solubility of AgBr(s) in water.
a)
2.5 x 10-13
b)
2.5 x 10-6
c)
2 x 10-6
d)
5.0 x10-7
|
|
Raghav Bansal answered |
Ksp = 4.0 x 10-12
For AB type salt, Solubility = Ksp1/2
= (4.0 x 10-12)1/2
= 2 x 10-6
For AB type salt, Solubility = Ksp1/2
= (4.0 x 10-12)1/2
= 2 x 10-6
A steel rod 2.0 m long has a cross-sectional area of 0.30 cm2. It is hung by one end from a support, and a 550-kg milling machine is hung from its other end. Determine the elongation. Take Young's modulus of steel as 20 × 1010 Pa- a)2.0 mm
- b)1.6 mm
- c)2.2 mm
- d)1.8 mm
Correct answer is option 'D'. Can you explain this answer?
A steel rod 2.0 m long has a cross-sectional area of 0.30 cm2. It is hung by one end from a support, and a 550-kg milling machine is hung from its other end. Determine the elongation. Take Young's modulus of steel as 20 × 1010 Pa
a)
2.0 mm
b)
1.6 mm
c)
2.2 mm
d)
1.8 mm
|
Gaurav Kumar answered |
σ=Stress and ε=strain
σ=F/A= (550kg) × (9.81m/s2)3×10-5m2/=0.18GPA
ε=Δl/l0=σ/Υ=0.18×109/200×109=9×10-4
Δl=εl0= (9×10-4) (2m) = 0.0018m=1.8mm
σ=F/A= (550kg) × (9.81m/s2)3×10-5m2/=0.18GPA
ε=Δl/l0=σ/Υ=0.18×109/200×109=9×10-4
Δl=εl0= (9×10-4) (2m) = 0.0018m=1.8mm
The following equilibrium exists in aqueous solutionCH3COOH 
CH3COO- + H+
If dilute HCl is added:- a)Acetate ion concentration will increase
- b)Acetate ion concentration will decrease
- c)The equilibrium constant will decrease
- d)The equilibrium constant will increase.
Correct answer is option 'B'. Can you explain this answer?
The following equilibrium exists in aqueous solution
CH3COOH CH3COO- + H+
If dilute HCl is added:
CH3COO- + H+If dilute HCl is added:
a)
Acetate ion concentration will increase
b)
Acetate ion concentration will decrease
c)
The equilibrium constant will decrease
d)
The equilibrium constant will increase.
|
|
Sahana Marigoudar answered |
H+ concentration increases which makes the reaction to proceed through reverse direction due to which acetic acid concentration increases.
volume strain is defined- a)as the change in volume ΔV
- b)as the ratio of change in volume (ΔV) to the original volume V
- c)as the ratio of change in volume (ΔV) to thrice the original volume V
- d)as the ratio of change in volume (ΔV) to twice the original volume V
Correct answer is option 'B'. Can you explain this answer?
volume strain is defined
a)
as the change in volume ΔV
b)
as the ratio of change in volume (ΔV) to the original volume V
c)
as the ratio of change in volume (ΔV) to thrice the original volume V
d)
as the ratio of change in volume (ΔV) to twice the original volume V
|
Imk Pathsala answered |
Volume Strain Definition
- Definition: Volume strain is defined as the ratio of change in volume (ΔV) to the original volume V.
Detailed Explanation
- Volume strain is a measure of how much a material changes in volume under stress.
- It is calculated by taking the change in volume and dividing it by the original volume of the material.
- Volume strain is usually expressed as a decimal or a percentage.
- It is an important concept in physics and engineering, especially in the study of materials and structures.
- Understanding volume strain is crucial for predicting how materials will behave under different conditions and loads.
Rectangular section is rarely used in beams because- a)stresses are uniform in a rectangular section
- b)more material in kilos is required
- c)stresses are always plastic in rectangular section
- d)less material in kilos is required
Correct answer is option 'B'. Can you explain this answer?
Rectangular section is rarely used in beams because
a)
stresses are uniform in a rectangular section
b)
more material in kilos is required
c)
stresses are always plastic in rectangular section
d)
less material in kilos is required
|
Anjali Iyer answered |
I section is generally used as a beam because of its high section modulus as it's most of the area is situated away from it's neutral axis hence it has high moment of inertia i.e high section modulus i.e high moment carrying capacity which is the major requirement for a good beam section.
A steel rod 2.0 m long has a cross-sectional area of 0.30 cm2 . It is hung by one end from a support, and a 550-kg milling machine is hung from its other end. Determine the resulting strain. Young's Modulus of Steel (Y) = 20×1010 Pa
- a)8.0 × 10−4
- b)10.0 × 10−4
- c)7.0 × 10−4
- d)9.0 × 10−4
Correct answer is option 'D'. Can you explain this answer?
A steel rod 2.0 m long has a cross-sectional area of 0.30 cm2 . It is hung by one end from a support, and a 550-kg milling machine is hung from its other end. Determine the resulting strain. Young's Modulus of Steel (Y) = 20×1010 Pa
a)
8.0 × 10−4
b)
10.0 × 10−4
c)
7.0 × 10−4
d)
9.0 × 10−4
|
|
Naina Bansal answered |
from the Hooke’s law :
ε = σ/Y = (1.8 x 10^8 Pa)/(20 x 10^10 Pa)
= 9.0 x 10^−4
The locus of the centre of a circle, which touches externally the circle x2 + y2 − 6x − 6y + 14 = 0 and also touches Y-axis, is given by the equation- a)x2−6x−10y+14=0
- b)x2−10x−6y+14=0
- c)y2−6x−10y+14=0
- d)y2−10x−6y+14=0
Correct answer is option 'D'. Can you explain this answer?
The locus of the centre of a circle, which touches externally the circle x2 + y2 − 6x − 6y + 14 = 0 and also touches Y-axis, is given by the equation
a)
x2−6x−10y+14=0
b)
x2−10x−6y+14=0
c)
y2−6x−10y+14=0
d)
y2−10x−6y+14=0
|
Ameya Tiwari answered |
Understanding the Circle Equation
The given circle is represented by the equation:
- x² + y² - 6x - 6y + 14 = 0
This can be converted into standard form. Completing the square for both x and y:
- (x - 3)² + (y - 3)² = 4
This represents a circle centered at (3, 3) with a radius of 2.
Locus of the Center of the New Circle
To find the locus of the center of a circle that touches this given circle externally and the Y-axis, consider the following:
- Let the center of the new circle be at (h, k).
- The radius of this new circle is denoted as r.
Conditions for the New Circle
1. Touching the Y-axis: The distance from the center (h, k) to the Y-axis must equal the radius r. Hence, we have:
- r = h
2. Touching the Given Circle Externally: The distance between the centers of the two circles must equal the sum of their radii:
- Distance = √[(h - 3)² + (k - 3)²] = r + 2
Substituting r = h into the distance formula gives:
- √[(h - 3)² + (k - 3)²] = h + 2
Squaring both sides and rearranging leads to the equation of the locus.
Final Equation
After simplification, the resulting equation of the locus of the center (h, k) is:
- y² - 10x - 6y + 14 = 0
This corresponds to option 'D'.
Conclusion
Hence, the locus of the center of the new circle touching both the given circle externally and the Y-axis is described by the equation:
- y² - 10x - 6y + 14 = 0
The given circle is represented by the equation:
- x² + y² - 6x - 6y + 14 = 0
This can be converted into standard form. Completing the square for both x and y:
- (x - 3)² + (y - 3)² = 4
This represents a circle centered at (3, 3) with a radius of 2.
Locus of the Center of the New Circle
To find the locus of the center of a circle that touches this given circle externally and the Y-axis, consider the following:
- Let the center of the new circle be at (h, k).
- The radius of this new circle is denoted as r.
Conditions for the New Circle
1. Touching the Y-axis: The distance from the center (h, k) to the Y-axis must equal the radius r. Hence, we have:
- r = h
2. Touching the Given Circle Externally: The distance between the centers of the two circles must equal the sum of their radii:
- Distance = √[(h - 3)² + (k - 3)²] = r + 2
Substituting r = h into the distance formula gives:
- √[(h - 3)² + (k - 3)²] = h + 2
Squaring both sides and rearranging leads to the equation of the locus.
Final Equation
After simplification, the resulting equation of the locus of the center (h, k) is:
- y² - 10x - 6y + 14 = 0
This corresponds to option 'D'.
Conclusion
Hence, the locus of the center of the new circle touching both the given circle externally and the Y-axis is described by the equation:
- y² - 10x - 6y + 14 = 0
Columns are loaded in- a)shear
- b)hydraulic stress
- c)tension
- d)compression
Correct answer is option 'D'. Can you explain this answer?
Columns are loaded in
a)
shear
b)
hydraulic stress
c)
tension
d)
compression
|
Madhavan Patel answered |
Alternation of generations (also known as metagenesis) is the type of life cycle that occurs in those plants and algae in the Archaeplastida and the Heterokontophyta that have distinct sexual haploid and asexual diploid stages.
When the value of Kc is very small then- a)reaction is at start
- b)reactant conc. Is maximum
- c)reactant conc. Is minimum
- d)reaction is completed
Correct answer is option 'B'. Can you explain this answer?
When the value of Kc is very small then
a)
reaction is at start
b)
reactant conc. Is maximum
c)
reactant conc. Is minimum
d)
reaction is completed
|
|
Rutuja Desai answered |
When the value of Kc is very small, it indicates that the equilibrium position of the reaction lies towards the left side, meaning that the concentration of the reactants is relatively high compared to the concentration of the products.
Let's understand this in detail:
Equilibrium Constant (Kc):
The equilibrium constant, Kc, is a measure of the extent of a chemical reaction at equilibrium. It is defined as the ratio of the product concentrations to the reactant concentrations, each raised to their respective stoichiometric coefficients, at equilibrium, with each concentration term raised to the power equal to its stoichiometric coefficient in the balanced chemical equation.
Kc = [Products]^n / [Reactants]^m
Where [Products] and [Reactants] represent the concentrations of the products and reactants at equilibrium, respectively, and n and m are the stoichiometric coefficients of the products and reactants, respectively.
Interpretation of a Very Small Kc Value:
When the value of Kc is very small, it means that the numerator (concentration of products) is much smaller compared to the denominator (concentration of reactants).
This implies that the concentration of the reactants is significantly higher than the concentration of the products at equilibrium.
Explanation of Correct Answer (Option B):
The correct answer, "reactant conc. is maximum," indicates that when the value of Kc is very small, the concentration of the reactants is at its maximum.
This is because the equilibrium position favors the reactants, and the reaction is not proceeding significantly towards the product side. As a result, the concentration of the reactants remains high, while the concentration of the products is relatively low.
In other words, the reaction is not proceeding to a significant extent, and the reactants are dominant in the equilibrium mixture.
Therefore, when the value of Kc is very small, it signifies that the reaction is at the start, and the concentration of the reactants is maximum.
Let's understand this in detail:
Equilibrium Constant (Kc):
The equilibrium constant, Kc, is a measure of the extent of a chemical reaction at equilibrium. It is defined as the ratio of the product concentrations to the reactant concentrations, each raised to their respective stoichiometric coefficients, at equilibrium, with each concentration term raised to the power equal to its stoichiometric coefficient in the balanced chemical equation.
Kc = [Products]^n / [Reactants]^m
Where [Products] and [Reactants] represent the concentrations of the products and reactants at equilibrium, respectively, and n and m are the stoichiometric coefficients of the products and reactants, respectively.
Interpretation of a Very Small Kc Value:
When the value of Kc is very small, it means that the numerator (concentration of products) is much smaller compared to the denominator (concentration of reactants).
This implies that the concentration of the reactants is significantly higher than the concentration of the products at equilibrium.
Explanation of Correct Answer (Option B):
The correct answer, "reactant conc. is maximum," indicates that when the value of Kc is very small, the concentration of the reactants is at its maximum.
This is because the equilibrium position favors the reactants, and the reaction is not proceeding significantly towards the product side. As a result, the concentration of the reactants remains high, while the concentration of the products is relatively low.
In other words, the reaction is not proceeding to a significant extent, and the reactants are dominant in the equilibrium mixture.
Therefore, when the value of Kc is very small, it signifies that the reaction is at the start, and the concentration of the reactants is maximum.
A mixture of NH4Cl and NH4OH shows no change in pH upon addition small amount of HCl. This is because it is- a)A neutral solution
- b)A buffer
- c)A basic solution due to presence of NH4OH
- d)An acidic solution due to presence of NH4Cl
Correct answer is option 'B'. Can you explain this answer?
A mixture of NH4Cl and NH4OH shows no change in pH upon addition small amount of HCl. This is because it is
a)
A neutral solution
b)
A buffer
c)
A basic solution due to presence of NH4OH
d)
An acidic solution due to presence of NH4Cl
|
|
Rajat Patel answered |
A mixture of weak base and its salt with a strong acid serves as an basic buffer which resists changes in pH upon addition of small amount of acid or base.
Elastomers are materials- a)which can be stretched without corresponding stress
- b)which cannot be stretched to cause large strains
- c)which cannot be stretched to beyond elastic limit
- d)which can be stretched to cause large strains
Correct answer is option 'D'. Can you explain this answer?
Elastomers are materials
a)
which can be stretched without corresponding stress
b)
which cannot be stretched to cause large strains
c)
which cannot be stretched to beyond elastic limit
d)
which can be stretched to cause large strains
|
|
Rajeev Saxena answered |
An elastomer is a polymer with viscoelasticity (i. e., both viscosity and elasticity) and very weak intermolecular forces, and generally low Young's modulus and high failure strain compared with other materials. Elastomer rubber compounds are made from five to ten ingredients, each ingredient playing a specific role. Polymer is the main component, and determines heat and chemical resistance, as well as low- temperature performance. Reinforcing filler is used, typically carbon black, for strength properties.
A circular steel wire 2.00 m long must stretch no more than 0.25 cm when a tensile force of 400 N is applied to each end of the wire. What minimum diameter is required for the wire? Given that the Young's modulus for steel is Young's modulus of the material is 2.00×1011 N/m2)- a)1.4 mm
- b)10 mm
- c)1.5 mm
- d)12.4 mm
Correct answer is option 'A'. Can you explain this answer?
A circular steel wire 2.00 m long must stretch no more than 0.25 cm when a tensile force of 400 N is applied to each end of the wire. What minimum diameter is required for the wire? Given that the Young's modulus for steel is Young's modulus of the material is 2.00×1011 N/m2)
a)
1.4 mm
b)
10 mm
c)
1.5 mm
d)
12.4 mm
|
|
Swati Chauhan answered |
Understanding the Problem
To determine the minimum diameter required for a circular steel wire, we must consider the relationship between tensile stress, strain, and Young's modulus.
Key Given Data:
- Length of wire (L) = 2.00 m
- Maximum stretch (ΔL) = 0.25 cm = 0.0025 m
- Tensile force (F) = 400 N
- Young's modulus for steel (E) = 2.00 × 10^11 N/m²
Formulas to Use:
1. Strain (ε): ε = ΔL / L
2. Stress (σ): σ = F / A
3. Young's Modulus (E): E = σ / ε
Calculating Strain:
- Strain (ε) = ΔL / L
- ε = 0.0025 m / 2.00 m = 0.00125
Calculating Stress:
Using Young's modulus, we can rearrange the formula to find stress:
- σ = E × ε
- σ = (2.00 × 10^11 N/m²) × (0.00125) = 2.5 × 10^8 N/m²
Finding the Required Area:
From the stress formula, we can find the cross-sectional area (A):
- A = F / σ
- A = 400 N / (2.5 × 10^8 N/m²) = 1.6 × 10^-6 m²
Calculating Diameter:
The area of a circle is given by A = (π/4) × d². Rearranging gives:
- d² = (4A) / π
- d = √((4 × 1.6 × 10^-6 m²) / π)
- d ≈ 0.0014 m = 1.4 mm
Conclusion:
The minimum diameter required for the wire is 1.4 mm, confirming option 'A' as the correct answer.
To determine the minimum diameter required for a circular steel wire, we must consider the relationship between tensile stress, strain, and Young's modulus.
Key Given Data:
- Length of wire (L) = 2.00 m
- Maximum stretch (ΔL) = 0.25 cm = 0.0025 m
- Tensile force (F) = 400 N
- Young's modulus for steel (E) = 2.00 × 10^11 N/m²
Formulas to Use:
1. Strain (ε): ε = ΔL / L
2. Stress (σ): σ = F / A
3. Young's Modulus (E): E = σ / ε
Calculating Strain:
- Strain (ε) = ΔL / L
- ε = 0.0025 m / 2.00 m = 0.00125
Calculating Stress:
Using Young's modulus, we can rearrange the formula to find stress:
- σ = E × ε
- σ = (2.00 × 10^11 N/m²) × (0.00125) = 2.5 × 10^8 N/m²
Finding the Required Area:
From the stress formula, we can find the cross-sectional area (A):
- A = F / σ
- A = 400 N / (2.5 × 10^8 N/m²) = 1.6 × 10^-6 m²
Calculating Diameter:
The area of a circle is given by A = (π/4) × d². Rearranging gives:
- d² = (4A) / π
- d = √((4 × 1.6 × 10^-6 m²) / π)
- d ≈ 0.0014 m = 1.4 mm
Conclusion:
The minimum diameter required for the wire is 1.4 mm, confirming option 'A' as the correct answer.
A mild steel wire of length 1.0 m and cross-sectional area 0.50 × 10−2 cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the midpoint.- a)1.1 cm
- b)1.0 cm
- c)0.9 cm
- d)1.2 cm
Correct answer is option 'A'. Can you explain this answer?
A mild steel wire of length 1.0 m and cross-sectional area 0.50 × 10−2 cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the midpoint.
a)
1.1 cm
b)
1.0 cm
c)
0.9 cm
d)
1.2 cm
|
|
Siddharth Mehra answered |
Which of the following is an example of basic buffer?- a)A mixture of HCl and NaOH
- b)A mixture of NH4Cl and NH4OH
- c)A mixture of CH3COOH and OH3COONa
- d)1M solution of NaOH
Correct answer is option 'B'. Can you explain this answer?
Which of the following is an example of basic buffer?
a)
A mixture of HCl and NaOH
b)
A mixture of NH4Cl and NH4OH
c)
A mixture of CH3COOH and OH3COONa
d)
1M solution of NaOH
|
|
Nandini Iyer answered |
Acidic buffer solution contains equimolar quantities of a weak acid and its salt with strong base. For example: an acetic acid, CH3COOH and sodium acetate I.e. CH3COONa. Basic buffer solution contains equimolar quantities of a weak base and its salt with strong acid.
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched for a copper wire of the original length and diameter?- a)0.39 mm
- b)0.37 mm
- c)0.33 mm
- d)0.18 mm
Correct answer is option 'C'. Can you explain this answer?
You hang a flood lamp from the end of a vertical steel wire. The flood lamp stretches the wire 0.18 mm and the stress is proportional to the strain. How much would it have stretched for a copper wire of the original length and diameter?
a)
0.39 mm
b)
0.37 mm
c)
0.33 mm
d)
0.18 mm
|
Darshan Nagesh answered |
When a solid is deformed,- a)the atoms or molecules do not move from their equilibrium position
- b)only the atoms or molecules at some points move from their equilibrium position
- c)only the atoms or molecules of the surface move from their equilibrium position
- d)all the atoms or molecules are displaced from their equilibrium positions causing a change in inter atomic (or intermolecular) distances.
Correct answer is option 'D'. Can you explain this answer?
When a solid is deformed,
a)
the atoms or molecules do not move from their equilibrium position
b)
only the atoms or molecules at some points move from their equilibrium position
c)
only the atoms or molecules of the surface move from their equilibrium position
d)
all the atoms or molecules are displaced from their equilibrium positions causing a change in inter atomic (or intermolecular) distances.
|
Sravya Banerjee answered |
Explanation:External force permanently distubed the equilibrium position of the interatomic ( or intermolecular ) forces between the particles of solid bodies.
The circles x2+y2+6x+6y = 0 and x2+y2−12x−12y = 0- a)touch each other externally
- b)touch each other internally
- c)cut orthogonally
- d)intersect in two points
Correct answer is option 'A'. Can you explain this answer?
The circles x2+y2+6x+6y = 0 and x2+y2−12x−12y = 0
a)
touch each other externally
b)
touch each other internally
c)
cut orthogonally
d)
intersect in two points
|
|
Gaurav Kumar answered |
Given equation of circles are
x2+y2+6x+6y=0....(i)
and x2+y2−12x−12y=0....(ii)
Here, g1 = 3,f2 = 3, g2 = −6 and f2 = −6
∴ Centres of circles are C1(−3,−3) and C2(6,6) respectively and radii are r1 = 3√2 and r2 = 6√2 respectively.
Now, C1C2 = √[(6+3)2 + (6+3)2]
= 9√2
and r1 + r2
= 3(2)1/2 + 6(2)1/2
= 9(2)1/2
⇒ C1C2 = r1 + r2
∴ Both circles touch each other externally.
x2+y2+6x+6y=0....(i)
and x2+y2−12x−12y=0....(ii)
Here, g1 = 3,f2 = 3, g2 = −6 and f2 = −6
∴ Centres of circles are C1(−3,−3) and C2(6,6) respectively and radii are r1 = 3√2 and r2 = 6√2 respectively.
Now, C1C2 = √[(6+3)2 + (6+3)2]
= 9√2
and r1 + r2
= 3(2)1/2 + 6(2)1/2
= 9(2)1/2
⇒ C1C2 = r1 + r2
∴ Both circles touch each other externally.
A piece of copper having a rectangular cross-section of 15.2 mm × 19.1 mm is pulled in tension with 44,500 N force, producing only elastic deformation. Calculate the resulting strain? Take Young's modulus of copper as 42 × 109Pa
- a)3.65 × 10-8
- b)3.65 × 10-3
- c)3.65 × 10-9
- d)3.65 × 10-2
Correct answer is option 'B'. Can you explain this answer?
A piece of copper having a rectangular cross-section of 15.2 mm × 19.1 mm is pulled in tension with 44,500 N force, producing only elastic deformation. Calculate the resulting strain? Take Young's modulus of copper as 42 × 10
9
Paa)
3.65 × 10-8
b)
3.65 × 10-3
c)
3.65 × 10-9
d)
3.65 × 10-2
|
|
Anjana Sharma answered |
Given Data,
Length of the piece of copper = l = 19.1 mm = 19.1 × 10-3m
Breadth of the piece of copper = b = 15.2 mm = 15.2× 10-3m
Tension force applied on the piece of cooper, F = 44500N
Area of rectangular cross section of copper piece,
Area = l× b
⇒ Area = (19.1 × 10-3m) × (15.2× 10-3m)
⇒ Area = 2.9 × 10-4 m2
Modulus of elasticity of copper from standard list, η = 42× 109 N/m2
By definition, Modulus of elasticity, η = stress/strain
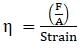
⇒ Strain = F/Aη
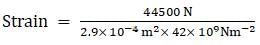
⇒ Strain = 3.65 × 10-3
Hence, the resulting strain is 3.65 × 10-3
Length of the piece of copper = l = 19.1 mm = 19.1 × 10-3m
Breadth of the piece of copper = b = 15.2 mm = 15.2× 10-3m
Tension force applied on the piece of cooper, F = 44500N
Area of rectangular cross section of copper piece,
Area = l× b
⇒ Area = (19.1 × 10-3m) × (15.2× 10-3m)
⇒ Area = 2.9 × 10-4 m2
Modulus of elasticity of copper from standard list, η = 42× 109 N/m2
By definition, Modulus of elasticity, η = stress/strain
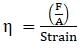
⇒ Strain = F/Aη
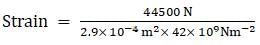
⇒ Strain = 3.65 × 10-3
Hence, the resulting strain is 3.65 × 10-3
A lead cube measures 6.00 cm on each side. The bottom face is held in place by very strong glue to a flat horizontal surface, while a horizontal force F is applied to the upper face parallel to one of the edges. How large must F be to cause the cube to deform by 0.250 mm? (Shear modulus of lead = 0.6 × 1010Pa)- a)7.0 * 105 N
- b)6* 105 N
- c)6.6 * 105 N
- d)5.6 * 105 N
Correct answer is option 'C'. Can you explain this answer?
A lead cube measures 6.00 cm on each side. The bottom face is held in place by very strong glue to a flat horizontal surface, while a horizontal force F is applied to the upper face parallel to one of the edges. How large must F be to cause the cube to deform by 0.250 mm? (Shear modulus of lead = 0.6 × 1010Pa)
a)
7.0 * 105 N
b)
6* 105 N
c)
6.6 * 105 N
d)
5.6 * 105 N
|
|
Sanchita Mukherjee answered |
The importance of the elastic behavior of materials is- a)that it is useful in making springs
- b)that it enables a safe and sound design of bridges, buildings, machinery parts.
- c)that it is useful in building sling shots
- d)that it gives methods for understanding materials
Correct answer is option 'B'. Can you explain this answer?
The importance of the elastic behavior of materials is
a)
that it is useful in making springs
b)
that it enables a safe and sound design of bridges, buildings, machinery parts.
c)
that it is useful in building sling shots
d)
that it gives methods for understanding materials
|
Puja Das answered |
Explanation:More the elastic a material is , more it has the property to regain its original position which is required in construction works.
Shear modulus or modulus of rigidity is- a)the ratio of shearing stress to the corresponding lateral strain
- b)the ratio of shearing stress to the corresponding shearing strain
- c)the ratio of longitudinal stress to the corresponding shearing strain
- d)the ratio of shearing strain to the corresponding shearing stress
Correct answer is option 'B'. Can you explain this answer?
Shear modulus or modulus of rigidity is
a)
the ratio of shearing stress to the corresponding lateral strain
b)
the ratio of shearing stress to the corresponding shearing strain
c)
the ratio of longitudinal stress to the corresponding shearing strain
d)
the ratio of shearing strain to the corresponding shearing stress
|
|
Ameya Choudhury answered |
Shear modulus or modulus of rigidity is the ratio of shearing stress to the corresponding shearing strain, by the definition of shear modulus.
In constructing a large mobile, an artist hangs an aluminum sphere of mass 6.0 kg from a vertical steel wire 0.50 m long and 2.5 × 10−3 cm2in cross-sectional area. On the bottom of the sphere he attaches a similar steel wire, from which he hangs a brass cube of mass 10.0 kg. Compute the elongation.- a)3.7 mm upper, 1.0 mm lower
- b)3.4 mm upper, 1.0 mm lower
- c)3.5 mm upper, 1.1 mm lower
- d)1.6 mm upper, 1.0 mm lower
Correct answer is option 'D'. Can you explain this answer?
In constructing a large mobile, an artist hangs an aluminum sphere of mass 6.0 kg from a vertical steel wire 0.50 m long and 2.5 × 10−3 cm2in cross-sectional area. On the bottom of the sphere he attaches a similar steel wire, from which he hangs a brass cube of mass 10.0 kg. Compute the elongation.
a)
3.7 mm upper, 1.0 mm lower
b)
3.4 mm upper, 1.0 mm lower
c)
3.5 mm upper, 1.1 mm lower
d)
1.6 mm upper, 1.0 mm lower
|
|
Muskaan Kumar answered |
Hence 1.6 mm upper, 1.0 mm lower is correct.
The equation of the circle with centre (2, 1) and touching the line 3x+4y=5 is- a)x2+y2−4x−2y+5=0
- b)x2+y2−4x−2y−5=0
- c)x2+y2−4x−2y+4=0
- d)x2+y2−4x−2y−4=0
Correct answer is option 'C'. Can you explain this answer?
The equation of the circle with centre (2, 1) and touching the line 3x+4y=5 is
a)
x2+y2−4x−2y+5=0
b)
x2+y2−4x−2y−5=0
c)
x2+y2−4x−2y+4=0
d)
x2+y2−4x−2y−4=0
|
KP Classes answered |
Distance from centre (2, 1) to the line 3x+4y−5= radius of circle
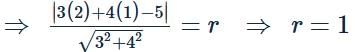
Equation of circle is
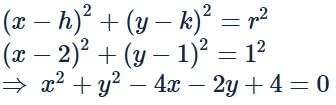
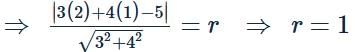
Equation of circle is
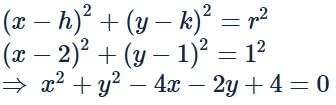
The locus of the midpoint of the chord of the circle x2 + y2 − 2x − 2y − 2 = 0 which makes an angle of 120° at the centre, is:- a)x2 + y2 − 2x − 2y − 1 = 0
- b)x2 + y2 + x + y − 1 = 0
- c)x2 + y2 − 2x − 2y + 1 = 0
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
The locus of the midpoint of the chord of the circle x2 + y2 − 2x − 2y − 2 = 0 which makes an angle of 120° at the centre, is:
a)
x2 + y2 − 2x − 2y − 1 = 0
b)
x2 + y2 + x + y − 1 = 0
c)
x2 + y2 − 2x − 2y + 1 = 0
d)
None of the above
|
|
KP Classes answered |
The coordinates of the centre and radius of the given circle are (1, 1) and 2 respectively. Let AB be the chord subtending an angle of 120° at the center. Let M be the midpoint of AB and let its coordinates be (h, k).
In ∆OAM,
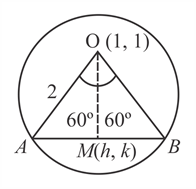
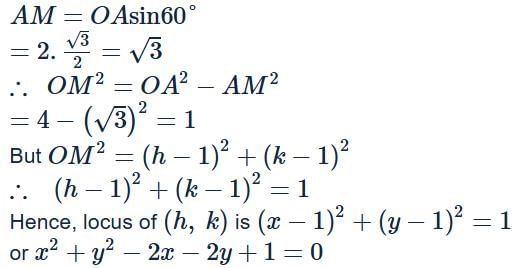
In ∆OAM,
Let P(x1, y1) and P(x2, y2) are two points such that their abscissas x1 and x2 are the roots of the equation x2 + 2x − 3 = 0 while the ordinates y1 and y2 are the roots of the equation y2 + 4y − 12 = 0.Then the centre of the circle with PQ as diameter is- a)(-1, -2)
- b)(1, 2)
- c)(1, -2)
- d)(-1, 2)
Correct answer is option 'A'. Can you explain this answer?
Let P(x1, y1) and P(x2, y2) are two points such that their abscissas x1 and x2 are the roots of the equation x2 + 2x − 3 = 0 while the ordinates y1 and y2 are the roots of the equation y2 + 4y − 12 = 0.Then the centre of the circle with PQ as diameter is
a)
(-1, -2)
b)
(1, 2)
c)
(1, -2)
d)
(-1, 2)
|
Nipuns Institute answered |
Given x1, x2 are the roots of the equation.
x2 + 2x − 3 = 0
⇒ x2 + 3x − x − 3 = 0
⇒x(x+3)−1(x+3)=0
⇒(x−1)(x+3)=0
⇒ x1 = −3, x2 = 1
And y1,y2 are the roots of the equation.
y2+4y−12=0
⇒y2+6y−2y−12=0
⇒y(y+6)−2(y+6)=0
⇒(y−2)(y+6)=0
⇒y1 = −6,
y2 = 2
Points are P(−3,−6) &Q(1,2)
Since Pand Q are the endpoints of a diameter.
∴ Centre = Mid point of PQ
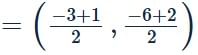
=(−1,) −2
x2 + 2x − 3 = 0
⇒ x2 + 3x − x − 3 = 0
⇒x(x+3)−1(x+3)=0
⇒(x−1)(x+3)=0
⇒ x1 = −3, x2 = 1
And y1,y2 are the roots of the equation.
y2+4y−12=0
⇒y2+6y−2y−12=0
⇒y(y+6)−2(y+6)=0
⇒(y−2)(y+6)=0
⇒y1 = −6,
y2 = 2
Points are P(−3,−6) &Q(1,2)
Since Pand Q are the endpoints of a diameter.
∴ Centre = Mid point of PQ
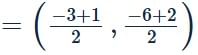
=(−1,) −2
Let A(1, 2), B(3, 4) be two points and C(x, y) be a point such that area of ∆ABC is 3 sq. units and (x − 1)(x − 3) + (y − 2)(y − 4) = 0. Then number of positions of C, in the xy plane, is- a)2
- b)4
- c)8
- d)0
Correct answer is option 'D'. Can you explain this answer?
Let A(1, 2), B(3, 4) be two points and C(x, y) be a point such that area of ∆ABC is 3 sq. units and (x − 1)(x − 3) + (y − 2)(y − 4) = 0. Then number of positions of C, in the xy plane, is
a)
2
b)
4
c)
8
d)
0
|
|
Nipuns Institute answered |
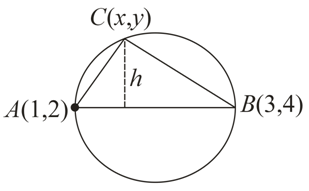
We observe that, (x−1)(x−3)+(y−2)(y−4)=0, is equation of circle in diametric form. Hence, AB is a diameter and (x,y) lies on the circle.
Diameter AB=2√2
So, radius = √2
Area(∆ABC)=3
Height h=3√2> Radius
Hence, no such C exists.
The number of points with integral coordinates which are interior to the circle (x − 2009)2 + (y − 2009)2 = 16, is- a)43
- b)45
- c)47
- d)46
Correct answer is option 'B'. Can you explain this answer?
The number of points with integral coordinates which are interior to the circle (x − 2009)2 + (y − 2009)2 = 16, is
a)
43
b)
45
c)
47
d)
46
|
|
Nipuns Institute answered |
Given,
(x−2009)2+(x−2009)2=16
We have to find the number of points with integral coordinates which are interior to the circle. for this
Number of integral (coordinate) solution = Number of points,
(x)2+(y)2 <(4)2 where x∈[−3,3] and y∈[−3,3]
clearly x and y∈{−3,−2,−1,0,1,2,3}
The ordered pairs of (x, y)={−3,−2,−1,0,1,2,3}×{−3,−2,−1,0,1,2,3}
⇒ The odered pairs
={(−3,−3),(−2,−3),(−1,−3),(0,−3),(1,−3),(2,−3),(3,−3)(−3,−2),(−2,−2),(−1,−2),(0,−2),(1,−2),(2,−2),(3,−2) .(−3 ,3) , (−2, 3), (−1, 3), (0, 3), (1, 3), (2, 3), (3, 3)}
The total number of ordered pairs =49
Out of these 49 ordered pairs, 4 ordered {(−3,−3),(−3,3),(3,−3),(3,3)} pairs doesn't satisfy.
⇒ The number of points with integral coordinates which are interior to the given circle =49−4=45
⇒ By shifting the origin to (2009,−2009), the number of points with integral coordinates will remain the same.
(x−2009)2+(x−2009)2=16
We have to find the number of points with integral coordinates which are interior to the circle. for this
Number of integral (coordinate) solution = Number of points,
(x)2+(y)2 <(4)2 where x∈[−3,3] and y∈[−3,3]
clearly x and y∈{−3,−2,−1,0,1,2,3}
The ordered pairs of (x, y)={−3,−2,−1,0,1,2,3}×{−3,−2,−1,0,1,2,3}
⇒ The odered pairs
={(−3,−3),(−2,−3),(−1,−3),(0,−3),(1,−3),(2,−3),(3,−3)(−3,−2),(−2,−2),(−1,−2),(0,−2),(1,−2),(2,−2),(3,−2) .(−3 ,3) , (−2, 3), (−1, 3), (0, 3), (1, 3), (2, 3), (3, 3)}
The total number of ordered pairs =49
Out of these 49 ordered pairs, 4 ordered {(−3,−3),(−3,3),(3,−3),(3,3)} pairs doesn't satisfy.
⇒ The number of points with integral coordinates which are interior to the given circle =49−4=45
⇒ By shifting the origin to (2009,−2009), the number of points with integral coordinates will remain the same.
Length of common chord of the circles x2+y2+2x+6y = 0 and x2+y2−4x−2y−6 = 0 is - a)
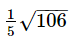
- b)
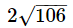
- c)
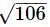
- d)
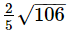
Correct answer is option 'D'. Can you explain this answer?
Length of common chord of the circles x2+y2+2x+6y = 0 and x2+y2−4x−2y−6 = 0 is
a)
b)
c)
d)
|
|
Pallabi Patel answered |
Given equation of circles are
S1 = x2 + y2 + 2x + 6y = 0 ..................1
S2 = x2 + y2 − 4x − 2y − 6 = 0 ............2
Subtract equation 1 - equation 2, we get
S1 - S2 = 6x + 8y + 6 = 0
=> 6x + 8y + 6 = 0 ............3
Cente of the circle S2 is (2, 1)
Now, the length of the perpendicular from the center (2, 1) of of the circle 2 upon the common chord 3 is
l = (6*2 + 8*1 + 6)/√{62 + 82 }
=> l = (12 + 8 + 6)/√{36 + 64}
=> l = 26/√100
=> l = 26/10
=> l = 13/5
Radius of the circle 2 is
r = √{22 + 12 - (-6)}
=> r = √{4 + 1 + 6}
=> r = √11
Now length of common chord = 2√{r2 - l2 }
= 2√{(√11)2 - (13/5)2 }
= 2√{11 - 169/25}
= 2√{(275 - 169)/25}
= 2√{106/25} unit
The point (3,−4) lies on both the circles x2 + y2 − 2x + 8y + 13 = 0 and x2 + y2 − 4x + 6y + 11 = 0. Then, the angle between the circles is- a)60∘
- b)
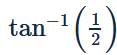
- c)
- d)135∘
Correct answer is option 'D'. Can you explain this answer?
The point (3,−4) lies on both the circles x2 + y2 − 2x + 8y + 13 = 0 and x2 + y2 − 4x + 6y + 11 = 0. Then, the angle between the circles is
a)
60∘
b)
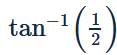
c)
d)
135∘
|
Nipun Tuteja answered |
Given circles are x2 + y2 − 2x + 8y + 13 = 0
and x2 + y2 − 4x + 6y + 11 = 0.
Here, C1 = (1,−4),C2 = (2,−3),
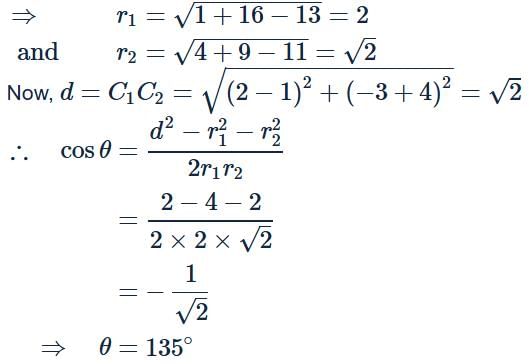
and x2 + y2 − 4x + 6y + 11 = 0.
Here, C1 = (1,−4),C2 = (2,−3),
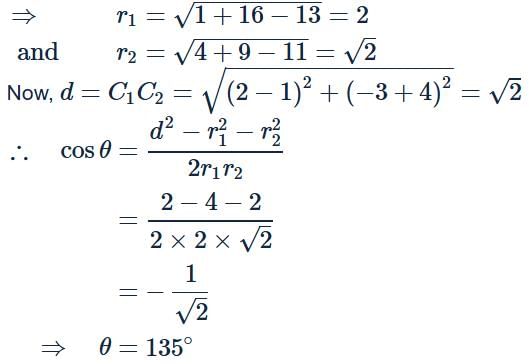
If there is a point (x,y) on circle x2+y2−4x−6y−3=0, then maximum value of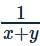 
is- a)5−4√2
- b)5+4√2
- c)
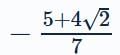
- d)
Correct answer is option 'C'. Can you explain this answer?
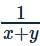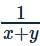If there is a point (x,y) on circle x2+y2−4x−6y−3=0, then maximum value of is
isa)
5−4√2
b)
5+4√2
c)
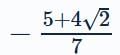
d)
|
|
KP Classes answered |
x2+y2−4x−6y−3=0
⇒ (x−2)2+(y−3)2=42
Parametric forms of circle will be
x−2=4cosθ and y−3=4sinθ
⇒ x=2+4cosθ and y=3+4sinθ
Now, x + y = 5 + 4(sinθ + cosθ), − √2 ≤ sinθ + cosθ ≤√2 for maximum value of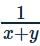
, value of (x+y) will be minimum, so (x + y) min = 5 + 4(−√2) = 5−4√2
Hence, answer is
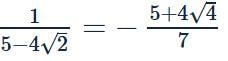
⇒ (x−2)2+(y−3)2=42
Parametric forms of circle will be
x−2=4cosθ and y−3=4sinθ
⇒ x=2+4cosθ and y=3+4sinθ
Now, x + y = 5 + 4(sinθ + cosθ), − √2 ≤ sinθ + cosθ ≤√2 for maximum value of
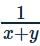, value of (x+y) will be minimum, so (x + y) min = 5 + 4(−√2) = 5−4√2Hence, answer is
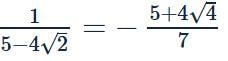
Find the sum of square of the length of the chords intercepted by the line x + y =n; n ∈ N on the circle x2 + y2 = 4.- a)22
- b)29
- c)25
- d)23
Correct answer is option 'A'. Can you explain this answer?
Find the sum of square of the length of the chords intercepted by the line x + y =n; n ∈ N on the circle x2 + y2 = 4.
a)
22
b)
29
c)
25
d)
23
|
|
Nipun Tuteja answered |
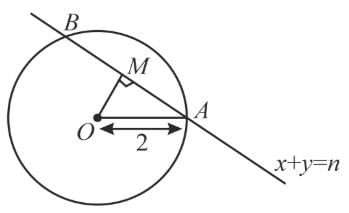
AB=2 AM
AB2=4 AM2
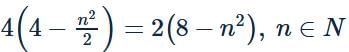
n=1 or n=2 (∵ length should be +ve)
Hence required sum
=2(8−12+8−22)
=2×11=22
Chapter doubts & questions for September Week 4 - Weekly Tests for JEE Preparation 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of September Week 4 - Weekly Tests for JEE Preparation in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily