All Exams >
JEE >
Weekly Tests for JEE Preparation >
All Questions
All questions of August Week 1 for JEE Exam
If we double the radius of a current carrying coil keeping the current unchanged. what happens to the magnetic field at its Centre?- a)halved
- b)doubled
- c)remains unchanged
- d)becomes four times
Correct answer is option 'A'. Can you explain this answer?
If we double the radius of a current carrying coil keeping the current unchanged. what happens to the magnetic field at its Centre?
a)
halved
b)
doubled
c)
remains unchanged
d)
becomes four times

|
Ciel Knowledge answered |
As,
B=μonI/2a
a ->radius
B ∝1/a
B1/B2=a2/a1
B1=2B2
B2=(1/2) x B1,
Magnetic field is halved.
B=μonI/2a
a ->radius
B ∝1/a
B1/B2=a2/a1
B1=2B2
B2=(1/2) x B1,
Magnetic field is halved.
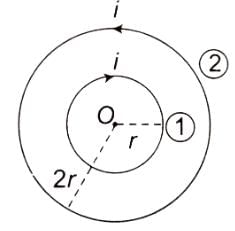
Two concentric coils carry the same current in opposite directions. The diameter of the inner coil is half that of the outer coil. If the magnetic field produced by the outer coil at the common centre are 1 T, the net field at the centre is
- a)4T
- b)2T
- c)1T
- d)3T
Correct answer is option 'C'. Can you explain this answer?
Two concentric coils carry the same current in opposite directions. The diameter of the inner coil is half that of the outer coil. If the magnetic field produced by the outer coil at the common centre are 1 T, the net field at the centre is
a)
4T
b)
2T
c)
1T
d)
3T
|
|
Krishna Iyer answered |
The magnetic field produced by a current-carrying coil at its center is given by the formula,
B = μ0 * (N*I/R),
where,
B is the magnetic field,
μ0 is the permeability of free space,
N is the number of turns in the coil,
I is the current through the coil, and
R is the radius of the coil.
In this case, both the coils carry the same current but in opposite directions. So, the fields produced by them will be in opposite directions. Also, the diameter of the inner coil is half that of the outer coil. Thus, the radius of the inner coil will be half that of the outer coil.
Therefore, the field at the center due to the inner coil will be double that due to the outer coil (because the magnetic field is inversely proportional to the radius).
Since the fields are in opposite directions, the net field at the center will be the difference between the two fields. That is, 2B (due to the inner coil) - B (due to the outer coil) = B.
So, if the field due to the outer coil is 1 T (Tesla), the net field at the center will also be 1 T.
Hence, the correct answer is 3. 1T.
The magnetic field due to circular coil of 200 turns of diameter 0.1m carrying a current of 5A at a point on the axis of the coil at a distance 0.15m from the center of the coil will be- a)
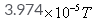
- b)
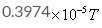
- c)
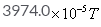
- d)
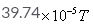
Correct answer is option 'D'. Can you explain this answer?
The magnetic field due to circular coil of 200 turns of diameter 0.1m carrying a current of 5A at a point on the axis of the coil at a distance 0.15m from the center of the coil will be
a)
b)
c)
d)
|
|
Krishna Iyer answered |
B=μ02πnIa2/4π (a2+x2)3/2
=10−7×2×(22/7)×200×5×(0⋅1/2)2/ [(0⋅1/2)2+(0⋅15)2]3/2
=39.74x10-5
=10−7×2×(22/7)×200×5×(0⋅1/2)2/ [(0⋅1/2)2+(0⋅15)2]3/2
=39.74x10-5
Wire of length l, carries a steady current I. It is bent first to form a circular coil of one turn. The same wire of same length is now bent more sharply to give two loops of smaller radius the magnetic field at the centre caused by the same current is- a)one third of its initial value
- b)nine times of its initial value
- c)four times of its initial value
- d)unaltered
Correct answer is option 'C'. Can you explain this answer?
Wire of length l, carries a steady current I. It is bent first to form a circular coil of one turn. The same wire of same length is now bent more sharply to give two loops of smaller radius the magnetic field at the centre caused by the same current is
a)
one third of its initial value
b)
nine times of its initial value
c)
four times of its initial value
d)
unaltered
|
|
Om Desai answered |
Let the radii be r1 and r2 respectively.
Since there are two turns of radius r2, r1=2r2
Magnetic field B at the centre of the coil of radius r1 B1=μoi/2r1=μoi/4r2
Magnetic field B at the center of the coil of radius r2 B2=2×μoi/2r2
∴ B2/B1 =(2× μoi/2r2)/(μoi /4r2) =4
Hence the answer is option C, four times its initial value.
Since there are two turns of radius r2, r1=2r2
Magnetic field B at the centre of the coil of radius r1 B1=μoi/2r1=μoi/4r2
Magnetic field B at the center of the coil of radius r2 B2=2×μoi/2r2
∴ B2/B1 =(2× μoi/2r2)/(μoi /4r2) =4
Hence the answer is option C, four times its initial value.
A circular coil of radius r carries current I. The magnetic field at its center is B. at what distance from the center on the axis of the coil magnetic field will be B/8- a)√3R
- b)√2R
- c)2R
- d)3R
Correct answer is option 'A'. Can you explain this answer?
A circular coil of radius r carries current I. The magnetic field at its center is B. at what distance from the center on the axis of the coil magnetic field will be B/8
a)
√3R
b)
√2R
c)
2R
d)
3R

|
Shilpa Saha answered |
As you know that magnetic field at point on the axis of current carrying ring is
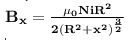
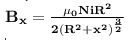
where x is the point on the axis of ring, R is the radius of ring , i is the current carrying on ring and N is the number of turns .
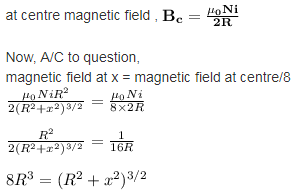
This is possible only when x = +-√3R
Hence, √3R distance from the centre magnetic field is equal to magnetic field at centre .
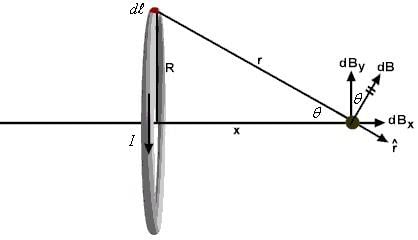

A straight conductor carrying current I is split into circular loop as shown in figure a , the magnetic induction at the center of the circular loop is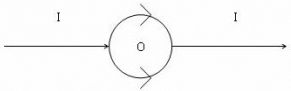
- a)Zero
- b)
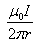
- c)
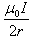
- d)Infinite
Correct answer is option 'A'. Can you explain this answer?
A straight conductor carrying current I is split into circular loop as shown in figure a , the magnetic induction at the center of the circular loop is
a)
Zero
b)
c)
d)
Infinite
|
|
Jayant Mishra answered |
The magnetic field at the center O due to the upper side of the semicircular current loop is equal and opposite to that due to the lower side of the loop.
A circular loop of radius 0.0157 m carries a current of 2 A. The magnetic field at the centre of the loop is- a)3.14 x 10-5 weber /m2
- b)1.57 x 10-5 weber /m2
- c)1.57 x 10-5 weber /m2
- d)8.0 x 10-5 weber /m2
Correct answer is option 'D'. Can you explain this answer?
A circular loop of radius 0.0157 m carries a current of 2 A. The magnetic field at the centre of the loop is
a)
3.14 x 10-5 weber /m2
b)
1.57 x 10-5 weber /m2
c)
1.57 x 10-5 weber /m2
d)
8.0 x 10-5 weber /m2
|
|
Hansa Sharma answered |
The magnetic field due to a circular loop is given by:
B= μ02πi/4πr
=10−7×2π×2/0.0157
=8×10−5 Wb/m2
B= μ02πi/4πr
=10−7×2π×2/0.0157
=8×10−5 Wb/m2

- a)

- b)
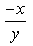
- c)
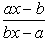
- d)
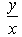
Correct answer is option 'D'. Can you explain this answer?
a)
b)
c)
d)
|
|
Rocky Gupta answered |
X^a y^b = (x + y)^(a + b)
taking ln on both sides :-
alnx + b lny = (a + b) ln(x + y)
diff both sides w.r.t x :-
a/x + by'/y = ( (a + b)/(x + y) ) + (((a + b) y'))/(x + y)
or,
a/x - (a +b)/(x + y) = y'[((a + b) / (x + y)) - b/y]
or,
(ax + ay - ax - bx)/x = y' [ (ay + by - bx - by)/y] (cancel (x + y))
or,
y' = dy/dx = ( y (ay - bx) )/(x( ay - bx)) = y/x
therefore we can easily say that the option (D) is the correct answer
taking ln on both sides :-
alnx + b lny = (a + b) ln(x + y)
diff both sides w.r.t x :-
a/x + by'/y = ( (a + b)/(x + y) ) + (((a + b) y'))/(x + y)
or,
a/x - (a +b)/(x + y) = y'[((a + b) / (x + y)) - b/y]
or,
(ax + ay - ax - bx)/x = y' [ (ay + by - bx - by)/y] (cancel (x + y))
or,
y' = dy/dx = ( y (ay - bx) )/(x( ay - bx)) = y/x
therefore we can easily say that the option (D) is the correct answer

- a)
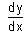
- b)

- c)
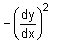
- d)
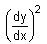
Correct answer is option 'D'. Can you explain this answer?
a)
b)
c)
d)

|
Knowledge Hub answered |
ey =1/ (x+5)
Taking log both side we get
log ey = log {1/(5+x)}
then, y = log {1/(5+x)}
Differentiating both side ,
dy/dx =( x+5) . {-1/(5+x)²}
dy/dx = -1/(5+x) ……..( 1)
Again Differentiating, d²y/dx²= 1/(5+x)²
d²y/dx²= {-1/(5+x)}²
From equation (1)
d²y/dx² = {dy/dx}²
Taking log both side we get
log ey = log {1/(5+x)}
then, y = log {1/(5+x)}
Differentiating both side ,
dy/dx =( x+5) . {-1/(5+x)²}
dy/dx = -1/(5+x) ……..( 1)
Again Differentiating, d²y/dx²= 1/(5+x)²
d²y/dx²= {-1/(5+x)}²
From equation (1)
d²y/dx² = {dy/dx}²
If f(x) = x + cot x, 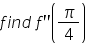
- a)-4
- b)2
- c)4
- d)-2
Correct answer is option 'C'. Can you explain this answer?
If f(x) = x + cot x, 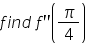
a)
-4
b)
2
c)
4
d)
-2
|
|
Aryan Khanna answered |
f(x) = x + cot x
f’(x) = 1 + (-cosec2 x)
f”(x) = 0 - 2cosec x(-cosec x cot x)
= 2 cosec2 x cot x
f”(π/4) = 2 cosec2 (π/4) cot(π/4)
= 2 [(2)^½]2 (1)
= 4
f’(x) = 1 + (-cosec2 x)
f”(x) = 0 - 2cosec x(-cosec x cot x)
= 2 cosec2 x cot x
f”(π/4) = 2 cosec2 (π/4) cot(π/4)
= 2 [(2)^½]2 (1)
= 4
Find the second derivative of excosx- a)-2exsinx
- b)-exsinx
- c)ex(sinx + cosx)
- d)-2excosx
Correct answer is option 'A'. Can you explain this answer?
Find the second derivative of excosx
a)
-2exsinx
b)
-exsinx
c)
ex(sinx + cosx)
d)
-2excosx
|
|
Rounak Nair answered |
**Solution:**
To find the second derivative of the given function, we need to differentiate it twice with respect to x.
First, let's find the first derivative of the function:
f(x) = ex * cosx
Using the product rule, the derivative of f(x) is:
f'(x) = (ex * (-sinx)) + (cosx * ex)
= -ex * sinx + ex * cosx
= ex * (cosx - sinx)
Now, let's find the second derivative of the function. Taking the derivative of f'(x):
f''(x) = (ex * (-sinx)) + (ex * (-cosx))
= -ex * sinx - ex * cosx
= -ex * (sinx + cosx)
Therefore, the second derivative of excosx is -2exsinx, which is option A.
To find the second derivative of the given function, we need to differentiate it twice with respect to x.
First, let's find the first derivative of the function:
f(x) = ex * cosx
Using the product rule, the derivative of f(x) is:
f'(x) = (ex * (-sinx)) + (cosx * ex)
= -ex * sinx + ex * cosx
= ex * (cosx - sinx)
Now, let's find the second derivative of the function. Taking the derivative of f'(x):
f''(x) = (ex * (-sinx)) + (ex * (-cosx))
= -ex * sinx - ex * cosx
= -ex * (sinx + cosx)
Therefore, the second derivative of excosx is -2exsinx, which is option A.
Find the differential coefficient y = (sec 5x)5x - a)log ( sec 5x) + 5x log (tan 5x)
- b)5(sec 5x)5x [log (sec 5x) + 5x tan 5x ]
- c)(sec 5x)5x [log( sec 5x) + 5x log (tan 5x)]
- d)log (sec 5x) + 5x tan 5x
Correct answer is option 'B'. Can you explain this answer?
Find the differential coefficient y = (sec 5x)5x
a)
log ( sec 5x) + 5x log (tan 5x)
b)
5(sec 5x)5x [log (sec 5x) + 5x tan 5x ]
c)
(sec 5x)5x [log( sec 5x) + 5x log (tan 5x)]
d)
log (sec 5x) + 5x tan 5x
|
|
Mehul Kulkarni answered |
Explanation:
Given: y = (sec 5x)^5x
Step 1: Apply the chain rule to find the differential coefficient of y with respect to x.
Step 2: Differentiate the function (sec 5x)^5x using the chain rule.
Step 3: Apply the chain rule to differentiate (sec 5x)^5x.
Step 4: The differential coefficient of y is given by 5(sec 5x)^5x[log(sec 5x) + 5x tan 5x].
Therefore, the correct answer is option B - 5(sec 5x)^5x[log(sec 5x) + 5x tan 5x].
Given: y = (sec 5x)^5x
Step 1: Apply the chain rule to find the differential coefficient of y with respect to x.
Step 2: Differentiate the function (sec 5x)^5x using the chain rule.
Step 3: Apply the chain rule to differentiate (sec 5x)^5x.
Step 4: The differential coefficient of y is given by 5(sec 5x)^5x[log(sec 5x) + 5x tan 5x].
Therefore, the correct answer is option B - 5(sec 5x)^5x[log(sec 5x) + 5x tan 5x].
The magnetic field B on the axis of a circular coil at distance x far away from its centre are related as:- a)Bαx-1
- b)Bαx-4
- c)Bαx-3
- d)Bαx-2
Correct answer is option 'C'. Can you explain this answer?
The magnetic field B on the axis of a circular coil at distance x far away from its centre are related as:
a)
Bαx-1
b)
Bαx-4
c)
Bαx-3
d)
Bαx-2
|
|
Naina Bansal answered |
The formula for the magnetic field B (flux density) at P at a distance d from the center of O the coil on the axis of the coil of radius r :
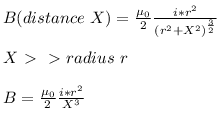
Put appropriate punctuation marks in the following sentences.Sorry to disturb you could I speak to you for a moment Correct answer is 'Sorry to disturb you – could I speak to you for a moment?'. Can you explain this answer?
Put appropriate punctuation marks in the following sentences.
Sorry to disturb you could I speak to you for a moment

|
Gowri Chakraborty answered |
In the sentence "Sorry to disturb you – could I speak to you for a moment?", the appropriate punctuation marks are a hyphen (-) after "disturb you" and a question mark (?) after "moment".
The hyphen is used to join two words together, in this case "disturb" and "you", to form a compound adjective. A compound adjective is an adjective made up of two or more words that describes a noun. In this sentence, the compound adjective "sorry to disturb you" describes the speaker and indicates that they feel apologetic about interrupting the person they are speaking to.
The question mark is used to indicate that the sentence is a question. In this case, the speaker is asking if they can speak to the person for a moment.
Overall, the punctuation in the sentence helps to clarify the meaning and structure of the sentence, making it easier for the reader to understand.
The general solution of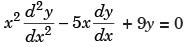 is
is- a)(c1 + c2x)e3x
- b)(c1 + c2 In x)x3
- c)(c1 + c2 x)x3
- d)(c1 + c2 In x)ex3
Correct answer is option 'B'. Can you explain this answer?
The general solution of
a)
(c1 + c2x)e3x
b)
(c1 + c2 In x)x3
c)
(c1 + c2 x)x3
d)
(c1 + c2 In x)ex3
|
|
Varun Kapoor answered |
The operator form of given equation is (x2D2 – 5xD + 9)y = 0 ...(*)
Let x = et ⇒ t = log x D′ ≡ d / dt
D ≡ d / dt
We have x2D2 = D′(D′ – 1)
xD = D′
[D′(D′ – 1) – 5D′ + 9]y = 0
The A.E. is m2 – 6m + 9 = 0
(m – 3)2 = 0, m = 3, 3
The C.F. is y = (c
The solution of (*) is
y = (c1 + c2 log x) x3.
Let x = et ⇒ t = log x D′ ≡ d / dt
D ≡ d / dt
We have x2D2 = D′(D′ – 1)
xD = D′
[D′(D′ – 1) – 5D′ + 9]y = 0
The A.E. is m2 – 6m + 9 = 0
(m – 3)2 = 0, m = 3, 3
The C.F. is y = (c
1
+ c2t)e3t The solution of (*) is
y = (c1 + c2 log x) x3.
Chapter doubts & questions for August Week 1 - Weekly Tests for JEE Preparation 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of August Week 1 - Weekly Tests for JEE Preparation in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Related JEE Content

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup













