All Exams >
Class 10 >
Weekly Tests for Class 10 Preparation >
All Questions
All questions of May Week 2 for Class 10 Exam
The pair of linear equations x + y + 10 = 0 and x + y – 7 = 0 has:- a)One solution
- b)Infinitely many solutions
- c)No solutions
- d)Two solutions
Correct answer is option 'C'. Can you explain this answer?
The pair of linear equations x + y + 10 = 0 and x + y – 7 = 0 has:
a)
One solution
b)
Infinitely many solutions
c)
No solutions
d)
Two solutions
|
Gaurav Kumar answered |
We have a1, a2 the coefficients of x2,b1 and b2 coefficients of x and c1 and c2 the constant terms.
So,
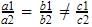a1a2=b1b2c1c2which is a case of parallel lines which which never meet. So there are no solutions obtainable for these equations.
So,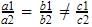a1a2=b1b2c1c2which is a case of parallel lines which which never meet. So there are no solutions obtainable for these equations.
Which of the following is not a solution of pair of equations 3x – 2y = 4 and 6x – 4y = 8?- a)x = 5, y = 3
- b)x = 2, y = 1
- c)x = 6, y = 7
- d)x = 4, y = 4
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not a solution of pair of equations 3x – 2y = 4 and 6x – 4y = 8?
a)
x = 5, y = 3
b)
x = 2, y = 1
c)
x = 6, y = 7
d)
x = 4, y = 4
|
Vikram Kapoor answered |
3x – 2y = 4 and 6x – 4y = 8
Putting x=5 and y=3
LHS=3(5)-2(3)
15-6=9
RHS=4
LHS ≠ RHS
Also,
6(5)-4(3)=30-12=18 ≠ 8
Putting x=5 and y=3
LHS=3(5)-2(3)
15-6=9
RHS=4
LHS ≠ RHS
Also,
6(5)-4(3)=30-12=18 ≠ 8
One equation of a pair of dependent linear equations is -5x + 7y = 2, the second equation can be :- a)-10x + 14y + 4 = 0
- b)-10x – 14x + 4 =
- c)10x – 14y = -4
- d)10x + 14y + 4 =0
Correct answer is option 'C'. Can you explain this answer?
One equation of a pair of dependent linear equations is -5x + 7y = 2, the second equation can be :
a)
-10x + 14y + 4 = 0
b)
-10x – 14x + 4 =
c)
10x – 14y = -4
d)
10x + 14y + 4 =0
|
|
Vikram Kapoor answered |
If a system of two linear equation is consistent system and has an infinite number of solutions, it is dependent . When you graph the equations, both equations represent the same line.So we have 
which is satisfied by 10x – 14y = -4 only.
which is satisfied by 10x – 14y = -4 only. For what value of ‘K’ will the system of equations: 3x + y = 1, (2K – 1) x + (K – 1) y = 2K + 1 have no solution- a)3
- b)2
- c)1
- d)-2
Correct answer is option 'B'. Can you explain this answer?
For what value of ‘K’ will the system of equations: 3x + y = 1, (2K – 1) x + (K – 1) y = 2K + 1 have no solution
a)
3
b)
2
c)
1
d)
-2
|
Krishna Iyer answered |
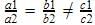is a case of parallel lines which never meet. So there are no solutions obtainable for these equations. So equations are inconsistent3x + y = 1, (2K – 1) x + (K – 1) y = 2K + 1
b1=1,b2=k-1,c1=-1,c2=-2k-1
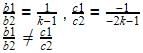
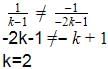
Can you explain the answer of this question below:The pair of equations y = 0 and y = -7 has :
- A:
no solution
- B:
infinitely many solutions
- C:
one solution
- D:
two solutions
The answer is a.
The pair of equations y = 0 and y = -7 has :
no solution
infinitely many solutions
one solution
two solutions
|
Raghav Bansal answered |
y=0 is x-axis… since every point has y=0. y=-7 is a line parallel to x-axis passing through x=0,y=-7. So the two lines are parallel to each other and are inconsistent which means that it has no solutions because it will never meet.
Which of following is not a solution of 3a + b = 12 ?
- a)(3, 3)
- b)(5, -3)
- c)(4, 0)
- d)(2, 4)
Correct answer is option 'D'. Can you explain this answer?
Which of following is not a solution of 3a + b = 12 ?
a)
(3, 3)
b)
(5, -3)
c)
(4, 0)
d)
(2, 4)
|
Prashant Gujjar Pgv answered |
D correct h 3(2)+4=10this is not a solution
Which of the following pair of linear equations is inconsistent?- a)5x – 3y = 11; 7x + 2y =13
- b)x – 2y = 6; 2x + 3y = 4
- c)9x – 8y = 17; 18x -16y = 34
- d)2x + 3y = 7; 4x + 6y = 5
Correct answer is option 'D'. Can you explain this answer?
Which of the following pair of linear equations is inconsistent?
a)
5x – 3y = 11; 7x + 2y =13
b)
x – 2y = 6; 2x + 3y = 4
c)
9x – 8y = 17; 18x -16y = 34
d)
2x + 3y = 7; 4x + 6y = 5
|
|
Krishna Iyer answered |
Pair of linear equations are inconsistent when they are parallel. When the two equations are parallel ,we have 
.
.In D, we have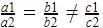 
which is 
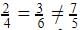, so it is inconsistent.
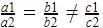which is 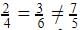, so it is inconsistent.The number of solutions of the pair of linear equations x + 2y – 8 = 0 and 2x + 4y = 16 are:- a)None
- b)Infinitely many
- c)0
- d)1
Correct answer is option 'B'. Can you explain this answer?
The number of solutions of the pair of linear equations x + 2y – 8 = 0 and 2x + 4y = 16 are:
a)
None
b)
Infinitely many
c)
0
d)
1
|
Pooja Shah answered |
We have the equations x + 2y – 8 = 0 and 2x + 4y = 16 Where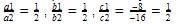 
Here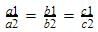
which is the case of coincident lines . So there are infinitely many solutions.
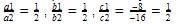
Here
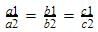which is the case of coincident lines . So there are infinitely many solutions.A system of simultaneous linear equations has infinitely many solutions if two lines:- a)are coincident
- b)intersect at two points
- c)are parallel
- d)intersect at one point
Correct answer is option 'A'. Can you explain this answer?
A system of simultaneous linear equations has infinitely many solutions if two lines:
a)
are coincident
b)
intersect at two points
c)
are parallel
d)
intersect at one point
|
|
Damini kumar answered |
Explanation:
Simultaneous linear equations are equations with two or more variables that are to be solved at the same time. These equations can be represented by lines, and the solutions represent the points where these lines intersect.
When two lines intersect at one point, there is only one solution to the system of equations. When two lines are parallel, there is no solution to the system of equations. However, when two lines are coincident, they overlap each other and have infinite solutions.
Example:
Consider the system of equations:
2x + 3y = 6
4x + 6y = 12
We can solve this system of equations by using elimination or substitution method.
Using the elimination method, we can multiply the first equation by 2 and subtract the second equation from it to eliminate x, which gives:
4x + 6y = 12
- (4x + 6y = 12)
-----------------
0x + 0y = 0
This equation is always true, which means that the two equations are equivalent. Therefore, they represent the same line, and there are infinitely many solutions to this system of equations.
Using the substitution method, we can solve for y in the first equation and substitute it into the second equation, which gives:
y = (6 - 2x)/3
4x + 6((6 - 2x)/3) = 12
Simplifying the second equation, we get:
4x + 4x = 12
Which gives:
x = 3/2
Substituting this value of x into the first equation, we get:
2(3/2) + 3y = 6
Simplifying, we get:
3y = 3
Which gives:
y = 1
Therefore, the solution to this system of equations is (3/2, 1). However, this is just one solution, and there are infinitely many solutions to this system of equations since the two lines are coincident.
Simultaneous linear equations are equations with two or more variables that are to be solved at the same time. These equations can be represented by lines, and the solutions represent the points where these lines intersect.
When two lines intersect at one point, there is only one solution to the system of equations. When two lines are parallel, there is no solution to the system of equations. However, when two lines are coincident, they overlap each other and have infinite solutions.
Example:
Consider the system of equations:
2x + 3y = 6
4x + 6y = 12
We can solve this system of equations by using elimination or substitution method.
Using the elimination method, we can multiply the first equation by 2 and subtract the second equation from it to eliminate x, which gives:
4x + 6y = 12
- (4x + 6y = 12)
-----------------
0x + 0y = 0
This equation is always true, which means that the two equations are equivalent. Therefore, they represent the same line, and there are infinitely many solutions to this system of equations.
Using the substitution method, we can solve for y in the first equation and substitute it into the second equation, which gives:
y = (6 - 2x)/3
4x + 6((6 - 2x)/3) = 12
Simplifying the second equation, we get:
4x + 4x = 12
Which gives:
x = 3/2
Substituting this value of x into the first equation, we get:
2(3/2) + 3y = 6
Simplifying, we get:
3y = 3
Which gives:
y = 1
Therefore, the solution to this system of equations is (3/2, 1). However, this is just one solution, and there are infinitely many solutions to this system of equations since the two lines are coincident.
Which of the following pairs of equations represent inconsistent system?- a)3x – y = -8 3x – y = 24
- b)5x – y = 10 10x – 2y = 20
- c)3x – 2y = 8 2x + 3y = 1
- d)lx – y = m x + my = l
Correct answer is option 'A'. Can you explain this answer?
Which of the following pairs of equations represent inconsistent system?
a)
3x – y = -8 3x – y = 24
b)
5x – y = 10 10x – 2y = 20
c)
3x – 2y = 8 2x + 3y = 1
d)
lx – y = m x + my = l
|
Amit Sharma answered |
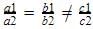is a case of parallel lines which never meet. So there are no solutions obtainable for these equations. So equations are inconsistent.3x – y = -8 ,3x – y = 24
3x – y +8=0 ,3x – y -24=0
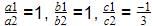
So,
Therefore the equations are inconsistent. The pair of linear equations 8x – 5y = 7 and 5x – 8y = -7 have :- a)No solution
- b)Many solutions
- c)One solution
- d)Two solutions
Correct answer is option 'C'. Can you explain this answer?
The pair of linear equations 8x – 5y = 7 and 5x – 8y = -7 have :
a)
No solution
b)
Many solutions
c)
One solution
d)
Two solutions
|
|
Raghav Bansal answered |
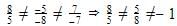So, they are intersecting lines. And intersecting lines meet at only one point. So only 1 solution is available.Which of the following equation is not a linear equation?- a)2a-b =1
- b)2a+b =1
- c)a+b =1
- d)√a+b =1
Correct answer is option 'D'. Can you explain this answer?
Which of the following equation is not a linear equation?
a)
2a-b =1
b)
2a+b =1
c)
a+b =1
d)
√a+b =1
|
|
Gaurav Kumar answered |
Linear equation is an equation between two variables that gives a straight line when plotted on a graph. Linear equations have degree 1 only which means that power of the variables is 1 only. Since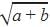 
does not have degree 1 its not a linear equation.
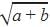does not have degree 1 its not a linear equation.The pair of equations 3x + 2y = 5 and 2x – 3y = 7 will have
- a)Consistent
- b)no solution
- c)infinite solution
- d)none of the above
Correct answer is option 'A'. Can you explain this answer?
The pair of equations 3x + 2y = 5 and 2x – 3y = 7 will have
a)
Consistent
b)
no solution
c)
infinite solution
d)
none of the above
|
|
Mehak Jaju answered |
A/a is not equal to B/b then its unique
If the pair of equation has no solution, then the pair of equation is :- a)inconsistent
- b)coincident
- c)consistent
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If the pair of equation has no solution, then the pair of equation is :
a)
inconsistent
b)
coincident
c)
consistent
d)
none of these
|
|
Vikas Kumar answered |
If two lines are parallel then, they have no solution pair of linear equations is inconsistent;
If two lines are coincident then, they have infinite solution and pair of linear equations is consistent;
If two lines are intersecting then, they have unique solution and pair of linear equations is consistent.
Chapter doubts & questions for May Week 2 - Weekly Tests for Class 10 Preparation 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of May Week 2 - Weekly Tests for Class 10 Preparation in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Weekly Tests for Class 10 Preparation
23 docs|109 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily