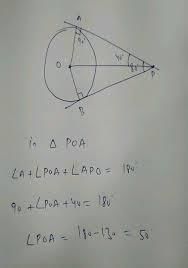All Exams >
Class 10 >
Weekly Tests for Class 10 Preparation >
All Questions
All questions of November Week 1 for Class 10 Exam
In the given figure, PQ is the tangent of the circle. Line segment PR intersects the circle at Nand R. PQ = 15 cm, PR = 25 cm, find PN: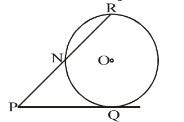
- a)15 cm
- b)10 cm
- c)9 cm
- d)6 cm
Correct answer is option 'C'. Can you explain this answer?
In the given figure, PQ is the tangent of the circle. Line segment PR intersects the circle at Nand R. PQ = 15 cm, PR = 25 cm, find PN:
a)
15 cm
b)
10 cm
c)
9 cm
d)
6 cm
|
|
Archana singh answered |
Given, PQ = 15 cm
PR = 25 cm
We know that, PQ² = PN × PR
15² = PN × 25
225 = PN × 25
PN = 9
15² = PN × 25
225 = PN × 25
PN = 9
The length of the tangent drawn from a point 8 cm away from the centre of a circle of radius 6 cm is- a)√7 cm
- b)2√7 cm
- c)10 cm
- d)5 cm
Correct answer is option 'B'. Can you explain this answer?
The length of the tangent drawn from a point 8 cm away from the centre of a circle of radius 6 cm is
a)
√7 cm
b)
2√7 cm
c)
10 cm
d)
5 cm
|
|
Pooja Shah answered |
Let P be the external point and PA and PB be the tangents and OA and OB be the radii.
So OP is the hypotenuse=8cm
Applying Pythagoras theorem,
H2 = P2 + B2
64 = AP2 + 36
AP =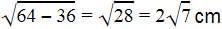
So OP is the hypotenuse=8cm
Applying Pythagoras theorem,
H2 = P2 + B2
64 = AP2 + 36
AP =
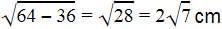
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB =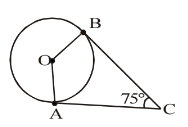
- a)75°
- b)85°
- c)95°
- d)105º
Correct answer is option 'D'. Can you explain this answer?
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB =
a)
75°
b)
85°
c)
95°
d)
105º
|
|
Kuldeep Kuldeep answered |
Solution:- The length of tangents drawn from an external point to the circle are equal.
In the figure, CA and CB are the tangents from external point of a circle and OA and OB are the two radius of a circle.
Draw a line OC, then you will get two triangles OAC and OBC.
In a ∆le AOC and ∆le BOC,
Angle OAC and OBC = 180 degree. Because, these are angles between the radii and tangents. So, there are two right angles.
The value for right angled triangle is 90 degree. Here, you can see both right angled triangle, so 90×2 = 180 degree.
Angle AOB = Angle OAC + Angle OBC - Angle ACB.
Given:- Angle ACB = 75 degree. , Angle OAC and OBC = 90 degree.
Angle AOB = 90 + 90 - 75.
Angle AOB = 180 -75.
Angle AOB =105 degree.
So, option d is correct friend.
In the figure, CA and CB are the tangents from external point of a circle and OA and OB are the two radius of a circle.
Draw a line OC, then you will get two triangles OAC and OBC.
In a ∆le AOC and ∆le BOC,
Angle OAC and OBC = 180 degree. Because, these are angles between the radii and tangents. So, there are two right angles.
The value for right angled triangle is 90 degree. Here, you can see both right angled triangle, so 90×2 = 180 degree.
Angle AOB = Angle OAC + Angle OBC - Angle ACB.
Given:- Angle ACB = 75 degree. , Angle OAC and OBC = 90 degree.
Angle AOB = 90 + 90 - 75.
Angle AOB = 180 -75.
Angle AOB =105 degree.
So, option d is correct friend.
A ray of light is reflected by the pole of a concave mirror at an angle of 80o. The angle of incidence will be
- a)80º
- b)180º
- c)0º
- d)50º
Correct answer is option 'A'. Can you explain this answer?
A ray of light is reflected by the pole of a concave mirror at an angle of 80o. The angle of incidence will be
a)
80º
b)
180º
c)
0º
d)
50º
|
|
Ashiii answered |
Angle of Reflection = Angle of Incidence
Angle of Reflection = 80॰
⁂ Angle of Incidence = 80॰
..v@.**
Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Circles" are available for CBSE Class 10 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 10 Mathematics (Maths)Q. A point P is 10 cm from the centre of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to- a)4 cm
- b)5 cm
- c)6 cm
- d)None of these.
Correct answer is option 'C'. Can you explain this answer?
Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Circles" are available for CBSE Class 10 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 10 Mathematics (Maths)
Q. A point P is 10 cm from the centre of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to
a)
4 cm
b)
5 cm
c)
6 cm
d)
None of these.
|
|
Krishna Iyer answered |
ΔPTO is a right angled triangle at T ,where the tangent touches the circle.
So applying pythagoras theorem,
H2=P2+B2
102=B2+82
B=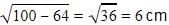
Radius is 6cm.
So applying pythagoras theorem,
H2=P2+B2
102=B2+82
B=
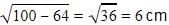
Radius is 6cm.
If the diagonals of a cyclic quadrilateral are equal, then the quadrilateral is- a)rhombus
- b)square
- c)rectangle
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If the diagonals of a cyclic quadrilateral are equal, then the quadrilateral is
a)
rhombus
b)
square
c)
rectangle
d)
none of these
|
|
Raghav Bansal answered |
Let ABCD be a cyclic quadrilateral having diagonals BD and AC, intersecting each other at point O.
(Consider BD as a chord)
∠BCD + ∠BAD = 180 (Cyclic quadrilateral)
∠BCD = 180− 90 = 90
(Considering AC as a chord)
∠ADC + ∠ABC = 180 (Cyclic quadrilateral)
90+ ∠ABC = 180
∠ABC = 90
Each interior angle of a cyclic quadrilateral is of 90.Hence it is a rectangle.
(Consider BD as a chord)
∠BCD + ∠BAD = 180 (Cyclic quadrilateral)
∠BCD = 180− 90 = 90
(Considering AC as a chord)
∠ADC + ∠ABC = 180 (Cyclic quadrilateral)
90+ ∠ABC = 180
∠ABC = 90
Each interior angle of a cyclic quadrilateral is of 90.Hence it is a rectangle.
A ray of light, which is parallel to the principal axis of the concave mirror, after reflection passes through the- a)Centre of curvature
- b)Focal length
- c)Pole of the mirror
- d)Principal focus of the mirror
Correct answer is option 'D'. Can you explain this answer?
A ray of light, which is parallel to the principal axis of the concave mirror, after reflection passes through the
a)
Centre of curvature
b)
Focal length
c)
Pole of the mirror
d)
Principal focus of the mirror
|
|
Vikas Kumar answered |
An incident ray which passes through the focus of the mirror is reflected parallel to the principal axis. An incident ray which passes through the centre of curvature of the mirror is reflected back along its own path (since it is normally incident on the mirror).
In the given figure, PT is tangent to the circle with centre O. If OT = 6 cm and OP = 10 cm then the length of tangent PT is 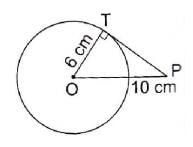
- a)6 cm
- b)15 cm
- c)18 cm
- d)8 cm
Correct answer is option 'D'. Can you explain this answer?
In the given figure, PT is tangent to the circle with centre O. If OT = 6 cm and OP = 10 cm then the length of tangent PT is

a)
6 cm
b)
15 cm
c)
18 cm
d)
8 cm

|
Learning Education answered |
In right triangle PTO By using Pythagoras theorem,
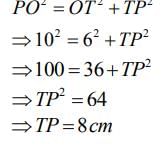
PO2 = OT2 + TP2
⇒ 102 = 62 + TP2
⇒ TP2 = 100 - 36
⇒ TP2 = 64
⇒ TP = 8
A ray of light passes through the focus of the mirror. After reflection, it- a)becomes parallel to the principal axis.
- b)Passes between the pole and focus of the mirror.
- c)goes through the pole of the mirror.
- d)goes through the centre of curvature.
Correct answer is option 'A'. Can you explain this answer?
A ray of light passes through the focus of the mirror. After reflection, it
a)
becomes parallel to the principal axis.
b)
Passes between the pole and focus of the mirror.
c)
goes through the pole of the mirror.
d)
goes through the centre of curvature.
|
|
Gaurav Kumar answered |
A ray which is parallel to the principal axis after reflection from mirror will always pass through principal focus. The distance between principal focus and pole is known as focal length and is half the centre of curvature of the mirror.
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is a:- a)rectangle
- b)square
- c)parallelogram
- d)cyclic quadrilateral
Correct answer is option 'D'. Can you explain this answer?
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is a:
a)
rectangle
b)
square
c)
parallelogram
d)
cyclic quadrilateral
|
|
Tejas Devarajan answered |
Cyclic quadrilaterals do not any definite rules unlike IIgram .The only rule that applies hear is that opp angles are supplementary.Hence it would'n matter if the angle bisectors form a quadrilateral
In the New Cartesian Sign Convention, which distance is considered positive?- a)Distance measured to the left of the mirror
- b)Distance measured above the principal axis
- c)Distance measured below the principal axis
- d)Distance measured to the left of the lens
Correct answer is option 'B'. Can you explain this answer?
In the New Cartesian Sign Convention, which distance is considered positive?
a)
Distance measured to the left of the mirror
b)
Distance measured above the principal axis
c)
Distance measured below the principal axis
d)
Distance measured to the left of the lens

|
Kamna Science Academy answered |
According to the New Cartesian Sign Convention, distances measured above the principal axis are taken as positive, while those below it are taken as negative. Distances measured to the right of the mirror are positive, and those to the left are negative.
For a spherical mirror with a focal length of 12 cm, what is the radius of curvature?- a)6 cm
- b)12 cm
- c)24 cm
- d)36 cm
Correct answer is option 'C'. Can you explain this answer?
For a spherical mirror with a focal length of 12 cm, what is the radius of curvature?
a)
6 cm
b)
12 cm
c)
24 cm
d)
36 cm

|
Kds Coaching answered |
The focal length (f) and radius of curvature (R) of a spherical mirror are related by the equation:
R = 2f
Given:
f = 12 cm
Calculate the radius of curvature:
R = 2 × 12 cm
R = 24 cm
Thus, the correct answer is:C: 24 cm
R = 2f
Given:
f = 12 cm
Calculate the radius of curvature:
R = 2 × 12 cm
R = 24 cm
Thus, the correct answer is:C: 24 cm
For spherical mirrors- a)Both laws of reflection are valid
- b)Only first law is valid
- c)Only second law is valid
- d)Laws of reflection are not valid
Correct answer is option 'A'. Can you explain this answer?
For spherical mirrors
a)
Both laws of reflection are valid
b)
Only first law is valid
c)
Only second law is valid
d)
Laws of reflection are not valid
|
|
Divyanshi Sharma Sharma answered |
Because spherical mirrors are two types first is concave and second is convex in first angle of reflection is equal to the angle of incidence and incidence angle ,reflected angle and normal ray all lie in same plane
To determine focal length of a concave mirror a student obtains the image of a well lit distant object on a screen. To determine the focal length of the given concave mirror he needs to measure the distance between:- a)Mirror and the object
- b)Cannot be determined
- c)Mirror and the screen
- d)Screen and the object
Correct answer is option 'C'. Can you explain this answer?
To determine focal length of a concave mirror a student obtains the image of a well lit distant object on a screen. To determine the focal length of the given concave mirror he needs to measure the distance between:
a)
Mirror and the object
b)
Cannot be determined
c)
Mirror and the screen
d)
Screen and the object
|
|
Rahul Kapoor answered |
The distance between mirror and the screen will give the focal length of the mirror as the mirror focuses the light on the screen.
An inverted image can be seen by using a convex mirror under what circumstances?- a)When the distance of the object from the mirror is equal to the focal length of the mirror.
- b)When the object is placed at infinity
- c)Under no circumstances
- d)When the object is at a distance equal to the radius of curvature of the mirror
Correct answer is option 'C'. Can you explain this answer?
An inverted image can be seen by using a convex mirror under what circumstances?
a)
When the distance of the object from the mirror is equal to the focal length of the mirror.
b)
When the object is placed at infinity
c)
Under no circumstances
d)
When the object is at a distance equal to the radius of curvature of the mirror
|
|
Krishna Iyer answered |
The image formed by a convex mirror is always virtual and erect irrespective of the position of the object.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q such that OQ = 12 cm. Length PQ is- a)12 cm
- b)13 cm
- c)8.5 cm
- d)√119 cm
Correct answer is option 'D'. Can you explain this answer?
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q such that OQ = 12 cm. Length PQ is
a)
12 cm
b)
13 cm
c)
8.5 cm
d)
√119 cm

|
Kds Coaching answered |
In the given problem, PQ is a tangent to the circle at point P, and OP is the radius to the point of tangency. By the property of tangents, OP is perpendicular to PQ, i.e., OP ⟂ PQ.
Given:
- Radius, OP = 5 cm
- OQ = 12 cm
Since OP ⟂ PQ, triangle OPQ is a right-angled triangle with the right angle at P.
Applying the Pythagorean theorem in triangle OPQ:
OQ² = OP² + PQ²
Substituting the known values:
12² = 5² + PQ²
144 = 25 + PQ²
PQ² = 144 - 25 = 119
Therefore, PQ = √119 cm.
AB is a chord of the circle and AOC is its diameter such that angle ACB = 50°. If AT is the tangent to the circle at the point A, then BAT is equal to- a) 65°
- b) 60°
- c)50°
- d)40°
Correct answer is option 'C'. Can you explain this answer?
AB is a chord of the circle and AOC is its diameter such that angle ACB = 50°. If AT is the tangent to the circle at the point A, then BAT is equal to
a)
65°
b)
60°
c)
50°
d)
40°

|
Kds Coaching answered |
Answer: (c) 50°
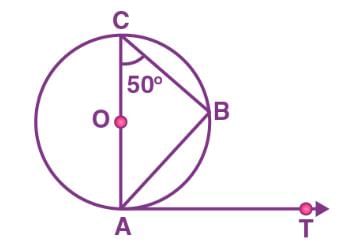

∠ABC = 90° (angle in Semicircle is right angle)
In ∆ACB
∠A + ∠B + ∠C = 180°
∠A = 180° – (90° + 50°)
∠A = 40°
Or ∠OAB = 40°
Therefore, ∠BAT = 90° – 40° = 50°
In ∆ACB
∠A + ∠B + ∠C = 180°
∠A = 180° – (90° + 50°)
∠A = 40°
Or ∠OAB = 40°
Therefore, ∠BAT = 90° – 40° = 50°
An object 2 cm tall is placed 10 cm in front of a concave mirror with a focal length of 5 cm. What is the size of the image?
- a)4 cm
- b)-4 cm
- c)-2 cm
- d)2 cm
Correct answer is option 'C'. Can you explain this answer??
An object 2 cm tall is placed 10 cm in front of a concave mirror with a focal length of 5 cm. What is the size of the image?
a)
4 cm
b)
-4 cm
c)
-2 cm
d)
2 cm
|
|
Abhinav joshi answered |
Concave Mirror Basics
Concave mirrors converge light rays, and their properties can be analyzed using the mirror formula:
1/f = 1/v + 1/u, where:
- f = focal length
- v = image distance
- u = object distance
Given Data
- Object height (h_o) = 2 cm
- Object distance (u) = -10 cm (negative as per sign convention)
- Focal length (f) = -5 cm (negative for concave mirrors)
Finding the Image Distance (v)
Using the mirror formula:
1/f = 1/v + 1/u
Substituting the values:
1/(-5) = 1/v + 1/(-10)
This simplifies to:
-1/5 = 1/v - 1/10
Finding a common denominator (10v):
-2v = -2 + v
Rearranging gives:
3v = 10
So, v = 10/3 cm or approximately 3.33 cm.
Determining Image Height (h_i)
To find the image height, we use the magnification formula:
Magnification (m) = h_i/h_o = -v/u
Substituting the values:
m = - (10/3) / (-10) = 1/3
Now, calculate the image height:
h_i = m * h_o = (1/3) * 2 cm = 2/3 cm or approximately 0.67 cm.
Since the image is inverted, the final image height is -2/3 cm, but we typically state sizes as positive values.
Conclusion
The image size is approximately 2 cm, which means for the given options, the correct answer is option 'c) -2 cm', indicating that the image is inverted and reduced in height.
Concave mirrors converge light rays, and their properties can be analyzed using the mirror formula:
1/f = 1/v + 1/u, where:
- f = focal length
- v = image distance
- u = object distance
Given Data
- Object height (h_o) = 2 cm
- Object distance (u) = -10 cm (negative as per sign convention)
- Focal length (f) = -5 cm (negative for concave mirrors)
Finding the Image Distance (v)
Using the mirror formula:
1/f = 1/v + 1/u
Substituting the values:
1/(-5) = 1/v + 1/(-10)
This simplifies to:
-1/5 = 1/v - 1/10
Finding a common denominator (10v):
-2v = -2 + v
Rearranging gives:
3v = 10
So, v = 10/3 cm or approximately 3.33 cm.
Determining Image Height (h_i)
To find the image height, we use the magnification formula:
Magnification (m) = h_i/h_o = -v/u
Substituting the values:
m = - (10/3) / (-10) = 1/3
Now, calculate the image height:
h_i = m * h_o = (1/3) * 2 cm = 2/3 cm or approximately 0.67 cm.
Since the image is inverted, the final image height is -2/3 cm, but we typically state sizes as positive values.
Conclusion
The image size is approximately 2 cm, which means for the given options, the correct answer is option 'c) -2 cm', indicating that the image is inverted and reduced in height.
What determines the position of the image of a point object formed by a spherical mirror?- a)The size of the mirror
- b)The color of the object
- c)The material of the mirror
- d)The intersection of reflected rays
Correct answer is option 'D'. Can you explain this answer?
What determines the position of the image of a point object formed by a spherical mirror?
a)
The size of the mirror
b)
The color of the object
c)
The material of the mirror
d)
The intersection of reflected rays

|
Elite Coaching Classes answered |
The position of the image of a point object formed by a spherical mirror is determined by the intersection of at least two reflected rays. These rays help locate the image of the object, showcasing the principles of reflection in optics.
In fig, O is the centre of the circle. PQ is tangent to the circle and secant PAB passes through the centre O. If PQ = 5 cm and PA = 1 cm, then the radius of the circle is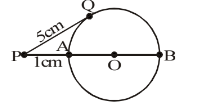
- a)8 cm
- b)12 cm
- c)10 cm
- d)6 cm
Correct answer is option 'B'. Can you explain this answer?
In fig, O is the centre of the circle. PQ is tangent to the circle and secant PAB passes through the centre O. If PQ = 5 cm and PA = 1 cm, then the radius of the circle is
a)
8 cm
b)
12 cm
c)
10 cm
d)
6 cm

|
Kds Coaching answered |
AOB is the diameter of the circle since POB passes through O.
Now PA is the segment of the secant POB outside the circle.
So, by the tangent–secant rule, the square of the tangent = secant segment × segment of the secant outside the circle when a secant and tangent to a circle are drawn from a point outside the circle.
PB × PA = PQ × PA ⇒ PB = (PQ²) / PA
PB = (25²) / 1 = 625 / 1 = 25 cm
The diameter AOB = PB - PA = (25 - 1) cm = 24 cm
The radius = x = AOB / 2 = 24 cm / 2 = 12 cm
Now PA is the segment of the secant POB outside the circle.
So, by the tangent–secant rule, the square of the tangent = secant segment × segment of the secant outside the circle when a secant and tangent to a circle are drawn from a point outside the circle.
PB × PA = PQ × PA ⇒ PB = (PQ²) / PA
PB = (25²) / 1 = 625 / 1 = 25 cm
The diameter AOB = PB - PA = (25 - 1) cm = 24 cm
The radius = x = AOB / 2 = 24 cm / 2 = 12 cm
Chapter doubts & questions for November Week 1 - Weekly Tests for Class 10 Preparation 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of November Week 1 - Weekly Tests for Class 10 Preparation in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup