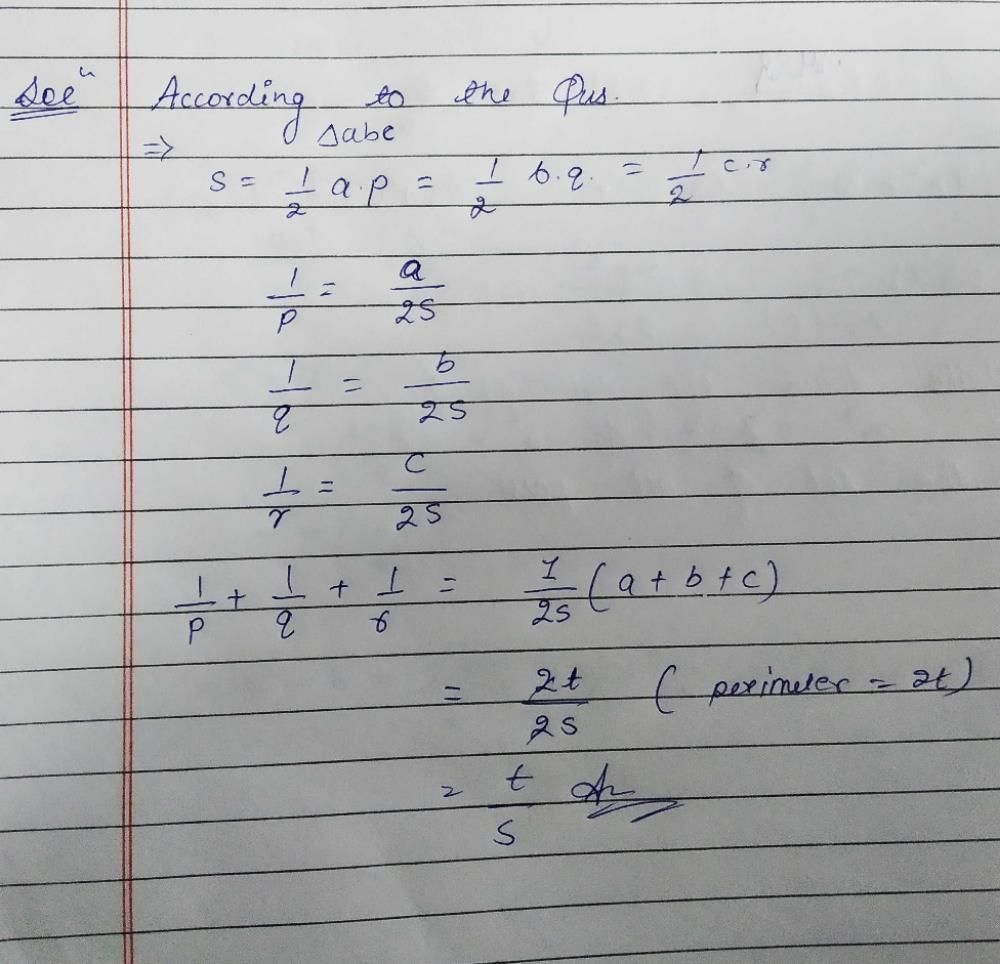All Exams >
JEE >
WBJEE Sample Papers, Section Wise & Full Mock Tests 2026 >
All Questions
All questions of 2012 for JEE Exam
Heat is produced at a rate given by H in a resistor when it is connected across a supply of voltage V. If now the resistance of the resistor is doubled and the supply voltage is made V/3 then the rate of production of heat in the resistor will be- a)H/18
- b)H/9
- c)6H
- d)18H
Correct answer is option 'A'. Can you explain this answer?
Heat is produced at a rate given by H in a resistor when it is connected across a supply of voltage V. If now the resistance of the resistor is doubled and the supply voltage is made V/3 then the rate of production of heat in the resistor will be
a)
H/18
b)
H/9
c)
6H
d)
18H
|
Rohit Jain answered |
The number of solutions of the equation log2(x2 + 2x –1) = 1 is- a)0
- b)1
- c)2
- d)3
Correct answer is option 'C'. Can you explain this answer?
The number of solutions of the equation log2(x2 + 2x –1) = 1 is
a)
0
b)
1
c)
2
d)
3
|
|
Arnab Choudhary answered |
x2 + 2x –1 = 2
x2 + 2x – 3=0
(x + 3) (x – 1) = 0;
x = 1, –3
The total number of injections (one-one into mappings) from {a1, a2, a3 , a4} to {b1,b2 ,b3 ,b4 ,b5 ,b6 , b7 is}- a)400
- b)420
- c)800
- d)840
Correct answer is option 'D'. Can you explain this answer?
The total number of injections (one-one into mappings) from {a1, a2, a3 , a4} to {b1,b2 ,b3 ,b4 ,b5 ,b6 , b7 is}
a)
400
b)
420
c)
800
d)
840
|
Ananya Das answered |
So total = 7 × 6 × 5 × 4 = 840 one-one into functions
Let f(x) = ax2 + bx + c, g(x) = px2 + qx + r, such that f(1) = g(1), f(2) = g(2) and f(3) – g(3) = 2. Then f(4) – g(4) is- a)4
- b)5
- c)6
- d)7
Correct answer is option 'C'. Can you explain this answer?
Let f(x) = ax2 + bx + c, g(x) = px2 + qx + r, such that f(1) = g(1), f(2) = g(2) and f(3) – g(3) = 2. Then f(4) – g(4) is
a)
4
b)
5
c)
6
d)
7
|
Ashwini Pillai answered |
= g(3).
From the given information, we can set up the following equations:
f(1) = a(1)2 + b(1) + c = p(1)2 + q(1) + r
f(2) = a(2)2 + b(2) + c = p(2)2 + q(2) + r
f(3) = a(3)2 + b(3) + c = p(3)2 + q(3) + r
Simplifying these equations, we get:
a + b + c = p + q + r (equation 1)
4a + 2b + c = 4p + 2q + r (equation 2)
9a + 3b + c = 9p + 3q + r (equation 3)
To find the values of a, b, and c, we can solve these equations simultaneously. Subtracting equation 1 from equation 2 and equation 3, we get:
3a + b = 3p + q (equation 4)
8a + 2b = 8p + 2q (equation 5)
Next, we subtract equation 4 from equation 5:
5a = 5p
Simplifying, we get:
a = p
Now we substitute this value of a into equation 4:
3p + b = 3p + q
Simplifying, we get:
b = q
Finally, we substitute the values of a and b into equation 1:
p + q + c = p + q + r
Simplifying, we get:
c = r
Therefore, we have found that a = p, b = q, and c = r. This means that f(x) = g(x) for all values of x.
From the given information, we can set up the following equations:
f(1) = a(1)2 + b(1) + c = p(1)2 + q(1) + r
f(2) = a(2)2 + b(2) + c = p(2)2 + q(2) + r
f(3) = a(3)2 + b(3) + c = p(3)2 + q(3) + r
Simplifying these equations, we get:
a + b + c = p + q + r (equation 1)
4a + 2b + c = 4p + 2q + r (equation 2)
9a + 3b + c = 9p + 3q + r (equation 3)
To find the values of a, b, and c, we can solve these equations simultaneously. Subtracting equation 1 from equation 2 and equation 3, we get:
3a + b = 3p + q (equation 4)
8a + 2b = 8p + 2q (equation 5)
Next, we subtract equation 4 from equation 5:
5a = 5p
Simplifying, we get:
a = p
Now we substitute this value of a into equation 4:
3p + b = 3p + q
Simplifying, we get:
b = q
Finally, we substitute the values of a and b into equation 1:
p + q + c = p + q + r
Simplifying, we get:
c = r
Therefore, we have found that a = p, b = q, and c = r. This means that f(x) = g(x) for all values of x.
Which of the following will show a negative deviation from Raoult’s law?- a)Acetone-benzene
- b)Acetone-ethanol
- c) Benzene-methanol
- d)Acetone-chloroform
Correct answer is option 'D'. Can you explain this answer?
Which of the following will show a negative deviation from Raoult’s law?
a)
Acetone-benzene
b)
Acetone-ethanol
c)
Benzene-methanol
d)
Acetone-chloroform
|
Tejas Verma answered |
Acetone – chloroform due to formation of intermolecular Hydrogen bonding
In a reversible chemical reaction at equilibrium, if the concentration of any one of the reactants is doubled, then the equilibrium constant will- a)also be doubled
- b)be halved
- c)remain the same
- d)become one-fourth
Correct answer is option 'C'. Can you explain this answer?
In a reversible chemical reaction at equilibrium, if the concentration of any one of the reactants is doubled, then the equilibrium constant will
a)
also be doubled
b)
be halved
c)
remain the same
d)
become one-fourth
|
|
Tejas Verma answered |
Equilibrium constant does not depend on conc. It is only a function of temperature
Identify the correct statement from the following in a chemical reaction.- a)The entropy always increases
- b)The change in entropy along with suitable change in enthalpy decides the fate of a reaction
- c)The enthalpy always decreases
- d)Both the enthalpy and the entropy remain constant
Correct answer is option 'B'. Can you explain this answer?
Identify the correct statement from the following in a chemical reaction.
a)
The entropy always increases
b)
The change in entropy along with suitable change in enthalpy decides the fate of a reaction
c)
The enthalpy always decreases
d)
Both the enthalpy and the entropy remain constant
|
Shahbaz Ahmad answered |
Option (b) is correct because the change in entropy Along with suitable change in enthalpy decides the fate of a reaction either it is spontaneous or non-spontaneous reaction .
From the top of a tower, 80 m high from the ground, a stone is thrown in the horizontal direction with a velocity of 8 ms–1. The stone reaches the ground after a time ‘t’ and falls at a distance of ‘d’ from the foot of the tower. Assuming g = 10 ms–2, the time t and distance d are given respectively by- a)6 s, 64 m
- b)6 s, 48 m
- c)4 s, 32 m
- d)4 s, 16 m
Correct answer is option 'C'. Can you explain this answer?
From the top of a tower, 80 m high from the ground, a stone is thrown in the horizontal direction with a velocity of 8 ms–1. The stone reaches the ground after a time ‘t’ and falls at a distance of ‘d’ from the foot of the tower. Assuming g = 10 ms–2, the time t and distance d are given respectively by
a)
6 s, 64 m
b)
6 s, 48 m
c)
4 s, 32 m
d)
4 s, 16 m
|
|
Poulomi Gupta answered |
time of flight (t) =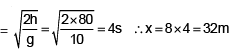 
If four distinct points (2k, 3k), (2, 0), (0, 3) (0, 0) lie on a circle, then- a)k < 0
- b)o < k < 1
- c)k = 1
- d)k > 1
Correct answer is option 'C'. Can you explain this answer?
If four distinct points (2k, 3k), (2, 0), (0, 3) (0, 0) lie on a circle, then
a)
k < 0
b)
o < k < 1
c)
k = 1
d)
k > 1
|
Nilotpal Ghosh answered |
Equation of circle x(x – 2) + y (y – 3) = 0
(2k, 3k) will satisfy
So, K = 1
(2k, 3k) will satisfy
So, K = 1
By passing excess Cl2(g) in boiling toluene, which one of the following compounds is exclusively formed?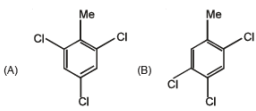
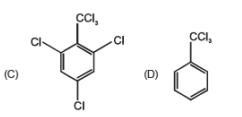
- a)A
- b)B
- c)C
- d)D
Correct answer is option 'D'. Can you explain this answer?
By passing excess Cl2(g) in boiling toluene, which one of the following compounds is exclusively formed?
a)
A
b)
B
c)
C
d)
D
|
|
Ashfaque Usmani answered |
In excess of Cl2 all the Hydrogen atom in CH3 are removed and chlorine take the place in toluene
On passing ‘C’ Ampere of current for time ‘t’ sec through 1 litre of 2 (M) CuSO4 solution (atomic weight of Cu = 63.5), the amount ‘m’ of Cu (in gm) deposited on cathode will be- a)m = Ct / (63.5 × 96500)
- b) m = Ct/ (31.25 × 96500)
- c)m = (C × 96500) / (31.25 × t)
- d)m = (31.25 × C × t) / 96500
Correct answer is option 'D'. Can you explain this answer?
On passing ‘C’ Ampere of current for time ‘t’ sec through 1 litre of 2 (M) CuSO4 solution (atomic weight of Cu = 63.5), the amount ‘m’ of Cu (in gm) deposited on cathode will be
a)
m = Ct / (63.5 × 96500)
b)
m = Ct/ (31.25 × 96500)
c)
m = (C × 96500) / (31.25 × t)
d)
m = (31.25 × C × t) / 96500
|
Megha Ahuja answered |
1000 ml 2(M) CuSO4 ≡ 2(M) CuSO4 solution contains 2 moles Cu+2
Cu2 + 2 →Cu
2F 63.5g
2F 63.5g
q = c × t coulomb
or, 2 × 96500C
Which of the following is correct?- a)Evaporation of water causes an increase in disorder of the system
- b)Melting of ice causes a decrease in randomness of the system
- c)Condensation of steam causes an increase in disorder of the system
- d)There is practically no change in the randomness of the system when water is evaporated
Correct answer is option 'A'. Can you explain this answer?
Which of the following is correct?
a)
Evaporation of water causes an increase in disorder of the system
b)
Melting of ice causes a decrease in randomness of the system
c)
Condensation of steam causes an increase in disorder of the system
d)
There is practically no change in the randomness of the system when water is evaporated
|
Dishani Datta answered |
Evaparation increases randomness as liquid water is converted to water vapours.
A Wheatstone bridge has the resistances 10 Ω , 10 Ω , 10Ω and 30 Ω in its four arms. What resistance joined in parallel to the 30 resistance will bring it to the balanced condition?- a)2Ω
- b)5Ω
- c)10Ω
- d)15Ω
Correct answer is option 'D'. Can you explain this answer?
A Wheatstone bridge has the resistances 10 Ω , 10 Ω , 10Ω and 30 Ω in its four arms. What resistance joined in parallel to the 30 resistance will bring it to the balanced condition?
a)
2Ω
b)
5Ω
c)
10Ω
d)
15Ω
|
|
Kiran Nair answered |
for a balanced bridge. R = 10 Ω
The stability of Me2C=CH2 is more than that of MeCH2CH = CH2 due to- a)inductive effect of the Me group
- b) resonance effect of the Me group
- c)hyperconjugative effect of the Me group
- d)resonance as well as inductive effect of the Me group
Correct answer is option 'C'. Can you explain this answer?
The stability of Me2C=CH2 is more than that of MeCH2CH = CH2 due to
a)
inductive effect of the Me group
b)
resonance effect of the Me group
c)
hyperconjugative effect of the Me group
d)
resonance as well as inductive effect of the Me group
|
Charvi Chopra answered |
Me2C = CH2 is more stable than MeCH2CH = CH2 due to hyperconjugative effect.
A straight line through the point of intersection of the lines x + 2y = 4 and 2x + y = 4 meets the coordinate axes at A and B. The locus of the midpoint of AB is- a)3(x + y) = 2xy
- b)2(x + y) = 3xy
- c)2(x + y) = xy
- d)x + y = 3xy
Correct answer is option 'B'. Can you explain this answer?
A straight line through the point of intersection of the lines x + 2y = 4 and 2x + y = 4 meets the coordinate axes at A and B. The locus of the midpoint of AB is
a)
3(x + y) = 2xy
b)
2(x + y) = 3xy
c)
2(x + y) = xy
d)
x + y = 3xy
|
Deepika Chavan answered |
Point of intersection of given lines x = 4/3, y = 4/3
The remainder obtained when 1!+2!+...+95! is divided by 15 is- a)14
- b)3
- c)1
- d)0
Correct answer is option 'B'. Can you explain this answer?
The remainder obtained when 1!+2!+...+95! is divided by 15 is
a)
14
b)
3
c)
1
d)
0
|
Ritika Mehta answered |
Starting from 5! all the other numbers are divisible by 15 since 15 will be a factor So 1! + 2! + 3! + 4! = 1 + 2 + 6 + 24 = 33 So the remainder on dividing 33 by 15 is 3.
When a certain metal surface is illuminated with light of frequency ν , the stopping potential for photoelectric current is νo When the same surface is illuminated by light of frequency v/2 the stopping potential is v0/4 The threshold frequency for photoelectric emission is- a)v/6
- b)v/3
- c)2v/3
- d)4v/3
Correct answer is option 'B'. Can you explain this answer?
When a certain metal surface is illuminated with light of frequency ν , the stopping potential for photoelectric current is νo When the same surface is illuminated by light of frequency v/2 the stopping potential is v0/4 The threshold frequency for photoelectric emission is
a)
v/6
b)
v/3
c)
2v/3
d)
4v/3
|
Parth Yadav answered |
solving equation (1) and (2) ,v/3
The line x = 2y intersects the ellipse x2/4 + y2 = 1 at the points P and Q. The equation of the circle with PQ as diameter is- a)x2 + y2 = 1/2
- b)x2 + y2 = 1
- c)x2 + y2 = 2
- d)x2 + y2 = 5/2
Correct answer is option 'D'. Can you explain this answer?
The line x = 2y intersects the ellipse x2/4 + y2 = 1 at the points P and Q. The equation of the circle with PQ as diameter is
a)
x2 + y2 = 1/2
b)
x2 + y2 = 1
c)
x2 + y2 = 2
d)
x2 + y2 = 5/2
|
|
Srestha Iyer answered |
Solving the given equations then common points are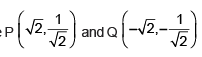 
Eqn. of Circle PQ as
diameter
diameter
then the value of the determinant of Q is equal to
Equal weights of CH4 and H2 are mixed in an empty container at 25oC. The fraction of the total pressure exerted by H2 is- a)1/9
- b)1/2
- c)8/9
- d)16/17
Correct answer is option 'C'. Can you explain this answer?
Equal weights of CH4 and H2 are mixed in an empty container at 25oC. The fraction of the total pressure exerted by H2 is
a)
1/9
b)
1/2
c)
8/9
d)
16/17
|
|
Nitin Gupta answered |
Let equal weights be w g.
Partial pressure = mole fraction × Total pressure
PH2 = 8/9 x Total pressure
The number of real values of for which the system of equationsx + 3y+5z = αx
5x+y+3z =α y
3x+5y+z = αz- a)1
- b)2
- c)4
- d)6
Correct answer is option 'A'. Can you explain this answer?
The number of real values of for which the system of equations
x + 3y+5z = αx
5x+y+3z =α y
3x+5y+z = αz
5x+y+3z =α y
3x+5y+z = αz
a)
1
b)
2
c)
4
d)
6
|
|
Sneha Sengupta answered |
Understanding the System of Equations
- Given system of equations:
1. x + 3y + 5z = α
2. 5x + y + 3z = α
3. 3x + 5y + z = α
Analysis of the System
- To find the number of real values of α for which the system has a solution, we need to analyze the system of equations.
- We can represent the system in matrix form as AX = B, where A is the coefficient matrix, X is the variable matrix, and B is the constant matrix.
Determinant of Coefficient Matrix
- The determinant of the coefficient matrix A is given by |A| = -144.
- If |A| ≠ 0, then the system has a unique solution for any value of α.
Calculating the Determinant
- Since |A| ≠ 0, the system of equations has a unique solution for any value of α.
- Therefore, the number of real values of α for which the system has a solution is 1.
Therefore, the correct answer is option 'A'.
A box of mass 2 kg is placed on the roof of a car. The box would remain stationary until the car attains a maximum acceleration. Coefficient of static friction between the box and the roof of the car is 0.2 and g = 10 ms–2.This maximum acceleration of the car, for the box to remain stationary, is- a)8 ms–2
- b)6 ms–2
- c)4 ms–2
- d)2 ms–2
Correct answer is option 'D'. Can you explain this answer?
A box of mass 2 kg is placed on the roof of a car. The box would remain stationary until the car attains a maximum acceleration. Coefficient of static friction between the box and the roof of the car is 0.2 and g = 10 ms–2.This maximum acceleration of the car, for the box to remain stationary, is
a)
8 ms–2
b)
6 ms–2
c)
4 ms–2
d)
2 ms–2
|
Naina Nambiar answered |
amax = μg =0.2x 10 = 2 m/s2
22320 cal of heat is supplied to 100 g of ice at 0oC If the latent heat of fusion of ice is 80 cal g–1 and latent heat of vaporization of water is 540 cal g–1, the final amount of water thus obtained and its temperature respectively are- a)8g, 100oC
- b)100 g, 90oC
- c)92g, 100oC
- d)82g, 100oC
Correct answer is option 'C'. Can you explain this answer?
22320 cal of heat is supplied to 100 g of ice at 0oC If the latent heat of fusion of ice is 80 cal g–1 and latent heat of vaporization of water is 540 cal g–1, the final amount of water thus obtained and its temperature respectively are
a)
8g, 100oC
b)
100 g, 90oC
c)
92g, 100oC
d)
82g, 100oC
|
|
Vaibhav Dasgupta answered |
total energy required to melt and boil at 100oC is
(Q)min = 8000 + 10000 = 18000 cal,
(Qrequired)min < Qgiven for amount of vapour 22320=18000+ m x 540
= m = 8 gm. temperature = 100oC and water remaining = 92 gm.
If 64, 27, 36 are the Pth , Qth and Rth terms of a G.P., then P + 2Q is equal to- a)R
- b)2R
- c)3 R
- d)4 R
Correct answer is option 'C'. Can you explain this answer?
If 64, 27, 36 are the Pth , Qth and Rth terms of a G.P., then P + 2Q is equal to
a)
R
b)
2R
c)
3 R
d)
4 R
|
|
Nisha Sen answered |
tP = 64,
tR = 36,
a . rP–1 = 64.............(1);
tQ = 27, a . rQ–1 = 27.............(2)
a . rR–1 = 36.............(3)
(2)2x (1)/(3)3 ; 2 Q + P = 3R
Which of the following is correct ?- a)radius of Ca2+ < Cl- < S2-
- b)radius of Cl- < S2- < Ca2+
- c) radius of S2- = Cl- = Ca2+
- d)radius of S2- < Cl- < Ca2+
Correct answer is option 'A'. Can you explain this answer?
Which of the following is correct ?
a)
radius of Ca2+ < Cl- < S2-
b)
radius of Cl- < S2- < Ca2+
c)
radius of S2- = Cl- = Ca2+
d)
radius of S2- < Cl- < Ca2+
|
|
Nishtha Rane answered |
Ca+2, S–2, Cl– are isoelectronic (consist of 18e–) and for isoelectronic species, ionic radii ∞e/z
A point moves in such a way that the difference of its distance from two points (8, 0) and (–8, 0) always remains 4.Then the locus of the point is- a)a circle
- b)a parabola
- c)an ellipse
- d)a hyperbola
Correct answer is option 'D'. Can you explain this answer?
A point moves in such a way that the difference of its distance from two points (8, 0) and (–8, 0) always remains 4.Then the locus of the point is
a)
a circle
b)
a parabola
c)
an ellipse
d)
a hyperbola
|
|
Pallabi Basak answered |
Let P(h, k) be the moving point
Conjugate equation of (i)
Two elements A and B with atomic numbers ZA and ZB are used to produce characteristic x–rays with frequencies A and B respectively. If ZA : ZB= 1 : 2, then vA : vB will be- a)1 :√2
- b)1 : 8
- c)4 : 1
- d)1 : 4
Correct answer is option 'D'. Can you explain this answer?
Two elements A and B with atomic numbers ZA and ZB are used to produce characteristic x–rays with frequencies A and B respectively. If ZA : ZB= 1 : 2, then vA : vB will be
a)
1 :√2
b)
1 : 8
c)
4 : 1
d)
1 : 4
|
|
Saranya Choudhary answered |
√v = a(z - b) , Ignoring screening effect (i.e. b=0)
The de Broglie wavelength of an electron moving with a velocity c/2 (c = velocity of light in vacuum) is equal to the wavelength of a photon. The ratio of the kinetic energies of electron and photon is- a)1 : 4
- b)1 : 2
- c)1 : 1
- d)2 : 1
Correct answer is option 'A'. Can you explain this answer?
The de Broglie wavelength of an electron moving with a velocity c/2 (c = velocity of light in vacuum) is equal to the wavelength of a photon. The ratio of the kinetic energies of electron and photon is
a)
1 : 4
b)
1 : 2
c)
1 : 1
d)
2 : 1
|
|
Sakshi Shah answered |
The equivalent weight of K2Cr2O7 in acidic medium is expressed in terms of its molecular weight (M) as- a)M/3
- b)M/4
- c)M/6
- d)M/7
Correct answer is option 'C'. Can you explain this answer?
The equivalent weight of K2Cr2O7 in acidic medium is expressed in terms of its molecular weight (M) as
a)
M/3
b)
M/4
c)
M/6
d)
M/7
|
Navya Hegde answered |
Because k2Cr2O7 loses 6 elections. equivalent weight is the mass divided by the no of electrons lost or gained. that is why M/6 is the correct answer.
A vehicle registration number consists of 2 letters of English alphabets followed by 4 digits, where the first digit is not zero. Then the total number of vehicles with distinct registration numbers is- a)262 x 104
- b)26P2 x 10 P4
- c)26 P2 x 9 x 10 P3
- d)262 x 9 x 103
Correct answer is option 'D'. Can you explain this answer?
A vehicle registration number consists of 2 letters of English alphabets followed by 4 digits, where the first digit is not zero. Then the total number of vehicles with distinct registration numbers is
a)
262 x 104
b)
26P2 x 10 P4
c)
26 P2 x 9 x 10 P3
d)
262 x 9 x 103
|
|
Khaja Moinuddin answered |
The coefficient of x10 in the expansion of 1 + (1 + x) + ......... + (1 + x)20 is- a)19C9
- b)20C10
- c)21C11
- d)22C12
Correct answer is option 'C'. Can you explain this answer?
The coefficient of x10 in the expansion of 1 + (1 + x) + ......... + (1 + x)20 is
a)
19C9
b)
20C10
c)
21C11
d)
22C12
|
|
Nisha Kaur answered |
1 + (1 + x) + ......... + (1 + x)20
A straight wire of length 2 m carries a current of 10 A. If this wire is placed in a uniform magnetic field of 0.15 T making an angle of 45o with the magnetic field, the applied force on the wire will be- a)1.5 N
- b)3 N
- c)3√2N
- d)3/√2 N
Correct answer is option 'D'. Can you explain this answer?
A straight wire of length 2 m carries a current of 10 A. If this wire is placed in a uniform magnetic field of 0.15 T making an angle of 45o with the magnetic field, the applied force on the wire will be
a)
1.5 N
b)
3 N
c)
3√2N
d)
3/√2 N
|
|
Nishtha Sengupta answered |
Under identical conditions, the SN1 reaction will occur most efficiently with- a)tert-butyl chloride
- b)1-chlorobutane
- c)2-methyl-1-chloropropane
- d)2-chlorobutane
Correct answer is option 'A'. Can you explain this answer?
Under identical conditions, the SN1 reaction will occur most efficiently with
a)
tert-butyl chloride
b)
1-chlorobutane
c)
2-methyl-1-chloropropane
d)
2-chlorobutane
|
|
Lavanya Menon answered |
Reactivity order for SN1 reaction in case of alkyl halide is 3°> 2°> 1°
Chapter doubts & questions for 2012 - WBJEE Sample Papers, Section Wise & Full Mock Tests 2026 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of 2012 - WBJEE Sample Papers, Section Wise & Full Mock Tests 2026 in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
WBJEE Sample Papers, Section Wise & Full Mock Tests 2026
3 videos|21 docs|54 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup