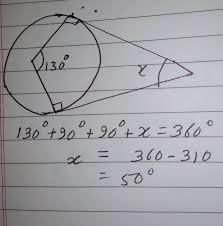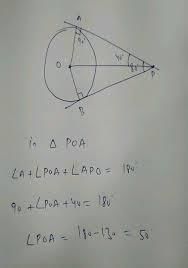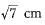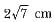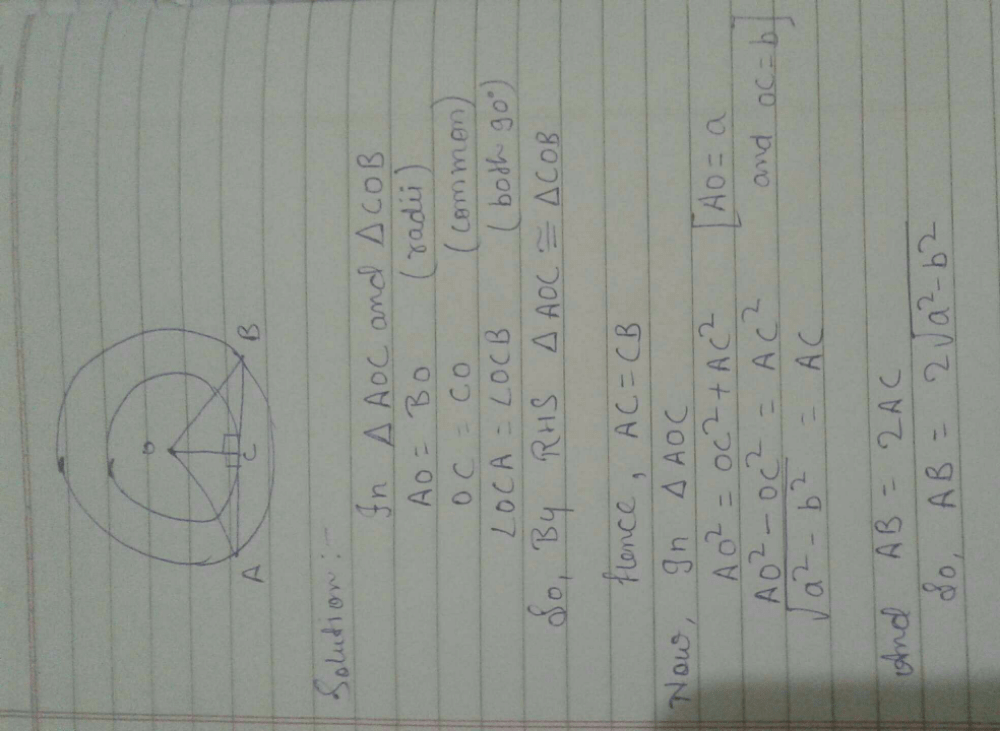All Exams >
Class 10 >
Mathematics Class 10 (Maharashtra SSC Board) >
All Questions
All questions of Circle for Class 10 Exam
In Fig. 8.6, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠PAB is equal to
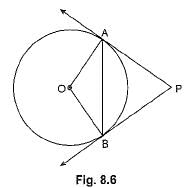
- a)35°
- b)65°
- c)40°
- d)70°
Correct answer is option 'B'. Can you explain this answer?
In Fig. 8.6, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠PAB is equal to
a)
35°
b)
65°
c)
40°
d)
70°
|
Crafty Classes answered |
In triangle PAB
∠A+∠B+∠P=180
x+x+50=180 [ if tangents are drawn from same point then they are equal so PAB is a isoceles triangle ]
2x=130
x=65
∠A+∠B+∠P=180
x+x+50=180 [ if tangents are drawn from same point then they are equal so PAB is a isoceles triangle ]
2x=130
x=65
A circle can pass through
- a)2 collinear points
- b)3 collinear points
- c)4 collinear points
- d)4 collinear points
Correct answer is option 'A'. Can you explain this answer?
A circle can pass through
a)
2 collinear points
b)
3 collinear points
c)
4 collinear points
d)
4 collinear points
|
Krishna Iyer answered |
The answer can be 2 collinear points as well. We have three collinear points. Join one point to the other two points and then draw the perpendicular bisector for both the lines
Join the perpendicular bisectors. The point is the centre of the circle. And a circle can be formed then. Also two points can form a circle as the two points joines becomes a diameter.
Join the perpendicular bisectors. The point is the centre of the circle. And a circle can be formed then. Also two points can form a circle as the two points joines becomes a diameter.
Option D : The number of circles which can pass through three given non-collinear points is exactly one.
So, A is the correct Option
In fig., two circles with centres A and B touch each other externally at k. The length of PQ (in cm) is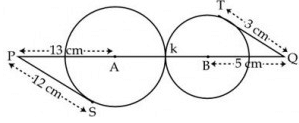
- a)24 cm
- b)20 cm
- c)27 cm
- d)18 cm
Correct answer is option 'C'. Can you explain this answer?
In fig., two circles with centres A and B touch each other externally at k. The length of PQ (in cm) is
a)
24 cm
b)
20 cm
c)
27 cm
d)
18 cm
|
Vikas Kumar answered |
Constructions - join AS and join BT.
Case 1 (triangle ASP)
We know, ∠ASP = 900 (radius is perpendicular to tangent at point of contact)
So, in triangle ASP,
AP2 = PS2 + AS2
=> 132 = 122 + AS2
=> 169 = 144 + AS2
+> AS2 = 169 - 144 = 25
=> AS = √25 = 5cm
Since AS is radius, AP = Ak = 5 cm.
Case 2 (triangle BTQ)
We know, ∠BTQ = 900 (radius is perpendicular to tangent at point of contact)
So, in triangle BTQ,
BQ2 = QT2 + BT2
= 52 = 32 + BT2
=> 25 = 9 + BT2
=> BT2 = 25 - 9 = 9
=> BT = √16 = 4cm
Since BT is radius, BT = Bk 4cm
Now, PQ = AP + Ak + Bk + BQ
=> PQ = 13 + 5 + 4 + 5
=> PQ = 27 cm
In the given figure, PQ is the tangent of the circle. Line segment PR intersects the circle at Nand R. PQ = 15 cm, PR = 25 cm, find PN: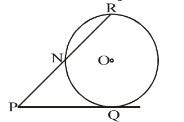
- a)15 cm
- b)10 cm
- c)9 cm
- d)6 cm
Correct answer is option 'C'. Can you explain this answer?
In the given figure, PQ is the tangent of the circle. Line segment PR intersects the circle at Nand R. PQ = 15 cm, PR = 25 cm, find PN:
a)
15 cm
b)
10 cm
c)
9 cm
d)
6 cm
|
Archana singh answered |
Given, PQ = 15 cm
PR = 25 cm
We know that, PQ² = PN × PR
15² = PN × 25
225 = PN × 25
PN = 9
15² = PN × 25
225 = PN × 25
PN = 9
Two parallel lines touch the circle at points A and B respectively, If area of the circle is 25πcm2, then AB is equal to- a)5 cm
- b)8 cm
- c)10 cm
- d)25 cm
Correct answer is option 'C'. Can you explain this answer?
Two parallel lines touch the circle at points A and B respectively, If area of the circle is 25πcm2, then AB is equal to
a)
5 cm
b)
8 cm
c)
10 cm
d)
25 cm
|
|
Vivek Rana answered |
Let radius of circle = R
∴ πR2 = 25π
⇒ R = 5cm
∴ Distance between two parallel tangents
= diameter = 2 x 5 = 10 cm.
∴ πR2 = 25π
⇒ R = 5cm
∴ Distance between two parallel tangents
= diameter = 2 x 5 = 10 cm.
The length of the tangent drawn from a point 8 cm away from the centre of a circle of radius 6 cm is- a)√7 cm
- b)2√7 cm
- c)10 cm
- d)5 cm
Correct answer is option 'B'. Can you explain this answer?
The length of the tangent drawn from a point 8 cm away from the centre of a circle of radius 6 cm is
a)
√7 cm
b)
2√7 cm
c)
10 cm
d)
5 cm
|
Pooja Shah answered |
Let P be the external point and PA and PB be the tangents and OA and OB be the radii.
So OP is the hypotenuse=8cm
Applying Pythagoras theorem,
H2 = P2 + B2
64 = AP2 + 36
AP =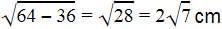
So OP is the hypotenuse=8cm
Applying Pythagoras theorem,
H2 = P2 + B2
64 = AP2 + 36
AP =
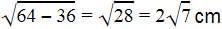
A tangent PA is drawn from an external point P to a circle of radius 3√2 cm such that the distance of the point P from O is 6 cm as shown figure. The value of ∠APO is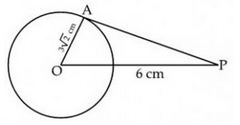
- a)30°
- b)60°
- c)45°
- d)75°
Correct answer is option 'C'. Can you explain this answer?
A tangent PA is drawn from an external point P to a circle of radius 3√2 cm such that the distance of the point P from O is 6 cm as shown figure. The value of ∠APO is
a)
30°
b)
60°
c)
45°
d)
75°
|
Sushil Kumar answered |
The correct answer is c
In right angled triangle, OAP
sin of angle APO = AO/OP = 1/root2
sin 45 = 1/root2
angle APO = 45 degree
In the given figure, AR=5cm, BR=4cm and AC =11cm. What is the length of BC?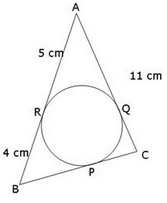
- a)6 cm
- b)10 cm
- c)4 cm
- d)8 cm
Correct answer is option 'B'. Can you explain this answer?
In the given figure, AR=5cm, BR=4cm and AC =11cm. What is the length of BC?
a)
6 cm
b)
10 cm
c)
4 cm
d)
8 cm
|
|
Vivek Rana answered |
Since the sides of the triangles are tangent to the circle. BR = BP,AR = AQ and CP = CQ
So, BP = 4cm and AQ = 5
CQ = 11-5 = 6 = CP
BC = BP + CP = 4 + 6 = 10 cm
So, BP = 4cm and AQ = 5
CQ = 11-5 = 6 = CP
BC = BP + CP = 4 + 6 = 10 cm
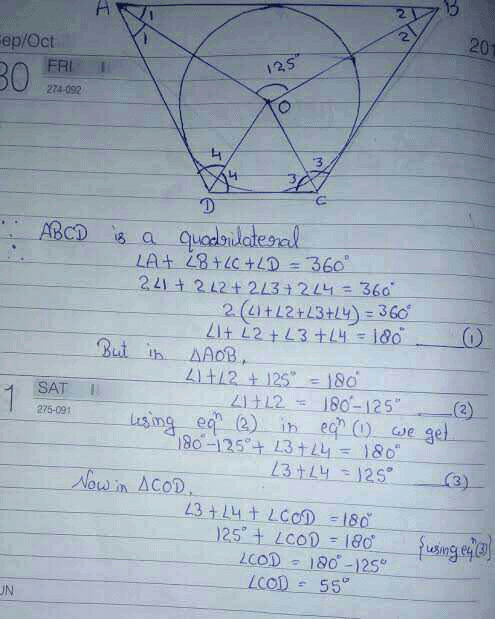
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB =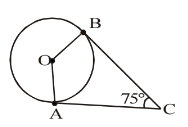
- a)75°
- b)85°
- c)95°
- d)105º
Correct answer is option 'D'. Can you explain this answer?
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB =
a)
75°
b)
85°
c)
95°
d)
105º
|
|
Kuldeep Kuldeep answered |
Solution:- The length of tangents drawn from an external point to the circle are equal.
In the figure, CA and CB are the tangents from external point of a circle and OA and OB are the two radius of a circle.
Draw a line OC, then you will get two triangles OAC and OBC.
In a ∆le AOC and ∆le BOC,
Angle OAC and OBC = 180 degree. Because, these are angles between the radii and tangents. So, there are two right angles.
The value for right angled triangle is 90 degree. Here, you can see both right angled triangle, so 90×2 = 180 degree.
Angle AOB = Angle OAC + Angle OBC - Angle ACB.
Given:- Angle ACB = 75 degree. , Angle OAC and OBC = 90 degree.
Angle AOB = 90 + 90 - 75.
Angle AOB = 180 -75.
Angle AOB =105 degree.
So, option d is correct friend.
In the figure, CA and CB are the tangents from external point of a circle and OA and OB are the two radius of a circle.
Draw a line OC, then you will get two triangles OAC and OBC.
In a ∆le AOC and ∆le BOC,
Angle OAC and OBC = 180 degree. Because, these are angles between the radii and tangents. So, there are two right angles.
The value for right angled triangle is 90 degree. Here, you can see both right angled triangle, so 90×2 = 180 degree.
Angle AOB = Angle OAC + Angle OBC - Angle ACB.
Given:- Angle ACB = 75 degree. , Angle OAC and OBC = 90 degree.
Angle AOB = 90 + 90 - 75.
Angle AOB = 180 -75.
Angle AOB =105 degree.
So, option d is correct friend.
A circle may have…….- a)2 tangent
- b)1 tangent
- c)Infinite tangents
- d)No tangent
Correct answer is option 'C'. Can you explain this answer?
A circle may have…….
a)
2 tangent
b)
1 tangent
c)
Infinite tangents
d)
No tangent
|
|
Vedashree V answered |
Because a tangent intersect only one point on circle so it can form infinite tangents
If figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P. If ∠POQ = 70o, then ∠TPQ is equal to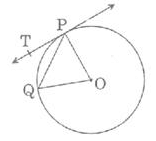
- a)45°
- b)5°
- c)35°
- d)70°
Correct answer is 'C'. Can you explain this answer?
If figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P. If ∠POQ = 70o, then ∠TPQ is equal to
a)
45°
b)
5°
c)
35°
d)
70°
|
Ananya Das answered |
POQ is an isosceles triangle because of 2 radii as sides. So by angle sum property, 2*angle OPQ=180-70=110
Angle OPQ=55°
Since Angle TPO is a right angle , because PT is a tangent,
Angle OPQ+Angle TPQ=90
Angle TPQ=90° - 55° = 35°
Angle OPQ=55°
Since Angle TPO is a right angle , because PT is a tangent,
Angle OPQ+Angle TPQ=90
Angle TPQ=90° - 55° = 35°
The length of the tangent drawn from a point 8 cm away from the centre of a circle, of radius 6 cm, is :- a)10 cm
- b)5 cm
- c)√7 cm
- d)2√7 cm
Correct answer is option 'D'. Can you explain this answer?
The length of the tangent drawn from a point 8 cm away from the centre of a circle, of radius 6 cm, is :
a)
10 cm
b)
5 cm
c)
√7 cm
d)
2√7 cm
|
Dronacharya Institute answered |
Since tangent is perpendicular to radius, the triangle so formed is a right angled triangle,
So using Pythagoras Theorem,
Line joining centre and And the point outside the circle is hypotenuse and tangent and radius are the two sides
H2=P2+B2
64=P2+36
P=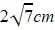
So using Pythagoras Theorem,
Line joining centre and And the point outside the circle is hypotenuse and tangent and radius are the two sides
H2=P2+B2
64=P2+36
P=
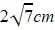
How many tangents can be drawn to a circle from a point in its interior?- a)One
- b)Two
- c)infinite
- d)None
Correct answer is option 'D'. Can you explain this answer?
How many tangents can be drawn to a circle from a point in its interior?
a)
One
b)
Two
c)
infinite
d)
None
|
Shiva Tiwari answered |
Tangent can only be drawn from outside.and from a point outside the circle only two tangent can be drawn
Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Circles" are available for CBSE Class 10 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 10 Mathematics (Maths)Q. A point P is 10 cm from the centre of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to- a)4 cm
- b)5 cm
- c)6 cm
- d)None of these.
Correct answer is option 'C'. Can you explain this answer?
Practice Test/Quiz or MCQ (Multiple Choice Questions) with Solutions of Chapter "Circles" are available for CBSE Class 10 Mathematics (Maths) and have been compiled as per the syllabus of CBSE Class 10 Mathematics (Maths)
Q. A point P is 10 cm from the centre of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to
a)
4 cm
b)
5 cm
c)
6 cm
d)
None of these.
|
|
Krishna Iyer answered |
ΔPTO is a right angled triangle at T ,where the tangent touches the circle.
So applying pythagoras theorem,
H2=P2+B2
102=B2+82
B=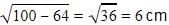
Radius is 6cm.
So applying pythagoras theorem,
H2=P2+B2
102=B2+82
B=
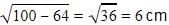
Radius is 6cm.
If the diagonals of a cyclic quadrilateral are equal, then the quadrilateral is- a)rhombus
- b)square
- c)rectangle
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If the diagonals of a cyclic quadrilateral are equal, then the quadrilateral is
a)
rhombus
b)
square
c)
rectangle
d)
none of these
|
|
Raghav Bansal answered |
Let ABCD be a cyclic quadrilateral having diagonals BD and AC, intersecting each other at point O.
(Consider BD as a chord)
∠BCD + ∠BAD = 180 (Cyclic quadrilateral)
∠BCD = 180− 90 = 90
(Considering AC as a chord)
∠ADC + ∠ABC = 180 (Cyclic quadrilateral)
90+ ∠ABC = 180
∠ABC = 90
Each interior angle of a cyclic quadrilateral is of 90.Hence it is a rectangle.
(Consider BD as a chord)
∠BCD + ∠BAD = 180 (Cyclic quadrilateral)
∠BCD = 180− 90 = 90
(Considering AC as a chord)
∠ADC + ∠ABC = 180 (Cyclic quadrilateral)
90+ ∠ABC = 180
∠ABC = 90
Each interior angle of a cyclic quadrilateral is of 90.Hence it is a rectangle.
From a point A, the length of a tangent to a circle is 8cm and distance of A from the circle is 10cm. The length of the diameter of the circle is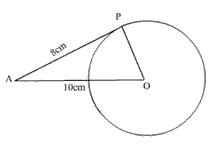
- a)6 cm
- b)12 cm
- c)16 cm
- d)14 cm
Correct answer is option 'B'. Can you explain this answer?
From a point A, the length of a tangent to a circle is 8cm and distance of A from the circle is 10cm. The length of the diameter of the circle is
a)
6 cm
b)
12 cm
c)
16 cm
d)
14 cm
|
|
Himaja Ammu answered |
Angle APO=90[radius is always perpendicular to the tangent)]
now by Pythagoras theorem AO^2=AP^2+OP^2
10^2=8^2+OP^2
OP^2=36
OP=6cm
here OP is nothing but the radius of circle
we know diameter is twice the radius...so
diameter=(2×6)=12 cm
now by Pythagoras theorem AO^2=AP^2+OP^2
10^2=8^2+OP^2
OP^2=36
OP=6cm
here OP is nothing but the radius of circle
we know diameter is twice the radius...so
diameter=(2×6)=12 cm
Number of tangents, that can be drawn to a circle, parallel to a given chord is- a)3
- b)Zero
- c)Infinite
- d)2
Correct answer is option 'D'. Can you explain this answer?
Number of tangents, that can be drawn to a circle, parallel to a given chord is
a)
3
b)
Zero
c)
Infinite
d)
2
|
Gaurav Kumar answered |
There are only two tangents that can be drawn parallel to a given chord. That is the tangents are drawn on either side of the chord so that both are parallel to the chord.
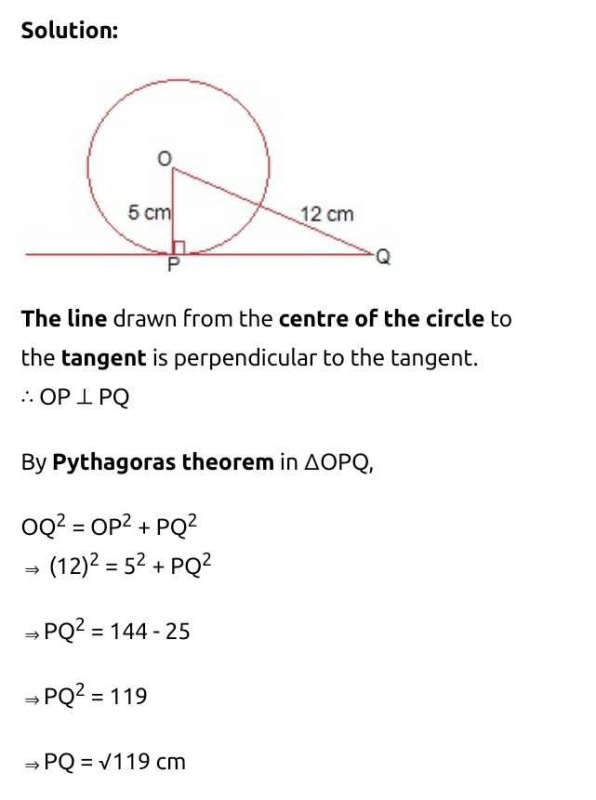
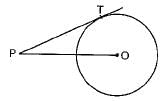
In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is
- a)25 cm
- b)26 cm
- c)24 cm
- d)10 cm
Correct answer is option 'D'. Can you explain this answer?
In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is
a)
25 cm
b)
26 cm
c)
24 cm
d)
10 cm
|
|
Vikram Kapoor answered |
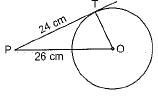
∵ OT is radius and PT is tangent
∴ OT ⊥ PT
Now, in ΔOTP,
OP2 = PT2 + OT2
⇒ 262 = 242 + OT2
⇒ 676 - 576 -OT2
⇒ 100 = OT2 ⇒ 10 cm = OT
The tangents drawn at the ends of a diameter of a circle are:- a)intersecting at a point inside the circle
- b)perpendicular
- c)intersecting at the centre of the circle
- d)parallel
Correct answer is option 'D'. Can you explain this answer?
The tangents drawn at the ends of a diameter of a circle are:
a)
intersecting at a point inside the circle
b)
perpendicular
c)
intersecting at the centre of the circle
d)
parallel
|
|
Rahul Kapoor answered |
Here AB is a diameter of the circle with centre O, two tangents PQ and RS drawn at points A and B respectively.
Radius will be perpendicular to these tangents.
Thus, OA ⊥ RS and OB ⊥ PQ
∠OAR = ∠OAS = ∠OBP = ∠OBQ = 90degree
Therefore,
∠OAR = ∠OBQ (Alternate interior angles)
∠OAS = ∠OBP (Alternate interior angles)
Since alternate interior angles are equal, lines PQ and RS will be parallel.
In the given figure, PT is tangent to the circle with centre O. If OT = 6 cm and OP = 10 cm then the length of tangent PT is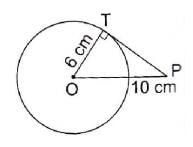 
- a)6 cm
- b)15 cm
- c)18 cm
- d)8 cm
Correct answer is option 'D'. Can you explain this answer?
In the given figure, PT is tangent to the circle with centre O. If OT = 6 cm and OP = 10 cm then the length of tangent PT is
a)
6 cm
b)
15 cm
c)
18 cm
d)
8 cm
|
Learning Education answered |
In right triangle PTO By using Pythagoras theorem,
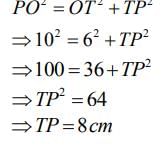
PO2 = OT2 + TP2
⇒ 102 = 62 + TP2
⇒ TP2 = 100 - 36
⇒ TP2 = 64
⇒ TP = 8
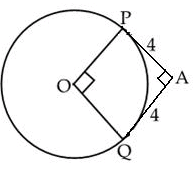
In the figure, the pair of tangents AP and AQ, drawn from an external point A to a circle with centre O, are perpendicular to each other and length of each tangent is 4 cm, then the radius of the circle is
- a)10 cm
- b)4 cm
- c)7.5 cm
- d)2.5 cm
Correct answer is option 'B'. Can you explain this answer?
In the figure, the pair of tangents AP and AQ, drawn from an external point A to a circle with centre O, are perpendicular to each other and length of each tangent is 4 cm, then the radius of the circle is
a)
10 cm
b)
4 cm
c)
7.5 cm
d)
2.5 cm
|
|
Arun Yadav answered |
Join OA.
Triangles OPA and OQA are congruent.
⇒∠PAO = ∠QAO = 45o
Tangent and radius are perpendicular at the point of contact.
∠OPA = 90o
⇒∠OAP = ∠AOP = 45o
⇒OP = AP = 4cm
So the radius of the circle is 4 cm.
PT is a tangent from an external point P and PAB is a secant. If PT = 6cm and PA = 3cm, then the length of PB is __- a)6
- b)36
- c)12
- d)2
Correct answer is option 'C'. Can you explain this answer?
PT is a tangent from an external point P and PAB is a secant. If PT = 6cm and PA = 3cm, then the length of PB is __
a)
6
b)
36
c)
12
d)
2
|
|
Rahul Kapoor answered |
We know that:
PT^2 = PA X PB
therfore PB = PT^2/PA = 36/3 = 12
ABC is a right triangle right angled at B such that BC = 6 cm and AB = 8 cm. The radius of its incircle is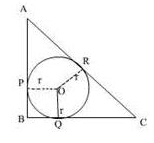
- a)3 cm
- b)8 cm
- c)2 cm
- d)5 cm
Correct answer is option 'C'. Can you explain this answer?
ABC is a right triangle right angled at B such that BC = 6 cm and AB = 8 cm. The radius of its incircle is
a)
3 cm
b)
8 cm
c)
2 cm
d)
5 cm
|
Coachify answered |
By pythagoras theorem ,
H2 = P2 + B2
=36 + 64=100
H=10
We have a square BPOQ so all sides are equal.
Since tangents from a point are equal in length
Let AP = AR = x
BP=BQ=y
RC = QC = z
x + y = 8
x = 8 - y
x + z = 10 ⇒ 8 - y + z = 10 ⇒ z = 2 + y
y + z = 6 ⇒ y + 2 + y = 6 ⇒ y = 2
x = 6, z= 4
Since BP = OQ = y = 2
H2 = P2 + B2
=36 + 64=100
H=10
We have a square BPOQ so all sides are equal.
Since tangents from a point are equal in length
Let AP = AR = x
BP=BQ=y
RC = QC = z
x + y = 8
x = 8 - y
x + z = 10 ⇒ 8 - y + z = 10 ⇒ z = 2 + y
y + z = 6 ⇒ y + 2 + y = 6 ⇒ y = 2
x = 6, z= 4
Since BP = OQ = y = 2
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is a:- a)rectangle
- b)square
- c)parallelogram
- d)cyclic quadrilateral
Correct answer is option 'D'. Can you explain this answer?
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is a:
a)
rectangle
b)
square
c)
parallelogram
d)
cyclic quadrilateral
|
|
Tejas Devarajan answered |
Cyclic quadrilaterals do not any definite rules unlike IIgram .The only rule that applies hear is that opp angles are supplementary.Hence it would'n matter if the angle bisectors form a quadrilateral
C (O, r1) and C (O, r2) are two concentric circles with r1 > r2. AB is a chord of C (O, r1) touching C (O, r2) at C then- a)AB = r1
- b)AB = r2
- c)AC = BC
- d) AB = r1 + r2
Correct answer is option 'C'. Can you explain this answer?
C (O, r1) and C (O, r2) are two concentric circles with r1 > r2. AB is a chord of C (O, r1) touching C (O, r2) at C then
a)
AB = r1
b)
AB = r2
c)
AC = BC
d)
AB = r1 + r2
|
Arjun Dasgupta answered |
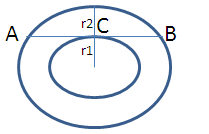
Given that AB is chord of bigger circle and it is tangent to a smaller circle touching at C.
Then AB is perpendicular to OC. C is mid point of AB then AC = BC.
The angle between two tangents drawn from an external point to a circle is 110°. The angle subtended at the centre by the segments joining the points of contact to the centre of circle is:- a)70°
- b)90°
- c)55°
- d)110°
Correct answer is option 'A'. Can you explain this answer?
The angle between two tangents drawn from an external point to a circle is 110°. The angle subtended at the centre by the segments joining the points of contact to the centre of circle is:
a)
70°
b)
90°
c)
55°
d)
110°
|
Divisha mehta answered |
Degrees.
This is a common result in geometry, known as the "angle between tangents theorem." It states that the angle between two tangents drawn from an external point to a circle is equal to the measure of the arc they intercept on the circle.
In this case, we know that the two tangents intersect an arc of measure 110 degrees on the circle. Therefore, the angle between the tangents is also 110 degrees.
This is a common result in geometry, known as the "angle between tangents theorem." It states that the angle between two tangents drawn from an external point to a circle is equal to the measure of the arc they intercept on the circle.
In this case, we know that the two tangents intersect an arc of measure 110 degrees on the circle. Therefore, the angle between the tangents is also 110 degrees.
A line that intersects a circle in exactly one point is called a- a)Diameter
- b)Tangent
- c)Radius
- d)Chord
Correct answer is option 'B'. Can you explain this answer?
A line that intersects a circle in exactly one point is called a
a)
Diameter
b)
Tangent
c)
Radius
d)
Chord
|
|
Aditya Kumar answered |
A TANGENT IS THE ONLY LINE WHICH INTERSECT CIRCLE AT ONLY ONE POINT.
A line that intersects a circle in two distinct points is called a- a)Tangent
- b)Chord
- c)Diameter
- d)Secant
Correct answer is option 'D'. Can you explain this answer?
A line that intersects a circle in two distinct points is called a
a)
Tangent
b)
Chord
c)
Diameter
d)
Secant
|
|
Krishna Iyer answered |
A chord is the actual line segment determined by these two points, that is, the interval on the secant whose ends are at these positions But a secant of a curve is a line that intersects the curve at a minimum of two distinct points. The difference is that the secant is not just limited to the circle it extends further.
A circle is inscribed in a ΔABC having AB= 10cm, BC = 12cm and CA = 8cm and touching these sides at D, E, F respectively. The lengths of AD, BE and CF will be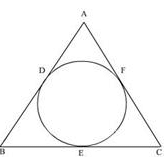
- a)AD = 4cm, BE = 6cm, CF = 8cm
- b)AD = 5cm, BE = 9cm, CF = 4cm
- c)AD = 3cm, BE = 7cm, CF = 5cm
- d)AD = 2cm, BE = 6cm, CF = 7cm
Correct answer is option 'C'. Can you explain this answer?
A circle is inscribed in a ΔABC having AB= 10cm, BC = 12cm and CA = 8cm and touching these sides at D, E, F respectively. The lengths of AD, BE and CF will be
a)
AD = 4cm, BE = 6cm, CF = 8cm
b)
AD = 5cm, BE = 9cm, CF = 4cm
c)
AD = 3cm, BE = 7cm, CF = 5cm
d)
AD = 2cm, BE = 6cm, CF = 7cm
|
Tanishka Gupta answered |
Read the following text and answer the following question on the basis of the same:A farmer has a field in the shape of triangle with AB = 13 cm, BC = 14 cm and AE = 7 cm. He wants to leave a space in the form of a circular field for growing wheat and the remaining for growing vegetables.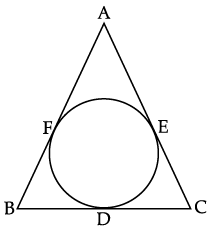
Q. The measure of CE + CD is:- a)15 cm
- b)16 cm
- c)10 cm
- d)14 cm
Correct answer is option 'B'. Can you explain this answer?
Read the following text and answer the following question on the basis of the same:
A farmer has a field in the shape of triangle with AB = 13 cm, BC = 14 cm and AE = 7 cm. He wants to leave a space in the form of a circular field for growing wheat and the remaining for growing vegetables.
a)
15 cm
b)
16 cm
c)
10 cm
d)
14 cm
|
|
Swati Malkani answered |
16 cm.
Segment joining the points of contact of two parallel tangents- a)may or may not pass through the centre.
- b)will pass through the centre.
- c)will not pass through the centre.
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Segment joining the points of contact of two parallel tangents
a)
may or may not pass through the centre.
b)
will pass through the centre.
c)
will not pass through the centre.
d)
none of these
|
Omprakash Meena answered |
Because that is diameter which definitely pass through the centre
What is the distance between two parallel tangents of a circle of the radius 4 cm?- a)8 cm
- b)4 cm
- c)2 cm
- d)6 cm
Correct answer is option 'A'. Can you explain this answer?
What is the distance between two parallel tangents of a circle of the radius 4 cm?
a)
8 cm
b)
4 cm
c)
2 cm
d)
6 cm
|
|
El Cerebro answered |
Let O is the centre of the circle. l and m are two parallel tangents of the circle.
Radius of the circle = 4cm
Distance between two parallel tangents
= AB
= OA + OB
= 4cm + 4cm
= 8cm
Thus, distance between the parallel tangents land m is 8cm.
Radius of the circle = 4cm
Distance between two parallel tangents
= AB
= OA + OB
= 4cm + 4cm
= 8cm
Thus, distance between the parallel tangents land m is 8cm.
Chapter doubts & questions for Circle - Mathematics Class 10 (Maharashtra SSC Board) 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Circle - Mathematics Class 10 (Maharashtra SSC Board) in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
Mathematics Class 10 (Maharashtra SSC Board)
26 videos|208 docs|38 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup