All Exams >
UGC NET >
3 Months Preparation for UGC NET Paper 1 >
All Questions
All questions of Percentages for UGC NET Exam
The price of an article is increased by 16 (2/3)%. By what percentage the customer should reduce his consumption such the expenditure is increased by only 12%?- a)5%
- b)6%
- c)7%
- d)4%
- e)Not Attempted
Correct answer is option 'D'. Can you explain this answer?
The price of an article is increased by 16 (2/3)%. By what percentage the customer should reduce his consumption such the expenditure is increased by only 12%?
a)
5%
b)
6%
c)
7%
d)
4%
e)
Not Attempted

|
Elite Coaching Classes answered |
We know that
Product of price and consumption is equal to the expenditure
Let the original price of article be x units
According to the question,
Price is increased by 24%
New price of article = x + 16(2/3)% of x = 7x/6
Let the original consumption be y
Original expenditure = xy
Expenditure is increased by 12%
New expenditure = xy + (12/100) × xy = 28xy/25
New consumption = (New expenditure)/(New Price)
New consumption = (28xy/25)/(7x/6) = 24y/25
Decrease in consumption = (y) – (24y/25) = y/25
Required percentage = (y/25)/y × 100 = 4%
There were two candidates in an election, 10% of voters did not vote and 48 votes were found invalid. The winning candidate got 53% of all the voters in the list and won by 304 votes. Find the total number of votes enrolled.- a)1600
- b)1230
- c)4561
- d)1653
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
There were two candidates in an election, 10% of voters did not vote and 48 votes were found invalid. The winning candidate got 53% of all the voters in the list and won by 304 votes. Find the total number of votes enrolled.
a)
1600
b)
1230
c)
4561
d)
1653
e)
None of these

|
Elite Coaching Classes answered |
Let total number of votes be 100 units,
10% voters did not cast their vote
⇒ Votes polled = 90 units
The winning candidate got 53% of all the voters in the list and won by 304 votes,
⇒ Winning candidate got = 53 units votes
⇒ Other candidate got = 37 units votes
⇒ Difference in votes = 53 units votes - 37 units votes = 304 - 48 = 256 votes
⇒ 16 units = 256
∴ 100 units votes = 256/16 × 100 = 1600 votes
∴ Total number of voters = 1600.
In two successive years, 100 and 75 students of a school appeared at the final examination. Respectively 75 % and 60 % of them passed. The average rate of pass is:- a)68 4/7 %
- b)78 %
- c)80 %
- d)80 4/7 %
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
In two successive years, 100 and 75 students of a school appeared at the final examination. Respectively 75 % and 60 % of them passed. The average rate of pass is:
a)
68 4/7 %
b)
78 %
c)
80 %
d)
80 4/7 %
e)
None of these

|
Elite Coaching Classes answered |
Total candidates = (100 + 75) = 175
Total passed = (75/100 Ã- 100) + (60/100 Ã- 75)
= (75 + 45) = 120
Therefore Pass % = (120/175 Ã -100)%
= 480/7 % = 68 4/7 %
Total passed = (75/100 Ã- 100) + (60/100 Ã- 75)
= (75 + 45) = 120
Therefore Pass % = (120/175 Ã -100)%
= 480/7 % = 68 4/7 %
In a school, 40 % of the students play football and 50 % play cricket. If 18 % of the students play neither football nor cricket, the percentage of students playing both is- a)40 %
- b)32 %
- c)22 %
- d)8 %
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
In a school, 40 % of the students play football and 50 % play cricket. If 18 % of the students play neither football nor cricket, the percentage of students playing both is
a)
40 %
b)
32 %
c)
22 %
d)
8 %
e)
None of these

|
Elite Coaching Classes answered |
Let A = set of students who play football and
B = set of students play cricket.
Then n(A) = 40, n (B) = 50 and
n(A U B) = (100 - 18) = 82
n(A U B) = n(A) + n(B) “ n(A ∩ B)
n(A∩B) = n(A) + n(B) “ n(AUB) = (40 + 50 -82) = 8
Percentage of the students who play both = 8%
If the numerator of a fraction is increased by 140 % and the denominator is increased by 150 % the resultant fraction is 4/15 what is the original fraction?- a)3/5
- b)5/16
- c)2/9
- d)18
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
If the numerator of a fraction is increased by 140 % and the denominator is increased by 150 % the resultant fraction is 4/15 what is the original fraction?
a)
3/5
b)
5/16
c)
2/9
d)
18
e)
None of these

|
Elite Coaching Classes answered |
Let the original fraction be x/y.
Then new fraction
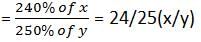
Then new fraction
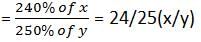
Therefore 24/25(x/y) = 4/15
⇒ x/y = (4/15 Ã - 25/24) = 5/18
Therefore Original Fraction = 5/18
⇒ x/y = (4/15 Ã - 25/24) = 5/18
Therefore Original Fraction = 5/18
Ankit scored 25% of the total marks and failed by 15 marks in the examination. Had he scored 55% of the total marks, he would have got 15 marks more than the passing marks. What is the passing mark in the examination?- a)40
- b)50
- c)35
- d)45
- e)Not Attempted
Correct answer is option 'A'. Can you explain this answer?
Ankit scored 25% of the total marks and failed by 15 marks in the examination. Had he scored 55% of the total marks, he would have got 15 marks more than the passing marks. What is the passing mark in the examination?
a)
40
b)
50
c)
35
d)
45
e)
Not Attempted

|
Elite Coaching Classes answered |
Let the total marks be 100x.
Passing marks = 25 x + 15 and 55 x - 15
25x + 15 = 55x - 15
30x = 30
x = 1
Hence, passing marks are 25 + 15 = 40.
In measuring the sides of a rectangle errors of 5 % and 3 % in excess are made. The error percent in the calculates area is- a)8. 35 %
- b)7.15 %
- c)8.15 %
- d)6. 25%
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
In measuring the sides of a rectangle errors of 5 % and 3 % in excess are made. The error percent in the calculates area is
a)
8. 35 %
b)
7.15 %
c)
8.15 %
d)
6. 25%
e)
None of these

|
Elite Coaching Classes answered |
Let length = x units and breadth = Y units
Then actual area = xy sq.units
Length shown = (105/100 Ã - x)units = 21x/20 units;
Breadth shown = (103/100 Ã - Y)
Calculated area = (21x/20 Ã - 103y/100)sq.units
Error = 2163xy/2000 sq.units
Error = (2163xy/2000 - xy)
Error = 163xy/2000
Error % = (163xy/2000 à - 1/xy à - 100)%
= 163/20 % = 8.15 %
Then actual area = xy sq.units
Length shown = (105/100 Ã - x)units = 21x/20 units;
Breadth shown = (103/100 Ã - Y)
Calculated area = (21x/20 Ã - 103y/100)sq.units
Error = 2163xy/2000 sq.units
Error = (2163xy/2000 - xy)
Error = 163xy/2000
Error % = (163xy/2000 à - 1/xy à - 100)%
= 163/20 % = 8.15 %
Two students appeared for an examination. One of them secured 22 marks more than the other and his marks were 55% of the sum of their marks. The marks obtained by them are _______.- a)121 and 99
- b)43 and 21
- c)58 and 36
- d)86 and 64
- e) None of these
Correct answer is option 'A'. Can you explain this answer?
Two students appeared for an examination. One of them secured 22 marks more than the other and his marks were 55% of the sum of their marks. The marks obtained by them are _______.
a)
121 and 99
b)
43 and 21
c)
58 and 36
d)
86 and 64
e)
None of these

|
Elite Coaching Classes answered |
Two students appeared for an examination. One of them secured 22
marks more than the other and his marks were 55% of the sum of
their marks
Let the students be A and B
Let the marks secured by B = x
Marks secured by A = x + 22
Sum of their marks of A & B = x + x + 22 = 2x + 22
Accoring to question,
Marks of A = 55% of the sum of marks
⇒ x + 22 = 0.55 × (2x + 22)
⇒ x + 22 = 1.1x + 12.1
⇒ 0.1x = 9.9
⇒ x = 9.9/0.1 = 99 marks
Marks secured by A = 99 + 22 = 121 marks
Therefore the correct answer is 121.
A fruit seller sells 45% of the oranges that he has along with one more orange to a customer. He then sells 20% of the remaining oranges and 2 more oranges to a second customer. He then sells 90% of the now remaining oranges to a third customer and is still left with 5 oranges. How many oranges did the fruit seller have initially?- a)121
- b)111
- c)100
- d)120
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A fruit seller sells 45% of the oranges that he has along with one more orange to a customer. He then sells 20% of the remaining oranges and 2 more oranges to a second customer. He then sells 90% of the now remaining oranges to a third customer and is still left with 5 oranges. How many oranges did the fruit seller have initially?
a)
121
b)
111
c)
100
d)
120
e)
None of these
|
|
Amelia Johnson answered |
To solve this problem, let's break it down step by step.
Step 1: Calculate the number of oranges the fruit seller had after selling to the first customer.
Let's assume the initial number of oranges the fruit seller had is x.
The fruit seller sells 45% of the oranges to the first customer, which is 0.45x.
He also sells one more orange to the customer, so the total number of oranges sold to the first customer is 0.45x + 1.
Therefore, the number of oranges remaining after the first sale is x - (0.45x + 1) = 0.55x - 1.
Step 2: Calculate the number of oranges the fruit seller had after selling to the second customer.
The fruit seller sells 20% of the remaining oranges to the second customer, which is 0.2(0.55x - 1).
He also sells two more oranges to the second customer, so the total number of oranges sold to the second customer is 0.2(0.55x - 1) + 2.
Therefore, the number of oranges remaining after the second sale is 0.55x - 1 - (0.2(0.55x - 1) + 2) = 0.35x - 3.
Step 3: Calculate the number of oranges the fruit seller had after selling to the third customer.
The fruit seller sells 90% of the remaining oranges to the third customer, which is 0.9(0.35x - 3).
Therefore, the number of oranges remaining after the third sale is 0.35x - 3 - 0.9(0.35x - 3) = 0.35x - 3 - 0.315x + 2.7 = 0.035x - 0.3.
Step 4: Set up an equation using the information from step 3 and solve for x.
According to the problem, the fruit seller is left with 5 oranges after the third sale. Therefore, we have the equation 0.035x - 0.3 = 5.
Solving this equation gives us x = 120.
Therefore, the fruit seller initially had 120 oranges, which is option D.
Step 1: Calculate the number of oranges the fruit seller had after selling to the first customer.
Let's assume the initial number of oranges the fruit seller had is x.
The fruit seller sells 45% of the oranges to the first customer, which is 0.45x.
He also sells one more orange to the customer, so the total number of oranges sold to the first customer is 0.45x + 1.
Therefore, the number of oranges remaining after the first sale is x - (0.45x + 1) = 0.55x - 1.
Step 2: Calculate the number of oranges the fruit seller had after selling to the second customer.
The fruit seller sells 20% of the remaining oranges to the second customer, which is 0.2(0.55x - 1).
He also sells two more oranges to the second customer, so the total number of oranges sold to the second customer is 0.2(0.55x - 1) + 2.
Therefore, the number of oranges remaining after the second sale is 0.55x - 1 - (0.2(0.55x - 1) + 2) = 0.35x - 3.
Step 3: Calculate the number of oranges the fruit seller had after selling to the third customer.
The fruit seller sells 90% of the remaining oranges to the third customer, which is 0.9(0.35x - 3).
Therefore, the number of oranges remaining after the third sale is 0.35x - 3 - 0.9(0.35x - 3) = 0.35x - 3 - 0.315x + 2.7 = 0.035x - 0.3.
Step 4: Set up an equation using the information from step 3 and solve for x.
According to the problem, the fruit seller is left with 5 oranges after the third sale. Therefore, we have the equation 0.035x - 0.3 = 5.
Solving this equation gives us x = 120.
Therefore, the fruit seller initially had 120 oranges, which is option D.
If the price of petrol has increased from Rs. 40 per litre to Rs. 60 per litre, by how much percent a person has to decrease his consumption so that his expenditure remains same.- a)66.67%
- b)40%
- c)33.33%
- d)45%
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
If the price of petrol has increased from Rs. 40 per litre to Rs. 60 per litre, by how much percent a person has to decrease his consumption so that his expenditure remains same.
a)
66.67%
b)
40%
c)
33.33%
d)
45%
e)
None of these

|
Elite Coaching Classes answered |
If the price of petrol has increased from Rs. 40 per litre to Rs. 60 per litre
Let the consumption be 100 litres.
When price is Rs. 40 per litres, then, the expenditure = 100 × 40
⇒ Rs. 4,000.
At Rs. 60 per litre, the 60 × consumption = 4000
Consumption = 4,000/60 = 66.67 litres.
∴ Required decreased % = 100 - 66.67 = 33.33%
The sum of two numbers is 2490. If 6.5 % of one number is equal to 8.5 % of the other then the numbers are:- a)989, 1501
- b)1011, 1479
- c)1401, 1089
- d)1411, 1079
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
The sum of two numbers is 2490. If 6.5 % of one number is equal to 8.5 % of the other then the numbers are:
a)
989, 1501
b)
1011, 1479
c)
1401, 1089
d)
1411, 1079
e)
None of these

|
Elite Coaching Classes answered |
Let the number be x and (2490 - x).
Then 6.5 % of x = 8.5 % of (2490 - x)
⇒ 6.5/100 Ã - x = 8.5/100 Ã - (2490 - x)
⇒ 65x/1000 = 85(2490 - x)/1000
⇒ 65x = (85 Ã - 2490) “ 85x
⇒ 150x =(85 Ã - 2490)
⇒ x = 211650/150 = 1411
Hence the numbers are 1411 and (2490 - 1411) = 1079
Then 6.5 % of x = 8.5 % of (2490 - x)
⇒ 6.5/100 Ã - x = 8.5/100 Ã - (2490 - x)
⇒ 65x/1000 = 85(2490 - x)/1000
⇒ 65x = (85 Ã - 2490) “ 85x
⇒ 150x =(85 Ã - 2490)
⇒ x = 211650/150 = 1411
Hence the numbers are 1411 and (2490 - 1411) = 1079
If the price of the eraser is reduced by 25% a person buy 2 more erasers for a rupee. How many erasers available for a rupee?- a)8
- b)6
- c)4
- d)2
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
If the price of the eraser is reduced by 25% a person buy 2 more erasers for a rupee. How many erasers available for a rupee?
a)
8
b)
6
c)
4
d)
2
e)
None of these

|
Elite Coaching Classes answered |
Let n erasers be available for a rupee
Reduced Price = (75/100 Ã - 1) = Re ¾
3/4 rupee fetch n erasers = 1 Rupee will fetch (n à - 4/3) erasers
Therefore, 4n/3 = n +2 ⇒ 4n = 3n +6 ⇒ n =6
Reduced Price = (75/100 Ã - 1) = Re ¾
3/4 rupee fetch n erasers = 1 Rupee will fetch (n à - 4/3) erasers
Therefore, 4n/3 = n +2 ⇒ 4n = 3n +6 ⇒ n =6
Fresh grapes contain 80 % water dry grapes contain 10 % water. If the weight of dry grapes is 250 kg. What was its total weight when it was fresh?- a)1000 kg
- b)1100 kg
- c)1125 kg
- d)1225 kg
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Fresh grapes contain 80 % water dry grapes contain 10 % water. If the weight of dry grapes is 250 kg. What was its total weight when it was fresh?
a)
1000 kg
b)
1100 kg
c)
1125 kg
d)
1225 kg
e)
None of these

|
Elite Coaching Classes answered |
Let the weight of fresh grapes be x kg
Quantity of water in it = (80/100 Ã - x)kg = 4x/5 kg
Quantity of pulp in it = (x “ 4x/5)kg = x/5 kg
Quantity of water in 250 kg dry grapes
= (10/100 Ã- 250)kg = 25kg
Quantity of pulp in it = (250 - 25)kg = 225 kg
Therefore, x/5 = 225
⇒ x = 1125
Quantity of water in it = (80/100 Ã - x)kg = 4x/5 kg
Quantity of pulp in it = (x “ 4x/5)kg = x/5 kg
Quantity of water in 250 kg dry grapes
= (10/100 Ã- 250)kg = 25kg
Quantity of pulp in it = (250 - 25)kg = 225 kg
Therefore, x/5 = 225
⇒ x = 1125
If the number of person infected by corona virus is 230000. Out of them 10000 people died. Out of the remaining 43% has been cured. Then the number of persons still infected is what percent of the total number of infected person initially.- a)56.5%
- b)54.5%
- c)60%
- d)47%
- e)Not Attempted
Correct answer is option 'B'. Can you explain this answer?
If the number of person infected by corona virus is 230000. Out of them 10000 people died. Out of the remaining 43% has been cured. Then the number of persons still infected is what percent of the total number of infected person initially.
a)
56.5%
b)
54.5%
c)
60%
d)
47%
e)
Not Attempted

|
Elite Coaching Classes answered |
Total number of infected person initially = 230000
Number of people died = 10000
Remaining persons = 230000 – 10000 = 220000
Number of person cured = 43% of 220000 = 94600
Number of person still infected = 220000 - 94600 = 125400
∴ Required percentage = 125400/230000 × 100 = 54.5
Fresh fruit contains 68 % water and dry fruit contains 20 % water. How much dry fruit can be obtained from 100 kg of fresh fruits?- a)32 kg
- b)40 kg
- c)52 kg
- d)80 kg
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Fresh fruit contains 68 % water and dry fruit contains 20 % water. How much dry fruit can be obtained from 100 kg of fresh fruits?
a)
32 kg
b)
40 kg
c)
52 kg
d)
80 kg
e)
None of these
|
|
Swati Sharma answered |
Quantity of water in 100kg of fresh fruits =(68/100 × 100)kg
Quantity of pulp in it = (100 - 68)kg = 32 kg
Let the dry fruit be x kg
Water in it = (20/100 Ã - x)kg = x/5 kg
Quantity of pulp in it = (x “ x/5)kg = 4x/5 kg
Therefore, 4x/5 = 32 ⇒ x = 160/4 = 40 kg
Quantity of pulp in it = (100 - 68)kg = 32 kg
Let the dry fruit be x kg
Water in it = (20/100 Ã - x)kg = x/5 kg
Quantity of pulp in it = (x “ x/5)kg = 4x/5 kg
Therefore, 4x/5 = 32 ⇒ x = 160/4 = 40 kg
8 % of the voters in an election did not cast their votes in the election, there were only two candidates. The winner by obtaining 48 % of the total votes defeated his contestant by 1100 votes. The total number of voters in the election was.- a)21000
- b)2200
- c)23500
- d)27500
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
8 % of the voters in an election did not cast their votes in the election, there were only two candidates. The winner by obtaining 48 % of the total votes defeated his contestant by 1100 votes. The total number of voters in the election was.
a)
21000
b)
2200
c)
23500
d)
27500
e)
None of these
|
|
Swati Sharma answered |
Let the total number of voters be x
Votes cast = 92 % of x = (92/100 Ã - x) = 23x/25
Votes in favour of winning candidate = 48/100 Ã - x
= 12x/25
Votes polled by defeated candidate = (23x/25 “ 12x/25)
= 11x/25 12x/25 “ 11x/25 = 1100
⇒ 12x “ 11x = 27500
⇒ x = 27500
Votes cast = 92 % of x = (92/100 Ã - x) = 23x/25
Votes in favour of winning candidate = 48/100 Ã - x
= 12x/25
Votes polled by defeated candidate = (23x/25 “ 12x/25)
= 11x/25 12x/25 “ 11x/25 = 1100
⇒ 12x “ 11x = 27500
⇒ x = 27500
The price of petrol is increased by 25 %. By how much percent a car owner should reduce his consumption of petrol. So that expenditure on petrol would not be increased?- a)25 %
- b)30 %
- c)50 %
- d)20 %
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
The price of petrol is increased by 25 %. By how much percent a car owner should reduce his consumption of petrol. So that expenditure on petrol would not be increased?
a)
25 %
b)
30 %
c)
50 %
d)
20 %
e)
None of these

|
Elite Coaching Classes answered |
Reduction % in consumption = {r/(100+ r) Ã -100}%
= (25/125 Ã - 100)%
= 20%
= (25/125 Ã - 100)%
= 20%
If 170% of a number added to 66, then the result becomes equal to twice of the number. What is the number?- a)200
- b)220
- c)210
- d)236
- e)Not Attempted
Correct answer is option 'B'. Can you explain this answer?
If 170% of a number added to 66, then the result becomes equal to twice of the number. What is the number?
a)
200
b)
220
c)
210
d)
236
e)
Not Attempted
|
|
Swati Sharma answered |
Given:
170% of a number added to 66,
the result becomes equal twice
Calculation:
Let the number be = x
According to the question
⇒ x × 170/100 + 66 = 2x
⇒ 17x/10 + 66 = 2x
⇒ 2x - 17x/10 = 66
⇒ 3x/10 = 66
⇒ x = 220
∴ The correct answer is 220.
Out of two numbers, 65% of the smaller number is equal to 45% of the larger number. If the sum of two numbers is 2574, then what is the value of the larger number?- a)1521
- b)1471
- c)1641
- d)1419
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
Out of two numbers, 65% of the smaller number is equal to 45% of the larger number. If the sum of two numbers is 2574, then what is the value of the larger number?
a)
1521
b)
1471
c)
1641
d)
1419
e)
None of these
|
|
Swati Sharma answered |
From the problem, it is given that
65%x = 45%y
⇒ 13x = 9y
⇒ x = (9/13)y ----(1)
Given the sum of the numbers = 2574
⇒ (x + y) = 2574 ----(2)
Substituting the value of ‘x’ from Equation 1 in Equation 2, we get
(9/13)y + y = 2574
⇒ (9y + 13y) = 2574 × 13
⇒ 22y = (2574 × 13)
⇒ y = (2574 × 13)/22 = 1521
∴ Value of the larger number is 1521
The ratio 5 ∶ 4 expressed as a percent equals - a)1
- b)5% 2.40%
- c)80%
- d)125%
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
The ratio 5 ∶ 4 expressed as a percent equals
a)
1
b)
5% 2.40%
c)
80%
d)
125%
e)
None of these

|
Elite Coaching Classes answered |
Given:
Ratio = 5:4
Formula used:-
Required percentage = (x/y) × 100
Calculation:-
Required percentage = (5/4) × 100
Required percentage = 125%
∴ 5:4 is equal to 125%.
Chapter doubts & questions for Percentages - 3 Months Preparation for UGC NET Paper 1 2025 is part of UGC NET exam preparation. The chapters have been prepared according to the UGC NET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for UGC NET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Percentages - 3 Months Preparation for UGC NET Paper 1 in English & Hindi are available as part of UGC NET exam.
Download more important topics, notes, lectures and mock test series for UGC NET Exam by signing up for free.
3 Months Preparation for UGC NET Paper 1
231 videos|447 docs|128 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup









