All Exams >
JEE >
6 Months Preparation for JEE >
All Questions
All questions of Circle for JEE Exam
The angle between the two tangents from the origin to the circle (x – 7)2 + (y + 1)2 = 25 equals- a)π/2
- b)π/3
- c)π/4
- d)None
Correct answer is option 'A'. Can you explain this answer?
The angle between the two tangents from the origin to the circle (x – 7)2 + (y + 1)2 = 25 equals
a)
π/2
b)
π/3
c)
π/4
d)
None
|
|
Krishna Iyer answered |
Let tangent from origin be y = mx
Using the condition of tangency, we get
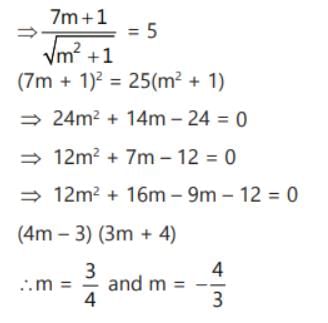
The angle between tangents = π/2
Using the condition of tangency, we get
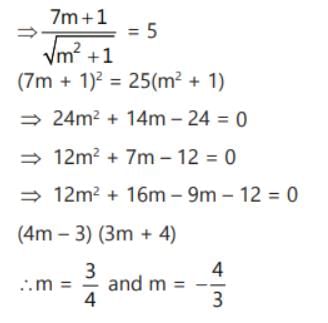
The angle between tangents = π/2
The equation of circle of radius 5 units touches the coordinates axes in the second quadrant is:- a)x2 + y2 + 10x – 10y + 25 = 0
- b)x2 + y2 – 10x – 10y + 25 = 0
- c)x2 + y2 + 10x + 10y + 25 = 0
- d)x2 + y2 – 10x – 10y – 25 = 0
Correct answer is option 'A'. Can you explain this answer?
The equation of circle of radius 5 units touches the coordinates axes in the second quadrant is:
a)
x2 + y2 + 10x – 10y + 25 = 0
b)
x2 + y2 – 10x – 10y + 25 = 0
c)
x2 + y2 + 10x + 10y + 25 = 0
d)
x2 + y2 – 10x – 10y – 25 = 0
|
|
Suresh Reddy answered |
If the circle lies in second quadrant
The equation of a circle touches both the coordinate axes and has radius a is
x2 + y2 + 2ax - 2ay + a2 = 0
Radius of circle, a = 5
x2 + y2 + 10x - 10y + 25 = 0
The equation of a circle touches both the coordinate axes and has radius a is
x2 + y2 + 2ax - 2ay + a2 = 0
Radius of circle, a = 5
x2 + y2 + 10x - 10y + 25 = 0
The equation of circle whose centre is (2, 1) and which passes through the point (3, – 5) is:- a)
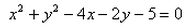
- b)
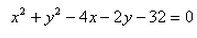
- c)
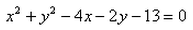
- d)
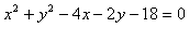
Correct answer is option 'B'. Can you explain this answer?
The equation of circle whose centre is (2, 1) and which passes through the point (3, – 5) is:
a)
b)
c)
d)
|
|
Poonam Reddy answered |
Radius of circle is given by -
r = √[(h-x1)² + (k-y1)²]
r = √[(2-3)² + (1+5)²]
r = √(-1² + 6²)
r = √(1 + 36)
r = √37
if centre (2,-]1) and radius=√26 are given,
(x-h)2+(y-k)2=r2
equation is (x-2)2 + (y-1)2 = (√37)2
x2 + 4 - 4x + y2 + 1 - 2y = 37
x2 + y2 - 4x - 2y - 32 = 0
r = √[(h-x1)² + (k-y1)²]
r = √[(2-3)² + (1+5)²]
r = √(-1² + 6²)
r = √(1 + 36)
r = √37
if centre (2,-]1) and radius=√26 are given,
(x-h)2+(y-k)2=r2
equation is (x-2)2 + (y-1)2 = (√37)2
x2 + 4 - 4x + y2 + 1 - 2y = 37
x2 + y2 - 4x - 2y - 32 = 0
The equation of the circle passing through (0, 0) and making intercepts 2 and 4 on the coordinate axes is:- a)
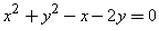
- b)
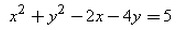
- c)
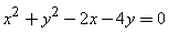
- d)
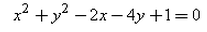
Correct answer is option 'C'. Can you explain this answer?
The equation of the circle passing through (0, 0) and making intercepts 2 and 4 on the coordinate axes is:
a)
b)
c)
d)
|
|
Geetika Shah answered |
The circle intercept the co-ordinate axes at a and b. it means x - intercept at ( a, 0) and y-intercept at (0, b) .
Now, we observed that circle passes through points (0, 0) , (a, 0) and (0, b) .
we also know, General equation of circle is
x² + y² + 2gx + 2fy + C = 0
when point (0,0)
(0)² + (0)² + 2g(0) + 2f(0) + C = 0
0 + 0 + 0 + 0 + C = 0
C = 0 -------(1)
when point (a,0)
(a)² + (0)² + 2g(a) + 2f(0) + C = 0
a² + 2ag + C = 0
from equation (1)
a² + 2ag = 0
a(a + 2g) = 0
g = -a/2
when point ( 0, b)
(0)² + (b)² + 2g(0) + 2f(b) + C = 0
b² + 2fb + C = 0
f = -b/2
Now, equation of circle is
x² + y² + 2x(-a/2) + 2y(-b/2) + 0 = 0 { after putting values of g, f and C }
x² + y² - ax - by = 0
As we know that, a=2, b=4
x^2 + y^2 - 2x - 4y = 0
Now, we observed that circle passes through points (0, 0) , (a, 0) and (0, b) .
we also know, General equation of circle is
x² + y² + 2gx + 2fy + C = 0
when point (0,0)
(0)² + (0)² + 2g(0) + 2f(0) + C = 0
0 + 0 + 0 + 0 + C = 0
C = 0 -------(1)
when point (a,0)
(a)² + (0)² + 2g(a) + 2f(0) + C = 0
a² + 2ag + C = 0
from equation (1)
a² + 2ag = 0
a(a + 2g) = 0
g = -a/2
when point ( 0, b)
(0)² + (b)² + 2g(0) + 2f(b) + C = 0
b² + 2fb + C = 0
f = -b/2
Now, equation of circle is
x² + y² + 2x(-a/2) + 2y(-b/2) + 0 = 0 { after putting values of g, f and C }
x² + y² - ax - by = 0
As we know that, a=2, b=4
x^2 + y^2 - 2x - 4y = 0
The centre and radius of the circle x2 + y2 + 4x – 6y = 5 is:- a)(2, – 3), 2√2
- b)(– 2, 3), 3√2
- c)(– 2, 3), 2√2
- d)(2, – 3), 3√2
Correct answer is option 'B'. Can you explain this answer?
The centre and radius of the circle x2 + y2 + 4x – 6y = 5 is:
a)
(2, – 3), 2√2
b)
(– 2, 3), 3√2
c)
(– 2, 3), 2√2
d)
(2, – 3), 3√2
|
|
Riya Banerjee answered |
x2+y2+4x-6y=5
Circle Equation
(x-a)2+(y-b)2=r2 is the circle equation with a radius r, centered at (a,b)
Rewrite x2+y24x-6y=5 in the form of circle standard circle equation
(x-(-2))
Therefore the circle properties are:
(a,b) = (-2,3), r = 3√2
Circle Equation
(x-a)2+(y-b)2=r2 is the circle equation with a radius r, centered at (a,b)
Rewrite x2+y24x-6y=5 in the form of circle standard circle equation
(x-(-2))
2
+(y-3)2=(3
√2)2Therefore the circle properties are:
(a,b) = (-2,3), r = 3√2
The equation of a circle which is concentric to the given circle x2 + y2 - 4x - 6y - 3 = 0 and which touches the Y-axis is:
- a)x2 + y2 + 4x + 6y + 13 = 0
- b)x2 + y2 - 4x - 6y + 13 = 0
- c)x2 + y2 - 4x - 6y + 9 = 0
- d)x2 + y2 - 4x - 6y + 4 = 0
Correct answer is option 'C'. Can you explain this answer?
The equation of a circle which is concentric to the given circle x2 + y2 - 4x - 6y - 3 = 0 and which touches the Y-axis is:
a)
x2 + y2 + 4x + 6y + 13 = 0
b)
x2 + y2 - 4x - 6y + 13 = 0
c)
x2 + y2 - 4x - 6y + 9 = 0
d)
x2 + y2 - 4x - 6y + 4 = 0
|
|
Aryan Khanna answered |
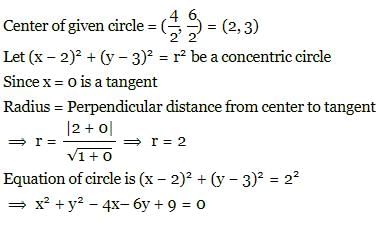
Point (-2, – 5) lies on the circle x2 + y2 = 25.- a)On the axis outside the circle
- b)Outside
- c)Inside
- d)On the circle
Correct answer is option 'B'. Can you explain this answer?
Point (-2, – 5) lies on the circle x2 + y2 = 25.
a)
On the axis outside the circle
b)
Outside
c)
Inside
d)
On the circle
|
|
Hansa Sharma answered |
X2 +Y2 =25 Points =(-2,-5)
Put the points in the variables
(-2)2 + (-5)2 = 29
As 29 > 25 (lies outside).
Put the points in the variables
(-2)2 + (-5)2 = 29
As 29 > 25 (lies outside).
If y=c is a tangent to the circle x2+y2–2x+2y–2 =0 at (1, 1), then the value of c is- a)1
- b)2
- c)–1
- d)–2
Correct answer is option 'A'. Can you explain this answer?
If y=c is a tangent to the circle x2+y2–2x+2y–2 =0 at (1, 1), then the value of c is
a)
1
b)
2
c)
–1
d)
–2
|
|
Raghav Bansal answered |
For line y=c to be tangent to the given circle at point (1,1)
It has to pass through (1,1)
⇒ c = 1
It has to pass through (1,1)
⇒ c = 1
The equation of the circle having the lines y2 – 2y + 4x – 2xy = 0 as its normals & passing through the point (2, 1) is- a)x2 + y2 – 2x – 4y + 3 = 0
- b)x2 + y2 – 2x + 4y – 5 = 0
- c)x2 + y2 + 2x + 4y – 13 = 0
- d)None
Correct answer is option 'A'. Can you explain this answer?
The equation of the circle having the lines y2 – 2y + 4x – 2xy = 0 as its normals & passing through the point (2, 1) is
a)
x2 + y2 – 2x – 4y + 3 = 0
b)
x2 + y2 – 2x + 4y – 5 = 0
c)
x2 + y2 + 2x + 4y – 13 = 0
d)
None
|
|
Geetika Shah answered |
The normal line to circle is →y² - 2 y + 4 x -2 xy=0
→ y(y-2) - 2x(y-2)=0
→ (y-2)(y-2x)=0
the two lines are , y=2 and 2 x -y =0
The point of intersection of normals are centre of circle.
→ Put , y=2 in 2 x -y=0, we get
→2 x -2=0
→2 x=2
→ x=1
So, the point of intersection of normals is (1,2) which is the center of circle.
Also, the circle passes through (2,1).
Radius of circle is given by distance formula = [(1-2)² + (2-1)²]½
=(1+1)½ =(2)½
The equation of circle having center (1,2) and radius √2 is
= (x-1)²+(y-2)²=[√2]²
→ (x-1)²+(y-2)²= 2
x²+y² -2x-4y+3 = 0
→ y(y-2) - 2x(y-2)=0
→ (y-2)(y-2x)=0
the two lines are , y=2 and 2 x -y =0
The point of intersection of normals are centre of circle.
→ Put , y=2 in 2 x -y=0, we get
→2 x -2=0
→2 x=2
→ x=1
So, the point of intersection of normals is (1,2) which is the center of circle.
Also, the circle passes through (2,1).
Radius of circle is given by distance formula = [(1-2)² + (2-1)²]½
=(1+1)½ =(2)½
The equation of circle having center (1,2) and radius √2 is
= (x-1)²+(y-2)²=[√2]²
→ (x-1)²+(y-2)²= 2
x²+y² -2x-4y+3 = 0
The equations of the tangents drawn from the point (0, 1) to the circle x2 + y2 - 2x + 4y = 0 are- a)2x - y + 1 = 0, x + 2y - 2 = 0
- b)2x - y - 1 = 0, x + 2y - 2 = 0
- c)2x - y + 1 = 0, x + 2y + 2 = 0
- d)2x - y - 1 = 0, x + 2y + 2 = 0
Correct answer is option 'A'. Can you explain this answer?
The equations of the tangents drawn from the point (0, 1) to the circle x2 + y2 - 2x + 4y = 0 are
a)
2x - y + 1 = 0, x + 2y - 2 = 0
b)
2x - y - 1 = 0, x + 2y - 2 = 0
c)
2x - y + 1 = 0, x + 2y + 2 = 0
d)
2x - y - 1 = 0, x + 2y + 2 = 0
|
|
Geetika Shah answered |
Let equation of tangent with slope =m and point (0,1)
(y−1)=m(x−0)⇒y=mx+1
Intersection point
x2+(mx+1)2−2x+4(mx+1)=0
(1+m2)x2+(−2+6m)x+5=0
For y=mx+1 to be tangent, discriminant =0
(6m−2)2−4×5(1+m2)=0
36m2+4−24m−20m2+20=0
16m2−20m+24=0
⇒ 2m2−3m−2=0
(2m+1)(m−2)=0
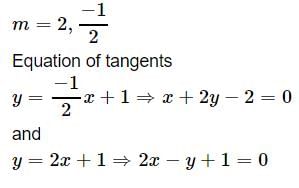
(y−1)=m(x−0)⇒y=mx+1
Intersection point
x2+(mx+1)2−2x+4(mx+1)=0
(1+m2)x2+(−2+6m)x+5=0
For y=mx+1 to be tangent, discriminant =0
(6m−2)2−4×5(1+m2)=0
36m2+4−24m−20m2+20=0
16m2−20m+24=0
⇒ 2m2−3m−2=0
(2m+1)(m−2)=0
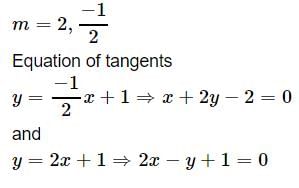
The locus of the mid-points of the chords of the circle x2 + y2 – 2x – 4y – 11 = 0 which subtend 60º at the centre is- a)x2 + y2 – 4x – 2y – 7 = 0
- b)x2 + y2 + 4x + 2y – 7 = 0
- c)x2 + y2 – 2x – 4y – 7 = 0
- d)x2 + y2 + 2x + 4y + 7 = 0
Correct answer is option 'C'. Can you explain this answer?
The locus of the mid-points of the chords of the circle x2 + y2 – 2x – 4y – 11 = 0 which subtend 60º at the centre is
a)
x2 + y2 – 4x – 2y – 7 = 0
b)
x2 + y2 + 4x + 2y – 7 = 0
c)
x2 + y2 – 2x – 4y – 7 = 0
d)
x2 + y2 + 2x + 4y + 7 = 0
|
|
Preeti Iyer answered |
Let AB be the chord of the circle and P be the midpoint of AB.
It is known that perpendicular from the center bisects a chord.
Thus △ACP is a right-angled triangle.
Now AC=BC= radius.
The equation of the give circle can be written as
(x−1)2+(y−2)2=16
Hence, centre C=(1,2) and radius =r=4 units.
PC=ACsin60degree
= rsin60degree
= 4([2(3)½]/2
= 2(3)1/2 units
Therefore, PC=2(3)1/2
⇒ PC2=12
⇒ (x−1)2+(y−2)2=12
⇒ x2+y2−2x−4y+5=12
⇒ x2+y2−2x−4y−7=0
It is known that perpendicular from the center bisects a chord.
Thus △ACP is a right-angled triangle.
Now AC=BC= radius.
The equation of the give circle can be written as
(x−1)2+(y−2)2=16
Hence, centre C=(1,2) and radius =r=4 units.
PC=ACsin60degree
= rsin60degree
= 4([2(3)½]/2
= 2(3)1/2 units
Therefore, PC=2(3)1/2
⇒ PC2=12
⇒ (x−1)2+(y−2)2=12
⇒ x2+y2−2x−4y+5=12
⇒ x2+y2−2x−4y−7=0
The number of common tangents of the circles x2 + y2 – 2x – 1 = 0 and x2 + y2 – 2y – 7 = 0- a)1
- b)2
- c)3
- d)4
Correct answer is option 'A'. Can you explain this answer?
The number of common tangents of the circles x2 + y2 – 2x – 1 = 0 and x2 + y2 – 2y – 7 = 0
a)
1
b)
2
c)
3
d)
4
|
|
Neha Joshi answered |
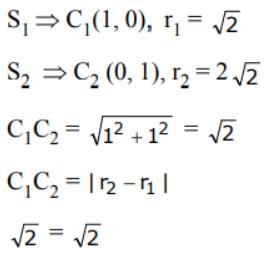
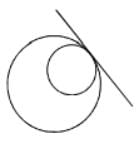
Internally touch ∴ common tangent is one.
y = √3x + c1 & y = √3x + c2 are two parallel tangents of a circle of radius 2 units, then |c1 – c2| is equal to
- a)8
- b)4
- c)2
- d)1
Correct answer is option 'A'. Can you explain this answer?
y = √3x + c1 & y = √3x + c2 are two parallel tangents of a circle of radius 2 units, then |c1 – c2| is equal to
a)
8
b)
4
c)
2
d)
1
|
|
Anmol Chauhan answered |
For both lines to be parallel tangent the distance between both lines
should be equal to the diameter of the circle
⇒ 4 = |c1−c2|/(1+3)1/2
⇒∣c1−c2∣ = 8
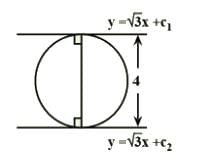
should be equal to the diameter of the circle
⇒ 4 = |c1−c2|/(1+3)1/2
⇒∣c1−c2∣ = 8

Pair of tangents are drawn from every point on the line 3x + 4y = 12 on the circle x2+ y2 = 4. Their variable chord of contact always passes through a fixed point whose co-ordinates are- a)
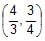
- b)
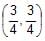
- c)(1, 1)
- d)
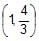
Correct answer is option 'D'. Can you explain this answer?
Pair of tangents are drawn from every point on the line 3x + 4y = 12 on the circle x2+ y2 = 4. Their variable chord of contact always passes through a fixed point whose co-ordinates are
a)
b)
c)
(1, 1)
d)
|
|
Geetika Shah answered |
Let P(x1,y1) be a point on the line 3x + 4y = 12
Equation of variable chord of contact of P(x1,y1) w.r.t circle x2 + y2 = 4
xx1 + yy1 − 4 = 0 ...(1)
Also 3x1 + 4y1 − 12 = 0
⇒ x1 + 4/3y1 − 4 = 0 ...(2)
Comparing (1) and (2), we get
x = 1; y = 4/3
∴ Variable chord of contact always passes through (1, 4/3)
Equation of variable chord of contact of P(x1,y1) w.r.t circle x2 + y2 = 4
xx1 + yy1 − 4 = 0 ...(1)
Also 3x1 + 4y1 − 12 = 0
⇒ x1 + 4/3y1 − 4 = 0 ...(2)
Comparing (1) and (2), we get
x = 1; y = 4/3
∴ Variable chord of contact always passes through (1, 4/3)
A circle is drawn touching the x-axis and centre at the point which is the reflection of (a, b) in the line y – x = 0. The equation of the circle is- a)x2 + y2 – 2bx – 2ay + a2 = 0
- b)x2 + y2 – 2bx – 2ay + b2 = 0
- c)x2 + y2 – 2ax – 2by + b2 = 0
- d)x2 + y2 – 2ax – 2by + a2 = 0
Correct answer is option 'B'. Can you explain this answer?
A circle is drawn touching the x-axis and centre at the point which is the reflection of (a, b) in the line y – x = 0. The equation of the circle is
a)
x2 + y2 – 2bx – 2ay + a2 = 0
b)
x2 + y2 – 2bx – 2ay + b2 = 0
c)
x2 + y2 – 2ax – 2by + b2 = 0
d)
x2 + y2 – 2ax – 2by + a2 = 0
|
|
Geetika Shah answered |
Radius of the circle = a
and centre ≡ (b,a)
And circle is touching the x-axis.
The equation of the circle :
x2+y2−2bx−2ay+b2 = 0
and centre ≡ (b,a)
And circle is touching the x-axis.
The equation of the circle :
x2+y2−2bx−2ay+b2 = 0
If a be the radius of a circle which touches x-axis at the origin, then its equation is- a)x2 + y2 + ax = 0
- b)x2 + y2 ± 2ya = 0
- c)x2 + y2 ± 2xa = 0
- d)x2 + y2 + ya = 0
Correct answer is option 'B'. Can you explain this answer?
If a be the radius of a circle which touches x-axis at the origin, then its equation is
a)
x2 + y2 + ax = 0
b)
x2 + y2 ± 2ya = 0
c)
x2 + y2 ± 2xa = 0
d)
x2 + y2 + ya = 0
|
|
Sushant Ghosh answered |
The equation of the circle with centre at (h,k) and radius equal to a is (x−h)2 +(y−k)2 = a2
When the circle passes through the origin and centre lies on x− axis
⇒h = a and k = 0
Then the equation (x−h)2+(y−k)2=a2 becomes (x−a)2+y2=a2
If a circle passes through the origin and centre lies on x−axis then the abscissa will be equal to the radius of the circle and the y−co-ordinate of the centre will be zero Hence, the equation of the circle will be of the form
(x±a)2+y2=a2⇒x2+a2 ±2ax+y2=a2
=x2 +y2 ±2ax=0 is the required equation of the circle.
When the circle passes through the origin and centre lies on x− axis
⇒h = a and k = 0
Then the equation (x−h)2+(y−k)2=a2 becomes (x−a)2+y2=a2
If a circle passes through the origin and centre lies on x−axis then the abscissa will be equal to the radius of the circle and the y−co-ordinate of the centre will be zero Hence, the equation of the circle will be of the form
(x±a)2+y2=a2⇒x2+a2 ±2ax+y2=a2
=x2 +y2 ±2ax=0 is the required equation of the circle.
If the line 2x – y + λ = 0 is a diameter of the circle x2+y2+6x−6y+5 = 0 then λ =- a)6
- b)9
- c)3
- d)12
Correct answer is option 'B'. Can you explain this answer?
If the line 2x – y + λ = 0 is a diameter of the circle x2+y2+6x−6y+5 = 0 then λ =
a)
6
b)
9
c)
3
d)
12
|
|
Rajesh Gupta answered |
x2 + y2 + 6x − 6y + 5 = 0
Center O = (-3, 3)
radius r = √{(-3)2 + (3)2 - 5}
= √{9 + 9 - 5}
= √13
Since diameter of the circle passes through the center of the circle.
So (-3, 3) satisfies the equation 2x – y + λ = 0
=> -3*2 - 3 + λ = 0
=> -6 - 3 + λ = 0
=> -9 + λ = 0
=> λ = 9
Center O = (-3, 3)
radius r = √{(-3)2 + (3)2 - 5}
= √{9 + 9 - 5}
= √13
Since diameter of the circle passes through the center of the circle.
So (-3, 3) satisfies the equation 2x – y + λ = 0
=> -3*2 - 3 + λ = 0
=> -6 - 3 + λ = 0
=> -9 + λ = 0
=> λ = 9
The equation of a circle which passes through the three points (3, 0) (1, –6), (4, –1) is- a)2x2 + 2y2 + 5x – 11y + 3 = 0
- b)x2 + y2 – 5x + 11y – 3 = 0
- c)x2 + y2 + 5x – 11y + 3 = 0
- d)2x2 + 2y2 – 5x + 11y – 3 = 0
Correct answer is option 'D'. Can you explain this answer?
The equation of a circle which passes through the three points (3, 0) (1, –6), (4, –1) is
a)
2x2 + 2y2 + 5x – 11y + 3 = 0
b)
x2 + y2 – 5x + 11y – 3 = 0
c)
x2 + y2 + 5x – 11y + 3 = 0
d)
2x2 + 2y2 – 5x + 11y – 3 = 0
|
|
Pooja Shah answered |
Gen equation of a circle is (x−h)2+(y−k)2=r2 (3,0),(1,−6),(4,−1) circle passes through these points
∴ These three points should satisfy the equation
of circle.
(3−h)2+k2=r2 ___ (I)
(1−h)2 +(−6−k)2 = r2(1−h)2+(6+k)2=r2 ___ (II)
From (I) & (II)
(3−h)2+k2 =(1−h)2+(6+k)2
9+h2−6h+k2 =1+h2 2h+36+k2+12k
9−6h=1−2h+36+12k
9−37=4h+12k
−28=4h+12k
h+3k=−7
h=−7−3k ___ (III)
(4−h)2+(−1−k)2=r2 ___ (IV)
From (I) & (IV)
(3−h)2+k2 = (4−h)2 +(1+k)2
9+h2 −6h+k2
=16+h2 −8h+1+k2+2k
9−6h=17−8h+2k
9−17=−2h+2k
−8=−2h+2k
−h+k=−4
k=−4+h ___ (V)
Put (V) in (III)
h=−7−3(−4+h)
h=−7+12−3h
h=5/4,k=−11/4,r=170/16
Eq of circle: (x−5/4)2 +(y+11/4)2 =170/16
x2+25/16−10x/4+y2 +121/16+22y/4=170/16
Simplifying, we get 2x2+xy2−5x+11y−3=0
∴ These three points should satisfy the equation
of circle.
(3−h)2+k2=r2 ___ (I)
(1−h)2 +(−6−k)2 = r2(1−h)2+(6+k)2=r2 ___ (II)
From (I) & (II)
(3−h)2+k2 =(1−h)2+(6+k)2
9+h2−6h+k2 =1+h2 2h+36+k2+12k
9−6h=1−2h+36+12k
9−37=4h+12k
−28=4h+12k
h+3k=−7
h=−7−3k ___ (III)
(4−h)2+(−1−k)2=r2 ___ (IV)
From (I) & (IV)
(3−h)2+k2 = (4−h)2 +(1+k)2
9+h2 −6h+k2
=16+h2 −8h+1+k2+2k
9−6h=17−8h+2k
9−17=−2h+2k
−8=−2h+2k
−h+k=−4
k=−4+h ___ (V)
Put (V) in (III)
h=−7−3(−4+h)
h=−7+12−3h
h=5/4,k=−11/4,r=170/16
Eq of circle: (x−5/4)2 +(y+11/4)2 =170/16
x2+25/16−10x/4+y2 +121/16+22y/4=170/16
Simplifying, we get 2x2+xy2−5x+11y−3=0
The locus of the centres of the circles such that the point (2, 3) is the mid point of the chord5x + 2y = 16 is- a) 2x – 5y + 11 = 0
- b)2x + 5y – 11 = 0
- c)2x + 5y + 11 = 0
- d)None
Correct answer is option 'A'. Can you explain this answer?
The locus of the centres of the circles such that the point (2, 3) is the mid point of the chord
5x + 2y = 16 is
a)
2x – 5y + 11 = 0
b)
2x + 5y – 11 = 0
c)
2x + 5y + 11 = 0
d)
None
|
|
Nandini Patel answered |
Let locus lie on
Y = mx +C
Slope of a line = -5/2
Hence slope of its perpendicular line = 2/5
Hence
y = 2x/5 +C
5y = 2x + 5C
(2, 3) satisfies this
C = 11/5
Hence
Line will be
5y = 2x + 5*11/5
2x - 5y + 11 = 0
The equation of parabola whose focus is (– 3, 0) and directrix x + 5 = 0 is:- a)y2 = 4(x + 1)
- b)y2 = 4x
- c)y2 = 4(x + 16)
- d)y2 = 4(x + 4)
Correct answer is option 'D'. Can you explain this answer?
The equation of parabola whose focus is (– 3, 0) and directrix x + 5 = 0 is:
a)
y2 = 4(x + 1)
b)
y2 = 4x
c)
y2 = 4(x + 16)
d)
y2 = 4(x + 4)
|
|
Gaurav Kumar answered |
Given, focus : (-3,0)
directrix : x + 5 = 0
Let (x ,y) is the point on the parabola .
∴ distance of point from focus = distance of point from directrix
⇒ √{(x + 3)² + y²} = |x + 5|/√(1² + 0²)
⇒ √{(x + 3)² + y² } = |x + 5|
squaring both sides,
(x + 3)² + y² = (x + 5)²
⇒y² = (x + 5)² - (x + 3)²
⇒y² = (x + 5 - x - 3)(x + 5 + x + 3)
⇒y² = 2(2x + 8) = 4(x + 4)
Hence, equation of parabola is y² = 4(x + 4)
directrix : x + 5 = 0
Let (x ,y) is the point on the parabola .
∴ distance of point from focus = distance of point from directrix
⇒ √{(x + 3)² + y²} = |x + 5|/√(1² + 0²)
⇒ √{(x + 3)² + y² } = |x + 5|
squaring both sides,
(x + 3)² + y² = (x + 5)²
⇒y² = (x + 5)² - (x + 3)²
⇒y² = (x + 5 - x - 3)(x + 5 + x + 3)
⇒y² = 2(2x + 8) = 4(x + 4)
Hence, equation of parabola is y² = 4(x + 4)
The greatest distance of the point P(10, 7) from the circle x2 + y2 – 4x – 2y – 20 = 0 is- a)5
- b)15
- c)10
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The greatest distance of the point P(10, 7) from the circle x2 + y2 – 4x – 2y – 20 = 0 is
a)
5
b)
15
c)
10
d)
None of these
|
|
Sankar Mehta answered |
The equation of the circle is x^2 + y^2 = r^2, where r is the radius of the circle. We need to find the value of r first.
The circle passes through the origin (0,0), since x^2 + y^2 = 0^2 when x = 0 and y = 0. Therefore, the distance from the center of the circle to the origin is equal to the radius.
The center of the circle is at (0,0), so the distance from the center to the point P(10,7) is:
d = sqrt((10-0)^2 + (7-0)^2) = sqrt(149)
Therefore, the radius of the circle is r = sqrt(149).
The greatest distance from the point P(10,7) to the circle is the distance from the point to the edge of the circle along a line that passes through the center of the circle. This is equal to the difference between the distance from the center to the point and the radius of the circle.
The distance from the center of the circle to the point P(10,7) is d = sqrt((10-0)^2 + (7-0)^2) = sqrt(149).
Therefore, the greatest distance of the point P(10,7) from the circle is:
d - r = sqrt(149) - sqrt(149) = 0.
Therefore, the greatest distance is 0, which means that the point P(10,7) is on the circle.
The circle passes through the origin (0,0), since x^2 + y^2 = 0^2 when x = 0 and y = 0. Therefore, the distance from the center of the circle to the origin is equal to the radius.
The center of the circle is at (0,0), so the distance from the center to the point P(10,7) is:
d = sqrt((10-0)^2 + (7-0)^2) = sqrt(149)
Therefore, the radius of the circle is r = sqrt(149).
The greatest distance from the point P(10,7) to the circle is the distance from the point to the edge of the circle along a line that passes through the center of the circle. This is equal to the difference between the distance from the center to the point and the radius of the circle.
The distance from the center of the circle to the point P(10,7) is d = sqrt((10-0)^2 + (7-0)^2) = sqrt(149).
Therefore, the greatest distance of the point P(10,7) from the circle is:
d - r = sqrt(149) - sqrt(149) = 0.
Therefore, the greatest distance is 0, which means that the point P(10,7) is on the circle.
The number of points on X-axis which are at a distance c units (c < 3) from (2, 3) is- a)1
- b)0
- c)3
- d)2
Correct answer is option 'B'. Can you explain this answer?
The number of points on X-axis which are at a distance c units (c < 3) from (2, 3) is
a)
1
b)
0
c)
3
d)
2

|
Mohit Rajpoot answered |
Distance of 'c' units from (2,3)
Let the no: of points be (x,0)
By distance formula
{(2−x)2+(3−0)2}=c
4−4x+x2+9=c
⇒x2−4x+13 = c:c=2,2
There are the points of c,such that when they are applied back to the equations,the number of points will become zero.
Let the no: of points be (x,0)
By distance formula
{(2−x)2+(3−0)2}=c
4−4x+x2+9=c
⇒x2−4x+13 = c:c=2,2
There are the points of c,such that when they are applied back to the equations,the number of points will become zero.
The point from which the tangents to the circles x2 + y2 – 8x + 40 = 0, 5x2 + 5y2 – 25 x + 80 = 0, x2 + y2 – 8x + 16y + 160 = 0 are equal in length is- a)
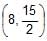
- b)
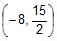
- c)
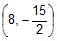
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The point from which the tangents to the circles x2 + y2 – 8x + 40 = 0, 5x2 + 5y2 – 25 x + 80 = 0, x2 + y2 – 8x + 16y + 160 = 0 are equal in length is
a)
b)
c)
d)
None of these
|
|
Hansa Sharma answered |
The Required point is the radical centre of the three given circles. The radical axes of the three circles taken in pairs are 3x - 24 = 0,16y + 120 = 0 and - 3x + 16y + 80 = 0. On solving, the required point is (8, -15/2).
The locus of the centre of a circle, which touches externally the circle x2 + y2 − 6x − 6y + 14 = 0 and also touches Y-axis, is given by the equation- a)x2−6x−10y+14=0
- b)x2−10x−6y+14=0
- c)y2−6x−10y+14=0
- d)y2−10x−6y+14=0
Correct answer is option 'D'. Can you explain this answer?
The locus of the centre of a circle, which touches externally the circle x2 + y2 − 6x − 6y + 14 = 0 and also touches Y-axis, is given by the equation
a)
x2−6x−10y+14=0
b)
x2−10x−6y+14=0
c)
y2−6x−10y+14=0
d)
y2−10x−6y+14=0

|
Nipun Tuteja answered |
Let the equation of circle be x2+y2+2gx+2fy+c=0.
Then the radius,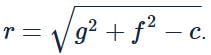
Centre: (−g,−f).
But since circle touches Y-axis, the absolute value of abscissa is equal to the radius, |−g|=r.
⇒g2=r2⇒g2=g2+f2−c
⇒c=f2
Centre of the circle, x2+y2−6x−6y+14=0: (3,3)
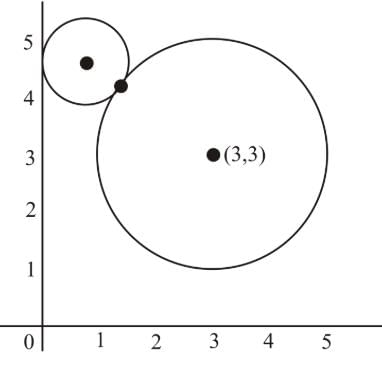
As the two circles touch externally, the distance between
centres is equal to the sum of radii.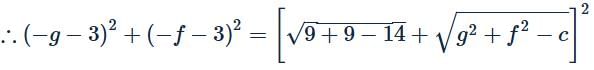
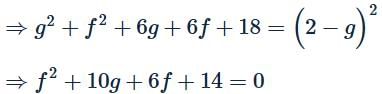
Hence, locus of the centre (−g,−f) obtained by substituting −g=x, −f=y⇒g=−x, f=−y, is y2−10x−6y+14=0.
Then the radius,
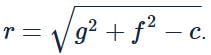
Centre: (−g,−f).
But since circle touches Y-axis, the absolute value of abscissa is equal to the radius, |−g|=r.
⇒g2=r2⇒g2=g2+f2−c
⇒c=f2
Centre of the circle, x2+y2−6x−6y+14=0: (3,3)

As the two circles touch externally, the distance between
centres is equal to the sum of radii.
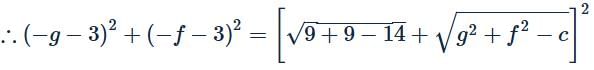
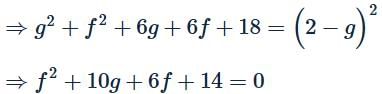
Hence, locus of the centre (−g,−f) obtained by substituting −g=x, −f=y⇒g=−x, f=−y, is y2−10x−6y+14=0.
The equations x = at2, y = 4at ; t ∈ R represent- a)a parabola
- b)a circle
- c)an ellipse
- d)a hyperbola
Correct answer is option 'A'. Can you explain this answer?
The equations x = at2, y = 4at ; t ∈ R represent
a)
a parabola
b)
a circle
c)
an ellipse
d)
a hyperbola

|
Anjali Mehla answered |
Firstly I think you have to know the equation of a parabola and it's proff
The equation of the circle passing through (0, 0) and making intercepts a and b on the coordinate axes is:- a)x2 + y2 - 2ax - 2by = 0
- b)x2 + y2 - ax - by = a2 + b2
- c)x2 + y2 - ax - by = 0
- d)x2 + y2 + 4x + 6y + 13 = 0
Correct answer is option 'C'. Can you explain this answer?
The equation of the circle passing through (0, 0) and making intercepts a and b on the coordinate axes is:
a)
x2 + y2 - 2ax - 2by = 0
b)
x2 + y2 - ax - by = a2 + b2
c)
x2 + y2 - ax - by = 0
d)
x2 + y2 + 4x + 6y + 13 = 0
|
|
Rithika Sarkar answered |
Given information:
- The circle passes through the point (0, 0).
- The circle intercepts on the coordinate axes are a and b.
To find the equation of the circle, we can use the standard form of the equation of a circle:
(x - h)² + (y - k)² = r²
where (h, k) is the center of the circle and r is the radius.
Let's find the center of the circle first:
Since the circle passes through the point (0, 0), the center must lie on the perpendicular bisectors of the intercepts on the coordinate axes.
The perpendicular bisector of the x-axis intercept (a, 0) is the line y = 0.
The perpendicular bisector of the y-axis intercept (0, b) is the line x = 0.
Therefore, the center of the circle is the intersection of these two lines, which is the point (0, 0).
Now, let's find the radius of the circle:
The radius can be found using the distance formula between the center (0, 0) and any point on the circle. Let's take the x-axis intercept (a, 0).
The distance between (0, 0) and (a, 0) is given by:
r = √[(a - 0)² + (0 - 0)²]
= √[a²]
= a
So, the radius of the circle is a.
Therefore, the equation of the circle is:
(x - 0)² + (y - 0)² = a²
x² + y² = a²
However, none of the given options match this equation.
Let's check the options again:
a) x² + y² - 2ax - 2by = 0
b) x² + y² - ax - by = a² + b²
c) x² + y² - ax - by = 0
d) x² + y² + 4x + 6y + 13 = 0
Option C (x² + y² - ax - by = 0) is the closest match to the equation we derived (x² + y² = a²).
Therefore, the correct answer is option C.
- The circle passes through the point (0, 0).
- The circle intercepts on the coordinate axes are a and b.
To find the equation of the circle, we can use the standard form of the equation of a circle:
(x - h)² + (y - k)² = r²
where (h, k) is the center of the circle and r is the radius.
Let's find the center of the circle first:
Since the circle passes through the point (0, 0), the center must lie on the perpendicular bisectors of the intercepts on the coordinate axes.
The perpendicular bisector of the x-axis intercept (a, 0) is the line y = 0.
The perpendicular bisector of the y-axis intercept (0, b) is the line x = 0.
Therefore, the center of the circle is the intersection of these two lines, which is the point (0, 0).
Now, let's find the radius of the circle:
The radius can be found using the distance formula between the center (0, 0) and any point on the circle. Let's take the x-axis intercept (a, 0).
The distance between (0, 0) and (a, 0) is given by:
r = √[(a - 0)² + (0 - 0)²]
= √[a²]
= a
So, the radius of the circle is a.
Therefore, the equation of the circle is:
(x - 0)² + (y - 0)² = a²
x² + y² = a²
However, none of the given options match this equation.
Let's check the options again:
a) x² + y² - 2ax - 2by = 0
b) x² + y² - ax - by = a² + b²
c) x² + y² - ax - by = 0
d) x² + y² + 4x + 6y + 13 = 0
Option C (x² + y² - ax - by = 0) is the closest match to the equation we derived (x² + y² = a²).
Therefore, the correct answer is option C.
The line y = c is a tangent to the parabola 7/2 if c is equal to- a)a
- b)0
- c)2a
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
The line y = c is a tangent to the parabola 7/2 if c is equal to
a)
a
b)
0
c)
2a
d)
none of these
|
|
Sravya Nair answered |
y = x is tangent to the parabola
y=ax2+c
if a= then c=?
y′ =2ax
y’ = 2(7/2)x =1
x = 1/7
1/7 = 2(1/7)2 + c
c = 1/7 * 2/49
c = 7/2
y=ax2+c
if a= then c=?
y′ =2ax
y’ = 2(7/2)x =1
x = 1/7
1/7 = 2(1/7)2 + c
c = 1/7 * 2/49
c = 7/2
A and B are two distinct points, Locus of a point P satisfying |PA| + |PB| = 2k, a constant is- a)nothing can be said
- b)the line segment [AB]
- c)an ellipse
- d)a hyperbola
Correct answer is option 'A'. Can you explain this answer?
A and B are two distinct points, Locus of a point P satisfying |PA| + |PB| = 2k, a constant is
a)
nothing can be said
b)
the line segment [AB]
c)
an ellipse
d)
a hyperbola
|
|
Ram Mohith answered |
I think the locus of P is an ellipse because if yo... moreu take any point on the ellipse then the sum of distance from focii to that
If the circle x2 + y2 = 9 touches the circle x2 + y2 + 6y + c = 0, then c is equal to- a)27
- b)36
- c)–36
- d)–27
Correct answer is option 'A'. Can you explain this answer?
If the circle x2 + y2 = 9 touches the circle x2 + y2 + 6y + c = 0, then c is equal to
a)
27
b)
36
c)
–36
d)
–27
|
|
Jithin Roy answered |
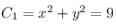
touches the another circle
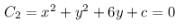
Now, Central first circle will be
And its radius will be 3 units.
Also,centre of second circle
And radius,
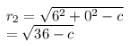
As both touches each other
So,

The equation of the circle passing through (3, 6) and whose centre is (2, –1) is- a)x2 + y2 – 4x + 2y = 45
- b)x2 + y2 – 4x – 2y + 45 = 0
- c)x2 + y2 + 4x – 2y = 45
- d)x2 + y2 – 4x + 2y + 45 = 0
Correct answer is option 'A'. Can you explain this answer?
The equation of the circle passing through (3, 6) and whose centre is (2, –1) is
a)
x2 + y2 – 4x + 2y = 45
b)
x2 + y2 – 4x – 2y + 45 = 0
c)
x2 + y2 + 4x – 2y = 45
d)
x2 + y2 – 4x + 2y + 45 = 0
|
|
Meghana Pillai answered |
To find the equation of the circle passing through (3, 6) and with center (2, c), we can use the distance formula.
The distance between the center (2, c) and the point (3, 6) should be equal to the radius of the circle. Let's call the radius r.
Using the distance formula:
√((3 - 2)^2 + (6 - c)^2) = r
Simplifying this equation:
√(1 + (6 - c)^2) = r
Squaring both sides of the equation:
1 + (6 - c)^2 = r^2
Now we need one more piece of information to find the value of c and r.
The distance between the center (2, c) and the point (3, 6) should be equal to the radius of the circle. Let's call the radius r.
Using the distance formula:
√((3 - 2)^2 + (6 - c)^2) = r
Simplifying this equation:
√(1 + (6 - c)^2) = r
Squaring both sides of the equation:
1 + (6 - c)^2 = r^2
Now we need one more piece of information to find the value of c and r.
The angle between the tangents drawn from the origin to the circle = (x−7)2+(y+1)2 = 25 is - a)π/8
- b)π/2
- c)π/6
- d)π/3
Correct answer is option 'B'. Can you explain this answer?
The angle between the tangents drawn from the origin to the circle = (x−7)2+(y+1)2 = 25 is
a)
π/8
b)
π/2
c)
π/6
d)
π/3
|
|
Shalini Yadav answered |
Let the equation of tangent drawn from (0,0) to the circle be y=mx. Then, p = a ⇒ 7m+1/(m2+1)1/2= 5
⇒24m2 + 14m−24=0
⇒12m2 + 7m−12=0
⇒m1m2 = −12/12 =−1
∴ Required angle = π/2
⇒24m2 + 14m−24=0
⇒12m2 + 7m−12=0
⇒m1m2 = −12/12 =−1
∴ Required angle = π/2
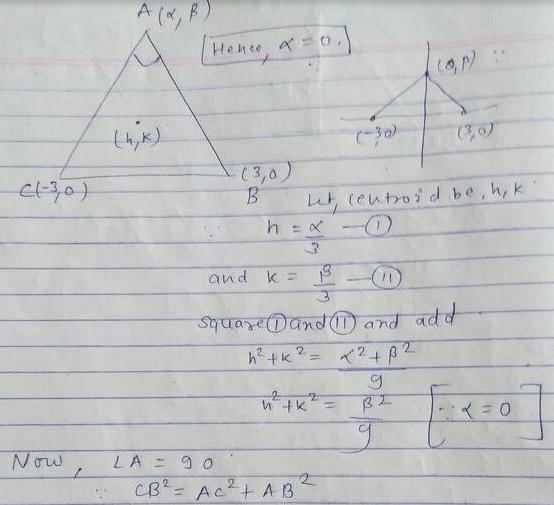
B and C are fixed point having co-ordinates (3, 0) and (–3, 0) respectively. If the vertical angle BAC is 90º, then the locus of the centroid of the DABC has the equation- a)x2 + y2 = 1
- b) x2 + y2 = 2
- c)9(x2 + y2) = 1
- d)9(x2 + y2) = 4
Correct answer is option 'A'. Can you explain this answer?
B and C are fixed point having co-ordinates (3, 0) and (–3, 0) respectively. If the vertical angle BAC is 90º, then the locus of the centroid of the DABC has the equation
a)
x2 + y2 = 1
b)
x2 + y2 = 2
c)
9(x2 + y2) = 1
d)
9(x2 + y2) = 4

|
Maheshwar Malik answered |
Ans.
Option (a)
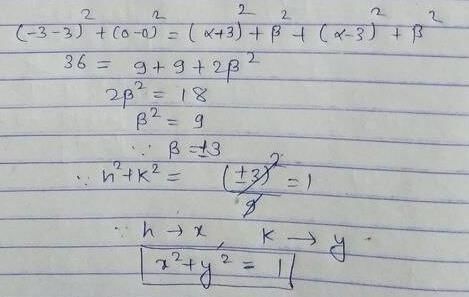
Line 3x + 4y = 25 touches the circle x2 + y2 = 25 at the point- a)(4, 3)
- b)(3, 4)
- c)(–3, –4)
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Line 3x + 4y = 25 touches the circle x2 + y2 = 25 at the point
a)
(4, 3)
b)
(3, 4)
c)
(–3, –4)
d)
None of these

|
Anagha Sharma answered |
Method to Solve :
Y= 4; x=3
Get X in terms of y from first eq.
X=(25-4y)/3
Substitute in second eq.
By solving you will get
Y2-8y+16=0
Here you will get y value as 4
Substitute in first eq we will get X value as 3
The circles x2+y2+6x+6y = 0 and x2+y2−12x−12y = 0- a)touch each other externally
- b)touch each other internally
- c)cut orthogonally
- d)intersect in two points
Correct answer is option 'A'. Can you explain this answer?
The circles x2+y2+6x+6y = 0 and x2+y2−12x−12y = 0
a)
touch each other externally
b)
touch each other internally
c)
cut orthogonally
d)
intersect in two points
|
|
Gaurav Kumar answered |
Given equation of circles are
x2+y2+6x+6y=0....(i)
and x2+y2−12x−12y=0....(ii)
Here, g1 = 3,f2 = 3, g2 = −6 and f2 = −6
∴ Centres of circles are C1(−3,−3) and C2(6,6) respectively and radii are r1 = 3√2 and r2 = 6√2 respectively.
Now, C1C2 = √[(6+3)2 + (6+3)2]
= 9√2
and r1 + r2
= 3(2)1/2 + 6(2)1/2
= 9(2)1/2
⇒ C1C2 = r1 + r2
∴ Both circles touch each other externally.
x2+y2+6x+6y=0....(i)
and x2+y2−12x−12y=0....(ii)
Here, g1 = 3,f2 = 3, g2 = −6 and f2 = −6
∴ Centres of circles are C1(−3,−3) and C2(6,6) respectively and radii are r1 = 3√2 and r2 = 6√2 respectively.
Now, C1C2 = √[(6+3)2 + (6+3)2]
= 9√2
and r1 + r2
= 3(2)1/2 + 6(2)1/2
= 9(2)1/2
⇒ C1C2 = r1 + r2
∴ Both circles touch each other externally.
The eccentricity of the conic 9x2 − 16y2 = 144 is- a)4/3
- b)5/4
- c)√7
- d)4/5
Correct answer is option 'B'. Can you explain this answer?
The eccentricity of the conic 9x2 − 16y2 = 144 is
a)
4/3
b)
5/4
c)
√7
d)
4/5
|
|
Mihir Chaudhary answered |
+16y2=144 is:
To find the eccentricity of a conic, we need to first identify the type of conic. We can rewrite the given equation as:
9x^2/144 + 16y^2/144 = 1
Dividing both sides by 144, we get:
x^2/16 + y^2/9 = 1
This is the equation of an ellipse. To find the eccentricity, we need to first find the distance between the center of the ellipse and one of its foci. The center of the ellipse is at the point (0,0). We can find the length of the semi-major axis (a) and the semi-minor axis (b) using the equation:
a^2 = 16, b^2 = 9
a = 4, b = 3
The distance between the center and one of the foci (c) can be found using the equation:
c^2 = a^2 - b^2
c^2 = 16 - 9 = 7
c = sqrt(7)
The eccentricity (e) of the ellipse is given by the equation:
e = c/a
e = sqrt(7)/4
Therefore, the eccentricity of the conic 9x^2+16y^2=144 is sqrt(7)/4.
To find the eccentricity of a conic, we need to first identify the type of conic. We can rewrite the given equation as:
9x^2/144 + 16y^2/144 = 1
Dividing both sides by 144, we get:
x^2/16 + y^2/9 = 1
This is the equation of an ellipse. To find the eccentricity, we need to first find the distance between the center of the ellipse and one of its foci. The center of the ellipse is at the point (0,0). We can find the length of the semi-major axis (a) and the semi-minor axis (b) using the equation:
a^2 = 16, b^2 = 9
a = 4, b = 3
The distance between the center and one of the foci (c) can be found using the equation:
c^2 = a^2 - b^2
c^2 = 16 - 9 = 7
c = sqrt(7)
The eccentricity (e) of the ellipse is given by the equation:
e = c/a
e = sqrt(7)/4
Therefore, the eccentricity of the conic 9x^2+16y^2=144 is sqrt(7)/4.
Chapter doubts & questions for Circle - 6 Months Preparation for JEE 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Circle - 6 Months Preparation for JEE in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily







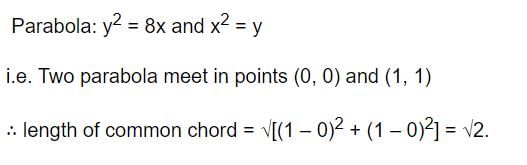

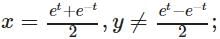 t ∈ R represents
t ∈ R represents