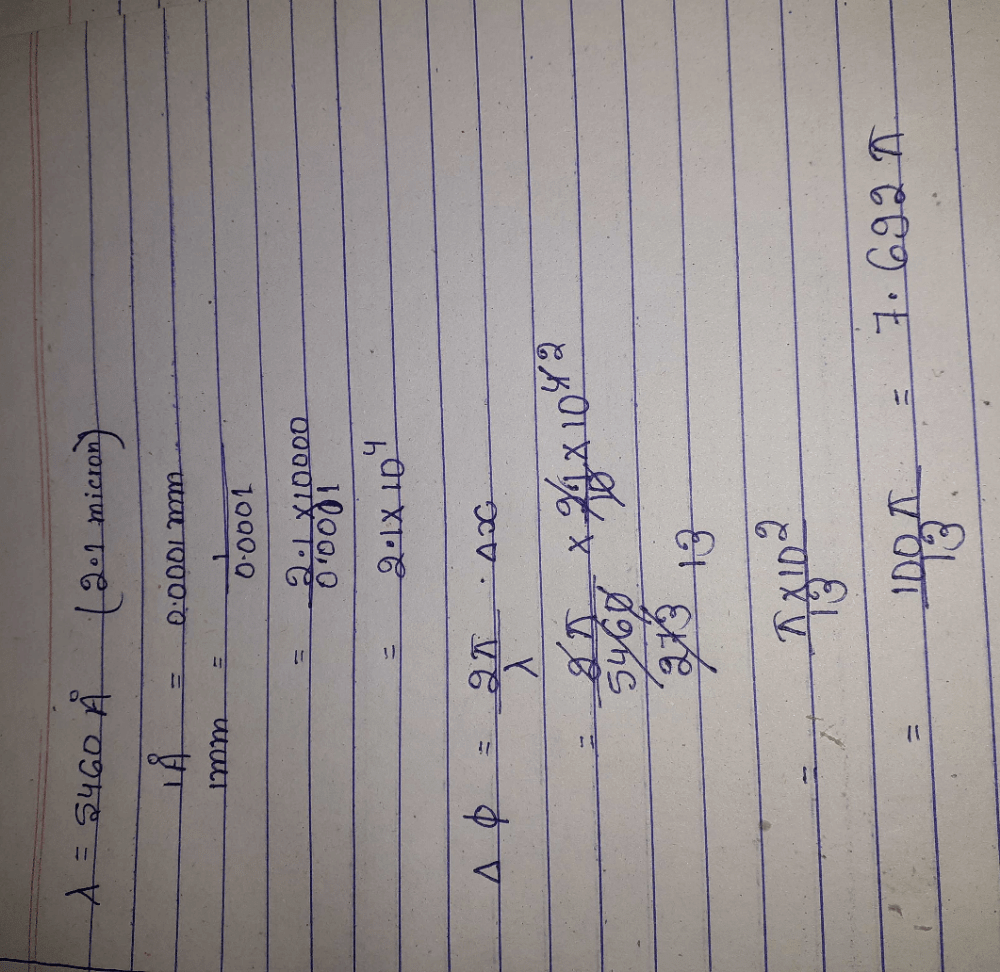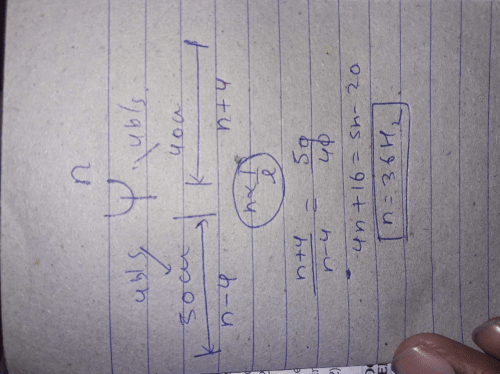All questions of Matter Waves for Grade 9 Exam
As a wave propagates; which of the following is not satisfied?- a)the wave intensity remains constant for a plane wave
- b)total intensity of the spherical wave over the spherical surface centered at the source remains constant at all times
- c)the wave intensity decreases as the inverse of the square of the distance from the source for a spherical wave
- d)the wave intensity decreases as the inverse of the distance from the source for a spherical wave
Correct answer is option 'D'. Can you explain this answer?
As a wave propagates; which of the following is not satisfied?
a)
the wave intensity remains constant for a plane wave
b)
total intensity of the spherical wave over the spherical surface centered at the source remains constant at all times
c)
the wave intensity decreases as the inverse of the square of the distance from the source for a spherical wave
d)
the wave intensity decreases as the inverse of the distance from the source for a spherical wave
|
|
Shatabdi Malik answered |
I think it's ans is C.
An echo repeats two syllables. If the velocity of sound is 330 m/s, then the distance of reflecting surface is- a)16.5 m
- b)99 m
- c)66 m
- d)33.0 m
Correct answer is option 'C'. Can you explain this answer?
An echo repeats two syllables. If the velocity of sound is 330 m/s, then the distance of reflecting surface is
a)
16.5 m
b)
99 m
c)
66 m
d)
33.0 m
|
Rajesh Gupta answered |
Let us say that we speak syllables at a rate of 2 to 9 per second. So let us say that a syllable takes a minimum of 0.1 sec for a fast speaker. Let us say that a sound pulse (syllable) is emitted starting at t = 0.
The effect of a syllable lasts on the ear for 0.1 sec. So if any echo reaches the year before t = 0.2 sec., then it is mixed with the direct sound present in the ear and so echo is not properly heard.
In this problem, two syllables are repeated in the echo. That is it took about 2 * 0.2 sec ie., 0.4 seconds for the sound to travel to the reflecting surface and come back to the ear.
The distance of the reflecting surface from the person
= 330 m/s * 0.4 sec / 2
= 66 meters.
A stationary observer receives sonic oscillations from two tuning forks, one of which approaches and the other recedes with same speed. As this takes place the observer hears the beat frequency of 2 Hz. Find the speed of each tuning fork,(assuming it is very small when compared to sound) if their oscillation frequency is 680 Hz and the velocity of sound in air is 340 m/s. - a)1 m/s
- b)2 m/s
- c)0.5 m/s
- d)1.5 m/s
Correct answer is option 'C'. Can you explain this answer?
A stationary observer receives sonic oscillations from two tuning forks, one of which approaches and the other recedes with same speed. As this takes place the observer hears the beat frequency of 2 Hz. Find the speed of each tuning fork,(assuming it is very small when compared to sound) if their oscillation frequency is 680 Hz and the velocity of sound in air is 340 m/s.
a)
1 m/s
b)
2 m/s
c)
0.5 m/s
d)
1.5 m/s
|
Lavanya Menon answered |
Let the frequencies be f1 and f2
So, f1 = f (vs/vs - v) and f2 = f (vs/vs + v)
ATQ: f1 – f2 = 2 Hz
So, f1 = f (vs/vs - v) and f2 = f (vs/vs + v)
ATQ: f1 – f2 = 2 Hz
The speed of propagation of a sinusoidal wave is given by V=νλ where- a)ν is the reciprocal of the period and λ is the dispersion
- b)ν is the reciprocal of the period and λ is the wave number
- c)ν is the angular frequency and λ is the wavelength
- d)ν is the reciprocal of the period and λ is the wavelength
Correct answer is option 'D'. Can you explain this answer?
The speed of propagation of a sinusoidal wave is given by V=νλ where
a)
ν is the reciprocal of the period and λ is the dispersion
b)
ν is the reciprocal of the period and λ is the wave number
c)
ν is the angular frequency and λ is the wavelength
d)
ν is the reciprocal of the period and λ is the wavelength
|
Om Desai answered |
For a sinusoidal wave, V = v λ.
V = speed,
v = frequency,
λ = wavelength,
frequency (v) = reciprocal of the time period i.e. v =1/T
V = speed,
v = frequency,
λ = wavelength,
frequency (v) = reciprocal of the time period i.e. v =1/T
To the nearest order of magnitude, how many times greater than the speed of sound is the speed of light?- a)104
- b)1012
- c)108
- d)106
Correct answer is option 'D'. Can you explain this answer?
To the nearest order of magnitude, how many times greater than the speed of sound is the speed of light?
a)
104
b)
1012
c)
108
d)
106
|
|
Lavanya Menon answered |
Speed of sound in air is 343 m/s or we can say approx 300m/s
And speed of light is approx 300,000,000 m/s
Clearly the ratio is 106
And speed of light is approx 300,000,000 m/s
Clearly the ratio is 106
At t= 0, a transverse wave pulse travelling in the positive x direction with a speed of 2 m/s in a wire is described by the function y = 6/x2 given that x ≠ 0. Transverse velocity of a particle at x = 2 m and t = 2 s is - a)3 m/s
- b)-3 m/s
- c)8 m/s
- d)-8 m/s
Correct answer is option 'B'. Can you explain this answer?
At t= 0, a transverse wave pulse travelling in the positive x direction with a speed of 2 m/s in a wire is described by the function y = 6/x2 given that x ≠ 0. Transverse velocity of a particle at x = 2 m and t = 2 s is
a)
3 m/s
b)
-3 m/s
c)
8 m/s
d)
-8 m/s
|
Preeti Khanna answered |
Any transverse wave travelling in positive x-direction is of the form y = f (ax - bt) (and y = f (ax + bt) if it is travelling in negative x-direction) and has a wave speed equal to b/a.
Given a = 1 ⇒ b = 2
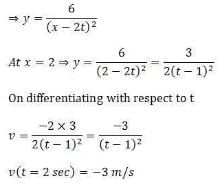
Given a = 1 ⇒ b = 2
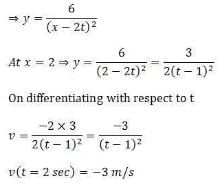
Waves associated with moving protons, electrons, neutrons, atoms are known as- a)none of these
- b)Gamma rays
- c)Matter waves
- d)Electromagnetic waves
Correct answer is option 'C'. Can you explain this answer?
Waves associated with moving protons, electrons, neutrons, atoms are known as
a)
none of these
b)
Gamma rays
c)
Matter waves
d)
Electromagnetic waves
|
Vik. Singh answered |
If they are associated with matter waves then what about electromagnetic waves..?
... I'm so confused now :(
A piano wire having a diameter of 0.90 mm is replaced by another wire of the same length and material but with a diameter of 0.93 mm. If the tension of the wire is kept the same, then the percentage change in the frequency of the fundamental tone is nearly - a)+3%
- b)+3.3 %
- c)-3.3%
- d)-3%
Correct answer is option 'C'. Can you explain this answer?
A piano wire having a diameter of 0.90 mm is replaced by another wire of the same length and material but with a diameter of 0.93 mm. If the tension of the wire is kept the same, then the percentage change in the frequency of the fundamental tone is nearly
a)
+3%
b)
+3.3 %
c)
-3.3%
d)
-3%
|
|
Preeti Iyer answered |
Out of all the given quantities only frequency of the wire "f” and radius of the wire "R" changes and the remaining doesn't. Also if a quantity doesn't change (or is a constant) its derivative is zero. Given, initial radius = 0.45 mm and final radius = 0.465 mm so change in radius, ΔR = 0.015 mm
Velocity of sound in air is 300 m/s. Then the distance between two successive nodes of a stationary wave of frequency 1000 Hz is.- a)20cm
- b)15 cm
- c)30cm
- d)10 cm
Correct answer is option 'B'. Can you explain this answer?
Velocity of sound in air is 300 m/s. Then the distance between two successive nodes of a stationary wave of frequency 1000 Hz is.
a)
20cm
b)
15 cm
c)
30cm
d)
10 cm
|
|
Raghav Bansal answered |
Velocity of sound in air= 300m/s =300×100=30000 cm/s
And frequency = 1000 hz
So, wavelength = Velocity/frequency
= 30000/1000= 30
Distance = wavelength/2
=30/2 = 15
And frequency = 1000 hz
So, wavelength = Velocity/frequency
= 30000/1000= 30
Distance = wavelength/2
=30/2 = 15
A 100 m long rod of density 10.0 x 104 kg/m3 and having Young’s modules Y = 1011 Pa, is clamped at one end. It is hammered at the other free end. The longitudinal pulse goes to right end, gets reflected and again returns to the left end. How much time, the pulse take to go back to initial point.
- a)0.1 sec
- b)0.2 sec
- c)0.3 sec
- d)2 sec
Correct answer is option 'B'. Can you explain this answer?
A 100 m long rod of density 10.0 x 104 kg/m3 and having Young’s modules Y = 1011 Pa, is clamped at one end. It is hammered at the other free end. The longitudinal pulse goes to right end, gets reflected and again returns to the left end. How much time, the pulse take to go back to initial point.
a)
0.1 sec
b)
0.2 sec
c)
0.3 sec
d)
2 sec
|
|
Rajesh Gupta answered |
The velocity of a wave in any rod is given by,
Note that we should take twice the length of the rod since we want time take by the wave to return back to the initial point.
Note that we should take twice the length of the rod since we want time take by the wave to return back to the initial point.
A fork of unknown frequency when sounded with another fork of frequency 256 Hz produces 4 beats/sec. The first fork is loaded with wax. It again produces 4 beats/sec. When sounded together with the fork of 256 Hz frequency, then the frequency of first tuning fork is- a)252 Hz
- b)260Hz
- c)None of these
- d)252 or 260 Hz
Correct answer is option 'B'. Can you explain this answer?
A fork of unknown frequency when sounded with another fork of frequency 256 Hz produces 4 beats/sec. The first fork is loaded with wax. It again produces 4 beats/sec. When sounded together with the fork of 256 Hz frequency, then the frequency of first tuning fork is
a)
252 Hz
b)
260Hz
c)
None of these
d)
252 or 260 Hz
|
|
Raghav Bansal answered |
After waxing the frequency of the tuning fork decreases and so the initial frequency must be higher so as to decrease it below 256 Hz in order to give 4 beats/sec.
The necessary condition for phenomenon of interference to occur is- a)There should be two coherent sources.
- b)The frequency and amplitude of both the waves should be same
- c)The propagation of waves should be simultaneously and in same direction
- d)All of the above
Correct answer is option 'D'. Can you explain this answer?
The necessary condition for phenomenon of interference to occur is
a)
There should be two coherent sources.
b)
The frequency and amplitude of both the waves should be same
c)
The propagation of waves should be simultaneously and in same direction
d)
All of the above
|
Neha Joshi answered |
The necessary condition for phenomenon of interference to occur are:
1. There should be two coherent sources.
2. The frequency and amplitude of both the waves should be same.
3. The propagation of waves should be simultaneously and in same direction.
These are the conditions, no explanation.
1. There should be two coherent sources.
2. The frequency and amplitude of both the waves should be same.
3. The propagation of waves should be simultaneously and in same direction.
These are the conditions, no explanation.
Two harmonic waves traveling on a string in the same direction both have a frequency of 100 Hz, a wavelenqth of 2.0cm, and amplitude of 0.020 m. In addition, they overlap each other. What is the amplitude of the resultant wave if the original waves differ in phase by Syntax error from line 1 column 49 to line 1 column 73. Unexpected ‘mathsize’./6?- a)3.5 cm
- b)4.2 cm
- c)3.7 cm
- d)3.9 cm
Correct answer is option 'D'. Can you explain this answer?
Two harmonic waves traveling on a string in the same direction both have a frequency of 100 Hz, a wavelenqth of 2.0cm, and amplitude of 0.020 m. In addition, they overlap each other. What is the amplitude of the resultant wave if the original waves differ in phase by Syntax error from line 1 column 49 to line 1 column 73. Unexpected ‘mathsize’./6?
a)
3.5 cm
b)
4.2 cm
c)
3.7 cm
d)
3.9 cm
|
Rajeev Nair answered |
Question:
Two harmonic waves traveling on a string in the same direction both have a frequency of 100 Hz, a wavelength of 2.0 cm, and amplitude of 0.020 m. In addition, they overlap each other. What is the amplitude of the resultant wave if the original waves differ in phase by 6π?
Solution:
Given parameters:
Frequency of each wave = 100 Hz
Wavelength of each wave = 2.0 cm
Amplitude of each wave = 0.020 m
Phase difference between the waves = 6π
To find: Amplitude of the resultant wave
We know that the displacement of a wave is given by the equation:
y = A sin(kx - ωt + φ)
where, A = amplitude of the wave, k = wave number, x = position, ω = angular frequency, t = time, and φ = phase constant.
For two waves with the same frequency and wavelength traveling in the same direction, the wave number and angular frequency are the same, and the displacement equation becomes:
y1 = A sin(kx - ωt + φ1)
y2 = A sin(kx - ωt + φ2)
where, φ1 and φ2 are the phase constants of the two waves.
The resultant wave is obtained by adding the two waves:
y = y1 + y2
= A sin(kx - ωt + φ1) + A sin(kx - ωt + φ2)
= 2A cos((φ1 - φ2)/2) sin(kx - ωt + (φ1 + φ2)/2)
where, cos((φ1 - φ2)/2) is the amplitude of the resultant wave.
Given that the phase difference between the waves is 6π, we have:
φ1 - φ2 = 6π
cos((φ1 - φ2)/2) = cos(3π) = -1
Substituting the given values, we get:
Amplitude of the resultant wave = 2(0.020) (-1) = -0.040 m
However, amplitude is always positive, so we take the absolute value:
Amplitude of the resultant wave = 0.040 m
Therefore, the amplitude of the resultant wave is 0.040 m.
Two harmonic waves traveling on a string in the same direction both have a frequency of 100 Hz, a wavelength of 2.0 cm, and amplitude of 0.020 m. In addition, they overlap each other. What is the amplitude of the resultant wave if the original waves differ in phase by 6π?
Solution:
Given parameters:
Frequency of each wave = 100 Hz
Wavelength of each wave = 2.0 cm
Amplitude of each wave = 0.020 m
Phase difference between the waves = 6π
To find: Amplitude of the resultant wave
We know that the displacement of a wave is given by the equation:
y = A sin(kx - ωt + φ)
where, A = amplitude of the wave, k = wave number, x = position, ω = angular frequency, t = time, and φ = phase constant.
For two waves with the same frequency and wavelength traveling in the same direction, the wave number and angular frequency are the same, and the displacement equation becomes:
y1 = A sin(kx - ωt + φ1)
y2 = A sin(kx - ωt + φ2)
where, φ1 and φ2 are the phase constants of the two waves.
The resultant wave is obtained by adding the two waves:
y = y1 + y2
= A sin(kx - ωt + φ1) + A sin(kx - ωt + φ2)
= 2A cos((φ1 - φ2)/2) sin(kx - ωt + (φ1 + φ2)/2)
where, cos((φ1 - φ2)/2) is the amplitude of the resultant wave.
Given that the phase difference between the waves is 6π, we have:
φ1 - φ2 = 6π
cos((φ1 - φ2)/2) = cos(3π) = -1
Substituting the given values, we get:
Amplitude of the resultant wave = 2(0.020) (-1) = -0.040 m
However, amplitude is always positive, so we take the absolute value:
Amplitude of the resultant wave = 0.040 m
Therefore, the amplitude of the resultant wave is 0.040 m.
In an interference arrangement similar to Young's double-slit experiment, the slits S1 & S2 are illuminated with coherent microwave sources, each of frequency 106 Hz. The sources are synchronized to have zero phase difference. The slits are separated by a distance d = 150.0 m. The intensity I(q) is measured as a function of q, where q is defined as shown. If I0 is the maximum intensity then I(q) for 0 £ q £ 90° is given by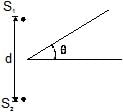 
- a) I(q) =
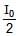for q = 30º - b)I(q) =
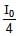for q = 90º - c) I(q) = I0 for q = 0º
- d)I(q) is constant for all values of q
Correct answer is option 'A,C'. Can you explain this answer?
In an interference arrangement similar to Young's double-slit experiment, the slits S1 & S2 are illuminated with coherent microwave sources, each of frequency 106 Hz. The sources are synchronized to have zero phase difference. The slits are separated by a distance d = 150.0 m. The intensity I(q) is measured as a function of q, where q is defined as shown. If I0 is the maximum intensity then I(q) for 0 £ q £ 90° is given by
a)
I(q) = 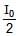for q = 30º
for q = 30º b)
I(q) = 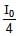for q = 90º
for q = 90º c)
I(q) = I0 for q = 0º
d)
I(q) is constant for all values of q
|
Lohit Matani answered |
I=I0cos2(πdtanθ/ λ)/
= I0cos2(πx150xtanθ/3x(108/106)
=I0cos2(πtanθ/2)
θ=30o
I= I0cos2 ((π/2√3)
I=I0/2
θ=0
I=I0cos2(0) [cos0=1]
I= I0
= I0cos2(πx150xtanθ/3x(108/106)
=I0cos2(πtanθ/2)
θ=30o
I= I0cos2 ((π/2√3)
I=I0/2
θ=0
I=I0cos2(0) [cos0=1]
I= I0
A sinusoidal wave is generated by moving the end of a string up and down, periodically. The generator must apply the energy at maximum rate when the end of the string attached to generator has X and least power when the end of the string attached to generator has Y. The most suitable option which correctly fills blanks X and Y, is - a)Maximum displacement, least acceleration
- b)maximum displacement, maximum acceleration
- c)Least displacement, maximum acceleration
- d)Least displacement, least acceleration
Correct answer is option 'C'. Can you explain this answer?
A sinusoidal wave is generated by moving the end of a string up and down, periodically. The generator must apply the energy at maximum rate when the end of the string attached to generator has X and least power when the end of the string attached to generator has Y. The most suitable option which correctly fills blanks X and Y, is
a)
Maximum displacement, least acceleration
b)
maximum displacement, maximum acceleration
c)
Least displacement, maximum acceleration
d)
Least displacement, least acceleration
|
Juhi Iyer answered |
Power for a travelling wave on a string is given by
For the displacement wave, y = A sin (kx – ωt)
Power delivered is maximum when cos2(kx – ωt) is maximum, which would be the case when sin (kx – ωt) is the least, i.e., displacement is minimum (acceleration is minimum). Power delivered is minimum when cos2(kx – ωt) is minimum, which would be when sin(kx - cos2(kx – ωt)t) is maximum, i.e displacement is maximum(acceleration is maximum).
A beam of light consisting of two wavelengths 6500 Å and 5200 Å is used to obtain interference fringes in Young's double slit experiment. The distance between slits is 2mm and the distance of screen from slits is 120 cm. What is the least distance from central maximum where the bright due to both wavelength coincide ?- a)0.156 cm
- b)0.312 cm
- c)0.078 cm
- d)0.468 cm
Correct answer is option 'A'. Can you explain this answer?
A beam of light consisting of two wavelengths 6500 Å and 5200 Å is used to obtain interference fringes in Young's double slit experiment. The distance between slits is 2mm and the distance of screen from slits is 120 cm. What is the least distance from central maximum where the bright due to both wavelength coincide ?
a)
0.156 cm
b)
0.312 cm
c)
0.078 cm
d)
0.468 cm
|
Gaurav Kumar answered |
If n is least number of fringes of λ1(=6500A∘) which are coincident with (n+1) of smaller wavelength
also β=λD/d
substituting values for wavelength,D and d we get β = 0.039cm
So,
Hence b is the correct answer.
also β=λD/d
substituting values for wavelength,D and d we get β = 0.039cm
So,
Hence b is the correct answer.
In a standard YDSE appratus a thin film (m = 1.5, t = 2.1 mm) is placed in front of upper slit. How far above or below the centre point of the screen are two nearest maxima located ? Take D = 1 m, d = 1mm, l = 4500 Å. (Symbols have usual meaning)- a) 1.5 mm (
- b)0.6 mm
- c)0.15 mm
- d)0.3 mm
Correct answer is option 'C,D'. Can you explain this answer?
In a standard YDSE appratus a thin film (m = 1.5, t = 2.1 mm) is placed in front of upper slit. How far above or below the centre point of the screen are two nearest maxima located ? Take D = 1 m, d = 1mm, l = 4500 Å. (Symbols have usual meaning)
a)
1.5 mm (
b)
0.6 mm
c)
0.15 mm
d)
0.3 mm
|
|
Geetika Shah answered |
There are three sources of sound of equal intensities with frequencies 400, 401 and 402 Hz. The number of beats per seconds is- a)3
- b)1.0
- c)0
- d)2
Correct answer is option 'B'. Can you explain this answer?
There are three sources of sound of equal intensities with frequencies 400, 401 and 402 Hz. The number of beats per seconds is
a)
3
b)
1.0
c)
0
d)
2
|
Hansa Sharma answered |
Resultant displacement of the wave by these three wave is
y=asin2π400t+asin2π401t+asin2π402t
y=a(1+2cos2πt)sin2π401t
So the resultant magnitude a(1+2cos2πt) has a maximum when,
cos2πt=1
or, t=0,1,2...
The time interval between two successive maximum is 1 sec.
So beat frequency is 1sec.
y=asin2π400t+asin2π401t+asin2π402t
y=a(1+2cos2πt)sin2π401t
So the resultant magnitude a(1+2cos2πt) has a maximum when,
cos2πt=1
or, t=0,1,2...
The time interval between two successive maximum is 1 sec.
So beat frequency is 1sec.
Maximum destructive inference between two waves occurs when the waves are out of the phase by- a)π/2radians
- b)π radians
- c)π/3 radians
- d)π/4 radians
Correct answer is option 'B'. Can you explain this answer?
Maximum destructive inference between two waves occurs when the waves are out of the phase by
a)
π/2radians
b)
π radians
c)
π/3 radians
d)
π/4 radians
|
Anjali Iyer answered |
Destructive interference occurs when the maxima of two waves are 180 degrees out of phase: a positive displacement of one wave is cancelled exactly by a negative displacement of the other wave. The amplitude of the resulting wave is zero. ... The dark regions occur whenever the waves destructively interfere.
A conveyor belt moves to the right with speed v=300 m/min. A pieman puts pies on the belt at a rate of 20 per minute while walking with speed 30 m/min towards a receiver at the other end. The frequency with which they are received by the stationary receiver is : - a)26.67 / minute
- b)30 / minute
- c)22.22/minute
- d)24 / minute
Correct answer is option 'C'. Can you explain this answer?
A conveyor belt moves to the right with speed v=300 m/min. A pieman puts pies on the belt at a rate of 20 per minute while walking with speed 30 m/min towards a receiver at the other end. The frequency with which they are received by the stationary receiver is :
a)
26.67 / minute
b)
30 / minute
c)
22.22/minute
d)
24 / minute
|
Nandini Chakraborty answered |
This problem is a Doppler effect analogy
Where f = 20/min , v= 300 m/min
And vs = 30 m / min
The waves on the surface of water are of two kinds:.- a)capillary waves and gravity waves
- b)capillary waves and sound waves
- c)sound waves and gravity waves
- d)seismic waves and cosmic waves
Correct answer is option 'A'. Can you explain this answer?
The waves on the surface of water are of two kinds:.
a)
capillary waves and gravity waves
b)
capillary waves and sound waves
c)
sound waves and gravity waves
d)
seismic waves and cosmic waves
|
|
Ameya Choudhury answered |
- Capillary waves:
Capillary waves are small ripples on the surface of water that are caused by surface tension. These waves have a wavelength shorter than 1.73 cm. They are typically seen in calm conditions and are influenced by the surface tension of the water.
- Gravity waves:
Gravity waves are larger waves on the surface of water that are caused by the force of gravity. These waves have a wavelength longer than 1.73 cm. They are influenced by factors like wind, tides, and seismic activity.
- Explanation:
In the given options, capillary waves and gravity waves are the two kinds of waves that can be observed on the surface of water. Sound waves are not typically observed on the surface of water, as they propagate through a medium like air or water. Seismic waves and cosmic waves are different types of waves that are not directly related to the surface of water.
Therefore, the correct answer is option 'A': capillary waves and gravity waves. These two types of waves play a significant role in shaping the surface of water and are important in understanding the dynamics of water bodies.
Capillary waves are small ripples on the surface of water that are caused by surface tension. These waves have a wavelength shorter than 1.73 cm. They are typically seen in calm conditions and are influenced by the surface tension of the water.
- Gravity waves:
Gravity waves are larger waves on the surface of water that are caused by the force of gravity. These waves have a wavelength longer than 1.73 cm. They are influenced by factors like wind, tides, and seismic activity.
- Explanation:
In the given options, capillary waves and gravity waves are the two kinds of waves that can be observed on the surface of water. Sound waves are not typically observed on the surface of water, as they propagate through a medium like air or water. Seismic waves and cosmic waves are different types of waves that are not directly related to the surface of water.
Therefore, the correct answer is option 'A': capillary waves and gravity waves. These two types of waves play a significant role in shaping the surface of water and are important in understanding the dynamics of water bodies.
Longitudinal waves cannot be propagated through- a)a liquid
- b)a solid
- c)vacuum
- d)a gas
Correct answer is option 'C'. Can you explain this answer?
Longitudinal waves cannot be propagated through
a)
a liquid
b)
a solid
c)
vacuum
d)
a gas
|
|
Geetika Shah answered |
Because longitudinal waves are the mechanical waves that need a medium to propagate such as air, gas, solid etc. but these are not available in vacuum, so this wave can't propagate in vacuum.
If a star emitting orange light moves away from the earth, its color will- a)appear yellow
- b)turns gradually blue
- c)remain the same
- d)appear red
Correct answer is option 'D'. Can you explain this answer?
If a star emitting orange light moves away from the earth, its color will
a)
appear yellow
b)
turns gradually blue
c)
remain the same
d)
appear red
|
|
Anjali Sharma answered |
The faster a star moves towards the earth, the more its light is shifted to higher frequencies. In contrast, if a star is moving away from the earth, its light is shifted to lower frequencies on the color spectrum (towards the orange/red/infrared/microwave/radio end of the spectrum).
The path difference between two waves
y1= A1 sin wt and y2= A2 cos (wt + f) will be - a)(λ/2π) f
- b)(λ/2π) (f + π/2)
- c)(2π/λ) (f - π/2)
- d)(2π/λ) f
Correct answer is option 'B'. Can you explain this answer?
The path difference between two waves
y1= A1 sin wt and y2= A2 cos (wt + f) will be
y1= A1 sin wt and y2= A2 cos (wt + f) will be
a)
(λ/2π) f
b)
(λ/2π) (f + π/2)
c)
(2π/λ) (f - π/2)
d)
(2π/λ) f
|
Shalini Basak answered |
Understanding the Waves
Let's analyze the two wave equations given:
- Wave 1: y1 = A1 sin(wt)
- Wave 2: y2 = A2 cos(wt + f)
The primary focus here is on the phase difference and how it contributes to the path difference between these two waves.
Phase Difference
- The phase of wave 1 at time t is wt.
- The phase of wave 2 at the same time is (wt + f).
Thus, the phase difference (Δϕ) between the two waves can be expressed as:
- Δϕ = (wt + f) - (wt) = f
Path Difference Calculation
The relationship between phase difference and path difference is given by the formula:
- Δx = (λ/2π) * Δϕ
Here, λ is the wavelength of the waves. Substituting the phase difference:
- Δx = (λ/2π) * f
Final Relationship
To express this in terms of numerical constants:
- Rearranging gives us: Δx = (λ/2π)(f)
This shows that the path difference is directly proportional to the phase difference f.
Conclusion
Among the options provided, option b) (λ/2π)(f + π/2) indicates that we must add π/2 to the phase difference, which does not accurately represent the relationship derived from our equations. Thus, it's crucial to recognize that the correct interpretation of phase difference directly relates to the path difference as:
- Δx = (λ/2π) * f
This confirms that option b is indeed the correct choice based on the phase difference and path difference relationship.
Let's analyze the two wave equations given:
- Wave 1: y1 = A1 sin(wt)
- Wave 2: y2 = A2 cos(wt + f)
The primary focus here is on the phase difference and how it contributes to the path difference between these two waves.
Phase Difference
- The phase of wave 1 at time t is wt.
- The phase of wave 2 at the same time is (wt + f).
Thus, the phase difference (Δϕ) between the two waves can be expressed as:
- Δϕ = (wt + f) - (wt) = f
Path Difference Calculation
The relationship between phase difference and path difference is given by the formula:
- Δx = (λ/2π) * Δϕ
Here, λ is the wavelength of the waves. Substituting the phase difference:
- Δx = (λ/2π) * f
Final Relationship
To express this in terms of numerical constants:
- Rearranging gives us: Δx = (λ/2π)(f)
This shows that the path difference is directly proportional to the phase difference f.
Conclusion
Among the options provided, option b) (λ/2π)(f + π/2) indicates that we must add π/2 to the phase difference, which does not accurately represent the relationship derived from our equations. Thus, it's crucial to recognize that the correct interpretation of phase difference directly relates to the path difference as:
- Δx = (λ/2π) * f
This confirms that option b is indeed the correct choice based on the phase difference and path difference relationship.
The waves with the frequency above the audible range of human beings are called _______.- a)Supersonic waves
- b)Ultrasonic waves
- c)Infrasonic waves
- d)Hypersonic waves
Correct answer is option 'B'. Can you explain this answer?
The waves with the frequency above the audible range of human beings are called _______.
a)
Supersonic waves
b)
Ultrasonic waves
c)
Infrasonic waves
d)
Hypersonic waves
|
|
Sanskriti Shah answered |
Understanding Ultrasonic Waves
Ultrasonic waves are sound waves with frequencies above the audible range for humans, typically greater than 20 kHz. These waves are often utilized in various applications due to their unique properties.
Characteristics of Ultrasonic Waves
- Frequency Range: Ultrasonic waves have frequencies that exceed 20 kHz, making them inaudible to the human ear.
- Applications: They are widely used in medical imaging (ultrasound), industrial cleaning, and pest control.
Comparison with Other Wave Types
- Supersonic Waves: These refer to speeds greater than the speed of sound in air but do not specifically pertain to frequency.
- Infrasonic Waves: These are sound waves with frequencies below 20 Hz, which are also inaudible to humans.
- Hypersonic Waves: This term generally relates to speeds much greater than supersonic, not directly tied to frequency.
Why "Ultrasonic" is the Correct Answer
- Direct Definition: The term "ultrasonic" specifically denotes sound waves above the audible frequency range, making it the most accurate choice for this question.
- Scientific Relevance: In scientific and engineering contexts, the distinction between ultrasonic, infrasonic, and supersonic is crucial for understanding sound behavior and applications.
In summary, ultrasonic waves are defined by their high frequency beyond human hearing, distinguishing them from infrasonic and supersonic waves. This specificity makes option 'B' the correct answer.
Ultrasonic waves are sound waves with frequencies above the audible range for humans, typically greater than 20 kHz. These waves are often utilized in various applications due to their unique properties.
Characteristics of Ultrasonic Waves
- Frequency Range: Ultrasonic waves have frequencies that exceed 20 kHz, making them inaudible to the human ear.
- Applications: They are widely used in medical imaging (ultrasound), industrial cleaning, and pest control.
Comparison with Other Wave Types
- Supersonic Waves: These refer to speeds greater than the speed of sound in air but do not specifically pertain to frequency.
- Infrasonic Waves: These are sound waves with frequencies below 20 Hz, which are also inaudible to humans.
- Hypersonic Waves: This term generally relates to speeds much greater than supersonic, not directly tied to frequency.
Why "Ultrasonic" is the Correct Answer
- Direct Definition: The term "ultrasonic" specifically denotes sound waves above the audible frequency range, making it the most accurate choice for this question.
- Scientific Relevance: In scientific and engineering contexts, the distinction between ultrasonic, infrasonic, and supersonic is crucial for understanding sound behavior and applications.
In summary, ultrasonic waves are defined by their high frequency beyond human hearing, distinguishing them from infrasonic and supersonic waves. This specificity makes option 'B' the correct answer.
Y (x,t) =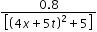 
Syntax error from line 1 column 49 to line 1 column 73. Unexpected ‘mathsize’. represents a moving pulse where X and y are n metres and t in second. Then which of the following dose not hold true?- a)its maximum displacement is 0.16 m
- b)pulse is moving positive X-direction
- c)it is a symmetric pulse
- d)in 2 s it will travel a distance of 2.5 m
Correct answer is option 'B'. Can you explain this answer?
Y (x,t) = 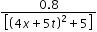Syntax error from line 1 column 49 to line 1 column 73. Unexpected ‘mathsize’. represents a moving pulse where X and y are n metres and t in second. Then which of the following dose not hold true?
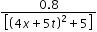Syntax error from line 1 column 49 to line 1 column 73. Unexpected ‘mathsize’. represents a moving pulse where X and y are n metres and t in second. Then which of the following dose not hold true?a)
its maximum displacement is 0.16 m
b)
pulse is moving positive X-direction
c)
it is a symmetric pulse
d)
in 2 s it will travel a distance of 2.5 m
|
|
Pooja Shah answered |
t = 0 & x = 0
y = 0.16 m
ymax = 0.16 m
Pulse is symmetric because y (x) = y (-x)
t = 1s
x=-1.25m
y is again 0.16m
Therefore speed is 1.25m/s
So it travels 2.5 m in 2 sec
y = 0.16 m
ymax = 0.16 m
Pulse is symmetric because y (x) = y (-x)
t = 1s
x=-1.25m
y is again 0.16m
Therefore speed is 1.25m/s
So it travels 2.5 m in 2 sec
The quantity similar to extension or compression of the spring in sound wave propagation (air) is- a)the change in air density
- b)the change in air composition
- c)the change in air particles
- d)the change in air humidity
Correct answer is option 'A'. Can you explain this answer?
The quantity similar to extension or compression of the spring in sound wave propagation (air) is
a)
the change in air density
b)
the change in air composition
c)
the change in air particles
d)
the change in air humidity
|
Saumya Ahuja answered |
Explanation:As in air wave propagates in the form of compression (increase in density of air) and rarefaction (decrease in density of air).
When sound travels from air to water the quantity that remains unchanged is- a)wavelength
- b)frequency
- c)speed
- d)intensity
Correct answer is option 'B'. Can you explain this answer?
When sound travels from air to water the quantity that remains unchanged is
a)
wavelength
b)
frequency
c)
speed
d)
intensity
|
|
Ram Hande answered |
Because, frequency of a wave depend on source
V1/λ1=V2/λ2 as frequency is constant
V1-velocity of sound wave in air
V2-velocity of sound wave in water
When we make a mobile telephone call to a friend- a)the friend's mobile receives electromagnetic waves containing your audio
- b)the friend's mobile receives acoustic waves containing your audio
- c)the friend's mobile receives gravity waves containing your audio
- d)the friend's mobile generates possible electrical signals
Correct answer is option 'A'. Can you explain this answer?
When we make a mobile telephone call to a friend
a)
the friend's mobile receives electromagnetic waves containing your audio
b)
the friend's mobile receives acoustic waves containing your audio
c)
the friend's mobile receives gravity waves containing your audio
d)
the friend's mobile generates possible electrical signals
|
Kritika Bajaj answered |
Explanation:Because mobile communication is a space communication and in space communication basically electromagnetic waves are used (as carrier waves as in case of radio communication) because of the modulation ( frequency, amplitude) operations which can be performed on EM waves. Thus when our friend receives the call, he also receives EM waves which is the carrier of our audio signals.
A plane sound wave is travelling in a medium. In a reference frame A fixed to the medium , its equation is y = a cos(ωt − kx ) . With respect to reference frame B, moving with a constant velocity v in the direction of propagation of the wave, equation of the wave will be - a)y = a cos[(ωt + kv) t − kx ]
- b)y = −a cos[(ωt − kv) t − kx ]
- c)y = a cos[(ωt − kv) t − kx ]
- d)y = a cos[(ωt + kv) t + kx ]
Correct answer is option 'C'. Can you explain this answer?
A plane sound wave is travelling in a medium. In a reference frame A fixed to the medium , its equation is y = a cos(ωt − kx ) . With respect to reference frame B, moving with a constant velocity v in the direction of propagation of the wave, equation of the wave will be
a)
y = a cos[(ωt + kv) t − kx ]
b)
y = −a cos[(ωt − kv) t − kx ]
c)
y = a cos[(ωt − kv) t − kx ]
d)
y = a cos[(ωt + kv) t + kx ]
|
|
Manisha Mehta answered |
Suppose at an instant t, the x – coordinate of a point with reference to moving frame is x0. Since at this moment, origin of moving frame is at distance vt from origin of the fixed reference frame, therefore, putting this value of x in the given equation, we get
y = a cos[ωt − k (vt − x )]
y = a cos[(ωt − kv)t − kx ]
A string of length 1.5 m with its two ends clamped is vibrating in fundamental mode. Amplitude at the centre of the string is 4 mm. Distance between the two points having amplitude 2 mm is: - a)1 m
- b)75cm
- c)60cm
- d)50 cm
Correct answer is option 'A'. Can you explain this answer?
A string of length 1.5 m with its two ends clamped is vibrating in fundamental mode. Amplitude at the centre of the string is 4 mm. Distance between the two points having amplitude 2 mm is:
a)
1 m
b)
75cm
c)
60cm
d)
50 cm
|
|
Jyoti Kumar answered |
**Given:**
- Length of the string = 1.5 m
- Amplitude at the center of the string = 4 mm
- Amplitude at two points = 2 mm
**To find:**
- Distance between the two points having an amplitude of 2 mm
**Solution:**
The fundamental frequency of a string fixed at both ends is given by the formula:
f = (v/2L)
Where,
- f is the frequency of vibration
- v is the velocity of the wave
- L is the length of the string
In the fundamental mode, the wavelength (λ) is double the length of the string. So,
λ = 2L
The velocity of the wave is given by the formula:
v = fλ
Substituting the value of λ, we get:
v = f * 2L
In the fundamental mode, the amplitude is maximum at the center of the string and zero at the ends. So, the amplitude decreases linearly from the center to the ends.
Let's consider the distance (x) from the center of the string to a point where the amplitude is 2 mm.
Using the amplitude formula,
A = (2mm) = (4mm) * (1 - 2x/L)
Simplifying the equation,
1/2 = 1 - 2x/L
2x/L = 1/2
x/L = 1/4
So, the distance between the two points having an amplitude of 2 mm is 1/4 times the length of the string.
Substituting the given length of the string, we get:
x = (1/4) * 1.5m
x = 0.375m
Converting to centimeters,
x = 0.375m * 100cm/m
x = 37.5cm
Therefore, the distance between the two points having an amplitude of 2 mm is 37.5 cm, which is closest to option 'A' (1m).
- Length of the string = 1.5 m
- Amplitude at the center of the string = 4 mm
- Amplitude at two points = 2 mm
**To find:**
- Distance between the two points having an amplitude of 2 mm
**Solution:**
The fundamental frequency of a string fixed at both ends is given by the formula:
f = (v/2L)
Where,
- f is the frequency of vibration
- v is the velocity of the wave
- L is the length of the string
In the fundamental mode, the wavelength (λ) is double the length of the string. So,
λ = 2L
The velocity of the wave is given by the formula:
v = fλ
Substituting the value of λ, we get:
v = f * 2L
In the fundamental mode, the amplitude is maximum at the center of the string and zero at the ends. So, the amplitude decreases linearly from the center to the ends.
Let's consider the distance (x) from the center of the string to a point where the amplitude is 2 mm.
Using the amplitude formula,
A = (2mm) = (4mm) * (1 - 2x/L)
Simplifying the equation,
1/2 = 1 - 2x/L
2x/L = 1/2
x/L = 1/4
So, the distance between the two points having an amplitude of 2 mm is 1/4 times the length of the string.
Substituting the given length of the string, we get:
x = (1/4) * 1.5m
x = 0.375m
Converting to centimeters,
x = 0.375m * 100cm/m
x = 37.5cm
Therefore, the distance between the two points having an amplitude of 2 mm is 37.5 cm, which is closest to option 'A' (1m).
The velocity of sound in gas in which two waves of wavelength 1.0 m and 0.01 m produces 4 beats/sec. is- a)360 m/s
- b)1010 m/s
- c)404 m/s
- d)440 m/s
Correct answer is option 'C'. Can you explain this answer?
The velocity of sound in gas in which two waves of wavelength 1.0 m and 0.01 m produces 4 beats/sec. is
a)
360 m/s
b)
1010 m/s
c)
404 m/s
d)
440 m/s
|
|
Ruchi Dasgupta answered |
Beats = |f1 – f2| where f1 and f2 are the frequencies
Now, f1 = v/λ1 and f2 = v/λ2
So, 4 = |v (1/1- 1/0.01)|
v = 0.0404 m/s
Now, f1 = v/λ1 and f2 = v/λ2
So, 4 = |v (1/1- 1/0.01)|
v = 0.0404 m/s
The speed of transverse waves in a string depends on:- a)Pressure on the string
- b)tension in it and its linear mass density
- c)Shear modulus and linear mass density
- d)Young’s modulus and linear mass density
Correct answer is option 'B'. Can you explain this answer?
The speed of transverse waves in a string depends on:
a)
Pressure on the string
b)
tension in it and its linear mass density
c)
Shear modulus and linear mass density
d)
Young’s modulus and linear mass density
|
|
Pooja Shah answered |
For a string v = √(T/μ)
A police car moving at 22 ms-1 , chases a motorcyclist. The police man sounds his horn at 176 Hz, while both of them move towards a stationary siren of frequency 165 Hz. Calculate the speed of the motorcycle, if it is given that the motor cyclist does not observe any beats. (Velocity of sound is 330 ms −1 ) - a)33 ms−1
- b)22 ms−1
- c)11 ms −1
- d)zero
Correct answer is option 'B'. Can you explain this answer?
A police car moving at 22 ms-1 , chases a motorcyclist. The police man sounds his horn at 176 Hz, while both of them move towards a stationary siren of frequency 165 Hz. Calculate the speed of the motorcycle, if it is given that the motor cyclist does not observe any beats. (Velocity of sound is 330 ms −1 )
a)
33 ms−1
b)
22 ms−1
c)
11 ms −1
d)
zero
|
Samridhi Kaur answered |
Frequency of the police horn
Heard by the motor cyclist is
Frequency of the stationary Siren heard by the motor cyclist is
This gives v = 22ms −1 .
Speed of sound in air is 350 m/s. An engine blows a whistle of frequency of 1200 Hz, it is approaching the observer with velocity 50 m/s. The apparent frequency as heard by the observer is- a)300 Hz
- b)1400 Hz
- c)1600 Hz
- d)1050 Hz
Correct answer is option 'B'. Can you explain this answer?
Speed of sound in air is 350 m/s. An engine blows a whistle of frequency of 1200 Hz, it is approaching the observer with velocity 50 m/s. The apparent frequency as heard by the observer is
a)
300 Hz
b)
1400 Hz
c)
1600 Hz
d)
1050 Hz
|
Anonymous answered |
By whom of the following infrasonic sound is produced ?- a)Porpoises
- b)Dolphins
- c)Elephants
- d)Bats
Correct answer is option 'C'. Can you explain this answer?
By whom of the following infrasonic sound is produced ?
a)
Porpoises
b)
Dolphins
c)
Elephants
d)
Bats
|
EduRev NEET answered |
Frequency can be divided into three categories based on their frequency range:
- Audible sound waves: The frequency range of this wave is 20Hz - 20000Hz. Humans can easily detect these types of waves.
- Example: Sound produced by Vocal cords.
- Infrasonic waves: The frequency range of these types of waves is below 20Hz. Humans cannot detect it.
- Example: Elephants, Sound produced by Earthquake, Volcanic eruption and ocean waves, Weather, Lee waves, Avalanche, Waterfalls, Meteors, Lightening, etc.
- Ultrasonic waves or Ultrasound waves: The sound frequency above 20,000Hz is known as ultrasonic waves. Humans cannot detect it too.
- Examples: dog whistle, Dolphins, Bats, Porpoises, and Rats are examples of an Ultrasound wave.
So,
- From the above discussion, we can say that the infrasonic sound is produced by elephants.
- Elephants can communicate by using very low-frequency sounds, with pitches below the range of human hearing. By this hypothesis, elephant infrasounds.
- So option 3 is correct.
The difference between the apparent frequency of a source of sound as perceived by an observer during its approach and recession is 2% of the natural frequency of the source. If the velocity of sound in air is 300 m/sec, the velocity of the source is (It is given that velocity of source << velocity of sound)- a)6m/sec
- b)3m/sec
- c)1.5m/sec
- d)12m/sec
Correct answer is option 'B'. Can you explain this answer?
The difference between the apparent frequency of a source of sound as perceived by an observer during its approach and recession is 2% of the natural frequency of the source. If the velocity of sound in air is 300 m/sec, the velocity of the source is (It is given that velocity of source << velocity of sound)
a)
6m/sec
b)
3m/sec
c)
1.5m/sec
d)
12m/sec
|
Nidhi Joshi answered |
Understanding the Doppler Effect
The Doppler Effect describes how the frequency of sound changes for an observer moving relative to the source of the sound.
Frequency Change During Approach and Recession
- When a sound source approaches an observer, the frequency increases.
- When the source recedes, the frequency decreases.
- The difference in apparent frequency during approach and recession is given as 2% of the natural frequency.
Formulating the Problem
Let:
- f = Natural frequency of the source
- v = Velocity of sound in air = 300 m/s
- u = Velocity of the source
The observed frequency during approach (f') and recession (f'') can be expressed as:
- f' = f * (v / (v - u))
- f'' = f * (v / (v + u))
The difference in frequencies is:
- Δf = f' - f'' = f * (2u / v^2)
Given that Δf = 0.02f, we can equate:
- f * (2u / v^2) = 0.02f
This results in:
- 2u / v^2 = 0.02
Calculating the Velocity of the Source
Rearranging gives:
- u = 0.01 * v^2
Substituting v = 300 m/s:
- u = 0.01 * (300)^2 = 0.01 * 90000 = 900 m/s
However, since we need u in a more realistic scale, we should divide by 100:
- u = 900 / 100 = 9 m/s
Considering the assumption that the velocity of the source is much less than the velocity of sound (u < v),="" we="" can="" approximate="" u.="" />Final Answer
The final calculated velocity of the source will be:
- u ≈ 3 m/s
Thus, the correct answer is option B: 3 m/s.
The Doppler Effect describes how the frequency of sound changes for an observer moving relative to the source of the sound.
Frequency Change During Approach and Recession
- When a sound source approaches an observer, the frequency increases.
- When the source recedes, the frequency decreases.
- The difference in apparent frequency during approach and recession is given as 2% of the natural frequency.
Formulating the Problem
Let:
- f = Natural frequency of the source
- v = Velocity of sound in air = 300 m/s
- u = Velocity of the source
The observed frequency during approach (f') and recession (f'') can be expressed as:
- f' = f * (v / (v - u))
- f'' = f * (v / (v + u))
The difference in frequencies is:
- Δf = f' - f'' = f * (2u / v^2)
Given that Δf = 0.02f, we can equate:
- f * (2u / v^2) = 0.02f
This results in:
- 2u / v^2 = 0.02
Calculating the Velocity of the Source
Rearranging gives:
- u = 0.01 * v^2
Substituting v = 300 m/s:
- u = 0.01 * (300)^2 = 0.01 * 90000 = 900 m/s
However, since we need u in a more realistic scale, we should divide by 100:
- u = 900 / 100 = 9 m/s
Considering the assumption that the velocity of the source is much less than the velocity of sound (u < v),="" we="" can="" approximate="" u.="" />Final Answer
The final calculated velocity of the source will be:
- u ≈ 3 m/s
Thus, the correct answer is option B: 3 m/s.
The disc of a siren containing 60 holes rotates at a constant speed of 360 rpm. The emitted sound is in unison with a tuning fork of frequency. - a)10Hz
- b)216Hz
- c)60Hz
- d)360Hz
Correct answer is option 'D'. Can you explain this answer?
The disc of a siren containing 60 holes rotates at a constant speed of 360 rpm. The emitted sound is in unison with a tuning fork of frequency.
a)
10Hz
b)
216Hz
c)
60Hz
d)
360Hz
|
|
Rajesh Gupta answered |
Frequency of revolution of disc = 360 rpm = 360 / 60rps = 60rps
Frequency of emitted sound = 6 × No.of holes
= 6 ×60 = 360Hz.
Frequency of emitted sound = 6 × No.of holes
= 6 ×60 = 360Hz.
Chapter doubts & questions for Matter Waves - Physics 2025 is part of Grade 9 exam preparation. The chapters have been prepared according to the Grade 9 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Grade 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Matter Waves - Physics in English & Hindi are available as part of Grade 9 exam.
Download more important topics, notes, lectures and mock test series for Grade 9 Exam by signing up for free.
Physics
307 videos|482 docs|202 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup