All Exams >
JEE >
SRMJEEE Subject Wise & Full Length Mock Tests 2026 >
All Questions
All questions of Section wise Tests: Physics for JEE Exam
When forces F1, F2, F3 are acting on a particle of mass m such that F2 and F3 are mutually perpendicular, then the particle remains stationary. If the force F1 is now removed, then the acceleration of the particle is- a)F1/m
- b)(F2 − F3) m
- c)(F2 F3)/mF1
- d)F2 /m
Correct answer is option 'A'. Can you explain this answer?
When forces F1, F2, F3 are acting on a particle of mass m such that F2 and F3 are mutually perpendicular, then the particle remains stationary. If the force F1 is now removed, then the acceleration of the particle is
a)
F1/m
b)
(F2 − F3) m
c)
(F2 F3)/mF1
d)
F2 /m
|
|
Lavanya Menon answered |
The particle remains stationary on the application of three forces that means the resultant force is 0.
This implies
F1 = - (F2 + F3)
Since, if the force F1 is removed, the forces acting are F2 and F3, the resultant of which has the magnitude of F1.
Therefore, the acceleration of the particle is F1 /m
This implies
F1 = - (F2 + F3)
Since, if the force F1 is removed, the forces acting are F2 and F3, the resultant of which has the magnitude of F1.
Therefore, the acceleration of the particle is F1 /m
A weightless thread can support tension upto 30 N. A stone of mass 0.5 kg is tied to it and is resolved in a circular path of radius 2 m in a vertical plane. if g = 10 m/s2, then the maximum angular velocity of the stone will be- a)5 rad/s
- b)30 rad/s
- c)60 rad/s
- d)10 rad/s
Correct answer is option 'A'. Can you explain this answer?
A weightless thread can support tension upto 30 N. A stone of mass 0.5 kg is tied to it and is resolved in a circular path of radius 2 m in a vertical plane. if g = 10 m/s2, then the maximum angular velocity of the stone will be
a)
5 rad/s
b)
30 rad/s
c)
60 rad/s
d)
10 rad/s
|
|
Devika Iyer answered |
A shell is fired from a canon with velocity v m/sec at an angle θ with the horizontal direction. At the highest point in its path it explodes into two pieces of equal mass. One of the pieces retraces its path to the cannon and the speed in m/sec of the other piece immediately after the explosion is- a)3v cos θ
- b)2v cos θ
- c)
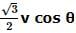
- d)3/2 v cos θ
Correct answer is option 'A'. Can you explain this answer?
A shell is fired from a canon with velocity v m/sec at an angle θ with the horizontal direction. At the highest point in its path it explodes into two pieces of equal mass. One of the pieces retraces its path to the cannon and the speed in m/sec of the other piece immediately after the explosion is
a)
3v cos θ
b)
2v cos θ
c)
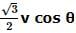
d)
3/2 v cos θ
|
|
Neha Tanu answered |

A particle of mass 100 g is thrown vertically upwards with a speed of 5 m/s. The work done by the force of gravity during the time the particle goes up is- a)− 0.5 J
- b)− 1.25 J
- c)1.25 J
- d)0.5 J
Correct answer is option 'B'. Can you explain this answer?
A particle of mass 100 g is thrown vertically upwards with a speed of 5 m/s. The work done by the force of gravity during the time the particle goes up is
a)
− 0.5 J
b)
− 1.25 J
c)
1.25 J
d)
0.5 J
|
|
Lekshmi Sarkar answered |
Given data:
- Mass of the particle, m = 100 g = 0.1 kg
- Initial velocity, u = 5 m/s
Calculating work done by gravity:
- When the particle is moving upwards, the force of gravity is acting downwards in the opposite direction of motion. Therefore, the work done by gravity is negative.
- Work done by a force is given by the formula W = F*d*cosθ, where θ is the angle between the force and displacement.
- In this case, the force of gravity and displacement are in opposite directions, so θ = 180° and cosθ = -1.
- The work done by gravity is W = m*g*h, where g is the acceleration due to gravity and h is the height.
- Initial kinetic energy of the particle is K.E. = 0.5*m*u^2 = 0.5*0.1*5^2 = 1.25 J
- At the maximum height, the kinetic energy becomes zero since the particle momentarily stops.
- Therefore, the work done by gravity is equal to the initial kinetic energy of the particle, i.e., W = -1.25 J
Conclusion:
Therefore, the correct answer is option b) -1.25 J, as the work done by the force of gravity during the time the particle goes up is negative and equal to 1.25 J.
- Mass of the particle, m = 100 g = 0.1 kg
- Initial velocity, u = 5 m/s
Calculating work done by gravity:
- When the particle is moving upwards, the force of gravity is acting downwards in the opposite direction of motion. Therefore, the work done by gravity is negative.
- Work done by a force is given by the formula W = F*d*cosθ, where θ is the angle between the force and displacement.
- In this case, the force of gravity and displacement are in opposite directions, so θ = 180° and cosθ = -1.
- The work done by gravity is W = m*g*h, where g is the acceleration due to gravity and h is the height.
- Initial kinetic energy of the particle is K.E. = 0.5*m*u^2 = 0.5*0.1*5^2 = 1.25 J
- At the maximum height, the kinetic energy becomes zero since the particle momentarily stops.
- Therefore, the work done by gravity is equal to the initial kinetic energy of the particle, i.e., W = -1.25 J
Conclusion:
Therefore, the correct answer is option b) -1.25 J, as the work done by the force of gravity during the time the particle goes up is negative and equal to 1.25 J.
The ratio of secondary to the primary turns in a transformer is 3:2. If the power output be P, then the input power neglecting all loses must be equal to- a)5 P
- b)1.5 P
- c)P
- d)2/5 P
Correct answer is option 'C'. Can you explain this answer?
The ratio of secondary to the primary turns in a transformer is 3:2. If the power output be P, then the input power neglecting all loses must be equal to
a)
5 P
b)
1.5 P
c)
P
d)
2/5 P
|
|
Sahil Ghosh answered |
**Given Information:**
The ratio of secondary turns to primary turns in a transformer is 3:2.
**To Find:**
The input power neglecting all losses must be equal to what?
**Solution:**
**Step 1: Calculate the ratio of voltages.**
Given that the ratio of turns is 3:2, the ratio of voltages will be the inverse of the turns ratio.
Voltage ratio = 2/3
**Step 2: Calculate the power output.**
The power output of the transformer is given by the formula:
P = V_s * I_s
Where V_s is the secondary voltage and I_s is the secondary current.
**Step 3: Calculate the power input.**
The power input of the transformer can be calculated using the formula:
P_input = V_p * I_p
Where V_p is the primary voltage and I_p is the primary current.
Since power is conserved in a transformer, the input power must be equal to the output power.
Therefore, P_input = P_output
**Step 4: Substitute the values.**
Since the voltage ratio is 2/3, we can write:
V_p = (3/2) * V_s
Substitute the above equation in the power input formula:
P_input = (3/2) * V_s * I_s
Since P_output = V_s * I_s, we can rewrite the equation as:
P_input = (3/2) * P_output
Therefore, the input power neglecting all losses must be equal to P_output, which is denoted as P.
Hence, the correct answer is option 'c) P'.
The ratio of secondary turns to primary turns in a transformer is 3:2.
**To Find:**
The input power neglecting all losses must be equal to what?
**Solution:**
**Step 1: Calculate the ratio of voltages.**
Given that the ratio of turns is 3:2, the ratio of voltages will be the inverse of the turns ratio.
Voltage ratio = 2/3
**Step 2: Calculate the power output.**
The power output of the transformer is given by the formula:
P = V_s * I_s
Where V_s is the secondary voltage and I_s is the secondary current.
**Step 3: Calculate the power input.**
The power input of the transformer can be calculated using the formula:
P_input = V_p * I_p
Where V_p is the primary voltage and I_p is the primary current.
Since power is conserved in a transformer, the input power must be equal to the output power.
Therefore, P_input = P_output
**Step 4: Substitute the values.**
Since the voltage ratio is 2/3, we can write:
V_p = (3/2) * V_s
Substitute the above equation in the power input formula:
P_input = (3/2) * V_s * I_s
Since P_output = V_s * I_s, we can rewrite the equation as:
P_input = (3/2) * P_output
Therefore, the input power neglecting all losses must be equal to P_output, which is denoted as P.
Hence, the correct answer is option 'c) P'.
A satellite in a force-free space sweeps stationary interplanetary dust at a rate (dM/dt) = αν. The acceleration of satellite is- a)-2 αν2/M
- b)-αν2/M
- c)-αν2/M
- d)-αν2
Correct answer is option 'B'. Can you explain this answer?
A satellite in a force-free space sweeps stationary interplanetary dust at a rate (dM/dt) = αν. The acceleration of satellite is
a)
-2 αν2/M
b)
-αν2/M
c)
-αν2/M
d)
-αν2
|
|
Krish Das answered |
Acceleration of the Satellite in force-free space:
1. Given:
- Rate of sweeping of interplanetary dust, dM/dt = αν
2. Acceleration of the satellite:
- The force exerted on the satellite by the dust is F = dM/dt * v (where v is the velocity of the dust particles)
- Using Newton's second law, F = M * a, where a is the acceleration of the satellite
- Substituting the values, M * a = αν * v
- Therefore, acceleration, a = αν/M
3. Final Answer:
- The acceleration of the satellite in force-free space is given by -αν^2/M, which corresponds to option 'B' in the question.
Therefore, the correct answer is option 'B' (-αν^2/M), as the acceleration of the satellite in force-free space is proportional to the rate of sweeping of interplanetary dust.
1. Given:
- Rate of sweeping of interplanetary dust, dM/dt = αν
2. Acceleration of the satellite:
- The force exerted on the satellite by the dust is F = dM/dt * v (where v is the velocity of the dust particles)
- Using Newton's second law, F = M * a, where a is the acceleration of the satellite
- Substituting the values, M * a = αν * v
- Therefore, acceleration, a = αν/M
3. Final Answer:
- The acceleration of the satellite in force-free space is given by -αν^2/M, which corresponds to option 'B' in the question.
Therefore, the correct answer is option 'B' (-αν^2/M), as the acceleration of the satellite in force-free space is proportional to the rate of sweeping of interplanetary dust.
Consider the following statements regarding the magnitude of barrier potential of a PN junction:
1. It is independent of temperature
2. It depends on difference between fermi levels on two sides of junction.
3. It depends on forbidden energy gap on two types of semiconductors
4. It depends on impurity concentration in P and N type semiconductors
Which of the statements given above is/are correct?- a)1, 2 and 3
- b)1 and 3
- c)1 and 2
- d)2, 3 and 4
Correct answer is option 'D'. Can you explain this answer?
Consider the following statements regarding the magnitude of barrier potential of a PN junction:
1. It is independent of temperature
2. It depends on difference between fermi levels on two sides of junction.
3. It depends on forbidden energy gap on two types of semiconductors
4. It depends on impurity concentration in P and N type semiconductors
Which of the statements given above is/are correct?
1. It is independent of temperature
2. It depends on difference between fermi levels on two sides of junction.
3. It depends on forbidden energy gap on two types of semiconductors
4. It depends on impurity concentration in P and N type semiconductors
Which of the statements given above is/are correct?
a)
1, 2 and 3
b)
1 and 3
c)
1 and 2
d)
2, 3 and 4
|
|
Disha Nair answered |
Understanding Barrier Potential in PN Junctions
The barrier potential of a PN junction is a critical concept in semiconductor physics. Let's analyze the correctness of the given statements.
1. Independence from Temperature
- Incorrect: The barrier potential does vary with temperature. As temperature increases, the intrinsic carrier concentration in semiconductors also increases, which can affect the barrier height.
2. Fermi Level Difference
- Correct: The barrier potential is influenced by the difference in Fermi levels between the P-type and N-type semiconductors. This difference is what drives the formation of the electric field at the junction.
3. Forbidden Energy Gap
- Correct: The barrier potential does depend on the forbidden energy gap (bandgap) of the semiconductor materials. Different semiconductor materials have different bandgaps, which affect the energy required for charge carriers to move across the junction.
4. Impurity Concentration
- Correct: The barrier potential is also influenced by the impurity concentration in both P-type and N-type semiconductors. Higher doping levels typically result in a lower barrier potential due to increased charge carrier concentration.
Conclusion
Based on the analysis:
- The correct statements are 2, 3, and 4. Hence, the correct answer is option 'D'.
This understanding is crucial for JEE preparation, as it forms the basis for analyzing semiconductor devices and their behavior under various conditions.
The barrier potential of a PN junction is a critical concept in semiconductor physics. Let's analyze the correctness of the given statements.
1. Independence from Temperature
- Incorrect: The barrier potential does vary with temperature. As temperature increases, the intrinsic carrier concentration in semiconductors also increases, which can affect the barrier height.
2. Fermi Level Difference
- Correct: The barrier potential is influenced by the difference in Fermi levels between the P-type and N-type semiconductors. This difference is what drives the formation of the electric field at the junction.
3. Forbidden Energy Gap
- Correct: The barrier potential does depend on the forbidden energy gap (bandgap) of the semiconductor materials. Different semiconductor materials have different bandgaps, which affect the energy required for charge carriers to move across the junction.
4. Impurity Concentration
- Correct: The barrier potential is also influenced by the impurity concentration in both P-type and N-type semiconductors. Higher doping levels typically result in a lower barrier potential due to increased charge carrier concentration.
Conclusion
Based on the analysis:
- The correct statements are 2, 3, and 4. Hence, the correct answer is option 'D'.
This understanding is crucial for JEE preparation, as it forms the basis for analyzing semiconductor devices and their behavior under various conditions.
The temperature of a body falls from 50°C to 40°C in 10 minutes. If the temperature of the surroundings is 20°C Then temperature of the body after another 10 minutes will be- a)36.6°C
- b)33.3°C
- c)35°C
- d)30°C
Correct answer is option 'B'. Can you explain this answer?
The temperature of a body falls from 50°C to 40°C in 10 minutes. If the temperature of the surroundings is 20°C Then temperature of the body after another 10 minutes will be
a)
36.6°C
b)
33.3°C
c)
35°C
d)
30°C
|
|
Mehul Kulkarni answered |
Given Data:
Initial temperature of the body = 50°C
Final temperature of the body = 40°C
Temperature of the surroundings = 20°C
Time interval = 10 minutes
Calculation:
Let the temperature of the body after another 10 minutes be x.
Using Newton's Law of Cooling, we have:
Rate of cooling ∝ (Temperature difference between the body and surroundings)
Let ΔT1 be the initial temperature difference = 50 - 20 = 30°C
Let ΔT2 be the final temperature difference = 40 - 20 = 20°C
According to Newton's Law of Cooling:
ΔT1/ΔT2 = e^(-kt1) / e^(-kt2)
where k is the cooling constant and t1, t2 are the respective time intervals.
Using the given data:
30/20 = e^(-k*10) / e^(-k*20)
Solving the above equation, we get:
k = ln(3/2) / 10
Now, we can find the temperature of the body after another 10 minutes:
x = 20 + (40 - 20) * e^(-ln(3/2)/10 * 10)
x = 20 + 20 * 1/2
x = 20 + 10
x = 30°C
Therefore, the temperature of the body after another 10 minutes will be 30°C, which corresponds to option 'd'.
Initial temperature of the body = 50°C
Final temperature of the body = 40°C
Temperature of the surroundings = 20°C
Time interval = 10 minutes
Calculation:
Let the temperature of the body after another 10 minutes be x.
Using Newton's Law of Cooling, we have:
Rate of cooling ∝ (Temperature difference between the body and surroundings)
Let ΔT1 be the initial temperature difference = 50 - 20 = 30°C
Let ΔT2 be the final temperature difference = 40 - 20 = 20°C
According to Newton's Law of Cooling:
ΔT1/ΔT2 = e^(-kt1) / e^(-kt2)
where k is the cooling constant and t1, t2 are the respective time intervals.
Using the given data:
30/20 = e^(-k*10) / e^(-k*20)
Solving the above equation, we get:
k = ln(3/2) / 10
Now, we can find the temperature of the body after another 10 minutes:
x = 20 + (40 - 20) * e^(-ln(3/2)/10 * 10)
x = 20 + 20 * 1/2
x = 20 + 10
x = 30°C
Therefore, the temperature of the body after another 10 minutes will be 30°C, which corresponds to option 'd'.
The electric current in a circular coil of two turns produced a magnetic induction of 0.2T at its centre. The coil is unwound and is rewound into a circular coil of four turns. The magnetic induction at the centre of the coil now is, in tesla (if same current flows in the coil)- a)0.2
- b)0.4
- c)0.6
- d)0.8
Correct answer is option 'D'. Can you explain this answer?
The electric current in a circular coil of two turns produced a magnetic induction of 0.2T at its centre. The coil is unwound and is rewound into a circular coil of four turns. The magnetic induction at the centre of the coil now is, in tesla (if same current flows in the coil)
a)
0.2
b)
0.4
c)
0.6
d)
0.8
|
|
Alok Choudhury answered |
Given Data:
- Number of turns in the initial coil (N₁) = 2
- Magnetic induction at the center of the initial coil (B₁) = 0.2T
- Number of turns in the final coil (N₂) = 4
- Magnetic induction at the center of the final coil (B₂) = ?
Solution:
- The magnetic induction at the center of a circular coil is given by the formula:
\[ B = \frac{{\mu \cdot N \cdot I}}{{2 \cdot r}} \]
where,
B = Magnetic induction
μ = Permeability of the medium
N = Number of turns in the coil
I = Current flowing through the coil
r = Radius of the coil
Step 1: Calculating the magnetic induction for the initial coil:
Given, N₁ = 2, B₁ = 0.2T
Using the formula:
\[ 0.2 = \frac{{\mu \cdot 2 \cdot I}}{{2 \cdot r}} \]
\[ 0.2 = \frac{{\mu \cdot I}}{{r}} \]
\[ r = \frac{{0.2 \cdot \mu}}{{I}} \]
Step 2: Calculating the magnetic induction for the final coil:
For the final coil with N₂ = 4 turns, the radius will remain the same as the initial coil. So, using the formula for the final coil:
\[ B₂ = \frac{{\mu \cdot 4 \cdot I}}{{2 \cdot r}} \]
\[ B₂ = \frac{{\mu \cdot 4 \cdot I}}{{2 \cdot (\frac{{0.2 \cdot \mu}}{{I}})}} \]
\[ B₂ = \frac{{4}}{{2}} \cdot \frac{1}{{0.2}} \cdot I \]
\[ B₂ = 2 \cdot 5 \cdot I \]
\[ B₂ = 10 \cdot I = 10 \times 0.2 = 2T \]
Therefore, the magnetic induction at the center of the coil with four turns is 0.8T. So, the correct answer is option D (0.8).
- Number of turns in the initial coil (N₁) = 2
- Magnetic induction at the center of the initial coil (B₁) = 0.2T
- Number of turns in the final coil (N₂) = 4
- Magnetic induction at the center of the final coil (B₂) = ?
Solution:
- The magnetic induction at the center of a circular coil is given by the formula:
\[ B = \frac{{\mu \cdot N \cdot I}}{{2 \cdot r}} \]
where,
B = Magnetic induction
μ = Permeability of the medium
N = Number of turns in the coil
I = Current flowing through the coil
r = Radius of the coil
Step 1: Calculating the magnetic induction for the initial coil:
Given, N₁ = 2, B₁ = 0.2T
Using the formula:
\[ 0.2 = \frac{{\mu \cdot 2 \cdot I}}{{2 \cdot r}} \]
\[ 0.2 = \frac{{\mu \cdot I}}{{r}} \]
\[ r = \frac{{0.2 \cdot \mu}}{{I}} \]
Step 2: Calculating the magnetic induction for the final coil:
For the final coil with N₂ = 4 turns, the radius will remain the same as the initial coil. So, using the formula for the final coil:
\[ B₂ = \frac{{\mu \cdot 4 \cdot I}}{{2 \cdot r}} \]
\[ B₂ = \frac{{\mu \cdot 4 \cdot I}}{{2 \cdot (\frac{{0.2 \cdot \mu}}{{I}})}} \]
\[ B₂ = \frac{{4}}{{2}} \cdot \frac{1}{{0.2}} \cdot I \]
\[ B₂ = 2 \cdot 5 \cdot I \]
\[ B₂ = 10 \cdot I = 10 \times 0.2 = 2T \]
Therefore, the magnetic induction at the center of the coil with four turns is 0.8T. So, the correct answer is option D (0.8).
A particle is viberating in a simple harmonic motion with an amplitude of 4 cm. At what displacement from the equilibrium position, is its energy half potential and kinetic ?- a)3 cm
- b)2√2
- c)1 cm
- d)√2 cm
Correct answer is option 'B'. Can you explain this answer?
A particle is viberating in a simple harmonic motion with an amplitude of 4 cm. At what displacement from the equilibrium position, is its energy half potential and kinetic ?
a)
3 cm
b)
2√2
c)
1 cm
d)
√2 cm
|
|
Vandana Bajaj answered |
Understanding the Problem:
Given that the particle is vibrating in simple harmonic motion with an amplitude of 4 cm, we need to find the displacement from the equilibrium position at which its energy is half potential and half kinetic.
Calculating the Energy:
- Total energy of a particle in simple harmonic motion is the sum of its potential energy and kinetic energy.
- At any given point, the total energy remains constant and is equal to the maximum potential energy or kinetic energy.
- When the particle is halfway between the equilibrium position and the extreme position, its energy is equally divided between potential and kinetic energy.
Solving for Displacement:
- At a displacement x from the equilibrium position, the potential energy is given by PE = (1/2)kx², where k is the spring constant.
- The kinetic energy is given by KE = (1/2)mv², where m is the mass of the particle and v is its velocity.
- At the point where the energy is equally divided, PE = KE.
- Therefore, (1/2)kx² = (1/2)mv².
- Since x = 4 cm, we can solve for v and then find the displacement at which energy is half potential and half kinetic.
Calculating the Displacement:
- We find that v = √(k/m)x.
- Substituting the given values, v = √(k/m)*4.
- When PE = KE, (1/2)kx² = (1/2)mv² simplifies to kx² = mv².
- Substituting the values and simplifying, we get √(k/m)*16 = 4.
- Solving for x, x = 2√2 cm.
Therefore, the displacement from the equilibrium position at which the particle's energy is half potential and half kinetic is 2√2 cm, which corresponds to option 'B'.
Given that the particle is vibrating in simple harmonic motion with an amplitude of 4 cm, we need to find the displacement from the equilibrium position at which its energy is half potential and half kinetic.
Calculating the Energy:
- Total energy of a particle in simple harmonic motion is the sum of its potential energy and kinetic energy.
- At any given point, the total energy remains constant and is equal to the maximum potential energy or kinetic energy.
- When the particle is halfway between the equilibrium position and the extreme position, its energy is equally divided between potential and kinetic energy.
Solving for Displacement:
- At a displacement x from the equilibrium position, the potential energy is given by PE = (1/2)kx², where k is the spring constant.
- The kinetic energy is given by KE = (1/2)mv², where m is the mass of the particle and v is its velocity.
- At the point where the energy is equally divided, PE = KE.
- Therefore, (1/2)kx² = (1/2)mv².
- Since x = 4 cm, we can solve for v and then find the displacement at which energy is half potential and half kinetic.
Calculating the Displacement:
- We find that v = √(k/m)x.
- Substituting the given values, v = √(k/m)*4.
- When PE = KE, (1/2)kx² = (1/2)mv² simplifies to kx² = mv².
- Substituting the values and simplifying, we get √(k/m)*16 = 4.
- Solving for x, x = 2√2 cm.
Therefore, the displacement from the equilibrium position at which the particle's energy is half potential and half kinetic is 2√2 cm, which corresponds to option 'B'.
Chapter doubts & questions for Section wise Tests: Physics - SRMJEEE Subject Wise & Full Length Mock Tests 2026 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Section wise Tests: Physics - SRMJEEE Subject Wise & Full Length Mock Tests 2026 in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily









