All Exams >
CLAT >
4 Months Preparation Course for CLAT UG >
All Questions
All questions of Profit And Loss for CLAT Exam
A retailer sold 12 notes at a profit of 20% and 8 notes at a profit of 10%. If he had sold all the 20 notes at a profit of 15%, then his profit would have been reduced by Rs.36. What is the cost price of each note?
- a)Rs.160
- b)Rs.190
- c)Rs.120
- d)Rs.180
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A retailer sold 12 notes at a profit of 20% and 8 notes at a profit of 10%. If he had sold all the 20 notes at a profit of 15%, then his profit would have been reduced by Rs.36. What is the cost price of each note?
a)
Rs.160
b)
Rs.190
c)
Rs.120
d)
Rs.180
e)
None of these
|
|
Nikita Singh answered |
Answer - D.Rs.180
Explanation :
Cost Price = x
Total Profit
= 12x * 20/100 + 8x * 10/100 = 320x/100 = 3.2x
= 20x * 15/100 — (ii) Profit of 15% on 20 notes
Total Profit
3.2x - 3x = 36
0.2x = 36
x = 180
Explanation :
Cost Price = x
Total Profit
= 12x * 20/100 + 8x * 10/100 = 320x/100 = 3.2x
= 20x * 15/100 — (ii) Profit of 15% on 20 notes
Total Profit
3.2x - 3x = 36
0.2x = 36
x = 180
The marked price of an article is 20% above the cost price. When the selling price of an article is increased by 30% the profit doubles. If the marked price of an article is 480, then original selling price is.
A.531.15
B.537.14
C.571.4
D.582.12
E.None of these- a)531.15
- b)537.14
- c)571.4
- d)582.12
- e).None of these
Correct answer is option 'C'. Can you explain this answer?
The marked price of an article is 20% above the cost price. When the selling price of an article is increased by 30% the profit doubles. If the marked price of an article is 480, then original selling price is.
A.531.15
B.537.14
C.571.4
D.582.12
E.None of these
A.531.15
B.537.14
C.571.4
D.582.12
E.None of these
a)
531.15
b)
537.14
c)
571.4
d)
582.12
e)
.None of these

|
KS Coaching Center answered |
Given MP = 120/100*CP. So, CP = 400.
SP -400 = P (Profit)
(130/100)*SP – 400 = 2P
Solving both equation we get, SP = 4000/7 = 571.4
SP -400 = P (Profit)
(130/100)*SP – 400 = 2P
Solving both equation we get, SP = 4000/7 = 571.4
A dealer marked the price of an item 20% above cost price. He allowed two successive discounts of 20% and 25% to a customer. As a result he incurred a loss of Rs.812. At what price did he sell the item to the customer?- a)1875
- b)2088
- c)2155
- d)2258
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A dealer marked the price of an item 20% above cost price. He allowed two successive discounts of 20% and 25% to a customer. As a result he incurred a loss of Rs.812. At what price did he sell the item to the customer?
a)
1875
b)
2088
c)
2155
d)
2258
e)
None of these

|
Target Study Academy answered |
CP = 100
MP = 120
120*80/100 = 96; 96*75/100 = 72
Loss = 100 – 72 = 28%
CP = 100/28*812 = 2900
SP = 2900*72/100 = 2088
MP = 120
120*80/100 = 96; 96*75/100 = 72
Loss = 100 – 72 = 28%
CP = 100/28*812 = 2900
SP = 2900*72/100 = 2088
Sriram purchased 40 dozen notebooks at Rs. 50 per dozen. He sold 10 dozens of it at 15% profit and the remaining 30 dozens at 25% profit. What is his percentage profit in the whole transaction?- a)18.8%
- b)20%
- c)22.5%
- d)25%
- e)28.5%
Correct answer is option 'C'. Can you explain this answer?
Sriram purchased 40 dozen notebooks at Rs. 50 per dozen. He sold 10 dozens of it at 15% profit and the remaining 30 dozens at 25% profit. What is his percentage profit in the whole transaction?
a)
18.8%
b)
20%
c)
22.5%
d)
25%
e)
28.5%
|
|
Faizan Khan answered |
C.P = 4*50 = 2000
S.P = 10*50*115 /100 + 30*50*125/100 = 2450
Profit = 2450- 2000 = 450
Profit% = 450/2000 * 100 = 22.5
S.P = 10*50*115 /100 + 30*50*125/100 = 2450
Profit = 2450- 2000 = 450
Profit% = 450/2000 * 100 = 22.5
A Shopkeeper bought 30 kg of rice at the rate of Rs. 40 per kg. He sold 40% of the total quantity at the rate of Rs. 50 per kg. At what price per kg should he sell the remaining quantity to make 25% overall profit?- a)Rs.54
- b) Rs.50
- c)Rs.40
- d)Rs.30
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A Shopkeeper bought 30 kg of rice at the rate of Rs. 40 per kg. He sold 40% of the total quantity at the rate of Rs. 50 per kg. At what price per kg should he sell the remaining quantity to make 25% overall profit?
a)
Rs.54
b)
Rs.50
c)
Rs.40
d)
Rs.30
e)
None of these

|
Cstoppers Instructors answered |
Total CP of Rice = 30 * 40 = 1200
40% of Total Quantity = 40% of 30 = 12
SP = 12*50 = 600
SP = 1200 * 125/100 = 1500
SP of Remaining Quantity = 1500 – 600 = 900
Remaining Quantity = 18kg
Rice per Kg = 900/18 = Rs. 50
40% of Total Quantity = 40% of 30 = 12
SP = 12*50 = 600
SP = 1200 * 125/100 = 1500
SP of Remaining Quantity = 1500 – 600 = 900
Remaining Quantity = 18kg
Rice per Kg = 900/18 = Rs. 50
A man buys some quantity of rice for Rs 5100. He sells one third of it at a profit of 10%. At what percent gain should he sell the remaining two-third so as to make an overall profit of 20% on the whole transaction?- a)10%
- b)15%
- c)20%
- d)25%
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A man buys some quantity of rice for Rs 5100. He sells one third of it at a profit of 10%. At what percent gain should he sell the remaining two-third so as to make an overall profit of 20% on the whole transaction?
a)
10%
b)
15%
c)
20%
d)
25%
e)
None of these

|
Target Study Academy answered |
10………………….X
…………20……………
x-20…………….10
1:2
X=25
…………20……………
x-20…………….10
1:2
X=25
A milkman buys some milk. If he sells it at rupees 10 a litre, he losses 400 rupees but when he sells it at 12 a litre, he gains 800 rupees. How much milk did he purchase?- a)400 litre
- b)550 litre
- c)600 litre
- d)800 litre
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A milkman buys some milk. If he sells it at rupees 10 a litre, he losses 400 rupees but when he sells it at 12 a litre, he gains 800 rupees. How much milk did he purchase?
a)
400 litre
b)
550 litre
c)
600 litre
d)
800 litre
e)
None of these

|
Bank Exams India answered |
10x=s-400
12x=s+800
2x=1200
X=600
12x=s+800
2x=1200
X=600
Arun sells an article at 20% profit to Bala, Bala sells it to Catherine at 10% profit. Catherine sells it to Dinesh at Rs. 16 profit. The difference between the cost price of Dinesh and cost price of Arun was Rs. 500. How much did Bala pay to Arun for the article? - a)Rs.1350
- b)Rs.1815
- c)Rs.1650
- d)Rs.1750
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Arun sells an article at 20% profit to Bala, Bala sells it to Catherine at 10% profit. Catherine sells it to Dinesh at Rs. 16 profit. The difference between the cost price of Dinesh and cost price of Arun was Rs. 500. How much did Bala pay to Arun for the article?
a)
Rs.1350
b)
Rs.1815
c)
Rs.1650
d)
Rs.1750
e)
None of these
|
|
Kirti Dahiya answered |
"use of successive percentage"
Let article cost is 100x...,,
100x -> 120x -> 132x -> (132+16)
Arun. Bala. Catherine Dinesh
The difference between the cost price of Dinesh and cost price of Arun was Rs. 500
So, (132x+16) - 100x = 500
X= 121/8
Bala pay to Arun for the article is
120x => 120* 121/8 => 1815
A reputed company sells a wrist watch to a wholesaler making a profit of 10%. The wholesaler, in turn, sells it to the retailer making a profit of 10%. A customer purchases it by paying Rs. 990. Thus the profit of retailer is 2(3/11)% What is the cost incurred by the the company to produce it?- a)700
- b) 600
- c)800
- d)900
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A reputed company sells a wrist watch to a wholesaler making a profit of 10%. The wholesaler, in turn, sells it to the retailer making a profit of 10%. A customer purchases it by paying Rs. 990. Thus the profit of retailer is 2(3/11)% What is the cost incurred by the the company to produce it?
a)
700
b)
600
c)
800
d)
900
e)
None of these

|
Future Foundation Institute answered |
Answer — C. 800
Explanation :
Explanation :
x*110/100*110/100*(100 + 25/11)/100 = 990
x = 800
x = 800
The profit Percentage on 3 bikes are 15%, 35% and 10% and the ratio of CP is 5:3:1. Also the ratio of the Bike sold of P, Q and R is 2:3:5. Then the overall approximate Profit Percentage is?- a)19%
- b)20%
- c)16%
- d)21%
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
The profit Percentage on 3 bikes are 15%, 35% and 10% and the ratio of CP is 5:3:1. Also the ratio of the Bike sold of P, Q and R is 2:3:5. Then the overall approximate Profit Percentage is?
a)
19%
b)
20%
c)
16%
d)
21%
e)
None of these

|
Future Foundation Institute answered |
Answer - D.
Explanation :
5x * 2y + 3x * 3y + 5y = 24xy
Total Profit —
= 515xy/100
= 5.15xy
Overall Profit Percentage
= 5.15xy * 100/24xy
= 21.46%
Explanation :
5x * 2y + 3x * 3y + 5y = 24xy
Total Profit —
= 515xy/100
= 5.15xy
Overall Profit Percentage
= 5.15xy * 100/24xy
= 21.46%
A trader gains 10% while buying the goods and gains 20% while selling the goods. Find the gain percent of the trader.- a)30
- b)31
- c)32
- d)34
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A trader gains 10% while buying the goods and gains 20% while selling the goods. Find the gain percent of the trader.
a)
30
b)
31
c)
32
d)
34
e)
None of these

|
Cstoppers Instructors answered |
- Traders gain 10% on buying means an article cost 110rs, he buy it for 100.
Now he sell it for 20% profit means 110*(120/100) = 132. So gain% is 32.
Raman buys some apples at the rate of four for a rupee and same numbers of oranges at three for a rupee. To make a profit of 25%, Raman should sell a 6 apples for. - a)3.75
- b)4.375
- c)5.75
- d)6.75
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Raman buys some apples at the rate of four for a rupee and same numbers of oranges at three for a rupee. To make a profit of 25%, Raman should sell a 6 apples for.
a)
3.75
b)
4.375
c)
5.75
d)
6.75
e)
None of these

|
Divey Sethi answered |
Let Raman buys ‘X’ apples at rate four for a rupee and ‘X’ apples at three for a rupee.
So, cost price = X/4 + X/3
CP = 6/4 + 6/3 = 3.5
Now SP = (125/100)*3.5 = 4.375
So, cost price = X/4 + X/3
CP = 6/4 + 6/3 = 3.5
Now SP = (125/100)*3.5 = 4.375
An article is sold for rupees 400 in which the seller fetches 25% profit. If 6 such articles are sold for rupees 2400, then the percent profit/loss incurred by the seller- a)25% loss
- b)20% profit
- c)25% profit
- d)20% loss
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
An article is sold for rupees 400 in which the seller fetches 25% profit. If 6 such articles are sold for rupees 2400, then the percent profit/loss incurred by the seller
a)
25% loss
b)
20% profit
c)
25% profit
d)
20% loss
e)
None of these

|
Cstoppers Instructors answered |
400 = (125/100)*CP
CP = 320.
Selling price = 2400/6 = 400.
% profit = [(400 – 320)/320]*100 = 25
CP = 320.
Selling price = 2400/6 = 400.
% profit = [(400 – 320)/320]*100 = 25
A reduction of 20% in the price of sugar enables a housewife to purchase 6 kg more for Rs. 240. What is original price per kg of sugar?- a)Rs.10 per Kg
- b)Rs.8 per Kg
- c)Rs.6 per Kg
- d)Rs.5 per Kg
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A reduction of 20% in the price of sugar enables a housewife to purchase 6 kg more for Rs. 240. What is original price per kg of sugar?
a)
Rs.10 per Kg
b)
Rs.8 per Kg
c)
Rs.6 per Kg
d)
Rs.5 per Kg
e)
None of these
|
|
Kavya Saxena answered |
Explanation:
Reduction in price = 1/5 = 20%
Increase in Quantity = 25%
25% = 6 Kg.
original amount of Sugar = 6*4 = 24Kg.
Original price of the sugar = 240/24 = Rs. 10 per kg.
Reduction in price = 1/5 = 20%
Increase in Quantity = 25%
25% = 6 Kg.
original amount of Sugar = 6*4 = 24Kg.
Original price of the sugar = 240/24 = Rs. 10 per kg.
Rahul purchased an article for Rs. 8400 and sold it for a loss of 5%. From that money he purchased another article and sold it for a gain of 5%. What is the overall gain or loss?- a)Profit of Rs.21
- b)Profit of Rs.24
- c)Loss of Rs.21
- d)Loss of Rs.24
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Rahul purchased an article for Rs. 8400 and sold it for a loss of 5%. From that money he purchased another article and sold it for a gain of 5%. What is the overall gain or loss?
a)
Profit of Rs.21
b)
Profit of Rs.24
c)
Loss of Rs.21
d)
Loss of Rs.24
e)
None of these

|
KS Coaching Center answered |
CP = 8400
SP = 8400 * 95/100 = 7980
CP = 7980
SP = 7980 * 105/100 = 8379
Difference = 8400 – 8379 = 21
SP = 8400 * 95/100 = 7980
CP = 7980
SP = 7980 * 105/100 = 8379
Difference = 8400 – 8379 = 21
The profit earned after selling an article for Rs. 1680 is the same as the loss incurred after selling the article for Rs. 1512. What is the cost price of the article?- a)Rs.1602
- b)Rs.1912
- c)Rs.1200
- d)Rs.1596
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
The profit earned after selling an article for Rs. 1680 is the same as the loss incurred after selling the article for Rs. 1512. What is the cost price of the article?
a)
Rs.1602
b)
Rs.1912
c)
Rs.1200
d)
Rs.1596
e)
None of these

|
Divey Sethi answered |
CP = x
1680 – x = x – 1512
2x = 3192
x = 1596
1680 – x = x – 1512
2x = 3192
x = 1596
A person saves 20 percent of his income. If the income of that person increased by 16 percent and he decided to save 25 percent, then find the percent increase in his saving as compared to previous one.- a)40%
- b)45%
- c)50%
- d)55%
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A person saves 20 percent of his income. If the income of that person increased by 16 percent and he decided to save 25 percent, then find the percent increase in his saving as compared to previous one.
a)
40%
b)
45%
c)
50%
d)
55%
e)
None of these

|
Target Study Academy answered |
Let initial income = 100 so his saving is rupees = 20.
Now his income is 116 and he save = 116*25/100 = 29
So % increase in saving = (9/20)*100 = 45
Now his income is 116 and he save = 116*25/100 = 29
So % increase in saving = (9/20)*100 = 45
A company declared 20 percent discount on its garments. Rakesh bought garments worth rupees 30000 after getting discount. Now he fixed the selling price of the garments in such a way that he got a profit of 15 percent on the marked price. Find the selling price of the garments.- a)34000
- b)34225
- c)35625
- d)36000
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A company declared 20 percent discount on its garments. Rakesh bought garments worth rupees 30000 after getting discount. Now he fixed the selling price of the garments in such a way that he got a profit of 15 percent on the marked price. Find the selling price of the garments.
a)
34000
b)
34225
c)
35625
d)
36000
e)
None of these
|
|
Rajeev Kumar answered |
(80/100)*MP = 30000
MP = 37500, CP = 30000
Profit = (15/100)*37500 =5625
SP = 30000+5625 = 35625 rupee
MP = 37500, CP = 30000
Profit = (15/100)*37500 =5625
SP = 30000+5625 = 35625 rupee
Pinkey and Shalini invested some amount of money in the ratio of 3:5 for the same period in the business. They decided that at the end of the year 20% profit was to be given to an organization as a donation. Out of the remaining, 75% was to be reinvested and the rest of the profit was to be divided as interest on their capitals. If the difference in their share is Rs. 2400. What is the total profit?- a)49800
- b)49400
- c)48000
- d)49500
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Pinkey and Shalini invested some amount of money in the ratio of 3:5 for the same period in the business. They decided that at the end of the year 20% profit was to be given to an organization as a donation. Out of the remaining, 75% was to be reinvested and the rest of the profit was to be divided as interest on their capitals. If the difference in their share is Rs. 2400. What is the total profit?
a)
49800
b)
49400
c)
48000
d)
49500
e)
None of these
|
|
Preeti Khanna answered |
Let the total profit = 100
Amount left after donation = 50
Amount left after reinvestment = 20
Now, 5x/8 – 3x/8 = 2400
⇒ 2x/8 = 2400 = 9600
⇒ 1/5 of y = 9600 => y = 48000
Amount left after donation = 50
Amount left after reinvestment = 20
Now, 5x/8 – 3x/8 = 2400
⇒ 2x/8 = 2400 = 9600
⇒ 1/5 of y = 9600 => y = 48000
Rahul sells his laptop to Ravi at a loss of 20% who subsequently sells it to Suresh at a profit of 25%. Suresh after finding some defect in the laptop, returns it to Ravi but could recover only Rs.4.50 for every Rs. 5 he had paid. Find the amount of Suresh’s loss if Rahul had paid Rs.50,000 for the laptop ?
- a)Rs.6000
- b)Rs.7000
- c)Rs.2000
- d)Rs.5000
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
Rahul sells his laptop to Ravi at a loss of 20% who subsequently sells it to Suresh at a profit of 25%. Suresh after finding some defect in the laptop, returns it to Ravi but could recover only Rs.4.50 for every Rs. 5 he had paid. Find the amount of Suresh’s loss if Rahul had paid Rs.50,000 for the laptop ?
a)
Rs.6000
b)
Rs.7000
c)
Rs.2000
d)
Rs.5000
e)
None of these
|
|
Ravi Singh answered |
Solution:
Given:
- Rahul's cost price of laptop = Rs.50,000
- Rahul sells laptop to Ravi at a loss of 20%
- Ravi sells laptop to Suresh at a profit of 25%
- Suresh returns laptop to Ravi and recovers Rs.4.50 for every Rs.5 he paid
Calculations:
1. Rahul's selling price to Ravi:
- Rahul's selling price = 80% of Rs.50,000 (20% loss)
- Rahul's selling price = Rs.40,000
2. Ravi's cost price of laptop:
- Ravi's cost price = Rs.40,000
3. Ravi's selling price to Suresh:
- Ravi's selling price = 125% of Rs.40,000 (25% profit)
- Ravi's selling price = Rs.50,000
4. Amount recovered by Suresh after returning laptop:
- Amount recovered = Rs.4.50 for every Rs.5 paid
- Amount recovered = Rs.4.50 / Rs.5 = 90% of the cost price
5. Suresh's cost price of laptop:
- Suresh's cost price = Rs.50,000
6. Suresh's loss:
- Suresh's loss = Rs.50,000 - Rs.45,000 (Amount recovered)
- Suresh's loss = Rs.5,000
Therefore, the amount of Suresh's loss is Rs.5,000. So, the correct answer is option D: Rs.5,000.0.50/5 * 50,000 = 5000
Given:
- Rahul's cost price of laptop = Rs.50,000
- Rahul sells laptop to Ravi at a loss of 20%
- Ravi sells laptop to Suresh at a profit of 25%
- Suresh returns laptop to Ravi and recovers Rs.4.50 for every Rs.5 he paid
Calculations:
1. Rahul's selling price to Ravi:
- Rahul's selling price = 80% of Rs.50,000 (20% loss)
- Rahul's selling price = Rs.40,000
2. Ravi's cost price of laptop:
- Ravi's cost price = Rs.40,000
3. Ravi's selling price to Suresh:
- Ravi's selling price = 125% of Rs.40,000 (25% profit)
- Ravi's selling price = Rs.50,000
4. Amount recovered by Suresh after returning laptop:
- Amount recovered = Rs.4.50 for every Rs.5 paid
- Amount recovered = Rs.4.50 / Rs.5 = 90% of the cost price
5. Suresh's cost price of laptop:
- Suresh's cost price = Rs.50,000
6. Suresh's loss:
- Suresh's loss = Rs.50,000 - Rs.45,000 (Amount recovered)
- Suresh's loss = Rs.5,000
Therefore, the amount of Suresh's loss is Rs.5,000. So, the correct answer is option D: Rs.5,000.0.50/5 * 50,000 = 5000
A shopkeeper bought 120 chairs at the rate of 250 each. He spends 3000 rupees on transportation. He marked the price of each chair at 400 rupee. On the marked price he gives 10% discount, then find the profit incurred by the shopkeeper.- a)340/11%
- b)350/11%
- c)330/13%
- d)330/11%
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A shopkeeper bought 120 chairs at the rate of 250 each. He spends 3000 rupees on transportation. He marked the price of each chair at 400 rupee. On the marked price he gives 10% discount, then find the profit incurred by the shopkeeper.
a)
340/11%
b)
350/11%
c)
330/13%
d)
330/11%
e)
None of these

|
Bank Exams India answered |
cost price of each chair = 250 + 3000/120 = 275
selling price = 400*90/100 = 360
% profit = [(360 – 275)/275]*100
selling price = 400*90/100 = 360
% profit = [(360 – 275)/275]*100
A and B, there are two companies, selling the packs of cold-drinks. For the same selling price A gives two successive discounts of 10% and 25%. While B sells it by giving two successive discounts of 15% and 20%. What is the ratio of their marked price?- a)143 : 144
- b)19 : 11
- c)136 : 135
- d)73 : 77
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A and B, there are two companies, selling the packs of cold-drinks. For the same selling price A gives two successive discounts of 10% and 25%. While B sells it by giving two successive discounts of 15% and 20%. What is the ratio of their marked price?
a)
143 : 144
b)
19 : 11
c)
136 : 135
d)
73 : 77
e)
None of these
|
|
Rajeev Kumar answered |
A = 90/100*75/100
= .675
B = 85/100*80/100
= .68
680:675
136:135
= .675
B = 85/100*80/100
= .68
680:675
136:135
Rohit bought an article at 25 percent discount on labelled price. He again sells the article at 20 percent on labelled price. Find the percent profit earned by rohit in whole transaction- a)30%
- b)40%
- c)50%
- d)60%
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
Rohit bought an article at 25 percent discount on labelled price. He again sells the article at 20 percent on labelled price. Find the percent profit earned by rohit in whole transaction
a)
30%
b)
40%
c)
50%
d)
60%
e)
None of these
|
|
Preeti Khanna answered |
Let labelled price is 100. Rohit bought it for 75 after getting 25% discount.
Now he sells the article at (120/100)*100 = 120. So % profit he earns = (45/75)*100 =60
Now he sells the article at (120/100)*100 = 120. So % profit he earns = (45/75)*100 =60
Rahul bought 20kg of rice at rupees 30 per kg and 40 kg of rice at 35 rupees per kg. Now he sold the entire lot at 45 rupees per kg. Find the amount of loss and profit made by rahul.- a)650
- b)700
- c)750
- d)800
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Rahul bought 20kg of rice at rupees 30 per kg and 40 kg of rice at 35 rupees per kg. Now he sold the entire lot at 45 rupees per kg. Find the amount of loss and profit made by rahul.
a)
650
b)
700
c)
750
d)
800
e)
None of these
|
|
Rajeev Kumar answered |
total cost price = 20*30 + 40*35 = 2000
total selling price = 45*60 = 2700
profit made = 700
total selling price = 45*60 = 2700
profit made = 700
An item was bought at Rs. X and sold at Rs.Y, thereby earning a profit of 20%. Had the value of X been 15% less and the value of Y been Rs.60 less, a profit of 20% would have been earned, What was the value of Y ?- a)350
- b)400
- c)450
- d)500
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
An item was bought at Rs. X and sold at Rs.Y, thereby earning a profit of 20%. Had the value of X been 15% less and the value of Y been Rs.60 less, a profit of 20% would have been earned, What was the value of Y ?
a)
350
b)
400
c)
450
d)
500
e)
None of these
|
|
Gurutav Patle answered |
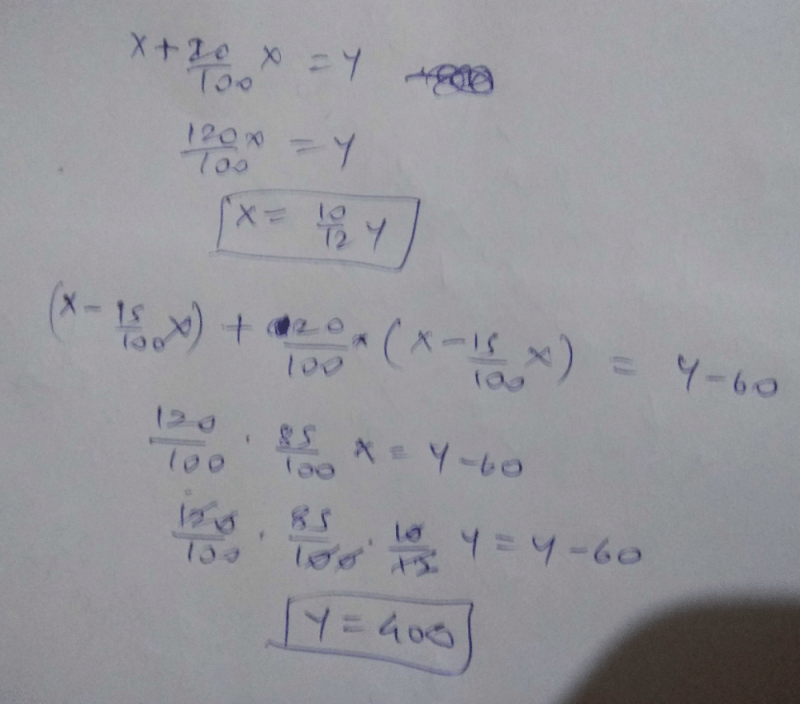
A shopkeeper sold a smartphone for Rs.15000. Had he offered discount of 10% on the Selling Price, he would have earned a profit of 8%. What is the Cost Price of that Smartphone?- a)11300
- b)11500
- c)12500
- d)12300
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A shopkeeper sold a smartphone for Rs.15000. Had he offered discount of 10% on the Selling Price, he would have earned a profit of 8%. What is the Cost Price of that Smartphone?
a)
11300
b)
11500
c)
12500
d)
12300
e)
None of these
|
|
Kavya Saxena answered |
S.P of Smart Phone = Rs.15000
Discount = 10%
New SP = 15000 – 1500 = Rs. 13500
Profit = 8%
CP = 13500 * 100/108 = 12500
Discount = 10%
New SP = 15000 – 1500 = Rs. 13500
Profit = 8%
CP = 13500 * 100/108 = 12500
By selling 22 meters of cloth a shopkeeper gains cost price of 4 meter cloth. Find the percent profit/loss occurred by the shopkeeper.- a)profit 200/9 %
- b)loss 200/11 %
- c)profit 200/11 %
- d)loss 200/11 %
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
By selling 22 meters of cloth a shopkeeper gains cost price of 4 meter cloth. Find the percent profit/loss occurred by the shopkeeper.
a)
profit 200/9 %
b)
loss 200/11 %
c)
profit 200/11 %
d)
loss 200/11 %
e)
None of these

|
Himanshu Somani answered |
It's simple, Selling Price is 22 and Profit is 4. so profit earned on selling price is 4/22 which is 18.18% or 200/11%.
The profit percentage of P and Q is same on selling the articles at Rs. 1800 each but P calculates his profit on the selling price while Q calculates it correctly on the cost price which is equal to 20%. What is the difference in their profits?
- a)40
- b)50
- c)60
- d)70
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
The profit percentage of P and Q is same on selling the articles at Rs. 1800 each but P calculates his profit on the selling price while Q calculates it correctly on the cost price which is equal to 20%. What is the difference in their profits?
a)
40
b)
50
c)
60
d)
70
e)
None of these
|
|
Kavya Saxena answered |
Explanation:
Profit(Calculated on SP) = 20% of 1800 = 360
Profit(calculated on CP)
x + x/5 = 1800
x = 1500
Profit = 300
Difference = 360 – 300 = 60
Profit(Calculated on SP) = 20% of 1800 = 360
Profit(calculated on CP)
x + x/5 = 1800
x = 1500
Profit = 300
Difference = 360 – 300 = 60
A person sold a pen at Rs. 96 in such a way that his percentage profit is same as the cost price of the watch. If he sells it at twice the percentage profit of its previous percentage profit then new selling price will be?- a)Rs.132
- b)Rs.150
- c)Rs.192
- d)Rs.180
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A person sold a pen at Rs. 96 in such a way that his percentage profit is same as the cost price of the watch. If he sells it at twice the percentage profit of its previous percentage profit then new selling price will be?
a)
Rs.132
b)
Rs.150
c)
Rs.192
d)
Rs.180
e)
None of these

|
Cstoppers Instructors answered |
CP = x
Profit Percentage = x%
SP = x(100 + x)/100
x(100 + x)/100 = 96
x = 60
Profit Percentage = 60%
New SP = 60 * 220 / 100 = 132
Profit Percentage = x%
SP = x(100 + x)/100
x(100 + x)/100 = 96
x = 60
Profit Percentage = 60%
New SP = 60 * 220 / 100 = 132
A scientist mixes 10% water in his solution but he is not content with it so he again mixes 10% more water in the previous mixture. What is the profit percentage of the scientist if he sells it at cost price:- a)15%
- b)21%
- c)18%
- d)16%
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A scientist mixes 10% water in his solution but he is not content with it so he again mixes 10% more water in the previous mixture. What is the profit percentage of the scientist if he sells it at cost price:
a)
15%
b)
21%
c)
18%
d)
16%
e)
None of these

|
Future Foundation Institute answered |
Let Initial Quantity of Solution = 100 litre
After mixing 10% water, Quantity of the mixture = 110 * 110 / 100 = 121 litre
CP of One litre of Solution = Rs.1
Total CP = Rs.100
Total SP = Rs.121
Profit = 121 – 100 = 21
Profit % = 21 * 100/100 = 21%
After mixing 10% water, Quantity of the mixture = 110 * 110 / 100 = 121 litre
CP of One litre of Solution = Rs.1
Total CP = Rs.100
Total SP = Rs.121
Profit = 121 – 100 = 21
Profit % = 21 * 100/100 = 21%
P calculates his profit percent on selling price while Q calculates his profit percent on cost price. They notice that difference between their profits is 1000 rupees. If selling price of both P and Q are same and P gets 40% profit and Q gets 60% profit. Then find their selling price - a)77500
- b)40000
- c)97500
- d)10500
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
P calculates his profit percent on selling price while Q calculates his profit percent on cost price. They notice that difference between their profits is 1000 rupees. If selling price of both P and Q are same and P gets 40% profit and Q gets 60% profit. Then find their selling price
a)
77500
b)
40000
c)
97500
d)
10500
e)
None of these

|
Iq Funda answered |
Given:
- Profit Calculation Methods:
- P calculates profit on Selling Price (SP).
- Q calculates profit on Cost Price (CP).
- Profits:
- P's profit: 40% of SP.
- Q's profit: 60% of CP.
- Difference in Profits: ₹1,000.
- Selling Price for both P and Q: Same and denoted as S.
<
Steps to Calculate the Selling Price
- Calculate P's Cost Price (CPP):
- P's profit is 40% of SP.
- ProfitP = 0.40 x S
- CPP = SP - ProfitP = S - 0.40S = 0.60S
- Calculate Q's Cost Price (CPQ):
- Q's profit is 60% of CPQ.
- ProfitQ = 0.60 x CPQ
- Selling Price for Q: SP = CPQ + ProfitQ = CPQ + 0.60CPQ = 1.60CPQ
- Therefore, CPQ = SP / 1.60 = S / 1.60
- ProfitQ = 0.60 x (S / 1.60) = 0.375S
- Set Up the Profit Difference Equation:
- Difference in profits: ProfitP - ProfitQ = ₹1,000
- Substitute the expressions for profits:
- 0.40S - 0.375S = 1,000
- 0.025S = 1,000
- S = 1,000 / 0.025 = 40,000
- Conclusion:
- The selling price for both P and Q is ₹40,000.
Final Answer
The selling price for both P and Q is ₹40,000.
A TV was purchased for Rs. 54000. Its price was marked up by 40%.It was sold at a discount of 20% on the marked price. What was the profit percent of the cost price?- a)10%
- b)11%
- c)15%
- d)12%
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A TV was purchased for Rs. 54000. Its price was marked up by 40%.It was sold at a discount of 20% on the marked price. What was the profit percent of the cost price?
a)
10%
b)
11%
c)
15%
d)
12%
e)
None of these
|
|
Aarav Sharma answered |
Let's break down the given information and solve the problem step by step.
Given information:
- The TV was purchased for Rs. 54000.
- The price was marked up by 40%.
- It was sold at a discount of 20% on the marked price.
Step 1: Finding the marked price
Since the price was marked up by 40%, we can find the marked price by adding 40% of the purchase price to the purchase price itself.
Marked price = Purchase price + 40% of the purchase price
= Rs. 54000 + 40% of Rs. 54000
= Rs. 54000 + (40/100) * Rs. 54000
= Rs. 54000 + (2/5) * Rs. 54000
= Rs. 54000 + Rs. 21600
= Rs. 75600
So, the marked price of the TV is Rs. 75600.
Step 2: Finding the selling price
Since the TV was sold at a discount of 20% on the marked price, we can find the selling price by deducting 20% of the marked price from the marked price itself.
Selling price = Marked price - 20% of the marked price
= Rs. 75600 - 20% of Rs. 75600
= Rs. 75600 - (20/100) * Rs. 75600
= Rs. 75600 - (1/5) * Rs. 75600
= Rs. 75600 - Rs. 15120
= Rs. 60480
So, the selling price of the TV is Rs. 60480.
Step 3: Finding the profit percentage
Profit percentage can be calculated using the formula:
Profit percentage = (Profit / Cost price) * 100
In this case, the profit is the difference between the selling price and the purchase price, and the cost price is the purchase price.
Profit = Selling price - Purchase price
= Rs. 60480 - Rs. 54000
= Rs. 6480
Profit percentage = (6480 / 54000) * 100
= (12 / 100) * 100
= 12%
Therefore, the profit percentage of the cost price is 12%.
Hence, the correct answer is option D) 12%.
Given information:
- The TV was purchased for Rs. 54000.
- The price was marked up by 40%.
- It was sold at a discount of 20% on the marked price.
Step 1: Finding the marked price
Since the price was marked up by 40%, we can find the marked price by adding 40% of the purchase price to the purchase price itself.
Marked price = Purchase price + 40% of the purchase price
= Rs. 54000 + 40% of Rs. 54000
= Rs. 54000 + (40/100) * Rs. 54000
= Rs. 54000 + (2/5) * Rs. 54000
= Rs. 54000 + Rs. 21600
= Rs. 75600
So, the marked price of the TV is Rs. 75600.
Step 2: Finding the selling price
Since the TV was sold at a discount of 20% on the marked price, we can find the selling price by deducting 20% of the marked price from the marked price itself.
Selling price = Marked price - 20% of the marked price
= Rs. 75600 - 20% of Rs. 75600
= Rs. 75600 - (20/100) * Rs. 75600
= Rs. 75600 - (1/5) * Rs. 75600
= Rs. 75600 - Rs. 15120
= Rs. 60480
So, the selling price of the TV is Rs. 60480.
Step 3: Finding the profit percentage
Profit percentage can be calculated using the formula:
Profit percentage = (Profit / Cost price) * 100
In this case, the profit is the difference between the selling price and the purchase price, and the cost price is the purchase price.
Profit = Selling price - Purchase price
= Rs. 60480 - Rs. 54000
= Rs. 6480
Profit percentage = (6480 / 54000) * 100
= (12 / 100) * 100
= 12%
Therefore, the profit percentage of the cost price is 12%.
Hence, the correct answer is option D) 12%.
A trader mixes 25% of solution A to his Solution B and then he sells the whole mixture at the price of Solution B. If the cost price of Solution A be 50% of the cost price of Solution B, what is the net profit percentage?- a)100/3%
- b)200/7%
- c)100/9%
- d)200/3%
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A trader mixes 25% of solution A to his Solution B and then he sells the whole mixture at the price of Solution B. If the cost price of Solution A be 50% of the cost price of Solution B, what is the net profit percentage?
a)
100/3%
b)
200/7%
c)
100/9%
d)
200/3%
e)
None of these
|
|
Preeti Khanna answered |
Quantity of Solution B = 100 litre
Quantity of Solution A = 25 litre
CP of 1 litre Solution B = Rs.10
CP of 1 litre Solution A = Rs.5
CP = 100 * 10 + 25 * 5 = 1125
SP = (100 + 25)*10 = 1250
Profit = 1250 – 1125 = 125
% = 125 * 100 / 1125 = 100/9%
Quantity of Solution A = 25 litre
CP of 1 litre Solution B = Rs.10
CP of 1 litre Solution A = Rs.5
CP = 100 * 10 + 25 * 5 = 1125
SP = (100 + 25)*10 = 1250
Profit = 1250 – 1125 = 125
% = 125 * 100 / 1125 = 100/9%
Pinkey sold a machine to Shalini at a profit of 30%. Shalini sold this machine to Arun at a loss of 20%. If Pinkey paid Rs.5000 for this machine, then find the cost price of machine for Arun?- a)6200
- b)5200
- c)4800
- d)4750
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Pinkey sold a machine to Shalini at a profit of 30%. Shalini sold this machine to Arun at a loss of 20%. If Pinkey paid Rs.5000 for this machine, then find the cost price of machine for Arun?
a)
6200
b)
5200
c)
4800
d)
4750
e)
None of these
|
|
Kavya Saxena answered |
R1 = 30% R2 = 20%
5000 * 130/100 * 80/100 = Rs. 5200
5000 * 130/100 * 80/100 = Rs. 5200
A shopkeeper bought 150 pen drives at the rate of Rs. 500 per pen drive. He spent Rs. 500 on transportation and packing. If the marked price of pen drive is Rs. 550 per pen drive and the shopkeeper gives a discount of 5% on the marked price then what will be the percentage profit gained by the shopkeeper?- a)4.5%
- b)5.5%
- c)3.8%
- d)1.2%
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A shopkeeper bought 150 pen drives at the rate of Rs. 500 per pen drive. He spent Rs. 500 on transportation and packing. If the marked price of pen drive is Rs. 550 per pen drive and the shopkeeper gives a discount of 5% on the marked price then what will be the percentage profit gained by the shopkeeper?
a)
4.5%
b)
5.5%
c)
3.8%
d)
1.2%
e)
None of these
|
|
Alok Verma answered |
C.P. of 150 pendrives = 150 x 500 = Rs. 75000
∴ Total C.P. = 75000 + 500 = Rs. 75500
Marked price of 150 pendrive = 150 x 550 = Rs. 82500
Selling price after discount = 82500 x 95 / 100 = Rs. 78375
∴ percentage profit = [(78375 – 75500) / 75500] x 100 = 3.8%
∴ Total C.P. = 75000 + 500 = Rs. 75500
Marked price of 150 pendrive = 150 x 550 = Rs. 82500
Selling price after discount = 82500 x 95 / 100 = Rs. 78375
∴ percentage profit = [(78375 – 75500) / 75500] x 100 = 3.8%
A tradesman marks the price of his goods such that after allowing a discount of 25%, he earns a profit of 40%. What is the marked price of an article whose cost price is Rs.180?- a)285
- b)336
- c)358
- d)375
- e)390
Correct answer is option 'B'. Can you explain this answer?
A tradesman marks the price of his goods such that after allowing a discount of 25%, he earns a profit of 40%. What is the marked price of an article whose cost price is Rs.180?
a)
285
b)
336
c)
358
d)
375
e)
390
|
|
Nikita Singh answered |
S.P = (100+profit%)*cp /100 = 140*180/100 = 252
M.P – 25% of M.P = SP
X – 25/100 X = 252
X = 336
M.P – 25% of M.P = SP
X – 25/100 X = 252
X = 336
A vendor sold two magazines namely A and B. He sold magazine ‘A’ at a loss of 30% and magazine ‘B’ at a profit of 35% but finally there is no loss or no gain. If the total Selling price of both magazines is Rs.572. Find the difference between the Cost Price of Magazine ‘A’ and ‘B’?- a)Rs. 32
- b)Rs. 44
- c)Rs. 56
- d)Rs. 62
- e)None of the Above
Correct answer is option 'B'. Can you explain this answer?
A vendor sold two magazines namely A and B. He sold magazine ‘A’ at a loss of 30% and magazine ‘B’ at a profit of 35% but finally there is no loss or no gain. If the total Selling price of both magazines is Rs.572. Find the difference between the Cost Price of Magazine ‘A’ and ‘B’?
a)
Rs. 32
b)
Rs. 44
c)
Rs. 56
d)
Rs. 62
e)
None of the Above
|
|
Anaya Patel answered |
30% of x = 35% of y ; x + y = 572
x/y = 7/6
Difference = Rs.44
x/y = 7/6
Difference = Rs.44
A trader sold an article for rupees 810 after giving a discount of 10 percent on the labelled price and gain 20% percent. What will be the profit percent when the article is sold at labelled price.- a)100/7 %
- b)100/3 %
- c)200/3 %
- d)200/7 %
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A trader sold an article for rupees 810 after giving a discount of 10 percent on the labelled price and gain 20% percent. What will be the profit percent when the article is sold at labelled price.
a)
100/7 %
b)
100/3 %
c)
200/3 %
d)
200/7 %
e)
None of these
|
|
Sagar Sharma answered |
To solve this problem, we need to calculate the profit percentage when the article is sold at the labeled price. Let's break down the steps to find the solution:
1. Find the cost price (CP):
We know that the trader sold the article for Rs. 810 after giving a discount of 10%. Therefore, the selling price (SP) is 90% of the labeled price (LP).
SP = LP - (10% of LP)
810 = LP - (0.10LP)
810 = 0.90LP
LP = 810 / 0.90
LP = 900
So, the labeled price (LP) is Rs. 900.
2. Find the profit:
The trader gained 20% on the cost price (CP). To find the profit, we need to calculate 20% of the cost price.
Profit = 20% of CP
Profit = 20/100 * CP
Profit = 1/5 * CP
3. Find the cost price (CP):
To find the cost price (CP), we can use the formula:
SP = CP + Profit
Since the selling price (SP) is the labeled price (LP), we can substitute LP for SP:
LP = CP + Profit
900 = CP + 1/5 * CP
900 = 6/5 * CP
CP = 900 * 5/6
CP = 750
4. Find the profit percentage:
Now that we have the cost price (CP) and the selling price (LP), we can calculate the profit percentage:
Profit Percentage = (Profit / CP) * 100
Profit Percentage = (1/5 * CP / CP) * 100
Profit Percentage = (1/5) * 100
Profit Percentage = 20%
Therefore, the profit percentage when the article is sold at the labeled price is 20%. The correct answer is option 'B' - 100/3%.
1. Find the cost price (CP):
We know that the trader sold the article for Rs. 810 after giving a discount of 10%. Therefore, the selling price (SP) is 90% of the labeled price (LP).
SP = LP - (10% of LP)
810 = LP - (0.10LP)
810 = 0.90LP
LP = 810 / 0.90
LP = 900
So, the labeled price (LP) is Rs. 900.
2. Find the profit:
The trader gained 20% on the cost price (CP). To find the profit, we need to calculate 20% of the cost price.
Profit = 20% of CP
Profit = 20/100 * CP
Profit = 1/5 * CP
3. Find the cost price (CP):
To find the cost price (CP), we can use the formula:
SP = CP + Profit
Since the selling price (SP) is the labeled price (LP), we can substitute LP for SP:
LP = CP + Profit
900 = CP + 1/5 * CP
900 = 6/5 * CP
CP = 900 * 5/6
CP = 750
4. Find the profit percentage:
Now that we have the cost price (CP) and the selling price (LP), we can calculate the profit percentage:
Profit Percentage = (Profit / CP) * 100
Profit Percentage = (1/5 * CP / CP) * 100
Profit Percentage = (1/5) * 100
Profit Percentage = 20%
Therefore, the profit percentage when the article is sold at the labeled price is 20%. The correct answer is option 'B' - 100/3%.
A Bike is available at 40% discount at show room “A” and the same is available at only 25% discount at show room “B”. Mr. Arun has just sufficient amount of Rs. 60,000 to purchase it at show room “A”. What is the amount that Mr. Arun has less than the required amount to purchase it at that show room “B”?- a)Rs. 70000
- b) Rs. 50000
- c)Rs. 10000
- d)Rs. 15000
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A Bike is available at 40% discount at show room “A” and the same is available at only 25% discount at show room “B”. Mr. Arun has just sufficient amount of Rs. 60,000 to purchase it at show room “A”. What is the amount that Mr. Arun has less than the required amount to purchase it at that show room “B”?
a)
Rs. 70000
b)
Rs. 50000
c)
Rs. 10000
d)
Rs. 15000
e)
None of these
|
|
Nikita Singh answered |
Let the marked price be x.
Cost price (CP) = 40 % discount on MP = 0.6y = 60000
⇒ y= Rs.100000 MP
SP at Show Room “A” = Rs. 60000
SP at Show Room “B” = 100000 X 0.75 = 75000; Difference = 15000
Cost price (CP) = 40 % discount on MP = 0.6y = 60000
⇒ y= Rs.100000 MP
SP at Show Room “A” = Rs. 60000
SP at Show Room “B” = 100000 X 0.75 = 75000; Difference = 15000
Person A sold his car to Person B at a profit of 20% and B sold it to C at a profit of 10%. Person C sold it to mechanic at a loss of 9.09%. Mechanic spent 10% of his purchasing price and then sold it at a profit of 8.33% to Person “A” once again. What is the loss of person “A”?- a)23%
- b)29%
- c)50%
- d)40%
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
Person A sold his car to Person B at a profit of 20% and B sold it to C at a profit of 10%. Person C sold it to mechanic at a loss of 9.09%. Mechanic spent 10% of his purchasing price and then sold it at a profit of 8.33% to Person “A” once again. What is the loss of person “A”?
a)
23%
b)
29%
c)
50%
d)
40%
e)
None of these
|
|
Yash Patel answered |
CP = 100
SP = 120
B:
CP = 120
SP = 132
C:
CP = 132
SP = 120
Mechanic:
CP = 120 + 12 = 132
SP = 143
Loss of A = 143 – 120 = 23
% loss of A = (23 / 100) x 100 = 23%
SP = 120
B:
CP = 120
SP = 132
C:
CP = 132
SP = 120
Mechanic:
CP = 120 + 12 = 132
SP = 143
Loss of A = 143 – 120 = 23
% loss of A = (23 / 100) x 100 = 23%
A dealer sells a goat for rupees 600 and there by gains 20 percent. He sells another goat at 5 percent loss and on the whole there is no loss no profit. Find the cost price of the second goat- a)1000
- b)2000
- c)3000
- d)4000
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A dealer sells a goat for rupees 600 and there by gains 20 percent. He sells another goat at 5 percent loss and on the whole there is no loss no profit. Find the cost price of the second goat
a)
1000
b)
2000
c)
3000
d)
4000
e)
None of these
|
|
Kavya Saxena answered |
600 = (120/100)*cp
so cp of first goat = 500. So in the first deal he gains 100 rupees.
But on selling second horse he losses 5 percent, means (5/100)*CP = 100
So cp of second goat = 2000
so cp of first goat = 500. So in the first deal he gains 100 rupees.
But on selling second horse he losses 5 percent, means (5/100)*CP = 100
So cp of second goat = 2000
A shopkeeper sold certain articles at 380 after giving a discount of 5 percent. If the discount is not given he would have been gain 20 percent. What is the cost price of the articles (approx.)- a)332
- b)333
- c)334
- d)335
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A shopkeeper sold certain articles at 380 after giving a discount of 5 percent. If the discount is not given he would have been gain 20 percent. What is the cost price of the articles (approx.)
a)
332
b)
333
c)
334
d)
335
e)
None of these
|
|
Yash Patel answered |
(95/100)*MP = 380. Mp = 400
400 = (120/100)*Cp
CP = 333.33
400 = (120/100)*Cp
CP = 333.33
If a discount of 15 percent is given on an article then the shopkeeper make a profit of 5 percent. Find the percent profit made by the seller when a discount of 10 percent is given
- a)11.3/17 %
- b)11.4/17 %
- c)11.5/17 %
- d)11.7/17 %
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
If a discount of 15 percent is given on an article then the shopkeeper make a profit of 5 percent. Find the percent profit made by the seller when a discount of 10 percent is given
a)
11.3/17 %
b)
11.4/17 %
c)
11.5/17 %
d)
11.7/17 %
e)
None of these
|
|
Kavya Saxena answered |
(85/100)*mp = (105/100)*cp
(90/100)*mp = [(100+p)/100]*(85/105)*mp
(90/100)*mp = [(100+p)/100]*(85/105)*mp
When a shopkeeper reduces the selling price of an article from 1180 to 1126 his loss increases by 5% . What is the cost price of article?- a)1050
- b)1060
- c)1070
- d)1080
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
When a shopkeeper reduces the selling price of an article from 1180 to 1126 his loss increases by 5% . What is the cost price of article?
a)
1050
b)
1060
c)
1070
d)
1080
e)
None of these
|
|
Rhea Reddy answered |
5% of CP = 1180 – 1126
CP = 54 * 100 / 5 = 1080
CP = 54 * 100 / 5 = 1080
A person sell two horses for rupees 480 each. On the first horse he gains 25 percent and on the second horse he losses 25 percent. Find the percent gain or loss in the transaction.
- a)loss 6.75%
- b)gain 6.75%
- c)loss 6.25%
- d)gain 6.25%
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A person sell two horses for rupees 480 each. On the first horse he gains 25 percent and on the second horse he losses 25 percent. Find the percent gain or loss in the transaction.
a)
loss 6.75%
b)
gain 6.75%
c)
loss 6.25%
d)
gain 6.25%
e)
None of these
|
|
Rhea Reddy answered |



If a discount of 10 percent is given on the marked price of the article then the seller gains 20 percent profit. Find the percent profit if the article is sold at 20 percent discount.- a)10/3 %
- b)20/3 %
- c)25/3 %
- d)40/3 %
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
If a discount of 10 percent is given on the marked price of the article then the seller gains 20 percent profit. Find the percent profit if the article is sold at 20 percent discount.
a)
10/3 %
b)
20/3 %
c)
25/3 %
d)
40/3 %
e)
None of these
|
|
Anaya Patel answered |
Let marked price = 100
90 = (120/100)*cp, cp = 75
Now discount = 20% so, SP = 80
% profit = [(80 – 75)/75]*100 = 20/3
90 = (120/100)*cp, cp = 75
Now discount = 20% so, SP = 80
% profit = [(80 – 75)/75]*100 = 20/3
A and B both are dealers of Honda Motorcycles. The price of an used Honda Motorcycle is Rs.28,000. A gives a discount of 10% on whole, while B gives a discount of 12% on the first Rs. 20,000 and 8% on the rest Rs. 8000. What is the difference between their selling prices?- a)Rs.240
- b)Rs.420
- c)Rs.640
- d)Rs.740
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A and B both are dealers of Honda Motorcycles. The price of an used Honda Motorcycle is Rs.28,000. A gives a discount of 10% on whole, while B gives a discount of 12% on the first Rs. 20,000 and 8% on the rest Rs. 8000. What is the difference between their selling prices?
a)
Rs.240
b)
Rs.420
c)
Rs.640
d)
Rs.740
e)
None of these
|
|
Kavya Saxena answered |
Discount offer by A = 10 % of 28000 = 2800
Total Discount offer by B = 12% of 20,000 + 8% of 8000 = 3040
Required difference = 3040 – 2800 = 240
Total Discount offer by B = 12% of 20,000 + 8% of 8000 = 3040
Required difference = 3040 – 2800 = 240
A trader gives an additional concession of 35% on an article which is already get discounted by 20% on the marked price. If the buyer pays an amount of 1300 for the article, then the marked price is- a)2200
- b)2500
- c)2600
- d)2700
- e)None of thes
Correct answer is option 'B'. Can you explain this answer?
A trader gives an additional concession of 35% on an article which is already get discounted by 20% on the marked price. If the buyer pays an amount of 1300 for the article, then the marked price is
a)
2200
b)
2500
c)
2600
d)
2700
e)
None of thes
|
|
Aarav Sharma answered |
Given Information:
- The trader gives an additional concession of 35% on an article.
- The article is already discounted by 20% on the marked price.
- The buyer pays an amount of 1300 for the article.
To Find:
The marked price of the article.
Solution:
Let's assume the marked price of the article is 'x' dollars.
Step 1: Discount on the Marked Price:
The article is already discounted by 20% on the marked price. Therefore, the selling price after the 20% discount will be:
x - (20/100)x = (80/100)x = 0.8x dollars.
Step 2: Additional Concession:
The trader gives an additional concession of 35% on the selling price after the 20% discount. Therefore, the selling price after the additional concession will be:
0.8x - (35/100)(0.8x) = 0.8x - 0.28x = 0.52x dollars.
Step 3: Selling Price:
The buyer pays an amount of 1300 for the article. Therefore, we can equate the selling price to 1300 and solve for 'x':
0.52x = 1300
x = 1300 / 0.52
x ≈ 2500
Therefore, the marked price of the article is approximately 2500 dollars.
Conclusion:
The marked price of the article is option 'B' - 2500 dollars.
- The trader gives an additional concession of 35% on an article.
- The article is already discounted by 20% on the marked price.
- The buyer pays an amount of 1300 for the article.
To Find:
The marked price of the article.
Solution:
Let's assume the marked price of the article is 'x' dollars.
Step 1: Discount on the Marked Price:
The article is already discounted by 20% on the marked price. Therefore, the selling price after the 20% discount will be:
x - (20/100)x = (80/100)x = 0.8x dollars.
Step 2: Additional Concession:
The trader gives an additional concession of 35% on the selling price after the 20% discount. Therefore, the selling price after the additional concession will be:
0.8x - (35/100)(0.8x) = 0.8x - 0.28x = 0.52x dollars.
Step 3: Selling Price:
The buyer pays an amount of 1300 for the article. Therefore, we can equate the selling price to 1300 and solve for 'x':
0.52x = 1300
x = 1300 / 0.52
x ≈ 2500
Therefore, the marked price of the article is approximately 2500 dollars.
Conclusion:
The marked price of the article is option 'B' - 2500 dollars.
If the Cost Price of 25 articles is equal to the Selling Price of 20 articles, then what is the gain %?
- a)25%
- b)29%
- c)50%
- d)40%
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
If the Cost Price of 25 articles is equal to the Selling Price of 20 articles, then what is the gain %?
a)
25%
b)
29%
c)
50%
d)
40%
e)
None of these
|
|
Aarav Sharma answered |
Given:
- Cost Price of 25 articles = Selling Price of 20 articles
To find:
- Gain %
Solution:
To find the gain %, we need to find the profit and then calculate the profit %.
Step 1: Finding the Profit:
Let's assume the cost price of each article is 'x' and the selling price of each article is 'y'.
- Cost Price of 25 articles = 25x
- Selling Price of 20 articles = 20y
Given that the cost price of 25 articles is equal to the selling price of 20 articles:
25x = 20y
Step 2: Solving the Equation:
To solve the equation, we need to find the relation between 'x' and 'y'. Let's assume the relation is 'a'.
x = ay
Substituting the above relation in the equation 25x = 20y:
25(ay) = 20y
25a = 20
a = 20/25
a = 4/5
So, the relation between 'x' and 'y' is x = (4/5)y.
Step 3: Calculating the Gain %:
Profit = Selling Price - Cost Price
Profit = 20y - 25x
Profit = 20y - 25(4/5)y
Profit = 20y - 20y
Profit = 0
Since the profit is 0, the gain % is also 0.
The correct option is (A) 0%, not 25%.
- Cost Price of 25 articles = Selling Price of 20 articles
To find:
- Gain %
Solution:
To find the gain %, we need to find the profit and then calculate the profit %.
Step 1: Finding the Profit:
Let's assume the cost price of each article is 'x' and the selling price of each article is 'y'.
- Cost Price of 25 articles = 25x
- Selling Price of 20 articles = 20y
Given that the cost price of 25 articles is equal to the selling price of 20 articles:
25x = 20y
Step 2: Solving the Equation:
To solve the equation, we need to find the relation between 'x' and 'y'. Let's assume the relation is 'a'.
x = ay
Substituting the above relation in the equation 25x = 20y:
25(ay) = 20y
25a = 20
a = 20/25
a = 4/5
So, the relation between 'x' and 'y' is x = (4/5)y.
Step 3: Calculating the Gain %:
Profit = Selling Price - Cost Price
Profit = 20y - 25x
Profit = 20y - 25(4/5)y
Profit = 20y - 20y
Profit = 0
Since the profit is 0, the gain % is also 0.
The correct option is (A) 0%, not 25%.
A merchant earns a profit of 20% by selling a basket containing 80 Oranges whose cost is Rs.240 but he gives one-fourth of it to his friend at cost price and sells the remaining oranges. In order to earn the same profit, at what price must he sell each orange?- a)Rs. 4.80
- b)Rs. 4.90
- c)Rs. 3.80
- d)Rs. 4.50
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A merchant earns a profit of 20% by selling a basket containing 80 Oranges whose cost is Rs.240 but he gives one-fourth of it to his friend at cost price and sells the remaining oranges. In order to earn the same profit, at what price must he sell each orange?
a)
Rs. 4.80
b)
Rs. 4.90
c)
Rs. 3.80
d)
Rs. 4.50
e)
None of these
|
|
Anaya Patel answered |
CP of 80 Oranges = Rs.240
CP of 1 Orange = Rs.3
CP of 20 Oranges = Rs.60
120% of 240 = 288
SP of remaining 60 Oranges = 288 – 60 = 228
SP of 1 Orange = 228/60 = Rs.3.80
CP of 1 Orange = Rs.3
CP of 20 Oranges = Rs.60
120% of 240 = 288
SP of remaining 60 Oranges = 288 – 60 = 228
SP of 1 Orange = 228/60 = Rs.3.80
Chapter doubts & questions for Profit And Loss - 4 Months Preparation Course for CLAT UG 2025 is part of CLAT exam preparation. The chapters have been prepared according to the CLAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CLAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Profit And Loss - 4 Months Preparation Course for CLAT UG in English & Hindi are available as part of CLAT exam.
Download more important topics, notes, lectures and mock test series for CLAT Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









