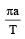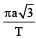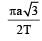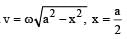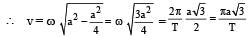All Exams >
NEET >
1 Year Dropper Course for NEET >
All Questions
All questions of Oscillations for NEET Exam
Find the amplitude of the S.H.M whose displacement y in cm is given by equation y= 3sin 157t +4cos157t where t is time in seconds.- a)20Hz
- b)25Hz
- c)50Hz
- d)40Hz
Correct answer is option 'B'. Can you explain this answer?
Find the amplitude of the S.H.M whose displacement y in cm is given by equation y= 3sin 157t +4cos157t where t is time in seconds.
a)
20Hz
b)
25Hz
c)
50Hz
d)
40Hz

|
Pioneer Academy answered |
When the displacement of a SHM is:
y=a sin wt+ b cos wt
y=a sin wt+ b cos wt
- Amplitude of the SHM will be:
A=√a2+b2
Here, a = 3, b = 4
Amplitude, A= √(32+42) = 5 cm
Amplitude, A= √(32+42) = 5 cm
Hence option B is correct.
A second pendulum is mounted in a space shuttle. Its period of oscillations will decrease when rocket is- a)moving in geostationary orbit
- b)ascending up with uniform acceleration
- c)descending down with uniform acceleration
- d)moving up with uniform velocity
Correct answer is option 'B'. Can you explain this answer?
A second pendulum is mounted in a space shuttle. Its period of oscillations will decrease when rocket is
a)
moving in geostationary orbit
b)
ascending up with uniform acceleration
c)
descending down with uniform acceleration
d)
moving up with uniform velocity

|
Top Rankers answered |
- Time Period, T = 2π √(l/g')where,
l = Length of seconds pendulum
g’ = Apparent Gravity - For the period of oscillations of Seconds Pendulum to decrease, the Apparent gravity (g’) has to increase because:
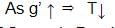
- Hence, Time Period of oscillations of Seconds Pendulum will decrease when the rocket is ascending up with uniform acceleration.
If a simple pendulum oscillates with an amplitude 50 mm and time period 2s, then its maximum velocity isa)0.15 m/sb)0.1 m/sc)0.16 m/sd)0.8 m/sCorrect answer is option 'A'. Can you explain this answer?
|
|
Neha Joshi answered |
We know that in a simple harmonic motion the maximum velocity,
Vmax = A⍵
Here A = 50 mm
Vmax = A⍵
Here A = 50 mm
And ⍵ = 2π / T
= 2π / 2
= π
= 2π / 2
= π
Hence Vmax = 50 x 10-3.π
= 0.15 m/s
= 0.15 m/s
The displacement of a particle along the x-axis is given by x = a sin2ωt. The motion of the particle corresponds to: [2010]
- a) non simple harmonic motion
- b)simple harmonic motion of frequency 3ω /2π
- c)simple harmonic motion of frequency ω /π
- d)simple harmonic motion of frequency ω /2π
Correct answer is option 'A'. Can you explain this answer?
The displacement of a particle along the x-axis is given by x = a sin2ωt. The motion of the particle corresponds to: [2010]
a)
non simple harmonic motion
b)
simple harmonic motion of frequency 3ω /2π
c)
simple harmonic motion of frequency ω /π
d)
simple harmonic motion of frequency ω /2π
|
|
Athira Krishnana answered |

What will be the phase difference between bigger pendulum (with time period 5T/4 )and smaller pendulum (with time period T) after one oscillation of bigger pendulum?- a)π/4
- b)π/2
- c)π/3
- d)π
Correct answer is option 'B'. Can you explain this answer?
What will be the phase difference between bigger pendulum (with time period 5T/4 )and smaller pendulum (with time period T) after one oscillation of bigger pendulum?
a)
π/4
b)
π/2
c)
π/3
d)
π
|
|
Preeti Iyer answered |
By the time bigger pendulum completes one vibration, the smaller pendulum would have completed 5/4 vibrations. That is smaller pendulum will be ahead by 1/4 vibration in phase. 1/4 vibration means λ/4 path or π/2 radians.
A frequency of 1Hz corresponds to:- a)2 vibrations per second
- b)1 vibration per second
- c)10 vibrations per second
- d)a time period of ½ second
Correct answer is option 'B'. Can you explain this answer?
A frequency of 1Hz corresponds to:
a)
2 vibrations per second
b)
1 vibration per second
c)
10 vibrations per second
d)
a time period of ½ second
|
|
Alok Mehta answered |
Frequency used to be measured in cycles per second, but now we use the unit of frequency - the Hertz (abbreviated Hz). One Hertz (1Hz) is equal to one vibration per second. So the weight above is bouncing with a frequency of about 1Hz. The sound wave corresponding to Middle C on a piano is around 256Hz.
What determines the natural frequency of a body?- a)Position of the body with respect to force applied
- b)Mass and speed of the body
- c)Oscillations in the body
- d)Elastic properties and dimensions of the body
Correct answer is option 'D'. Can you explain this answer?
What determines the natural frequency of a body?
a)
Position of the body with respect to force applied
b)
Mass and speed of the body
c)
Oscillations in the body
d)
Elastic properties and dimensions of the body
|
|
Lavanya Menon answered |
Natural frequency is the frequency at which a body tends to oscillate in the absence of any driving or damping force.
Free vibrations of any elastic body are called natural vibration and happen at a frequency called natural frequency. Natural vibrations are different from forced vibration which happen at frequency of applied force .
Free vibrations of any elastic body are called natural vibration and happen at a frequency called natural frequency. Natural vibrations are different from forced vibration which happen at frequency of applied force .
A particle executes linear simple harmonic motion with an amplitude of 2 cm. When the particle is at 1 cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then its time period in seconds is:- a)2π/√3
- b)2π√3
- c)√3/2π
- d)1/ 2π√3
Correct answer is option 'A'. Can you explain this answer?
A particle executes linear simple harmonic motion with an amplitude of 2 cm. When the particle is at 1 cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then its time period in seconds is:
a)
2π/√3
b)
2π√3
c)
√3/2π
d)
1/ 2π√3
|
|
Jyoti Kapoor answered |
velocity at distance x in shm is given as
v= w sqrt(A2-x2)
so A = 2 x =1
v = w sqrt(4-1) = wsqrt3
now acc at distance x is a= w2 x = w2
as mag a = mag v
w2 = wsqrt3
w= sqrt3
2pi/T= sqrt3
T = 2pi/sqrt3
If  is the natural frequency of the system and
is the natural frequency of the system and  is the frequency of the external force that acts on an oscillating system then at resonance
is the frequency of the external force that acts on an oscillating system then at resonance- a)ωd ≥ ω
- b)ωd = ω
- c)ωd ≤ ω
- d)ωd ≠ ω
Correct answer is option 'B'. Can you explain this answer?
If  is the natural frequency of the system and
is the natural frequency of the system and  is the frequency of the external force that acts on an oscillating system then at resonance
is the frequency of the external force that acts on an oscillating system then at resonance
 is the natural frequency of the system and
is the natural frequency of the system and  is the frequency of the external force that acts on an oscillating system then at resonance
is the frequency of the external force that acts on an oscillating system then at resonancea)
ωd ≥ ω
b)
ωd = ω
c)
ωd ≤ ω
d)
ωd ≠ ω
|
|
Om Desai answered |
When the natural frequency and external frequency of an object are equal the phenomenon is called resonance.
The restoring force in a simple harmonic motion is _________ in magnitude when the particle is instantaneously at rest.- a)zero
- b)maximum
- c)minimum
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The restoring force in a simple harmonic motion is _________ in magnitude when the particle is instantaneously at rest.
a)
zero
b)
maximum
c)
minimum
d)
none of these

|
Knowledge Hub answered |
The restoring force in a simple harmonic motion is maximum in magnitude when the particle is instantaneously at rest because in SHM object’s tendency is to return to mean position and here particle is instantaneously at rest after that instant restoring force will be max to bring particle to mean position.
If an external force with angular frequency ωd acts on an oscillating system with natural angular frequency ω, the system oscillates with angular frequency ωd. The amplitude of oscillations is the greatest when:- a)ωd > ω
- b)ωd < ω
- c)ωd ≥ ω
- d)ωd = ω
Correct answer is option 'D'. Can you explain this answer?
If an external force with angular frequency ωd acts on an oscillating system with natural angular frequency ω, the system oscillates with angular frequency ωd. The amplitude of oscillations is the greatest when:
a)
ωd > ω
b)
ωd < ω
c)
ωd ≥ ω
d)
ωd = ω
|
|
Jyoti Aiims Aspirant answered |
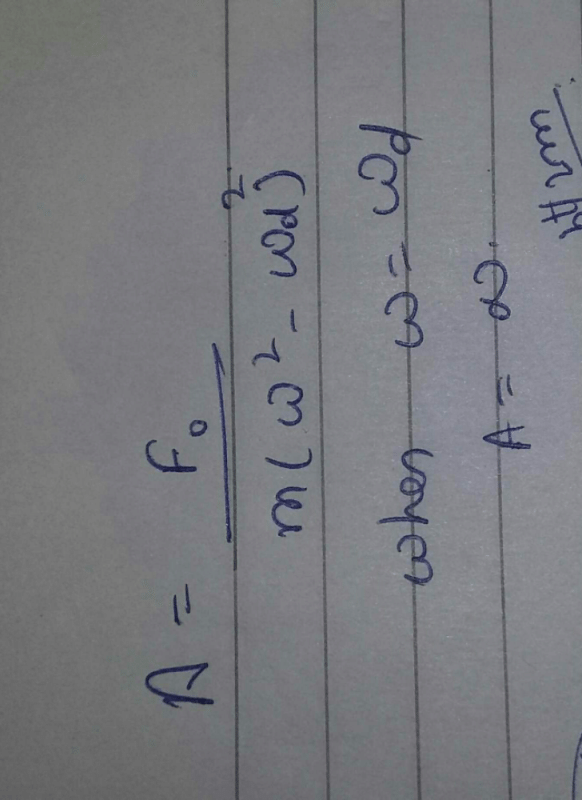
Under what condition angular frequency ω of the damped oscillator would be equivalent to angular velocity Ω of the undamped oscillator.- a)Velocity of oscillator is small
- b)Damping constant, b is small
- c)Damping constant ,b is large
- d)Force applied is small
Correct answer is option 'B'. Can you explain this answer?
Under what condition angular frequency ω of the damped oscillator would be equivalent to angular velocity Ω of the undamped oscillator.
a)
Velocity of oscillator is small
b)
Damping constant, b is small
c)
Damping constant ,b is large
d)
Force applied is small
|
|
Priya Patel answered |
The potential energy of a long spring when stretched by 2cm is U. If the spring is stretched by 8 cm, the potential energy stored in it is- a)8 U
- b)16 U [2006]
- c)U/ 4
- d)4 U
Correct answer is option 'B'. Can you explain this answer?
The potential energy of a long spring when stretched by 2cm is U. If the spring is stretched by 8 cm, the potential energy stored in it is
a)
8 U
b)
16 U [2006]
c)
U/ 4
d)
4 U
|
|
Geetika Shah answered |
The potential energy of a spring

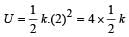
For x = 8 cm,
Energy stored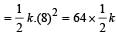
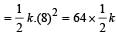
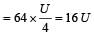
The amplitude of S.H.M at resonance is _______ in the ideal case of zero damping.- a)Maximum
- b)Minimum
- c)Zero
- d)Infinite
Correct answer is option 'D'. Can you explain this answer?
The amplitude of S.H.M at resonance is _______ in the ideal case of zero damping.
a)
Maximum
b)
Minimum
c)
Zero
d)
Infinite
|
|
Neha Joshi answered |
In an ideal environment where there is no resistance to oscillation motion i.e. damping is zero, when we oscillate a system at its resonant frequency since there is no opposition to oscillation, the amplitude will go on increasing and reach infinity.
The velocity of a particle moving with simple harmonic motion is . . . . at the mean position.- a)Zero
- b)Minimum
- c)Maximum
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
The velocity of a particle moving with simple harmonic motion is . . . . at the mean position.
a)
Zero
b)
Minimum
c)
Maximum
d)
None of the above
|
|
Niharika Nair answered |
V = ω√(A2 – x2)
So the velocity is maximum at mean position
So the velocity is maximum at mean position
A particle executes simple harmonic oscillation with an amplitude a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is[2007]- a)T/8
- b)T/12
- c)T/2
- d)T/4
Correct answer is option 'B'. Can you explain this answer?
A particle executes simple harmonic oscillation with an amplitude a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is[2007]
a)
T/8
b)
T/12
c)
T/2
d)
T/4

|
Anu Bajaj answered |
Displacement from the mean position
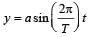
According to problem y = a/2
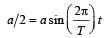
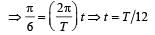
This is the minimum time taken by the particle to travel half of the amplitude from the equilibrium position.
In the ideal case of zero damping, the amplitude of simple harmonic motion at resonance is:- a)zero
- b)infinite
- c)cannot be said
- d)varies from zero to infinite
Correct answer is option 'B'. Can you explain this answer?
In the ideal case of zero damping, the amplitude of simple harmonic motion at resonance is:
a)
zero
b)
infinite
c)
cannot be said
d)
varies from zero to infinite
|
|
Priya Patel answered |
In an ideal environment where there is no resistance to oscillatory motion, that is, damping is zero, when we oscillate a system at its resonant frequency, since there is no opposition to oscillation, a very large value of amplitude will be recorded. Forced oscillation is when you apply an external oscillating force.
A block of mass M is attached to the lower end of a vertical spring. The spring is hung from a ceiling and has force constant value k. The mass is released from rest with the spring initially unstretched. The maximum extension produced in the length of the spring will be: [2009]- a) Mg/k
- b)4 Mg/k
- c)Mg/2k
- d)2 Mg/k
Correct answer is option 'D'. Can you explain this answer?
A block of mass M is attached to the lower end of a vertical spring. The spring is hung from a ceiling and has force constant value k. The mass is released from rest with the spring initially unstretched. The maximum extension produced in the length of the spring will be: [2009]
a)
Mg/k
b)
4 Mg/k
c)
Mg/2k
d)
2 Mg/k

|
Shourya Gupta answered |
By conservation of energy theorem
mgh=1/2 kh^²
mg=1/2kh
h=2mg/k
mgh=1/2 kh^²
mg=1/2kh
h=2mg/k
A point performs simple harmonic oscillation of period T and the equation of motion is given by x = a sin (ωt + π/6). After the elapse of what fraction of the time period the velocity of the point will be equal to half of its maximum velocity? [2008]
- a)T/8
- b)T/6
- c)T/3
- d)T/12
Correct answer is option 'D'. Can you explain this answer?
A point performs simple harmonic oscillation of period T and the equation of motion is given by x = a sin (ωt + π/6). After the elapse of what fraction of the time period the velocity of the point will be equal to half of its maximum velocity? [2008]
a)
T/8
b)
T/6
c)
T/3
d)
T/12
|
|
Surendra Bishnoi answered |
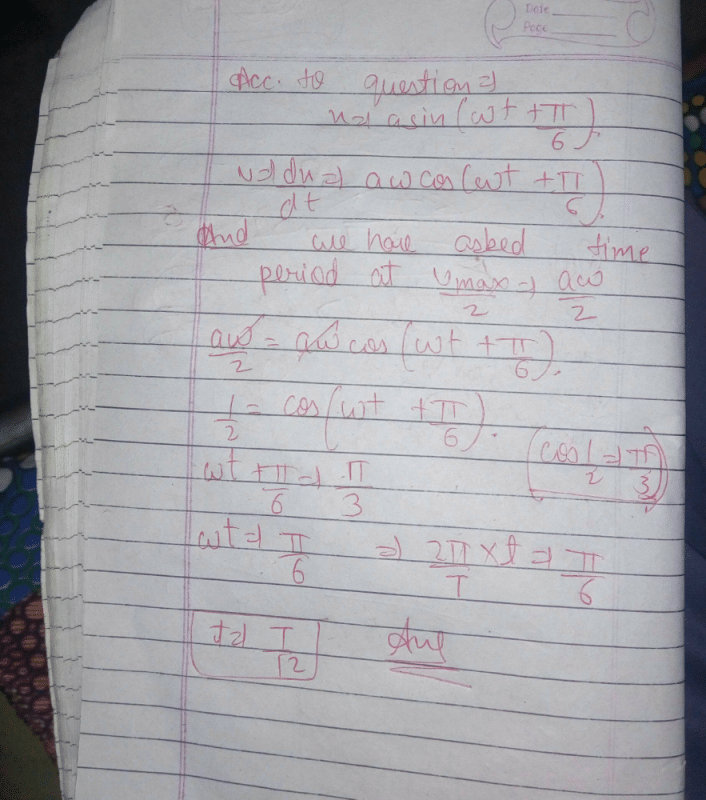
The particle executing simple harmonic motion has a kinetic energy K0 cos2ωt . The maximum values of the potential energy and the total energy are respectively [2007]- a)K0/2 and K0
- b)K0 and 2K0
- c)K0 and K0
- d)0 and 2K0.
Correct answer is option 'C'. Can you explain this answer?
The particle executing simple harmonic motion has a kinetic energy K0 cos2ωt . The maximum values of the potential energy and the total energy are respectively [2007]
a)
K0/2 and K0
b)
K0 and 2K0
c)
K0 and K0
d)
0 and 2K0.
|
|
Meera Singh answered |
Given, Kinetic energy=K0cos2ωt
Maximum kinetic energy=K (as ωt=0 and cos ωt=1
Since total energy remains conserved in SHM , hence when potential energy is maximum,Kinetic energy=0 i.e. E is also equal to Umax i.e. U max(maximum potential energy) = E(Total energy) = K0
A particle of mass m oscillates along x-axis according to equation x = a sinωt. The nature of the graph between momentum and displacement of the particle is [NEET Kar. 2013]- a)straight line passing through origin
- b)circle
- c)hyper bola
- d)ellipse
Correct answer is option 'D'. Can you explain this answer?
A particle of mass m oscillates along x-axis according to equation x = a sinωt. The nature of the graph between momentum and displacement of the particle is [NEET Kar. 2013]
a)
straight line passing through origin
b)
circle
c)
hyper bola
d)
ellipse
|
|
Tarun Saha answered |
(ωt + φ), where a is the amplitude, ω is the angular frequency, t is time, and φ is the phase angle. The displacement of the particle from its equilibrium position at any time t is given by x(t) = a sin(ωt + φ).
The velocity of the particle at any time t is the derivative of the displacement with respect to time, which is given by:
v(t) = aω cos(ωt + φ)
The acceleration of the particle at any time t is the second derivative of the displacement with respect to time, which is given by:
a(t) = -aω^2 sin(ωt + φ)
The negative sign indicates that the acceleration is in the opposite direction to the displacement. This means that when the particle is at its maximum displacement, the acceleration is zero, and when the particle passes through the equilibrium position, the acceleration is maximum.
The period of the motion is the time taken by the particle to complete one full oscillation. It is given by:
T = 2π/ω
The frequency of the motion is the number of oscillations per unit time. It is given by:
f = ω/2π
The maximum velocity of the particle is given by:
v_max = aω
The maximum acceleration of the particle is given by:
a_max = aω^2
The energy of the particle is the sum of its kinetic and potential energies. At any time t, the total energy of the particle is given by:
E(t) = (1/2)mv^2 + (1/2)kx^2
where k is the spring constant. The energy is constant throughout the motion, and is equal to the total energy at any other time.
The velocity of the particle at any time t is the derivative of the displacement with respect to time, which is given by:
v(t) = aω cos(ωt + φ)
The acceleration of the particle at any time t is the second derivative of the displacement with respect to time, which is given by:
a(t) = -aω^2 sin(ωt + φ)
The negative sign indicates that the acceleration is in the opposite direction to the displacement. This means that when the particle is at its maximum displacement, the acceleration is zero, and when the particle passes through the equilibrium position, the acceleration is maximum.
The period of the motion is the time taken by the particle to complete one full oscillation. It is given by:
T = 2π/ω
The frequency of the motion is the number of oscillations per unit time. It is given by:
f = ω/2π
The maximum velocity of the particle is given by:
v_max = aω
The maximum acceleration of the particle is given by:
a_max = aω^2
The energy of the particle is the sum of its kinetic and potential energies. At any time t, the total energy of the particle is given by:
E(t) = (1/2)mv^2 + (1/2)kx^2
where k is the spring constant. The energy is constant throughout the motion, and is equal to the total energy at any other time.
The phenomenon of increase in amplitude when the driving force is close to the natural frequency of the oscillator is known as- a)Accelerated Amplitude
- b)Epoch
- c)Resonance
- d)Dampening
Correct answer is option 'C'. Can you explain this answer?
The phenomenon of increase in amplitude when the driving force is close to the natural frequency of the oscillator is known as
a)
Accelerated Amplitude
b)
Epoch
c)
Resonance
d)
Dampening
|
|
Lavanya Menon answered |
The phenomenon of increase in amplitude when the driving force is close to the natural frequency of the oscillator is known as resonance. By the definition of resonance.
Which one of the following statements is true for the speed v and the acceleration a of a particle executing simple harmonic motion ?- a)When v is maximum, a is zero [2004]
- b)When v is maximum, a is maximum
- c)Value of a is zero, whatever may be the value of v
- d)When v is zero, a is zero
Correct answer is option 'A'. Can you explain this answer?
Which one of the following statements is true for the speed v and the acceleration a of a particle executing simple harmonic motion ?
a)
When v is maximum, a is zero [2004]
b)
When v is maximum, a is maximum
c)
Value of a is zero, whatever may be the value of v
d)
When v is zero, a is zero
|
|
Surendra Bishnoi answered |
Phase differences between acceleration and velocity is always 90 so if one equation is express in terms of sin and other express in cos terms so if one maximum then other is minimum
The periodic time (tp) is given by- a)ω / 2 π
- b)2 π / ω
- c)2 π × ω
- d)π/ω
Correct answer is option 'B'. Can you explain this answer?
The periodic time (tp) is given by
a)
ω / 2 π
b)
2 π / ω
c)
2 π × ω
d)
π/ω
|
|
Divyansh Saha answered |
Periodic time is the time taken for one complete revolution of the particle.
∴ Periodic time, tp = 2 π/ω seconds.
∴ Periodic time, tp = 2 π/ω seconds.
Under forced oscillation, the phase of the harmonic motion of the particle and phase of driving force- a)Are same
- b)Are different
- c)Both are zero
- d)Not present
Correct answer is option 'B'. Can you explain this answer?
Under forced oscillation, the phase of the harmonic motion of the particle and phase of driving force
a)
Are same
b)
Are different
c)
Both are zero
d)
Not present
|
|
Pratibha Sharma answered |
Harmonic motion is the natural motion of a body(we consider no air friction) under no force where as damped oscillation are under force hence the iscilation are different
Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes. They pass each other, moving in opposite directions when their displacement is half of the amplitude. The mean positions of the two particles lie on a straight line perpendicular to the paths of the two particles. The phase difference is [2011M]- a)0
- b)2π/3
- c)π
- d)π/6
Correct answer is option 'B'. Can you explain this answer?
Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes. They pass each other, moving in opposite directions when their displacement is half of the amplitude. The mean positions of the two particles lie on a straight line perpendicular to the paths of the two particles. The phase difference is [2011M]
a)
0
b)
2π/3
c)
π
d)
π/6
|
|
Rajeev Saxena answered |
Which one of the following equations of motion represents simple harmonic motion? [2009]where k, k0, k1 and a are all postive.- a)Acceleration = – k(x + a)
- b)Acceleration = k(x + a)
- c)Acceleration = kx
- d)Acceleration = – k0x + k1x2
Correct answer is option 'A'. Can you explain this answer?
Which one of the following equations of motion represents simple harmonic motion? [2009]
where k, k0, k1 and a are all postive.
a)
Acceleration = – k(x + a)
b)
Acceleration = k(x + a)
c)
Acceleration = kx
d)
Acceleration = – k0x + k1x2

|
Dipika Das answered |
a = – kX, X = x + a.
In simple harmonic motion acceleration is directly proportional to the displacement from the mean position. Also the acceleration is in the opposite direction of displacement.
In simple harmonic motion acceleration is directly proportional to the displacement from the mean position. Also the acceleration is in the opposite direction of displacement.
Energy is supplied to the damped oscillatory system at the same rate at which it is dissipating energy, then the amplitude of such oscillations would become constant. Such oscillations are called- a)Damped oscillations
- b)Undamped oscillations
- c)Coupled oscillations
- d)Maintained oscillations
Correct answer is option 'D'. Can you explain this answer?
Energy is supplied to the damped oscillatory system at the same rate at which it is dissipating energy, then the amplitude of such oscillations would become constant. Such oscillations are called
a)
Damped oscillations
b)
Undamped oscillations
c)
Coupled oscillations
d)
Maintained oscillations
|
|
Anoushka Basu answered |
Energy is supplied to the damped oscillatory system at the same rate at which it is dissipating energy, and then the amplitude of such oscillations would become constant. Such oscillations are called maintained oscillations. By the definition of maintained oscillations.
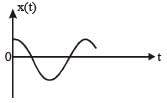
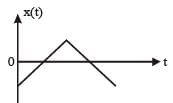
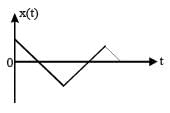
A par ticle of mass m is r eleased fr om rest and follows a parabolic path as shown.
Assuming that the displacement of the mass from the origin is small, which graph correctly depicts the position of the particle as a function of time [2011]
- a)
- b)
- c)
- d)
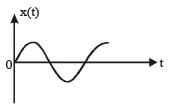
Correct answer is option 'A'. Can you explain this answer?
A par ticle of mass m is r eleased fr om rest and follows a parabolic path as shown.
Assuming that the displacement of the mass from the origin is small, which graph correctly depicts the position of the particle as a function of time [2011]
Assuming that the displacement of the mass from the origin is small, which graph correctly depicts the position of the particle as a function of time [2011]

a)

b)

c)

d)


|
Shruti Chauhan answered |
The given velocity-position graph depicts that the motion of the particle is SHM.
In SHM, at t = 0, v = 0 and x = xmax
So, option (a) is correct.
In SHM, at t = 0, v = 0 and x = xmax
So, option (a) is correct.
Two simple harmonic motions of angular frequency 100 and 1000 rad s–1 have the same displacement amplitude. The ratio of their maximum accelerations is: [2008]- a)1 : 10
- b)1 : 102
- c)1 : 103
- d)1 : 104
Correct answer is option 'B'. Can you explain this answer?
Two simple harmonic motions of angular frequency 100 and 1000 rad s–1 have the same displacement amplitude. The ratio of their maximum accelerations is: [2008]
a)
1 : 10
b)
1 : 102
c)
1 : 103
d)
1 : 104

|
Ruchi Chopra answered |
Maximum acceleration of a particle in the simple harmonic motion is directly proportional to the square of angular frequency i.e.
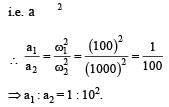
In case of a forced vibration, the resonance wave becomes very sharp when the [2003]- a)quality factor is small
- b)damping force is small
- c)restoring force is small
- d)applied periodic force is small
Correct answer is option 'B'. Can you explain this answer?
In case of a forced vibration, the resonance wave becomes very sharp when the [2003]
a)
quality factor is small
b)
damping force is small
c)
restoring force is small
d)
applied periodic force is small

|
Priyanka Iyer answered |
The resonan ce wave becomes very sharp when damping force is small.
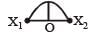
A particle of mass m oscillates with simple harmonic motion between points x1 and x2, the equilibrium position being O. Its potential energy is plotted. It will be as given below in the graph. [2003]- a)
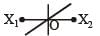
- b)
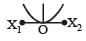
- c)
- d)

Correct answer is option 'B'. Can you explain this answer?
A particle of mass m oscillates with simple harmonic motion between points x1 and x2, the equilibrium position being O. Its potential energy is plotted. It will be as given below in the graph. [2003]
a)

b)

c)

d)


|
Arpita Tiwari answered |
Potential energy ∝ (Amplitude)2 ∝ (Displacement)2 P.E.is maximum at maximum distance.
P.E. is zero at equilibrium point.
P.E. curve is parabolic.
P.E. is zero at equilibrium point.
P.E. curve is parabolic.
Out of the following functions, representing motion of a particle, which represents SHM?
(A) y = sin ωt - cosωt [2011]
(B) y = sin3 ωt(C) 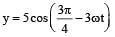 (D) y = 1 + ωt + ω2t2
(D) y = 1 + ωt + ω2t2- a)Only (A)
- b)Only (D) does not represent SHM
- c)Only (A) and (C)
- d)Only (A) and (B)
Correct answer is option 'C'. Can you explain this answer?
Out of the following functions, representing motion of a particle, which represents SHM?
(A) y = sin ωt - cosωt [2011]
(B) y = sin3 ωt
(A) y = sin ωt - cosωt [2011]
(B) y = sin3 ωt
(C) 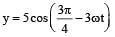
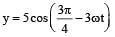
(D) y = 1 + ωt + ω2t2
a)
Only (A)
b)
Only (D) does not represent SHM
c)
Only (A) and (C)
d)
Only (A) and (B)

|
Sonal Kulkarni answered |
Only functions given in (A) & (C) represent SHM.
A mass of 2.0 kg is put on a flat pan attached to a vertical spring fixed on the ground as shown in the figure. The mass of the spring and the pan is negligible. When pressed slightly and released the mass executes a simple harmonic motion. The spring constant is 200 N/m. What should be the minimum amplitude of the motion so that the mass gets detached from the pan (take g = 10 m/s2)?[2007]
- a)10.0 cm
- b)any value less than 12.0 cm
- c)4.0 cm
- d)8.0 cm
Correct answer is option 'A'. Can you explain this answer?
A mass of 2.0 kg is put on a flat pan attached to a vertical spring fixed on the ground as shown in the figure. The mass of the spring and the pan is negligible. When pressed slightly and released the mass executes a simple harmonic motion. The spring constant is 200 N/m. What should be the minimum amplitude of the motion so that the mass gets detached from the pan (take g = 10 m/s2)?[2007]

a)
10.0 cm
b)
any value less than 12.0 cm
c)
4.0 cm
d)
8.0 cm

|
Sonal Kulkarni answered |
Mass gets detached at the upper extreme position when pan returns to its mean position.
R = mg – mω2a = 0
R = mg – mω2a = 0
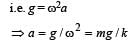
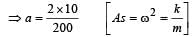
⇒ a = 1/10m = 10cm
The time period of a mass suspended from a spring is T. If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be- a)2T
- b)
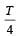 [2003]
[2003] - c)2
- d)

Correct answer is option 'D'. Can you explain this answer?
The time period of a mass suspended from a spring is T. If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be
a)
2T
b)
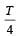 [2003]
[2003]c)
2
d)


|
Shruti Chauhan answered |
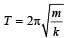
When a spring is cut into n parts Spring constant for each part = nk Here, n = 4

Chapter doubts & questions for Oscillations - 1 Year Dropper Course for NEET 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Oscillations - 1 Year Dropper Course for NEET in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily


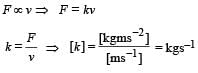

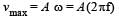


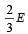
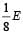
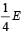
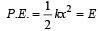
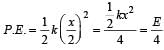

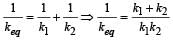
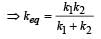



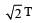


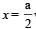 will be:[2009]
will be:[2009]