All Exams >
Civil Engineering (CE) >
6 Months Preparation for GATE Civil Engg >
All Questions
All questions of Turbulent Flow for Civil Engineering (CE) Exam
A pipe line carrying water has surface-protrusions of average height 0.10 mm. If the shear stress developed is 7.85 N/m2, then the pipe surface will act as- a)smooth
- b)rough
- c)transition
- d)data insufficient
Correct answer is option 'C'. Can you explain this answer?
A pipe line carrying water has surface-protrusions of average height 0.10 mm. If the shear stress developed is 7.85 N/m2, then the pipe surface will act as
a)
smooth
b)
rough
c)
transition
d)
data insufficient

|
Anmol Roy answered |

Since roughness value lies between 4 and 100 the pipe act as in transition.
In a laminar flow between two parallel plates with a separation distance of 6 mm, the centre line Velocity is 1.8 m/s. The velocity at a distance of 1 mm from the boundary is: - a)0.15 m/s
- b)1.0 m/s
- c)0.55 m/s
- d)0.75 m/s
Correct answer is option 'B'. Can you explain this answer?
In a laminar flow between two parallel plates with a separation distance of 6 mm, the centre line Velocity is 1.8 m/s. The velocity at a distance of 1 mm from the boundary is:
a)
0.15 m/s
b)
1.0 m/s
c)
0.55 m/s
d)
0.75 m/s
|
|
Sanya Agarwal answered |
Concept:
Laminar flow between the parallel fixed plate
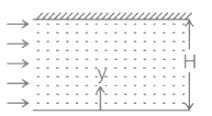
Velocity distribution equation is given by:
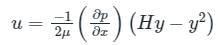
Where,
u = velocity of the fluid at any distance y from the boundary
H = Distance between two parallel fixed plates.
Calculation:
H = 6 mm, ucentre = 1.8 m/sec
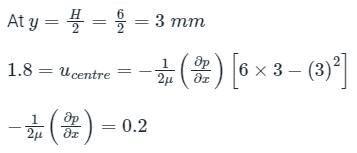
Now, at y = 1 mm
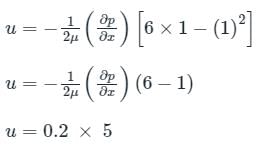
u = 1 m/s.
Laminar flow between the parallel fixed plate

Velocity distribution equation is given by:
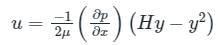
Where,
u = velocity of the fluid at any distance y from the boundary
H = Distance between two parallel fixed plates.
Calculation:
H = 6 mm, ucentre = 1.8 m/sec
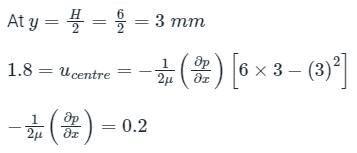
Now, at y = 1 mm
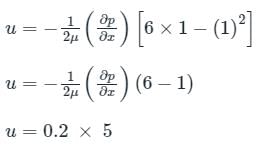
u = 1 m/s.
If you double the kinetic energy of an arrow, by what factor does its speed increase?- a)2
- b)4
- c)√2
- d)None
Correct answer is option 'C'. Can you explain this answer?
If you double the kinetic energy of an arrow, by what factor does its speed increase?
a)
2
b)
4
c)
√2
d)
None

|
Sagnik Sen answered |
To find the factor by which the speed increases, we need to use the equation for kinetic energy:
KE = 1/2mv^2
Where KE is the kinetic energy, m is the mass of the arrow, and v is the velocity (speed) of the arrow.
If we double the kinetic energy, we can write it as KE' = 2KE.
Therefore, 2KE = 1/2mv'^2, where v' is the new velocity.
Dividing both sides of the equation by 1/2m, we get:
4KE = mv'^2
Dividing both sides of the equation by m, we get:
4KE/m = v'^2
Taking the square root of both sides of the equation, we get:
√(4KE/m) = v'
Simplifying the equation, we have:
2√(KE/m) = v'
Therefore, the speed increases by a factor of 2, or the correct option is a)2.
KE = 1/2mv^2
Where KE is the kinetic energy, m is the mass of the arrow, and v is the velocity (speed) of the arrow.
If we double the kinetic energy, we can write it as KE' = 2KE.
Therefore, 2KE = 1/2mv'^2, where v' is the new velocity.
Dividing both sides of the equation by 1/2m, we get:
4KE = mv'^2
Dividing both sides of the equation by m, we get:
4KE/m = v'^2
Taking the square root of both sides of the equation, we get:
√(4KE/m) = v'
Simplifying the equation, we have:
2√(KE/m) = v'
Therefore, the speed increases by a factor of 2, or the correct option is a)2.
If the kinetic energy is increased 4 times its initial value, then how does its momentum change?- a)100%
- b)50%
- c)200%
- d)150%
Correct answer is option 'A'. Can you explain this answer?
If the kinetic energy is increased 4 times its initial value, then how does its momentum change?
a)
100%
b)
50%
c)
200%
d)
150%
|
|
Sanya Agarwal answered |
Kinetic energy depends upon velocity and mass. The relation is K.E = 0.5mv2. If we increase the kinetic energy by 4 times its initial value, the momentum has to be increased by 100% its initial value.
In a laminar flow between two fixed parallel plates, the shear stress is- a)constant across the passage
- b)maximum at centre and zero at boundary
- c)zero all through the passage
- d)maximum at the boundary and zero at the centre
Correct answer is option 'D'. Can you explain this answer?
In a laminar flow between two fixed parallel plates, the shear stress is
a)
constant across the passage
b)
maximum at centre and zero at boundary
c)
zero all through the passage
d)
maximum at the boundary and zero at the centre
|
|
Sanvi Kapoor answered |
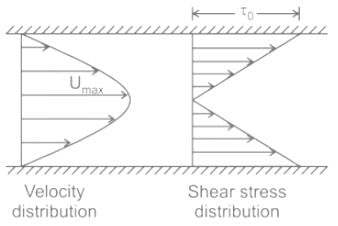
For the flow between two parallel spaced plates (as shown in the figure below):
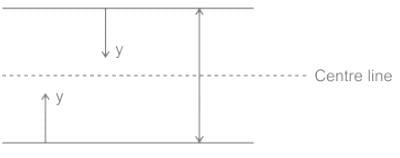
The velocity distribution is given by:
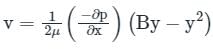
Shear stress is given by:
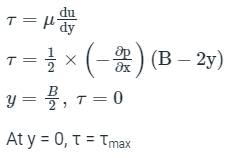
Thus, the stress distribution across a section is depicted below:
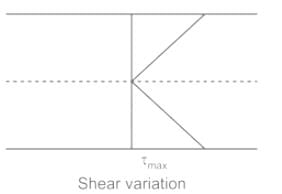
∴ The shear stress is maximum at the boundaries and zero at the center.

The velocity distribution is given by:
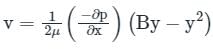
Shear stress is given by:
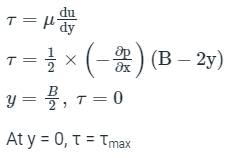
Thus, the stress distribution across a section is depicted below:

∴ The shear stress is maximum at the boundaries and zero at the center.
For laminar flow in a circular conduits, the energy correction factor α is taken as:-- a)1.33
- b)1.03
- c)2.00
- d)2.50
Correct answer is option 'C'. Can you explain this answer?
For laminar flow in a circular conduits, the energy correction factor α is taken as:-
a)
1.33
b)
1.03
c)
2.00
d)
2.50

|
Aaditya Jain answered |
Is given by the Darcy-Weisbach equation:
f = (64/Re)
Where:
- f is the energy correction factor
- Re is the Reynolds number, which is a dimensionless quantity that represents the ratio of inertial forces to viscous forces in the flow.
In laminar flow, the Reynolds number is typically less than 2,000, indicating that viscous forces dominate over inertial forces. Therefore, the energy correction factor for laminar flow in circular conduits is typically small, approaching zero.
f = (64/Re)
Where:
- f is the energy correction factor
- Re is the Reynolds number, which is a dimensionless quantity that represents the ratio of inertial forces to viscous forces in the flow.
In laminar flow, the Reynolds number is typically less than 2,000, indicating that viscous forces dominate over inertial forces. Therefore, the energy correction factor for laminar flow in circular conduits is typically small, approaching zero.
Turbulent flow generally occurs- a)at very low velocities
- b)in flows of highly viscous fluids
- c)in flows through very narrow passages
- d)in flows at high velocities through large passages
Correct answer is option 'D'. Can you explain this answer?
Turbulent flow generally occurs
a)
at very low velocities
b)
in flows of highly viscous fluids
c)
in flows through very narrow passages
d)
in flows at high velocities through large passages

|
Sahana Dey answered |
Turbulent flow generally occurs in flows at high velocities through large passages. Here is the explanation:
1. Introduction
Turbulent flow is characterized by irregular and chaotic motion of fluid particles. It is the opposite of laminar flow, which is smooth and orderly. Turbulent flow is usually observed in situations where the fluid velocity is high or the flow passage is large.
2. Flow Velocity
Turbulent flow occurs at high velocities. When the fluid velocity exceeds a certain critical value, the flow transitions from laminar to turbulent. This critical velocity is known as the critical Reynolds number. As the velocity increases beyond this point, the flow becomes more turbulent.
3. Large Passages
Turbulent flow is more likely to occur in flows through large passages. When the flow passage is large, there is more space for the fluid particles to move around and interact with each other. This leads to a higher likelihood of turbulence. In contrast, in flows through narrow passages, the fluid particles are restricted in their motion, resulting in a more laminar flow.
4. Reynolds Number
The Reynolds number is a dimensionless parameter that determines the flow regime. It is defined as the ratio of inertial forces to viscous forces in the flow. In the case of turbulent flow, the Reynolds number is typically large, indicating that the inertial forces dominate over the viscous forces. This is why turbulent flow is more commonly observed in flows at high velocities.
Conclusion
In conclusion, turbulent flow generally occurs in flows at high velocities through large passages. The high velocity and large passage size promote the development of turbulence in the flow. Understanding the factors that influence the occurrence of turbulent flow is important in various engineering applications, such as in designing pipelines, channels, and hydraulic structures.
1. Introduction
Turbulent flow is characterized by irregular and chaotic motion of fluid particles. It is the opposite of laminar flow, which is smooth and orderly. Turbulent flow is usually observed in situations where the fluid velocity is high or the flow passage is large.
2. Flow Velocity
Turbulent flow occurs at high velocities. When the fluid velocity exceeds a certain critical value, the flow transitions from laminar to turbulent. This critical velocity is known as the critical Reynolds number. As the velocity increases beyond this point, the flow becomes more turbulent.
3. Large Passages
Turbulent flow is more likely to occur in flows through large passages. When the flow passage is large, there is more space for the fluid particles to move around and interact with each other. This leads to a higher likelihood of turbulence. In contrast, in flows through narrow passages, the fluid particles are restricted in their motion, resulting in a more laminar flow.
4. Reynolds Number
The Reynolds number is a dimensionless parameter that determines the flow regime. It is defined as the ratio of inertial forces to viscous forces in the flow. In the case of turbulent flow, the Reynolds number is typically large, indicating that the inertial forces dominate over the viscous forces. This is why turbulent flow is more commonly observed in flows at high velocities.
Conclusion
In conclusion, turbulent flow generally occurs in flows at high velocities through large passages. The high velocity and large passage size promote the development of turbulence in the flow. Understanding the factors that influence the occurrence of turbulent flow is important in various engineering applications, such as in designing pipelines, channels, and hydraulic structures.
The value of kinetic energy correction factor for laminar flow through a circular pipe of radius R is _____. (Correct up to 2 decimals)
Correct answer is '2'. Can you explain this answer?
The value of kinetic energy correction factor for laminar flow through a circular pipe of radius R is _____. (Correct up to 2 decimals)

|
Sneha Roy answered |
Introduction
In fluid mechanics, the kinetic energy correction factor is a dimensionless parameter that accounts for the deviation of actual flow velocity from the average velocity in a pipe. It is commonly used in the calculation of pressure drop in pipe flow.
Explanation
The kinetic energy correction factor, denoted as "C", is given by the equation:
C = (2ln(D/2r) - 1)/(ln(D/r) - 1)
where D is the pipe diameter and r is the hydraulic radius (half of the pipe diameter in the case of a circular pipe).
Derivation
To understand why the kinetic energy correction factor is 2 for laminar flow through a circular pipe, let's consider the flow profile within the pipe.
In laminar flow, the velocity distribution across the pipe is parabolic, with the maximum velocity occurring at the centerline and decreasing towards the pipe walls. The average velocity is obtained by integrating the velocity profile across the pipe cross-section.
Key Points:
- Laminar flow has a parabolic velocity profile.
- Maximum velocity occurs at the centerline.
- Average velocity is obtained by integrating the velocity profile.
Integration of the Velocity Profile
To calculate the average velocity, we need to integrate the velocity profile across the pipe cross-section. The velocity at any radial position, "r", can be given by the equation:
v(r) = (2 * Vmax) * (1 - (r/R)^2)
where Vmax is the maximum velocity at the centerline and R is the pipe radius.
Key Points:
- Velocity at any radial position, "r", is given by v(r) = (2 * Vmax) * (1 - (r/R)^2).
- Vmax is the maximum velocity at the centerline.
- R is the pipe radius.
Calculation of the Average Velocity
To calculate the average velocity, we need to integrate the velocity profile across the pipe cross-section. The integration can be performed from r = 0 to r = R, which gives:
Vavg = (2/3) * Vmax
Key Points:
- Average velocity is given by Vavg = (2/3) * Vmax.
Calculating the Kinetic Energy Correction Factor
The kinetic energy correction factor, C, is defined as the ratio of the actual kinetic energy to the kinetic energy calculated using average velocity. It can be calculated using the equation:
C = (actual kinetic energy)/(kinetic energy using average velocity)
The actual kinetic energy is given by:
KE_actual = (1/2) * ρ * Vmax^2 * (π * R^2)
The kinetic energy using average velocity is given by:
KE_avg = (1/2) * ρ * Vavg^2 * (π * R^2)
Substituting the values of Vmax and Vavg, we get:
C = (2/3)^2 = 4/9 ≈ 0.44
Key Points:
- Kinetic energy correction factor, C, is the ratio of actual kinetic energy to kinetic energy using average velocity.
- Actual kinetic energy is (1/2) * ρ * Vmax^2 * (π * R^2).
- Kinetic energy using average velocity
In fluid mechanics, the kinetic energy correction factor is a dimensionless parameter that accounts for the deviation of actual flow velocity from the average velocity in a pipe. It is commonly used in the calculation of pressure drop in pipe flow.
Explanation
The kinetic energy correction factor, denoted as "C", is given by the equation:
C = (2ln(D/2r) - 1)/(ln(D/r) - 1)
where D is the pipe diameter and r is the hydraulic radius (half of the pipe diameter in the case of a circular pipe).
Derivation
To understand why the kinetic energy correction factor is 2 for laminar flow through a circular pipe, let's consider the flow profile within the pipe.
In laminar flow, the velocity distribution across the pipe is parabolic, with the maximum velocity occurring at the centerline and decreasing towards the pipe walls. The average velocity is obtained by integrating the velocity profile across the pipe cross-section.
Key Points:
- Laminar flow has a parabolic velocity profile.
- Maximum velocity occurs at the centerline.
- Average velocity is obtained by integrating the velocity profile.
Integration of the Velocity Profile
To calculate the average velocity, we need to integrate the velocity profile across the pipe cross-section. The velocity at any radial position, "r", can be given by the equation:
v(r) = (2 * Vmax) * (1 - (r/R)^2)
where Vmax is the maximum velocity at the centerline and R is the pipe radius.
Key Points:
- Velocity at any radial position, "r", is given by v(r) = (2 * Vmax) * (1 - (r/R)^2).
- Vmax is the maximum velocity at the centerline.
- R is the pipe radius.
Calculation of the Average Velocity
To calculate the average velocity, we need to integrate the velocity profile across the pipe cross-section. The integration can be performed from r = 0 to r = R, which gives:
Vavg = (2/3) * Vmax
Key Points:
- Average velocity is given by Vavg = (2/3) * Vmax.
Calculating the Kinetic Energy Correction Factor
The kinetic energy correction factor, C, is defined as the ratio of the actual kinetic energy to the kinetic energy calculated using average velocity. It can be calculated using the equation:
C = (actual kinetic energy)/(kinetic energy using average velocity)
The actual kinetic energy is given by:
KE_actual = (1/2) * ρ * Vmax^2 * (π * R^2)
The kinetic energy using average velocity is given by:
KE_avg = (1/2) * ρ * Vavg^2 * (π * R^2)
Substituting the values of Vmax and Vavg, we get:
C = (2/3)^2 = 4/9 ≈ 0.44
Key Points:
- Kinetic energy correction factor, C, is the ratio of actual kinetic energy to kinetic energy using average velocity.
- Actual kinetic energy is (1/2) * ρ * Vmax^2 * (π * R^2).
- Kinetic energy using average velocity
The shear stress between two fixed parallel plates with a laminar flow between them- a)a constant across the gap
- b)varies parabolically as the distance from the mid plane
- c)varies inversely as the distance from the mid plane
- d)varies directly as the distance from the mid plane
Correct answer is option 'D'. Can you explain this answer?
The shear stress between two fixed parallel plates with a laminar flow between them
a)
a constant across the gap
b)
varies parabolically as the distance from the mid plane
c)
varies inversely as the distance from the mid plane
d)
varies directly as the distance from the mid plane

|
Abhay Banerjee answered |
Understanding Shear Stress in Laminar Flow
When analyzing laminar flow between two fixed parallel plates, the behavior of shear stress is essential for understanding fluid dynamics.
Key Concepts of Shear Stress:
- Definition of Shear Stress: Shear stress is defined as the force per unit area acting parallel to the surface of the plates. In laminar flow, the fluid moves in layers, and the velocity gradient influences shear stress.
- Laminar Flow Characteristics: In laminar flow, the velocity profile is typically linear across the gap between the plates. This means that the fluid near the plates moves slower due to viscosity, while the fluid near the midplane moves faster.
Variation of Shear Stress:
- Inversely Related to Distance: The shear stress varies directly with the distance from the mid-plane of the two plates. This is because as you move away from the mid-plane towards either plate, the velocity gradient (which is the change in velocity per unit distance) increases.
- Mathematical Justification: The shear stress τ can be expressed as τ = μ(dv/dy), where μ is the dynamic viscosity, dv is the change in velocity, and dy is the change in distance from the mid-plane. As the distance from the mid-plane increases, the rate of change of velocity increases, leading to higher shear stress.
Conclusion:
Thus, the correct answer is option 'D': shear stress varies directly as the distance from the mid-plane. This relationship is crucial for engineers to understand when designing systems involving fluid flow between surfaces.
Understanding these principles helps in applications ranging from mechanical systems to civil engineering structures where fluid dynamics are a factor.
When analyzing laminar flow between two fixed parallel plates, the behavior of shear stress is essential for understanding fluid dynamics.
Key Concepts of Shear Stress:
- Definition of Shear Stress: Shear stress is defined as the force per unit area acting parallel to the surface of the plates. In laminar flow, the fluid moves in layers, and the velocity gradient influences shear stress.
- Laminar Flow Characteristics: In laminar flow, the velocity profile is typically linear across the gap between the plates. This means that the fluid near the plates moves slower due to viscosity, while the fluid near the midplane moves faster.
Variation of Shear Stress:
- Inversely Related to Distance: The shear stress varies directly with the distance from the mid-plane of the two plates. This is because as you move away from the mid-plane towards either plate, the velocity gradient (which is the change in velocity per unit distance) increases.
- Mathematical Justification: The shear stress τ can be expressed as τ = μ(dv/dy), where μ is the dynamic viscosity, dv is the change in velocity, and dy is the change in distance from the mid-plane. As the distance from the mid-plane increases, the rate of change of velocity increases, leading to higher shear stress.
Conclusion:
Thus, the correct answer is option 'D': shear stress varies directly as the distance from the mid-plane. This relationship is crucial for engineers to understand when designing systems involving fluid flow between surfaces.
Understanding these principles helps in applications ranging from mechanical systems to civil engineering structures where fluid dynamics are a factor.
Which among the following is not an application of the Bernoulli?- a)Sailing
- b)Flow through a venture tube
- c)Flow through a sharp-edged orifice.
- d)Closing of tap water
Correct answer is option 'B'. Can you explain this answer?
Which among the following is not an application of the Bernoulli?
a)
Sailing
b)
Flow through a venture tube
c)
Flow through a sharp-edged orifice.
d)
Closing of tap water

|
Shivani Choudhury answered |
Solution:
The Bernoulli equation is a fundamental principle in fluid mechanics that relates the pressure, velocity, and elevation in a fluid flow system. It is based on the principle of conservation of energy for fluid flow. The Bernoulli equation can be applied to various fluid flow problems, but not all applications are suitable for its use.
Explanation:
The Bernoulli equation can be applied to a wide range of fluid flow problems, including the following applications:
a) Sailing: The Bernoulli equation can be used to explain the lift force acting on the sails of a boat. As the wind flows over the curved surface of the sails, it accelerates and creates a lower pressure region on the side facing the wind. This pressure difference generates a lift force that propels the boat forward.
c) Flow through a sharp-edged orifice: An orifice is a small opening through which a fluid flows. When the fluid flows through a sharp-edged orifice, the velocity increases and the pressure decreases according to the Bernoulli equation. This principle is applied in various engineering applications, such as flow measurement devices.
d) Closing of tap water: When a tap is closed, the fluid flow is restricted, leading to an increase in velocity and a decrease in pressure according to the Bernoulli equation. This principle is used in faucets and valves to control the flow of water.
However, option B, flow through a venturi tube, is not an application of the Bernoulli equation. A venturi tube is a device used to measure fluid flow rate by creating a pressure difference. Although the Bernoulli equation is commonly used to explain the principle of a venturi tube, it is not directly applied to the flow through the venturi tube itself.
The venturi tube operates on the principle of conservation of mass rather than energy. It uses the narrowing of the tube to increase the flow velocity and decrease the pressure, which can be measured to determine the flow rate. The Bernoulli equation can be used to explain the pressure difference, but it is not directly applied to the flow through the venturi tube.
In conclusion, the correct answer is option B, flow through a venturi tube, as it is not an application of the Bernoulli equation.
The Bernoulli equation is a fundamental principle in fluid mechanics that relates the pressure, velocity, and elevation in a fluid flow system. It is based on the principle of conservation of energy for fluid flow. The Bernoulli equation can be applied to various fluid flow problems, but not all applications are suitable for its use.
Explanation:
The Bernoulli equation can be applied to a wide range of fluid flow problems, including the following applications:
a) Sailing: The Bernoulli equation can be used to explain the lift force acting on the sails of a boat. As the wind flows over the curved surface of the sails, it accelerates and creates a lower pressure region on the side facing the wind. This pressure difference generates a lift force that propels the boat forward.
c) Flow through a sharp-edged orifice: An orifice is a small opening through which a fluid flows. When the fluid flows through a sharp-edged orifice, the velocity increases and the pressure decreases according to the Bernoulli equation. This principle is applied in various engineering applications, such as flow measurement devices.
d) Closing of tap water: When a tap is closed, the fluid flow is restricted, leading to an increase in velocity and a decrease in pressure according to the Bernoulli equation. This principle is used in faucets and valves to control the flow of water.
However, option B, flow through a venturi tube, is not an application of the Bernoulli equation. A venturi tube is a device used to measure fluid flow rate by creating a pressure difference. Although the Bernoulli equation is commonly used to explain the principle of a venturi tube, it is not directly applied to the flow through the venturi tube itself.
The venturi tube operates on the principle of conservation of mass rather than energy. It uses the narrowing of the tube to increase the flow velocity and decrease the pressure, which can be measured to determine the flow rate. The Bernoulli equation can be used to explain the pressure difference, but it is not directly applied to the flow through the venturi tube.
In conclusion, the correct answer is option B, flow through a venturi tube, as it is not an application of the Bernoulli equation.
In a turbulent flow in a pipe, the shear stress is- a)maximum at the centre
- b)maximum at the boundary and decreases linearly to zero value at the centre
- c)maximum at the wall and decreases logarithmically towards the centre
- d)maximum at a finite distance from the wall
Correct answer is option 'B'. Can you explain this answer?
In a turbulent flow in a pipe, the shear stress is
a)
maximum at the centre
b)
maximum at the boundary and decreases linearly to zero value at the centre
c)
maximum at the wall and decreases logarithmically towards the centre
d)
maximum at a finite distance from the wall

|
Rahul Chauhan answered |
In turbulent flow shear stress 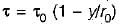
where,
r0 = Radius of pipe
y = Distance measured from pipe wall
ζ0 = Shear stress at boundary
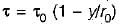
where,
r0 = Radius of pipe
y = Distance measured from pipe wall
ζ0 = Shear stress at boundary
A flat plate 0.1 m2 area is pulled at 30 cm/s relative to another plate located at a distance of 0.01 cm from it, the fluid separating them being water with viscosity of 0.001 Ns/m2. The power required to maintain velocity will be- a)0.05 W
- b)0.07 W
- c)0.09 W
- d)0.11 W
Correct answer is option 'C'. Can you explain this answer?
A flat plate 0.1 m2 area is pulled at 30 cm/s relative to another plate located at a distance of 0.01 cm from it, the fluid separating them being water with viscosity of 0.001 Ns/m2. The power required to maintain velocity will be
a)
0.05 W
b)
0.07 W
c)
0.09 W
d)
0.11 W
|
|
Sanvi Kapoor answered |
Concept:
The tangential shear stress between two adjoining is proportional to velocity gradient in direction of perpendicular to the layer. This is known as law of viscosity.
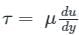
Shear force acting on the moving plate is given by F = τ × A
Power required to maintain velocity U is given by P = F × U
The tangential shear stress between two adjoining is proportional to velocity gradient in direction of perpendicular to the layer. This is known as law of viscosity.
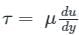
Shear force acting on the moving plate is given by F = τ × A
Power required to maintain velocity U is given by P = F × U
Calculation:
Given μ = 0.001 Ns/m2, U = 0.3 m/s, Y = 0.01 cm = 0.01 × 10-2 m, A = 0.1 m.;
Velocity gradient or rate of shear strain is given by

τ = 0.001 × 3000 = 3 N/m2
F = 3 × 0.1 = 0.3 N,
P = 0.3 × 0.3 = 0.09 W
Given μ = 0.001 Ns/m2, U = 0.3 m/s, Y = 0.01 cm = 0.01 × 10-2 m, A = 0.1 m.;
Velocity gradient or rate of shear strain is given by

τ = 0.001 × 3000 = 3 N/m2
F = 3 × 0.1 = 0.3 N,
P = 0.3 × 0.3 = 0.09 W
The distance from pipe boundary, at which the turbulent shear stress is one-third the wall shear stress, is- a)1/3 R
- b)1/2 R
- c)2/3 R
- d)3/4 R
Correct answer is option 'C'. Can you explain this answer?
The distance from pipe boundary, at which the turbulent shear stress is one-third the wall shear stress, is
a)
1/3 R
b)
1/2 R
c)
2/3 R
d)
3/4 R

|
Sarthak Menon answered |
In turbulent flow shear stress at distance y from pipe boundary,
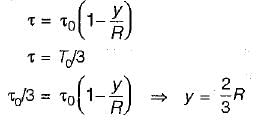
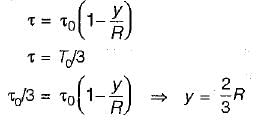
A flow in which the quantity of liquid flowing per second is not constant, is called- a)Stream line flow
- b)Turbulent flow
- c)Steady flow
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A flow in which the quantity of liquid flowing per second is not constant, is called
a)
Stream line flow
b)
Turbulent flow
c)
Steady flow
d)
None of these

|
Simran Mukherjee answered |
A fluid motion is said to be turbulent when the fluid particles move in an entirely haphazard or disorderly manner, that results in a rapid and continuous mixing of the fluid leading to momentum transfer as flow occurs. At any point in a turbulent flow the velocity and pressure are the functions of time thereby rendering such a flow as unsteady.
Which of following conditions would entail a greater energy dissipation in turbulent flow?
1. Smaller eddy size
2. Lower viscosity
3. Large intensity of turbulence
Select the correct answer using the codes given below:
- a)1 and 3
- b)1, 2 and 3
- c)2 and 3
- d)1 and 2
Correct answer is option 'B'. Can you explain this answer?
Which of following conditions would entail a greater energy dissipation in turbulent flow?
1. Smaller eddy size
2. Lower viscosity
3. Large intensity of turbulence
1. Smaller eddy size
2. Lower viscosity
3. Large intensity of turbulence
Select the correct answer using the codes given below:
a)
1 and 3
b)
1, 2 and 3
c)
2 and 3
d)
1 and 2

|
Gauri Roy answered |
Explanation:
Turbulent flow is characterized by irregular fluctuations and eddies of various sizes. When fluid particles move in turbulent flow, they transfer momentum and energy to each other, causing the dissipation of energy. The dissipation rate of energy in a turbulent flow depends on several factors, including the eddy size, viscosity, and intensity of turbulence.
Smaller eddy size:
- In turbulent flow, energy is dissipated at the smallest scales of motion, which are associated with the smallest eddies.
- Smaller eddies have higher velocities and shorter lifetimes, which leads to faster dissipation of energy.
- Therefore, smaller eddies would entail a greater energy dissipation in turbulent flow.
Lower viscosity:
- Viscosity is a measure of a fluid's resistance to deformation.
- In turbulent flow, viscosity plays a role in the dissipation of energy by converting kinetic energy into heat.
- Lower viscosity fluids have less resistance to deformation, which results in faster dissipation of energy.
- Therefore, lower viscosity would entail a greater energy dissipation in turbulent flow.
Large intensity of turbulence:
- Intensity of turbulence refers to the amount of energy contained in the turbulent fluctuations.
- Higher intensity of turbulence means that there is more energy available for dissipation.
- Therefore, large intensity of turbulence would entail a greater energy dissipation in turbulent flow.
Conclusion:
- From the above discussion, it can be concluded that options 1 and 3 (smaller eddy size and large intensity of turbulence) would entail a greater energy dissipation in turbulent flow.
- Option 2 (lower viscosity) would not entail a greater energy dissipation, as lower viscosity fluids have less resistance to deformation, which results in faster dissipation of energy.
Turbulent flow is characterized by irregular fluctuations and eddies of various sizes. When fluid particles move in turbulent flow, they transfer momentum and energy to each other, causing the dissipation of energy. The dissipation rate of energy in a turbulent flow depends on several factors, including the eddy size, viscosity, and intensity of turbulence.
Smaller eddy size:
- In turbulent flow, energy is dissipated at the smallest scales of motion, which are associated with the smallest eddies.
- Smaller eddies have higher velocities and shorter lifetimes, which leads to faster dissipation of energy.
- Therefore, smaller eddies would entail a greater energy dissipation in turbulent flow.
Lower viscosity:
- Viscosity is a measure of a fluid's resistance to deformation.
- In turbulent flow, viscosity plays a role in the dissipation of energy by converting kinetic energy into heat.
- Lower viscosity fluids have less resistance to deformation, which results in faster dissipation of energy.
- Therefore, lower viscosity would entail a greater energy dissipation in turbulent flow.
Large intensity of turbulence:
- Intensity of turbulence refers to the amount of energy contained in the turbulent fluctuations.
- Higher intensity of turbulence means that there is more energy available for dissipation.
- Therefore, large intensity of turbulence would entail a greater energy dissipation in turbulent flow.
Conclusion:
- From the above discussion, it can be concluded that options 1 and 3 (smaller eddy size and large intensity of turbulence) would entail a greater energy dissipation in turbulent flow.
- Option 2 (lower viscosity) would not entail a greater energy dissipation, as lower viscosity fluids have less resistance to deformation, which results in faster dissipation of energy.
A fluid (specific gravity = 0.9 and μ = 1.2 Pa.s) flows in a laminar regime between two parallel plates fixed 3 cm apart. If the discharge is 600 cm3/s/cm width of plate, the shear stress on the boundary, in Pa, is- a)800
- b)640
- c)480
- d)240
Correct answer is option 'C'. Can you explain this answer?
A fluid (specific gravity = 0.9 and μ = 1.2 Pa.s) flows in a laminar regime between two parallel plates fixed 3 cm apart. If the discharge is 600 cm3/s/cm width of plate, the shear stress on the boundary, in Pa, is
a)
800
b)
640
c)
480
d)
240

|
Ishita Patel answered |
Density = 900 kg/m3) is flowing through a pipe with a velocity of 3 m/s. The pipe has a diameter of 0.2 m. What is the mass flow rate of the fluid?
For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is- a)linear with zero value at the plates
- b)linear with zero value at the center
- c)quadratic with zero value at the plates
- d)quadratic with zero value at the center
Correct answer is option 'B'. Can you explain this answer?
For a steady incompressible laminar flow between two infinite parallel stationary plates, the shear stress variation is
a)
linear with zero value at the plates
b)
linear with zero value at the center
c)
quadratic with zero value at the plates
d)
quadratic with zero value at the center

|
Sparsh Unni answered |
The shear stress variation in a steady incompressible laminar flow between two infinite parallel stationary plates is linear with zero value at the center.
Explanation:
In a steady incompressible laminar flow between two infinite parallel stationary plates, the fluid moves in layers parallel to the plates. This type of flow is also known as a Couette flow.
Shear Stress:
Shear stress is the force per unit area acting tangentially to the surface of the fluid. In the case of a flow between parallel plates, the shear stress is caused by the relative motion of the fluid layers.
Shear Stress Variation:
The shear stress varies across the fluid layer from the bottom plate to the top plate. The variation of shear stress can be determined using the velocity distribution of the fluid.
Linear Variation:
In a Couette flow, the velocity of the fluid varies linearly from the bottom plate to the top plate. This means that the velocity gradient, which is directly proportional to the shear stress, also varies linearly.
So, the shear stress variation is linear with zero value at the center. This means that the shear stress is maximum at the plates and decreases linearly towards the center of the fluid layer.
Zero Value at the Center:
At the center of the fluid layer, the velocity is maximum and the velocity gradient is zero. This results in zero shear stress at the center of the fluid layer.
Conclusion:
In summary, the shear stress variation in a steady incompressible laminar flow between two infinite parallel stationary plates is linear with zero value at the center. This is because the velocity varies linearly across the fluid layer, resulting in a linear variation of shear stress.
Explanation:
In a steady incompressible laminar flow between two infinite parallel stationary plates, the fluid moves in layers parallel to the plates. This type of flow is also known as a Couette flow.
Shear Stress:
Shear stress is the force per unit area acting tangentially to the surface of the fluid. In the case of a flow between parallel plates, the shear stress is caused by the relative motion of the fluid layers.
Shear Stress Variation:
The shear stress varies across the fluid layer from the bottom plate to the top plate. The variation of shear stress can be determined using the velocity distribution of the fluid.
Linear Variation:
In a Couette flow, the velocity of the fluid varies linearly from the bottom plate to the top plate. This means that the velocity gradient, which is directly proportional to the shear stress, also varies linearly.
So, the shear stress variation is linear with zero value at the center. This means that the shear stress is maximum at the plates and decreases linearly towards the center of the fluid layer.
Zero Value at the Center:
At the center of the fluid layer, the velocity is maximum and the velocity gradient is zero. This results in zero shear stress at the center of the fluid layer.
Conclusion:
In summary, the shear stress variation in a steady incompressible laminar flow between two infinite parallel stationary plates is linear with zero value at the center. This is because the velocity varies linearly across the fluid layer, resulting in a linear variation of shear stress.
The maximum velocity of a one-dimensional incompressible fully developed viscous flow, between two fixed parallel plates, is 6 ms-1. The mean velocity (in ms-1) of the flow is- a)2
- b)3
- c)4
- d)5
Correct answer is option 'C'. Can you explain this answer?
The maximum velocity of a one-dimensional incompressible fully developed viscous flow, between two fixed parallel plates, is 6 ms-1. The mean velocity (in ms-1) of the flow is
a)
2
b)
3
c)
4
d)
5

|
Sankar Dasgupta answered |
To explain why the correct answer is option 'C' (4 m/s), we need to understand the concept of fully developed viscous flow between two parallel plates.
Fully Developed Viscous Flow:
A fully developed flow refers to a flow in which the velocity profile remains constant along the flow direction. In the case of a viscous flow between two parallel plates, the flow is fully developed when the flow is no longer affected by the entrance region and reaches a steady state.
Maximum Velocity in Fully Developed Flow:
In a fully developed flow between two parallel plates, the velocity profile is parabolic, with the maximum velocity occurring at the center of the channel. The velocity at the centerline is directly related to the maximum velocity.
The Hagen-Poiseuille Equation:
The Hagen-Poiseuille equation is used to calculate the maximum velocity in a fully developed viscous flow between two parallel plates. It is given by:
Vmax = (ΔP / (2μL)) * (h²/4 - y²)
Where:
Vmax = Maximum velocity
ΔP = Pressure drop across the plates
μ = Dynamic viscosity of the fluid
L = Distance between the plates
h = Height of the channel
y = Distance from the centerline
Applying the Hagen-Poiseuille Equation:
In this question, the maximum velocity (Vmax) is given as 6 m/s. We need to find the mean velocity, which is the average velocity of the flow.
In a fully developed flow, the mean velocity (Vmean) is related to the maximum velocity (Vmax) as follows:
Vmean = (2/3) * Vmax
Substituting the given value of Vmax into the equation, we get:
Vmean = (2/3) * 6
Vmean = 4 m/s
Therefore, the correct answer is option 'C' (4 m/s).
Fully Developed Viscous Flow:
A fully developed flow refers to a flow in which the velocity profile remains constant along the flow direction. In the case of a viscous flow between two parallel plates, the flow is fully developed when the flow is no longer affected by the entrance region and reaches a steady state.
Maximum Velocity in Fully Developed Flow:
In a fully developed flow between two parallel plates, the velocity profile is parabolic, with the maximum velocity occurring at the center of the channel. The velocity at the centerline is directly related to the maximum velocity.
The Hagen-Poiseuille Equation:
The Hagen-Poiseuille equation is used to calculate the maximum velocity in a fully developed viscous flow between two parallel plates. It is given by:
Vmax = (ΔP / (2μL)) * (h²/4 - y²)
Where:
Vmax = Maximum velocity
ΔP = Pressure drop across the plates
μ = Dynamic viscosity of the fluid
L = Distance between the plates
h = Height of the channel
y = Distance from the centerline
Applying the Hagen-Poiseuille Equation:
In this question, the maximum velocity (Vmax) is given as 6 m/s. We need to find the mean velocity, which is the average velocity of the flow.
In a fully developed flow, the mean velocity (Vmean) is related to the maximum velocity (Vmax) as follows:
Vmean = (2/3) * Vmax
Substituting the given value of Vmax into the equation, we get:
Vmean = (2/3) * 6
Vmean = 4 m/s
Therefore, the correct answer is option 'C' (4 m/s).
What is the relation between kinetic energy and momentum?- a)p = m/v
- b)p = mva
- c)p = mv
- d)p = m
Correct answer is option 'C'. Can you explain this answer?
What is the relation between kinetic energy and momentum?
a)
p = m/v
b)
p = mva
c)
p = mv
d)
p = m

|
Pallabi Bajaj answered |
The relation between kinetic energy and momentum is given by the equation p = mvd, where p represents momentum, m represents mass, v represents velocity, and d represents direction. This equation shows that momentum is directly proportional to both mass and velocity.
Explanation:
1. Kinetic Energy (KE):
- Kinetic energy is the energy possessed by an object due to its motion.
- It is given by the equation KE = 0.5mv^2, where KE represents kinetic energy, m represents mass, and v represents velocity.
- This equation shows that kinetic energy is directly proportional to both mass and the square of velocity.
2. Momentum (p):
- Momentum is a vector quantity that represents the motion of an object.
- It is given by the equation p = mv, where p represents momentum, m represents mass, and v represents velocity.
- This equation shows that momentum is directly proportional to both mass and velocity.
Relation between Kinetic Energy and Momentum:
1. Substituting the equation p = mv into the equation KE = 0.5mv^2, we get:
KE = 0.5(p/m)(v)
KE = 0.5(pv/m)
KE = (pv)/(2m)
2. Comparing this equation with the equation p = mv, we can see that:
- (pv) represents the product of momentum and velocity, which is equal to the square of momentum.
- 2m represents twice the mass.
3. Therefore, we can rewrite the equation for kinetic energy as:
KE = (p^2)/(2m)
Conclusion:
The relation between kinetic energy and momentum is given by the equation KE = (p^2)/(2m). This equation shows that kinetic energy is directly proportional to the square of momentum and inversely proportional to twice the mass. This means that an object with a larger momentum will have a greater kinetic energy, while an object with a smaller mass will also have a greater kinetic energy for the same momentum.
Explanation:
1. Kinetic Energy (KE):
- Kinetic energy is the energy possessed by an object due to its motion.
- It is given by the equation KE = 0.5mv^2, where KE represents kinetic energy, m represents mass, and v represents velocity.
- This equation shows that kinetic energy is directly proportional to both mass and the square of velocity.
2. Momentum (p):
- Momentum is a vector quantity that represents the motion of an object.
- It is given by the equation p = mv, where p represents momentum, m represents mass, and v represents velocity.
- This equation shows that momentum is directly proportional to both mass and velocity.
Relation between Kinetic Energy and Momentum:
1. Substituting the equation p = mv into the equation KE = 0.5mv^2, we get:
KE = 0.5(p/m)(v)
KE = 0.5(pv/m)
KE = (pv)/(2m)
2. Comparing this equation with the equation p = mv, we can see that:
- (pv) represents the product of momentum and velocity, which is equal to the square of momentum.
- 2m represents twice the mass.
3. Therefore, we can rewrite the equation for kinetic energy as:
KE = (p^2)/(2m)
Conclusion:
The relation between kinetic energy and momentum is given by the equation KE = (p^2)/(2m). This equation shows that kinetic energy is directly proportional to the square of momentum and inversely proportional to twice the mass. This means that an object with a larger momentum will have a greater kinetic energy, while an object with a smaller mass will also have a greater kinetic energy for the same momentum.
The boundary layer on a flat plate is called laminar boundary layer if- a)Re is less than 2000
- b)Re is less than 4000
- c)Re is less than 5 × 105
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The boundary layer on a flat plate is called laminar boundary layer if
a)
Re is less than 2000
b)
Re is less than 4000
c)
Re is less than 5 × 105
d)
None of these

|
Srestha Datta answered |
Understanding the Laminar Boundary Layer
The laminar boundary layer on a flat plate is an essential concept in fluid mechanics, particularly in the study of flow behavior. The transition from laminar to turbulent flow is primarily governed by the Reynolds number (Re).
Reynolds Number Definition
- The Reynolds number is a dimensionless quantity used to predict flow patterns in different fluid flow situations. It is defined as the ratio of inertial forces to viscous forces and is calculated using the formula:
Re = (ρVD) / μ
Where:
- ρ = fluid density
- V = flow velocity
- D = characteristic length (e.g., plate length)
- μ = dynamic viscosity of the fluid
Criteria for Laminar Flow
- The flow over a flat plate is considered laminar when the Reynolds number is low. Specifically:
- Re < 5="" ×="" />: This threshold indicates that the flow remains predominantly laminar. Flow in this regime is smooth and orderly.
- Re < />: The generally accepted value for the onset of turbulence in many applications. Below this, the flow is typically stable and laminar.
- Re < />: This value marks the upper limit for transitional flow, where flow begins to fluctuate between laminar and turbulent states.
Correct Answer Explanation
- The correct answer is option C (Re < 5="" ×="" />, as it encompasses a broader range of laminar flow conditions. While Re < 2000="" signifies="" a="" strictly="" laminar="" flow,="" the="" range="" up="" to="" 5="" ×="" 10^5="" includes="" various="" practical="" applications="" before="" turbulence="" fully="" />
In summary, understanding the boundaries of laminar flow based on Reynolds number is crucial for engineers and designers when analyzing fluid behavior over surfaces.
The laminar boundary layer on a flat plate is an essential concept in fluid mechanics, particularly in the study of flow behavior. The transition from laminar to turbulent flow is primarily governed by the Reynolds number (Re).
Reynolds Number Definition
- The Reynolds number is a dimensionless quantity used to predict flow patterns in different fluid flow situations. It is defined as the ratio of inertial forces to viscous forces and is calculated using the formula:
Re = (ρVD) / μ
Where:
- ρ = fluid density
- V = flow velocity
- D = characteristic length (e.g., plate length)
- μ = dynamic viscosity of the fluid
Criteria for Laminar Flow
- The flow over a flat plate is considered laminar when the Reynolds number is low. Specifically:
- Re < 5="" ×="" />: This threshold indicates that the flow remains predominantly laminar. Flow in this regime is smooth and orderly.
- Re < />: The generally accepted value for the onset of turbulence in many applications. Below this, the flow is typically stable and laminar.
- Re < />: This value marks the upper limit for transitional flow, where flow begins to fluctuate between laminar and turbulent states.
Correct Answer Explanation
- The correct answer is option C (Re < 5="" ×="" />, as it encompasses a broader range of laminar flow conditions. While Re < 2000="" signifies="" a="" strictly="" laminar="" flow,="" the="" range="" up="" to="" 5="" ×="" 10^5="" includes="" various="" practical="" applications="" before="" turbulence="" fully="" />
In summary, understanding the boundaries of laminar flow based on Reynolds number is crucial for engineers and designers when analyzing fluid behavior over surfaces.
In the case of turbulent flows in circular pipes, the maximum velocity um and the mean velocity V are related as (um - V)lu =- a)3.75 for rough boundary flow only
- b)3.75 for smooth boundary flow only
- c)3.75 for both rough and smooth boundaries
- d)5.75 for both rough and smooth boundaries
Correct answer is option 'C'. Can you explain this answer?
In the case of turbulent flows in circular pipes, the maximum velocity um and the mean velocity V are related as (um - V)lu =
a)
3.75 for rough boundary flow only
b)
3.75 for smooth boundary flow only
c)
3.75 for both rough and smooth boundaries
d)
5.75 for both rough and smooth boundaries

|
Anagha Mehta answered |
Turbulent flow
For smooth pipe,
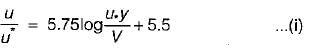
Average velocity,
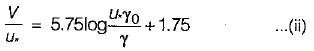
g0 = radius of pipe
y = distance measured from pipe boundary
u = shear velocity
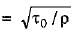
from equation (i)
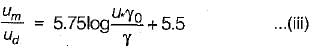
(iii) - (ii) gives
(b) Rough pipe
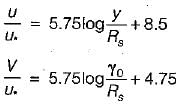
It gives,
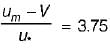
same for both pipes rough or smooth
For smooth pipe,
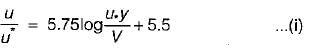
Average velocity,
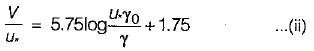
g0 = radius of pipe
y = distance measured from pipe boundary
u = shear velocity
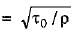
from equation (i)
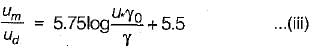
(iii) - (ii) gives
(b) Rough pipe
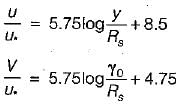
It gives,
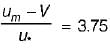
same for both pipes rough or smooth
If you double the kinetic energy of an arrow, by what factor does its speed increase?- a)2
- b)4
- c)√2
- d)None
Correct answer is option 'C'. Can you explain this answer?
If you double the kinetic energy of an arrow, by what factor does its speed increase?
a)
2
b)
4
c)
√2
d)
None
|
|
Sanya Agarwal answered |
Kinetic energy depends upon velocity and mass. The relation between K.E with mass and velocity is K.E = 0.5mv2. If we double the kinetic energy, the velocity has to be increased by a factor equal to the square root of two.
In a flow between two stationary parallel plates, the shear stress is zero- a)both at the base and at the top
- b)at the base
- c)at the top
- d)at the center where velocity is maximum
Correct answer is option 'D'. Can you explain this answer?
In a flow between two stationary parallel plates, the shear stress is zero
a)
both at the base and at the top
b)
at the base
c)
at the top
d)
at the center where velocity is maximum

|
Rhea Dasgupta answered |
Shear stress in a flow between two stationary parallel plates
Introduction:
In fluid mechanics, shear stress is the force per unit area that acts parallel to the surface of an object when there is a velocity gradient between the fluid layers. In the case of a flow between two stationary parallel plates, the shear stress distribution can be analyzed. The question asks where the shear stress is zero in this scenario.
Shear stress distribution:
When a fluid flows between two stationary parallel plates, the velocity of the fluid varies across the gap between the plates. This variation in velocity results in a shear stress distribution.
- At the base of the flow, near the stationary plate, the velocity of the fluid is zero. As a result, the shear stress is also zero at the base.
- At the top of the flow, near the other stationary plate, the velocity of the fluid is also zero. Hence, the shear stress is zero at the top as well.
- In the center of the flow, where the velocity is maximum, the shear stress is not zero. This is because the velocity gradient is the highest at the center, resulting in a non-zero shear stress.
Explanation:
The correct answer is option 'D' - at the center where the velocity is maximum. This is because the shear stress is zero at both the base and the top of the flow, but it is not zero at the center where the velocity is maximum.
Conclusion:
In a flow between two stationary parallel plates, the shear stress is zero at the base and the top of the flow, but it is not zero at the center where the velocity is maximum. This understanding of shear stress distribution is important in various engineering applications, such as fluid flow analysis and design of fluid handling systems.
Introduction:
In fluid mechanics, shear stress is the force per unit area that acts parallel to the surface of an object when there is a velocity gradient between the fluid layers. In the case of a flow between two stationary parallel plates, the shear stress distribution can be analyzed. The question asks where the shear stress is zero in this scenario.
Shear stress distribution:
When a fluid flows between two stationary parallel plates, the velocity of the fluid varies across the gap between the plates. This variation in velocity results in a shear stress distribution.
- At the base of the flow, near the stationary plate, the velocity of the fluid is zero. As a result, the shear stress is also zero at the base.
- At the top of the flow, near the other stationary plate, the velocity of the fluid is also zero. Hence, the shear stress is zero at the top as well.
- In the center of the flow, where the velocity is maximum, the shear stress is not zero. This is because the velocity gradient is the highest at the center, resulting in a non-zero shear stress.
Explanation:
The correct answer is option 'D' - at the center where the velocity is maximum. This is because the shear stress is zero at both the base and the top of the flow, but it is not zero at the center where the velocity is maximum.
Conclusion:
In a flow between two stationary parallel plates, the shear stress is zero at the base and the top of the flow, but it is not zero at the center where the velocity is maximum. This understanding of shear stress distribution is important in various engineering applications, such as fluid flow analysis and design of fluid handling systems.
The kinetic energy correction factor for laminar flow through circular pipes is- a)1
- b)2
- c)4/3
- d)3/4
Correct answer is option 'B'. Can you explain this answer?
The kinetic energy correction factor for laminar flow through circular pipes is
a)
1
b)
2
c)
4/3
d)
3/4

|
Madhurima Banerjee answered |
Understanding Kinetic Energy Correction Factor
The kinetic energy correction factor (KECF) is crucial in fluid dynamics, particularly for flow in pipes. For laminar flow through a circular pipe, this factor accounts for the variation in velocity across the pipe's cross-section.
Definition of Kinetic Energy Correction Factor
- The KECF is defined as the ratio of the actual kinetic energy of the flow to the kinetic energy calculated using the average velocity.
- It corrects for the non-uniform velocity profile in the flow.
Velocity Profile in Laminar Flow
- In laminar flow, the velocity profile is parabolic.
- The maximum velocity occurs at the centerline, while the velocity at the pipe walls is zero.
Calculation of KECF for Laminar Flow
- The average velocity (V_avg) in laminar flow can be determined through integration across the pipe's cross-section.
- The actual kinetic energy is influenced by the distribution of velocities, leading to a correction factor.
Value of KECF for Laminar Flow
- For laminar flow through a circular pipe, the KECF can be mathematically shown to equal 2.
- This means that the kinetic energy associated with the actual flow is twice that calculated using the average velocity.
Conclusion
- Therefore, the correct answer to the question is option 'B', which states that the kinetic energy correction factor for laminar flow through circular pipes is 2.
- Understanding this concept is essential for accurate calculations in civil engineering and fluid mechanics.
This correction factor is vital for ensuring the integrity and efficiency of hydraulic systems in engineering applications.
The kinetic energy correction factor (KECF) is crucial in fluid dynamics, particularly for flow in pipes. For laminar flow through a circular pipe, this factor accounts for the variation in velocity across the pipe's cross-section.
Definition of Kinetic Energy Correction Factor
- The KECF is defined as the ratio of the actual kinetic energy of the flow to the kinetic energy calculated using the average velocity.
- It corrects for the non-uniform velocity profile in the flow.
Velocity Profile in Laminar Flow
- In laminar flow, the velocity profile is parabolic.
- The maximum velocity occurs at the centerline, while the velocity at the pipe walls is zero.
Calculation of KECF for Laminar Flow
- The average velocity (V_avg) in laminar flow can be determined through integration across the pipe's cross-section.
- The actual kinetic energy is influenced by the distribution of velocities, leading to a correction factor.
Value of KECF for Laminar Flow
- For laminar flow through a circular pipe, the KECF can be mathematically shown to equal 2.
- This means that the kinetic energy associated with the actual flow is twice that calculated using the average velocity.
Conclusion
- Therefore, the correct answer to the question is option 'B', which states that the kinetic energy correction factor for laminar flow through circular pipes is 2.
- Understanding this concept is essential for accurate calculations in civil engineering and fluid mechanics.
This correction factor is vital for ensuring the integrity and efficiency of hydraulic systems in engineering applications.
Which among the following is not an application of the Bernoulli?- a)Sailing
- b)Flow through a venture tube
- c)Flow through a sharp-edged orifice.
- d)Closing of tap water
Correct answer is option 'B'. Can you explain this answer?
Which among the following is not an application of the Bernoulli?
a)
Sailing
b)
Flow through a venture tube
c)
Flow through a sharp-edged orifice.
d)
Closing of tap water
|
|
Sanya Agarwal answered |
This is mainly because, Bernoulli’s equation is applied only when the fluid is irrotational. It means that the stream lines are not supposed to intersect each other. Also, the equation does not take viscosity into account. Thus, the flow rate decreases when you close the valve.
What is the value of kinetic energy factor during a laminar flow?- a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
What is the value of kinetic energy factor during a laminar flow?
a)
1
b)
2
c)
3
d)
4
|
|
Sanvi Kapoor answered |
Kinetic energy factor for a fully developed laminar flow is around 2. Laminar flow occurs when a fluid flows in parallel layers. The flow must not have any sort of disruption between the layers of fluid. The fluid flows without a lateral mixing which makes it slide past one another.
In case of steady incompressible laminar viscous flow between two stationary parallel plates, the velocity distribution is- a)Linear
- b)Quadratic
- c)Parabolic
- d)Hyperbolic
Correct answer is option 'C'. Can you explain this answer?
In case of steady incompressible laminar viscous flow between two stationary parallel plates, the velocity distribution is
a)
Linear
b)
Quadratic
c)
Parabolic
d)
Hyperbolic
|
|
Sanya Agarwal answered |
The velocity distribution across a section of two fixed parallel plates is parabolically given by
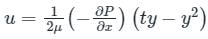
where ∂P/∂x = pressure gradient along the length of the plate
y = point of consideration from lower fixed plate
t = distance between the two fixed parallel plates
Note: The shear stress distribution across a section of two fixed parallel plates is Linear.
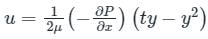
where ∂P/∂x = pressure gradient along the length of the plate
y = point of consideration from lower fixed plate
t = distance between the two fixed parallel plates

Note: The shear stress distribution across a section of two fixed parallel plates is Linear.
If a cricket ball moves with a velocity ‘v’ and collides with a tiny table tennis ball. After an elastic collision, at what velocity will the second ball move?- a)v
- b)v/2
- c)2v
- d)v2
Correct answer is option 'C'. Can you explain this answer?
If a cricket ball moves with a velocity ‘v’ and collides with a tiny table tennis ball. After an elastic collision, at what velocity will the second ball move?
a)
v
b)
v/2
c)
2v
d)
v2
|
|
Sanvi Kapoor answered |
Since the collision is elastic, the cricket ball having a higher mass than that of the tiny table tennis ball will hit and generate a higher velocity. After immediate impact, the table tennis ball will move exactly with twice the velocity of the cricket ball.
When a charged body enters a uniform magnetic field. How will it’s kinetic energy change?- a)Doubles
- b)4 times
- c)Constant
- d)Triples
Correct answer is option 'C'. Can you explain this answer?
When a charged body enters a uniform magnetic field. How will it’s kinetic energy change?
a)
Doubles
b)
4 times
c)
Constant
d)
Triples
|
|
Sanya Agarwal answered |
The kinetic energy remains a constant as the magnetic field always exerts a force perpendicular to the particle’s velocity. So, there is no change in the velocity of the fluid. Therefore, kinetic energy remains the same.
What is the function of Reynolds number?- a)To detect pressure changes
- b)To predict flow patterns
- c)Temperature
- d)Viscosity
Correct answer is option 'B'. Can you explain this answer?
What is the function of Reynolds number?
a)
To detect pressure changes
b)
To predict flow patterns
c)
Temperature
d)
Viscosity
|
|
Sanvi Kapoor answered |
Reynolds number is a dimensionless quantity. It is used to predict flow patterns in different types of fluid flow. At lower Reynold’s number, the flow is laminar. At higher Reynolds number, the flow is turbulent.
When a bullet hits a solid block and gets embedded into it. What is conserved?- a)Momentum only
- b)Kinetic energy only
- c)Momentum and kinetic energy
- d)Mass
Correct answer is option 'A'. Can you explain this answer?
When a bullet hits a solid block and gets embedded into it. What is conserved?
a)
Momentum only
b)
Kinetic energy only
c)
Momentum and kinetic energy
d)
Mass
|
|
Sanvi Kapoor answered |
When the bullet is released from the gun, it moves through the individual air molecules. These molecules tend to vibrate which cannot be seen though our naked eye. The solid block acts as a “momentum sink”. It’s so big when compared to a tiny bullet that it can absorb all the momentum without visibly moving.
What is the value of kinetic energy factor during a laminar flow?- a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
What is the value of kinetic energy factor during a laminar flow?
a)
1
b)
2
c)
3
d)
4
|
|
Sanya Agarwal answered |
Kinetic energy factor for a fully developed laminar flow is around 2. Laminar flow occurs when a fluid flows in parallel layers. The flow must not have any sort of disruption between the layers of fluid. The fluid flows without a lateral mixing which makes it slide past one another.
What is the function of Reynolds number?- a)To detect pressure changes
- b)To predict flow patterns
- c)Temperature
- d)Viscosity
Correct answer is option 'B'. Can you explain this answer?
What is the function of Reynolds number?
a)
To detect pressure changes
b)
To predict flow patterns
c)
Temperature
d)
Viscosity
|
|
Sanya Agarwal answered |
Reynolds number is a dimensionless quantity. It is used to predict flow patterns in different types of fluid flow. At lower Reynold’s number, the flow is laminar. At higher Reynolds number, the flow is turbulent.
The cause of turbulence in fluid flow may be- a)critical Reynold’s number
- b)abrupt discontinuity in velocity distribution
- c)very high Reynolds number
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The cause of turbulence in fluid flow may be
a)
critical Reynold’s number
b)
abrupt discontinuity in velocity distribution
c)
very high Reynolds number
d)
none of these

|
Shilpa Pillai answered |
S number
b)irregularities in the surface of the object
c)sudden changes in the direction or speed of the flow
d)all of the above
Answer: d) all of the above
b)irregularities in the surface of the object
c)sudden changes in the direction or speed of the flow
d)all of the above
Answer: d) all of the above
How can you slow down a fast neutron?- a)Applying an electric field
- b)Using shield
- c)Elastic collision
- d)Heavy water
Correct answer is option 'D'. Can you explain this answer?
How can you slow down a fast neutron?
a)
Applying an electric field
b)
Using shield
c)
Elastic collision
d)
Heavy water
|
|
Sanya Agarwal answered |
The fast neutrons are converted to thermal neutrons when they are passed through heavy water(D2O). The key factor for the neutrons to slow down are its atomic number. The velocity of the fast neutrons decreases with a few collisions.
If a cricket ball moves with a velocity ‘v’ and collides with a tiny table tennis ball. After an elastic collision, at what velocity will the second ball move?- a)v
- b)v/2
- c)2v
- d)v2
Correct answer is option 'C'. Can you explain this answer?
If a cricket ball moves with a velocity ‘v’ and collides with a tiny table tennis ball. After an elastic collision, at what velocity will the second ball move?
a)
v
b)
v/2
c)
2v
d)
v2
|
|
Sanya Agarwal answered |
Since the collision is elastic, the cricket ball having a higher mass than that of the tiny table tennis ball will hit and generate a higher velocity. After immediate impact, the table tennis ball will move exactly with twice the velocity of the cricket ball.
When a charged body enters a uniform magnetic field. How will it’s kinetic energy change?- a)Doubles
- b)4 times
- c)Constant
- d)Triples
Correct answer is option 'C'. Can you explain this answer?
When a charged body enters a uniform magnetic field. How will it’s kinetic energy change?
a)
Doubles
b)
4 times
c)
Constant
d)
Triples
|
|
Sanvi Kapoor answered |
The kinetic energy remains a constant as the magnetic field always exerts a force perpendicular to the particle’s velocity. So, there is no change in the velocity of the fluid. Therefore, kinetic energy remains the same.
When a bullet hits a solid block and gets embedded into it. What is conserved?- a)Momentum only
- b)Kinetic energy only
- c)Momentum and kinetic energy
- d)Mass
Correct answer is option 'A'. Can you explain this answer?
When a bullet hits a solid block and gets embedded into it. What is conserved?
a)
Momentum only
b)
Kinetic energy only
c)
Momentum and kinetic energy
d)
Mass
|
|
Sanya Agarwal answered |
When the bullet is released from the gun, it moves through the individual air molecules. These molecules tend to vibrate which cannot be seen though our naked eye. The solid block acts as a “momentum sink”. It’s so big when compared to a tiny bullet that it can absorb all the momentum without visibly moving.
Chapter doubts & questions for Turbulent Flow - 6 Months Preparation for GATE Civil Engg 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Turbulent Flow - 6 Months Preparation for GATE Civil Engg in English & Hindi are available as part of Civil Engineering (CE) exam.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
6 Months Preparation for GATE Civil Engg
488 videos|1261 docs|878 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









