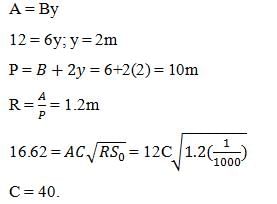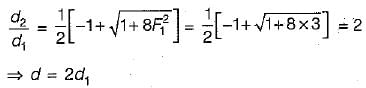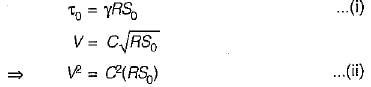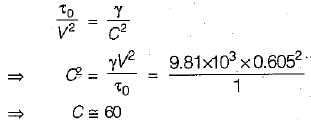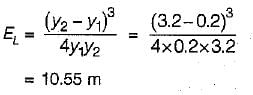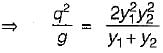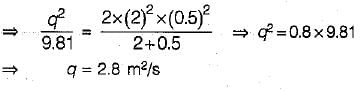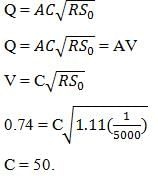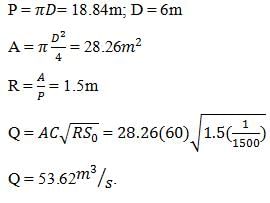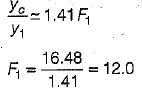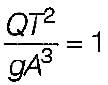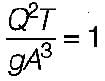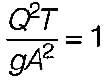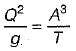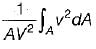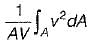All Exams >
Civil Engineering (CE) >
6 Months Preparation for GATE Civil Engg >
All Questions
All questions of Open Channel Flow for Civil Engineering (CE) Exam
The dimensions of the Chezy coefficient C in [MLT] notation system are- a)L
- b)M0 L0 T0
- c)L1/2 T-1
- d)L-1/4 T2
Correct answer is option 'C'. Can you explain this answer?
The dimensions of the Chezy coefficient C in [MLT] notation system are
a)
L
b)
M0 L0 T0
c)
L1/2 T-1
d)
L-1/4 T2
|
Gate Funda answered |
The Chezy equation can be used to calculate mean flow velocity in open channel.
Chezy’s constant is given by:
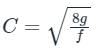
f = friction factor
Its unit is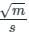
So, the dimensions of Chezy coefficient C is L1/2 T-1
Chezy’s constant is given by:
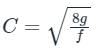
f = friction factor
Its unit is
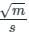
So, the dimensions of Chezy coefficient C is L1/2 T-1
Most efficient channel section is- a)half hexagon in the form of trapezoid
- b)triangular
- c)rectangular
- d)semicircular
Correct answer is option 'A'. Can you explain this answer?
Most efficient channel section is
a)
half hexagon in the form of trapezoid
b)
triangular
c)
rectangular
d)
semicircular
|
Aayan Tamboli answered |
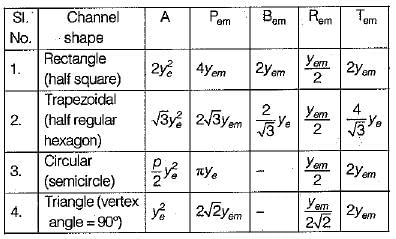
The actual answer is semicircular as it has the least wetted perimeter and maximum hydraulic radius but as it is not practically possible to construct semicircular channel we adopt trapezoidal channel .
Theoretically semicircular channel is the most efficient channel.
In a triangular notch there is an error of 4% in observing the head, the error in the computation of discharge- a)10%
- b)4%
- c)6%
- d)2.5%
Correct answer is option 'A'. Can you explain this answer?
In a triangular notch there is an error of 4% in observing the head, the error in the computation of discharge
a)
10%
b)
4%
c)
6%
d)
2.5%
|
Sanya Agarwal answered |
Concept:
Discharge through a triangular notch,
Q = 8/15 Cd √2 g tan θ/2 × H5/2
Where Q = discharge, Cd = Co-efficient of discharge, H = Head above the bottom of the notch, and θ = enclosed angle of the vee.
Differentiating equation w.r.t. H,
we have
dQ / dH = 8/15 Cd √2 g tanθ/2 × 5 /2 H3 / 2
dQ = 8/15 Cd √ 2 g tanθ/2 × 5 /2 H3/2 × d H
∴ dQ/Q = 5/2 dH/H = 2.5 dH/H
Calculation:
Given:
dH/H X 100 = 4%
The percentage error in computing discharge
= 2.5 dH/H = 2.5 x 4 = 10%
Discharge through a triangular notch,
Q = 8/15 Cd √2 g tan θ/2 × H5/2
Where Q = discharge, Cd = Co-efficient of discharge, H = Head above the bottom of the notch, and θ = enclosed angle of the vee.
Differentiating equation w.r.t. H,
we have
dQ / dH = 8/15 Cd √2 g tanθ/2 × 5 /2 H3 / 2
dQ = 8/15 Cd √ 2 g tanθ/2 × 5 /2 H3/2 × d H
∴ dQ/Q = 5/2 dH/H = 2.5 dH/H
Calculation:
Given:
dH/H X 100 = 4%
The percentage error in computing discharge
= 2.5 dH/H = 2.5 x 4 = 10%
A concrete or masonary structure placed in an open channel over which the flow occurs is called a/an:- a)Notch
- b)Weir
- c)Orifice
- d)Mouthpiece
Correct answer is option 'B'. Can you explain this answer?
A concrete or masonary structure placed in an open channel over which the flow occurs is called a/an:
a)
Notch
b)
Weir
c)
Orifice
d)
Mouthpiece
|
|
Sanya Agarwal answered |
Weirs:
Weirs are sharp-crested, overflow structures that are built across open canals. They are easy to construct and can measure the discharge accurately when correctly installed. It is important that the water level downstream is always below the weir crest, otherwise the discharge reading will be incorrect.
According to the discharge conditions the weirs are classified as follows:
Weirs are sharp-crested, overflow structures that are built across open canals. They are easy to construct and can measure the discharge accurately when correctly installed. It is important that the water level downstream is always below the weir crest, otherwise the discharge reading will be incorrect.
According to the discharge conditions the weirs are classified as follows:
Freely discharging weir:
If the water level on the downstream of a weir is well below the weir crest , then the nappe emerges freely in the atmosphere and thus it is called as freely discharging weir.
If the water level on the downstream of a weir is well below the weir crest , then the nappe emerges freely in the atmosphere and thus it is called as freely discharging weir.
Submerged weir:
If the water level downstream of a weir is above the crest level of the weir, then the weir is known as submerged weir.
If the water level downstream of a weir is above the crest level of the weir, then the weir is known as submerged weir.
Trapezoidal weir has another popular name. What is it?- a)Cipolletti weir
- b)Hagen Poiseuille’s weir
- c)Reynold’s weir
- d)Euler’s weir
Correct answer is option 'A'. Can you explain this answer?
Trapezoidal weir has another popular name. What is it?
a)
Cipolletti weir
b)
Hagen Poiseuille’s weir
c)
Reynold’s weir
d)
Euler’s weir
|
Arjun Unni answered |
Trapezoidal Weir
As per the question, the popular name for a trapezoidal weir is the Cipolletti weir. Here is a detailed explanation of this term:
Definition
A trapezoidal weir, also known as a Cipolletti weir, is a flow measurement structure commonly used in open channel flow applications. It consists of a trapezoidal-shaped notch or opening in a channel through which water flows, allowing for the measurement of flow rate based on the height of the water surface above the weir crest.
Reason for Name
The name "Cipolletti weir" comes from the Italian engineer who first introduced this specific shape of weir, Raffaele Cipolletti. He developed this design to improve the accuracy and efficiency of flow measurement in open channels, leading to its widespread adoption in hydraulic engineering.
Features
- The trapezoidal shape of the weir allows for a more accurate measurement of flow compared to other weir shapes.
- It is particularly useful for measuring flow rates in irrigation canals, stormwater drains, and other open channel systems.
- The design of the weir facilitates smooth flow over the crest, reducing turbulence and ensuring accurate flow readings.
Applications
- Cipolletti weirs are commonly used in water resource management, hydrology, and civil engineering projects for monitoring and controlling water flow.
- They can be found in various settings such as agricultural fields, urban drainage systems, and experimental hydraulic laboratories.
In conclusion, the term "Cipolletti weir" is synonymous with a trapezoidal weir due to its association with the engineer who popularized this particular design for flow measurement in open channels.
As per the question, the popular name for a trapezoidal weir is the Cipolletti weir. Here is a detailed explanation of this term:
Definition
A trapezoidal weir, also known as a Cipolletti weir, is a flow measurement structure commonly used in open channel flow applications. It consists of a trapezoidal-shaped notch or opening in a channel through which water flows, allowing for the measurement of flow rate based on the height of the water surface above the weir crest.
Reason for Name
The name "Cipolletti weir" comes from the Italian engineer who first introduced this specific shape of weir, Raffaele Cipolletti. He developed this design to improve the accuracy and efficiency of flow measurement in open channels, leading to its widespread adoption in hydraulic engineering.
Features
- The trapezoidal shape of the weir allows for a more accurate measurement of flow compared to other weir shapes.
- It is particularly useful for measuring flow rates in irrigation canals, stormwater drains, and other open channel systems.
- The design of the weir facilitates smooth flow over the crest, reducing turbulence and ensuring accurate flow readings.
Applications
- Cipolletti weirs are commonly used in water resource management, hydrology, and civil engineering projects for monitoring and controlling water flow.
- They can be found in various settings such as agricultural fields, urban drainage systems, and experimental hydraulic laboratories.
In conclusion, the term "Cipolletti weir" is synonymous with a trapezoidal weir due to its association with the engineer who popularized this particular design for flow measurement in open channels.
For a hydraulically efficient rectangular section, the ratio of width to normal depth is- a)0.5
- b)1.0
- c)2.0
- d)2√3
Correct answer is option 'C'. Can you explain this answer?
For a hydraulically efficient rectangular section, the ratio of width to normal depth is
a)
0.5
b)
1.0
c)
2.0
d)
2√3
|
Simran Saha answered |
For hydraulically efficient rectangular section.
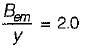
What is not the way of classifying weir based on the emerging nappe?- a)Weir with end contraction
- b)Weir without end contraction
- c)Weir contraction at the beginning
- d)Weir with absence of end contraction
Correct answer is option 'C'. Can you explain this answer?
What is not the way of classifying weir based on the emerging nappe?
a)
Weir with end contraction
b)
Weir without end contraction
c)
Weir contraction at the beginning
d)
Weir with absence of end contraction
|
Sanskriti Datta answered |
Classification of Weirs based on the Emerging Nappe
Weirs are hydraulic structures used to measure or control the flow of water in open channels. They are classified based on various factors, including the emerging nappe, which refers to the sheet of water that flows over the weir crest. The classification based on the emerging nappe helps in understanding the flow characteristics and behavior of the weir.
There are four ways of classifying weirs based on the emerging nappe:
1. Weir with End Contraction:
A weir with end contraction is one where the nappe contracts after passing over the crest. This contraction occurs at both ends of the weir and is due to the surface tension of the water. The contraction causes the effective width of the weir to be less than the actual width, resulting in an increase in the discharge coefficient. Weirs with end contraction are commonly used in practice and are considered the most efficient type of weirs.
2. Weir without End Contraction:
Weirs without end contraction are those where the nappe does not contract after passing over the crest. The flow over the weir is free and not influenced by surface tension. As a result, the effective width of the weir is equal to the actual width. Weirs without end contraction are less efficient compared to weirs with end contraction.
3. Weir Contraction at the Beginning:
Weirs with contraction at the beginning are those where the nappe contracts before passing over the crest. This contraction occurs at the upstream end of the weir and is caused by the converging shape of the channel leading to the weir. The contraction at the beginning affects the discharge coefficient and reduces the efficiency of the weir.
4. Weir with Absence of End Contraction:
Weirs with the absence of end contraction are similar to weirs without end contraction, but they have an additional feature. In these weirs, the flow over the crest is free and not influenced by surface tension, and the effective width is equal to the actual width. However, these weirs have an extended downstream apron that helps in dissipating energy and controlling the flow downstream. The absence of end contraction and the presence of an extended apron make these weirs suitable for locations where downstream scouring needs to be controlled.
Conclusion:
Among the given options, the classification based on "Weir Contraction at the Beginning" is not a correct way of classifying weirs based on the emerging nappe. Weirs can be classified as either having end contraction, absence of end contraction, or without end contraction, but the classification based on contraction at the beginning is not a recognized category.
Weirs are hydraulic structures used to measure or control the flow of water in open channels. They are classified based on various factors, including the emerging nappe, which refers to the sheet of water that flows over the weir crest. The classification based on the emerging nappe helps in understanding the flow characteristics and behavior of the weir.
There are four ways of classifying weirs based on the emerging nappe:
1. Weir with End Contraction:
A weir with end contraction is one where the nappe contracts after passing over the crest. This contraction occurs at both ends of the weir and is due to the surface tension of the water. The contraction causes the effective width of the weir to be less than the actual width, resulting in an increase in the discharge coefficient. Weirs with end contraction are commonly used in practice and are considered the most efficient type of weirs.
2. Weir without End Contraction:
Weirs without end contraction are those where the nappe does not contract after passing over the crest. The flow over the weir is free and not influenced by surface tension. As a result, the effective width of the weir is equal to the actual width. Weirs without end contraction are less efficient compared to weirs with end contraction.
3. Weir Contraction at the Beginning:
Weirs with contraction at the beginning are those where the nappe contracts before passing over the crest. This contraction occurs at the upstream end of the weir and is caused by the converging shape of the channel leading to the weir. The contraction at the beginning affects the discharge coefficient and reduces the efficiency of the weir.
4. Weir with Absence of End Contraction:
Weirs with the absence of end contraction are similar to weirs without end contraction, but they have an additional feature. In these weirs, the flow over the crest is free and not influenced by surface tension, and the effective width is equal to the actual width. However, these weirs have an extended downstream apron that helps in dissipating energy and controlling the flow downstream. The absence of end contraction and the presence of an extended apron make these weirs suitable for locations where downstream scouring needs to be controlled.
Conclusion:
Among the given options, the classification based on "Weir Contraction at the Beginning" is not a correct way of classifying weirs based on the emerging nappe. Weirs can be classified as either having end contraction, absence of end contraction, or without end contraction, but the classification based on contraction at the beginning is not a recognized category.
A hydraulically efficient trapezoidal section of open channel flow carries water at the optimal depth of 0.6 m. Chezy coefficient is 75 and bed slope is 1 in 250. What is the discharge through the channel?- a)1.44 m3/s
- b)1.62 m3/s
- c)1.92 m3/s
- d)2.24 m3/s
Correct answer is option 'B'. Can you explain this answer?
A hydraulically efficient trapezoidal section of open channel flow carries water at the optimal depth of 0.6 m. Chezy coefficient is 75 and bed slope is 1 in 250. What is the discharge through the channel?
a)
1.44 m3/s
b)
1.62 m3/s
c)
1.92 m3/s
d)
2.24 m3/s
|
Sparsh Unni answered |
To calculate the discharge through the channel, we can use the Manning's equation, which relates the cross-sectional properties of the channel to the flow rate. The equation is as follows:
Q = (1/n) * A * R^(2/3) * S^(1/2)
where:
Q is the discharge (m^3/s)
n is the Manning's roughness coefficient
A is the cross-sectional area of flow (m^2)
R is the hydraulic radius (m)
S is the bed slope (m/m)
Given:
n = 75
depth (y) = 0.6 m
bed slope (S) = 1/250
1. Determine the cross-sectional properties:
The channel has a trapezoidal section, which can be divided into a rectangle and a triangle. The area (A) of the flow can be calculated as the sum of these two areas:
A = A_rectangle + A_triangle
A_rectangle = base_rectangle * y
A_triangle = (1/2) * base_triangle * y
2. Determine the hydraulic radius:
The hydraulic radius (R) can be calculated as the ratio of the flow area to the wetted perimeter (P):
R = A / P
The wetted perimeter can be calculated as the sum of the rectangle and triangle perimeters:
P = P_rectangle + P_triangle
P_rectangle = 2 * base_rectangle + 2 * y
P_triangle = base_triangle + 2 * sqrt(base_triangle^2 + y^2)
3. Calculate the discharge:
Substitute the values into the Manning's equation:
Q = (1/n) * A * R^(2/3) * S^(1/2)
Simplify the equation using the values calculated above and solve for Q.
The correct answer is option B: 1.62 m^3/s.
Q = (1/n) * A * R^(2/3) * S^(1/2)
where:
Q is the discharge (m^3/s)
n is the Manning's roughness coefficient
A is the cross-sectional area of flow (m^2)
R is the hydraulic radius (m)
S is the bed slope (m/m)
Given:
n = 75
depth (y) = 0.6 m
bed slope (S) = 1/250
1. Determine the cross-sectional properties:
The channel has a trapezoidal section, which can be divided into a rectangle and a triangle. The area (A) of the flow can be calculated as the sum of these two areas:
A = A_rectangle + A_triangle
A_rectangle = base_rectangle * y
A_triangle = (1/2) * base_triangle * y
2. Determine the hydraulic radius:
The hydraulic radius (R) can be calculated as the ratio of the flow area to the wetted perimeter (P):
R = A / P
The wetted perimeter can be calculated as the sum of the rectangle and triangle perimeters:
P = P_rectangle + P_triangle
P_rectangle = 2 * base_rectangle + 2 * y
P_triangle = base_triangle + 2 * sqrt(base_triangle^2 + y^2)
3. Calculate the discharge:
Substitute the values into the Manning's equation:
Q = (1/n) * A * R^(2/3) * S^(1/2)
Simplify the equation using the values calculated above and solve for Q.
The correct answer is option B: 1.62 m^3/s.
Consider the following statements in regard to the critical flow:
1. Specific energy is maximum for a given discharge.
2. Specific force is maximum for a given discharge
3. Discharge is maximum for a given specific force.
4. Discharge is maximum for a given specific energy.Which of these statements are correct?- a)1, 2, 3 and 4
- b)1 and 2
- c)2 and 3
- d)3 and 4
Correct answer is option 'D'. Can you explain this answer?
Consider the following statements in regard to the critical flow:
1. Specific energy is maximum for a given discharge.
2. Specific force is maximum for a given discharge
3. Discharge is maximum for a given specific force.
4. Discharge is maximum for a given specific energy.
1. Specific energy is maximum for a given discharge.
2. Specific force is maximum for a given discharge
3. Discharge is maximum for a given specific force.
4. Discharge is maximum for a given specific energy.
Which of these statements are correct?
a)
1, 2, 3 and 4
b)
1 and 2
c)
2 and 3
d)
3 and 4
|
Nilesh Kapoor answered |
Critical flow is a flow condition in open channel hydraulics where the flow velocity equals the wave velocity, resulting in the maximum flow rate for a given channel geometry. In critical flow, the flow depth and flow velocity are uniquely related to each other, and specific energy and specific force are important parameters used to analyze and design open channel flows.
1. Specific energy is maximum for a given discharge:
Specific energy is defined as the energy per unit weight of the fluid flowing in the channel. It is given by the sum of the elevation head and the velocity head. In critical flow, the specific energy is maximum for a given discharge. This is because the flow is at its maximum efficiency, and any increase or decrease in specific energy would result in a decrease in discharge.
2. Specific force is maximum for a given discharge:
Specific force is defined as the force per unit weight of the fluid acting on the channel bottom. It is given by the sum of the gravitational force and the inertial force. In critical flow, the specific force is also maximum for a given discharge. This is because the flow is at its maximum efficiency, and any increase or decrease in specific force would result in a decrease in discharge.
3. Discharge is maximum for a given specific force:
Discharge refers to the volume of fluid passing through a cross-section of the channel per unit time. In critical flow, the discharge is maximum for a given specific force. This is because the specific force is directly related to the flow velocity, and the maximum flow velocity corresponds to the maximum discharge.
4. Discharge is maximum for a given specific energy:
Contrary to the previous statement, discharge is not maximum for a given specific energy. While specific energy is maximum in critical flow, the discharge is not necessarily at its maximum. The discharge is determined by the channel geometry, and specific energy alone does not dictate the maximum flow rate.
In summary, the correct statements regarding critical flow are:
- Specific energy is maximum for a given discharge.
- Specific force is maximum for a given discharge.
- Discharge is maximum for a given specific force.
- Discharge is not maximum for a given specific energy.
1. Specific energy is maximum for a given discharge:
Specific energy is defined as the energy per unit weight of the fluid flowing in the channel. It is given by the sum of the elevation head and the velocity head. In critical flow, the specific energy is maximum for a given discharge. This is because the flow is at its maximum efficiency, and any increase or decrease in specific energy would result in a decrease in discharge.
2. Specific force is maximum for a given discharge:
Specific force is defined as the force per unit weight of the fluid acting on the channel bottom. It is given by the sum of the gravitational force and the inertial force. In critical flow, the specific force is also maximum for a given discharge. This is because the flow is at its maximum efficiency, and any increase or decrease in specific force would result in a decrease in discharge.
3. Discharge is maximum for a given specific force:
Discharge refers to the volume of fluid passing through a cross-section of the channel per unit time. In critical flow, the discharge is maximum for a given specific force. This is because the specific force is directly related to the flow velocity, and the maximum flow velocity corresponds to the maximum discharge.
4. Discharge is maximum for a given specific energy:
Contrary to the previous statement, discharge is not maximum for a given specific energy. While specific energy is maximum in critical flow, the discharge is not necessarily at its maximum. The discharge is determined by the channel geometry, and specific energy alone does not dictate the maximum flow rate.
In summary, the correct statements regarding critical flow are:
- Specific energy is maximum for a given discharge.
- Specific force is maximum for a given discharge.
- Discharge is maximum for a given specific force.
- Discharge is not maximum for a given specific energy.
A rectangular channel is 6 m wide and discharges 30 m3s-1. The upstream depth is 2.0 m, acceleration due to gravity is 10 ms-2. Then, what is the specific energy (approximate)?- a)2.5
- b)0.3
- c)2.3
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
A rectangular channel is 6 m wide and discharges 30 m3s-1. The upstream depth is 2.0 m, acceleration due to gravity is 10 ms-2. Then, what is the specific energy (approximate)?
a)
2.5
b)
0.3
c)
2.3
d)
None of these
|
|
Amar Desai answered |
We know that,
Q = AV
⇒ \/ = 2.5 m/s
The specific energy may be given as,
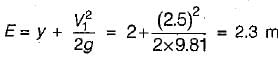
Q = AV
⇒ \/ = 2.5 m/s
The specific energy may be given as,
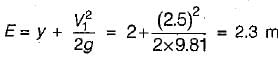
For a smooth hump in a subcritical flow to function as a broad crested weir, the height ΔZ of the hump above the bed must satisfy which one of the following?
(E1 = Specific head upstream of the hump, Ec = Specific head at the critical" depth yc) (Neglect friction effects)- a)
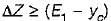
- b)
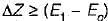
- c)
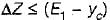
- d)
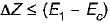
Correct answer is option 'D'. Can you explain this answer?
For a smooth hump in a subcritical flow to function as a broad crested weir, the height ΔZ of the hump above the bed must satisfy which one of the following?
(E1 = Specific head upstream of the hump, Ec = Specific head at the critical" depth yc) (Neglect friction effects)
(E1 = Specific head upstream of the hump, Ec = Specific head at the critical" depth yc) (Neglect friction effects)
a)
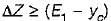
b)
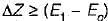
c)
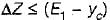
d)
|
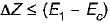
Mrinalini Chavan answered |
Explanation:
Given Parameters:
- E1 = Specific head upstream of the hump
- Ec = Specific head at the critical depth yc
Key Concept:
- For a smooth hump in a subcritical flow to function as a broad crested weir, the height ΔZ of the hump above the bed must satisfy certain conditions.
Condition for a Broad Crested Weir:
- In this case, we need to ensure that the specific energy at the upstream location (E1) is greater than the specific energy at the critical depth (Ec) for the flow to behave as a broad crested weir.
Analysis:
- The specific energy at a point is given by the sum of the depth of flow (Y) and the velocity head (V^2/2g).
- At critical depth, the specific energy is minimum and equal to the critical specific energy Ec.
- Therefore, the specific energy at the upstream location E1 must be greater than Ec for the flow to behave as a broad crested weir.
Conclusion:
- The height ΔZ of the hump above the bed must be such that the specific energy at the upstream location (E1) is greater than the specific energy at the critical depth (Ec).
- Therefore, the correct condition is ΔZ ≤ (E1 - E0), which is option 'd'.
Given Parameters:
- E1 = Specific head upstream of the hump
- Ec = Specific head at the critical depth yc
Key Concept:
- For a smooth hump in a subcritical flow to function as a broad crested weir, the height ΔZ of the hump above the bed must satisfy certain conditions.
Condition for a Broad Crested Weir:
- In this case, we need to ensure that the specific energy at the upstream location (E1) is greater than the specific energy at the critical depth (Ec) for the flow to behave as a broad crested weir.
Analysis:
- The specific energy at a point is given by the sum of the depth of flow (Y) and the velocity head (V^2/2g).
- At critical depth, the specific energy is minimum and equal to the critical specific energy Ec.
- Therefore, the specific energy at the upstream location E1 must be greater than Ec for the flow to behave as a broad crested weir.
Conclusion:
- The height ΔZ of the hump above the bed must be such that the specific energy at the upstream location (E1) is greater than the specific energy at the critical depth (Ec).
- Therefore, the correct condition is ΔZ ≤ (E1 - E0), which is option 'd'.
Which of the following is not a way of classifying based on the shape of opening?- a)Rectangular notch
- b)Circular notch
- c)Trapezoidal notch
- d)Stepped notch
Correct answer is option 'B'. Can you explain this answer?
Which of the following is not a way of classifying based on the shape of opening?
a)
Rectangular notch
b)
Circular notch
c)
Trapezoidal notch
d)
Stepped notch
|
|
Sanskriti Datta answered |
Classification based on the shape of the opening
The shape of the opening is an important factor when classifying different types of notches. It helps determine the flow characteristics and the behavior of the fluid passing through the opening. The options provided are rectangular notch, circular notch, trapezoidal notch, and stepped notch. Let's discuss each of these options and identify the one that does not fit the classification based on the shape of the opening.
1. Rectangular notch: A rectangular notch is a type of opening with a rectangular shape. It has two vertical sides and a horizontal base. The flow characteristics through a rectangular notch are influenced by the width and height of the notch, as well as the head of water above the notch.
2. Circular notch: A circular notch, as the name suggests, has a circular shape. It is characterized by a circular hole or opening. The flow through a circular notch is determined by the diameter of the opening and the head of water above it.
3. Trapezoidal notch: A trapezoidal notch has a trapezoidal shape. It is defined by its inclined sides and a horizontal base. The flow behavior through a trapezoidal notch is influenced by the dimensions of the notch, including the base width, side slope angles, and the head of water.
4. Stepped notch: A stepped notch is a type of notch that consists of multiple rectangular steps. Each step has its own width and height, creating a staircase-like structure. The flow characteristics through a stepped notch are influenced by the dimensions of each step, as well as the head of water above the notch.
Correct answer: Option 'B' - Circular notch is not a way of classifying based on the shape of the opening. Circular notches have their own characteristics and are classified separately from notches with other shapes, such as rectangular, trapezoidal, or stepped notches.
In conclusion, while rectangular, trapezoidal, and stepped notches are all classified based on the shape of their openings, circular notches are not categorized in the same manner.
The shape of the opening is an important factor when classifying different types of notches. It helps determine the flow characteristics and the behavior of the fluid passing through the opening. The options provided are rectangular notch, circular notch, trapezoidal notch, and stepped notch. Let's discuss each of these options and identify the one that does not fit the classification based on the shape of the opening.
1. Rectangular notch: A rectangular notch is a type of opening with a rectangular shape. It has two vertical sides and a horizontal base. The flow characteristics through a rectangular notch are influenced by the width and height of the notch, as well as the head of water above the notch.
2. Circular notch: A circular notch, as the name suggests, has a circular shape. It is characterized by a circular hole or opening. The flow through a circular notch is determined by the diameter of the opening and the head of water above it.
3. Trapezoidal notch: A trapezoidal notch has a trapezoidal shape. It is defined by its inclined sides and a horizontal base. The flow behavior through a trapezoidal notch is influenced by the dimensions of the notch, including the base width, side slope angles, and the head of water.
4. Stepped notch: A stepped notch is a type of notch that consists of multiple rectangular steps. Each step has its own width and height, creating a staircase-like structure. The flow characteristics through a stepped notch are influenced by the dimensions of each step, as well as the head of water above the notch.
Correct answer: Option 'B' - Circular notch is not a way of classifying based on the shape of the opening. Circular notches have their own characteristics and are classified separately from notches with other shapes, such as rectangular, trapezoidal, or stepped notches.
In conclusion, while rectangular, trapezoidal, and stepped notches are all classified based on the shape of their openings, circular notches are not categorized in the same manner.
A rectangular channel is 5 m wide and 3 m deep. Water is flowing in the channel for a depth of 2.5 m. The hydraulic radius is- a)0.50
- b)1.25
- c)2.00
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A rectangular channel is 5 m wide and 3 m deep. Water is flowing in the channel for a depth of 2.5 m. The hydraulic radius is
a)
0.50
b)
1.25
c)
2.00
d)
None of these
|
|
Samarth Ghoshal answered |
Hydraulic radius (R) is a parameter used in fluid mechanics to characterize the flow of water in open channels. It is defined as the ratio of the cross-sectional area of flow (A) to the wetted perimeter (P) of the channel.
To find the hydraulic radius in this rectangular channel, we need to calculate the cross-sectional area and wetted perimeter.
Cross-sectional area (A):
The cross-sectional area of the flow can be calculated by multiplying the width of the channel (5 m) by the depth of the flow (2.5 m).
A = width × depth
A = 5 m × 2.5 m
A = 12.5 m²
Wetted perimeter (P):
The wetted perimeter is the sum of all the sides that come into contact with the water. In a rectangular channel, the wetted perimeter is given by the sum of the width and two times the depth.
P = width + 2 × depth
P = 5 m + 2 × 2.5 m
P = 5 m + 5 m
P = 10 m
Hydraulic radius (R):
Now, we can calculate the hydraulic radius by dividing the cross-sectional area (A) by the wetted perimeter (P).
R = A / P
R = 12.5 m² / 10 m
R = 1.25 m
The hydraulic radius of the rectangular channel is 1.25 m. Therefore, the correct answer is option (B) 1.25.
To find the hydraulic radius in this rectangular channel, we need to calculate the cross-sectional area and wetted perimeter.
Cross-sectional area (A):
The cross-sectional area of the flow can be calculated by multiplying the width of the channel (5 m) by the depth of the flow (2.5 m).
A = width × depth
A = 5 m × 2.5 m
A = 12.5 m²
Wetted perimeter (P):
The wetted perimeter is the sum of all the sides that come into contact with the water. In a rectangular channel, the wetted perimeter is given by the sum of the width and two times the depth.
P = width + 2 × depth
P = 5 m + 2 × 2.5 m
P = 5 m + 5 m
P = 10 m
Hydraulic radius (R):
Now, we can calculate the hydraulic radius by dividing the cross-sectional area (A) by the wetted perimeter (P).
R = A / P
R = 12.5 m² / 10 m
R = 1.25 m
The hydraulic radius of the rectangular channel is 1.25 m. Therefore, the correct answer is option (B) 1.25.
A steady discharge of 1 cumec flows uniformly in a rectangular channel 1 m wide at a depth of 250 mm. The slope of the channel bed is- a)Adverse
- b)Steep
- c)Critical
- d)Mild
Correct answer is option 'B'. Can you explain this answer?
A steady discharge of 1 cumec flows uniformly in a rectangular channel 1 m wide at a depth of 250 mm. The slope of the channel bed is
a)
Adverse
b)
Steep
c)
Critical
d)
Mild
|
|
Pallabi Kulkarni answered |
Critical depth of flow :
q = Q/B = 1
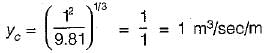
⇒ Yc = 0.467
Yc = 0.5
And normal depth of flow = yn = 0.25 m
since yn < yc therefore channel has steep slope.
q = Q/B = 1
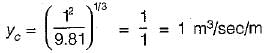
⇒ Yc = 0.467
Yc = 0.5
And normal depth of flow = yn = 0.25 m
since yn < yc therefore channel has steep slope.
Open channel flow is the one in which- a)A closed conduit is full of flowing liquid
- b)The liquid flowing in a closed conduit has a : free surface
- c)A covered channel flows full under pressure
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
Open channel flow is the one in which
a)
A closed conduit is full of flowing liquid
b)
The liquid flowing in a closed conduit has a : free surface
c)
A covered channel flows full under pressure
d)
None of the above
|
|
Dipika Nambiar answered |
Flow in a conduit with a free surface is known as open channel flow, flows in irrigation channels, streams and rivers, navigation channels, drainage channels and severs are some examples of open channel flow.
The depth and widths of a rectangular channel are 2m and 5m respectively, calculate the discharge of water through the channel if the bed slope is 1 in 500 and Chezy’s constant being 60.- a)28.27 m3/s
- b)38.27 m3/s
- c)48.27 m3/s
- d)58.27 m3/s
Correct answer is option 'A'. Can you explain this answer?
The depth and widths of a rectangular channel are 2m and 5m respectively, calculate the discharge of water through the channel if the bed slope is 1 in 500 and Chezy’s constant being 60.
a)
28.27 m3/s
b)
38.27 m3/s
c)
48.27 m3/s
d)
58.27 m3/s
|
|
Sanya Agarwal answered |
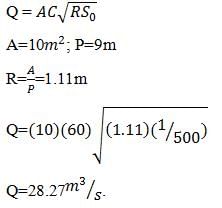
The relation between Manning' 'n' and Chezy's 'C' is given by
Where R = hydraulic mean depth- a)
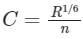
- b)
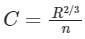
- c)
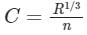
- d)
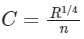
Correct answer is option 'A'. Can you explain this answer?
The relation between Manning' 'n' and Chezy's 'C' is given by
Where R = hydraulic mean depth
Where R = hydraulic mean depth
a)
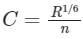
b)
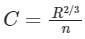
c)
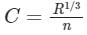
d)
|
|
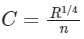
Sanvi Kapoor answered |
Manning's Formula:
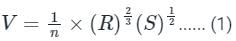
Chezy formula:
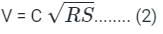
where
n = Manning’s Coefficient
R = Hydraulic radius = (Wetted Area/ Wetted Perimeter)
S = Bed Slope
C = Chezy's Coefficient
From Equations 1 and 2
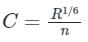
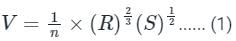
Chezy formula:
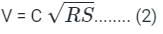
where
n = Manning’s Coefficient
R = Hydraulic radius = (Wetted Area/ Wetted Perimeter)
S = Bed Slope
C = Chezy's Coefficient
From Equations 1 and 2
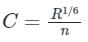
Gradually varied flow in open channel is caused when- a)There is an equilibrium between the forces causing the flow and those opposing it
- b)The pressure forces and the change in momentum are different from each other
- c)The force causing the flow is not equal to the resistance force
- d)The channel slope is equal to the normal slope
Correct answer is option 'D'. Can you explain this answer?
Gradually varied flow in open channel is caused when
a)
There is an equilibrium between the forces causing the flow and those opposing it
b)
The pressure forces and the change in momentum are different from each other
c)
The force causing the flow is not equal to the resistance force
d)
The channel slope is equal to the normal slope
|
|
Divya Mehta answered |
If the flow is subcritical, then after the introduction of hump the specific energy will decrease by ΔZ (height of hump).
The MoM (Material of Manufacture) of notch is,- a)Thermoplastic
- b)Metals
- c)Fibre
- d)Wood
Correct answer is option 'B'. Can you explain this answer?
The MoM (Material of Manufacture) of notch is,
a)
Thermoplastic
b)
Metals
c)
Fibre
d)
Wood
|
Sameer Verma answered |
Material of Manufacture of Notch
Metals
- Notches are commonly made from metals such as steel, aluminum, or titanium.
- Metals are preferred for notches due to their durability, strength, and resistance to wear and tear.
- The use of metals ensures that the notch can withstand high loads and harsh environmental conditions.
- Additionally, metals can be easily machined or welded to create precise and complex notch designs.
- Overall, metals are the preferred material of manufacture for notches in various engineering applications due to their superior mechanical properties and versatility.
Metals
- Notches are commonly made from metals such as steel, aluminum, or titanium.
- Metals are preferred for notches due to their durability, strength, and resistance to wear and tear.
- The use of metals ensures that the notch can withstand high loads and harsh environmental conditions.
- Additionally, metals can be easily machined or welded to create precise and complex notch designs.
- Overall, metals are the preferred material of manufacture for notches in various engineering applications due to their superior mechanical properties and versatility.
Find the discharge through a circular channel section having diameter of 5m, the value of Chezy’s constant is 90 and the bed slope is 1 in 4000.- a)13.61 m3/s
- b)14.61 m3/s
- c)15.61 m3/s
- d)16.61 m3/s
Correct answer is option 'C'. Can you explain this answer?
Find the discharge through a circular channel section having diameter of 5m, the value of Chezy’s constant is 90 and the bed slope is 1 in 4000.
a)
13.61 m3/s
b)
14.61 m3/s
c)
15.61 m3/s
d)
16.61 m3/s
|
|
Gowri Singh answered |
The discharge through a circular channel can be calculated using the Chezy-Manning equation:
Q = (1/n) * A * R^(2/3) * S^(1/2)
Where:
Q = Discharge (m^3/s)
n = Manning's roughness coefficient (dimensionless)
A = Cross-sectional area of the channel (m^2)
R = Hydraulic radius (m)
S = Slope of the channel (m/m)
In this case, the diameter of the circular channel is given as 5m. The cross-sectional area can be calculated as:
A = π * (D/2)^2
A = π * (5/2)^2
A = 19.63 m^2
The hydraulic radius can be calculated as:
R = A / P
R = A / (π * D)
R = 19.63 / (π * 5)
R = 1.25 m
Now, let's assume a value for the Manning's roughness coefficient (n). This value depends on the type of channel material and flow conditions. Let's assume a value of 0.03, which is commonly used for concrete channels.
Finally, let's assume a slope (S) of 0.001, which means a 0.1% slope.
Plugging in these values into the equation, we get:
Q = (1/0.03) * 19.63 * (1.25)^(2/3) * (0.001)^(1/2)
Q ≈ 218.52 m^3/s
Therefore, the discharge through the circular channel section is approximately 218.52 m^3/s.
Q = (1/n) * A * R^(2/3) * S^(1/2)
Where:
Q = Discharge (m^3/s)
n = Manning's roughness coefficient (dimensionless)
A = Cross-sectional area of the channel (m^2)
R = Hydraulic radius (m)
S = Slope of the channel (m/m)
In this case, the diameter of the circular channel is given as 5m. The cross-sectional area can be calculated as:
A = π * (D/2)^2
A = π * (5/2)^2
A = 19.63 m^2
The hydraulic radius can be calculated as:
R = A / P
R = A / (π * D)
R = 19.63 / (π * 5)
R = 1.25 m
Now, let's assume a value for the Manning's roughness coefficient (n). This value depends on the type of channel material and flow conditions. Let's assume a value of 0.03, which is commonly used for concrete channels.
Finally, let's assume a slope (S) of 0.001, which means a 0.1% slope.
Plugging in these values into the equation, we get:
Q = (1/0.03) * 19.63 * (1.25)^(2/3) * (0.001)^(1/2)
Q ≈ 218.52 m^3/s
Therefore, the discharge through the circular channel section is approximately 218.52 m^3/s.
A hydraulic jump is always needed in case of- a)an A2 profile followed by an A3 profile
- b)an A3 profile followed by an A2 profile
- c)an H2 profile followed by an M2 profile
- d)an M1 profile followed by an M3 profile
Correct answer is option 'D'. Can you explain this answer?
A hydraulic jump is always needed in case of
a)
an A2 profile followed by an A3 profile
b)
an A3 profile followed by an A2 profile
c)
an H2 profile followed by an M2 profile
d)
an M1 profile followed by an M3 profile
|
|
Sreemoyee Deshpande answered |
Hydraulic jump is needed when critical depth line is to be crossed.
The flow characteristic before and after a hydraulic jump are such that:- a)Specific forces are equal but specific energies are unequal
- b)Specific forces are unequal but specific energies are equal
- c)Neither specific forces nor specific energies are equal
- d)Specific forces as well as specific energies are equal
Correct answer is option 'A'. Can you explain this answer?
The flow characteristic before and after a hydraulic jump are such that:
a)
Specific forces are equal but specific energies are unequal
b)
Specific forces are unequal but specific energies are equal
c)
Neither specific forces nor specific energies are equal
d)
Specific forces as well as specific energies are equal
|
|
Rishika Sen answered |
The loss of energy in a hydraulic jump leads to unequal specific energies at downstream and upstream sections.
What is the normal depth in a wide rectangular channel carrying 0.5 m2/s discharge at a bed slope of 0.0004 and Manning’s n = 0.01?- a)0.13 m
- b)0.32 m
- c)0.43 m
- d)0.50 m
Correct answer is option 'C'. Can you explain this answer?
What is the normal depth in a wide rectangular channel carrying 0.5 m2/s discharge at a bed slope of 0.0004 and Manning’s n = 0.01?
a)
0.13 m
b)
0.32 m
c)
0.43 m
d)
0.50 m
|
|
Partho Choudhary answered |
For a wide rectangular channel, the hydraulic radius (F) is approximately equal to the depth of flow. By Manning’s equation, we have,
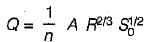
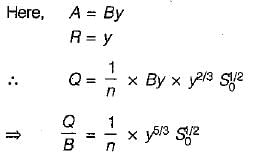
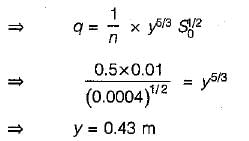
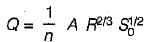
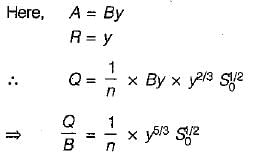
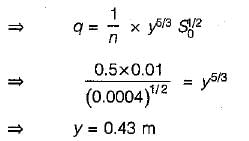
The Chezy’s constant C in the Chezy’s equation for mean velocity in open channels is- a)Is a dimensionless constant
- b)Has a constant value for different types of channels
- c)Has dimension L1/2T-1
- d)Does not depend on the quality of channel surface
Correct answer is option 'C'. Can you explain this answer?
The Chezy’s constant C in the Chezy’s equation for mean velocity in open channels is
a)
Is a dimensionless constant
b)
Has a constant value for different types of channels
c)
Has dimension L1/2T-1
d)
Does not depend on the quality of channel surface
|
|
Ameya Sen answered |
Chezy’s equation, V =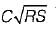 
Substituting dimensions of each term in above equation.
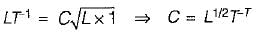
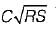
Substituting dimensions of each term in above equation.
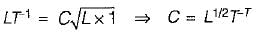
The Chezy’s and Manning’s formulae are related by- a)C = 1/n(R1/6)
- b)C = nR1/6
- c)C = Rn1/6
- d)C = 1/R(n1/6)
Correct answer is option 'C'. Can you explain this answer?
The Chezy’s and Manning’s formulae are related by
a)
C = 1/n(R1/6)
b)
C = nR1/6
c)
C = Rn1/6
d)
C = 1/R(n1/6)
|
|
Yash Joshi answered |
The Chezy is a term used to describe a characteristic of flow in fluid mechanics. It is named after the French engineer Antoine Chezy, who developed the Chezy equation in the 18th century to calculate the velocity of flow in open channels.
The Chezy equation is given as:
V = C * sqrt(R * S)
Where:
V is the velocity of flow
C is the Chezy coefficient, which is a dimensionless parameter that depends on the roughness of the channel.
R is the hydraulic radius, which is the ratio of the cross-sectional area of flow to the wetted perimeter.
S is the slope of the channel.
The Chezy coefficient is determined empirically and varies depending on the type of channel and the roughness of its surface. It is often determined through field measurements or laboratory experiments.
The Chezy equation is widely used in hydraulic engineering to calculate the velocity of flow in open channels, such as rivers, canals, and stormwater drains. It is an important tool for designing and analyzing hydraulic structures, such as dams, culverts, and flood control systems.
Overall, the Chezy equation and the concept of the Chezy are fundamental in understanding and predicting the behavior of fluid flow in open channels.
The Chezy equation is given as:
V = C * sqrt(R * S)
Where:
V is the velocity of flow
C is the Chezy coefficient, which is a dimensionless parameter that depends on the roughness of the channel.
R is the hydraulic radius, which is the ratio of the cross-sectional area of flow to the wetted perimeter.
S is the slope of the channel.
The Chezy coefficient is determined empirically and varies depending on the type of channel and the roughness of its surface. It is often determined through field measurements or laboratory experiments.
The Chezy equation is widely used in hydraulic engineering to calculate the velocity of flow in open channels, such as rivers, canals, and stormwater drains. It is an important tool for designing and analyzing hydraulic structures, such as dams, culverts, and flood control systems.
Overall, the Chezy equation and the concept of the Chezy are fundamental in understanding and predicting the behavior of fluid flow in open channels.
A right-angled triangular channel symmetrical in section about the vertical carries a discharge of 5 m3/s with a velocity of 1.25 m/s. What is the approximate value of the Froude number of the flow?- a)0.3
- b)0.4
- c)0.5
- d)0.6
Correct answer is option 'B'. Can you explain this answer?
A right-angled triangular channel symmetrical in section about the vertical carries a discharge of 5 m3/s with a velocity of 1.25 m/s. What is the approximate value of the Froude number of the flow?
a)
0.3
b)
0.4
c)
0.5
d)
0.6
|
|
Harshad Iyer answered |
We know that,
Q = AV
⇒ 5 = A x 1.25 ⇒ A = 4 m2
For a symmetrical right angled triangular channel,
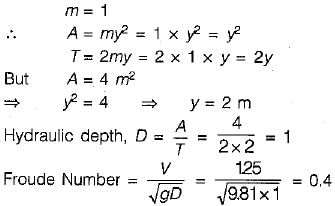
Q = AV
⇒ 5 = A x 1.25 ⇒ A = 4 m2
For a symmetrical right angled triangular channel,
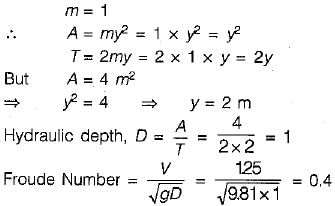
The Froude number of a hydraulic jump is 5.5. The jump can be classified as a/an- a)unduiarjump
- b)oscillating jump
- c)weak jump
- d)steady jump
Correct answer is option 'D'. Can you explain this answer?
The Froude number of a hydraulic jump is 5.5. The jump can be classified as a/an
a)
unduiarjump
b)
oscillating jump
c)
weak jump
d)
steady jump
|
|
Sarthak Menon answered |
The hydraulic jumps in horizontal rectangular channels are classified into five categories based on Froude number F1 of the super-critical flow as:
Water flows through a pipe of length 3 km at the rate of 250 litres/s and head lost due to friction is 5 m. Find the diameter of this pipe (in cm) ________ (Take chezy’s constant, c = 50)
Correct answer is between '60,65'. Can you explain this answer?
Water flows through a pipe of length 3 km at the rate of 250 litres/s and head lost due to friction is 5 m. Find the diameter of this pipe (in cm) ________ (Take chezy’s constant, c = 50)
|
|
Gowri Singh answered |
The Darcy-Weisbach equation can be used to find the diameter of the pipe:
hf = 4f(L/D)(V^2/2g)
Where:
hf = head loss due to friction (5 m)
f = Darcy-Weisbach friction factor (unknown)
L = length of the pipe (3 km = 3000 m)
D = diameter of the pipe (unknown)
V = flow velocity (250 L/s = 0.25 m^3/s)
g = acceleration due to gravity (9.81 m/s^2)
Converting the flow velocity from m^3/s to m^2/s:
V = Q/A, where Q is the flow rate (0.25 m^3/s) and A is the cross-sectional area of the pipe (unknown)
A = (π/4)(D^2)
Plugging in the values into the Darcy-Weisbach equation:
5 = 4f(3000/D)((0.25/(π/4)(D^2))^2/2(9.81))
Simplifying:
5 = 4f(3000/D)(0.25^2/(π/4)(D^2)^2/2(9.81))
5 = 4f(3000/D)(0.25^2/(π/4)(D^4)/(2(9.81)))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(
hf = 4f(L/D)(V^2/2g)
Where:
hf = head loss due to friction (5 m)
f = Darcy-Weisbach friction factor (unknown)
L = length of the pipe (3 km = 3000 m)
D = diameter of the pipe (unknown)
V = flow velocity (250 L/s = 0.25 m^3/s)
g = acceleration due to gravity (9.81 m/s^2)
Converting the flow velocity from m^3/s to m^2/s:
V = Q/A, where Q is the flow rate (0.25 m^3/s) and A is the cross-sectional area of the pipe (unknown)
A = (π/4)(D^2)
Plugging in the values into the Darcy-Weisbach equation:
5 = 4f(3000/D)((0.25/(π/4)(D^2))^2/2(9.81))
Simplifying:
5 = 4f(3000/D)(0.25^2/(π/4)(D^2)^2/2(9.81))
5 = 4f(3000/D)(0.25^2/(π/4)(D^4)/(2(9.81)))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(π/4)(D^4))
5 = 4f(3000/D)(0.25^2(9.81)/(
The discharge of water through a trapezoidal channel is 1.5 m3/s, the base width of the channel is 7m, the depth is 2m and the side slope is 1H:3V. Bed slope is 1 in 2000, determine the value of the Chezy’s constant.
- a)50
- b)60
- c)55
- d)65
Correct answer is option 'C'. Can you explain this answer?
The discharge of water through a trapezoidal channel is 1.5 m3/s, the base width of the channel is 7m, the depth is 2m and the side slope is 1H:3V. Bed slope is 1 in 2000, determine the value of the Chezy’s constant.
a)
50
b)
60
c)
55
d)
65
|
|
Sanya Agarwal answered |
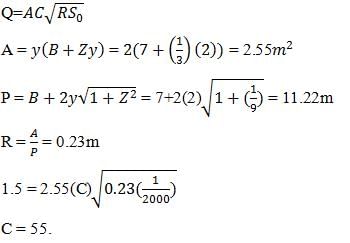
Identify the flow control device shown in image:
- a)Parshall flume
- b)Proportional weir
- c)Sutro weir
- d)Notch
Correct answer is option 'A'. Can you explain this answer?
Identify the flow control device shown in image:
a)
Parshall flume
b)
Proportional weir
c)
Sutro weir
d)
Notch
|
|
Sanya Agarwal answered |
Sutro weir:
- The Sutro weirs are special sharp-crested weirs.
- These weirs are widely used in industry and irrigation because they are easily controlled by float-regulated dosing devices.
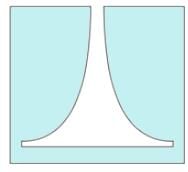
Parshall flume:
- Parshall flumes are calibrated devices for the measurement of water in open channels.
- The flume consists of a converging section with a level floor, a throat section with a downward sloping floor, and a diverging section with an upward sloping floor.
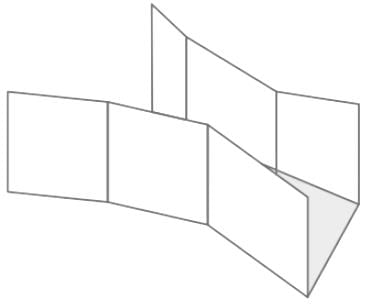
Weir and notch:
- A notch may be defined as an opening provided on one side of a tank or reservoir with an upstream liquid level below the top edge of the opening.
- A weir may be defined as a structure constructed across a river or a canal to store water on the upstream side.
Which of the following is FALSE regarding triangular weir?- a)The flow through the weir depends on the vertex angle
- b)Coefficient of discharge is fairly constant for all the heads
- c)Triangular weir is more effective under small discharges than a rectangular weir
- d)Ventilation of triangular weir is necessary
Correct answer is option 'D'. Can you explain this answer?
Which of the following is FALSE regarding triangular weir?
a)
The flow through the weir depends on the vertex angle
b)
Coefficient of discharge is fairly constant for all the heads
c)
Triangular weir is more effective under small discharges than a rectangular weir
d)
Ventilation of triangular weir is necessary
|
|
Sanya Agarwal answered |
Statement 4: False Ventilation of triangular weir is not necessary.
Weir:
A weir is a concrete or masonary structure, placed in an open channel over which the flow occurs. It is generally in the form of vertical wall, with a sharp edge at the top, running all the way across the open channel. The notch is of small size while the weir is of a bigger size. The notch is generally made of metallic plate while weir is made of concrete or masonary structure.
A weir is a concrete or masonary structure, placed in an open channel over which the flow occurs. It is generally in the form of vertical wall, with a sharp edge at the top, running all the way across the open channel. The notch is of small size while the weir is of a bigger size. The notch is generally made of metallic plate while weir is made of concrete or masonary structure.
Triangular weir:
The expression for the discharge over a triangular weir or notch is
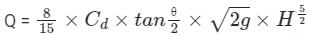
From this expression flow through the weir depend upon the vertex angle (θ) and coefficient of discharge (Cd) is constant for all the heads, the value of Cd is nearly equal to 0.6.
The expression for the discharge over a triangular weir or notch is
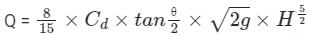
From this expression flow through the weir depend upon the vertex angle (θ) and coefficient of discharge (Cd) is constant for all the heads, the value of Cd is nearly equal to 0.6.
Rectangular weir:
The expression for the discharge over a rectangular weir or notch is
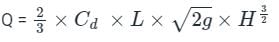
The expression for the discharge over a rectangular weir or notch is
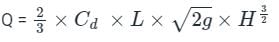
Advantage of triangular weir over rectangular weir:
A triangular weir is preferred to a rectangular weir due to following reason.
(1) The expression for discharge for a right angled V- notch or weir is very simple.
(2) For measuring low discharge, a triangular weir gives more accurate results than a rectangular weir.
(3) In case of triangular weir, only one reading, (H) is required for the computation of discharge.
(4) Ventilation of triangular weir is not necessary.
A triangular weir is preferred to a rectangular weir due to following reason.
(1) The expression for discharge for a right angled V- notch or weir is very simple.
(2) For measuring low discharge, a triangular weir gives more accurate results than a rectangular weir.
(3) In case of triangular weir, only one reading, (H) is required for the computation of discharge.
(4) Ventilation of triangular weir is not necessary.
The stage in a river is 4.8 m, the water surface- slope is 1 in 10,000 and the discharge in the stream is 600 m3/s. If the stage remains the same and the water surface slope is 1 in 14,400, then the discharge in the stream will be- a)300 m3/s
- b)400 m3/s
- c)600 m3/s
- d)500 m3/s
Correct answer is option 'D'. Can you explain this answer?
The stage in a river is 4.8 m, the water surface- slope is 1 in 10,000 and the discharge in the stream is 600 m3/s. If the stage remains the same and the water surface slope is 1 in 14,400, then the discharge in the stream will be
a)
300 m3/s
b)
400 m3/s
c)
600 m3/s
d)
500 m3/s
|
|
Anuj Verma answered |
∴
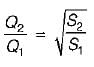
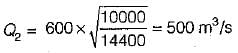
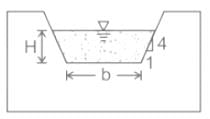
The horizontal to vertical side slope in case of Cipoletti weir is-- a)1 : 1
- b)1 : 3
- c)1 : 2
- d)1 : 4
Correct answer is option 'D'. Can you explain this answer?
The horizontal to vertical side slope in case of Cipoletti weir is-
a)
1 : 1
b)
1 : 3
c)
1 : 2
d)
1 : 4
|
|
Sanya Agarwal answered |
Concept:
Cippoletti weir
Cippoletti weir
- The Cippoletti weir is a trapezoidal weir, having side slopes 1 horizontal to 4 vertical.
- The purpose of the slope, on the sides, is to obtain an increased discharge through the triangular portions of the weir, which otherwise would have been decreased due to end contractions in the case of rectangular weirs.
- A type of contracted weir that is related to the rectangular sharp-crested weir is Cippoletti weir, which has a trapezoidal cross-section with side slopes 1: 4 (H: V).
Water surface profiles that are asymptotic at one end and terminated at the other end would include- a)H2 and S2
- b)H3 and S2
- c)M2 and H2
- d)M2 and H3
Correct answer is option 'C'. Can you explain this answer?
Water surface profiles that are asymptotic at one end and terminated at the other end would include
a)
H2 and S2
b)
H3 and S2
c)
M2 and H2
d)
M2 and H3
|
|
Rohan Singh answered |
The curves which are asymptotic at one end and terminated at the other end are M2 and H2.
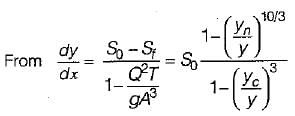
Using Manning’s equation for wide rectangular channel.
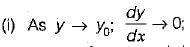i.e. the water surface approaches normal depth line asymptotically
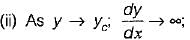i.e. the water surface meets the criticai depth line vertically in region 2 and 3.
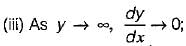i.e. the water surface meets a very large depth as horizontal asymptote in region 1.
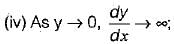it means that the surface profile meets the channel bed vertically in region 3.
Thus,
(i) M1, M2, S2 and S3 meet y0 line asymptotically
(ii) M1 and S1 curve tend to horizontal as y → ∞
(iii) M2, M3 and S2 meet yc line normally
(iv) M3 and S3 meet channel bed. normally.
The slope of:
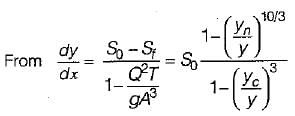
Using Manning’s equation for wide rectangular channel.
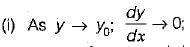i.e. the water surface approaches normal depth line asymptotically 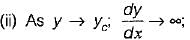i.e. the water surface meets the criticai depth line vertically in region 2 and 3. 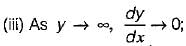i.e. the water surface meets a very large depth as horizontal asymptote in region 1. 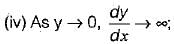it means that the surface profile meets the channel bed vertically in region 3.Thus,
(i) M1, M2, S2 and S3 meet y0 line asymptotically
(ii) M1 and S1 curve tend to horizontal as y → ∞
(iii) M2, M3 and S2 meet yc line normally
(iv) M3 and S3 meet channel bed. normally.
The slope of:
- C1 and C3 curves comes out to be equal to critical slope of the bed, if Chezy’s equation is used. Otherwise they are slightly curved.
If F1 and F2 are the Froude numbers of flow before and after the hydraulic jump occurring in a rectangular channel, then- a)
- b)
- c)
- d)
Correct answer is option 'B'. Can you explain this answer?
If F1 and F2 are the Froude numbers of flow before and after the hydraulic jump occurring in a rectangular channel, then
a)
b)
c)
d)
|
|
Raghavendra Dasgupta answered |
Equating the equation (i) with inverse of equation (ii) we get,
In a subdritica! flow, as the specific energy in a channel is decreased, the depth of flow- a)Also decrease
- b)Increases
- c)Does not vary
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
In a subdritica! flow, as the specific energy in a channel is decreased, the depth of flow
a)
Also decrease
b)
Increases
c)
Does not vary
d)
None of these
|
|
Arjun Menon answered |
Explanation:
To understand why the depth of flow decreases as the specific energy in a channel is decreased in a subcritical flow, we need to consider the principles of open channel hydraulics.
Subcritical Flow:
- In subcritical flow, the Froude number (Fr) is less than 1, indicating that the flow velocity is less than the wave velocity.
- Subcritical flow occurs when the specific energy in the channel is decreased.
Relationship between Specific Energy and Depth of Flow:
- Specific energy (E) in an open channel is the sum of the elevation head (z), the pressure head (p/γ), and the velocity head (V^2/2g).
- As the specific energy decreases, it means that either the velocity of flow or the depth of flow (or both) must decrease.
Depth of Flow Decreases:
- When the specific energy in a channel decreases, the velocity of flow decreases as well. This reduction in velocity leads to a decrease in the depth of flow.
- The decrease in velocity reduces the kinetic energy of the flow, causing a corresponding decrease in the depth of flow to maintain the conservation of energy.
Therefore, in a subcritical flow where the specific energy in a channel is decreased, the depth of flow also decreases as a result of the decrease in velocity. This relationship is essential in understanding the behavior of open channel flows and designing hydraulic structures to manage water resources effectively.
To understand why the depth of flow decreases as the specific energy in a channel is decreased in a subcritical flow, we need to consider the principles of open channel hydraulics.
Subcritical Flow:
- In subcritical flow, the Froude number (Fr) is less than 1, indicating that the flow velocity is less than the wave velocity.
- Subcritical flow occurs when the specific energy in the channel is decreased.
Relationship between Specific Energy and Depth of Flow:
- Specific energy (E) in an open channel is the sum of the elevation head (z), the pressure head (p/γ), and the velocity head (V^2/2g).
- As the specific energy decreases, it means that either the velocity of flow or the depth of flow (or both) must decrease.
Depth of Flow Decreases:
- When the specific energy in a channel decreases, the velocity of flow decreases as well. This reduction in velocity leads to a decrease in the depth of flow.
- The decrease in velocity reduces the kinetic energy of the flow, causing a corresponding decrease in the depth of flow to maintain the conservation of energy.
Therefore, in a subcritical flow where the specific energy in a channel is decreased, the depth of flow also decreases as a result of the decrease in velocity. This relationship is essential in understanding the behavior of open channel flows and designing hydraulic structures to manage water resources effectively.
The depth of flow for maximum velocity in a circular channel section with diameter equal to 1.5 m is- a)0.75 m
- b)1.065 m
- c)1.215 m
- d)1.425 m
Correct answer is option 'C'. Can you explain this answer?
The depth of flow for maximum velocity in a circular channel section with diameter equal to 1.5 m is
a)
0.75 m
b)
1.065 m
c)
1.215 m
d)
1.425 m
|
|
Arnab Choudhury answered |
**Explanation:**
When the flow in a circular channel is at maximum velocity, it is known as critical flow. In critical flow, the water surface is at its lowest point, resulting in the maximum velocity.
To determine the depth of flow for maximum velocity in a circular channel section, we can use the concept of critical depth. Critical depth is the depth of flow at which the specific energy is minimum for a given discharge. It is calculated using the Manning's equation or the Chezy's equation.
In this case, we are given the diameter of the circular channel section as 1.5 m.
To find the depth of flow for maximum velocity, we can use the concept of critical depth. Critical depth (dc) can be calculated using the following formula:
dc = 0.81 * D
Where:
dc = critical depth
D = diameter of the circular channel section
Substituting the given value of D = 1.5 m into the formula, we get:
dc = 0.81 * 1.5
= 1.215 m
Therefore, the depth of flow for maximum velocity in a circular channel section with a diameter of 1.5 m is 1.215 m.
Hence, the correct answer is option C) 1.215 m.
When the flow in a circular channel is at maximum velocity, it is known as critical flow. In critical flow, the water surface is at its lowest point, resulting in the maximum velocity.
To determine the depth of flow for maximum velocity in a circular channel section, we can use the concept of critical depth. Critical depth is the depth of flow at which the specific energy is minimum for a given discharge. It is calculated using the Manning's equation or the Chezy's equation.
In this case, we are given the diameter of the circular channel section as 1.5 m.
To find the depth of flow for maximum velocity, we can use the concept of critical depth. Critical depth (dc) can be calculated using the following formula:
dc = 0.81 * D
Where:
dc = critical depth
D = diameter of the circular channel section
Substituting the given value of D = 1.5 m into the formula, we get:
dc = 0.81 * 1.5
= 1.215 m
Therefore, the depth of flow for maximum velocity in a circular channel section with a diameter of 1.5 m is 1.215 m.
Hence, the correct answer is option C) 1.215 m.
The mild slope profile M2 ocdufs for depth- a)Above normal but below critical
- b)Above critical but below normal
- c)Below normal and below critical
- d)Above normal and above critical
Correct answer is option 'B'. Can you explain this answer?
The mild slope profile M2 ocdufs for depth
a)
Above normal but below critical
b)
Above critical but below normal
c)
Below normal and below critical
d)
Above normal and above critical
|
|
Gauri Sarkar answered |
Understanding Mild Slope Profile M2
In the context of open channel hydraulics, the mild slope profile M2 occurs under specific conditions related to the water surface elevation in relation to normal and critical depths.
Definitions:
- Normal Depth (y_n): The depth at which flow is uniform and steady for a given slope and discharge.
- Critical Depth (y_c): The depth at which the gravitational force and inertial force are balanced, indicating a transition between subcritical and supercritical flow.
Characteristics of Mild Slope Profile M2:
- Flow Conditions: In a mild slope channel, the flow is typically subcritical, which means that the flow depth is greater than the critical depth (y > y_c) but can still be less than normal depth (y < y_n).="" -="" />energy="" considerations:="" the="" mild="" slope="" ensures="" that="" the="" total="" energy="" of="" the="" flow="" is="" maintained,="" allowing="" for="" a="" gradual="" transition="" from="" one="" flow="" regime="" to="" another="" without="" sudden="" changes.="">Why Option B is Correct:
- Above Critical but Below Normal: This scenario indicates that the flow is stable and not experiencing any rapid changes. Here, the water surface is above the critical depth but remains below the normal depth, which is characteristic of a mild slope profile.
- Implications on Design: Understanding this profile helps engineers design channels that can effectively manage flow rates without risking instability or erosion.
In summary, the mild slope profile M2 signifies a flow condition that is above critical depth but below normal depth, which ensures a stable flow regime conducive to efficient hydraulic design and management.
In the context of open channel hydraulics, the mild slope profile M2 occurs under specific conditions related to the water surface elevation in relation to normal and critical depths.
Definitions:
- Normal Depth (y_n): The depth at which flow is uniform and steady for a given slope and discharge.
- Critical Depth (y_c): The depth at which the gravitational force and inertial force are balanced, indicating a transition between subcritical and supercritical flow.
Characteristics of Mild Slope Profile M2:
- Flow Conditions: In a mild slope channel, the flow is typically subcritical, which means that the flow depth is greater than the critical depth (y > y_c) but can still be less than normal depth (y < y_n).="" -="" />energy="" considerations:="" the="" mild="" slope="" ensures="" that="" the="" total="" energy="" of="" the="" flow="" is="" maintained,="" allowing="" for="" a="" gradual="" transition="" from="" one="" flow="" regime="" to="" another="" without="" sudden="" changes.="">Why Option B is Correct:
- Above Critical but Below Normal: This scenario indicates that the flow is stable and not experiencing any rapid changes. Here, the water surface is above the critical depth but remains below the normal depth, which is characteristic of a mild slope profile.
- Implications on Design: Understanding this profile helps engineers design channels that can effectively manage flow rates without risking instability or erosion.
In summary, the mild slope profile M2 signifies a flow condition that is above critical depth but below normal depth, which ensures a stable flow regime conducive to efficient hydraulic design and management.
If velocity is zero over 1/3rd of a cross-section and is uniform over remaining 2/3rd of the cross- section, then the correction factor for kinetic energy is- a)4/3
- b)3/2
- c)9/4
- d)27/8
Correct answer is option 'C'. Can you explain this answer?
If velocity is zero over 1/3rd of a cross-section and is uniform over remaining 2/3rd of the cross- section, then the correction factor for kinetic energy is
a)
4/3
b)
3/2
c)
9/4
d)
27/8
|
|
Srestha Datta answered |
Solution:
Given,
- Velocity is zero over 1/3rd of a cross-section and uniform over the remaining 2/3rd of the cross-section.
We need to find the correction factor for kinetic energy.
To find the correction factor, we can use the following formula:
Correction factor = (1 + α^2)
Where,
α = (Area of zero velocity / Total area)^(1/2)
Let's calculate the value of α.
Area of zero velocity = (1/3) x Total area
Area of uniform velocity = (2/3) x Total area
Therefore, α = [(1/3) x Total area / Total area]^(1/2) = (1/3)^(1/2)
Now, let's substitute the value of α in the formula of the correction factor.
Correction factor = (1 + (1/3))
= (4/3)
Hence, the correct answer is option C (9/4).
Given,
- Velocity is zero over 1/3rd of a cross-section and uniform over the remaining 2/3rd of the cross-section.
We need to find the correction factor for kinetic energy.
To find the correction factor, we can use the following formula:
Correction factor = (1 + α^2)
Where,
α = (Area of zero velocity / Total area)^(1/2)
Let's calculate the value of α.
Area of zero velocity = (1/3) x Total area
Area of uniform velocity = (2/3) x Total area
Therefore, α = [(1/3) x Total area / Total area]^(1/2) = (1/3)^(1/2)
Now, let's substitute the value of α in the formula of the correction factor.
Correction factor = (1 + (1/3))
= (4/3)
Hence, the correct answer is option C (9/4).
The critical depth of flow in a most economical triangular channel section for a discharge of 1 m3/sec is given by- a)
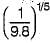metre - b)
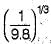metre - c)
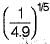metre - d)
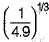metre
Correct answer is option 'C'. Can you explain this answer?
The critical depth of flow in a most economical triangular channel section for a discharge of 1 m3/sec is given by
a)
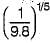metreb)
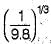metrec)
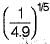metred)
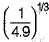metre|
|
S P CHAKRABORTY answered |
Critical depth= (2Q^2/(gm^2))^(1/5) for triangular channel
m= side slope= tan 45 degree= 1 for most economical channel
Q =1 m^3/s
yc= (2*1^2/(9.8*1^2))^(1/5)= (1/4.9)^(1/5)
m= side slope= tan 45 degree= 1 for most economical channel
Q =1 m^3/s
yc= (2*1^2/(9.8*1^2))^(1/5)= (1/4.9)^(1/5)
Chapter doubts & questions for Open Channel Flow - 6 Months Preparation for GATE Civil Engg 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Open Channel Flow - 6 Months Preparation for GATE Civil Engg in English & Hindi are available as part of Civil Engineering (CE) exam.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
6 Months Preparation for GATE Civil Engg
488 videos|1261 docs|878 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily