All Exams >
Civil Engineering (CE) >
6 Months Preparation for GATE Civil Engg >
All Questions
All questions of Work & Energy for Civil Engineering (CE) Exam
For what angle between Force and Displacement will the work done be positive?- a)

- b)
- c)

- d)

Correct answer is option 'C'. Can you explain this answer?
For what angle between Force and Displacement will the work done be positive?
a)
b)
c)
d)
|
|
Om Desai answered |
- If a force acting on a body has a component in the opposite direction of displacement, the work done is negative.
- So when a body slides against a rough horizontal surface, its displacement is opposite to that of the force of friction. The work done by the friction is negative.
Time rate at which work is done by a force is- a)Power
- b)Torque
- c)Centrifugal Force
- d)Acceleration
Correct answer is option 'A'. Can you explain this answer?
Time rate at which work is done by a force is
a)
Power
b)
Torque
c)
Centrifugal Force
d)
Acceleration
|
|
Gaurav Kumar answered |
We know that Work done, W = F.s
where F is force and s is displacement due to that force.
Thus rate of work done is:
where F is force and s is displacement due to that force.
Thus rate of work done is:
dW/dt = d(F.s)/dt
So as F is constant we get,
dW/dt = F.d(s)/dt = F.v = P (Power)
dW/dt = F.d(s)/dt = F.v = P (Power)
By how much does kinetic energy increase if the momentum is increased by 20%?- a)55 %
- b)20 %
- c)44 %
- d)60 %
Correct answer is option 'C'. Can you explain this answer?
By how much does kinetic energy increase if the momentum is increased by 20%?
a)
55 %
b)
20 %
c)
44 %
d)
60 %
|
|
Hansa Sharma answered |
The kinetic energy is given by:
KE= p2/2m
So, ΔKE = 2pΔp / 2m = pΔp / m
ΔKE / KE = (pΔp/m) * (2m/p2) = 2Δp / p
Since the momentum p increases by 20%, so the final momentum becomes 1.2p.
Hence, KEfinal = (1.2p)2 / 2m = 1.44p2 / 2m = 1.44KE
So, % change in KE = 44%
ΔKE / KE = (pΔp/m) * (2m/p2) = 2Δp / p
Since the momentum p increases by 20%, so the final momentum becomes 1.2p.
Hence, KEfinal = (1.2p)2 / 2m = 1.44p2 / 2m = 1.44KE
So, % change in KE = 44%
Output of a truck is 4500 J and its efficiency is 50%, the input energy provided to the truck is- a)5000 J
- b)900 J
- c)9000 J
- d)500 J
Correct answer is option 'C'. Can you explain this answer?
Output of a truck is 4500 J and its efficiency is 50%, the input energy provided to the truck is
a)
5000 J
b)
900 J
c)
9000 J
d)
500 J
|
|
Naina Sharma answered |
► η = work output / heat input
► η = 50% = 50/100 = 1/2
► 1/2 = 4500 / Heat input
► Heat input = 9000 J
► η = 50% = 50/100 = 1/2
► 1/2 = 4500 / Heat input
► Heat input = 9000 J
There are two bodies X and Y with equal kinetic energy but different masses m and 4m respectively. The ratio of their linear momentum is-- a)1:2
- b)4:1
- c)1:√2
- d)1:4
Correct answer is option 'A'. Can you explain this answer?
There are two bodies X and Y with equal kinetic energy but different masses m and 4m respectively. The ratio of their linear momentum is-
a)
1:2
b)
4:1
c)
1:√2
d)
1:4
|
|
Suresh Iyer answered |
X and Y have equal kinetic energy but their masses are m and 4m respectively.
► 1/2 m1v12 = 1/2 m2v22
► mv12 = 4m * v22
► v1 : v2 = 2 : 1
Hence the ratio of their linear momentum is:
m1v1 : m2v2 = m * 2v : 4m * v = 1 : 2
► 1/2 m1v12 = 1/2 m2v22
► mv12 = 4m * v22
► v1 : v2 = 2 : 1
Hence the ratio of their linear momentum is:
m1v1 : m2v2 = m * 2v : 4m * v = 1 : 2
A machine gun fires 60 bullets per minute, with a velocity of 700 m/s. If each bullet has a mass of 50g, find the power developed by the gun.
- a)1225 W
- b)12250 W
- c)122.5 W
- d)122 W
Correct answer is option 'B'. Can you explain this answer?
A machine gun fires 60 bullets per minute, with a velocity of 700 m/s. If each bullet has a mass of 50g, find the power developed by the gun.
a)
1225 W
b)
12250 W
c)
122.5 W
d)
122 W
|
|
Tejas Verma answered |
Each bullet will have KE = 1/2 * 0.05 * 700 * 700 = 12250 J
So for 60 bullets the energy given by machine in 60 second = 60 x 12250 J
Hence power developed = Energy / time =60 x12250/60 =12250W
Or power = 12.250 kW.
So for 60 bullets the energy given by machine in 60 second = 60 x 12250 J
Hence power developed = Energy / time =60 x12250/60 =12250W
Or power = 12.250 kW.
Which of the following is not a unit of energy?- a)newton meter
- b)electron volt
- c)joule/meter
- d)kilowatt hour
Correct answer is option 'C'. Can you explain this answer?
Which of the following is not a unit of energy?
a)
newton meter
b)
electron volt
c)
joule/meter
d)
kilowatt hour

|
Gargey Dudhe answered |
C is correct option because energy The joule ( symbol: J) is a derived unit of energy in the International System of Units. It is equal to the energy transferred to (or work done on) an object when a force of one newton acts on that object in the direction of its motion through a distance of one metre (1 newton metreor N⋅m). pls upvote and follow me.
Which of the following statements is false:- a)kinetic energy is positiv
- b)potential energy is positive
- c)kinetic energy is negative
- d)potential energy is negative
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements is false:
a)
kinetic energy is positiv
b)
potential energy is positive
c)
kinetic energy is negative
d)
potential energy is negative

|
Aiims answered |
K.E never negative as velocity negative then its square becomes it positive.
If a force acts perpendicular to the direction of motion of a body, what is the amount of work done?- a)Infinity
- b)Constant
- c)Zero
- d)sinθ
Correct answer is option 'C'. Can you explain this answer?
If a force acts perpendicular to the direction of motion of a body, what is the amount of work done?
a)
Infinity
b)
Constant
c)
Zero
d)
sinθ
|
|
Anjali Sharma answered |
If a force acts perpendicular to the direction of a body, the amount of work done is zero because there is no displacement in the direction of a force.
Virtual Work done is saved in the form of potential energy. It is best given by ___________- a)δU = Fδrcosθ
- b)δU = Fδrsinθ
- c)δU = Fδrcotθ
- d)δU = Fδrδθ
Correct answer is option 'A'. Can you explain this answer?
Virtual Work done is saved in the form of potential energy. It is best given by ___________
a)
δU = Fδrcosθ
b)
δU = Fδrsinθ
c)
δU = Fδrcotθ
d)
δU = Fδrδθ
|
|
Anmol Saini answered |
The work is defined as the dot product of the δ force and the δ distance. This means that the work done does depends upon the angle of the force. That is the angle which is being made by the force vector to the surface of action of the force.
Which of the following needs to zero for the perfect equilibrium for the calculation of the work?- a)∑F=0, ∑M=0 and ∑θ = 0
- b)∑F=0, ∑M≠0 and ∑θ = 0
- c)∑F≠0, ∑M=0 and ∑θ = 0
- d)∑F=0, ∑M=0 and ∑θ≠0
Correct answer is option 'D'. Can you explain this answer?
Which of the following needs to zero for the perfect equilibrium for the calculation of the work?
a)
∑F=0, ∑M=0 and ∑θ = 0
b)
∑F=0, ∑M≠0 and ∑θ = 0
c)
∑F≠0, ∑M=0 and ∑θ = 0
d)
∑F=0, ∑M=0 and ∑θ≠0
|
|
Bhargavi Chauhan answered |
The summation of the forces needs to be zero. So does the summation of the moments need to zero. But talking about the angles, they not needed to zero. But the forces which are acting at particular angles, must needed to be equal to zero. The basic need of the forces to make the body in equilibrium.
∑Fx=0, ∑Fy=0 and ∑Fz=0 are vector equations for the three dimensions. They are satisfied when the body is achieved it state of equilibrium and the net work done is zero.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
∑Fx=0, ∑Fy=0 and ∑Fz=0 are vector equations for the three dimensions. They are satisfied when the body is achieved it state of equilibrium and the net work done is zero.
a)
True
b)
False
|
|
Divya Banerjee answered |
The answer is false as the equations asked are scalars. As we make the net sum of the forces along the axis equal to zero. Of course this equation comes from the solving the vector forms, but still the result is a scalar, hence the equations are scalar.
Work done is best given by _____________- a)dU = F.dr
- b)dU = Fdrsinθ
- c)dU = F.drcotθ
- d)dU = Fxdrdθ
Correct answer is option 'A'. Can you explain this answer?
Work done is best given by _____________
a)
dU = F.dr
b)
dU = Fdrsinθ
c)
dU = F.drcotθ
d)
dU = Fxdrdθ
|
|
Keerthana Joshi answered |
The work is defined as the dot product of the force and the distance. This means that the work done does depends upon the angle of the force. That is the angle which is being made by the force vector to the surface of action of the force.
The supports in the 3D are having more than three reaction forces. Because they are having three axis on which the components of the work needs to be zero.- a)The first part of the statement is false and other part is true
- b)The first part of the statement is false and other part is false too
- c)The first part of the statement is true and other part is false
- d)The first part of the statement is true and other part is true too
Correct answer is option 'D'. Can you explain this answer?
The supports in the 3D are having more than three reaction forces. Because they are having three axis on which the components of the work needs to be zero.
a)
The first part of the statement is false and other part is true
b)
The first part of the statement is false and other part is false too
c)
The first part of the statement is true and other part is false
d)
The first part of the statement is true and other part is true too
|
|
Jhanvi Datta answered |
As 3D is defined as the three axis system, we have to consider the equilibrium in all the three axis. This will make the equilibrium go on all the axis of the 3D space. And hence will cancel all the forces.
What is the sum of squares of the cosine angles made by the conservative force vector with the coordinate axis?- a)1
- b)½
- c)2
- d)3
Correct answer is option 'A'. Can you explain this answer?
What is the sum of squares of the cosine angles made by the conservative force vector with the coordinate axis?
a)
1
b)
½
c)
2
d)
3
|
|
Mahi Kaur answered |
The sum of the squares of the cosines of the vector will give you the squares of the components in the numerator, and the vector’s magnitude’s square in the denominator. But the numerator sum is equal to the vector’s magnitude’s square. Thus, the answer = 1.
For the conditions of the equilibrium of the body, i.e. the rigid body only the external forces defines the equilibrium. And the support reactions only cancels out the rotation part of the body and thus the potential energy of the body is stored in it.- a)The first part of the statement is false and other part is true
- b)The first part of the statement is false and other part is false too
- c)The first part of the statement is true and other part is false
- d)The first part of the statement is true and other part is true too
Correct answer is option 'C'. Can you explain this answer?
For the conditions of the equilibrium of the body, i.e. the rigid body only the external forces defines the equilibrium. And the support reactions only cancels out the rotation part of the body and thus the potential energy of the body is stored in it.
a)
The first part of the statement is false and other part is true
b)
The first part of the statement is false and other part is false too
c)
The first part of the statement is true and other part is false
d)
The first part of the statement is true and other part is true too
|
|
Prateek Mukherjee answered |
The application of the support reaction forces does affect the conditions of the equilibrium of the body. Not only the external but the support reaction forces that are developed by the sake of external forces does develop a tending effect on the equilibrium of the body. Thus the support reaction forces also cancels the external forces.
Which statement is right for conservative force vector F = Ai + Bj + Ck?- a)In rectangular components representation of any vector we have vector F = Ai + Bj + Ck
- b)In rectangular components representation of any vector we have vector F = Ax + By + Cz
- c)In rectangular components representation of any vector we have vector F = Fx + Fy + Fz
- d)In rectangular components representation of any vector we have vector F = Fi + Fj + Fk
Correct answer is option 'C'. Can you explain this answer?
Which statement is right for conservative force vector F = Ai + Bj + Ck?
a)
In rectangular components representation of any vector we have vector F = Ai + Bj + Ck
b)
In rectangular components representation of any vector we have vector F = Ax + By + Cz
c)
In rectangular components representation of any vector we have vector F = Fx + Fy + Fz
d)
In rectangular components representation of any vector we have vector F = Fi + Fj + Fk
|
|
Divya Banerjee answered |
Rectangular Components Representation of Vector F:
The correct statement for the conservative force vector F = Ai Bj Ck is:
In rectangular components representation of any vector we have vector F = Fx Fy Fz
Explanation:
- When representing a vector in rectangular components, we typically use the notation F = Fx Fy Fz, where Fx, Fy, and Fz are the components of the vector in the x, y, and z directions respectively.
- In the given force vector F = Ai Bj Ck, A, B, and C are scalar constants representing the magnitudes of the vector components along the x, y, and z axes respectively.
- Therefore, in rectangular component form, the vector F would be represented as F = Ax By Cz, where Ax, By, and Cz are the components of the vector along the x, y, and z axes respectively.
- Hence, the correct representation for the conservative force vector F = Ai Bj Ck in rectangular components would be F = Fx Fy Fz, where Fx = A, Fy = B, and Fz = C.
Therefore, option 'C' is the correct statement for the given conservative force vector F = Ai Bj Ck in rectangular components representation.
The correct statement for the conservative force vector F = Ai Bj Ck is:
In rectangular components representation of any vector we have vector F = Fx Fy Fz
Explanation:
- When representing a vector in rectangular components, we typically use the notation F = Fx Fy Fz, where Fx, Fy, and Fz are the components of the vector in the x, y, and z directions respectively.
- In the given force vector F = Ai Bj Ck, A, B, and C are scalar constants representing the magnitudes of the vector components along the x, y, and z axes respectively.
- Therefore, in rectangular component form, the vector F would be represented as F = Ax By Cz, where Ax, By, and Cz are the components of the vector along the x, y, and z axes respectively.
- Hence, the correct representation for the conservative force vector F = Ai Bj Ck in rectangular components would be F = Fx Fy Fz, where Fx = A, Fy = B, and Fz = C.
Therefore, option 'C' is the correct statement for the given conservative force vector F = Ai Bj Ck in rectangular components representation.
Principle of virtual work done is having condition___________- a)δU = 0
- b)δU = δF
- c)δU = δM
- d)δU = δD
Correct answer is option 'A'. Can you explain this answer?
Principle of virtual work done is having condition___________
a)
δU = 0
b)
δU = δF
c)
δU = δM
d)
δU = δD
|
|
Aditya Chavan answered |
The virtual work done is working on the equation: δU = 0. This means that the body must be in the equilibrium and the net work done must be zero. Thus the unknown forces are being determined by the same technique.
What is the relation between work done by external loads and work done by internal loads.- a)They are unequal
- b)They are equal
- c)Can’t say
- d)Depends upon load
Correct answer is option 'B'. Can you explain this answer?
What is the relation between work done by external loads and work done by internal loads.
a)
They are unequal
b)
They are equal
c)
Can’t say
d)
Depends upon load
|
|
Neha Joshi answered |
External and internal displacements must be related by compatibility of displacement.
A bucket of water weighing 10 kg is pulled up from a 20 m deep well by a rope weighing 1 kg/m length, then the work done is _______.- a)200 kg-m
- b)400 kg-m
- c)500 kg-m
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
A bucket of water weighing 10 kg is pulled up from a 20 m deep well by a rope weighing 1 kg/m length, then the work done is _______.
a)
200 kg-m
b)
400 kg-m
c)
500 kg-m
d)
None of these
|
|
Neha Joshi answered |
Work done = Force applied × Displacement
Calculation
Here 10 kg block will be displaced by 20m hence work done displace bucket by 20 meters = 10 × 20 = 200 kg-m and the total weight of rope mass per unit length × length = 1 × 20 = 20kg and it will be concentrated at the center of the rope hence net displacement of rope = 10m, therefore, work done to displace rope 20 × 10 = 200 kg-m
Hence net work done = 200 + 200 = 400 kg-m
Calculation
Here 10 kg block will be displaced by 20m hence work done displace bucket by 20 meters = 10 × 20 = 200 kg-m and the total weight of rope mass per unit length × length = 1 × 20 = 20kg and it will be concentrated at the center of the rope hence net displacement of rope = 10m, therefore, work done to displace rope 20 × 10 = 200 kg-m
Hence net work done = 200 + 200 = 400 kg-m
Find the potential energy stored in a ball of mass 5 kg placed at a height of 3 m above the ground.- a)121.20 J
- b)227.31 J
- c)147.15 J
- d)182.21 J
Correct answer is option 'C'. Can you explain this answer?
Find the potential energy stored in a ball of mass 5 kg placed at a height of 3 m above the ground.
a)
121.20 J
b)
227.31 J
c)
147.15 J
d)
182.21 J
|
|
Mira Joshi answered |
m = 5 kg,
h = 3 m,
g = 9.81 m/s-2
h = 3 m,
g = 9.81 m/s-2
We know that,
Potential energy = mgh
Potential energy = mgh
= 5 * 9.81 * 3 = 147.15 J
Hence, the correct answer is Option C.
At time t = 0 s particle starts moving along the x-axis. If its kinetic energy increases uniformly with time ‘t’, the net force acting on it must be proportional to- a) √t
- b) 1/√t
- c)constant
- d)t
Correct answer is option 'B'. Can you explain this answer?
At time t = 0 s particle starts moving along the x-axis. If its kinetic energy increases uniformly with time ‘t’, the net force acting on it must be proportional to
a)
√t
b)
1/√t
c)
constant
d)
t
|
|
Sinjini Choudhury answered |
, then its acceleration is also constant. We can use the following kinematic equation to relate the acceleration, time, initial velocity, and displacement:
x = x0 + v0*t + (1/2)*a*t^2
where x is the displacement, x0 is the initial position (assumed to be zero), v0 is the initial velocity, t is the time, and a is the acceleration.
Since the kinetic energy increases uniformly with time, we can assume that the acceleration is also constant. Let's call this acceleration a. Then, the velocity at time t is:
v(t) = v0 + a*t
The kinetic energy is given by:
KE = (1/2)*m*v^2
where m is the mass of the particle.
Since the kinetic energy increases uniformly with time, we can write:
dKE/dt = constant
Taking the derivative with respect to time, we get:
dKE/dt = m*v*(dv/dt)
Substituting v(t) and dv/dt = a, we get:
dKE/dt = m*(v0 + a*t)*a
Since dKE/dt is constant, we can write:
dKE/dt = m*a*(v0 + a*t) = constant
Solving for a, we get:
a = constant/dt
where dt is a small time interval.
Now, we can use the kinematic equation to find the displacement x at time t:
x = (1/2)*a*t^2 + v0*t
Substituting a = constant/dt and v0 = 0, we get:
x = (1/2)*(constant/dt)*t^2
Simplifying, we get:
x = (constant/2)*t
Therefore, the particle moves with a constant velocity given by:
v = dx/dt = constant/2
This means that the velocity increases linearly with time, and the displacement increases quadratically with time.
x = x0 + v0*t + (1/2)*a*t^2
where x is the displacement, x0 is the initial position (assumed to be zero), v0 is the initial velocity, t is the time, and a is the acceleration.
Since the kinetic energy increases uniformly with time, we can assume that the acceleration is also constant. Let's call this acceleration a. Then, the velocity at time t is:
v(t) = v0 + a*t
The kinetic energy is given by:
KE = (1/2)*m*v^2
where m is the mass of the particle.
Since the kinetic energy increases uniformly with time, we can write:
dKE/dt = constant
Taking the derivative with respect to time, we get:
dKE/dt = m*v*(dv/dt)
Substituting v(t) and dv/dt = a, we get:
dKE/dt = m*(v0 + a*t)*a
Since dKE/dt is constant, we can write:
dKE/dt = m*a*(v0 + a*t) = constant
Solving for a, we get:
a = constant/dt
where dt is a small time interval.
Now, we can use the kinematic equation to find the displacement x at time t:
x = (1/2)*a*t^2 + v0*t
Substituting a = constant/dt and v0 = 0, we get:
x = (1/2)*(constant/dt)*t^2
Simplifying, we get:
x = (constant/2)*t
Therefore, the particle moves with a constant velocity given by:
v = dx/dt = constant/2
This means that the velocity increases linearly with time, and the displacement increases quadratically with time.
What is the shape of load-deformation curve for a non-linear elastic member?- a)Straight line with constant slope
- b)Straight line with varying slope
- c)Curve
- d)Circle
Correct answer is option 'C'. Can you explain this answer?
What is the shape of load-deformation curve for a non-linear elastic member?
a)
Straight line with constant slope
b)
Straight line with varying slope
c)
Curve
d)
Circle

|
Baishali Chopra answered |
Load-Deformation Curve for Non-Linear Elastic Member
The shape of the load-deformation curve is an important characteristic of a material. In the case of a linear elastic member, the load-deformation curve is a straight line with a constant slope. However, for a non-linear elastic member, the load-deformation curve is curved.
Explanation:
The load-deformation curve for a non-linear elastic member is curved because the deformation of the member is not proportional to the applied load. The relationship between the load and deformation is non-linear, which means that the slope of the curve changes as the load increases.
The load-deformation curve for a non-linear elastic member can be divided into three regions:
1. Elastic Region:
In this region, the material behaves like a linear elastic member, and the load-deformation curve is a straight line with a constant slope. The slope of the curve is equal to the elastic modulus of the material.
2. Yielding Region:
In this region, the material undergoes plastic deformation, and the load-deformation curve starts to deviate from the linear path. The slope of the curve decreases as the load increases.
3. Strain Hardening Region:
In this region, the material undergoes strain hardening, and the slope of the curve increases as the load increases. The material becomes stiffer and stronger in this region.
Conclusion:
In conclusion, the load-deformation curve for a non-linear elastic member is curved because the relationship between the load and deformation is non-linear. The curve can be divided into three regions, namely the elastic region, yielding region, and strain hardening region. Understanding the shape of the load-deformation curve is important in designing structures and selecting materials for different applications.
The shape of the load-deformation curve is an important characteristic of a material. In the case of a linear elastic member, the load-deformation curve is a straight line with a constant slope. However, for a non-linear elastic member, the load-deformation curve is curved.
Explanation:
The load-deformation curve for a non-linear elastic member is curved because the deformation of the member is not proportional to the applied load. The relationship between the load and deformation is non-linear, which means that the slope of the curve changes as the load increases.
The load-deformation curve for a non-linear elastic member can be divided into three regions:
1. Elastic Region:
In this region, the material behaves like a linear elastic member, and the load-deformation curve is a straight line with a constant slope. The slope of the curve is equal to the elastic modulus of the material.
2. Yielding Region:
In this region, the material undergoes plastic deformation, and the load-deformation curve starts to deviate from the linear path. The slope of the curve decreases as the load increases.
3. Strain Hardening Region:
In this region, the material undergoes strain hardening, and the slope of the curve increases as the load increases. The material becomes stiffer and stronger in this region.
Conclusion:
In conclusion, the load-deformation curve for a non-linear elastic member is curved because the relationship between the load and deformation is non-linear. The curve can be divided into three regions, namely the elastic region, yielding region, and strain hardening region. Understanding the shape of the load-deformation curve is important in designing structures and selecting materials for different applications.
To apply virtual work method it is :-- a)Compulsory for external and internal forces to be in equilibrium
- b)Not compulsory for external and internal forces to be in equilibrium
- c)Compulsory for external and internal forces to be in equilibrium in higher loads
- d)Compulsory for external and internal forces to be in equilibrium in lesser loads
Correct answer is option 'A'. Can you explain this answer?
To apply virtual work method it is :-
a)
Compulsory for external and internal forces to be in equilibrium
b)
Not compulsory for external and internal forces to be in equilibrium
c)
Compulsory for external and internal forces to be in equilibrium in higher loads
d)
Compulsory for external and internal forces to be in equilibrium in lesser loads

|
Sarthak Menon answered |
**The Application of Virtual Work Method**
The virtual work method is a powerful technique used in structural analysis to determine the displacements and reactions of a structure subjected to external loads. It is based on the principle of virtual work, which states that the work done by the external forces on a structure is equal to the work done by the internal forces within the structure.
**Equilibrium of External and Internal Forces**
In order to apply the virtual work method, it is indeed compulsory for the external and internal forces to be in equilibrium. This means that the sum of the external forces acting on the structure must be equal to zero, and the sum of the internal forces within the structure must also be equal to zero. This condition ensures that the structure is in a state of static equilibrium.
**Importance of Equilibrium**
The requirement for equilibrium is essential in the virtual work method because it allows us to simplify the analysis and solve for the unknown displacements and reactions. If the external and internal forces are not in equilibrium, it would introduce additional unknowns and complications to the analysis, making it difficult to determine the desired quantities accurately.
**Higher Loads**
The statement in option 'C' that equilibrium is compulsory for external and internal forces in higher loads is incorrect. The requirement for equilibrium holds true regardless of the magnitude of the loads. Whether the loads are high or low, the condition of equilibrium is always necessary for applying the virtual work method.
**Conclusion**
In conclusion, when applying the virtual work method in structural analysis, it is compulsory for the external and internal forces to be in equilibrium. This condition ensures that the structure is in a state of static equilibrium and allows for the accurate determination of displacements and reactions. The requirement for equilibrium holds true regardless of the magnitude of the loads being applied.
The virtual work method is a powerful technique used in structural analysis to determine the displacements and reactions of a structure subjected to external loads. It is based on the principle of virtual work, which states that the work done by the external forces on a structure is equal to the work done by the internal forces within the structure.
**Equilibrium of External and Internal Forces**
In order to apply the virtual work method, it is indeed compulsory for the external and internal forces to be in equilibrium. This means that the sum of the external forces acting on the structure must be equal to zero, and the sum of the internal forces within the structure must also be equal to zero. This condition ensures that the structure is in a state of static equilibrium.
**Importance of Equilibrium**
The requirement for equilibrium is essential in the virtual work method because it allows us to simplify the analysis and solve for the unknown displacements and reactions. If the external and internal forces are not in equilibrium, it would introduce additional unknowns and complications to the analysis, making it difficult to determine the desired quantities accurately.
**Higher Loads**
The statement in option 'C' that equilibrium is compulsory for external and internal forces in higher loads is incorrect. The requirement for equilibrium holds true regardless of the magnitude of the loads. Whether the loads are high or low, the condition of equilibrium is always necessary for applying the virtual work method.
**Conclusion**
In conclusion, when applying the virtual work method in structural analysis, it is compulsory for the external and internal forces to be in equilibrium. This condition ensures that the structure is in a state of static equilibrium and allows for the accurate determination of displacements and reactions. The requirement for equilibrium holds true regardless of the magnitude of the loads being applied.
The conservative frictional force always acts ____________ to the surface of the application of the friction.- a)Tangential
- b)Perpendicular
- c)Parallel
- d)Normal
Correct answer is option 'A'. Can you explain this answer?
The conservative frictional force always acts ____________ to the surface of the application of the friction.
a)
Tangential
b)
Perpendicular
c)
Parallel
d)
Normal
|
|
Sagarika Mukherjee answered |
The friction is the phenomena that defines that there is a resistance which is present there between the two surfaces. This friction is applied tangentially to the surfaces in contact. Thus the main thing is that the forces on both of the surfaces act tangential to each other.
For equilibrium the net moment acting on the body by various conservative forces is zero.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
For equilibrium the net moment acting on the body by various conservative forces is zero.
a)
True
b)
False
|
|
Rajat Basu answered |
Explanation:
For equilibrium, the net moment acting on the body by various conservative forces must be zero. This means that the sum of the moments produced by all the conservative forces acting on the body should be equal to zero.
Moments:
- A moment is the turning effect of a force about a point or axis. It is a measure of the tendency of a force to rotate an object around an axis.
- Moments are calculated by multiplying the force by the perpendicular distance from the point or axis of rotation.
- Moments can be either clockwise or counterclockwise, depending on the direction of the force and the direction of rotation.
Conservative Forces:
- Conservative forces are those forces that conserve mechanical energy.
- Examples of conservative forces include gravity, elastic forces, electric forces, and magnetic forces.
- Conservative forces have the property that the work done by the force depends only on the initial and final positions, and not on the path taken between the positions.
- This means that the work done by conservative forces is path-independent.
Equilibrium:
- Equilibrium occurs when an object is at rest or moving with a constant velocity.
- In equilibrium, the sum of the forces acting on the body is zero (ΣF = 0) and the sum of the moments acting on the body is zero (ΣM = 0).
Net Moment and Equilibrium:
- The net moment is the sum of all the moments produced by the individual forces acting on the body.
- If the net moment is zero, it means that the clockwise moments and counterclockwise moments balance each other out, resulting in no overall tendency for the body to rotate.
- When the net moment is zero, the body is in rotational equilibrium.
Conclusion:
- In conclusion, for equilibrium, the net moment acting on the body by various conservative forces must be zero.
- This is because equilibrium requires both the sum of the forces and the sum of the moments to be zero.
- Therefore, option 'A' is the correct answer.
For equilibrium, the net moment acting on the body by various conservative forces must be zero. This means that the sum of the moments produced by all the conservative forces acting on the body should be equal to zero.
Moments:
- A moment is the turning effect of a force about a point or axis. It is a measure of the tendency of a force to rotate an object around an axis.
- Moments are calculated by multiplying the force by the perpendicular distance from the point or axis of rotation.
- Moments can be either clockwise or counterclockwise, depending on the direction of the force and the direction of rotation.
Conservative Forces:
- Conservative forces are those forces that conserve mechanical energy.
- Examples of conservative forces include gravity, elastic forces, electric forces, and magnetic forces.
- Conservative forces have the property that the work done by the force depends only on the initial and final positions, and not on the path taken between the positions.
- This means that the work done by conservative forces is path-independent.
Equilibrium:
- Equilibrium occurs when an object is at rest or moving with a constant velocity.
- In equilibrium, the sum of the forces acting on the body is zero (ΣF = 0) and the sum of the moments acting on the body is zero (ΣM = 0).
Net Moment and Equilibrium:
- The net moment is the sum of all the moments produced by the individual forces acting on the body.
- If the net moment is zero, it means that the clockwise moments and counterclockwise moments balance each other out, resulting in no overall tendency for the body to rotate.
- When the net moment is zero, the body is in rotational equilibrium.
Conclusion:
- In conclusion, for equilibrium, the net moment acting on the body by various conservative forces must be zero.
- This is because equilibrium requires both the sum of the forces and the sum of the moments to be zero.
- Therefore, option 'A' is the correct answer.
What does the Newton’s third law states for the conservative forces?- a)The rate of change of momentum is equal to the force applied
- b)For every reaction there is an opposite reaction
- c)The body is tend to be rotated if the force is applied tangentially
- d)The body is rest until a force is applied
Correct answer is option 'B'. Can you explain this answer?
What does the Newton’s third law states for the conservative forces?
a)
The rate of change of momentum is equal to the force applied
b)
For every reaction there is an opposite reaction
c)
The body is tend to be rotated if the force is applied tangentially
d)
The body is rest until a force is applied
|
|
Ashutosh Sharma answered |
The requirement of the third law is important in the equilibrium of the body. Specially the rigid bodies. The rigid body particles are in the equilibrium and are thus facing the forces and to be in the equilibrium they also react and apply the opposite force and thus the third law of newton.It is same for all the methods.
We use sometimes the measures to know the direction of moment in the calculations of the moments caused by the gravitational forces over the body above the ground level. Which one is right about it(consider the mentioned axis to be positive)?- a)Thumb is z-axis, fingers curled from x-axis to y-axis
- b)Thumb is x-axis, fingers curled from z-axis to y-axis
- c)Thumb is y-axis, fingers curled from x-axis to z-axis
- d)Thumb is z-axis, fingers curled from y-axis to x-axis
Correct answer is option 'A'. Can you explain this answer?
We use sometimes the measures to know the direction of moment in the calculations of the moments caused by the gravitational forces over the body above the ground level. Which one is right about it(consider the mentioned axis to be positive)?
a)
Thumb is z-axis, fingers curled from x-axis to y-axis
b)
Thumb is x-axis, fingers curled from z-axis to y-axis
c)
Thumb is y-axis, fingers curled from x-axis to z-axis
d)
Thumb is z-axis, fingers curled from y-axis to x-axis
|
|
Mansi Rane answered |
Explanation:
To determine the direction of the moment caused by gravitational forces over a body, we can use the right-hand rule. The right-hand rule is a convention used in physics to determine the direction of a vector or moment in a three-dimensional coordinate system.
The right-hand rule states that if you align your thumb with the positive direction of a specified axis, and then curl your fingers towards the other specified axis, the direction in which your fingers point is the positive direction of the cross product of the two specified axes.
In this case, we are considering the direction of the moment caused by gravitational forces over a body above the ground level. The specified axis for the thumb is the z-axis. We need to determine the direction of the cross product between the x-axis and the y-axis.
Using the right-hand rule:
- Align your thumb with the positive direction of the z-axis.
- Curl your fingers from the positive direction of the x-axis towards the positive direction of the y-axis.
Result:
The direction in which your fingers point is the positive direction of the cross product between the x-axis and the y-axis. In this case, the direction is from the x-axis to the y-axis.
Conclusion:
Therefore, the correct answer is option 'A', where the thumb is aligned with the z-axis, and the fingers are curled from the x-axis to the y-axis.
To determine the direction of the moment caused by gravitational forces over a body, we can use the right-hand rule. The right-hand rule is a convention used in physics to determine the direction of a vector or moment in a three-dimensional coordinate system.
The right-hand rule states that if you align your thumb with the positive direction of a specified axis, and then curl your fingers towards the other specified axis, the direction in which your fingers point is the positive direction of the cross product of the two specified axes.
In this case, we are considering the direction of the moment caused by gravitational forces over a body above the ground level. The specified axis for the thumb is the z-axis. We need to determine the direction of the cross product between the x-axis and the y-axis.
Using the right-hand rule:
- Align your thumb with the positive direction of the z-axis.
- Curl your fingers from the positive direction of the x-axis towards the positive direction of the y-axis.
Result:
The direction in which your fingers point is the positive direction of the cross product between the x-axis and the y-axis. In this case, the direction is from the x-axis to the y-axis.
Conclusion:
Therefore, the correct answer is option 'A', where the thumb is aligned with the z-axis, and the fingers are curled from the x-axis to the y-axis.
Potential energy is stored in the body if some work is done on it. Work done is best given by:- a)dU = Fdrcosθ
- b)dU = Fdrsinθ
- c)dU = Fdrcotθ
- d)dU = Fdrdθ
Correct answer is option 'A'. Can you explain this answer?
Potential energy is stored in the body if some work is done on it. Work done is best given by:
a)
dU = Fdrcosθ
b)
dU = Fdrsinθ
c)
dU = Fdrcotθ
d)
dU = Fdrdθ
|
|
Mehul Yadav answered |
The work is defined as the dot product of the force and the distance. This means that the work done does depends upon the angle of the force. That is the angle which is being made by the force vector to the surface of action of the force.
Which of the following is correct for the forces which are considered in the potential energy calculations?- a)The application of the conditions of the equilibrium of the body is valid only if the forces are collinear
- b)The application of the conditions of the equilibrium of the body is valid only if the forces are parallel
- c)The application of the conditions of the equilibrium of the body is valid only if the forces are perpendicular
- d)The application of the conditions of the equilibrium of the body is valid throughout
Correct answer is option 'D'. Can you explain this answer?
Which of the following is correct for the forces which are considered in the potential energy calculations?
a)
The application of the conditions of the equilibrium of the body is valid only if the forces are collinear
b)
The application of the conditions of the equilibrium of the body is valid only if the forces are parallel
c)
The application of the conditions of the equilibrium of the body is valid only if the forces are perpendicular
d)
The application of the conditions of the equilibrium of the body is valid throughout
|
|
Sharmila Chauhan answered |
The application of the conditions of the equilibrium of the body is valid throughout. This means that the conditions are irrespective of the types of forces. The conditions are the basic rules that defines the equilibrium of the body and thus are applicable in any type of forces of the real axis.
What is the shape of load-deformation curve for a linear elastic member?- a)Straight line with constant slope
- b)Straight line with varying slope
- c)Curve
- d)Sine wave
Correct answer is option 'A'. Can you explain this answer?
What is the shape of load-deformation curve for a linear elastic member?
a)
Straight line with constant slope
b)
Straight line with varying slope
c)
Curve
d)
Sine wave
|
|
Sarita Yadav answered |
In these cases, both are directly proportional.
Which of the following is an example of zero work?- a)The work done by the tension in the string, when a body tied with the string move along a circular path
- b)When a person holds some amount of load but, does not move from his position.
- c)The work done by a coolie when he travels on a horizontal platform, with a load on his head.
- d)When a horse pulls a cart on a level road.
Correct answer is option 'B'. Can you explain this answer?
Which of the following is an example of zero work?
a)
The work done by the tension in the string, when a body tied with the string move along a circular path
b)
When a person holds some amount of load but, does not move from his position.
c)
The work done by a coolie when he travels on a horizontal platform, with a load on his head.
d)
When a horse pulls a cart on a level road.
|
|
Megha Desai answered |
Work done, W = Force x Δdisplacement
So, when a person holds some amount of load but does not move from his position, the displacement is 0. Hence, W done = 0.
Work done is best given by___________- a)dU = Fdrcosθ
- b)dU = Fdrsinθ
- c)dU = Fdrcotθ
- d)dU = Fdrdθ
Correct answer is option 'A'. Can you explain this answer?
Work done is best given by___________
a)
dU = Fdrcosθ
b)
dU = Fdrsinθ
c)
dU = Fdrcotθ
d)
dU = Fdrdθ
|
|
Mrinalini Sharma answered |
The work is defined as the dot product of the force and the distance. This means that the work done does depends upon the angle of the force. That is the angle which is being made by the force vector to the surface of action of the force.
____________ is the phenomena that resist the movement of the two surfaces in contact. This phenomena is also having its scope in the work and the conservative nature of the force.- a)Friction
- b)Motion
- c)Circular movement
- d)Rotation
Correct answer is option 'A'. Can you explain this answer?
____________ is the phenomena that resist the movement of the two surfaces in contact. This phenomena is also having its scope in the work and the conservative nature of the force.
a)
Friction
b)
Motion
c)
Circular movement
d)
Rotation
|
|
Ayush Chawla answered |
The friction is the phenomena that defines that there is a resistance which is present there between the two surfaces. The two surfaces are in contact and the friction applies at that surface only, resisting the motion of the surface.
Which statement is correct about the vector F in the showing the gravitational nature of the forces?- a)F= Fcos β + Fcos α + Fcosγ
- b)F= Fsin β + Fcos α + Fcosγ
- c)F= Fcos β + Fsin α + Fcosγ
- d)F= Fcos β + Fcos α + Fsinγ
Correct answer is option 'A'. Can you explain this answer?
Which statement is correct about the vector F in the showing the gravitational nature of the forces?
a)
F= Fcos β + Fcos α + Fcosγ
b)
F= Fsin β + Fcos α + Fcosγ
c)
F= Fcos β + Fsin α + Fcosγ
d)
F= Fcos β + Fcos α + Fsinγ
|
|
Stuti Bajaj answered |
Understanding the Gravitational Forces
In the context of gravitational forces, the vector F often represents the resultant force acting on an object due to gravity. The resolution of forces into components is crucial for analyzing the system's behavior.
Components of the Force Vector
The correct expression for the force vector F can be derived from the components of the force acting in different directions. In this case, the angles α, β, and γ represent the angles at which the forces are applied relative to the coordinate axes.
Explanation of Option A
Option A states:
F = Fcos(β) + Fcos(α) + Fcos(γ)
This expression is correct because:
- Cosine Function: The cosine function is used to resolve the force vector into its components along the respective axes (X, Y, Z). The use of cosines indicates that the components are being taken along the horizontal directions.
- Directionality: Each term, Fcos(β), Fcos(α), and Fcos(γ), represents the contribution of the force F in the direction of each angle. This means that the total force F can be calculated by summing these horizontal components.
Why Other Options are Incorrect
- Option B: F = Fsin(β) + Fcos(α) + Fcos(γ) - Incorrect because sine is not used for horizontal components.
- Option C: F = Fcos(β) + Fsin(α) + Fcos(γ) - Incorrect due to the use of sine for the vertical component instead of the horizontal one.
- Option D: F = Fcos(β) + Fcos(α) + Fsin(γ) - Also incorrect for the same reason as above.
In conclusion, the correct representation of the gravitational forces in terms of the vector F is indeed option A, which effectively sums the horizontal components of the gravitational force.
In the context of gravitational forces, the vector F often represents the resultant force acting on an object due to gravity. The resolution of forces into components is crucial for analyzing the system's behavior.
Components of the Force Vector
The correct expression for the force vector F can be derived from the components of the force acting in different directions. In this case, the angles α, β, and γ represent the angles at which the forces are applied relative to the coordinate axes.
Explanation of Option A
Option A states:
F = Fcos(β) + Fcos(α) + Fcos(γ)
This expression is correct because:
- Cosine Function: The cosine function is used to resolve the force vector into its components along the respective axes (X, Y, Z). The use of cosines indicates that the components are being taken along the horizontal directions.
- Directionality: Each term, Fcos(β), Fcos(α), and Fcos(γ), represents the contribution of the force F in the direction of each angle. This means that the total force F can be calculated by summing these horizontal components.
Why Other Options are Incorrect
- Option B: F = Fsin(β) + Fcos(α) + Fcos(γ) - Incorrect because sine is not used for horizontal components.
- Option C: F = Fcos(β) + Fsin(α) + Fcos(γ) - Incorrect due to the use of sine for the vertical component instead of the horizontal one.
- Option D: F = Fcos(β) + Fcos(α) + Fsin(γ) - Also incorrect for the same reason as above.
In conclusion, the correct representation of the gravitational forces in terms of the vector F is indeed option A, which effectively sums the horizontal components of the gravitational force.
For the conditions of the equilibrium of the body, i.e. the rigid body only the external conservative forces defines the equilibrium. Because the internal conservative forces cancels out so not to be considered.- a)The first part of the statement is false and other part is true
- b)The first part of the statement is false and other part is false too
- c)The first part of the statement is true and other part is false
- d)The first part of the statement is true and other part is true too
Correct answer is option 'C'. Can you explain this answer?
For the conditions of the equilibrium of the body, i.e. the rigid body only the external conservative forces defines the equilibrium. Because the internal conservative forces cancels out so not to be considered.
a)
The first part of the statement is false and other part is true
b)
The first part of the statement is false and other part is false too
c)
The first part of the statement is true and other part is false
d)
The first part of the statement is true and other part is true too
|
|
Nitin Joshi answered |
The application of the internal forces does affect the conditions of the equilibrium of the body. Not only the external but the internal forces that are developed by the sake of external forces does develop a tending effect on the equilibrium of the body. Thus the internal forces doesn’t cancels out.
Virtual work method can be applied when- a)Supports are moving
- b)Supports are not moving
- c)Can be applied in both case
- d)Can be applied in neither cases
Correct answer is option 'B'. Can you explain this answer?
Virtual work method can be applied when
a)
Supports are moving
b)
Supports are not moving
c)
Can be applied in both case
d)
Can be applied in neither cases
|
|
Keerthana Joshi answered |
Supports moving vs. Supports not moving in Virtual work method:
- Supports moving:
In virtual work method, the principle of virtual work is based on the equilibrium of forces and moments. When supports are moving, the forces and moments acting on the structure are constantly changing, making it difficult to apply the virtual work method accurately. The calculations become complex as the system is dynamic and the equilibrium conditions keep changing.
- Supports not moving:
On the other hand, when supports are not moving, the system is in a static equilibrium. This means that the forces and moments acting on the structure are constant and can be easily analyzed using the virtual work method. The static nature of the system allows for simpler calculations and accurate results when applying the virtual work method.
Therefore, the virtual work method can be effectively applied when supports are not moving, as it simplifies the analysis and ensures accurate results.
Conservation of energy will be applicable only when:-- a)Static load is applied
- b)Dynamic load is applied
- c)Can be anything
- d)Large load is applied
Correct answer is option 'A'. Can you explain this answer?
Conservation of energy will be applicable only when:-
a)
Static load is applied
b)
Dynamic load is applied
c)
Can be anything
d)
Large load is applied

|
Akash Mukherjee answered |
Conservation of energy is a fundamental principle in physics that states that the total energy of an isolated system remains constant over time. In other words, energy cannot be created or destroyed, only transformed from one form to another. However, the conservation of energy is not only applicable under specific circumstances.
a) Static load is applied:
When a static load is applied, it means that the load is not moving or changing over time. In this case, the conservation of energy is applicable because the energy of the system remains constant. The potential energy stored in the load and the surrounding objects is balanced by the external force applied, such as gravity or compression forces.
b) Dynamic load is applied:
When a dynamic load is applied, it means that the load is in motion or changing over time. In this case, the conservation of energy is still applicable. The kinetic energy of the load is balanced by the work done by external forces, such as friction or air resistance. The total energy of the system, including potential and kinetic energy, remains constant as long as no external energy is added or lost.
c) Can be anything:
The conservation of energy is a fundamental principle that applies to all physical systems, regardless of the nature of the load or the type of energy involved. Whether it is a static load, dynamic load, or any other type of load, the principle of conservation of energy still holds true. Energy may be transferred or transformed from one form to another, but the total energy of the system remains constant.
d) Large load is applied:
The size or magnitude of the load does not affect the applicability of the conservation of energy principle. Whether the load is small or large, the conservation of energy still applies. The total energy of the system is conserved, regardless of the magnitude of the load or the forces involved.
In conclusion, the conservation of energy principle is applicable in all situations, including when a static load is applied. This principle holds true for static and dynamic loads, as well as for loads of any size or magnitude. The conservation of energy is a fundamental law of nature that governs the behavior of physical systems.
a) Static load is applied:
When a static load is applied, it means that the load is not moving or changing over time. In this case, the conservation of energy is applicable because the energy of the system remains constant. The potential energy stored in the load and the surrounding objects is balanced by the external force applied, such as gravity or compression forces.
b) Dynamic load is applied:
When a dynamic load is applied, it means that the load is in motion or changing over time. In this case, the conservation of energy is still applicable. The kinetic energy of the load is balanced by the work done by external forces, such as friction or air resistance. The total energy of the system, including potential and kinetic energy, remains constant as long as no external energy is added or lost.
c) Can be anything:
The conservation of energy is a fundamental principle that applies to all physical systems, regardless of the nature of the load or the type of energy involved. Whether it is a static load, dynamic load, or any other type of load, the principle of conservation of energy still holds true. Energy may be transferred or transformed from one form to another, but the total energy of the system remains constant.
d) Large load is applied:
The size or magnitude of the load does not affect the applicability of the conservation of energy principle. Whether the load is small or large, the conservation of energy still applies. The total energy of the system is conserved, regardless of the magnitude of the load or the forces involved.
In conclusion, the conservation of energy principle is applicable in all situations, including when a static load is applied. This principle holds true for static and dynamic loads, as well as for loads of any size or magnitude. The conservation of energy is a fundamental law of nature that governs the behavior of physical systems.
The principle of work was proposed by________________- a)Mathematician Jean Bernoulli
- b)Physios Jean Bernoulli
- c)Chemist Jean Bernoulli
- d)John Jean Bernoulli
Correct answer is option 'A'. Can you explain this answer?
The principle of work was proposed by________________
a)
Mathematician Jean Bernoulli
b)
Physios Jean Bernoulli
c)
Chemist Jean Bernoulli
d)
John Jean Bernoulli
|
|
Rashi Chauhan answered |
The concept of work was proposed by Jean Bernoulli. He was a mathematician. It was proposed in 18th century. It gave us various alternative methods to calculate the work done. Thus the answer.
Work done by the couple is best given by___________- a)dU = Mdθ
- b)dU = M.dθ
- c)dU = Mxdθ
- d)dU = Mθ
Correct answer is option 'A'. Can you explain this answer?
Work done by the couple is best given by___________
a)
dU = Mdθ
b)
dU = M.dθ
c)
dU = Mxdθ
d)
dU = Mθ
|
|
Bhargavi Chauhan answered |
The work done by the couple is defined as the product of the moment and the del angle. This means that the work done does depends upon the angle of the moment. That is the angle which is being made by the moment vector to the surface of action of the moment.
Determine the horizontal force acting in the given figure.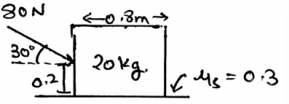
- a)80cos30
- b)60cos30
- c)40cos30
- d)8cos30
Correct answer is option 'A'. Can you explain this answer?
Determine the horizontal force acting in the given figure.
a)
80cos30
b)
60cos30
c)
40cos30
d)
8cos30

|
Janhavi Datta answered |
The net forces acting on the body is shown by the help of the resultant forces. There are two types, first the frictional and the second is the normal. This is because the resultant forces have the sum of all the forces which are acting on the direction which is same.
Find the tension in the cable AC.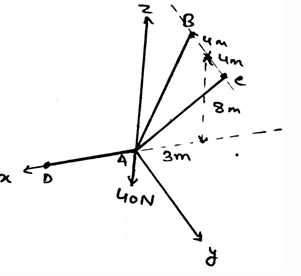
- a)23.6N
- b)55N
- c)89N
- d)-29N
Correct answer is option 'A'. Can you explain this answer?
Find the tension in the cable AC.
a)
23.6N
b)
55N
c)
89N
d)
-29N
|
|
Shruti Bose answered |
First represent the forces in their vector form. Then equate the net sum of the forces in the x, y and z directions to be zero. You will get FB = FC and 2(.848) = 40N. This gives the answer as 23.6N.
What is not the condition for the equilibrium in three dimensional system of axis so as to calculate the unknown forces acting on the body?- a)∑Fx=0
- b)∑Fy=0
- c)∑Fz=0
- d)∑F≠0
Correct answer is option 'D'. Can you explain this answer?
What is not the condition for the equilibrium in three dimensional system of axis so as to calculate the unknown forces acting on the body?
a)
∑Fx=0
b)
∑Fy=0
c)
∑Fz=0
d)
∑F≠0
|
|
Stuti Bajaj answered |
For the equilibrium in the three dimensional system of axis we have all the conditions true as, ∑Fx=0, ∑Fy=0 and ∑Fz=0. Also we have the summation of the forces equal to zero. Which is not a non-zero value.
Free body diagrams doesn’t play any role in making the calculations on the conditions of the equilibrium of the body when there is the involvement of the potential energy.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
Free body diagrams doesn’t play any role in making the calculations on the conditions of the equilibrium of the body when there is the involvement of the potential energy.
a)
True
b)
False
|
|
Sharmila Chauhan answered |
The free body diagrams does play an important role in the formation of the conditions of the equilibrium of the rigid body. As the net forces are zero, the fbd helps us to take the measure of the same. That is to see whether the summation is really zero or not.
If solving the question in 3D calculations is difficult, then use the 2D system and then equate the total work done to zero.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
If solving the question in 3D calculations is difficult, then use the 2D system and then equate the total work done to zero.
a)
True
b)
False
|
|
Isha Nambiar answered |
The answer is obviously yes. If we are having any difficulty in making the vector components, then we can go in 2D. As if the particle is in equilibrium, the net force will be zero. No matter where you see first. Net work done is zero.
We use sometimes the measures to know the direction of moment in the calculations of the moments caused by the conservative forces. Which one is right about it(consider the mentioned axis to be positive)?- a)Thumb is z-axis, fingers curled from x-axis to y-axis
- b)Thumb is x-axis, fingers curled from z-axis to y-axis
- c)Thumb is y-axis, fingers curled from x-axis to z-axis
- d)Thumb is z-axis, fingers curled from y-axis to x-axis
Correct answer is option 'A'. Can you explain this answer?
We use sometimes the measures to know the direction of moment in the calculations of the moments caused by the conservative forces. Which one is right about it(consider the mentioned axis to be positive)?
a)
Thumb is z-axis, fingers curled from x-axis to y-axis
b)
Thumb is x-axis, fingers curled from z-axis to y-axis
c)
Thumb is y-axis, fingers curled from x-axis to z-axis
d)
Thumb is z-axis, fingers curled from y-axis to x-axis
|
|
Pritam Das answered |
As right handed coordinate system means that you are curling your fingers from positive x-axis towards y-axis and the thumb which is projected is pointed to the positive z-axis. Thus visualizing the same and knowing the basic members of axis will not create much problem.
In the explanation of the theory of friction over which conservative forces were acted upon, the block used have an assumption. That is the upper portion of the block is considered to be rigid.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
In the explanation of the theory of friction over which conservative forces were acted upon, the block used have an assumption. That is the upper portion of the block is considered to be rigid.
a)
True
b)
False
|
|
Nitin Joshi answered |
The block used to explain the theory of friction is placed on a deformable surface. As we know that the theory of friction says that when there is no lubricating fluid present between the surfaces in contact, the dry friction occurs. Thus to show the same, experiments are done over a non-rigid/deformable surface which is having a rigid shape.
Ram and sham together can complete a vocation in 8 days. Ram can do likewise work all alone in 12 days. To what extent will sham take to carry out the occupation without anyone else's input?- a)16 days
- b)24 days
- c)20 days
- d)30 days
Correct answer is option 'B'. Can you explain this answer?
Ram and sham together can complete a vocation in 8 days. Ram can do likewise work all alone in 12 days. To what extent will sham take to carry out the occupation without anyone else's input?
a)
16 days
b)
24 days
c)
20 days
d)
30 days
|
|
Rajesh Gupta answered |
(Ram + sham)'s 1 day work = 1 / 8,
Ram 1 day work = 1 / 12
Sham 1 day work = (1 / 8 - 1 / 12) = 1 / 24
∴ Sham alone can finish the work in 24 days.
Ram 1 day work = 1 / 12
Sham 1 day work = (1 / 8 - 1 / 12) = 1 / 24
∴ Sham alone can finish the work in 24 days.
Determine the vertical force acting in the given figure.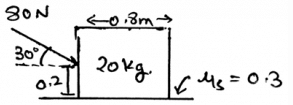
- a)236N
- b)600n
- c)403N
- d)830N
Correct answer is option 'A'. Can you explain this answer?
Determine the vertical force acting in the given figure.
a)
236N
b)
600n
c)
403N
d)
830N
|
|
Ashish Pillai answered |
The net forces acting on the body is shown by the help of the resultant forces. There are two types, first the frictional and the second is the normal. This is because the resultant forces have the sum of all the forces which are acting on the direction which is same.
Chapter doubts & questions for Work & Energy - 6 Months Preparation for GATE Civil Engg 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Work & Energy - 6 Months Preparation for GATE Civil Engg in English & Hindi are available as part of Civil Engineering (CE) exam.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
6 Months Preparation for GATE Civil Engg
488 videos|1261 docs|878 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup










