All Exams >
Computer Science Engineering (CSE) >
6 Months Preparation for GATE CSE >
All Questions
All questions of Recursion for Computer Science Engineering (CSE) Exam
Predict output of following program
#include <stdio.h>
int fun(int n)
{
if (n == 4)
return n;
else return 2*fun(n+1);
}
int main()
{
printf("%d ", fun(2));
return 0;- a)4
- b)8
- c)16
- d)Runtime Error
Correct answer is option 'C'. Can you explain this answer?
Predict output of following program
#include <stdio.h>
int fun(int n)
{
if (n == 4)
return n;
else return 2*fun(n+1);
}
int main()
{
printf("%d ", fun(2));
return 0;
#include <stdio.h>
int fun(int n)
{
if (n == 4)
return n;
else return 2*fun(n+1);
}
int main()
{
printf("%d ", fun(2));
return 0;
a)
4
b)
8
c)
16
d)
Runtime Error

|
Cstoppers Instructors answered |
Fun(2) = 2 * Fun(3) and Fun(3) = 2 * Fun(4) ....(i)
Fun(4) = 4 ......(ii)
From equation (i) and (ii),
Fun(2) = 2 * 2 * Fun(4)
Fun(2) = 2 * 2 * 4
Fun(2) = 16.
Fun(4) = 4 ......(ii)
From equation (i) and (ii),
Fun(2) = 2 * 2 * Fun(4)
Fun(2) = 2 * 2 * 4
Fun(2) = 16.
So, C is the correct answer
#include<stdio.h>
int f(int *a, int n)
{
if(n <= 0) return 0;
else if(*a % 2 == 0) return *a + f(a+1, n-1);
else return *a - f(a+1, n-1);
}
int main()
{
int a[] = {12, 7, 13, 4, 11, 6};
printf("%d", f(a, 6));
getchar();
return 0;
}- a)-9
- b)5
- c)15
- d)19
Correct answer is option 'C'. Can you explain this answer?
#include<stdio.h>
int f(int *a, int n)
{
if(n <= 0) return 0;
else if(*a % 2 == 0) return *a + f(a+1, n-1);
else return *a - f(a+1, n-1);
}
int main()
{
int a[] = {12, 7, 13, 4, 11, 6};
printf("%d", f(a, 6));
getchar();
return 0;
}
int f(int *a, int n)
{
if(n <= 0) return 0;
else if(*a % 2 == 0) return *a + f(a+1, n-1);
else return *a - f(a+1, n-1);
}
int main()
{
int a[] = {12, 7, 13, 4, 11, 6};
printf("%d", f(a, 6));
getchar();
return 0;
}
a)
-9
b)
5
c)
15
d)
19
|
|
Sanya Agarwal answered |
f() is a recursive function which adds f(a+1, n-1) to *a if *a is even. If *a is odd then f() subtracts f(a+1, n-1) from *a. See below recursion tree for execution of f(a, 6). .
f(add(12), 6) /*Since 12 is first element. a contains address of 12 */
|
|
12 + f(add(7), 5) /* Since 7 is the next element, a+1 contains address of 7 */
|
|
7 - f(add(13), 4)
|
|
13 - f(add(4), 3)
|
|
4 + f(add(11), 2)
|
|
11 - f(add(6), 1)
|
|
6 + 0
So, the final returned value is 12 + (7 – (13 – (4 + (11 – (6 + 0))))) = 15
f(add(12), 6) /*Since 12 is first element. a contains address of 12 */
|
|
12 + f(add(7), 5) /* Since 7 is the next element, a+1 contains address of 7 */
|
|
7 - f(add(13), 4)
|
|
13 - f(add(4), 3)
|
|
4 + f(add(11), 2)
|
|
11 - f(add(6), 1)
|
|
6 + 0
So, the final returned value is 12 + (7 – (13 – (4 + (11 – (6 + 0))))) = 15
What does the following function print for n = 25?void fun(int n){if (n == 0)return;printf("%d", n%2);fun(n/2);- a)11001
- b)10011
- c)11111
- d)00000
Correct answer is option 'B'. Can you explain this answer?
What does the following function print for n = 25?
void fun(int n)
{
if (n == 0)
return;
printf("%d", n%2);
fun(n/2);
a)
11001
b)
10011
c)
11111
d)
00000
|
|
Ravi Singh answered |
The function mainly prints binary representation in reverse order.
Consider the following recursive C function that takes two arguments
unsigned int foo(unsigned int n, unsigned int r) {
if (n > 0) return (n%r) + foo (n/r, r));
else return 0;
}
What is the return value of the function foo when it is called as foo(345, 10) ?
- a)345
- b)12
- c)5
- d)3
Correct answer is option 'B'. Can you explain this answer?
Consider the following recursive C function that takes two arguments
unsigned int foo(unsigned int n, unsigned int r) {
if (n > 0) return (n%r) + foo (n/r, r));
else return 0;
}
What is the return value of the function foo when it is called as foo(345, 10) ?
a)
345
b)
12
c)
5
d)
3
|
|
Sanya Agarwal answered |
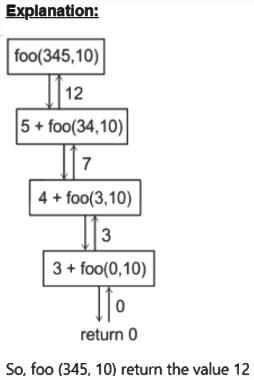
Consider the following C function:int f(int n){static int i = 1;if(n >= 5) return n;n = n+i; i++;return f(n);}The value returned by f(1) is- a)5
- b)6
- c)7
- d)8
Correct answer is option 'C'. Can you explain this answer?
Consider the following C function:
int f(int n)
{
static int i = 1;
if(n >= 5) return n;
n = n+i;
i++;
return f(n);
}
The value returned by f(1) is
a)
5
b)
6
c)
7
d)
8
|
|
Akshita Khanna answered |
answer is 7.as,
f(1):n=2,i=2
f(2):n=4,i=3
f(4):n=7,i=4
f(7):print(n)===>>> 7<ans>
f(1):n=2,i=2
f(2):n=4,i=3
f(4):n=7,i=4
f(7):print(n)===>>> 7<ans>
Output of following program?
#include <stdio.h>
int fun(int n, int *f_p)
{
int t, f;
if (n <= 1)
{
*f_p = 1;
return 1;
}
t = fun(n- 1,f_p);
f = t+ * f_p;
*f_p = t;
return f;
}
int main()
{
int x = 15;
printf (" %d n", fun(5, &x));
return 0;
}- a)6
- b)8
- c)14
- d)15
Correct answer is option 'B'. Can you explain this answer?
Output of following program?
#include <stdio.h>
int fun(int n, int *f_p)
{
int t, f;
if (n <= 1)
{
*f_p = 1;
return 1;
}
t = fun(n- 1,f_p);
f = t+ * f_p;
*f_p = t;
return f;
}
int main()
{
int x = 15;
printf (" %d n", fun(5, &x));
return 0;
}
#include <stdio.h>
int fun(int n, int *f_p)
{
int t, f;
if (n <= 1)
{
*f_p = 1;
return 1;
}
t = fun(n- 1,f_p);
f = t+ * f_p;
*f_p = t;
return f;
}
int main()
{
int x = 15;
printf (" %d n", fun(5, &x));
return 0;
}
a)
6
b)
8
c)
14
d)
15
|
|
Ravi Singh answered |
Let x is stored at location 2468 i.e. &x = 2468
(dots are use just to ensure alignment)
x = 15
fun(5, 2468)
...{t = fun(4, 2468)
.......{t = fun(3, 2468)
...........{t = fun(2,2468)
...............{t = fun(1, 2468)
...................{// x=1
........................return 1}
................t = 1
................f = 2 //1+1 //since *f_p is x
................x = t = 1
................return 2}
...........t = 2
...........f = 2+1
...........x = t = 2
...........return 3}
........t = 3
........f = 3+2
........x = t = 3
........return 5}
....t = 5
....f = 5+3
....x = t = 5
....return 8}
x = 15
fun(5, 2468)
...{t = fun(4, 2468)
.......{t = fun(3, 2468)
...........{t = fun(2,2468)
...............{t = fun(1, 2468)
...................{// x=1
........................return 1}
................t = 1
................f = 2 //1+1 //since *f_p is x
................x = t = 1
................return 2}
...........t = 2
...........f = 2+1
...........x = t = 2
...........return 3}
........t = 3
........f = 3+2
........x = t = 3
........return 5}
....t = 5
....f = 5+3
....x = t = 5
....return 8}
which implies fun (5,2468) is 8.
Consider the following recursive C function. If get(6) function is being called in main() then how many times will the get() function be invoked before returning to the main()?
void get (int n)
{
if (n < 1) return;
get(n-1);
get(n-3);
printf("%d", n);
}- a)15
- b)25
- c)35
- d)45
Correct answer is option 'B'. Can you explain this answer?
Consider the following recursive C function. If get(6) function is being called in main() then how many times will the get() function be invoked before returning to the main()?
void get (int n)
{
if (n < 1) return;
get(n-1);
get(n-3);
printf("%d", n);
}
void get (int n)
{
if (n < 1) return;
get(n-1);
get(n-3);
printf("%d", n);
}
a)
15
b)
25
c)
35
d)
45
|
|
Sanya Agarwal answered |
get(6) [25 Calls]
/ \
[17 Calls] get(5) get(3) [7 Calls]
/ \
get(4) get(2)[5 Calls]
/ \
[7 Calls] get(3) get(1)[3 Calls]
/ \
get(2) get(0)
/ \
[3 Calls]get(1) get(-1)
/ \
get(0) get(-2)
We can verify the same by running below program. [sourcecode language="CPP"] # include int count = 0; void get (int n) { count++; if (n < 1) return; get(n-1); get(n-3); } int main() { get(6); printf("%d ", count); } [/sourcecode] Output: 25
/ \
[17 Calls] get(5) get(3) [7 Calls]
/ \
get(4) get(2)[5 Calls]
/ \
[7 Calls] get(3) get(1)[3 Calls]
/ \
get(2) get(0)
/ \
[3 Calls]get(1) get(-1)
/ \
get(0) get(-2)
We can verify the same by running below program. [sourcecode language="CPP"] # include int count = 0; void get (int n) { count++; if (n < 1) return; get(n-1); get(n-3); } int main() { get(6); printf("%d ", count); } [/sourcecode] Output: 25
What does fun2() do in general?
int fun(int x, int y)
{
if (y == 0) return 0;
return (x + fun(x, y-1));
}
int fun2(int a, int b)
{
if (b == 0) return 1;
return fun(a, fun2(a, b-1));
}- a)x*y
- b)x+x*y
- c)xy
- d)yx
Correct answer is option 'C'. Can you explain this answer?
What does fun2() do in general?
int fun(int x, int y)
{
if (y == 0) return 0;
return (x + fun(x, y-1));
}
int fun2(int a, int b)
{
if (b == 0) return 1;
return fun(a, fun2(a, b-1));
}
int fun(int x, int y)
{
if (y == 0) return 0;
return (x + fun(x, y-1));
}
int fun2(int a, int b)
{
if (b == 0) return 1;
return fun(a, fun2(a, b-1));
}
a)
x*y
b)
x+x*y
c)
xy
d)
yx
|
|
Sanya Agarwal answered |
The function multiplies x to itself y times which is xy.
Consider the following computation rules. Parallel-outermost rule: Replace all the outermost occurrences of F (i.e., all occurrences of F which do not occur as arguments of other F's) simultaneously. Parallel - innermost rule: Replace all the innermost occurrences of F (i.e.,all occurrences of F with all arguments free of F's) simultaneously. Now consider the evaluations of the recursive program over the integers. F(x, y) <== if x = 0 then 0 else[ F(x + 1, F(x, y)) * F(x - 1, F(x, y))] where the multiplication functions * is extended as follows: 0 * w & w * 0 are 0a * w & w * a are w (for any non-zero integer a)w * w is w We say that F(x, y) = w when the evaluation of F(x, y) does not terminate. Computing F(1, 0) using the parallel - innermost and parallel - outermost rule yields- a)ω and 0 respectively
- b)0 and 0 respectively
- c)ω and ω respectively
- d)ω and 1 respectively
- e)none of the above
Correct answer is option 'A'. Can you explain this answer?
Consider the following computation rules. Parallel-outermost rule: Replace all the outermost occurrences of F (i.e., all occurrences of F which do not occur as arguments of other F's) simultaneously. Parallel - innermost rule: Replace all the innermost occurrences of F (i.e.,all occurrences of F with all arguments free of F's) simultaneously. Now consider the evaluations of the recursive program over the integers.
F(x, y) <== if x = 0 then 0 else
[ F(x + 1, F(x, y)) * F(x - 1, F(x, y))]
where the multiplication functions * is extended as follows:
0 * w & w * 0 are 0
a * w & w * a are w (for any non-zero integer a)
w * w is w
We say that F(x, y) = w when the evaluation of F(x, y) does not terminate. Computing F(1, 0) using the parallel - innermost and parallel - outermost rule yields
a)
ω and 0 respectively
b)
0 and 0 respectively
c)
ω and ω respectively
d)
ω and 1 respectively
e)
none of the above
|
|
Pritam Goyal answered |
Understanding the Function F(x, y)
The function F(x, y) is defined recursively with the condition that if x equals 0, it returns 0. Otherwise, it evaluates to a product involving recursive calls to itself.
Parallel-Outermost Rule
- This rule allows us to replace all outermost occurrences of F simultaneously.
- When computing F(1, 0), we consider the outermost F(1, 0).
- The evaluation leads to F(2, F(1, 0)) * F(0, F(1, 0)).
- Here, F(0, F(1, 0)) evaluates to 0, since x is 0.
Parallel-Innermost Rule
- This rule replaces all innermost occurrences of F simultaneously.
- In the case of F(1, 0), we first evaluate the innermost F calls.
- The innermost F(0, F(1, 0)) returns 0, and we are left with F(2, 0) * 0.
- According to the multiplication rules, anything multiplied by 0 yields 0.
Final Evaluation Results
- Using the parallel-outermost rule, we find that F(1, 0) evaluates to 0.
- Using the parallel-innermost rule, we also find that the evaluation of F(1, 0) leads to 0.
- Thus, the evaluation results in both cases yield 0.
Conclusion
- Therefore, the correct answer is option 'A': 0 and 0 respectively, as both methods yield the same result of 0.
The function F(x, y) is defined recursively with the condition that if x equals 0, it returns 0. Otherwise, it evaluates to a product involving recursive calls to itself.
Parallel-Outermost Rule
- This rule allows us to replace all outermost occurrences of F simultaneously.
- When computing F(1, 0), we consider the outermost F(1, 0).
- The evaluation leads to F(2, F(1, 0)) * F(0, F(1, 0)).
- Here, F(0, F(1, 0)) evaluates to 0, since x is 0.
Parallel-Innermost Rule
- This rule replaces all innermost occurrences of F simultaneously.
- In the case of F(1, 0), we first evaluate the innermost F calls.
- The innermost F(0, F(1, 0)) returns 0, and we are left with F(2, 0) * 0.
- According to the multiplication rules, anything multiplied by 0 yields 0.
Final Evaluation Results
- Using the parallel-outermost rule, we find that F(1, 0) evaluates to 0.
- Using the parallel-innermost rule, we also find that the evaluation of F(1, 0) leads to 0.
- Thus, the evaluation results in both cases yield 0.
Conclusion
- Therefore, the correct answer is option 'A': 0 and 0 respectively, as both methods yield the same result of 0.
What does the following function do?
int fun(int x, int y)
{
if (y == 0) return 0;
return (x + fun(x, y-1));- a)x + y
- b)x + x*y
- c)x*y
- d)xy
Correct answer is option 'C'. Can you explain this answer?
What does the following function do?
int fun(int x, int y)
{
if (y == 0) return 0;
return (x + fun(x, y-1));
int fun(int x, int y)
{
if (y == 0) return 0;
return (x + fun(x, y-1));
a)
x + y
b)
x + x*y
c)
x*y
d)
xy
|
|
Sanya Agarwal answered |
The function adds x to itself y times which is x*y.
What does the following function do?
int fun(unsigned int n)
{
if (n == 0 || n == 1)
return n;
if (n%3 != 0)
return 0;
return fun(n/3);
}- a)It returns 1 when n is a multiple of 3, otherwise returns 0
- b)It returns 1 when n is a power of 3, otherwise returns 0
- c)t returns 0 when n is a multiple of 3, otherwise returns 1
- d)It returns 0 when n is a power of 3, otherwise returns 1
Correct answer is option 'B'. Can you explain this answer?
What does the following function do?
int fun(unsigned int n)
{
if (n == 0 || n == 1)
return n;
if (n%3 != 0)
return 0;
return fun(n/3);
}
int fun(unsigned int n)
{
if (n == 0 || n == 1)
return n;
if (n%3 != 0)
return 0;
return fun(n/3);
}
a)
It returns 1 when n is a multiple of 3, otherwise returns 0
b)
It returns 1 when n is a power of 3, otherwise returns 0
c)
t returns 0 when n is a multiple of 3, otherwise returns 1
d)
It returns 0 when n is a power of 3, otherwise returns 1
|
|
Ravi Singh answered |
Lets solve with example, n = 27 which power of 3. First time if condition is false as n is neither equal to 0 nor equal to 1 then 27%3 = 0. Here, again if condition false because it is equal to 0. Then fun(27/3) will call. Second time if condition is false as n is neither equal to 0 nor equal to 1 then 9%3 = 0. Here again if condition false because it is equal to 0. Then fun (9/3) will call and third time if condition is false as n is neither equal to 0 nor equal to 1 then 3%3 = 0. Here again if condition false because it is equal to 0. Then fun(3/3) will call here n==1 if condition gets true and it return n i.e. 1. Option (B) is correct.
Consider the following C function.
int fun (int n)
{
int x=1, k;
if (n==1) return x;
for (k=1; k<n; ++k)
x = x + fun(k) * fun(n – k);
return x;
}
The return value of fun(5) is __________.- a)0
- b)26
- c)51
- d)71
Correct answer is option 'C'. Can you explain this answer?
Consider the following C function.
int fun (int n)
{
int x=1, k;
if (n==1) return x;
for (k=1; k<n; ++k)
x = x + fun(k) * fun(n – k);
return x;
}
The return value of fun(5) is __________.
int fun (int n)
{
int x=1, k;
if (n==1) return x;
for (k=1; k<n; ++k)
x = x + fun(k) * fun(n – k);
return x;
}
The return value of fun(5) is __________.
a)
0
b)
26
c)
51
d)
71
|
|
Sanya Agarwal answered |
fun(5) = 1 + fun(1) * fun(4) + fun(2) * fun(3) +
fun(3) * fun(2) + fun(4) * fun(1)
= 1 + 2*[fun(1)*fun(4) + fun(2)*fun(3)]
fun(3) * fun(2) + fun(4) * fun(1)
= 1 + 2*[fun(1)*fun(4) + fun(2)*fun(3)]
Substituting fun(1) = 1
= 1 + 2*[fun(4) + fun(2)*fun(3)]
= 1 + 2*[fun(4) + fun(2)*fun(3)]
Calculating fun(2), fun(3) and fun(4)
fun(2) = 1 + fun(1)*fun(1) = 1 + 1*1 = 2
fun(3) = 1 + 2*fun(1)*fun(2) = 1 + 2*1*2 = 5
fun(4) = 1 + 2*fun(1)*fun(3) + fun(2)*fun(2)
= 1 + 2*1*5 + 2*2 = 15
fun(2) = 1 + fun(1)*fun(1) = 1 + 1*1 = 2
fun(3) = 1 + 2*fun(1)*fun(2) = 1 + 2*1*2 = 5
fun(4) = 1 + 2*fun(1)*fun(3) + fun(2)*fun(2)
= 1 + 2*1*5 + 2*2 = 15
Substituting values of fun(2), fun(3) and fun(4)
fun(5) = 1 + 2*[15 + 2*5] = 51
fun(5) = 1 + 2*[15 + 2*5] = 51
Which of the following statements are CORRECT?1) Static allocation of all data areas by a compiler makes it impossible to implement recursion.2) Automatic garbage collection is essential to implement recursion3) Dynamic allocation of activation records is essential to implement recursion4) Both heap and stack are essential to implement recursion- a)1 and 2 only
- b)2 and 3 only
- c)3 and 4 only
- d)1 and 3 only
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements are CORRECT?
1) Static allocation of all data areas by a compiler makes it impossible to implement recursion.
2) Automatic garbage collection is essential to implement recursion
3) Dynamic allocation of activation records is essential to implement recursion
4) Both heap and stack are essential to implement recursion
a)
1 and 2 only
b)
2 and 3 only
c)
3 and 4 only
d)
1 and 3 only

|
Crack Gate answered |
Statement 1 – True
Dynamic memory allocation is necessary for implementing recursion because the number of function calls is not known in advance, requiring the use of a function call stack.
Statement 2 – False
Automatic garbage collection is not essential for recursion implementation, as languages provide specific functions for manual memory management.
Statement 3 – True
Dynamic memory allocation is required for recursion since the exact number of function calls cannot be predetermined.
Statement 4 – False
Recursion requires a stack structure. If a heap is used, it must be simulated as a stack for recursion purposes. The heap is generally used for user-driven dynamic memory allocation and is not needed for function calls. Thus, both stack and heap are not required simultaneously; either one is sufficient to implement recursion.
Therefore, statements 1 and 3 are true.
The function f is defined as follows:int f (int n) {if (n <= 1) return 1;else if (n % 2 == 0) return f(n/2);else return f(3n - 1);
}Assuming that arbitrarily large integers can be passed as a parameter to the function, consider the following statements.i. The function f terminates for finitely many different values of n ≥ 1.ii. The function f terminates for infinitely many different values of n ≥ 1.iii. The function f does not terminate for finitely many different values of n ≥ 1.iv. The function f does not terminate for infinitely many different values of n ≥ 1.Which one of the following options is true of the above?A. i and iiiB. i and ivC. ii and iiiD. ii and iv- a)A
- b)B
- c)C
- d)D
Correct answer is option 'D'. Can you explain this answer?
The function f is defined as follows:
int f (int n) {
if (n <= 1) return 1;
else if (n % 2 == 0) return f(n/2);
else return f(3n - 1);
}
}
Assuming that arbitrarily large integers can be passed as a parameter to the function, consider the following statements.
i. The function f terminates for finitely many different values of n ≥ 1.
ii. The function f terminates for infinitely many different values of n ≥ 1.
iii. The function f does not terminate for finitely many different values of n ≥ 1.
iv. The function f does not terminate for infinitely many different values of n ≥ 1.
Which one of the following options is true of the above?
A. i and iii
B. i and iv
C. ii and iii
D. ii and iv
a)
A
b)
B
c)
C
d)
D
|
|
Sagnik Desai answered |
The function terminates for all powers of 2 (which is infinite), hence (i) is false and (ii) is TRUE.
Let n = 5.
Now, recursive calls will go like 5 - 14 - 7 - 20 - 10 - 5 -
And this goes into infinite recursion. And if we multiply 5 with any power of 2, also result will be infinite recursion. Since, there are infinite powers of 2 possible, there are infinite recursions possible (even considering this case only). So, (iv) is TRUE and (iii) is false.
So, correct answer is (D)
Let n = 5.
Now, recursive calls will go like 5 - 14 - 7 - 20 - 10 - 5 -
And this goes into infinite recursion. And if we multiply 5 with any power of 2, also result will be infinite recursion. Since, there are infinite powers of 2 possible, there are infinite recursions possible (even considering this case only). So, (iv) is TRUE and (iii) is false.
So, correct answer is (D)
Consider the class of recursive and iterative programs. Which of the following is false?- a)Recursive programs are more powerful than iterative programs.
- b)For every iterative program there is an equivalent recursive program.
- c)Recursive programs require dynamic memory management.
- d)Recursive programs do not terminate sometimes.
- e)Iterative programs and recursive programs are equally expressive.
Correct answer is option 'E'. Can you explain this answer?
Consider the class of recursive and iterative programs. Which of the following is false?
a)
Recursive programs are more powerful than iterative programs.
b)
For every iterative program there is an equivalent recursive program.
c)
Recursive programs require dynamic memory management.
d)
Recursive programs do not terminate sometimes.
e)
Iterative programs and recursive programs are equally expressive.
|
|
Rajeev Menon answered |
Computable function: those which can be incorporated in a program using for/while loops.
Total Function: Defined for all possible inputs
Well Defined: if its definition assigns it a unique value.
It was a belief in early 1900s that every Computable function was also Primitively Recursive. But the discovery of Ackermann function provided a counter to it.
The class of primitive recursive functions is a small subclass of the class of recursive functions. This means that there are some functions which are Well-Defined Total Functions and are Computable BUT Not primitively recursive; eg. Ackermann function.
This makes all options from option A to option D as True.
But option E as FALSE. As iterative programs are equivalent to only Primitively Recursive class.
Output of following program?
#include<stdio.h>
void print(int n)
{
if (n > 4000)
return;
printf("%d ", n);
print(2*n);
printf("%d ", n);
}
int main()
{
print(1000);
getchar();
return 0;
}- a)1000 2000 4000
- b)1000 2000 4000 4000 2000 1000
- c)1000 2000 4000 2000 1000
- d)1000 2000 2000 1000
Correct answer is option 'B'. Can you explain this answer?
Output of following program?
#include<stdio.h>
void print(int n)
{
if (n > 4000)
return;
printf("%d ", n);
print(2*n);
printf("%d ", n);
}
int main()
{
print(1000);
getchar();
return 0;
}
#include<stdio.h>
void print(int n)
{
if (n > 4000)
return;
printf("%d ", n);
print(2*n);
printf("%d ", n);
}
int main()
{
print(1000);
getchar();
return 0;
}
a)
1000 2000 4000
b)
1000 2000 4000 4000 2000 1000
c)
1000 2000 4000 2000 1000
d)
1000 2000 2000 1000
|
|
Sanya Agarwal answered |
First time n=1000 Then 1000 is printed by first printf function then call print(2*1000) then again print 2000 by printf function then call print(2*2000) and it prints 4000 next time print(4000*2) is called. Here 8000 is greater than 4000 condition becomes true and it return at function(2*4000). Here n=4000 then 4000 will again print through second printf. Similarly print(2*2000) after that n=2000 then 2000 will print and come back at print(2*1000) here n=1000, so print 1000 through second printf. Option (B) is correct.
What will be the output of the following C program?void count (int n) {static int d=1;printf ("%d",n);printf ("%d",d); d++;if (n>1) count (n-1); printf ("%d",d);}void main(){ count (3);}- a)3 1 2 2 1 3 4 4 4
- b)3 1 2 1 1 1 2 2 2
- c)3 1 2 2 1 3 4
- d)3 1 2 1 1 1 2
Correct answer is option 'A'. Can you explain this answer?
What will be the output of the following C program?
void count (int n) {
static int d=1;
printf ("%d",n);
printf ("%d",d);
d++;
if (n>1) count (n-1);
printf ("%d",d);
}
void main(){
count (3);
}
a)
3 1 2 2 1 3 4 4 4
b)
3 1 2 1 1 1 2 2 2
c)
3 1 2 2 1 3 4
d)
3 1 2 1 1 1 2

|
Rahul Chatterjee answered |
Count(3) will print value of n and d. So 3 1 will be printed
and d will become 2.
Then count(2) will be called. It will print value of n and d.
So 2 2 will be printed and d will become 3.
Then count(1) will be called. It will print value of n and d.
So 1 3 will be printed and d will become 4.
Now count(1) will print value of d which is 4. count(1) will
finish its execution.
Then count(2) will print value of d which is 4.
Similarly, count(3) will print value of d which is 4.
So series will be A.
Consider the following two functions.void fun1(int n) {if(n == 0) return; printf("%d", n); fun2(n - 2); printf("%d", n);}void fun2(int n) {if(n == 0) return; printf("%d", n); fun1(++n); printf("%d", n);}The output printed when fun1 (5) is called is- a)53423122233445
- b)53423120112233
- c)53423122132435
- d)53423120213243
Correct answer is option 'A'. Can you explain this answer?
Consider the following two functions.
void fun1(int n) {
if(n == 0) return;
printf("%d", n);
fun2(n - 2);
printf("%d", n);
}
void fun2(int n) {
if(n == 0) return;
printf("%d", n);
fun1(++n);
printf("%d", n);
}
The output printed when fun1 (5) is called is
a)
53423122233445
b)
53423120112233
c)
53423122132435
d)
53423120213243
|
|
Raghav Basu answered |
- Unroll recursion up to a point where we can distinguish the given options and choose the correct one!
- Options B and D are eliminated.
- A is the answer.
The function f is defined as follows:
int f (int n) {
if (n <= 1) return 1;
else if (n % 2 == 0) return f(n/2);
else return f(3n - 1);
}
Assuming that arbitrarily large integers can be passed as a parameter to the function, consider the following statements.
1. The function f terminates for finitely many different values of n ≥ 1.
ii. The function f terminates for infinitely many different values of n ≥ 1.
iii. The function f does not terminate for finitely many different values of n ≥ 1.
iv. The function f does not terminate for infinitely many different values of n ≥ 1.
Which one of the following options is true of the above?- a)(i) and (iii)
- b)(i) and (iv)
- c)(ii) and (iii)
- d)(ii) and (iv)
Correct answer is option 'D'. Can you explain this answer?
The function f is defined as follows:
int f (int n) {
if (n <= 1) return 1;
else if (n % 2 == 0) return f(n/2);
else return f(3n - 1);
}
Assuming that arbitrarily large integers can be passed as a parameter to the function, consider the following statements.
1. The function f terminates for finitely many different values of n ≥ 1.
ii. The function f terminates for infinitely many different values of n ≥ 1.
iii. The function f does not terminate for finitely many different values of n ≥ 1.
iv. The function f does not terminate for infinitely many different values of n ≥ 1.
Which one of the following options is true of the above?
int f (int n) {
if (n <= 1) return 1;
else if (n % 2 == 0) return f(n/2);
else return f(3n - 1);
}
Assuming that arbitrarily large integers can be passed as a parameter to the function, consider the following statements.
1. The function f terminates for finitely many different values of n ≥ 1.
ii. The function f terminates for infinitely many different values of n ≥ 1.
iii. The function f does not terminate for finitely many different values of n ≥ 1.
iv. The function f does not terminate for infinitely many different values of n ≥ 1.
Which one of the following options is true of the above?
a)
(i) and (iii)
b)
(i) and (iv)
c)
(ii) and (iii)
d)
(ii) and (iv)
|
|
Ravi Singh answered |
The function terminates for all values having a factor of 2 {(2.x)2==0}
So, (i) is false and (ii) is TRUE.
Let n = 3, it will terminate in 2nd iteration.
Let n=5, it will go like 5 - 14 - 7 - 20 - 10 - 5 – and now it will repeat.
And any number with a factor of 5 and 2, there are infinite recursions possible.
So, (iv) is TRUE and (iii) is false.
So, (i) is false and (ii) is TRUE.
Let n = 3, it will terminate in 2nd iteration.
Let n=5, it will go like 5 - 14 - 7 - 20 - 10 - 5 – and now it will repeat.
And any number with a factor of 5 and 2, there are infinite recursions possible.
So, (iv) is TRUE and (iii) is false.
Consider the same recursive C function that takes two arguments
unsigned int foo(unsigned int n, unsigned int r) {
if (n > 0) return (n%r + foo (n/r, r ));
else return 0;
}What is the return value of the function foo when it is called as foo(513, 2)?- a)9
- b)8
- c)5
- d)2
Correct answer is option 'D'. Can you explain this answer?
Consider the same recursive C function that takes two arguments
unsigned int foo(unsigned int n, unsigned int r) {
if (n > 0) return (n%r + foo (n/r, r ));
else return 0;
}
unsigned int foo(unsigned int n, unsigned int r) {
if (n > 0) return (n%r + foo (n/r, r ));
else return 0;
}
What is the return value of the function foo when it is called as foo(513, 2)?
a)
9
b)
8
c)
5
d)
2
|
|
Yash Patel answered |
foo(513, 2) will return 1 + foo(256, 2). All subsequent recursive calls (including foo(256, 2)) will return 0 + foo(n/2, 2) except the last call foo(1, 2) . The last call foo(1, 2) returns 1. So, the value returned by foo(513, 2) is 1 + 0 + 0…. + 0 + 1. The function foo(n, 2) basically returns sum of bits (or count of set bits) in the number n.
Consider the C function given below.
int f(int j)
{
static int i = 50;
int k;
if (i == j)
{
printf(“something”);
k = f(i);
return 0;
}
else return 0;
}Which one of the following is TRUE?- a)The function returns 0 for all values of j
- b)The function prints the string something for all values of j.
- c)The function returns 0 when j = 50.
- d)The function will exhaust the runtime stack or run into an infinite loop when j = 50
Correct answer is option 'D'. Can you explain this answer?
Consider the C function given below.
int f(int j)
{
static int i = 50;
int k;
if (i == j)
{
printf(“something”);
k = f(i);
return 0;
}
else return 0;
}
int f(int j)
{
static int i = 50;
int k;
if (i == j)
{
printf(“something”);
k = f(i);
return 0;
}
else return 0;
}
Which one of the following is TRUE?
a)
The function returns 0 for all values of j
b)
The function prints the string something for all values of j.
c)
The function returns 0 when j = 50.
d)
The function will exhaust the runtime stack or run into an infinite loop when j = 50
|
|
Sanya Agarwal answered |
When j is 50, the function would call itself again and again as neither i nor j is changed inside the recursion.
Predict the output of following program
#include <stdio.h>
int f(int n)
{
if(n <= 1)
return 1;
if(n%2 == 0)
return f(n/2);
return f(n/2) + f(n/2+1);
}
int main()
{
printf("%d", f(11));
return 0;
}- a)Stack Overflow
- b)3
- c)4
- d)5
Correct answer is option 'D'. Can you explain this answer?
Predict the output of following program
#include <stdio.h>
int f(int n)
{
if(n <= 1)
return 1;
if(n%2 == 0)
return f(n/2);
return f(n/2) + f(n/2+1);
}
int main()
{
printf("%d", f(11));
return 0;
}
#include <stdio.h>
int f(int n)
{
if(n <= 1)
return 1;
if(n%2 == 0)
return f(n/2);
return f(n/2) + f(n/2+1);
}
int main()
{
printf("%d", f(11));
return 0;
}
a)
Stack Overflow
b)
3
c)
4
d)
5
|
|
Ravi Singh answered |
On successive recursion F(11) will be decomposed into F(5) + F(6) -> F(2) + F(3) + F(3) -> F(1) + 2 * [F(1) + F(2)] -> 1 + 2 * [1 + F(1)] -> 1 + 2 * (1 + 1) -> 5. Hence , option D is the correct answer i.e, 5.
Consider the following function
double f(double x){
if (abs(x*x - 3) < 0.01) return x;
else return f(x/2 + 1.5/x);
}
Give a value q (to 2 decimals) such that f(q) will return q:_____.- a)1.73
- b)2.24
- c)4.22
- d)3.42
Correct answer is option 'A'. Can you explain this answer?
Consider the following function
double f(double x){
if (abs(x*x - 3) < 0.01) return x;
else return f(x/2 + 1.5/x);
}
Give a value q (to 2 decimals) such that f(q) will return q:_____.
double f(double x){
if (abs(x*x - 3) < 0.01) return x;
else return f(x/2 + 1.5/x);
}
Give a value q (to 2 decimals) such that f(q) will return q:_____.
a)
1.73
b)
2.24
c)
4.22
d)
3.42
|
|
Harsh Sen answered |
The given function is incomplete. The condition inside the if statement is missing. Additionally, there is no return statement to specify the value to be returned by the function.
To complete the function, we need to provide the condition inside the if statement and specify the return value. Here's an example of a possible implementation:
```cpp
#include
double f(double x) {
if (std::abs(x*x - 3) < 0.0001)="" />
return x * x;
} else {
return x;
}
}
```
In this example, the condition inside the if statement checks if the absolute difference between `x*x` and 3 is less than 0.0001. If the condition is true, the function returns `x * x`, otherwise it returns `x`.
To complete the function, we need to provide the condition inside the if statement and specify the return value. Here's an example of a possible implementation:
```cpp
#include
double f(double x) {
if (std::abs(x*x - 3) < 0.0001)="" />
return x * x;
} else {
return x;
}
}
```
In this example, the condition inside the if statement checks if the absolute difference between `x*x` and 3 is less than 0.0001. If the condition is true, the function returns `x * x`, otherwise it returns `x`.
Consider the same recursive C function that takes two arguments Q. What is the return value of the function foo when it is called as foo(513, 2)?
Q. What is the return value of the function foo when it is called as foo(513, 2)?- a)9
- b)8
- c)5
- d)2
Correct answer is option 'D'. Can you explain this answer?
Consider the same recursive C function that takes two arguments
Q. What is the return value of the function foo when it is called as foo(513, 2)?
a)
9
b)
8
c)
5
d)
2
|
|
Yash Patel answered |
foo(513, 2) will return 1 + foo(256, 2). All subsequent recursive calls (including foo(256, 2)) will return 0 + foo(n/2, 2) except the last call foo(1, 2). The last call foo(1, 2) returns 1. So, the value returned by foo(513, 2) is 1 + 0 + 0…. + 0 + 1. The function foo(n, 2) basically returns sum of bits (or count of set bits) in the number n.
int f(int n){
static int r = 0; if (n <= 0) return1; if (n > 3) { r = n; return f(n-2) + 2; }
return f(n-1) + r;}What is the value of f(5)?- a)5
- b)7
- c)9
- d)18
Correct answer is option 'D'. Can you explain this answer?
int f(int n)
{
static int r = 0;
static int r = 0;
if (n <= 0) return1;
if (n > 3)
{ r = n;
return f(n-2) + 2;
}
return f(n-1) + r;
return f(n-1) + r;
}
What is the value of f(5)?
a)
5
b)
7
c)
9
d)
18

|
Rahul Chatterjee answered |
f(5) = f(3)+2
The line "r = n" changes value of r to 5. Since r
is static, its value is shared be all subsequence
calls. Also, all subsequent calls don't change r
because the statement "r = n" is in a if condition
with n > 3.
f(3) = f(2)+5
f(2) = f(1)+5
f(1) = f(0)+5
f(0) = 1
So f(5) = 1+5+5+5+2 = 18
A language with string manipulation facilities uses the following operationshead(s): first character of a stringtail(s): all but exclude the first character of a stringconcat(s1, s2): s1s2For the string "acbc" what will be the output ofconcat(head(s), head(tail(tail(s)))) - a)ac
- b)bc
- c)ab
- d)cc
Correct answer is option 'C'. Can you explain this answer?
A language with string manipulation facilities uses the following operations
head(s): first character of a string
tail(s): all but exclude the first character of a string
concat(s1, s2): s1s2
For the string "acbc" what will be the output of
concat(head(s), head(tail(tail(s))))
a)
ac
b)
bc
c)
ab
d)
cc
|
|
Akshay Singh answered |
concat(a,head(tail(tail(acbc))))
concat(a,head(tail(cbc)))
concat(a,head(bc))
concat(a,b)
ab.
concat(a,head(tail(cbc)))
concat(a,head(bc))
concat(a,b)
ab.
Consider the following recursive C function that takes two argumentsunsigned int foo(unsigned int n, unsigned int r){if(n >0) return (n%r + foo (n/r, r));else return 0;}Q.
What is the return value of the function foo when it is called as foo(345, 10) ?- a)345
- b)12
- c)5
- d)3
Correct answer is option 'B'. Can you explain this answer?
Consider the following recursive C function that takes two arguments
unsigned int foo(unsigned int n, unsigned int r){
if(n >0) return (n%r + foo (n/r, r));
else return 0;
}
Q.
What is the return value of the function foo when it is called as foo(345, 10) ?
What is the return value of the function foo when it is called as foo(345, 10) ?
a)
345
b)
12
c)
5
d)
3
|
|
Shubham Sharma answered |
The function foo takes two unsigned integer arguments n and r. It calculates the sum of the first r terms of the sequence {n, n+1, n+2, ...} using recursion.
The base case is when r equals 0, in which case the function returns 0. Otherwise, it recursively calls itself with n+1 and r-1, and adds the result to n.
For example, if we call foo(3, 4), it will calculate the sum of the first 4 terms of the sequence {3, 4, 5, 6}, which is 3+4+5+6=18.
The base case is when r equals 0, in which case the function returns 0. Otherwise, it recursively calls itself with n+1 and r-1, and adds the result to n.
For example, if we call foo(3, 4), it will calculate the sum of the first 4 terms of the sequence {3, 4, 5, 6}, which is 3+4+5+6=18.
double foo(int n){int i;double sum;if(n == 0){return 1.0;
}else{sum = 0.0;for(i = 0; i < n; i++){ sum += foo(i);}
return sum;}
}The space complexity of the above code is?- a)
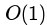
- b)
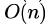
- c)
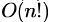
- d)
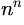
Correct answer is option 'B'. Can you explain this answer?
double foo(int n)
{
int i;
double sum;
if(n == 0)
{
return 1.0;
}
}
else
{
sum = 0.0;
for(i = 0; i < n; i++)
{
sum += foo(i);
}
return sum;
return sum;
}
}
}
The space complexity of the above code is?
a)
b)
c)
d)

|
Anirban Khanna answered |
Note that the function foo() is recursive. Space complexity is O(n) as there can be at most O(n) active functions (function call frames) at a time.
double foo(int n){int i;double sum;if(n == 0){return 1.0;}else{sum = 0.0;for(i = 0; i < n; i++){ sum += foo(i);}return sum;}
}Suppose we modify the above function foo() and stores the value of foo(i) 0 <= i < n, as and when they are computed. With this modification the time complexity for function foo() is significantly reduced. The space complexity of the modified function would be:- a)
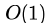
- b)
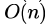
- c)
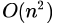
- d)
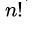
Correct answer is option 'B'. Can you explain this answer?
double foo(int n)
{
int i;
double sum;
if(n == 0)
{return 1.0;
}
else
{
sum = 0.0;
for(i = 0; i < n; i++)
{
sum += foo(i);
}
return sum;
}
}
}
Suppose we modify the above function foo() and stores the value of foo(i) 0 <= i < n, as and when they are computed. With this modification the time complexity for function foo() is significantly reduced. The space complexity of the modified function would be:
a)
b)
c)
d)
|
|
Akshay Singh answered |
The modification being proposed is tabulation method of Dynamic Programming.
So let we have an auxillary array which stores the value of foo(i) once it is computed and can be used at later stage .So foo(i) is not called again , instead lookup from the table takes place. It would be something like :
So let we have an auxillary array which stores the value of foo(i) once it is computed and can be used at later stage .So foo(i) is not called again , instead lookup from the table takes place. It would be something like :
#include <stdio.h>
#define max 1000
int foo[max];
#define max 1000
int foo[max];
foo(int n) {
if(foo[n] == -1) //compute it and store at foo[n] and return
else // return foo[n] directly
}
if(foo[n] == -1) //compute it and store at foo[n] and return
else // return foo[n] directly
}
int main(void) {
//initialize all elements of foo[max] to -1
return 0;
}Using this approach , we need an auxillary array of size n to store foo(i) where i ranges from 0 to n-1.
//initialize all elements of foo[max] to -1
return 0;
}Using this approach , we need an auxillary array of size n to store foo(i) where i ranges from 0 to n-1.
So space complexity of this method = O(n) And function foo(n) computes 2n - 1
What does the following function print for n = 25?
- a)11001
- b)10011
- c)11111
- d)00000
Correct answer is option 'B'. Can you explain this answer?
What does the following function print for n = 25?
a)
11001
b)
10011
c)
11111
d)
00000
|
|
Swara Basak answered |
The function mainly prints binary representation in reverse order.
What does fun2() do in general?
- a)x*y
- b)x+x*y
- c)xy
- d)yx
Correct answer is option 'C'. Can you explain this answer?
What does fun2() do in general?
a)
x*y
b)
x+x*y
c)
xy
d)
yx

|
Baishali Bajaj answered |
The function multiplies x to itself y times which is x^y.
What does the following function do?
- a)It returns 1 when n is a multiple of 3, otherwise returns 0
- b)It returns 1 when n is a power of 3, otherwise returns 0
- c)It returns 0 when n is a multiple of 3, otherwise returns 1
- d)It returns 0 when n is a power of 3, otherwise returns 1
Correct answer is option 'B'. Can you explain this answer?
What does the following function do?
a)
It returns 1 when n is a multiple of 3, otherwise returns 0
b)
It returns 1 when n is a power of 3, otherwise returns 0
c)
It returns 0 when n is a multiple of 3, otherwise returns 1
d)
It returns 0 when n is a power of 3, otherwise returns 1

|
Aryan Batheja answered |
Lets solve with example, n = 27 which power of 3. First time if condition is false as n is neither equal to 0 nor equal to 1 then 27%3 = 0. Here, again if condition false because it is equal to 0. Then fun(27/3) will call. Second time if condition is false as n is neither equal to 0 nor equal to 1 then 9%3 = 0. Here again if condition false because it is equal to 0. Then fun (9/3) will call and third time if condition is false as n is neither equal to 0 nor equal to 1 then 3%3 = 0. Here again if condition false because it is equal to 0. Then fun(3/3) will call here n==1 if condition gets true and it return n i.e. 1. Option (B) is correct.
Find the number of elements in the following array.float f [6] [4] [2]; - a)12
- b)26
- c)48
- d)20
Correct answer is option 'C'. Can you explain this answer?
Find the number of elements in the following array.
float f [6] [4] [2];
a)
12
b)
26
c)
48
d)
20

|
Crack Gate answered |
A number of elements present in the array can be found by calculating the length of the array.
Algorithm:
Step 1: Start
Step 2: Initialize arr[] = {1, 2, 3, 4, 5, 6}
Step 3: length = sizeof(arr) / sizeof(arr[0])
Step 4: Print "number of elements present in given array" by assigning length.
Step 5: Return 0
Step 6: End
Analysis:- float f [6] [4] [2]
Number of element = 6 × 4 × 2 = 48.
So, the number of elements in the array, float f [6] [4] [2] is 48.
Predict the output of following program
- a)Stack Overflow
- b)3
- c)4
- d)5
Correct answer is option 'D'. Can you explain this answer?
Predict the output of following program
a)
Stack Overflow
b)
3
c)
4
d)
5

|
Aditya Tiwari answered |
Whenever such small recursive programs are given, apply recursive tree method along with dynamic programming. Here f(11)=f(5)+f(6) f(5)=f(2)+f(3) f(2)=f(1)=1 f(3)=f(1)+f(2)=1+1=2 so f(5) becomes 3 Now, f(6)=f(3)=2 and finally f(11)=3+2=5
Consider the following code snippet:

What will happen when the above snippet is executed?- a)The code will be executed successfully and no output will be generated
- b)The code will be executed successfully and random output will be generated
- c)The code will show a compile time error
- d)The code will run for some time and stop when the stack overflows
Correct answer is option 'D'. Can you explain this answer?
Consider the following code snippet:

What will happen when the above snippet is executed?
What will happen when the above snippet is executed?
a)
The code will be executed successfully and no output will be generated
b)
The code will be executed successfully and random output will be generated
c)
The code will show a compile time error
d)
The code will run for some time and stop when the stack overflows
|
|
Krithika Gupta answered |
Every function call is stored in the stack memory. In this case, there is no terminating condition(base case). So, my_recursive_function() will be called continuously till the stack overflows and there is no more space to store the function calls. At this point of time, the program will stop abruptly.
Predict output of following program
- a)4
- b)8
- c)16
- d)Runtime Error
Correct answer is option 'C'. Can you explain this answer?
Predict output of following program
a)
4
b)
8
c)
16
d)
Runtime Error
|
|
Rashi Banerjee answered |
Fun(2)
|
2*fun(3)
|
2*fun(4)
|
4 After tree evaluation we get 16
So, C is the correct answer
|
2*fun(3)
|
2*fun(4)
|
4 After tree evaluation we get 16
So, C is the correct answer
What does the following function do?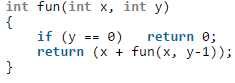
- a)x + y
- b)x + x*y
- c)x*y
- d)xy
Correct answer is option 'C'. Can you explain this answer?
What does the following function do?
a)
x + y
b)
x + x*y
c)
x*y
d)
xy
|
|
Mainak Kulkarni answered |
The function adds x to itself y times which is x*y.

- a)-9
- b)5
- c)15
- d)19
Correct answer is 'C'. Can you explain this answer?
a)
-9
b)
5
c)
15
d)
19
|
|
Shraddha Kaur answered |
f() is a recursive function which adds f(a+1, n-1) to *a if *a is even. If *a is odd then f() subtracts f(a+1, n-1) from *a. See below recursion tree for execution of f(a, 6).
So, the final returned value is 12 + (7 – (13 – (4 + (11 – (6 + 0))))) = 15
Consider the following recursive function fun(x, y). What is the value of fun(4, 3)
- a)13
- b)12
- c)9
- d)10
Correct answer is option 'A'. Can you explain this answer?
Consider the following recursive function fun(x, y). What is the value of fun(4, 3)
a)
13
b)
12
c)
9
d)
10
|
|
Soumya Dey answered |
The function fun() calculates and returns ((1 + 2 … + x-1 + x) +y) which is x(x+1)/2 + y.
Consider the C function given below.
Q. Which one of the following is TRUE?- a)The function returns 0 for all values of j.
- b)The function prints the string something for all values of j.
- c)The function returns 0 when j = 50.
- d)The function will exhaust the runtime stack or run into an infinite loop when j = 50
Correct answer is option 'D'. Can you explain this answer?
Consider the C function given below.
Q. Which one of the following is TRUE?
a)
The function returns 0 for all values of j.
b)
The function prints the string something for all values of j.
c)
The function returns 0 when j = 50.
d)
The function will exhaust the runtime stack or run into an infinite loop when j = 50
|
|
Akanksha Chauhan answered |
When j is 50, the function would call itself again and again as neither i nor j is changed inside the recursion.
The function f is defined as follows: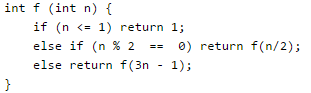 Assuming that arbitrarily large integers can be passed as a parameter to the function, consider the following statements.
Assuming that arbitrarily large integers can be passed as a parameter to the function, consider the following statements.
1. The function f terminates for finitely many different values of n ≥ 1.
ii. The function f terminates for infinitely many different values of n ≥ 1.
iii. The function f does not terminate for finitely many different values of n ≥ 1.
iv. The function f does not terminate for infinitely many different values of n ≥ 1.
Which one of the following options is true of the above?- a)(i) and (iii)
- b)(i) and (iv)
- c)(ii) and (iii)
- d)(ii) and (iv)
Correct answer is option 'D'. Can you explain this answer?
The function f is defined as follows:
Assuming that arbitrarily large integers can be passed as a parameter to the function, consider the following statements.
1. The function f terminates for finitely many different values of n ≥ 1.
ii. The function f terminates for infinitely many different values of n ≥ 1.
iii. The function f does not terminate for finitely many different values of n ≥ 1.
iv. The function f does not terminate for infinitely many different values of n ≥ 1.
Which one of the following options is true of the above?
1. The function f terminates for finitely many different values of n ≥ 1.
ii. The function f terminates for infinitely many different values of n ≥ 1.
iii. The function f does not terminate for finitely many different values of n ≥ 1.
iv. The function f does not terminate for infinitely many different values of n ≥ 1.
Which one of the following options is true of the above?
a)
(i) and (iii)
b)
(i) and (iv)
c)
(ii) and (iii)
d)
(ii) and (iv)
|
|
Shruti Tiwari answered |
The function terminates for all values having a factor of 2 {(2.x)2==0}
So, (i) is false and (ii) is TRUE.
Let n = 3, it will terminate in 2nd iteration.
Let n=5, it will go like 5 - 14 - 7 - 20 - 10 - 5 – and now it will repeat.
And any number with a factor of 5 and 2, there are infinite recursions possible.
So, (iv) is TRUE and (iii) is false.
So, (i) is false and (ii) is TRUE.
Let n = 3, it will terminate in 2nd iteration.
Let n=5, it will go like 5 - 14 - 7 - 20 - 10 - 5 – and now it will repeat.
And any number with a factor of 5 and 2, there are infinite recursions possible.
So, (iv) is TRUE and (iii) is false.
Match the pairs in the following questions: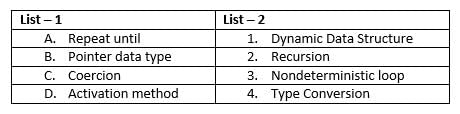
- a)A – 2, B – 1, C – 4, D – 3
- b)A – 3, B – 4, C – 1, D – 2
- c)A – 3, B – 1, C – 4, D – 2
- d)A – 2, B – 4, C – 1, D – 3
Correct answer is option 'C'. Can you explain this answer?
Match the pairs in the following questions:

a)
A – 2, B – 1, C – 4, D – 3
b)
A – 3, B – 4, C – 1, D – 2
c)
A – 3, B – 1, C – 4, D – 2
d)
A – 2, B – 4, C – 1, D – 3
|
|
Ravi Singh answered |
Correct matching is A – 3, B – 1, C – 4, D – 2 Option (C) is correct.
Output of following program?
- a)1000 2000 4000
- b)1000 2000 4000 4000 2000 1000
- c)1000 2000 4000 2000 1000
- d)1000 2000 2000 1000
Correct answer is option 'B'. Can you explain this answer?
Output of following program?
a)
1000 2000 4000
b)
1000 2000 4000 4000 2000 1000
c)
1000 2000 4000 2000 1000
d)
1000 2000 2000 1000

|
Aryan Batheja answered |
First time n=1000 Then 1000 is printed by first printf function then call print(2*1000) then again print 2000 by printf function then call print(2*2000) and it prints 4000 next time print(4000*2) is called. Here 8000 is greater than 4000 condition becomes true and it return at function(2*4000). Here n=4000 then 4000 will again print through second printf. Similarly print(2*2000) after that n=2000 then 2000 will print and come back at print(2*1000) here n=1000, so print 1000 through second printf. Option (B) is correct.
What will be the output of the following C program?
- a)3 1 2 2 1 3 4 4 4
- b)3 1 2 1 1 1 2 2 2
- c)3 1 2 2 1 3 4
- d)3 1 2 1 1 1 2
Correct answer is option 'A'. Can you explain this answer?
What will be the output of the following C program?
a)
3 1 2 2 1 3 4 4 4
b)
3 1 2 1 1 1 2 2 2
c)
3 1 2 2 1 3 4
d)
3 1 2 1 1 1 2
|
|
Kajal Sharma answered |
count(3) will print value of n and d. So 3 1 will be printed and d will become 2.
Then count(2) will be called. It will print value of n and d.
So 2 2 will be printed and d will become 3.
Then count(1) will be called. It will print value of n and d.
So 1 3 will be printed and d will become 4.
Now count(1) will print value of d which is 4. count(1) will finish its execution.
Then count(2) will print value of d which is 4.
Similarly, count(3) will print value of d which is 4.
So series will be A.
Then count(2) will be called. It will print value of n and d.
So 2 2 will be printed and d will become 3.
Then count(1) will be called. It will print value of n and d.
So 1 3 will be printed and d will become 4.
Now count(1) will print value of d which is 4. count(1) will finish its execution.
Then count(2) will print value of d which is 4.
Similarly, count(3) will print value of d which is 4.
So series will be A.
Chapter doubts & questions for Recursion - 6 Months Preparation for GATE CSE 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Recursion - 6 Months Preparation for GATE CSE in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
6 Months Preparation for GATE CSE
453 videos|1305 docs|700 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily









