All Exams >
Computer Science Engineering (CSE) >
6 Months Preparation for GATE CSE >
All Questions
All questions of Trees for Computer Science Engineering (CSE) Exam
What are the main applications of tree data structure? 1) Manipulate hierarchical data 2) Make information easy to search (see tree traversal). 3) Manipulate sorted lists of data 4) Router algorithms 5) Form of a multi-stage decision-making, like Chess Game. 6) As a workflow for compositing digital images for visual effects- a)1, 2, 3, 4 and 6
- b)1, 2, 3, 4 and 5
- c)1, 3, 4, 5 and 6
- d)1, 2, 3, 4, 5 and 6
Correct answer is 'D'. Can you explain this answer?
What are the main applications of tree data structure? 1) Manipulate hierarchical data 2) Make information easy to search (see tree traversal). 3) Manipulate sorted lists of data 4) Router algorithms 5) Form of a multi-stage decision-making, like Chess Game. 6) As a workflow for compositing digital images for visual effects
a)
1, 2, 3, 4 and 6
b)
1, 2, 3, 4 and 5
c)
1, 3, 4, 5 and 6
d)
1, 2, 3, 4, 5 and 6
|
Atharva Kulkarni answered |
Main Applications of Tree Data Structure:
1. Manipulate Hierarchical Data:
Trees are used to represent hierarchical data, such as file systems or organization charts, where each node represents a folder, file, or employee.
2. Make Information Easy to Search:
Tree traversal algorithms can be used to search for specific data within a tree structure, making it an efficient way to store and retrieve information.
3. Manipulate Sorted Lists of Data:
Binary search trees can be used to manipulate and search sorted lists of data, providing a faster search time than traditional linear searches.
4. Router Algorithms:
Trees are used in computer networking to represent routing algorithms that determine the path of data packets through a network.
5. Multi-Stage Decision Making:
Trees can be used to represent multi-stage decision-making processes, such as in a chess game, where each node represents a possible move and the branches represent subsequent moves.
6. Workflow for Compositing Digital Images:
Trees are used in visual effects to represent the workflow for compositing digital images, where each node represents a stage in the process and the branches represent the steps taken to achieve the final image.
Therefore, the correct answer is D, as all of these applications use tree data structures.
1. Manipulate Hierarchical Data:
Trees are used to represent hierarchical data, such as file systems or organization charts, where each node represents a folder, file, or employee.
2. Make Information Easy to Search:
Tree traversal algorithms can be used to search for specific data within a tree structure, making it an efficient way to store and retrieve information.
3. Manipulate Sorted Lists of Data:
Binary search trees can be used to manipulate and search sorted lists of data, providing a faster search time than traditional linear searches.
4. Router Algorithms:
Trees are used in computer networking to represent routing algorithms that determine the path of data packets through a network.
5. Multi-Stage Decision Making:
Trees can be used to represent multi-stage decision-making processes, such as in a chess game, where each node represents a possible move and the branches represent subsequent moves.
6. Workflow for Compositing Digital Images:
Trees are used in visual effects to represent the workflow for compositing digital images, where each node represents a stage in the process and the branches represent the steps taken to achieve the final image.
Therefore, the correct answer is D, as all of these applications use tree data structures.
If arity of operators is fixed, then which of the following notations can be used to parse expressions without parentheses? a) Infix Notation (Inorder traversal of a expression tree) b) Postfix Notation (Postorder traversal of a expression tree) c) Prefix Notation (Preorder traversal of a expression tree)- a)b and c
- b)Only b
- c)a, b and c
- d)None of them
Correct answer is option 'A'. Can you explain this answer?
If arity of operators is fixed, then which of the following notations can be used to parse expressions without parentheses? a) Infix Notation (Inorder traversal of a expression tree) b) Postfix Notation (Postorder traversal of a expression tree) c) Prefix Notation (Preorder traversal of a expression tree)
a)
b and c
b)
Only b
c)
a, b and c
d)
None of them
|
Swara Dasgupta answered |
Consider inorder traversal or infix as
a+b*c+d*e+f+g
its prefix is
++a*bc++*defg
And postfix expression is
abc*++de*f+g++
Here prefix and postfix can be calculated in right way by using algorithms.But inorder can give different values.
The elements 32, 15, 20, 30, 12, 25, 16 are inserted one by one in the given order into a Max Heap. The resultant Max Heap is.- a)
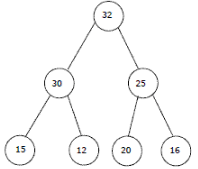
- b)
- c)
- d)
Correct answer is option 'A'. Can you explain this answer?
The elements 32, 15, 20, 30, 12, 25, 16 are inserted one by one in the given order into a Max Heap. The resultant Max Heap is.
a)
b)
c)
d)
|
Crack Gate answered |
32, 15, 20, 30, 12, 25, 16
After insertion of 32, 15 and 20
After insertion of 32, 15 and 20
After insertion of 30
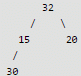
Max Heap property is violated, so 30 is swapped with 15
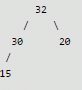
After insertion of 12
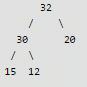
After insertion of 25
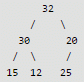
Max Heap property is violated, so 25 is swapped with 20
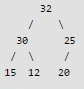
After insertion of 16
How many distinct binary search trees can be created out of 4 distinct keys?- a)4
- b)14
- c)24
- d)42
Correct answer is option 'B'. Can you explain this answer?
How many distinct binary search trees can be created out of 4 distinct keys?
a)
4
b)
14
c)
24
d)
42
|
Rajeev Menon answered |
Number of Binary Search trees for n nodes is given by = (2n)! / n! * (n+1)!
Hence for 4 keys or nodes-
= 8! /4! * 5!
= 14
Hence, 14 distinct binary search trees are possible for 4 keys.
So, the Correct Answer is Option B
So, the Correct Answer is Option B
You can solve many such questions & mock tests by going through the course:
What does the following function do for a given binary tree?int fun(struct node *root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 0;
return 1 + fun(root->left) + fun(root->right);
}- a)Counts leaf nodes
- b)Counts internal nodes
- c)Returns height where height is defined as number of edges on the path from root to deepest node
- d)Return diameter where diameter is number of edges on the longest path between any two nodes.
Correct answer is option 'B'. Can you explain this answer?
What does the following function do for a given binary tree?
int fun(struct node *root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 0;
return 1 + fun(root->left) + fun(root->right);
}
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 0;
return 1 + fun(root->left) + fun(root->right);
}
a)
Counts leaf nodes
b)
Counts internal nodes
c)
Returns height where height is defined as number of edges on the path from root to deepest node
d)
Return diameter where diameter is number of edges on the longest path between any two nodes.
|
Sanya Agarwal answered |
The function counts internal nodes. 1) If root is NULL or a leaf node, it returns 0. 2) Otherwise returns, 1 plus count of internal nodes in left subtree, plus count of internal nodes in right subtree.
Which traversal of tree resembles the breadth first search of the graph- a)Preorder
- b)Inorder
- c)Postorder
- d)Level order
Correct answer is option 'D'. Can you explain this answer?
Which traversal of tree resembles the breadth first search of the graph
a)
Preorder
b)
Inorder
c)
Postorder
d)
Level order
|
|
Sanya Agarwal answered |
Breadth first search visits all the neighbors first and then deepens into each neighbor one by one. The level order traversal of the tree also visits nodes on the current level and then goes to the next level.
Level of a node is distance from root to that node. For example, level of root is 1 and levels of left and right children of root is 2. The maximum number of nodes on level i of a binary tree is
In the following answers, the operator '^' indicates power.- a)2^(i-1)
- b)2^i
- c)2^(i+1)
- d)2^[(i+1)/2]
Correct answer is option 'A'. Can you explain this answer?
Level of a node is distance from root to that node. For example, level of root is 1 and levels of left and right children of root is 2. The maximum number of nodes on level i of a binary tree is
In the following answers, the operator '^' indicates power.
In the following answers, the operator '^' indicates power.
a)
2^(i-1)
b)
2^i
c)
2^(i+1)
d)
2^[(i+1)/2]
|
Milan Rane answered |
Explanation:
The maximum number of nodes on level i of a binary tree is given by the formula: 2^(i-1)
Proof:
Let's consider the levels of the binary tree from top to bottom. The root node is at level 1, its children are at level 2, their children are at level 3, and so on.
At level 1, there is only one node which is the root node. Therefore, the maximum number of nodes on level 1 is 2^(1-1) = 1.
At level 2, there can be at most two nodes because each node at level 1 can have at most two children. Therefore, the maximum number of nodes on level 2 is 2^(2-1) = 2.
At level 3, each node at level 2 can have at most two children. Therefore, the maximum number of nodes on level 3 is 2^(3-1) = 4.
Similarly, at level i, each node at level i-1 can have at most two children. Therefore, the maximum number of nodes on level i is 2^(i-1).
Hence, the correct answer is option 'A' which is 2^(i-1).
The maximum number of nodes on level i of a binary tree is given by the formula: 2^(i-1)
Proof:
Let's consider the levels of the binary tree from top to bottom. The root node is at level 1, its children are at level 2, their children are at level 3, and so on.
At level 1, there is only one node which is the root node. Therefore, the maximum number of nodes on level 1 is 2^(1-1) = 1.
At level 2, there can be at most two nodes because each node at level 1 can have at most two children. Therefore, the maximum number of nodes on level 2 is 2^(2-1) = 2.
At level 3, each node at level 2 can have at most two children. Therefore, the maximum number of nodes on level 3 is 2^(3-1) = 4.
Similarly, at level i, each node at level i-1 can have at most two children. Therefore, the maximum number of nodes on level i is 2^(i-1).
Hence, the correct answer is option 'A' which is 2^(i-1).
An array of integers of size n can be converted into a heap by adjusting the heaps rooted at each internal node of the complete binary tree starting at the node ⌊(n - 1) /2⌋, and doing this adjustment up to the root node (root node is at index 0) in the order ⌊(n - 1)/2⌋, ⌊(n - 3)/ 2⌋, ....., 0. The time required to construct a heap in this manner is- a)O(log n)
- b)O(n)
- c)O (n log log n)
- d)O(n log n)
Correct answer is option 'B'. Can you explain this answer?
An array of integers of size n can be converted into a heap by adjusting the heaps rooted at each internal node of the complete binary tree starting at the node ⌊(n - 1) /2⌋, and doing this adjustment up to the root node (root node is at index 0) in the order ⌊(n - 1)/2⌋, ⌊(n - 3)/ 2⌋, ....., 0. The time required to construct a heap in this manner is
a)
O(log n)
b)
O(n)
c)
O (n log log n)
d)
O(n log n)
|
Baishali Bajaj answered |
The above statement is actually algorithm for building a Heap of an input array A.
BUILD-HEAP(A)
heapsize := size(A);
for i := floor(heapsize/2) downto 1
do HEAPIFY(A, i);
end for
END
Upper bound of time complexity is O(n) for above algo
A binary tree with n > 1 nodes has n1, n2 and n3 nodes of degree one, two and three respectively. The degree of a node is defined as the number of its neighbors. n3 can be expressed as- a)n1 + n2 - 1
- b)n1 - 2
- c)[((n1 + n2)/2)]
- d)n2 - 1
Correct answer is option 'B'. Can you explain this answer?
A binary tree with n > 1 nodes has n1, n2 and n3 nodes of degree one, two and three respectively. The degree of a node is defined as the number of its neighbors. n3 can be expressed as
a)
n1 + n2 - 1
b)
n1 - 2
c)
[((n1 + n2)/2)]
d)
n2 - 1
|
Maitri Yadav answered |
Postorder traversal of a given binary search tree, T produces the following sequence of keys 10, 9, 23, 22, 27, 25, 15, 50, 95, 60, 40, 29 Which one of the following sequences of keys can be the result of an in-order traversal of the tree T? - a)9, 10, 15, 22, 23, 25, 27, 29, 40, 50, 60, 95
- b)9, 10, 15, 22, 40, 50, 60, 95, 23, 25, 27, 29
- c)29, 15, 9, 10, 25, 22, 23, 27, 40, 60, 50, 95
- d)95, 50, 60, 40, 27, 23, 22, 25, 10, 9, 15, 29
Correct answer is option 'A'. Can you explain this answer?
Postorder traversal of a given binary search tree, T produces the following sequence of keys 10, 9, 23, 22, 27, 25, 15, 50, 95, 60, 40, 29 Which one of the following sequences of keys can be the result of an in-order traversal of the tree T?
a)
9, 10, 15, 22, 23, 25, 27, 29, 40, 50, 60, 95
b)
9, 10, 15, 22, 40, 50, 60, 95, 23, 25, 27, 29
c)
29, 15, 9, 10, 25, 22, 23, 27, 40, 60, 50, 95
d)
95, 50, 60, 40, 27, 23, 22, 25, 10, 9, 15, 29
|
Saptarshi Nair answered |
Inorder traversal of a BST always gives elements in increasing order. Among all four options, a) is the only increasing order sequence.
What is common in three different types of traversals (Inorder, Preorder and Postorder)?- a)Root is visited before right subtree
- b)Left subtree is always visited before right subtree
- c)Root is visited after left subtree
- d)All of the above
- e)None of the above
Correct answer is option 'B'. Can you explain this answer?
What is common in three different types of traversals (Inorder, Preorder and Postorder)?
a)
Root is visited before right subtree
b)
Left subtree is always visited before right subtree
c)
Root is visited after left subtree
d)
All of the above
e)
None of the above
|
|
Sanya Agarwal answered |
The order of inorder traversal is LEFT ROOT RIGHT The order of preorder traversal is ROOT LEFT RIGHT The order of postorder traversal is LEFT RIGHT ROOT In all three traversals, LEFT is traversed before RIGHT
Which of the following traversal outputs the data in sorted order in a BST?- a)Preorder
- b)Inorder
- c)Postorder
- d)Level order
Correct answer is option 'B'. Can you explain this answer?
Which of the following traversal outputs the data in sorted order in a BST?
a)
Preorder
b)
Inorder
c)
Postorder
d)
Level order
|
Abhay Bhadouriya answered |
Inorder traversal of a BST outputs data in sorted order. Read here for details.
Choose the equivalent prefix form of the following expression
(a + (b − c))* ((d − e)/(f + g − h))- a)* +a − bc /− de − +fgh
- b)* +a −bc − /de − +fgh
- c)* +a − bc /− ed + −fgh
- d)* +ab − c /− ed + −fgh
Correct answer is option 'A'. Can you explain this answer?
Choose the equivalent prefix form of the following expression
(a + (b − c))* ((d − e)/(f + g − h))
(a + (b − c))* ((d − e)/(f + g − h))
a)
* +a − bc /− de − +fgh
b)
* +a −bc − /de − +fgh
c)
* +a − bc /− ed + −fgh
d)
* +ab − c /− ed + −fgh
|
Pranjal Sen answered |
The expression is incomplete. Please provide the complete expression for me to determine the equivalent prefix form.
Consider a node X in a Binary Tree. Given that X has two children, let Y be Inorder successor of X. Which of the following is true about Y?- a)Y has no right child
- b)Y has no left child
- c)Y has both children
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
Consider a node X in a Binary Tree. Given that X has two children, let Y be Inorder successor of X. Which of the following is true about Y?
a)
Y has no right child
b)
Y has no left child
c)
Y has both children
d)
None of the above
|
Sagarika Patel answered |
Since X has both children, Y must be leftmost node in right child of X.
A binary tree T has 20 leaves. The number of nodes in T having two children is- a)18
- b)19
- c)17
- d)Any number between 10 and 20
Correct answer is option 'B'. Can you explain this answer?
A binary tree T has 20 leaves. The number of nodes in T having two children is
a)
18
b)
19
c)
17
d)
Any number between 10 and 20
|
Amar Mukherjee answered |
Sum of all degrees = 2 * |E|. Here considering tree as a k-ary tree :
Sum of degrees of leaves + Sum of degrees for Internal Node except root + Root's degree = 2 * (No. of nodes - 1). Putting values of above terms,
L + (I-1)*(k+1) + k = 2 * (L + I - 1)
L + k*I - k + I -1 + k = 2*L + 2I - 2
L + K*I + I - 1 = 2*L + 2*I - 2
K*I + 1 - I = L
(K-1)*I + 1 = L
Given k = 2, L=20
==> (2-1)*I + 1 = 20
==> I = 19
==> T has 19 internal nodes which are having two children.
L + (I-1)*(k+1) + k = 2 * (L + I - 1)
L + k*I - k + I -1 + k = 2*L + 2I - 2
L + K*I + I - 1 = 2*L + 2*I - 2
K*I + 1 - I = L
(K-1)*I + 1 = L
Given k = 2, L=20
==> (2-1)*I + 1 = 20
==> I = 19
==> T has 19 internal nodes which are having two children.
A scheme for storing binary trees in an array X is as follows. Indexing of X starts at 1 instead of 0. the root is stored at X[1]. For a node stored at X[i], the left child, if any, is stored in X[2i] and the right child, if any, in X[2i 1]. To be able to store any binary tree on n vertices the minimum size of X should be.
- a) log2n
- b) n
- c) 2n + 1
- d) 2^n — 1
Correct answer is option 'D'. Can you explain this answer?
A scheme for storing binary trees in an array X is as follows. Indexing of X starts at 1 instead of 0. the root is stored at X[1]. For a node stored at X[i], the left child, if any, is stored in X[2i] and the right child, if any, in X[2i 1]. To be able to store any binary tree on n vertices the minimum size of X should be.
a)
log2nb)
nc)
2n + 1d)
2^n — 1|
|
Neha Choudhury answered |
For a right skewed binary tree, number of nodes will be 2^n – 1. For example, in below binary tree, node ‘A’ will be stored at index 1, ‘B’ at index 3, ‘C’ at index 7 and ‘D’ at index 15.
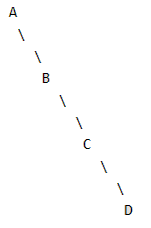
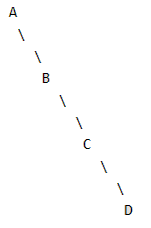
When searching for the key value 60 in a binary search tree, nodes containing the key values 10, 20, 40, 50, 70 80, 90 are traversed, not necessarily in the order given. How many different orders are possible in which these key values can occur on the search path from the root to the node containing the value 60?- a) 35
- b) 64
- c) 128
- d) 5040
Correct answer is option 'A'. Can you explain this answer?
When searching for the key value 60 in a binary search tree, nodes containing the key values 10, 20, 40, 50, 70 80, 90 are traversed, not necessarily in the order given. How many different orders are possible in which these key values can occur on the search path from the root to the node containing the value 60?
a)
35
b)
64
c)
128
d)
5040
|
|
Sudhir Patel answered |
There are two set of values, smaller than 60 and greater than 60. Smaller values 10, 20, 40 and 50 are visited, means they are visited in order. Similarly, 90, 80 and 70 are visited in order.
= 7!/(4!3!)
= 35
= 7!/(4!3!)
= 35
A binary tree with n > 1 nodes has n1, n2 and n3 nodes of degree one, two and three respectively. The degree of a node is defined as the number of its neighbors.
Starting with the above tree, while there remains a node v of degree two in the tree, add an edge between the two neighbors of v and then remove v from the tree. How many edges will remain at the end of the process?- a)2 * n1 - 3
- b)n2 + 2 * n1 - 2
- c)n3 - n2
- d)n2 + n1 - 2
Correct answer is option 'A'. Can you explain this answer?
A binary tree with n > 1 nodes has n1, n2 and n3 nodes of degree one, two and three respectively. The degree of a node is defined as the number of its neighbors.
Starting with the above tree, while there remains a node v of degree two in the tree, add an edge between the two neighbors of v and then remove v from the tree. How many edges will remain at the end of the process?
Starting with the above tree, while there remains a node v of degree two in the tree, add an edge between the two neighbors of v and then remove v from the tree. How many edges will remain at the end of the process?
a)
2 * n1 - 3
b)
n2 + 2 * n1 - 2
c)
n3 - n2
d)
n2 + n1 - 2
|
Rajveer Sharma answered |
With reference to figure of answer of previous question:
Breadth First Search (BFS) is started on a binary tree beginning from the root vertex. There is a vertex t at a distance four from the root. If t is the n-th vertex in this BFS traversal, then the maximum possible value of n is ________ [This Question was originally a Fill-in-the-blanks Question]- a)15
- b)16
- c)31
- d)32
Correct answer is option 'C'. Can you explain this answer?
Breadth First Search (BFS) is started on a binary tree beginning from the root vertex. There is a vertex t at a distance four from the root. If t is the n-th vertex in this BFS traversal, then the maximum possible value of n is ________ [This Question was originally a Fill-in-the-blanks Question]
a)
15
b)
16
c)
31
d)
32
|
Arya Kaur answered |
It would be node number 31 for given distance 4. For example if we consider at distance 2, below highlighted node G can be the farthest node at position 7.
Consider the pseudocode given below. The function DoSomething() takes as argument a pointer to the root of an arbitrary tree represented by the leftMostChild-rightSibling representation. Each node of the tree is of type treeNode.typedef struct treeNode* treeptr;
struct treeNode
{treeptr leftMostChild, rightSibling;
};int DoSomething (treeptr tree)
{
int value=0;
if (tree != NULL)
{
if (tree->leftMostChild == NULL)
value = 1;
else
value = DoSomething(tree->leftMostChild); value = value + DoSomething(tree->rightSibling);
}
return(value);
} Q. When the pointer to the root of a tree is passed as the argument to DoSomething, the value returned by the function corresponds to the- a)number of internal nodes in the tree.
- b)height of the tree.
- c)number of nodes without a right sibling in the tree.
- d)number of leaf nodes in the tree.
Correct answer is option 'D'. Can you explain this answer?
Consider the pseudocode given below. The function DoSomething() takes as argument a pointer to the root of an arbitrary tree represented by the leftMostChild-rightSibling representation. Each node of the tree is of type treeNode.
typedef struct treeNode* treeptr;
struct treeNode
{
struct treeNode
{
treeptr leftMostChild, rightSibling;
};
};
int DoSomething (treeptr tree)
{
int value=0;
if (tree != NULL)
{
if (tree->leftMostChild == NULL)
value = 1;
else
value = DoSomething(tree->leftMostChild); value = value + DoSomething(tree->rightSibling);
}
return(value);
}
{
int value=0;
if (tree != NULL)
{
if (tree->leftMostChild == NULL)
value = 1;
else
value = DoSomething(tree->leftMostChild); value = value + DoSomething(tree->rightSibling);
}
return(value);
}
Q. When the pointer to the root of a tree is passed as the argument to DoSomething, the value returned by the function corresponds to the
a)
number of internal nodes in the tree.
b)
height of the tree.
c)
number of nodes without a right sibling in the tree.
d)
number of leaf nodes in the tree.
|
Gauri Banerjee answered |
Explanation:
To understand why the value returned by the function corresponds to the number of leaf nodes in the tree, let's analyze the pseudocode step by step.
The function DoSomething() takes a pointer to the root of an arbitrary tree represented by the leftMostChild-rightSibling representation.
Step 1: Initialize a variable "value" to 0.
Step 2: Check if the tree pointer is not NULL. If it is NULL, it means that the tree is empty and there are no nodes. In this case, the function returns 0.
Step 3: If the tree pointer is not NULL, check if the leftMostChild pointer of the current node is NULL. If it is NULL, it means that the current node is a leaf node (a node with no children). In this case, set the value to 1.
Step 4: If the leftMostChild pointer is not NULL, recursively call the DoSomething() function with the leftMostChild pointer as the argument. This will traverse the subtree rooted at the leftMostChild pointer and count the number of leaf nodes in that subtree.
Step 5: After the recursive call, the value variable will hold the number of leaf nodes in the subtree rooted at the leftMostChild pointer.
Step 6: Call the DoSomething() function with the rightSibling pointer as the argument. This will traverse the remaining siblings of the current node and count the number of leaf nodes in each subtree rooted at the siblings.
Step 7: Finally, return the value variable.
Conclusion:
From the above analysis, we can conclude that the value returned by the DoSomething() function corresponds to the number of leaf nodes in the tree. This is because at each recursive call, the function checks whether the current node is a leaf node or not. If it is a leaf node, the value is set to 1. If it is not a leaf node, the function recursively counts the number of leaf nodes in the subtrees rooted at its children. By traversing the entire tree using the leftMostChild-rightSibling representation and counting the number of leaf nodes at each step, the function eventually returns the total number of leaf nodes in the tree.
To understand why the value returned by the function corresponds to the number of leaf nodes in the tree, let's analyze the pseudocode step by step.
The function DoSomething() takes a pointer to the root of an arbitrary tree represented by the leftMostChild-rightSibling representation.
Step 1: Initialize a variable "value" to 0.
Step 2: Check if the tree pointer is not NULL. If it is NULL, it means that the tree is empty and there are no nodes. In this case, the function returns 0.
Step 3: If the tree pointer is not NULL, check if the leftMostChild pointer of the current node is NULL. If it is NULL, it means that the current node is a leaf node (a node with no children). In this case, set the value to 1.
Step 4: If the leftMostChild pointer is not NULL, recursively call the DoSomething() function with the leftMostChild pointer as the argument. This will traverse the subtree rooted at the leftMostChild pointer and count the number of leaf nodes in that subtree.
Step 5: After the recursive call, the value variable will hold the number of leaf nodes in the subtree rooted at the leftMostChild pointer.
Step 6: Call the DoSomething() function with the rightSibling pointer as the argument. This will traverse the remaining siblings of the current node and count the number of leaf nodes in each subtree rooted at the siblings.
Step 7: Finally, return the value variable.
Conclusion:
From the above analysis, we can conclude that the value returned by the DoSomething() function corresponds to the number of leaf nodes in the tree. This is because at each recursive call, the function checks whether the current node is a leaf node or not. If it is a leaf node, the value is set to 1. If it is not a leaf node, the function recursively counts the number of leaf nodes in the subtrees rooted at its children. By traversing the entire tree using the leftMostChild-rightSibling representation and counting the number of leaf nodes at each step, the function eventually returns the total number of leaf nodes in the tree.
The numbers 1, 2, .... n are inserted in a binary search tree in some order. In the resulting tree, the right subtree of the root contains p nodes. The first number to be inserted in the tree must be- a)p
- b)p + 1
- c)n - p
- d)n - p + 1
Correct answer is option 'C'. Can you explain this answer?
The numbers 1, 2, .... n are inserted in a binary search tree in some order. In the resulting tree, the right subtree of the root contains p nodes. The first number to be inserted in the tree must be
a)
p
b)
p + 1
c)
n - p
d)
n - p + 1
|
Srishti Yadav answered |
Binary Search Tree, is a node-based binary tree data structure which has the following properties:
- The left subtree of a node contains only nodes with keys less than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- The left and right subtree each must also be a binary search tree. There must be no duplicate nodes.
So let us say n=10, p=4. According to BST property the root must be 10-4=6 (considering all unique elements in BST)
And according to BST insertion, root is the first element to be inserted in a BST.
Therefore, the answer is (n-p).
Let LASTPOST, LASTIN and LASTPRE denote the last vertex visited in a postorder, inorder and preorder traversal, respectively, of a complete binary tree. Which of the following is always true?- a)LASTIN = LASTPOST
- b)LASTIN = LASTPRE
- c)LASTPRE = LASTPOST
- d)None of the above
Correct answer is option 'D'. Can you explain this answer?
Let LASTPOST, LASTIN and LASTPRE denote the last vertex visited in a postorder, inorder and preorder traversal, respectively, of a complete binary tree. Which of the following is always true?
a)
LASTIN = LASTPOST
b)
LASTIN = LASTPRE
c)
LASTPRE = LASTPOST
d)
None of the above
|
Rishabh Menon answered |
Explanation:
In a complete binary tree, the number of nodes is always a power of 2. Let us consider a complete binary tree with 7 nodes numbered from 1 to 7 in level order traversal. The tree looks like:
```
1
/ \
2 3
/ \ / \
4 5 6 7
```
Let us now traverse the tree in inorder, preorder and postorder and observe the values of LASTIN, LASTPRE and LASTPOST.
Inorder traversal: 4 2 5 1 6 3 7
- LASTIN = 7 (last node visited in inorder traversal)
Preorder traversal: 1 2 4 5 3 6 7
- LASTPRE = 7 (last node visited in preorder traversal)
Postorder traversal: 4 5 2 6 7 3 1
- LASTPOST = 7 (last node visited in postorder traversal)
From the above example, we can see that none of the options (a), (b) or (c) are always true.
Conclusion:
Therefore, the correct answer is option (d) None of the above.
In a complete binary tree, the number of nodes is always a power of 2. Let us consider a complete binary tree with 7 nodes numbered from 1 to 7 in level order traversal. The tree looks like:
```
1
/ \
2 3
/ \ / \
4 5 6 7
```
Let us now traverse the tree in inorder, preorder and postorder and observe the values of LASTIN, LASTPRE and LASTPOST.
Inorder traversal: 4 2 5 1 6 3 7
- LASTIN = 7 (last node visited in inorder traversal)
Preorder traversal: 1 2 4 5 3 6 7
- LASTPRE = 7 (last node visited in preorder traversal)
Postorder traversal: 4 5 2 6 7 3 1
- LASTPOST = 7 (last node visited in postorder traversal)
From the above example, we can see that none of the options (a), (b) or (c) are always true.
Conclusion:
Therefore, the correct answer is option (d) None of the above.
Given two max heaps of size n each, what is the minimum possible time complexity to make a one max-heap of size from elements of two max heaps?- a)O(nLogn)
- b)O(nLogLogn)
- c)O(n)
- d)none
Correct answer is option 'C'. Can you explain this answer?
Given two max heaps of size n each, what is the minimum possible time complexity to make a one max-heap of size from elements of two max heaps?
a)
O(nLogn)
b)
O(nLogLogn)
c)
O(n)
d)
none
|
Niharika Ahuja answered |
Explanation:
To create a single max heap of size 2n from two max heaps of size n, we need to perform the following steps:
1. Merge the two heaps into a single array of size 2n.
2. Call the heapify function on the merged array to create a max heap.
Time Complexity:
1. Merging two heaps into a single array of size 2n takes O(n) time complexity.
2. Heapify function takes O(n) time complexity.
Therefore, the minimum possible time complexity to make a one max-heap of size from elements of two max heaps is O(n).
Conclusion:
Hence, option 'C' is the correct answer.
To create a single max heap of size 2n from two max heaps of size n, we need to perform the following steps:
1. Merge the two heaps into a single array of size 2n.
2. Call the heapify function on the merged array to create a max heap.
Time Complexity:
1. Merging two heaps into a single array of size 2n takes O(n) time complexity.
2. Heapify function takes O(n) time complexity.
Therefore, the minimum possible time complexity to make a one max-heap of size from elements of two max heaps is O(n).
Conclusion:
Hence, option 'C' is the correct answer.
In a binary tree with n nodes, every node has an odd number of descendants. Every node is considered to be its own descendant. What is the number of nodes in the tree that have exactly one child?- a)0
- b)1
- c)(n-1)/2
- d)n-1
Correct answer is option 'A'. Can you explain this answer?
In a binary tree with n nodes, every node has an odd number of descendants. Every node is considered to be its own descendant. What is the number of nodes in the tree that have exactly one child?
a)
0
b)
1
c)
(n-1)/2
d)
n-1
|
|
Anagha Choudhary answered |
It is mentioned that each node has odd number of descendants including node itself, so all nodes must have even number of descendants 0, 2, 4 so on. Which means each node should have either 0 or 2 children. So there will be no node with 1 child. Hence 0 is answer. Following are few examples.
Such a binary tree is full binary tree (a binary tree where every node has 0 or 2 children).
In a binary max heap containing n numbers, the smallest element can be found in time - a)0(n)
- b)O(logn)
- c)0(loglogn)
- d)0(1)
Correct answer is option 'A'. Can you explain this answer?
In a binary max heap containing n numbers, the smallest element can be found in time
a)
0(n)
b)
O(logn)
c)
0(loglogn)
d)
0(1)
|
Palak Khanna answered |
In a max heap, the smallest element is always present at a leaf node. So we need to check for all leaf nodes for the minimum value. Worst case complexity will be O(n)
A complete n-ary tree is a tree in which each node has n children or no children. Let I be the number of internal nodes and L be the number of leaves in a complete n-ary tree. If L = 41, and I = 10, what is the value of n?- a)6
- b)3
- c)4
- d)5
Correct answer is option 'D'. Can you explain this answer?
A complete n-ary tree is a tree in which each node has n children or no children. Let I be the number of internal nodes and L be the number of leaves in a complete n-ary tree. If L = 41, and I = 10, what is the value of n?
a)
6
b)
3
c)
4
d)
5
|
Soumya Dey answered |
For an n-ary tree where each node has n children or no children, following relation holds
L = (n-1)*I + 1
Where L is the number of leaf nodes and I is the number of internal nodes. Let us find out the value of n for the given data.
L = 41 , I = 10
41 = 10*(n-1) + 1
(n-1) = 4
n = 5
41 = 10*(n-1) + 1
(n-1) = 4
n = 5
Consider a complete binary tree where the left and the right subtrees of the root are max-heaps. The lower bound for the number of operations to convert the tree to a heap is- a)Ω(log n)
- b)Ω(n)
- c)Ω(n log n)
- d)Ω(n2)
Correct answer is option 'A'. Can you explain this answer?
Consider a complete binary tree where the left and the right subtrees of the root are max-heaps. The lower bound for the number of operations to convert the tree to a heap is
a)
Ω(log n)
b)
Ω(n)
c)
Ω(n log n)
d)
Ω(n2)
|
Prisha Sharma answered |
The answer to this question is simply max-heapify function. Time complexity of max-heapify is O(Log n) as it recurses at most through height of heap.
// A recursive method to heapify a subtree with root at given index
// This method assumes that the subtrees are already heapified void MinHeap::MaxHeapify(int i)
// This method assumes that the subtrees are already heapified void MinHeap::MaxHeapify(int i)
{
int l = left(i);
int r = right(i);
int largest = i;
if (l < heap_size && harr[l] < harr[i]) largest = l;
if (r < heap_size && harr[r] < harr[smallest]) largest = r;
if (largest != i) { swap(&harr[i], &harr[largest]); MinHeapify(largest);
}
}
int l = left(i);
int r = right(i);
int largest = i;
if (l < heap_size && harr[l] < harr[i]) largest = l;
if (r < heap_size && harr[r] < harr[smallest]) largest = r;
if (largest != i) { swap(&harr[i], &harr[largest]); MinHeapify(largest);
}
}
What is the maximum height of any AVL-tree with 7 nodes? Assume that the height of a tree with a single node is 0.- a)2
- b)3
- c)4
- d)5
Correct answer is option 'B'. Can you explain this answer?
What is the maximum height of any AVL-tree with 7 nodes? Assume that the height of a tree with a single node is 0.
a)
2
b)
3
c)
4
d)
5
|
|
Bijoy Iyer answered |
AVL trees are binary trees with the following restrictions. 1) the height difference of the children is at most 1. 2) both children are AVL trees Following is the most unbalanced AVL tree that we can get with 7 nodes
A Binary Search Tree (BST) stores values in the range 37 to 573. Consider the following sequence of keys.
I. 81, 537, 102, 439, 285, 376, 305
II. 52, 97, 121, 195, 242, 381, 472
III. 142, 248, 520, 386, 345, 270, 307
IV. 550, 149, 507, 395, 463, 402, 270
Q. Which of the following statements is TRUE?- a)I, II and IV are inorder sequences of three different BSTs
- b)I is a preorder sequence of some BST with 439 as the root
- c)II is an inorder sequence of some BST where 121 is the root and 52 is a leaf
- d)IV is a postorder sequence of some BST with 149 as the root
Correct answer is option 'C'. Can you explain this answer?
A Binary Search Tree (BST) stores values in the range 37 to 573. Consider the following sequence of keys.
I. 81, 537, 102, 439, 285, 376, 305
II. 52, 97, 121, 195, 242, 381, 472
III. 142, 248, 520, 386, 345, 270, 307
IV. 550, 149, 507, 395, 463, 402, 270
I. 81, 537, 102, 439, 285, 376, 305
II. 52, 97, 121, 195, 242, 381, 472
III. 142, 248, 520, 386, 345, 270, 307
IV. 550, 149, 507, 395, 463, 402, 270
Q. Which of the following statements is TRUE?
a)
I, II and IV are inorder sequences of three different BSTs
b)
I is a preorder sequence of some BST with 439 as the root
c)
II is an inorder sequence of some BST where 121 is the root and 52 is a leaf
d)
IV is a postorder sequence of some BST with 149 as the root
|
|
Milan Mukherjee answered |
A: I and IV are not in ascending order
B: If 439 is root, It should be 1st element in preorder
D: IV is a postorder sequence of some BST with 149 as the root, => False
B: If 439 is root, It should be 1st element in preorder
D: IV is a postorder sequence of some BST with 149 as the root, => False
You are given the postorder traversal, P, of a binary search tree on the n elements 1, 2, ..., n. You have to determine the unique binary search tree that has P as its postorder traversal. What is the time complexity of the most efficient algorithm for doing this?- a)O(Logn)
- b)O(n)
- c)O(nLogn)
- d)none of the above, as the tree cannot be uniquely determined.
Correct answer is option 'B'. Can you explain this answer?
You are given the postorder traversal, P, of a binary search tree on the n elements 1, 2, ..., n. You have to determine the unique binary search tree that has P as its postorder traversal. What is the time complexity of the most efficient algorithm for doing this?
a)
O(Logn)
b)
O(n)
c)
O(nLogn)
d)
none of the above, as the tree cannot be uniquely determined.
|
|
Sandeep Majumdar answered |
One important thing to note is, it is Binary Search Tree, not Binary Tree. In BST, inorder traversal can always be obtained by sorting all keys.
Given two Balanced binary search trees, B1 having n elements and B2 having m elements, what is the time complexity of the best known algorithm to merge these trees to form another balanced binary tree containing m+n elements ?- a)O(m+n)
- b)O(mlogn)
- c)O(nlogm)
- d)O(m2 + n2)
Correct answer is option 'A'. Can you explain this answer?
Given two Balanced binary search trees, B1 having n elements and B2 having m elements, what is the time complexity of the best known algorithm to merge these trees to form another balanced binary tree containing m+n elements ?
a)
O(m+n)
b)
O(mlogn)
c)
O(nlogm)
d)
O(m2 + n2)
|
|
Garima Bose answered |
The correct answer is option 'A' - O(mn). Let's understand why.
To merge two balanced binary search trees, we need to follow a specific algorithm that ensures the resulting tree is still balanced.
Here is a step-by-step explanation of the algorithm:
1. Convert B1 and B2 to sorted arrays using an inorder traversal. This step takes O(n) and O(m) time, respectively.
2. Merge the two sorted arrays into a single sorted array using the merge algorithm from Merge Sort. This step takes O(n+m) time.
3. Construct a balanced binary search tree from the merged sorted array. This step takes O(n+m) time.
4. The final balanced binary search tree contains n+m elements.
Now, let's analyze the time complexity of the algorithm:
- Converting B1 and B2 to sorted arrays takes O(n) and O(m) time, respectively.
- Merging the two sorted arrays takes O(n+m) time.
- Constructing a balanced binary search tree from the merged sorted array also takes O(n+m) time.
Therefore, the total time complexity of the algorithm is:
O(n) + O(m) + O(n+m) + O(n+m) = O(n+m) + O(n+m) = 2O(n+m) = O(n+m)
Since n and m are the number of elements in B1 and B2 respectively, the time complexity of the algorithm can be written as O(nm).
Hence, the best known algorithm to merge two balanced binary search trees to form another balanced binary tree containing n+m elements has a time complexity of O(nm), which is equivalent to O(mn). Therefore, the correct answer is option 'A' - O(mn).
To merge two balanced binary search trees, we need to follow a specific algorithm that ensures the resulting tree is still balanced.
Here is a step-by-step explanation of the algorithm:
1. Convert B1 and B2 to sorted arrays using an inorder traversal. This step takes O(n) and O(m) time, respectively.
2. Merge the two sorted arrays into a single sorted array using the merge algorithm from Merge Sort. This step takes O(n+m) time.
3. Construct a balanced binary search tree from the merged sorted array. This step takes O(n+m) time.
4. The final balanced binary search tree contains n+m elements.
Now, let's analyze the time complexity of the algorithm:
- Converting B1 and B2 to sorted arrays takes O(n) and O(m) time, respectively.
- Merging the two sorted arrays takes O(n+m) time.
- Constructing a balanced binary search tree from the merged sorted array also takes O(n+m) time.
Therefore, the total time complexity of the algorithm is:
O(n) + O(m) + O(n+m) + O(n+m) = O(n+m) + O(n+m) = 2O(n+m) = O(n+m)
Since n and m are the number of elements in B1 and B2 respectively, the time complexity of the algorithm can be written as O(nm).
Hence, the best known algorithm to merge two balanced binary search trees to form another balanced binary tree containing n+m elements has a time complexity of O(nm), which is equivalent to O(mn). Therefore, the correct answer is option 'A' - O(mn).
The number of ways in which the numbers 1, 2, 3, 4, 5, 6, 7 can be inserted in an empty binary search tree, such that the resulting tree has height 6, is _____________ Note: The height of a tree with a single node is 0. [This question was originally a Fill-in-the-Blanks question]- a)2
- b)4
- c)64
- d)32
Correct answer is option 'C'. Can you explain this answer?
The number of ways in which the numbers 1, 2, 3, 4, 5, 6, 7 can be inserted in an empty binary search tree, such that the resulting tree has height 6, is _____________ Note: The height of a tree with a single node is 0. [This question was originally a Fill-in-the-Blanks question]
a)
2
b)
4
c)
64
d)
32
|
|
Arnab Kapoor answered |
To get height 6, we need to put either 1 or 7 at root. So count can be written as T(n) = 2*T(n-1) with T(1) = 1
Therefore count is 26 = 64 Another Explanation: Consider these cases, 1 2 3 4 5 6 7 1 2 3 4 5 7 6 1 7 6 5 4 3 2 1 7 6 5 4 2 3 7 6 5 4 3 2 1 7 6 5 4 3 1 2 7 1 2 3 4 5 6 7 1 2 3 4 6 5 For height 6, we have 2 choices. Either we select the root as 1 or 7. Suppose we select 7. Now, we have 6 nodes and remaining height = 5. So, now we have 2 ways to select root for this sub-tree also. Now, we keep on repeating the same procedure till remaining height = 1 For this last case also, we have 2 ways. Therefore, total number of ways = 26= 64
If all the edge weights of an undirected graph are positive, then any subset of edges that connects all the vertices and has minimum total weight is a- a)Hamiltonian cycle
- b)grid
- c)hypercube
- d)tree
Correct answer is option 'D'. Can you explain this answer?
If all the edge weights of an undirected graph are positive, then any subset of edges that connects all the vertices and has minimum total weight is a
a)
Hamiltonian cycle
b)
grid
c)
hypercube
d)
tree
|
|
Varun Khanna answered |
Explanation:
To understand why the correct answer is option 'D' (tree), let's break down the characteristics of each option:
a) Hamiltonian cycle: A Hamiltonian cycle is a cycle in a graph that visits every vertex exactly once. While it does connect all the vertices, it is not guaranteed to have the minimum total weight. The weights of the edges can vary, and there is no guarantee that a Hamiltonian cycle will have the lowest total weight.
b) Grid: A grid is a graph formed by connecting vertices in a rectangular grid pattern. While it is possible to connect all the vertices in a grid, it is not necessary to use all the edges to achieve this. Additionally, the total weight of the edges in a grid can vary, so it is not necessarily the minimum.
c) Hypercube: A hypercube is a graph formed by connecting vertices in an n-dimensional cube. Similar to a grid, it is possible to connect all the vertices in a hypercube, but it is not necessary to use all the edges to achieve this. Also, the total weight of the edges can vary, so it is not necessarily the minimum.
d) Tree: A tree is a connected acyclic graph. In a tree, there is exactly one path between any two vertices, and all the vertices are connected. If all the edge weights of an undirected graph are positive, the minimum total weight subset of edges that connects all the vertices will form a tree. This is known as a minimum spanning tree (MST).
The reason a tree is the correct answer is because of the properties of an MST:
1. A tree connects all the vertices: In an MST, all the vertices of the graph are connected, ensuring that every vertex can be reached from any other vertex.
2. The total weight is minimized: An MST has the minimum total weight among all possible subsets of edges that connect all the vertices. This is because the algorithm for finding an MST (such as Prim's algorithm or Kruskal's algorithm) carefully selects edges with the minimum weight while ensuring that no cycles are formed.
So, in conclusion, if all the edge weights of an undirected graph are positive, the subset of edges that connects all the vertices and has the minimum total weight will form a tree (option 'D').
To understand why the correct answer is option 'D' (tree), let's break down the characteristics of each option:
a) Hamiltonian cycle: A Hamiltonian cycle is a cycle in a graph that visits every vertex exactly once. While it does connect all the vertices, it is not guaranteed to have the minimum total weight. The weights of the edges can vary, and there is no guarantee that a Hamiltonian cycle will have the lowest total weight.
b) Grid: A grid is a graph formed by connecting vertices in a rectangular grid pattern. While it is possible to connect all the vertices in a grid, it is not necessary to use all the edges to achieve this. Additionally, the total weight of the edges in a grid can vary, so it is not necessarily the minimum.
c) Hypercube: A hypercube is a graph formed by connecting vertices in an n-dimensional cube. Similar to a grid, it is possible to connect all the vertices in a hypercube, but it is not necessary to use all the edges to achieve this. Also, the total weight of the edges can vary, so it is not necessarily the minimum.
d) Tree: A tree is a connected acyclic graph. In a tree, there is exactly one path between any two vertices, and all the vertices are connected. If all the edge weights of an undirected graph are positive, the minimum total weight subset of edges that connects all the vertices will form a tree. This is known as a minimum spanning tree (MST).
The reason a tree is the correct answer is because of the properties of an MST:
1. A tree connects all the vertices: In an MST, all the vertices of the graph are connected, ensuring that every vertex can be reached from any other vertex.
2. The total weight is minimized: An MST has the minimum total weight among all possible subsets of edges that connect all the vertices. This is because the algorithm for finding an MST (such as Prim's algorithm or Kruskal's algorithm) carefully selects edges with the minimum weight while ensuring that no cycles are formed.
So, in conclusion, if all the edge weights of an undirected graph are positive, the subset of edges that connects all the vertices and has the minimum total weight will form a tree (option 'D').
Consider a complete binary tree where the left and the right subtrees of the root are max-heaps. The lower bound for the number of operations to convert the tree to a heap is- a)Ω(logn)
- b)Ω(n)
- c)Ω(nlogn)
- d)Ω(n2)
Correct answer is option 'A'. Can you explain this answer?
Consider a complete binary tree where the left and the right subtrees of the root are max-heaps. The lower bound for the number of operations to convert the tree to a heap is
a)
Ω(logn)
b)
Ω(n)
c)
Ω(nlogn)
d)
Ω(n2)
|
|
Sanya Agarwal answered |
The answer to this question is simply max-heapify function. Time complexity of max-heapify is O(Log n) as it recurses at most through height of heap.
// A recursive method to heapify a subtree with root at given index
// This method assumes that the subtrees are already heapified
void MinHeap::MaxHeapify(int i)
{
int l = left(i);
int r = right(i);
int largest = i;
if (l < heap_size && harr[l] < harr[i])
largest = l;
if (r < heap_size && harr[r] < harr[smallest])
largest = r;
if (largest != i)
{
swap(&harr[i], &harr[largest]);
MinHeapify(largest);
}
}
// This method assumes that the subtrees are already heapified
void MinHeap::MaxHeapify(int i)
{
int l = left(i);
int r = right(i);
int largest = i;
if (l < heap_size && harr[l] < harr[i])
largest = l;
if (r < heap_size && harr[r] < harr[smallest])
largest = r;
if (largest != i)
{
swap(&harr[i], &harr[largest]);
MinHeapify(largest);
}
}
The inorder and preorder Traversal of binary Tree are dbeafcg and abdecfg respectively. The post-order Traversal is __________.- a)dbefacg
- b)debfagc
- c)dbefcga
- d)debfgca
Correct answer is option 'D'. Can you explain this answer?
The inorder and preorder Traversal of binary Tree are dbeafcg and abdecfg respectively. The post-order Traversal is __________.
a)
dbefacg
b)
debfagc
c)
dbefcga
d)
debfgca
|
|
Saanvi Gupta answered |
Explanation:
Given Traversals:
- Inorder: dbeafcg
- Preorder: abdecfg
Steps to Find Post-order Traversal:
- The first element in the Preorder traversal is the root of the tree (a).
- Find the index of the root in the Inorder traversal (index 3).
- The elements to the left of the root in the Inorder traversal represent the left subtree (dbe).
- The elements to the right of the root in the Inorder traversal represent the right subtree (fcg).
- Recursively repeat the above steps for the left and right subtrees.
Post-order Traversal:
- Left Subtree: dbef
- Right Subtree: cg
- Root: a
- Combine the post-order traversals of the left subtree, right subtree, and root to get the final post-order traversal: debfgca
Therefore, the correct post-order Traversal of the binary tree is debfgca.
Given Traversals:
- Inorder: dbeafcg
- Preorder: abdecfg
Steps to Find Post-order Traversal:
- The first element in the Preorder traversal is the root of the tree (a).
- Find the index of the root in the Inorder traversal (index 3).
- The elements to the left of the root in the Inorder traversal represent the left subtree (dbe).
- The elements to the right of the root in the Inorder traversal represent the right subtree (fcg).
- Recursively repeat the above steps for the left and right subtrees.
Post-order Traversal:
- Left Subtree: dbef
- Right Subtree: cg
- Root: a
- Combine the post-order traversals of the left subtree, right subtree, and root to get the final post-order traversal: debfgca
Therefore, the correct post-order Traversal of the binary tree is debfgca.
Which of the following is a true about Binary Trees- a)Every binary tree is either complete or full.
- b)Every complete binary tree is also a full binary tree.
- c)Every full binary tree is also a complete binary tree.
- d)No binary tree is both complete and full.
- e)None of the above
Correct answer is option 'E'. Can you explain this answer?
Which of the following is a true about Binary Trees
a)
Every binary tree is either complete or full.
b)
Every complete binary tree is also a full binary tree.
c)
Every full binary tree is also a complete binary tree.
d)
No binary tree is both complete and full.
e)
None of the above
|
|
Avantika Yadav answered |
Introduction
In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the left child and the right child. Binary trees are widely used in many applications, such as representing hierarchical relationships, sorting, searching, and more.
Explanation
a) Every binary tree is either complete or full: This statement is false. A binary tree can be neither complete nor full. A binary tree is complete if all levels, except possibly the last level, are completely filled, and all nodes are as far left as possible. A binary tree is full if every node has either 0 or 2 children.
b) Every complete binary tree is also a full binary tree: This statement is false. A complete binary tree can have nodes with only one child, as long as all the levels are filled except possibly the last level, which should be filled from left to right. On the other hand, a full binary tree requires all nodes to have either 0 or 2 children.
c) Every full binary tree is also a complete binary tree: This statement is false. A full binary tree can have all levels completely filled, but it does not guarantee that the nodes are as far left as possible. A complete binary tree requires the nodes to be as far left as possible.
d) No binary tree is both complete and full: This statement is false. It is possible to have a binary tree that is both complete and full. For example, a binary tree with a single node is both complete and full.
e) None of the above: This is the correct answer. None of the statements a, b, c, or d are true. Each statement represents a different property of binary trees, and none of them are universally true for all binary trees.
Conclusion
In summary, none of the statements a, b, c, or d are true about binary trees. Each statement represents a different property, and binary trees can vary in terms of completeness and fullness. It is important to understand the specific properties and characteristics of binary trees to analyze and manipulate them effectively.
In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the left child and the right child. Binary trees are widely used in many applications, such as representing hierarchical relationships, sorting, searching, and more.
Explanation
a) Every binary tree is either complete or full: This statement is false. A binary tree can be neither complete nor full. A binary tree is complete if all levels, except possibly the last level, are completely filled, and all nodes are as far left as possible. A binary tree is full if every node has either 0 or 2 children.
b) Every complete binary tree is also a full binary tree: This statement is false. A complete binary tree can have nodes with only one child, as long as all the levels are filled except possibly the last level, which should be filled from left to right. On the other hand, a full binary tree requires all nodes to have either 0 or 2 children.
c) Every full binary tree is also a complete binary tree: This statement is false. A full binary tree can have all levels completely filled, but it does not guarantee that the nodes are as far left as possible. A complete binary tree requires the nodes to be as far left as possible.
d) No binary tree is both complete and full: This statement is false. It is possible to have a binary tree that is both complete and full. For example, a binary tree with a single node is both complete and full.
e) None of the above: This is the correct answer. None of the statements a, b, c, or d are true. Each statement represents a different property of binary trees, and none of them are universally true for all binary trees.
Conclusion
In summary, none of the statements a, b, c, or d are true about binary trees. Each statement represents a different property, and binary trees can vary in terms of completeness and fullness. It is important to understand the specific properties and characteristics of binary trees to analyze and manipulate them effectively.
Postorder traversal of a given binary search tree, T produces the following sequence of keys
10, 9, 23, 22, 27, 25, 15, 50, 95, 60, 40, 29
Which one of the following sequences of keys can be the result of an in-order traversal of the tree T? (GATE CS 2005)- a)9, 10, 15, 22, 23, 25, 27, 29, 40, 50, 60, 95
- b)9, 10, 15, 22, 40, 50, 60, 95, 23, 25, 27, 29
- c)29, 15, 9, 10, 25, 22, 23, 27, 40, 60, 50, 95
- d)95, 50, 60, 40, 27, 23, 22, 25, 10, 9, 15, 29
Correct answer is option 'A'. Can you explain this answer?
Postorder traversal of a given binary search tree, T produces the following sequence of keys
10, 9, 23, 22, 27, 25, 15, 50, 95, 60, 40, 29
Which one of the following sequences of keys can be the result of an in-order traversal of the tree T? (GATE CS 2005)
10, 9, 23, 22, 27, 25, 15, 50, 95, 60, 40, 29
Which one of the following sequences of keys can be the result of an in-order traversal of the tree T? (GATE CS 2005)
a)
9, 10, 15, 22, 23, 25, 27, 29, 40, 50, 60, 95
b)
9, 10, 15, 22, 40, 50, 60, 95, 23, 25, 27, 29
c)
29, 15, 9, 10, 25, 22, 23, 27, 40, 60, 50, 95
d)
95, 50, 60, 40, 27, 23, 22, 25, 10, 9, 15, 29
|
|
Ravi Singh answered |
Inorder traversal of a BST always gives elements in increasing order. Among all four options, a) is the only increasing order sequence.
The inorder and preorder traversal of a binary tree are d b e a f c g and a b d e c f g, respectively. The postorder traversal of the binary tree is:- a)d e b f g c a
- b)e d b g f c a
- c)e d b f g c a
- d)d e f g b c a
Correct answer is option 'A'. Can you explain this answer?
The inorder and preorder traversal of a binary tree are d b e a f c g and a b d e c f g, respectively. The postorder traversal of the binary tree is:
a)
d e b f g c a
b)
e d b g f c a
c)
e d b f g c a
d)
d e f g b c a
|
|
Hridoy Datta answered |
Explanation:
Given Traversals:
Inorder: d b e a f c g
Preorder: a b d e c f g
Steps to find Postorder:
1. The first element in the Preorder traversal is the root of the tree, which is 'a'.
2. Find the position of 'a' in the Inorder traversal. Everything to the left of 'a' in the Inorder traversal is the left subtree, and everything to the right is the right subtree.
3. In the Inorder traversal, the left subtree of 'a' is 'd b e' and the right subtree is 'f c g'.
4. From the Preorder traversal, the elements corresponding to the left subtree are 'b d e' and the elements corresponding to the right subtree are 'c f g'.
5. Recursively apply the above steps for the left and right subtrees to construct the Postorder traversal.
6. The Postorder traversal of the binary tree is 'd e b f g c a'.
Therefore, the correct answer is option 'A': d e b f g c a.
Given Traversals:
Inorder: d b e a f c g
Preorder: a b d e c f g
Steps to find Postorder:
1. The first element in the Preorder traversal is the root of the tree, which is 'a'.
2. Find the position of 'a' in the Inorder traversal. Everything to the left of 'a' in the Inorder traversal is the left subtree, and everything to the right is the right subtree.
3. In the Inorder traversal, the left subtree of 'a' is 'd b e' and the right subtree is 'f c g'.
4. From the Preorder traversal, the elements corresponding to the left subtree are 'b d e' and the elements corresponding to the right subtree are 'c f g'.
5. Recursively apply the above steps for the left and right subtrees to construct the Postorder traversal.
6. The Postorder traversal of the binary tree is 'd e b f g c a'.
Therefore, the correct answer is option 'A': d e b f g c a.
The number of leaf nodes in a rooted tree of n nodes, with each node having 0 or 3 children is:- a)n/2
- b)(n-1)/3
- c)(n-1)/2
- d)(2n+1)/3
Correct answer is option 'D'. Can you explain this answer?
The number of leaf nodes in a rooted tree of n nodes, with each node having 0 or 3 children is:
a)
n/2
b)
(n-1)/3
c)
(n-1)/2
d)
(2n+1)/3
|
|
Sanya Agarwal answered |
Let L be the number of leaf nodes and I be the number of internal nodes, then following relation holds for above given tree.
L = (3-1)I + 1 = 2I + 1
Total number of nodes(n) is sum of leaf nodes and internal nodes
Total number of nodes(n) is sum of leaf nodes and internal nodes
n = L + I
After solving above two, we get L = (2n+1)/3
After solving above two, we get L = (2n+1)/3
A scheme for storing binary trees in an array X is as follows. Indexing of X starts at 1 instead of 0. the root is stored at X[1]. For a node stored at X[i], the left child, if any, is stored in X[2i] and the right child, if any, in X[2i+1]. To be able to store any binary tree on n vertices the minimum size of X should be.- a) log2n
- b) n
- c) 2n + 1
- d) 2n — 1
Correct answer is option 'D'. Can you explain this answer?
A scheme for storing binary trees in an array X is as follows. Indexing of X starts at 1 instead of 0. the root is stored at X[1]. For a node stored at X[i], the left child, if any, is stored in X[2i] and the right child, if any, in X[2i+1]. To be able to store any binary tree on n vertices the minimum size of X should be.
a)
log2n
b)
n
c)
2n + 1
d)
2n — 1
|
|
Mayank Khanna answered |
The minimum size of X should be c) 2n - 1.
In a binary tree, each node can have at most two children (left and right). Therefore, the number of nodes in a binary tree with n vertices can be at most 2n.
In the given scheme, each node in the binary tree is stored at a specific index in the array X. If we have 2n nodes in the binary tree, we would need at least 2n indices in the array X to store each node.
However, indexing in X starts at 1 instead of 0. Therefore, we would need an additional index in the array X to account for this offset.
Hence, the minimum size of X should be 2n + 1 - 1, which simplifies to 2n - 1.
In a binary tree, each node can have at most two children (left and right). Therefore, the number of nodes in a binary tree with n vertices can be at most 2n.
In the given scheme, each node in the binary tree is stored at a specific index in the array X. If we have 2n nodes in the binary tree, we would need at least 2n indices in the array X to store each node.
However, indexing in X starts at 1 instead of 0. Therefore, we would need an additional index in the array X to account for this offset.
Hence, the minimum size of X should be 2n + 1 - 1, which simplifies to 2n - 1.
Consider the following tree
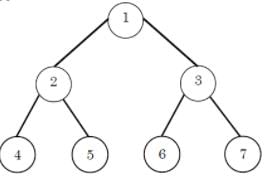If the post order traversal gives ab-cd*+ then the label of the nodes 1,2,3,… will be- a)+,-,*,a,b,c,d
- b)a,-,b,+,c,*,d
- c)a,b,c,d,-,*,+
- d)-,a,b,+,*,c,d
Correct answer is option 'A'. Can you explain this answer?
Consider the following tree
If the post order traversal gives ab-cd*+ then the label of the nodes 1,2,3,… will be
a)
+,-,*,a,b,c,d
b)
a,-,b,+,c,*,d
c)
a,b,c,d,-,*,+
d)
-,a,b,+,*,c,d
|
Riverdale Learning Institute answered |
Postorder traversal of the given binary tree will give the following sequence: 4 5 2 6 7 3 1.
Now comparing the sequence with a b – c d * + we get 1 = +, 2 = -, 3 = *, 4 = a, 5 = b, 6 = c and 7 = d.
So, option (A) is correct.
Now comparing the sequence with a b – c d * + we get 1 = +, 2 = -, 3 = *, 4 = a, 5 = b, 6 = c and 7 = d.
So, option (A) is correct.
Consider the following rooted tree with the vertex P labeled as root
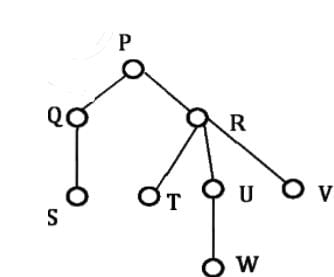
The order in which the nodes are visited during in-order traversal is- a)SQPTRWUV
- b)SQPTURWV
- c)SQPTWUVR
- d)SQPTRUWV
Correct answer is option 'A'. Can you explain this answer?
Consider the following rooted tree with the vertex P labeled as root
The order in which the nodes are visited during in-order traversal is
The order in which the nodes are visited during in-order traversal is
a)
SQPTRWUV
b)
SQPTURWV
c)
SQPTWUVR
d)
SQPTRUWV
|
|
Sudhir Patel answered |
Algorithm Inorder(tree) - Use of Recursion
Steps:
1. Traverse the left subtree,
i.e., call Inorder(left-subtree)
2. Visit the root.
3. Traverse the right subtree,
i.e., call Inorder(right-subtree)
Steps:
1. Traverse the left subtree,
i.e., call Inorder(left-subtree)
2. Visit the root.
3. Traverse the right subtree,
i.e., call Inorder(right-subtree)
Understanding this algorithm requires the basic
understanding of Recursion
understanding of Recursion
Therefore, We begin in the above tree with root as
the starting point, which is P.
the starting point, which is P.
# Step 1( for node P) :
Traverse the left subtree of node or root P.
So we have node Q on left of P.
Traverse the left subtree of node or root P.
So we have node Q on left of P.
-> Step 1( for node Q)
Traverse the left subtree of node Q.
So we have node S on left of Q.
Traverse the left subtree of node Q.
So we have node S on left of Q.
* Step 1 (for node S)
Now again traverse the left subtree of node S which is
NULL here.
Now again traverse the left subtree of node S which is
NULL here.
* Step 2(for node S)
Visit the node S, i.e print node S as the 1st element of
inorder traversal.
Visit the node S, i.e print node S as the 1st element of
inorder traversal.
* Step 3(for node S)
Traverse the right subtree of node S.
Which is NULL here.
Traverse the right subtree of node S.
Which is NULL here.
Now move up in the tree to Q which is parent
of S.( Recursion, function of Q called for function of S).
Hence we go back to Q.
of S.( Recursion, function of Q called for function of S).
Hence we go back to Q.
-> Step 2( for node Q):
Visit the node Q, i.e print node Q as the 2nd
element of inorder traversal.
Visit the node Q, i.e print node Q as the 2nd
element of inorder traversal.
-> Step 3 (for node Q)
Traverse the right subtree of node Q.
Which is NULL here.
Traverse the right subtree of node Q.
Which is NULL here.
Now move up in the tree to P which is parent
of Q.( Recursion, function of P called for function of Q).
Hence we go back to P.
of Q.( Recursion, function of P called for function of Q).
Hence we go back to P.
# Step 2(for node P)
Visit the node P, i.e print node S as the 3rd
element of inorder traversal.
Visit the node P, i.e print node S as the 3rd
element of inorder traversal.
# Step 3 (for node P)
Traverse the right subtree of node P.
Node R is at the right of P.
Traverse the right subtree of node P.
Node R is at the right of P.
Till now we have printed SQP as the inorder of the tree.
Similarly other elements can be obtained by traversing
the right subtree of P.
Similarly other elements can be obtained by traversing
the right subtree of P.
The final correct order of Inorder traversal would
be SQPTRWUV.
be SQPTRWUV.
Which of the following is a true about Binary Trees- a)Every binary tree is either complete or full.
- b)Every complete binary tree is also a full binary tree.
- c)Every full binary tree is also a complete binary tree.
- d)No binary tree is both complete and full.
- e)None of the above
Correct answer is 'E'. Can you explain this answer?
Which of the following is a true about Binary Trees
a)
Every binary tree is either complete or full.
b)
Every complete binary tree is also a full binary tree.
c)
Every full binary tree is also a complete binary tree.
d)
No binary tree is both complete and full.
e)
None of the above
|
Manisha Sharma answered |
Explanation:
Binary trees are the trees in which each node can have at most two children. Here are the statements given in the question and their explanations:
a) Every binary tree is either complete or full.
This statement is false. There are binary trees which are neither complete nor full. For example, consider a binary tree in which each node has only one child. Such a binary tree is neither complete nor full.
b) Every complete binary tree is also a full binary tree.
This statement is false. A complete binary tree is the one in which all levels except the last level are completely filled, and all nodes are as far left as possible. A full binary tree is the one in which every node has either 0 or 2 children. Consider the following binary tree:
```
1
/ \
2 3
/ \
4 5
```
This binary tree is complete but not full because node 2 has only one child.
c) Every full binary tree is also a complete binary tree.
This statement is true. A full binary tree is the one in which every node has either 0 or 2 children. Such a binary tree is always complete because all levels except the last level are completely filled. In the last level, all nodes are as far left as possible.
d) No binary tree is both complete and full.
This statement is false. Consider a binary tree with only one node. Such a binary tree is both complete and full.
e) None of the above.
This statement is true because statements a, b, and d are false, and statement c is true.
Binary trees are the trees in which each node can have at most two children. Here are the statements given in the question and their explanations:
a) Every binary tree is either complete or full.
This statement is false. There are binary trees which are neither complete nor full. For example, consider a binary tree in which each node has only one child. Such a binary tree is neither complete nor full.
b) Every complete binary tree is also a full binary tree.
This statement is false. A complete binary tree is the one in which all levels except the last level are completely filled, and all nodes are as far left as possible. A full binary tree is the one in which every node has either 0 or 2 children. Consider the following binary tree:
```
1
/ \
2 3
/ \
4 5
```
This binary tree is complete but not full because node 2 has only one child.
c) Every full binary tree is also a complete binary tree.
This statement is true. A full binary tree is the one in which every node has either 0 or 2 children. Such a binary tree is always complete because all levels except the last level are completely filled. In the last level, all nodes are as far left as possible.
d) No binary tree is both complete and full.
This statement is false. Consider a binary tree with only one node. Such a binary tree is both complete and full.
e) None of the above.
This statement is true because statements a, b, and d are false, and statement c is true.
In a complete k-ary tree, every internal node has exactly k children or no child. The number of leaves in such a tree with n internal nodes is:- a)nk
- b)(n – 1) k+ 1
- c)n( k – 1) + 1
- d)n(k – 1)
Correct answer is option 'C'. Can you explain this answer?
In a complete k-ary tree, every internal node has exactly k children or no child. The number of leaves in such a tree with n internal nodes is:
a)
nk
b)
(n – 1) k+ 1
c)
n( k – 1) + 1
d)
n(k – 1)
|
Anirban Khanna answered |
For an k-ary tree where each node has k children or no children, following relation holds
L = (k-1)*n + 1
Where L is the number of leaf nodes and n is the number of internal nodes.
What is the content of the array after two delete operations on the correct answer to the previous question?- a)14,13,12,10,8
- b)14,12,13,8,10
- c)14,13,8,12,10
- d)14,13,12,8,10
Correct answer is option 'D'. Can you explain this answer?
What is the content of the array after two delete operations on the correct answer to the previous question?
a)
14,13,12,10,8
b)
14,12,13,8,10
c)
14,13,8,12,10
d)
14,13,12,8,10
|
Megha Dasgupta answered |
For Heap trees, deletion of a node includes following two operations. 1) Replace the root with last element on the last level. 2) Starting from root, heapify the complete tree from top to bottom.. Let us delete the two nodes one by one: 1) Deletion of 25: Replace 25 with 12
13 10 8
Since heap property is violated for root (16 is greater than 12), make 16 as root of the tree.
2) Deletion of 16: Replace 16 with 8
Heapify from root to bottom.
Which of the following cannot generate the full binary tree?- a)Inorder and Preorder
- b)Inorder and Postorder
- c)Preorder and Postorder
- d)None of the above
Correct answer is option 'D'. Can you explain this answer?
Which of the following cannot generate the full binary tree?
a)
Inorder and Preorder
b)
Inorder and Postorder
c)
Preorder and Postorder
d)
None of the above
|
|
Subhankar Chawla answered |
To generate a binary tree, two traversals are necessary and one of them must be inorder. But, a full binary tree can be generated from preorder and postorder traversals. Read the algorithm here. Read Can tree be constructed from given traversals?
Which of the following Binary Min Heap operation has the highest time complexity?- a)Inserting an item under the assumption that the heap has capacity to accommodate one more item
- b)Merging with another heap under the assumption that the heap has capacity to accommodate items of other heap
- c)Deleting an item from heap D
- d)Decreasing value of a key
Correct answer is option 'B'. Can you explain this answer?
Which of the following Binary Min Heap operation has the highest time complexity?
a)
Inserting an item under the assumption that the heap has capacity to accommodate one more item
b)
Merging with another heap under the assumption that the heap has capacity to accommodate items of other heap
c)
Deleting an item from heap D
d)
Decreasing value of a key
|
|
Anisha Ahuja answered |
The merge operation takes O(n) time, all other operations given in question take O(Logn) time. The Binomial and Fibonacci Heaps do merge in better time complexity.
Consider a binary max-heap implemented using an array. Which one of the following array represents a binary max-heap? - a)25,12,16,13,10,8,14
- b)25,14,12,13,10,8,16
- c)25,14,16,13,10,8,12
- d)none
Correct answer is option 'C'. Can you explain this answer?
Consider a binary max-heap implemented using an array. Which one of the following array represents a binary max-heap?
a)
25,12,16,13,10,8,14
b)
25,14,12,13,10,8,16
c)
25,14,16,13,10,8,12
d)
none
|
|
Tushar Unni answered |
A tree is max-heap if data at every node in the tree is greater than or equal to it’s children’ s data. In array representation of heap tree, a node at index i has its left child at index 2i + 1 and right child at index 2i + 2.
Suppose we are sorting an array of eight integers using heapsort, and we have just finished some heapify (either maxheapify or minheapify) operations. The array now looks like this: 16 14 15 10 12 27 28 How many heapify operations have been performed on root of heap?- a)1
- b)2
- c)3 or 4
- d)5 or 6
Correct answer is option 'B'. Can you explain this answer?
Suppose we are sorting an array of eight integers using heapsort, and we have just finished some heapify (either maxheapify or minheapify) operations. The array now looks like this: 16 14 15 10 12 27 28 How many heapify operations have been performed on root of heap?
a)
1
b)
2
c)
3 or 4
d)
5 or 6
|
|
Sounak Joshi answered |
In Heapsort, we first build a heap, then we do following operations till the heap size becomes 1. a) Swap the root with last element b) Call heapify for root c) reduce the heap size by 1. In this question, it is given that heapify has been called few times and we see that last two elements in given array are the 2 maximum elements in array. So situation is clear, it is maxheapify whic has been called 2 times.
Chapter doubts & questions for Trees - 6 Months Preparation for GATE CSE 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Trees - 6 Months Preparation for GATE CSE in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
6 Months Preparation for GATE CSE
459 videos|1398 docs|786 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily