Explore Exams
Login Signup
Sign in Open App

All questions of Searching & Sorting for Computer Science Engineering (CSE) Exam

Which of the following is not a stable sorting algorithm in its typical implementation.
  • a)
    Insertion Sort
  • b)
    Merge Sort
  • c)
    Quick Sort
  • d)
    Bubble Sort
Correct answer is option 'C'. Can you explain this answer?

Anushka Khanna answered
Explanation:
- A sorting algorithm is said to be stable if two objects with equal keys appear in the same order in sorted output as they appear in the input array to be sorted.
- Means, a sorting algorithm is called stable if two identical elements do not change the order during the process of sorting.
- Some sorting algorithms are stable by nature like Insertion sort, Merge Sort, Bubble Sort, etc. and some sorting algorithms are not, like Heap Sort, Quick Sort, etc.
You can study about Sorting Algorithms through the document: 
Sorting Algorithms
Clear all your doubts with EduRev

Given an unsorted array. The array has this property that every element in array is at most k distance from its position in sorted array where k is a positive integer smaller than size of array. Which sorting algorithm can be easily modified for sorting this array and what is the obtainable time complexity?
  • a)
    Insertion Sort with time complexity O(kn)
  • b)
    Heap Sort with time complexity O(nLogk)
  • c)
    Quick Sort with time complexity O(kLogk)
  • d)
    Merge Sort with time complexity O(kLogk)
Correct answer is option 'B'. Can you explain this answer?

Sanya Agarwal answered
1) to sort the array firstly create a min-heap with first k+1 elements and a separate array as resultant array.
2) because elements are at most k distance apart from original position so, it is guranteed that the smallest element will be in this K+1 elements.
3) remove the smallest element from the min-heap(extract min) and put it in the result array.
4) Now,insert another element from the unsorted array into the mean-heap, now,the second smallest element will be in this, perform extract min and continue this process until no more elements are in the unsorted array.finally, use simple heap sort for the remaining elements Time Complexity ------------------------ 1) O(k) to build the initial min-heap 2) O((n-k)logk) for remaining elements... 3) 0(1) for extract min so overall O(k) + O((n-k)logk) + 0(1) = O(nlogk)

A hash table of length 10 uses open addressing with hash function h(k)=k mod 10, and linear probing. After inserting 6 values into an empty hash table, the table is as shown below.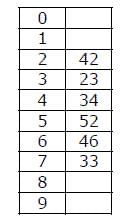
Which one of the following choices gives a possible order in which the key values could have been inserted in the table?
  • a)
    46, 42, 34, 52, 23, 33
  • b)
    34, 42, 23, 52, 33, 46
  • c)
    46, 34, 42, 23, 52, 33
  • d)
    42, 46, 33, 23, 34, 52
Correct answer is option 'C'. Can you explain this answer?

Sanya Agarwal answered
The sequence (A) doesn’t create the hash table as the element 52 appears before 23 in this sequence.
The sequence (B) doesn’t create the hash table as the element 33 appears before 46 in this sequence.
The sequence (C) creates the hash table as 42, 23 and 34 appear before 52 and 33, and 46 appears before 33.
The sequence (D) doesn’t create the hash table as the element 33 appears before 23 in this sequence.

Which sorting algorithm will take least time when all elements of input array are identical? Consider typical implementations of sorting algorithms.
  • a)
    Insertion Sort
  • b)
    Heap Sort
  • c)
    Merge Sort
  • d)
    Selection Sort
Correct answer is option 'A'. Can you explain this answer?

Dipika Chavan answered
Explanation:
When all elements of the input array are identical, it means that the array is already sorted. In such a case, some sorting algorithms perform better than others.

Insertion Sort:
Insertion Sort is an efficient algorithm when it comes to sorting an already sorted array. The algorithm simply traverses the array once, comparing each element with its predecessor. Since all elements are already identical, the algorithm will just compare each element with its predecessor and find no difference, thus completing the sort in minimum time.

Heap Sort:
Heap Sort is a comparison-based sorting algorithm that uses a binary heap data structure to sort elements. In the case of an array with identical elements, it takes the same amount of time as any other comparison-based sorting algorithm.

Merge Sort:
Merge Sort is a divide-and-conquer algorithm that divides an array into two halves, sorts them separately, and then merges them back together. In the case of an array with identical elements, Merge Sort still needs to perform the divide and merge operations, which takes more time than Insertion Sort.

Selection Sort:
Selection Sort is a simple sorting algorithm that selects the smallest element from an unsorted array and swaps it with the first element, then selects the second smallest element and swaps it with the second element, and so on. In the case of an array with identical elements, Selection Sort will still perform the same number of swaps as in any other case, making it slower than Insertion Sort.

Therefore, Insertion Sort is the best sorting algorithm when all elements of the input array are identical.

An advantage of chained hash table (external hashing) over the open addressing scheme is
  • a)
    Worst case complexity of search operations is less
  • b)
    Space used is less
  • c)
    Deletion is easier
  • d)
    None of the above
Correct answer is option 'C'. Can you explain this answer?

Sanya Agarwal answered
In Open Addressing scheme sometimes though element is present we can't delete it if empty bucket comes in between while searching for that element.
External hashing scheme is free from this limitations .
Hence, Option c is correct answer.

You have to sort 1 GB of data with only 100 MB of available main memory. Which sorting technique will be most appropriate?
  • a)
    Heap sort
  • b)
    Merge sort
  • c)
    Quick sort
  • d)
    Insertion sort
Correct answer is option 'B'. Can you explain this answer?

Ravi Singh answered
The data can be sorted using external sorting which uses merging technique. This can be done as follows:
1. Divide the data into 10 groups each of size 100.
2. Sort each group and write them to disk.
3. Load 10 items from each group into main memory.
4. Output the smallest item from the main memory to disk. Load the next item from the group whose item was chosen.
5. Loop step #4 until all items are not outputted. The step 3-5 is called as merging technique.

Example 1:
Consider array has 4 elements and a searching element 16.
A[4]= {10, 16, 22, 25} 
The number of iterations are required to search an element by using a binary search= T1
Example 2:
Consider array has 4 elements and a searching element 22.
A[4]= {10, 16, 22, 25} 
The number of iterations are required to search an element by using a binary search= T2
Note: Searching is successful.
Q.Which of the following statement are true?
  • a)
    T1 = T2
  • b)
    T1 < T2
  • c)
    T1 >T2
  • d)
    T2 < T1
Correct answer is option 'B'. Can you explain this answer?

Sankar Sarkar answered
Understanding Binary Search Iterations
Binary search is an efficient algorithm used to find an element in a sorted array. The number of iterations required to find an element can vary based on the position of the element being searched.
Example Analysis
- Array Elements: A[4] = {10, 16, 22, 25}
- Searching Element for Example 1: 16
- Searching Element for Example 2: 22
Iteration Details
- T1 (Searching for 16):
- Start with the entire array: indexes 0 to 3.
- Middle index = 1 (value = 16).
- Found in 1 iteration.
- T2 (Searching for 22):
- Start with the entire array: indexes 0 to 3.
- Middle index = 1 (value = 16).
- Since 22 > 16, search the right half (indexes 2 to 3).
- New middle index = 2 (value = 22).
- Found in 2 iterations.
Conclusion
- Comparison of Iterations:
- T1 (1 iteration) is less than T2 (2 iterations).
Thus, the statement T1 < /> is correct, making option b the true statement.
Summary of Options
- a) T1 = T2: False
- b) T1 < t2:="" />
- c) T1 > T2: False
- d) T2 < t1:="" />
Understanding the binary search algorithm's mechanics is crucial in determining how many iterations are needed based on the searched element's position.

Given an unsorted array. The array has this property that every element in array is at most k distance from its position in sorted array where k is a positive integer smaller than size of array. Which sorting algorithm can be easily modified for sorting this array and what is the obtainable time complexity?
  • a)
    Insertion Sort with time complexity O(kn)
  • b)
    Heap Sort with time complexity O(nLogk)
  • c)
    Quick Sort with time complexity O(kLogk)
  • d)
    Merge Sort with time complexity O(kLogk)
Correct answer is option 'B'. Can you explain this answer?

Swara Dasgupta answered
We can perform this in O(nlogK) time using heaps.

First, create a min-heap with first k+1 elements.Now, we are sure that the smallest element will be in this K+1 elements..Now,remove the smallest element from the min-heap(which is the root) and put it in the result array.Next,insert another element from the unsorted array into the mean-heap, now,the second smallest element will be in this..extract it from the mean-heap and continue this until no more elements are in the unsorted array.Next, use simple heap sort for the remaining elements.

Time Complexity---

O(k) to build the initial min-heap

O((n-k)logk) for remaining elements...

Thus we get O(nlogk)

Hence,B is the correct answer

The characters of the string K R P C S N Y T J M are inserted into a hash table of size 10 using hash function
h(x) = ((ord(x) - ord(A) + 1)) mod 10
If linear probing is used to resolve collisions, then the following insertion causes collision
  • a)
    Y
  • b)
    C
  • c)
    M
  • d)
    P
Correct answer is option 'C'. Can you explain this answer?

Ravi Singh answered
The hash table with size 10 will have index from 0 to 9. hash function = h(x) = ((ord(x) - ord(A) + 1)) mod 10 So for string K R P C S N Y T J M: K will be inserted at index : (11-1+1) mod 10 = 1 R at index: (18-1+1) mod 10 = 8 P at index: (16-1+1) mod 10 = 6 C at index: (3-1+1) mod 10 = 3 S at index: (19-1+1) mod 10 = 9 N at index: (14-1+1) mod 10 = 4 Y at index (25-1+1) mod 10 = 5 T at index (20-1+1) mod 10 = 0 J at index (10-1+1) mod 10 = 0 // first collision occurs. M at index (13-1+1) mod 10 = 3 //second collision occurs. Only J and M are causing the collision. Final Hash table will be:
0    T
1    K
2    J
3    C
4    N
5    Y
6    P
7    M
8    R
9    S
So, option (C) is correct.

Consider the array L = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]. Suppose you’re searching for the value 3 using binary search method. What is the value of the variable last after two iterations?
  • a)
    14
  • b)
    2
  • c)
    6
  • d)
    3
Correct answer is option 'B'. Can you explain this answer?

Nisha Das answered
Want to find the sum of all the even numbers in the array L.

To do this, you can iterate through each element in the array and check if it is even. If it is even, add it to a running total. Here is the code to achieve this:

```python
L = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
sum_even = 0

for num in L:
if num % 2 == 0:
sum_even += num

print(sum_even)
```

Output:
```
56
```

In this code, we initialize a variable `sum_even` to 0 to keep track of the sum of even numbers. Then, we iterate through each element `num` in the array `L`. Inside the loop, we use the modulo operator `%` to check if `num` is divisible by 2 (i.e., even). If it is, we add it to `sum_even`. Finally, we print `sum_even`, which gives us the sum of all even numbers in the array.

What is recurrence for worst case of QuickSort and what is the time complexity in Worst case?
  • a)
    Recurrence is T(n) = T(n-2) + O(n) and time complexity is O(n^2)
  • b)
    Recurrence is T(n) = T(n-1) + O(n) and time complexity is O(n^2)
  • c)
    Recurrence is T(n) = 2T(n/2) + O(n) and time complexity is O(nLogn)
  • d)
    Recurrence is T(n) = T(n/10) + T(9n/10) + O(n) and time complexity is O(nLogn)
Correct answer is option 'B'. Can you explain this answer?

Nabanita Saha answered
The worst case of QuickSort occurs when the picked pivot is always one of the corner elements in sorted array. In worst case, QuickSort recursively calls one subproblem with size 0 and other subproblem with size (n-1). So recurrence is T(n) = T(n-1) + T(0) + O(n) The above expression can be rewritten as T(n) = T(n-1) + O(n) 1
void exchange(int *a, int *b) 
{ 
int temp; 
temp = *a; 
*a = *b; 
*b = temp; 
} 
int partition(int arr[], int si, int ei) 
{ 
int x = arr[ei]; 
int i = (si - 1); 
int j; 
for (j = si; j <= ei - 1; j++) 
{ 
    if(arr[j] <= x) 
    { 
    i++; 
    exchange(&arr[i], &arr[j]); 
    } 
} 
exchange (&arr[i + 1], &arr[ei]); 
return (i + 1); 
} 
/* Implementation of Quick Sort 
arr[] --> Array to be sorted 
si --> Starting index 
ei --> Ending index 
*/
void quickSort(int arr[], int si, int ei) 
{ 
int pi; /* Partitioning index */
if(si < ei) 
{ 
    pi = partition(arr, si, ei); 
    quickSort(arr, si, pi - 1); 
    quickSort(arr, pi + 1, ei); 
} 
} 

What is the worst case time complexity of insertion sort where position of the data to be inserted is calculated using binary search?
  • a)
    N
  • b)
    NlogN
  • c)
    N^2
  • d)
    N(logN)^2
Correct answer is option 'C'. Can you explain this answer?

Kaavya Sengupta answered
Applying binary search to calculate the position of the data to be inserted doesn’t reduce the time complexity of insertion sort. This is because insertion of a data at an appropriate position involves two steps:
1. Calculate the position.
2. Shift the data from the position calculated in step #1 one step right to create a gap where the data will be inserted.

Using binary search reduces the time complexity in step #1 from O(N) to O(logN). But, the time complexity in step #2 still remains O(N). So, overall complexity remains O(N^2).

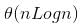
Number of comparisons required for an unsuccessful search of an element in a sequential search, organized, fixed length, symbol table of length L is
  • a)
    L
  • b)
    L/2
  • c)
    (L+1)/2
  • d)
    2L
Correct answer is option 'A'. Can you explain this answer?

Ravi Singh answered
In Sequential search, in order to find a particular element, each element of the table is searched sequentially until the desired element is not found. So, in case of an unsuccessful search, the element would be searched until the last element and it would be a worst case when number of searches are equal to the size of the table. So, option (A) is correct.

Assume that we use Bubble Sort to sort n distinct elements in ascending order. When does the best case of Bubble Sort occur?
  • a)
    When elements are sorted in ascending order
  • b)
    When elements are sorted in descending order
  • c)
    When elements are not sorted by any order
  • d)
    There is no best case for Bubble Sort. It always takes O(n*n) time
Correct answer is option 'A'. Can you explain this answer?

Nishtha Gupta answered
Explanation:

Bubble Sort is a simple sorting algorithm that repeatedly steps through the list, compares adjacent elements and swaps them if they are in the wrong order. The pass through the list is repeated until the list is sorted.

Best Case Scenario:

The Best case scenario for Bubble Sort occurs when the elements are already sorted in ascending order. In this case, the algorithm will only need to make a single pass through the list to identify that it is already sorted and no swaps are needed. Therefore, the time complexity of this scenario is O(n).

Worst Case Scenario:

The Worst case scenario for Bubble Sort occurs when the elements are sorted in descending order. In this case, the algorithm will need to make n-1 passes through the list and perform n-1 swaps in each pass. Therefore, the time complexity for this scenario is O(n*n).

Average Case Scenario:

In the average case scenario, the time complexity of Bubble Sort is O(n*n).

Conclusion:

In conclusion, the best case scenario for Bubble Sort occurs when the elements are already sorted in ascending order. In this scenario, the time complexity of Bubble Sort is O(n). However, in the worst-case scenario, Bubble Sort takes O(n*n) time to sort the list.

The average number of key comparisons required for a successful search for sequential search on items is
  • a)
    n/2
  • b)
    (n-1)/2
  • c)
    (n+1)/2
  • d)
    None of these
Correct answer is option 'C'. Can you explain this answer?

Sanya Agarwal answered
If element is at i-th position where 1 <= i <= n, then we need i comparisons. So average number of comparisons is (1 + 2 + 3 + ..... n)/n = (n * (n + 1)/ 2) / n = (n + 1)/2

The minimum number of comparisons for a particular record among 32 sorted records through binary search method will be: 
  • a)
    16
  • b)
    5
  • c)
    8
  • d)
    2
Correct answer is option 'B'. Can you explain this answer?

Niharika Ahuja answered
Explanation:

To find the minimum number of comparisons for a particular record among 32 sorted records through binary search, we need to determine the maximum number of comparisons required.

Binary Search:
Binary search is a divide and conquer algorithm that works by repeatedly dividing the search interval in half. It starts by comparing the target value with the middle element of the sorted array. If the target value matches the middle element, the search is successful. If the target value is less than the middle element, the search continues on the lower half of the array. If the target value is greater than the middle element, the search continues on the upper half of the array. This process continues until the target value is found or the search interval is empty.

Maximum Number of Comparisons:
In binary search, the search interval is halved at each step. The maximum number of comparisons required to find a particular record can be determined by finding the height of the binary search tree.

- In the first comparison, we compare the target value with the middle element of the array.
- If the target value is less than the middle element, we divide the search interval into two halves. The next comparison will be made with the middle element of one of the halves.
- Each subsequent comparison divides the search interval into half until the target value is found or the search interval is empty.

Height of Binary Search Tree:
The height of a binary search tree with n nodes is given by h = log2(n+1) - 1.

For 32 sorted records, the height of the binary search tree would be:
h = log2(32+1) - 1
= log2(33) - 1
= 5 - 1
= 4

Minimum Number of Comparisons:
The minimum number of comparisons required to find a particular record is equal to the height of the binary search tree. In this case, the height is 4.

Therefore, the minimum number of comparisons for a particular record among 32 sorted records through binary search method will be 4, which corresponds to option 'B'.

Suppose we have a O(n) time algorithm that finds median of an unsorted array. Now consider a QuickSort implementation where we first find median using the above algorithm, then use median as pivot. What will be the worst case time complexity of this modified QuickSort.
  • a)
    O(n^2 Logn)
  • b)
    O(nLogn)
  • c)
    O(n Logn Logn)
  • d)
    none
Correct answer is option 'B'. Can you explain this answer?

Raghav Sharma answered
Explanation:

- QuickSort is an efficient sorting algorithm with average case complexity of O(nLogn). However, its worst case complexity is O(n^2) when the pivot selected is either the smallest or largest element in the array, resulting in unbalanced partitions.
- To improve the efficiency of QuickSort, we can use a better pivot selection strategy. One such strategy is to choose the median element as the pivot, which ensures that the partitions are roughly equal in size and reduces the chances of worst case scenario.
- If we have an O(n) time algorithm to find the median element of an unsorted array, we can use it to select the pivot in QuickSort. This will result in a modified version of QuickSort with improved worst case complexity.
- The worst case scenario for this modified QuickSort will occur when the median element is selected as the pivot and it still results in unbalanced partitions. This can happen if the array is already sorted or has many duplicate elements, such that the median element is either the smallest or largest element in the array.
- In this worst case scenario, the time taken by the median finding algorithm will be O(n), and the time taken by QuickSort will be O(n^2), resulting in a worst case time complexity of O(n^2).
- However, this worst case scenario is unlikely to occur in practice, and the average case complexity of the modified QuickSort will still be O(nLogn).
- Therefore, the correct answer is option B, O(nLogn).

Consider a hash table with 100 slots. Collisions are resolved using chaining. Assuming simple uniform hashing, what is the probability that the first 3 slots are unfilled after the first 3 insertions?
  • a)
    (97 × 97 × 97) / 1003
  • b)
    (99 × 98 × 97) / 1003
  • c)
    (97 × 96 × 95) / 1003
  • d)
    (97 × 96 × 95) / (3! × 1003)
Correct answer is option 'A'. Can you explain this answer?

Sudhir Patel answered
Chaining:
  • Each slot may contain a chain of elements but in linear probing, we can insert only one element in every slot.
  • In order to insert element 1, we have 4 to 100 = 97 slots out of 100 slots
  • In order to insert second element, we have 4 to 100 = 97 slots out of 100 slots
  • In order to insert third element, we have 4 to 100 = 97 slots out of 100 slots
  • Required probability 
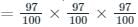
Hence option a is the correct option.

Which of the following sorting algorithms has the lowest worst-case complexity?
  • a)
    Merge Sort
  • b)
    Bubble Sort
  • c)
    Quick Sort
  • d)
    Selection Sort
Correct answer is option 'A'. Can you explain this answer?

Priyanka Chopra answered
Worst case complexities for the above sorting algorithms are as follows: Merge Sort — nLogn Bubble Sort — n^2 Quick Sort — n^2 Selection Sort — n^2

In the above question, the correction needed in the program to make it work properly is
  • a)
    Change line 6 to: if (Y[k] < x) i = k + 1; else j = k-1;
  • b)
    Change line 6 to: if (Y[k] < x) i = k - 1; else j = k+1;
  • c)
    Change line 6 to: if (Y[k] <= x) i = k; else j = k;
  • d)
    Change line 7 to: } while ((Y[k] == x) && (i < j));
Correct answer is option 'A'. Can you explain this answer?

Yash Patel answered
Below is the corrected function f(int Y[10], int x) { int i, j, k; i = 0; j = 9; do { k = (i + j) /2; if( Y[k] < x) i = k + 1; else j = k - 1; } while(Y[k] != x && i < j); if(Y[k] == x) printf ("x is in the array ") ; else printf (" x is not in the array ") ; }[/sourcecode] 

Choose true statement :
(I) Binary search is faster than linear search.
(II) Binary search may not be applied on all the input lists on which linear search can be applied.
  • a)
    Only I
  • b)
    Only II
  • c)
    Both I and II
  • d)
    Neither I nor II
Correct answer is option 'C'. Can you explain this answer?

Sudhir Patel answered
The correct answer is option C.
Concept:
Statement 1: Binary search is faster than linear search.
True, Unless the array size is tiny, binary search is faster than linear search. However, sorting the array is required before doing a binary search. In contrast to binary search, there exist specialized data structures created for quick searching, such as hash tables.
Statement 2:Binary search may not be applied on all the input lists on which linear search can be applied.
True, Binary search is applied only on the sorted list it can not apply to an unsorted list. Whereas linear search is applicable for all types of lists. It means the sorted or unsorted type of lists.
Hence the correct answer is Both I and II.

The time taken by binary search algorithm to search a key in a sorted array of n elements is
  • a)
    O ( log2n )
  • b)
    O ( n )
  • c)
    O ( n log2n )
  • d)
    O ( n2 )
Correct answer is option 'A'. Can you explain this answer?

Sanya Agarwal answered
Search a sorted array by repeatedly dividing the search interval in half. Begin with an interval covering the whole array. If the value of the search key is less than the item in the middle of the interval, narrow the interval to the lower half. Otherwise narrow it to the upper half. Repeatedly check until the value is found or the interval is empty. It takes a maximum of log(n) searches to search an element from the sorted array. Option (A) is correct.

Consider the Quicksort algorithm. Suppose there is a procedure for finding a pivot element which splits the list into two sub-lists each of which contains at least one-fifth of the elements. Let T(n) be the number of comparisons required to sort n elements. Then
  • a)
    T(n) <= 2T(n/5) + n
  • b)
    T(n) <= T(n/5) + T(4n/5) + n
  • c)
    T(n) <= 2T(4n/5) + n
  • d)
    T(n) <= 2T(n/2) + n
Correct answer is option 'B'. Can you explain this answer?

Shivam Sharma answered
For the case where n/5 elements are in one subset, T(n/5) comparisons are needed for the first subset with n/5 elements, T(4n/5) is for the rest 4n/5 elements, and n is for finding the pivot. If there are more than n/5 elements in one set then other set will have less than 4n/5 elements and time complexity will be less than T(n/5) + T(4n/5) + n because recursion tree will be more balanced. 

In binary search, the key to be searched is compared with the element in the __________ of a sorted list.
  • a)
    End
  • b)
    Front
  • c)
    Middle
  • d)
    None of these
Correct answer is option 'C'. Can you explain this answer?

Sudhir Patel answered
Concept:
The binary search algorithm is used to find a specific element in a sorted array. The target value is compared to the array's middle element in a binary search.
Key Points
  • Sequential search is substantially less efficient than binary search. The elements must, however, be presorted before using the binary search method.
  • It works by dividing the area of the list that could contain the item in half until the number of possible sites is reduced to just one.
  • Binary search is an efficient algorithm and is better than linear search in terms of time complexity.
  • Because it splits the array into two half as part of the process, it's called binary. A binary search will initially compare the item in the middle of the array to the search terms.
    ​​​​​​​

What will be the cipher text produced by the following cipher function for the plain text ISRO with key k =7. [Consider 'A' = 0, 'B' = 1, .......'Z' = 25]. Ck(M) = (kM + 13) mod 26
  • a)
    RJCH
  • b)
    QIBG
  • c)
    GQPM
  • d)
    XPIN
Correct answer is option 'A'. Can you explain this answer?

Yash Patel answered
Ck(M) = (kM + 13) mod 26 
Here, 'A' = 0, 'B' = 1, .......'Z' = 25
I = Ck(I) = (7*8 + 13) mod 26 = 17 = R
S = Ck(S) = (7*18 + 13) mod 26 = 9 = J
R = Ck(R) = (7*17 + 13) mod 26 = 2 = C
O = Ck(O) = (7*14 + 13) mod 26 = 7 = H  
So, option (A) is correct.

Insert the characters of the string K R P C S N Y T J M into a hash table of size 10. Use the hash function
h(x) = ( ord(x) – ord("a") + 1 ) mod10
If linear probing is used to resolve collisions, then the following insertion causes collision
  • a)
    Y
  • b)
    C
  • c)
    M
  • d)
    P
Correct answer is option 'C'. Can you explain this answer?

Sanya Agarwal answered
(a) The hash table with size 10 will have index from 0 to 9. hash function = h(x) = ((ord(x) - ord(A) + 1)) mod 10 So for string K R P C S N Y T J M: K will be inserted at index : (11-1+1) mod 10 = 1 R at index: (18-1+1) mod 10 = 8 P at index: (16-1+1) mod 10 = 6 C at index: (3-1+1) mod 10 = 3 S at index: (19-1+1) mod 10 = 9 N at index: (14-1+1) mod 10 = 4 Y at index (25-1+1) mod 10 = 5 T at index (20-1+1) mod 10 = 0 J at index (10-1+1) mod 10 = 0 // first collision occurs. M at index (13-1+1) mod 10 = 3 //second collision occurs. Only J and M are causing the collision. (b) Final Hash table will be:
0    T
1    K
2    J
3    C
4    N
5    Y
6    P
7    M
8    R
9    S

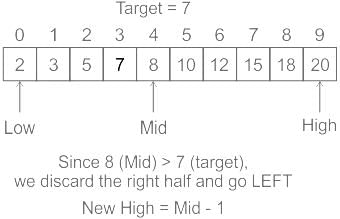
Consider the following C program that attempts to locate an element x in an array Y[] using binary search. The program is erroneous. (GATE CS 2008)
f(int Y[10], int x) {
int i, j, k;
i = 0; j = 9;
do {
k =  (i + j) /2;
if( Y[k] < x)  i = k; else j = k;
} while(Y[k] != x && i < j);
if(Y[k] == x) printf ("x is in the array ") ;
else printf (" x is not in the array ") ;
}
On which of the following contents of Y and x does the program fail?
  • a)
    Y is [1 2 3 4 5 6 7 8 9 10] and x < 10
  • b)
    Y is [1 3 5 7 9 11 13 15 17 19] and x < 1
  • c)
    Y is [2 2 2 2 2 2 2 2 2 2] and x > 2
  • d)
    Y is [2 4 6 8 10 12 14 16 18 20] and 2 < x < 20 and x is even
Correct answer is option 'C'. Can you explain this answer?

Yash Patel answered
The above program doesn’t work for the cases where element to be searched is the last element of Y[] or greater than the last element (or maximum element) in Y[]. For such cases, program goes in an infinite loop because i is assigned value as k in all iterations, and i never becomes equal to or greater than j. So while condition never becomes false.

Which of the following is true about merge sort?
  • a)
    Merge Sort works better than quick sort if data is accessed from slow sequential memory.
  • b)
    Merge Sort is stable sort by nature
  • c)
    Merge sort outperforms heap sort in most of the practical situations.
  • d)
    All of the above.
Correct answer is option 'D'. Can you explain this answer?

Ravi Singh answered
-An example of merge sort. First divide the list into the smallest unit (1 element), then compare each element with the adjacent list to sort and merge the two adjacent lists. Finally all the elements are sorted and merged.
-In computer science, merge sort is an efficient, general-purpose, and comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the order of equal elements is the same in the input and output.
-Merge Sort works better than quick sort if data is accessed from slow sequential memory. 
-Merge Sort is stable sort by nature. 
-Merge sort outperforms heap sort in most of the practical situations.

The average case occurs in the Linear Search Algorithm when:
  • a)
    The item to be searched is in some where middle of the Array
  • b)
    The item to be searched is not in the array
  • c)
    The item to be searched is in the last of the array
  • d)
    The item to be searched is either in the last or not in the array
Correct answer is option 'A'. Can you explain this answer?

Yash Patel answered
  • The average case occurs in the Linear Search Algorithm when the item to be searched is in some where middle of the Array.
  • The best case occurs in the Linear Search Algorithm when the item to be searched is in starting of the Array.
  • The worst case occurs in the Linear Search Algorithm when the item to be searched is in end of the Array.
So, option (A) is correct.

The worst case running times of Insertion sort, Merge sort and Quick sort, respectively, are:
  • a)
    Θ(n log n), Θ(n log n) and Θ(n2)
  • b)
    Θ(n2), Θ(n2) and Θ(n Log n)
  • c)
    Θ(n2), Θ(n log n) and Θ(n log n)
  • d)
    Θ(n2), Θ(n log n) and Θ(n2
Correct answer is option 'D'. Can you explain this answer?

Divya Kaur answered
  • Insertion Sort takes Θ(n2) in worst case as we need to run two loops. The outer loop is needed to one by one pick an element to be inserted at right position. Inner loop is used for two things, to find position of the element to be inserted and moving all sorted greater elements one position ahead. Therefore the worst case recursive formula is T(n) = T(n-1) + Θ(n).
  • Merge Sort takes Θ(n Log n) time in all cases. We always divide array in two halves, sort the two halves and merge them. The recursive formula is T(n) = 2T(n/2) + Θ(n).
  • QuickSort takes Θ(n2) in worst case. In QuickSort, we take an element as pivot and partition the array around it. In worst case, the picked element is always a corner element and recursive formula becomes T(n) = T(n-1) + Θ(n). An example scenario when worst case happens is, arrays is sorted and our code always picks a corner element as pivot.

What is the space complexity of the following binary search algorithm?
int BinSearch(int a[], int n, int data)
{
int low = 0;
int high = n-1;
while (low <= high)
{
mid = low + (high-low)/2;
if(a[mid] == data)
return mid;
else if(a[mid] < data)
low = mid + 1;
else
high = mid - 1;
}
return -1;
}
  • a)
    O(n)
  • b)
    O(n2)
  • c)
    O(log n)
  • d)
    O(1)
Correct answer is option 'D'. Can you explain this answer?

Tanishq Chavan answered


Space Complexity of Binary Search Algorithm

Explanation:

- The space complexity of an algorithm is the amount of memory space required by the algorithm to execute and store the data values.

Binary Search Algorithm:

- In the given binary search algorithm, the only extra space used is for the variables `low`, `high`, `mid`, and `data`.

Variables:
- low, high, mid: These variables are used to keep track of the indices in the array during the search process. They each take up constant space.
- data: This variable stores the value that is being searched for in the array. It also takes up constant space.

Space Complexity:
- Since the space used by the algorithm is constant regardless of the size of the input array, the space complexity of the binary search algorithm is O(1) (constant space complexity).

Which of the following is correct recurrence for worst case of Binary Search?
  • a)
    T(n) = 2T(n/2) + O(1) and T(1) = T(0) = O(1)
  • b)
    T(n) = T(n-1) + O(1) and T(1) = T(0) = O(1)
  • c)
    T(n) = T(n/2) + O(1) and T(1) = T(0) = O(1)
  • d)
    T(n) = T(n-2) + O(1) and T(1) = T(0) = O(1)
Correct answer is option 'C'. Can you explain this answer?

Yash Patel answered
Following is typical implementation of Binary Search. In Binary Search, we first compare the given element x with middle of the array. If x matches with middle element, then we return middle index. Otherwise, we either recur for left half of array or right half of array. So recurrence is T(n) = T(n/2) + O(1)

The tightest lower bound on the number of comparisons, in the worst case, for comparison-based sorting is of the order of
  • a)
    N
  • b)
    N^2
  • c)
    NlogN
  • d)
    N(logN)^2
Correct answer is option 'C'. Can you explain this answer?

Rajeev Menon answered
The number of comparisons that a comparison sort algorithm requires increases in proportion to Nlog(N), where N is the number of elements to sort. This bound is asymptotically tight:
Given a list of distinct numbers (we can assume this because this is a worst-case analysis), there are N factorial permutations exactly one of which is the list in sorted order. The sort algorithm must gain enough information from the comparisons to identify the correct permutations. If the algorithm always completes after at most f(N) steps, it cannot distinguish more than 2^f(N) cases because the keys are distinct and each comparison has only two possible outcomes. Therefore,
2^f(N) >= N! or equivalently f(N) >= log(N!).
Since log(N!) is Omega(NlogN), the answer is NlogN.

Assume that the algorithms considered here sort the input sequences in ascending order. If the input is already in ascending order, which of the following are TRUE?
I. Quicksort runs in Θ(n2) time
II. Bubblesort runs in Θ(n2) time
III. Mergesort runs in Θ(n) time
IV. Insertion sort runs in Θ(n) time
  • a)
    I and II only
  • b)
    I and III only
  • c)
    II and IV only
  • d)
    I and IV only
Correct answer is option 'D'. Can you explain this answer?

Kajal Sharma answered
I. Given an array in ascending order, Recurrence relation for total number of comparisons for quicksort will be T(n) = T(n-1)+O(n) //partition algo will take O(n) comparisons in any case. = O(n^2)
II. Bubble Sort runs in Θ(n^2) time If an array is in ascending order, we could make a small modification in Bubble Sort Inner for loop which is responsible for bubbling the kth largest element to the end in kth iteration. Whenever there is no swap after the completion of inner for loop of bubble sort in any iteration, we can declare that array is sorted in case of Bubble Sort taking O(n) time in Best Case.
III. Merge Sort runs in Θ(n) time Merge Sort relies on Divide and Conquer paradigm to sort an array and there is no such worst or best case input for merge sort. For any sequence, Time complexity will be given by following recurrence relation, T(n) = 2T(n/2) + Θ(n) // In-Place Merge algorithm will take Θ(n) due to copying an entire array. = Θ(nlogn)
IV. Insertion sort runs in Θ(n) time Whenever a new element which will be greater than all the elements of the intermediate sorted sub-array ( because given array is sorted) is added, there won't be any swap but a single comparison. In n-1 passes we will be having 0 swaps and n-1 comparisons. Total time complexity = O(n) // N-1 Comparisons
/// For an array already sorted in ascending order, Quicksort has a complexity Θ(n2) [Worst Case] Bubblesort has a complexity Θ(n) [Best Case] Mergesort has a complexity Θ(n log n) [Any Case] Insertsort has a complexity Θ(n) [Best Case]

Consider a hash table of size 7, with hash function H (k) = k % 7, and pseudo random i = (i + 5) % 7. We want to insert the following keys one by one from left to right.
15, 11, 25, 16, 9, 8, 12
What will be the position of the key 25, if we use random probing?
  • a)
    4
  • b)
    5
  • c)
    1
  • d)
    2
Correct answer is option 'D'. Can you explain this answer?

Arpita Gupta answered
Hash Table with Random Probing
In random probing, we use a pseudo-random function to determine the next position to probe if a collision occurs during insertion. In this case, the pseudo-random function is i = (i + 5) % 7.

Inserting Keys
Let's insert the keys one by one according to the given order: 15, 11, 25, 16, 9, 8, 12.
- Insert 15: H(15) = 1. Key 15 is inserted at position 1.
- Insert 11: H(11) = 4. Key 11 is inserted at position 4.
- Insert 25: H(25) = 4. Since position 4 is already occupied by key 11, we use random probing i = (4 + 5) % 7 = 2. Key 25 is inserted at position 2.
- Insert 16: H(16) = 2. Key 16 is inserted at position 2.
- Insert 9: H(9) = 2. Since position 2 is already occupied by key 16, we use random probing i = (2 + 5) % 7 = 0. Key 9 is inserted at position 0.
- Insert 8: H(8) = 1. Since position 1 is already occupied by key 15, we use random probing i = (1 + 5) % 7 = 6. Key 8 is inserted at position 6.
- Insert 12: H(12) = 5. Key 12 is inserted at position 5.

Position of Key 25
After inserting all keys, the final positions are: 0, 1, 2, 4, 5, 6. Key 25 is at position 2, as determined by random probing. Therefore, the correct answer is option 'D' - 2.

Suppose we have a O(n) time algorithm that finds median of an unsorted array. Now consider a QuickSort implementation where we first find median using the above algorithm, then use median as pivot. What will be the worst case time complexity of this modified QuickSort.
  • a)
    O(n^2 Logn)
  • b)
    O(n^2)
  • c)
    O(n Logn Logn)
  • d)
    O(nLogn)
Correct answer is option 'D'. Can you explain this answer?

Anand Chatterjee answered
Worst case time complexity of the modified QuickSort:

Explanation:
In the modified QuickSort algorithm, we first find the median of the unsorted array using the O(n) time algorithm. Then we use this median as the pivot for partitioning the array in the QuickSort algorithm.

Step 1: Finding the Median
Finding the median of an unsorted array takes O(n) time. This is because we can use the O(n) time algorithm to find the median in linear time. So, the first step of finding the median has a time complexity of O(n).

Step 2: Partitioning the Array
In the QuickSort algorithm, we partition the array around the pivot element. In the worst case scenario, if the pivot is always chosen as the median, the array will be evenly split into two halves. This means that each partitioning step will divide the array into two subarrays of roughly equal size. The worst case time complexity for partitioning is O(n) because we need to compare each element with the pivot and move them to the left or right subarray accordingly.

Step 3: Recursion
After partitioning the array, we recursively apply the QuickSort algorithm on the two subarrays. Since each partitioning step divides the array into two roughly equal halves, the size of the subarrays will be halved at each recursive call.

Time Complexity Analysis:
Let's denote the length of the array as n.

- In the first step, finding the median takes O(n) time.
- In the second step, partitioning the array around the median pivot takes O(n) time.
- In the third step, we recursively apply the QuickSort algorithm on two subarrays of size n/2.

The recurrence relation for the worst case time complexity of the modified QuickSort algorithm can be written as:
T(n) = T(n/2) + O(n)

Using the Master Theorem, we can solve this recurrence relation. In this case, the recurrence relation falls under Case 2 of the Master Theorem, which states that if the partitioning step divides the problem into two subproblems of size n/2, and the time complexity of the partitioning step is O(n), then the time complexity of the algorithm is O(n log n).

Therefore, the worst case time complexity of the modified QuickSort algorithm is O(n log n), which corresponds to option (d).

Consider an array of elements arr[5]= {5,4,3,2,1} , what are the steps of insertions done while doing insertion sort in the array.  
  • a)
    4 5 3 2 1 3 4 5 2 1 2 3 4 5 1 1 2 3 4 5
  • b)
    5 4 3 1 2 5 4 1 2 3 5 1 2 3 4 1 2 3 4 5
  • c)
    4 3 2 1 5 3 2 1 5 4 2 1 5 4 3 1 5 4 3 2
  • d)
    4 5 3 2 1 2 3 4 5 1 3 4 5 2 1 1 2 3 4 5
Correct answer is option 'A'. Can you explain this answer?

Mira Sharma answered
In the insertion sort , just imagine that the first element is already sorted and all the right side Elements are unsorted, we need to insert all elements one by one from left to right in the sorted Array. Sorted : 5
unsorted : 4 3 2 1 Insert all elements less than 5 on the left (Considering 5 as the key ) Now key value is 4 and array will look like this Sorted : 45 unsorted : 3 2 1 Similarly for all the cases the key will always be the newly inserted value and all the values will be compared to that key and inserted in to proper position

Chapter doubts & questions for Searching & Sorting - 6 Months Preparation for GATE CSE 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.

Chapter doubts & questions of Searching & Sorting - 6 Months Preparation for GATE CSE in English & Hindi are available as part of Computer Science Engineering (CSE) exam. Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.

6 Months Preparation for GATE CSE

453 videos|1305 docs|700 tests

Top Courses Computer Science Engineering (CSE)

© EduRev
Education Revolution
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup