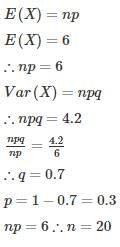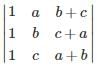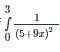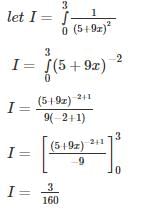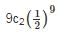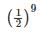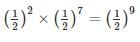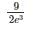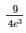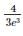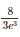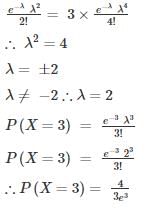All Exams >
Computer Science Engineering (CSE) >
6 Months Preparation for GATE CSE >
All Questions
All questions of Engineering Mathematics for Computer Science Engineering (CSE) Exam
In an examination, 20% of the students have failed in Computer Networks, 30% of the students have failed in Computer Architecture and 10% in Computer Networks and Computer Architecture. If a student is selected at random, then what is the probability that the student has failed in at least one subject?- a)1/5
- b)2/5
- c)3/5
- d)4/5
Correct answer is option 'B'. Can you explain this answer?
In an examination, 20% of the students have failed in Computer Networks, 30% of the students have failed in Computer Architecture and 10% in Computer Networks and Computer Architecture. If a student is selected at random, then what is the probability that the student has failed in at least one subject?
a)
1/5
b)
2/5
c)
3/5
d)
4/5
|
|
Mainak Kulkarni answered |
Let the number of students be 100.
P(N)→ probability that students failed in Computer Networks
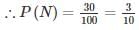
P(A)→ probability that students failed in Computer Architecture
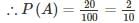
P(N∩A)→ probability that the student has failed in both the subject
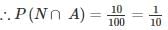
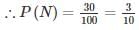
P(A)→ probability that students failed in Computer Architecture
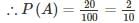
P(N∩A)→ probability that the student has failed in both the subject
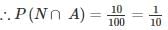
P(NUA)→ probability that the student has failed in atleast one subject
P(NUA) = P(N) + P(A) − P(N∩A)
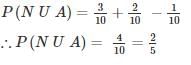
Matrix for which LU decomposition is not possible?- a)
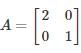
- b)
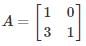
- c)
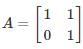
- d)
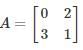
Correct answer is option 'D'. Can you explain this answer?
Matrix for which LU decomposition is not possible?
a)
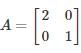
b)
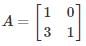
c)
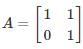
d)
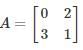
|
|
Rohit Mukherjee answered |
An invertible matrix A has an LU decomposition provided that all it's leading submatrices have non-zero determinants.
All the matrices in the options are invertible because
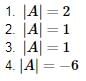
In option 4
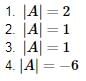
In option 4
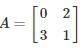 in this leading sub matrix A = [0]
in this leading sub matrix A = [0]Hence LU decomposition is not possible
As xx varies from −1 to +3, which one of the following describes the behaviour of the function f(x) = x3–3x2 + 1?- a)f(x)f(x) increases monotonically.
- b)f(x)f(x) increases, then decreases and increases again.
- c)f(x)f(x) decreases, then increases and decreases again.
- d)f(x)f(x) increases and then decreases.
Correct answer is option 'B'. Can you explain this answer?
As xx varies from −1 to +3, which one of the following describes the behaviour of the function f(x) = x3–3x2 + 1?
a)
f(x)f(x) increases monotonically.
b)
f(x)f(x) increases, then decreases and increases again.
c)
f(x)f(x) decreases, then increases and decreases again.
d)
f(x)f(x) increases and then decreases.
|
|
Athira Reddy answered |
Person to person, as it depends on their individual experiences, perspectives, and attitudes. Some individuals may view success as achieving financial stability and career advancement, while others may define success as having strong personal relationships and a sense of fulfillment in their daily life. Additionally, cultural and societal influences can also shape one's definition of success. Ultimately, success is a subjective concept that is unique to each individual.
An anti-aircraft gun can take a maximum of 4 shots at an enemy plane moving away from it. The probabilities of hitting the plane at the first, second, third and fourth shot are 0.4, 0.3, 0.2 and 0.1 respectively. The probability that the gun hits the plane is_____
Correct answer is between '0.69,0.7'. Can you explain this answer?
An anti-aircraft gun can take a maximum of 4 shots at an enemy plane moving away from it. The probabilities of hitting the plane at the first, second, third and fourth shot are 0.4, 0.3, 0.2 and 0.1 respectively. The probability that the gun hits the plane is_____
|
|
Arka Bajaj answered |
Let p1 = 0.4, p2 = 0.3, p3 = 0.2 and p4 = 0.1
P(the gun hits the plane) = P(the plane is hit at least once)
= 1 – P(the plane is hit in none of the shots)
= 1− (1−p1) (1−p2) (1−p3) (1−p4)
= 1− (0.6 × 0.7 × 0.8 × 0.9)
= (1− 0.3024) = 0.6976
= 1− (0.6 × 0.7 × 0.8 × 0.9)
= (1− 0.3024) = 0.6976
A dice is rolled 180180 times, find the probability that face 44 will turn up at least 3535 times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413- a)0.147
- b)0.158
- c)0.17
- d)0.2
Correct answer is option 'B'. Can you explain this answer?
A dice is rolled 180180 times, find the probability that face 44 will turn up at least 3535 times.(Assume normal distribution). Assume p(0 < z < 1) = 0.3413
a)
0.147
b)
0.158
c)
0.17
d)
0.2
|
|
Mainak Kulkarni answered |
Given that n = 180
Required Probability is given by 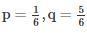
∴ mean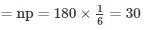
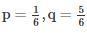
∴ mean
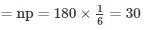
Variance = npq = 25


= 0.5 – 0.3413 = 0.1587
The system of equation, 5x + 2y + z = 3,7x + 10y + 2z = 7,2x + 8y + z = 4 has- a)One Solution
- b)Two Solutions
- c)No Solution
- d)Infinite Solutions
Correct answer is option 'D'. Can you explain this answer?
The system of equation, 5x + 2y + z = 3,7x + 10y + 2z = 7,2x + 8y + z = 4 has
a)
One Solution
b)
Two Solutions
c)
No Solution
d)
Infinite Solutions
|
|
Sandeep Majumdar answered |
The given system of equations are of the form AX = Bwhich represents the system of non homogeneous equations.
Augmented matrix is given by
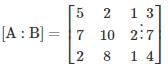
by applying row transformation R2 → R2 − (R1+R3), we get
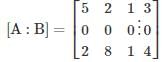
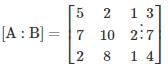
by applying row transformation R2 → R2 − (R1+R3), we get
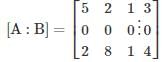
so, rank of matrix = rank of augmented matrix = 2 < number of variables
∴ System has infinite solutions
Alternatively we can simply observe that second equation is redundant as it can be obtained from rest two. Hence we have 2 primary equations and 3 variables hence infinite solution.
The probability that GATE CS/IT question has an error is 1/20 and 65 questions are made in such an exam. If the probability that at least 2 question has an error is [1−[a(19/20)64]] then what is the value of a (answer up to 2 decimal place)?
Correct answer is '4.2'. Can you explain this answer?
The probability that GATE CS/IT question has an error is 1/20 and 65 questions are made in such an exam. If the probability that at least 2 question has an error is [1−[a(19/20)64]] then what is the value of a (answer up to 2 decimal place)?
|
|
Megha Dasgupta answered |
Understanding the Problem
The problem is about calculating the probability of errors in questions on a GATE CS/IT exam. Given that the probability of a question having an error is 1/20 (or 0.05), we can analyze the situation using the complementary probability.
Calculating the Complementary Probability
- The probability that a question does not have an error is 1 - (1/20) = 19/20.
- For 65 questions, the probability that none of them have errors is (19/20)^65.
- The probability that at least 2 questions have errors can be calculated as:
P(at least 2 errors) = 1 - P(0 errors) - P(1 error)
Calculating the Individual Probabilities
1. No Errors:
- P(0 errors) = (19/20)^65
2. Exactly One Error:
- For exactly one error, we choose 1 question to have an error and the rest not:
- P(1 error) = C(65, 1) * (1/20)^1 * (19/20)^64
- C(65, 1) = 65 (the number of ways to choose 1 question from 65)
Therefore, P(1 error) = 65 * (1/20) * (19/20)^64.
Final Calculation
Combining these probabilities:
P(at least 2 errors) = 1 - [(19/20)^65 + 65 * (1/20) * (19/20)^64].
This can be factored as:
P(at least 2 errors) = 1 - [a * (19/20)^64], where a = (19/20) + 65 * (1/20).
Calculating a:
- a = (19/20) + 65 * (1/20) = (19 + 65) / 20 = 84 / 20 = 4.2.
Conclusion
Thus, the value of "a" is 4.2, which matches the given correct answer.
The problem is about calculating the probability of errors in questions on a GATE CS/IT exam. Given that the probability of a question having an error is 1/20 (or 0.05), we can analyze the situation using the complementary probability.
Calculating the Complementary Probability
- The probability that a question does not have an error is 1 - (1/20) = 19/20.
- For 65 questions, the probability that none of them have errors is (19/20)^65.
- The probability that at least 2 questions have errors can be calculated as:
P(at least 2 errors) = 1 - P(0 errors) - P(1 error)
Calculating the Individual Probabilities
1. No Errors:
- P(0 errors) = (19/20)^65
2. Exactly One Error:
- For exactly one error, we choose 1 question to have an error and the rest not:
- P(1 error) = C(65, 1) * (1/20)^1 * (19/20)^64
- C(65, 1) = 65 (the number of ways to choose 1 question from 65)
Therefore, P(1 error) = 65 * (1/20) * (19/20)^64.
Final Calculation
Combining these probabilities:
P(at least 2 errors) = 1 - [(19/20)^65 + 65 * (1/20) * (19/20)^64].
This can be factored as:
P(at least 2 errors) = 1 - [a * (19/20)^64], where a = (19/20) + 65 * (1/20).
Calculating a:
- a = (19/20) + 65 * (1/20) = (19 + 65) / 20 = 84 / 20 = 4.2.
Conclusion
Thus, the value of "a" is 4.2, which matches the given correct answer.
The simultaneous equations2x + ay + z = 20 x + 3y + 4z = bx + 2y + 3z = chas unique solution then what is the value of a, b and c respectively?- a)a ≠ ± 1, b and c can be any value
- b)a ≠ ± 1, b ≠ 0, c ≠ 1
- c)a ≠ -1, b and c can be any value
- d)a, b and c can be any value
Correct answer is option 'C'. Can you explain this answer?
The simultaneous equations
2x + ay + z = 20
x + 3y + 4z = b
x + 2y + 3z = c
has unique solution then what is the value of a, b and c respectively?
a)
a ≠ ± 1, b and c can be any value
b)
a ≠ ± 1, b ≠ 0, c ≠ 1
c)
a ≠ -1, b and c can be any value
d)
a, b and c can be any value
|
|
Kalyan Menon answered |
For given system of equations to have unique solution, the determinant of the coefficient matrix should be not equal to 0


2 (9−8) − a(3−4) + (2−3) ≠ 0
2 + a − 1 ≠ 0
a ≠ −1
Since Δ of coefficient matrix is not equal to 0 then b and c can take any value
Note:
If coefficient matrix’s Δ ≠ 0 then rank of coefficient matrix is always equal rank of augmented matrix so right-hand side of given equation can take any value
From an urn containing 3 red and 2 white balls, a man is to draw 2 balls at random without replacement, being promised Rs. 20 for each red ball he draws and Rs. 10 for each white one. Find his expectation (In rupees).
Correct answer is '32'. Can you explain this answer?
From an urn containing 3 red and 2 white balls, a man is to draw 2 balls at random without replacement, being promised Rs. 20 for each red ball he draws and Rs. 10 for each white one. Find his expectation (In rupees).
|
|
Bijoy Sharma answered |
A man is to draw 2 balls at random without replacement.
Probability to draw 2 red balls 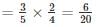
Probability to draw 2 white balls
Probability to draw one red ball and one white ball =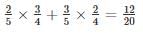
Let X be the random variable and it shows the money he earn.
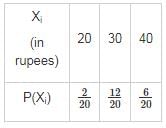
Expectation =
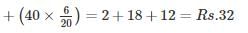
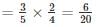
Probability to draw 2 white balls

Probability to draw one red ball and one white ball =
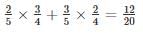
Let X be the random variable and it shows the money he earn.

Expectation =

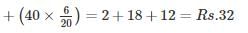
Let A be the 2 X 2 matrix with elements a11 = 2, a12 = 3, a21 = 1 and a22 = 4 then the Characteristic Equation:?
- a)λ2 − 6λ + 5
- b)λ2 + 6λ + 5
- c)λ2 − 6λ − 5
- d)λ2 + 6λ + 5
Correct answer is option 'A'. Can you explain this answer?
Let A be the 2 X 2 matrix with elements a11 = 2, a12 = 3, a21 = 1 and a22 = 4 then the Characteristic Equation:?
a)
λ2 − 6λ + 5
b)
λ2 + 6λ + 5
c)
λ2 − 6λ − 5
d)
λ2 + 6λ + 5
|
|
Divya Kaur answered |
Given Matrix:
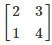
Characteristic Equation:
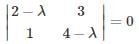
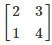
Characteristic Equation:
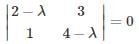
(2−λ) (4−λ) −3 = 0
λ2 − 6λ + 5 = 0
λ = 5 or λ = 1
Consider the following system of equations in three real variables x, y, z.2x – 3y + 7z = 53x + y – 3z = 132x + 19y – 47z = 32The system of the equation has- a)No solution
- b)A unique solution
- c)More than one but a finite number of solutions
- d)An infinite number of solutions
Correct answer is option 'A'. Can you explain this answer?
Consider the following system of equations in three real variables x, y, z.
2x – 3y + 7z = 5
3x + y – 3z = 13
2x + 19y – 47z = 32
The system of the equation has
a)
No solution
b)
A unique solution
c)
More than one but a finite number of solutions
d)
An infinite number of solutions
|
|
Akanksha Chauhan answered |
Augmented matrix will be
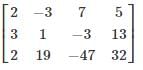
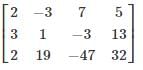
R3 → R3 – R1
R2 → 2R2 – 3R1
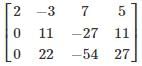
R3 → R3 – 2R2

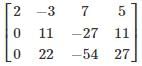
R3 → R3 – 2R2

Rank of A ≠ Rank of Augmented matrix
Hence given system of equations has no solution.
A sample of 15 data is as follows: 17, 18, 17, 17, 13, 18, 5, 5, 6, 7, 8, 9, 20, 17, 3. the mode of the data is- a)4
- b)13
- c)17
- d)20
Correct answer is option 'C'. Can you explain this answer?
A sample of 15 data is as follows: 17, 18, 17, 17, 13, 18, 5, 5, 6, 7, 8, 9, 20, 17, 3. the mode of the data is
a)
4
b)
13
c)
17
d)
20
|
|
Harshitha Sarkar answered |
Understanding Mode in Data Sets
The mode of a data set is defined as the value that appears most frequently. To determine the mode, we need to count the occurrences of each number in the given sample.
Data Sample
The provided data sample is as follows:
- 17
- 18
- 17
- 17
- 13
- 18
- 5
- 5
- 6
- 7
- 8
- 9
- 20
- 17
- 3
Counting Frequencies
Let's tally the occurrences of each number:
- **3**: 1 time
- **5**: 2 times
- **6**: 1 time
- **7**: 1 time
- **8**: 1 time
- **9**: 1 time
- **13**: 1 time
- **17**: 4 times
- **18**: 2 times
- **20**: 1 time
Identifying the Mode
From the frequency count, we can see that:
- **17** appears 4 times, which is more than any other number.
- The next highest frequencies are for **5** and **18**, which appear 2 times each.
Conclusion
Since **17** has the highest frequency, it is the mode of this data set. Therefore, the correct answer is:
- **Option C: 17**
This indicates that in this particular data sample, 17 is the most common value.
The mode of a data set is defined as the value that appears most frequently. To determine the mode, we need to count the occurrences of each number in the given sample.
Data Sample
The provided data sample is as follows:
- 17
- 18
- 17
- 17
- 13
- 18
- 5
- 5
- 6
- 7
- 8
- 9
- 20
- 17
- 3
Counting Frequencies
Let's tally the occurrences of each number:
- **3**: 1 time
- **5**: 2 times
- **6**: 1 time
- **7**: 1 time
- **8**: 1 time
- **9**: 1 time
- **13**: 1 time
- **17**: 4 times
- **18**: 2 times
- **20**: 1 time
Identifying the Mode
From the frequency count, we can see that:
- **17** appears 4 times, which is more than any other number.
- The next highest frequencies are for **5** and **18**, which appear 2 times each.
Conclusion
Since **17** has the highest frequency, it is the mode of this data set. Therefore, the correct answer is:
- **Option C: 17**
This indicates that in this particular data sample, 17 is the most common value.
A die is tossed thrice. Success is getting 2 or 5 on a toss. What is the variance of the number of success?- a)1/3
- b)2/3
- c)4/5
- d)35
Correct answer is option 'B'. Can you explain this answer?
A die is tossed thrice. Success is getting 2 or 5 on a toss. What is the variance of the number of success?
a)
1/3
b)
2/3
c)
4/5
d)
35
|
|
Meghana Rane answered |
Understanding the Problem
When a die is tossed, we define success as rolling a 2 or a 5. This gives us two successful outcomes out of six possible outcomes on a die.
Calculating Probability of Success
- The probability of success (rolling a 2 or 5) is:
- P(success) = 2 successful outcomes / 6 total outcomes = 1/3
- The probability of failure (not rolling a 2 or 5) is:
- P(failure) = 1 - P(success) = 1 - 1/3 = 2/3
Setting Up the Experiment
- The die is tossed three times, and we define the random variable X as the number of successes in these three tosses.
- Since each toss is independent, X follows a binomial distribution with parameters n = 3 (number of trials) and p = 1/3 (probability of success).
Calculating Variance
- The formula for the variance of a binomial distribution is given by:
- Variance = n * p * (1 - p)
- Substituting the values:
- Variance = 3 * (1/3) * (2/3)
- Variance = 3 * (1/3) * (2/3) = 2/3
Conclusion
The variance of the number of successes when tossing a die three times, where success is defined as rolling a 2 or 5, is indeed 2/3. Thus, the correct answer is option 'B'.
When a die is tossed, we define success as rolling a 2 or a 5. This gives us two successful outcomes out of six possible outcomes on a die.
Calculating Probability of Success
- The probability of success (rolling a 2 or 5) is:
- P(success) = 2 successful outcomes / 6 total outcomes = 1/3
- The probability of failure (not rolling a 2 or 5) is:
- P(failure) = 1 - P(success) = 1 - 1/3 = 2/3
Setting Up the Experiment
- The die is tossed three times, and we define the random variable X as the number of successes in these three tosses.
- Since each toss is independent, X follows a binomial distribution with parameters n = 3 (number of trials) and p = 1/3 (probability of success).
Calculating Variance
- The formula for the variance of a binomial distribution is given by:
- Variance = n * p * (1 - p)
- Substituting the values:
- Variance = 3 * (1/3) * (2/3)
- Variance = 3 * (1/3) * (2/3) = 2/3
Conclusion
The variance of the number of successes when tossing a die three times, where success is defined as rolling a 2 or 5, is indeed 2/3. Thus, the correct answer is option 'B'.
An open box is to be made out of square cardboard of 18 cm by cutting offs equal squares from the corners and turning up the sides. What is the maximum volume of the box in cm3?- a)423
- b)432
- c)412
- d)424
Correct answer is option 'B'. Can you explain this answer?
An open box is to be made out of square cardboard of 18 cm by cutting offs equal squares from the corners and turning up the sides. What is the maximum volume of the box in cm3?
a)
423
b)
432
c)
412
d)
424
|
|
Aman Menon answered |
Let x be the corner side which is cut off and v be volume.
v = l × b × h
v = l × b × h
v = (18 − 2x) × (18 − 2x) × x
v = 4x3 − 72x2 + 324x
v′ = 12x2 − 144x + 324v′
v′′ = 24x − 144
v′ = 12x2 − 144x + 324 = 0
x2 − 12x + 27=0
(x−3) (x−9) = 0
(x=3) or (x = 9)
atx = 3
v′= 24x −144 = 24(3) −144 = −72<0
at x = 3 we have volume maximum
v = 4(3)3 − 72(2)2 + 324(2)
∴ v = 432
Find the value of k for which the following system of equations will be consistent. 2x – 5y = 10 and 6x – 15y = k- a)40
- b)15
- c)60
- d)30
Correct answer is option 'D'. Can you explain this answer?
Find the value of k for which the following system of equations will be consistent.
2x – 5y = 10 and 6x – 15y = k
a)
40
b)
15
c)
60
d)
30
|
|
Maulik Iyer answered |
In the given system of equations, the ratio of the coefficients of x equals the ratio of coefficients of y.
Therefore, they would be consistent only if this ratio equals the constant terms.
That is, If 10/k = 2/6 = -5/-15
Hence if k = 30, then the given system of equations is consistent.
If a matrix A is given by f(x) = a0 + a1x + a2x2+…+ an−1xn−1 + anxn, then the determinant of A is- a)
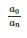
- b)
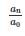
- c)
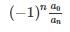
- d)
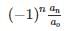
Correct answer is option 'C'. Can you explain this answer?
If a matrix A is given by f(x) = a0 + a1x + a2x2+…+ an−1xn−1 + anxn, then the determinant of A is
a)
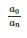
b)
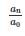
c)
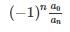
d)
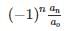
|
|
Gargi Menon answered |
matrix ‘A’ ⇒ f(x) = a0 + a1x + a2x2 +……….+an−1xn−1 + anxnf(x)
if 2 × 2 matrix then characteristic equation ⇒ aλ2 + bλ + c = 0
⇒ |A| = λ1.λ2. = c/a
where ao = c;an = a2 = a
if 3 × 3 matrix → then characteristic equation ⇒ aλ3 + bλ2 + cλ + d = 0
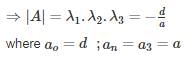
∴ For n × n matrix, |A| = λ1.λ2.λ3….λn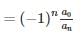
⇒ |A| = λ1.λ2. = c/a
where ao = c;an = a2 = a
if 3 × 3 matrix → then characteristic equation ⇒ aλ3 + bλ2 + cλ + d = 0
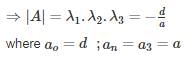
∴ For n × n matrix, |A| = λ1.λ2.λ3….λn
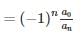
If A = then 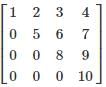 the value of adj (adj (A))?
the value of adj (adj (A))?- a)
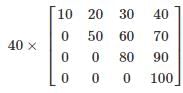
- b)
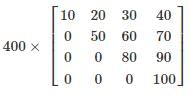
- c)
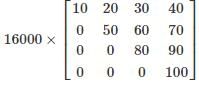
- d)

Correct answer is option 'C'. Can you explain this answer?
If A = then  the value of adj (adj (A))?
the value of adj (adj (A))?
 the value of adj (adj (A))?
the value of adj (adj (A))?a)

b)

c)

d)

|
|
Tanishq Banerjee answered |
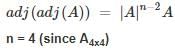
A is upper triangular matrix
∴ product of diagonal elements = |A|
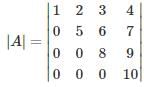 = 1 × 5 × 8 × 10 = 400
= 1 × 5 × 8 × 10 = 400

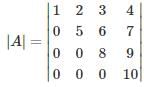 = 1 × 5 × 8 × 10 = 400
= 1 × 5 × 8 × 10 = 400
Note:
|A||A| is determinant of matrix A
In a Poisson distribution if 2P(X = 1) = P(X = 2), then what is the mean?- a)0
- b)2
- c)4
- d)± 2
Correct answer is option 'C'. Can you explain this answer?
In a Poisson distribution if 2P(X = 1) = P(X = 2), then what is the mean?
a)
0
b)
2
c)
4
d)
± 2
|
|
Ankit Mehta answered |
If X is random variable, then Poisson’s distribution is given by:
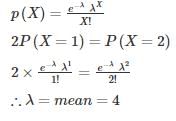
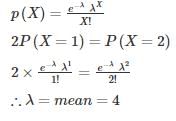
The chances of A, B, C becoming managers of a Testbook company are 4:2:3. The probability that the bonus scheme will be introduced if A, B, C become manager are 0.3, 0.5, 0.8 respectively.If the bonus scheme has introduced, what is the probability that A is appointed as the manager of Testbook (answer up to 2 decimal place)?
Correct answer is between '0.26,0.27'. Can you explain this answer?
The chances of A, B, C becoming managers of a Testbook company are 4:2:3. The probability that the bonus scheme will be introduced if A, B, C become manager are 0.3, 0.5, 0.8 respectively.
If the bonus scheme has introduced, what is the probability that A is appointed as the manager of Testbook (answer up to 2 decimal place)?
|
|
Samarth Ghosh answered |
P(X)→ probability that bonus scheme is introduced
P(A) → probability of A being a manager.
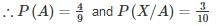
P(B) → probability of B being a manager.
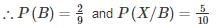
P(C) → probability of C being a manager.
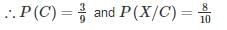
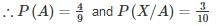
P(B) → probability of B being a manager.
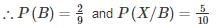
P(C) → probability of C being a manager.
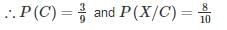
P(X) = P (A ∩ X) + P (B ∩ X) + P (C ∩ X)
P(X) = P(A)P(X/A) + P(B)P(X/B) + P(C)P(X/C)
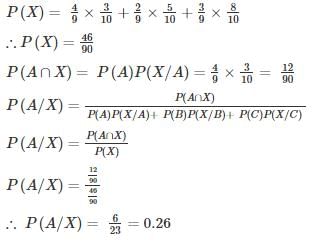
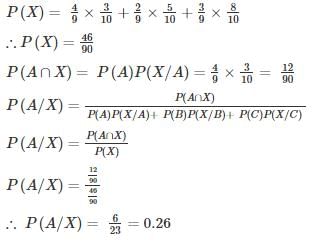
Given the following statements about a function f : R→R, select the right option:P: If f(x) is continuous at x = x0, then it is also differentiable at x = x0Q: If f(x) is continuous at x = x0, then it may not be differentiable at x = x0R: If f(x) is differentiable at x = x0, then it is also continuous at x = x0- a)P is true, Q is false, R is false
- b)P is false, Q is true, R is true
- c)P is false, Q is true, R is false
- d)P is true, Q is false, R is true
Correct answer is option 'B'. Can you explain this answer?
Given the following statements about a function f : R→R, select the right option:
P: If f(x) is continuous at x = x0, then it is also differentiable at x = x0
Q: If f(x) is continuous at x = x0, then it may not be differentiable at x = x0
R: If f(x) is differentiable at x = x0, then it is also continuous at x = x0
a)
P is true, Q is false, R is false
b)
P is false, Q is true, R is true
c)
P is false, Q is true, R is false
d)
P is true, Q is false, R is true
|
|
Subham Saha answered |
If the function is differentiable then always it is continuous but vice – versa is not true. If the function is continuous then it may (or) may not differentiable.
A bag contains 6 red, 5 blue balls, and another bag contains 5 red and 8 blue balls. A ball is drawn from the first bag without noticing the color is put in the second bag. A ball is drawn from the second bag. Find the probability that ball drawn is blue in color.- a)4/7
- b)9/14
- c)93/154
- d)91/154
Correct answer is option 'C'. Can you explain this answer?
A bag contains 6 red, 5 blue balls, and another bag contains 5 red and 8 blue balls. A ball is drawn from the first bag without noticing the color is put in the second bag. A ball is drawn from the second bag. Find the probability that ball drawn is blue in color.
a)
4/7
b)
9/14
c)
93/154
d)
91/154
|
|
Mansi Shah answered |
P(A)→ probability of getting a blue ball from the 2nd bag.
P(E1)→ probability of getting a red ball from the 1st bag.
P(E2)→ probability of getting a blue ball from the 1st bag.

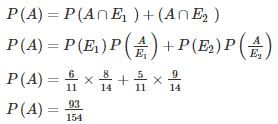

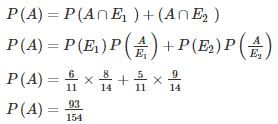
If the determinant of the matrix 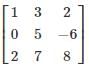 is 26, then the determinant of the matrix
is 26, then the determinant of the matrix  is
is
Correct answer is '-26'. Can you explain this answer?
If the determinant of the matrix 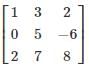 is 26, then the determinant of the matrix
is 26, then the determinant of the matrix  is
is
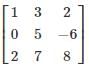 is 26, then the determinant of the matrix
is 26, then the determinant of the matrix  is
is|
|
Rajveer Sharma answered |
If two rows are interchanged in a determinant then the value of the determinant does not change but sign will change. In the given question, first and third rows are interchanged.
Among the given two sets which is/are consistent:
S1 = {3x + ay + 4z = 0,bx + 2y + z = 0,5x + 7z + 9z = 0
S2 = {2x + 6y= −11, 6x + 20y − 6z = −3, 6y − 18z = −1}- a)Only I
- b)Only II
- c)Both I and II
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Among the given two sets which is/are consistent:
S1 = {3x + ay + 4z = 0,bx + 2y + z = 0,5x + 7z + 9z = 0
S2 = {2x + 6y= −11, 6x + 20y − 6z = −3, 6y − 18z = −1}
S1 = {3x + ay + 4z = 0,bx + 2y + z = 0,5x + 7z + 9z = 0
S2 = {2x + 6y= −11, 6x + 20y − 6z = −3, 6y − 18z = −1}
a)
Only I
b)
Only II
c)
Both I and II
d)
None of these
|
|
Nitya Choudhury answered |
Set S1 contains homogeneous equations, homogeneous equations are always consistent because it always satisfied a trivial solution i.e. x = y = z = 0
For S2

R2 → 3R2


R2 → 3R2

Rank Augmented matrix is 3 while rank of coefficient matrix has rank is 2
Hence the S2 is inconsistent
∴ only S1 is consistent
Binomial distribution B(n,p) can be approximated to a normal distribution N(np, np(1−p)) if ____- a)n is large and p and 1-p are almost equal.
- b)n is small and p is almost 1.
- c)n is large and p is almost 0.
- d)n is small and p and 1-p are almost equal.
Correct answer is option 'A'. Can you explain this answer?
Binomial distribution B(n,p) can be approximated to a normal distribution N(np, np(1−p)) if ____
a)
n is large and p and 1-p are almost equal.
b)
n is small and p is almost 1.
c)
n is large and p is almost 0.
d)
n is small and p and 1-p are almost equal.
|
|
Jay Basu answered |
Explanation:
Binomial Distribution vs. Normal Distribution:
- Binomial distribution B(n,p) is used to model the number of successes in a fixed number of trials, where each trial has the same probability of success p.
- Normal distribution N(np, np(1-p)) is a continuous probability distribution that is symmetric and bell-shaped.
Conditions for Approximation:
- When n is large and p and 1-p are almost equal, the binomial distribution can be approximated by a normal distribution.
- This is because when n is large, the binomial distribution becomes more symmetric and bell-shaped, resembling a normal distribution.
Reason for Option A:
- Option A states that n is large and p and 1-p are almost equal, which satisfies the conditions for approximating the binomial distribution to a normal distribution.
- In this scenario, the mean of the normal distribution is np and the standard deviation is sqrt(np(1-p)), which closely approximates the binomial distribution.
Conclusion:
- Therefore, option A is the correct choice as it correctly identifies the conditions under which the binomial distribution can be approximated by a normal distribution.
Binomial Distribution vs. Normal Distribution:
- Binomial distribution B(n,p) is used to model the number of successes in a fixed number of trials, where each trial has the same probability of success p.
- Normal distribution N(np, np(1-p)) is a continuous probability distribution that is symmetric and bell-shaped.
Conditions for Approximation:
- When n is large and p and 1-p are almost equal, the binomial distribution can be approximated by a normal distribution.
- This is because when n is large, the binomial distribution becomes more symmetric and bell-shaped, resembling a normal distribution.
Reason for Option A:
- Option A states that n is large and p and 1-p are almost equal, which satisfies the conditions for approximating the binomial distribution to a normal distribution.
- In this scenario, the mean of the normal distribution is np and the standard deviation is sqrt(np(1-p)), which closely approximates the binomial distribution.
Conclusion:
- Therefore, option A is the correct choice as it correctly identifies the conditions under which the binomial distribution can be approximated by a normal distribution.
Find the value of x for the singular matrix?

- a)0
- b)4
- c)6
- d)8
Correct answer is option 'D'. Can you explain this answer?
Find the value of x for the singular matrix?


a)
0
b)
4
c)
6
d)
8
|
|
Arindam Malik answered |
Determinant of a singular matrix is 0
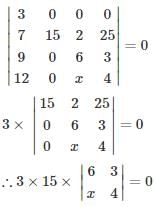
∴ 3×15×(24−3x)=0
∴ 3x=24
∴ x=8
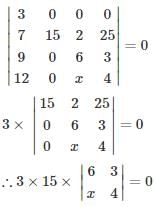
∴ 3×15×(24−3x)=0
∴ 3x=24
∴ x=8
If f(x) is continuous at x = 0 where
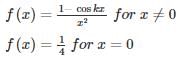
then what is the value of k?- a)

- b)
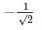
- c)

- d)1/2
Correct answer is option 'C'. Can you explain this answer?
If f(x) is continuous at x = 0 where
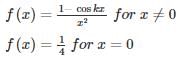
then what is the value of k?
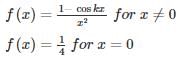
then what is the value of k?
a)

b)
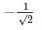
c)

d)
1/2
|
|
Maitri Yadav answered |
Since given function is continuous at x = 0
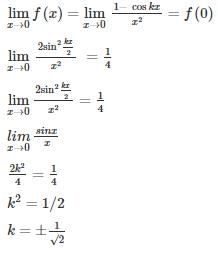
Alternate method:
0/0 form using L Hospital’s
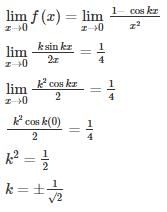
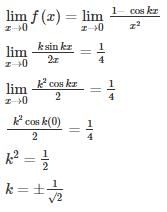
If f(x) is differentiable and g’(x) ≠ 0 such that f(1) = 4, f(2) = 16, f’(x)= 8g’(x) and g(2) = 4 then what is the value of g(1) ?- a)3/2
- b)5/2
- c)7-2
- d)9/2
Correct answer is option 'B'. Can you explain this answer?
If f(x) is differentiable and g’(x) ≠ 0 such that f(1) = 4, f(2) = 16, f’(x)= 8g’(x) and g(2) = 4 then what is the value of g(1) ?
a)
3/2
b)
5/2
c)
7-2
d)
9/2
|
|
Mohit Unni answered |
(x) is differentiable, then the function h(x) = f(x) + g(x) is differentiable.
To prove this, we need to show that h(x) satisfies the definition of differentiability.
First, we know that f(x) is differentiable, so we can write its derivative as f'(x). Similarly, g(x) is differentiable, so its derivative can be written as g'(x).
Now, let's find the derivative of h(x) using the limit definition of the derivative:
h'(x) = lim┬(Δx→0)〖(h(x+Δx)-h(x))/Δx〗
= lim┬(Δx→0)〖((f(x+Δx) + g(x+Δx)) - (f(x) + g(x)))/Δx〗
= lim┬(Δx→0)〖(f(x+Δx) - f(x))/Δx + (g(x+Δx) - g(x))/Δx〗
= lim┬(Δx→0)〖(f(x+Δx) - f(x))/Δx〗 + lim┬(Δx→0)〖(g(x+Δx) - g(x))/Δx〗
= f'(x) + g'(x)
Since f'(x) and g'(x) exist, the limit of the difference quotient exists and is equal to f'(x) + g'(x). Therefore, h(x) = f(x) + g(x) is differentiable.
To prove this, we need to show that h(x) satisfies the definition of differentiability.
First, we know that f(x) is differentiable, so we can write its derivative as f'(x). Similarly, g(x) is differentiable, so its derivative can be written as g'(x).
Now, let's find the derivative of h(x) using the limit definition of the derivative:
h'(x) = lim┬(Δx→0)〖(h(x+Δx)-h(x))/Δx〗
= lim┬(Δx→0)〖((f(x+Δx) + g(x+Δx)) - (f(x) + g(x)))/Δx〗
= lim┬(Δx→0)〖(f(x+Δx) - f(x))/Δx + (g(x+Δx) - g(x))/Δx〗
= lim┬(Δx→0)〖(f(x+Δx) - f(x))/Δx〗 + lim┬(Δx→0)〖(g(x+Δx) - g(x))/Δx〗
= f'(x) + g'(x)
Since f'(x) and g'(x) exist, the limit of the difference quotient exists and is equal to f'(x) + g'(x). Therefore, h(x) = f(x) + g(x) is differentiable.
What is the determinant of the below-given matrix?- a)766
- b)768
- c)786
- d)788
Correct answer is option 'B'. Can you explain this answer?
What is the determinant of the below-given matrix?
a)
766
b)
768
c)
786
d)
788
|
|
Madhurima Chakraborty answered |
Determinant of the given matrix is


Δ = (a − b) (a − c) (a − d) (b − c) (b − d)(c − d)
a = 3, b = 5, c = 7, d = 9
∴ Δ = 768
Given f(x) = x3 + ax2 + bx + c and y-intercept for the function is 1. Also f has local extrema at x = -4 and x = 2. Then a + b + c = ____
Correct answer is '-20'. Can you explain this answer?
Given f(x) = x3 + ax2 + bx + c and y-intercept for the function is 1. Also f has local extrema at x = -4 and x = 2. Then a + b + c = ____
|
|
Tanishq Yadav answered |
First, let's find the equation of the function f(x) based on the given information:
Given y-intercept is 1:
When x = 0, f(x) = 1
So, c = 1
Local extrema at x = -4 and x = 2:
Since f(x) has local extrema at x = -4 and x = 2, the derivative f'(x) will be zero at these points. This means:
f'(-4) = 0 and f'(2) = 0
### Finding the derivative of f(x)
Let's find the derivative of f(x) and set it to zero to find the values of a and b.
f(x) = x^3 + ax^2 + bx + 1
f'(x) = 3x^2 + 2ax + b
### Solving for a and b
1. f'(-4) = 0
3(-4)^2 + 2a(-4) + b = 0
48 - 8a + b = 0
-8a + b = -48
2. f'(2) = 0
3(2)^2 + 2a(2) + b = 0
12 + 4a + b = 0
4a + b = -12
### Solving the equations
By solving equations -8a + b = -48 and 4a + b = -12 simultaneously, we get:
a = -4 and b = -8
### Calculating a + b + c
Now that we have a, b, and c values:
a + b + c = -4 - 8 + 1 = -11
Therefore, a + b + c = -11.
Given y-intercept is 1:
When x = 0, f(x) = 1
So, c = 1
Local extrema at x = -4 and x = 2:
Since f(x) has local extrema at x = -4 and x = 2, the derivative f'(x) will be zero at these points. This means:
f'(-4) = 0 and f'(2) = 0
### Finding the derivative of f(x)
Let's find the derivative of f(x) and set it to zero to find the values of a and b.
f(x) = x^3 + ax^2 + bx + 1
f'(x) = 3x^2 + 2ax + b
### Solving for a and b
1. f'(-4) = 0
3(-4)^2 + 2a(-4) + b = 0
48 - 8a + b = 0
-8a + b = -48
2. f'(2) = 0
3(2)^2 + 2a(2) + b = 0
12 + 4a + b = 0
4a + b = -12
### Solving the equations
By solving equations -8a + b = -48 and 4a + b = -12 simultaneously, we get:
a = -4 and b = -8
### Calculating a + b + c
Now that we have a, b, and c values:
a + b + c = -4 - 8 + 1 = -11
Therefore, a + b + c = -11.
The number of values of k for which the system of equations (k + 1) x + 8y = 4k, kx + (k + 3)y = 3k – 1 has infinitely many solutions, is- a)0
- b)1
- c)2
- d)Infinite
Correct answer is option 'B'. Can you explain this answer?
The number of values of k for which the system of equations (k + 1) x + 8y = 4k, kx + (k + 3)y = 3k – 1 has infinitely many solutions, is
a)
0
b)
1
c)
2
d)
Infinite
|
|
Maulik Iyer answered |
(k + 1)x + 8y = 4k
kx + (k + 3)y = 3k – 1
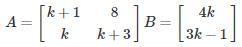 The given system of linear equations has infinitely many solutions if ρ(A) = ρ(A|B) < n = 2
The given system of linear equations has infinitely many solutions if ρ(A) = ρ(A|B) < n = 2
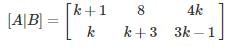
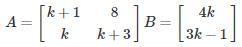 The given system of linear equations has infinitely many solutions if ρ(A) = ρ(A|B) < n = 2
The given system of linear equations has infinitely many solutions if ρ(A) = ρ(A|B) < n = 2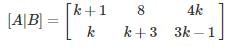
To get the rank less than 2, one row should be dependent on another.
nk = (k + 1), n(k + 3) = 8, n(3k – 1) = 4k
by solving the above equations, we get
n = 2, k = 1
Hence for k = 1 only the system has infinitely many solutions.
Find the value of x and y for the below given simultaneous equations that has no solutions?a + b + c = 182a + 4b + 6c = 122a + xc + 4b = y- a)x ≠ 6 and y ≠ 12
- b)x = 6 and y = 12
- c)x ≠ 6 and y = 12
- d)x = 6 and y ≠ 12
Correct answer is option 'D'. Can you explain this answer?
Find the value of x and y for the below given simultaneous equations that has no solutions?
a + b + c = 18
2a + 4b + 6c = 12
2a + xc + 4b = y
a)
x ≠ 6 and y ≠ 12
b)
x = 6 and y = 12
c)
x ≠ 6 and y = 12
d)
x = 6 and y ≠ 12
|
|
Rajveer Sharma answered |
For given system of equations to have no solution, the determinant of the coefficient matrix should be equal to 0
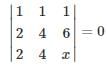
1 × (4x−24) − 1 × (2x−12) + 1(8−8) = 0
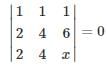
1 × (4x−24) − 1 × (2x−12) + 1(8−8) = 0
2x − 12 = 0
∴ x = 6
Augmented matrix is given by

For given system of equations to have no solution, rank of augmented matrix should be greater than coefficient matrix
∴ y − 12 ≠ 0
∴ y ≠ 12
Augmented matrix is given by

For given system of equations to have no solution, rank of augmented matrix should be greater than coefficient matrix
∴ y − 12 ≠ 0
∴ y ≠ 12
What are the minimum and maximum value of the below-given function respectively?f(x) = 3x3 − 9x2 − 27x + 30- a)45 and 51
- b)-51 and -45
- c)51 ad -45
- d)-51 and 45
Correct answer is option 'D'. Can you explain this answer?
What are the minimum and maximum value of the below-given function respectively?
f(x) = 3x3 − 9x2 − 27x + 30
a)
45 and 51
b)
-51 and -45
c)
51 ad -45
d)
-51 and 45
|
|
Abhijeet Mehta answered |
f(x) = 3x3 − 9x2 − 27x + 30
f′(x) = 9x2 − 18x − 27
f′′(x) = 18x − 18
Points at which maximum or minimum exists
f′(x) = 0
Points at which maximum or minimum exists
f′(x) = 0
9x2 − 18x − 27 = 0
x2 − 2x − 3 = 0
(x − 3) (x + 1 ) = 0
(x = 3) or (x = −1)
Substitute the value in (x = 3) or (x = −1)
f′′(−1) = 18(−1) − 18 = − 36 < 0
∴ at x = −1,maximum value exists
f(−1) = 3(−1)3 −9(−1)2 −27(−1) + 30
f (−1) = 45
f′′ (3) = 18(3) − 18 = 36 > 0
∴ at x = 3, mimimum value exists
f(3) = 3(3)3 − 9(3)2 − 27(3) + 30
f (3) = −51
Find C of Rolle’s theorem for f(x) = ex(sin x - cos x) in- a)0
- b)3π/4
- c)π
- d)Does not exist
Correct answer is option 'C'. Can you explain this answer?
Find C of Rolle’s theorem for f(x) = ex(sin x - cos x) in
a)
0
b)
3π/4
c)
π
d)
Does not exist
|
|
Aaditya Ghosh answered |
Given function f(x) = ex(sin x - cos x)
f(x) is continuous in 3π/4
f(x) is differentiable in 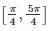

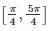

f(a) = f(b)
According to Rolle’s theorem,
there exists at least one value C ∈ (a,b)
such that f’(c) = 0
f’(c) = 0
f’(x) = ex (sin x – cos x) + ex (cos x + sin x)
f’(c) = ec (sin c – cos c) + ec (cos c + sin c) = 0
⇒ 2 ec sin c = 0
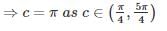
Find the point at which maximum value of f(x) = 2x3−3x2 occurs in interval [-2, 2]?- a)1
- b)0
- c)-1
- d)2
Correct answer is option 'D'. Can you explain this answer?
Find the point at which maximum value of f(x) = 2x3−3x2 occurs in interval [-2, 2]?
a)
1
b)
0
c)
-1
d)
2
|
|
Mrinalini Menon answered |
f(x) = 2x3 − 3x2
f′(x) = 6x2 − 6x
f′′(x) = 12x − 6
f′(x) = 6x2 − 6x = 0
6x (x−1) = 0
x = 0 or x = 1
Now check f(x) at x = 0, x = 1 and the end points of given interval since at end point tangent cannot be drawn so, above concept cannot be used to find maximum or minimum value for end points.
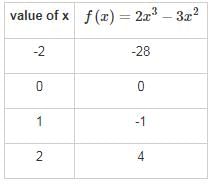
Now check f(x) at x = 0, x = 1 and the end points of given interval since at end point tangent cannot be drawn so, above concept cannot be used to find maximum or minimum value for end points.
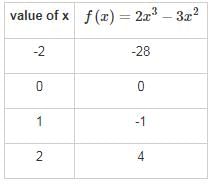
Which of the below-given statements is/are true?I. The eigenvalue of the lower triangular matrix is just the diagonal elements of the matrix.II. The product of the eigenvalue of a matrix is equal to its trace.III. If 1/λ is an eigenvalue of A’(inverse of A) then orthogonal of A also have 1/λ as its eigenvalue.- a)Only I
- b)I and II
- c)I and III
- d)I, II and III
Correct answer is option 'C'. Can you explain this answer?
Which of the below-given statements is/are true?
I. The eigenvalue of the lower triangular matrix is just the diagonal elements of the matrix.
II. The product of the eigenvalue of a matrix is equal to its trace.
III. If 1/λ is an eigenvalue of A’(inverse of A) then orthogonal of A also have 1/λ as its eigenvalue.
a)
Only I
b)
I and II
c)
I and III
d)
I, II and III
|
|
Navya Menon answered |
- The eigenvalue of the triangular (lower or upper) matrix are just the diagonal elements of matrix.
- The product of the eigenvalue of a matrix is equal to its determinants.
- If λ is the eigenvalue of matrix, then 1/λ is the eigenvalue of its inverse since orthogonal is equal to inverse matrix then it has 1/λ as its eigenvalue
Example:

Eigenvalues are 1, 4 and 6 (diagonal elements)
Product of eigen value = determinants = 1 × 4 × 6 = 24
Orthogonal matrix and Inverse of given matrix have eigenvalues: 1,1/4 and 1/6
If a random variable X has a Poisson distribution with variance 6, then expectation [E(X + 3)2] equals _____.
Correct answer is '87'. Can you explain this answer?
If a random variable X has a Poisson distribution with variance 6, then expectation [E(X + 3)2] equals _____.
|
|
Shubham Ghoshal answered |
Var(X) = E(X) = 6
Var(X) = E(X2) - (E(X))2
6 = E(X2) – 36
∴ E(X2) = 42
[E(X + 3)2]
= E(X2 + 6X + 9 )
= E(X2) + 6E(X) + 9
= 42 + 6× 6 + 9
= 87
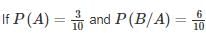 where A and B are exhaustive events, then find P(B)?
where A and B are exhaustive events, then find P(B)?- a)9/50
- b)22/25
- c)23/25
- d)24/25
Correct answer is option 'B'. Can you explain this answer?
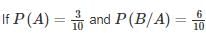 where A and B are exhaustive events, then find P(B)?
where A and B are exhaustive events, then find P(B)?a)
9/50
b)
22/25
c)
23/25
d)
24/25
|
|
Mahi Yadav answered |
Since A and B are exhaustive events
∴ P(A∪B) = 1
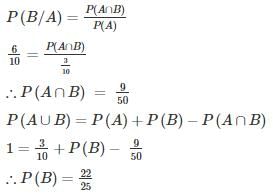
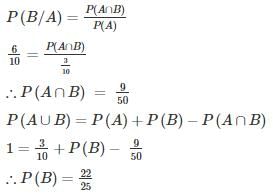
In the given matrix one of the eigenvalues is 1. The eigenvectors corresponding to the eigenvalue 1 are
one of the eigenvalues is 1. The eigenvectors corresponding to the eigenvalue 1 are- a){(4, 2, 1)| α ≠ 0, α ∈ ℝ}
- b){(−4, 2, 1)| α ≠ 0, α ∈ℝ}
- c)
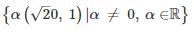
- d)
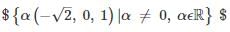
Correct answer is option 'B'. Can you explain this answer?
In the given matrix one of the eigenvalues is 1. The eigenvectors corresponding to the eigenvalue 1 are
one of the eigenvalues is 1. The eigenvectors corresponding to the eigenvalue 1 are
 one of the eigenvalues is 1. The eigenvectors corresponding to the eigenvalue 1 are
one of the eigenvalues is 1. The eigenvectors corresponding to the eigenvalue 1 area)
{(4, 2, 1)| α ≠ 0, α ∈ ℝ}
b)
{(−4, 2, 1)| α ≠ 0, α ∈ℝ}
c)
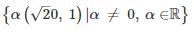
d)
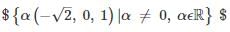
|
|
Palak Saini answered |
For a given matrix A if V is the eigen vector corresponding to the eigen value λ, then:
AV = λV
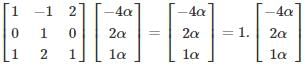
∴ {α (−4, 2, 1) |α ≠ 0, αϵR} are the corresponding eigenvectors.
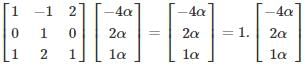
∴ {α (−4, 2, 1) |α ≠ 0, αϵR} are the corresponding eigenvectors.
In the LU decomposition of the matrix, 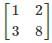 , if the diagonal elements of U are both 1, then the trace of L is:
, if the diagonal elements of U are both 1, then the trace of L is:
Correct answer is '3'. Can you explain this answer?
In the LU decomposition of the matrix, 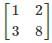 , if the diagonal elements of U are both 1, then the trace of L is:
, if the diagonal elements of U are both 1, then the trace of L is:
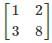 , if the diagonal elements of U are both 1, then the trace of L is:
, if the diagonal elements of U are both 1, then the trace of L is:|
|
Rohit Mukherjee answered |
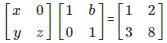
We get x = 1 and z = 2.
Hence tr(L) = 3.
The matrix  has one eigenvalue equal to 3. The sum of the other two eigenvalues is
has one eigenvalue equal to 3. The sum of the other two eigenvalues is- a)P
- b)P – 1
- c)P – 2
- d)P - 3
Correct answer is option 'C'. Can you explain this answer?
The matrix  has one eigenvalue equal to 3. The sum of the other two eigenvalues is
has one eigenvalue equal to 3. The sum of the other two eigenvalues is
 has one eigenvalue equal to 3. The sum of the other two eigenvalues is
has one eigenvalue equal to 3. The sum of the other two eigenvalues isa)
P
b)
P – 1
c)
P – 2
d)
P - 3
|
|
Avantika Shah answered |
Sum of the eigen values of matrix is = Sum of diagonal values present in the matrix
∴ 1 + 0 + P = 3 + λ2 + λ3
⇒ P + 1 = 3 + λ2 + λ3
⇒ λ2 + λ3 = P + 1 – 3 = P – 2
What is the absolute difference of the eigenvalues for the matrix 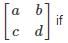 ad – bc = 6 and a + d = 7?
ad – bc = 6 and a + d = 7?- a)7
- b)6
- c)5
- d)4
Correct answer is option 'C'. Can you explain this answer?
What is the absolute difference of the eigenvalues for the matrix 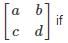 ad – bc = 6 and a + d = 7?
ad – bc = 6 and a + d = 7?
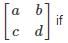 ad – bc = 6 and a + d = 7?
ad – bc = 6 and a + d = 7?a)
7
b)
6
c)
5
d)
4
|
|
Nilanjan Chavan answered |
Let λ1 and λ2 be the two eigen values
Product of eigen value is equal to determinant of matrix
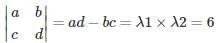
Sum of eigen value is equal to its trace
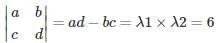
Sum of eigen value is equal to its trace
a + d = λ1 + λ2 = 7
λ1 × (7 − λ1) = 6
λ12 − 7λ + 6 = 0
λ1 = 6 or λ2 = 1
|λ1 − λ2| = 5
3, k, 2, 8, m, 3The arithmetic mean of the list of numbers above is 4. If k and m are integers and k ≠ m, what is the median of the list?- a)2
- b)2.5
- c)3
- d)3.5
Correct answer is option 'C'. Can you explain this answer?
3, k, 2, 8, m, 3
The arithmetic mean of the list of numbers above is 4. If k and m are integers and k ≠ m, what is the median of the list?
a)
2
b)
2.5
c)
3
d)
3.5
|
|
Aditya Nair answered |
Mean = 4
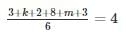
k ≠ m so k = m = 4 is out.
{k, m} = {1, 7} or {2, 6} or {3, 5}
for median of {3, k, 2, 8, m, 3}
{1, 2, 3, 3, 7, 8} or {2, 2, 3, 3, 6, 8} or {2, 3, 3, 3, 5, 8}
Median: (3 + 3) /2 = 3
Chapter doubts & questions for Engineering Mathematics - 6 Months Preparation for GATE CSE 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Engineering Mathematics - 6 Months Preparation for GATE CSE in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
6 Months Preparation for GATE CSE
459 videos|1398 docs|786 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily