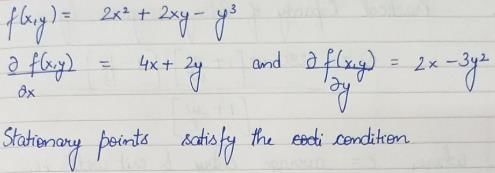All Exams >
Electrical Engineering (EE) >
6 Months Preparation for GATE Electrical >
All Questions
All questions of Calculus for Electrical Engineering (EE) Exam
Consider the function f(x) = |x|3, where x is real... more. Then the function f(x) at x = 0 isa)Continuous but not differentiable
b)Once differentiable but not twice
c)Twice differentiable but not thrice
d)Thrice differentiable
Correct answer is option 'C'. Can you explain this answer?
|
|
Diya Mukherjee answered |
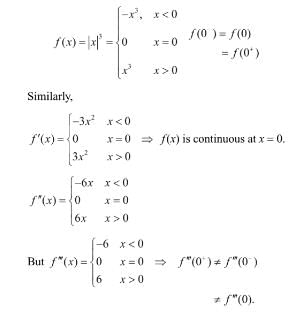
The minimum point of the function f(x) = (x2/3) – x is at - a) x = 1
- b)x = -1
- c) x = 0
- d)x = 1/√3
Correct answer is option 'A'. Can you explain this answer?
The minimum point of the function f(x) = (x2/3) – x is at
a)
x = 1
b)
x = -1
c)
x = 0
d)
x = 1/√3
|
|
Avinash Sharma answered |
Correct Answer :- a
Explanation : f(x) = (x^2/3) - x
f'(x) = 2/3(x-1/2) - 1
f"(x) = -1/3(x-3/2)
For critical points. f′(x)=0
=> 2/3(x-1/2) - 1 = 0
f has minimum value of x = 1
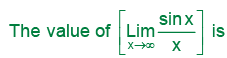
- a)∞
- b)2
- c)0
- d)1
Correct answer is option 'C'. Can you explain this answer?
a)
∞
b)
2
c)
0
d)
1
|
|
Yash Patel answered |
the squeeze theorem for this. Recall that sinx is only defined on −1≤sinx≤1. Therefore
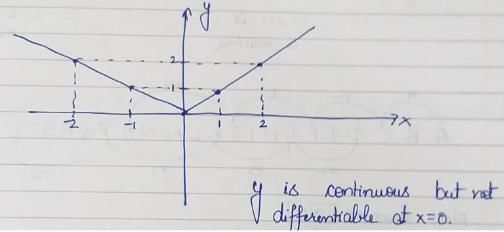
Consider the following two statements about the function f(x) = |x| P: f(x) is continuous for all real values of x Q: f(x) is differentiable for all real values of x Which of the f oll owi ng is TRU E? - a)P is true and Q is false
- b)P is false and Q is true
- c)Both P and Q are true
- d)Both P and Q are false
Correct answer is option 'A'. Can you explain this answer?
Consider the following two statements about the function f(x) = |x|
P: f(x) is continuous for all real values of x
Q: f(x) is differentiable for all real values of x
Which of the f oll owi ng is TRU E?
a)
P is true and Q is false
b)
P is false and Q is true
c)
Both P and Q are true
d)
Both P and Q are false
|
|
Avinash Sharma answered |
The graph of f(x) is
f(x) is continuous for all real values of x Lim |x| = Lim |x| = 0
as can be seen from graph of |x|.
and Lim f(x) = +1 as can be seen from graph of |x|
x → 0+
Left deriva tive ≠ Rig ht derivative
So |x| is continuous but not differentiable at x = 0.

- a)0
- b)π/2
- c)1/5
- d)π/3
Correct answer is option 'B'. Can you explain this answer?

a)
0
b)
π/2
c)
1/5
d)
π/3

|
Akash Kumar answered |
Explain the questions
The distance between the origin and the point nearest to it on the surface z2 = 1 + xy is - a)1
- b)√3/2
- c)√3
- d)-2
Correct answer is option 'A'. Can you explain this answer?
The distance between the origin and the point nearest to it on the surface z2 = 1 + xy is
a)
1
b)
√3/2
c)
√3
d)
-2

|
Baishali Bajaj answered |
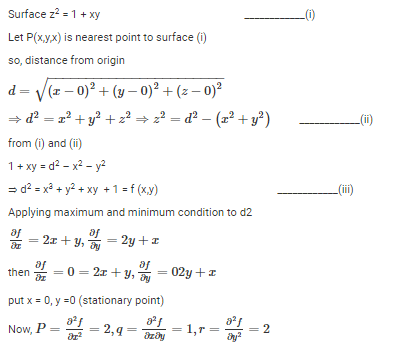
or pr – q^2 = 4 – 1 = 3 > 0 and r = +ve
so f(xy) is minimum at (0,0)
Hence, minimum value of d^2 at (0,0)
d2 = x^2 + y^2 + xy + 1 = (0)^2 + (0)^2 + (0)(0) + 1 = 1
Then the nearest point is
z^2 = 1 + xy = 1+ (0)(0) = 1
or z = 1
The Fourier series for the function f(x)=sin2x is - a)sinx+sin2x
- b)1-cos2x
- c)sin2x+cos2x
- d)0.5-0.5cos2x
Correct answer is option 'D'. Can you explain this answer?
The Fourier series for the function f(x)=sin2x is
a)
sinx+sin2x
b)
1-cos2x
c)
sin2x+cos2x
d)
0.5-0.5cos2x

|
Ashish Chakraborty answered |
Here f(x ) = sin2 x is even function, hence f( x ) has no sine term.
X(t) is a real valued function of a real variable with period T. Its trigonometric Fourier Series expansion contains no terms of frequency ω = 2π (2k ) /T ; k = 1, 2,.... Also, no sine terms are present. Then x(t) satisfies the equation - a)x ( t ) =−x(t − T)
- b)x (t) = −x(T − t)= −x (−t)
- c)x (t) = x(T− t) = −x (t −T / 2)
- d)x (t ) = x(t−T) = x (t −T / 2)
Correct answer is option 'D'. Can you explain this answer?
X(t) is a real valued function of a real variable with period T. Its trigonometric Fourier Series expansion contains no terms of frequency ω = 2π (2k ) /T ; k = 1, 2,.... Also, no sine terms are present. Then x(t) satisfies the equation
a)
x ( t ) =−x(t − T)
b)
x (t) = −x(T − t)= −x (−t)
c)
x (t) = x(T− t) = −x (t −T / 2)
d)
x (t ) = x(t−T) = x (t −T / 2)
|
|
Nandini Banerjee answered |
No sine terms are present.
∴x(t ) is even function.
If x is real, find the maximum value of (-x2 + 3x + 7)- a)36/5
- b)37/7
- c)37/4
- d)36/7
Correct answer is option 'C'. Can you explain this answer?
If x is real, find the maximum value of (-x2 + 3x + 7)
a)
36/5
b)
37/7
c)
37/4
d)
36/7

|
Bijoy Mehra answered |
Given Equation:
- x is real, find the maximum value of (-x^2 + 3x + 7)
Step 1: Find the vertex of the parabola
- The given equation is in the form of a quadratic equation, -x^2 + 3x + 7.
- To find the maximum value, we need to find the vertex of the parabola represented by this equation.
- The x-coordinate of the vertex is given by the formula: x = -b/2a, where a=-1 and b=3 in this case.
- Substituting the values of a and b, we get x = -3/(2*(-1)) = 3/2.
- Now, substitute x = 3/2 back into the equation to find the maximum value.
Step 2: Calculate the maximum value
- Substitute x = 3/2 into the equation: (-3/2)^2 + 3*(3/2) + 7
- Simplify the expression to find the maximum value: -9/4 + 9/2 + 7 = 37/4
Therefore, the maximum value of the given equation (-x^2 + 3x + 7) when x is real is 37/4. Hence, the correct answer is option 'C'.
- x is real, find the maximum value of (-x^2 + 3x + 7)
Step 1: Find the vertex of the parabola
- The given equation is in the form of a quadratic equation, -x^2 + 3x + 7.
- To find the maximum value, we need to find the vertex of the parabola represented by this equation.
- The x-coordinate of the vertex is given by the formula: x = -b/2a, where a=-1 and b=3 in this case.
- Substituting the values of a and b, we get x = -3/(2*(-1)) = 3/2.
- Now, substitute x = 3/2 back into the equation to find the maximum value.
Step 2: Calculate the maximum value
- Substitute x = 3/2 into the equation: (-3/2)^2 + 3*(3/2) + 7
- Simplify the expression to find the maximum value: -9/4 + 9/2 + 7 = 37/4
Therefore, the maximum value of the given equation (-x^2 + 3x + 7) when x is real is 37/4. Hence, the correct answer is option 'C'.
The value of the directional derivative of the function θ (x, y, z) = xy2 + yz2 + zx2 at the point (2, -1, 1) in the direction of the vector p = i + 2j + 2k is- a)1
- b)0.95
- c)0.93
- d)0.9
Correct answer is option 'A'. Can you explain this answer?
The value of the directional derivative of the function θ (x, y, z) = xy2 + yz2 + zx2 at the point (2, -1, 1) in the direction of the vector p = i + 2j + 2k is
a)
1
b)
0.95
c)
0.93
d)
0.9

|
Vertex Academy answered |
Given that,
ϕ = xy2 + yz2 + zx2
directional vector (p) = I + 2j + 2K
Directional derivative = 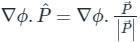
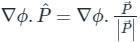
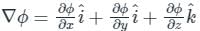
∇ϕ at the point (2, -1, 1) is
∇ϕ = ((-1)2 + 2(2)(1)) î + (2(2)(-1) + (1)2) ĵ + (2(-1)(1) + (2)2)k̂
= 5î - 3ĵ + 2k̂
Directional derivative = 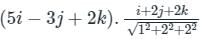
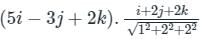
= 5 - 6 + 4 / 3
= 1
The Fourier series of a real periodic function has only P. cosine terms if it is even Q. sine terms if it is even R. cosine terms if it is odd S. sine terms if it is odd Which of the above statements are correct? - a)P and S
- b)P and R
- c)Q and S
- d)Q and R
Correct answer is option 'A'. Can you explain this answer?
The Fourier series of a real periodic function has only
P. cosine terms if it is even
Q. sine terms if it is even
R. cosine terms if it is odd
S. sine terms if it is odd
Which of the above statements are correct?
a)
P and S
b)
P and R
c)
Q and S
d)
Q and R
|
|
Bijoy Menon answered |
Because sine function is odd and cosine is even function.
The maximum value of f ( x) = (1 + cos x) sin x is- a)3
- b)3√3
- c)4
- d)3√3/4
Correct answer is option 'D'. Can you explain this answer?
The maximum value of f ( x) = (1 + cos x) sin x is
a)
3
b)
3√3
c)
4
d)
3√3/4
|
|
Radhika Sharma answered |
The given function is:
f(x) = (1 - cos(x))sin(x)
To find the maximum value of the function:
We can find the maximum value of the function by finding the critical points and determining whether they are maximum or minimum points.
Finding the critical points:
The critical points occur when the derivative of the function is zero or undefined. Let's find the derivative of the given function.
f'(x) = (1 - cos(x))cos(x) + sin(x)(-sin(x))
= cos(x) - cos^2(x) - sin^2(x)
= cos(x) - (1 - sin^2(x))
= cos(x) - 1 + sin^2(x)
= sin^2(x) + cos(x) - 1
Simplifying the derivative:
To find the critical points, we need to solve the equation f'(x) = 0.
sin^2(x) + cos(x) - 1 = 0
Using the identity sin^2(x) = 1 - cos^2(x):
1 - cos^2(x) + cos(x) - 1 = 0
Simplifying further:
-cos^2(x) + cos(x) = 0
Factoring out cos(x):
cos(x)(-cos(x) + 1) = 0
Setting each factor to zero:
cos(x) = 0 or -cos(x) + 1 = 0
Solving the first equation:
cos(x) = 0
This occurs when x = π/2 or x = 3π/2.
Solving the second equation:
-cos(x) + 1 = 0
cos(x) = 1
This occurs when x = 0 or x = 2π.
Therefore, the critical points are x = π/2, 3π/2, 0, and 2π.
Determining the nature of critical points:
To determine whether the critical points are maximum or minimum points, we can use the second derivative test. Let's find the second derivative of the function.
f''(x) = d/dx (sin^2(x) + cos(x) - 1)
= 2sin(x)cos(x) - sin(x)
Using the identity 2sin(x)cos(x) = sin(2x):
f''(x) = sin(2x) - sin(x)
Simplifying the second derivative:
f''(x) = 2sin(x)cos(x) - sin(x)
= sin(x)(2cos(x) - 1)
Evaluating the second derivative at the critical points:
f''(π/2) = sin(π/2)(2cos(π/2) - 1)
= 1(2(0) - 1)
= -1
f''(3π/2) = sin(3π/2)(2cos(3π/2) - 1)
= -1(2(0) - 1)
= 1
f''(0
f(x) = (1 - cos(x))sin(x)
To find the maximum value of the function:
We can find the maximum value of the function by finding the critical points and determining whether they are maximum or minimum points.
Finding the critical points:
The critical points occur when the derivative of the function is zero or undefined. Let's find the derivative of the given function.
f'(x) = (1 - cos(x))cos(x) + sin(x)(-sin(x))
= cos(x) - cos^2(x) - sin^2(x)
= cos(x) - (1 - sin^2(x))
= cos(x) - 1 + sin^2(x)
= sin^2(x) + cos(x) - 1
Simplifying the derivative:
To find the critical points, we need to solve the equation f'(x) = 0.
sin^2(x) + cos(x) - 1 = 0
Using the identity sin^2(x) = 1 - cos^2(x):
1 - cos^2(x) + cos(x) - 1 = 0
Simplifying further:
-cos^2(x) + cos(x) = 0
Factoring out cos(x):
cos(x)(-cos(x) + 1) = 0
Setting each factor to zero:
cos(x) = 0 or -cos(x) + 1 = 0
Solving the first equation:
cos(x) = 0
This occurs when x = π/2 or x = 3π/2.
Solving the second equation:
-cos(x) + 1 = 0
cos(x) = 1
This occurs when x = 0 or x = 2π.
Therefore, the critical points are x = π/2, 3π/2, 0, and 2π.
Determining the nature of critical points:
To determine whether the critical points are maximum or minimum points, we can use the second derivative test. Let's find the second derivative of the function.
f''(x) = d/dx (sin^2(x) + cos(x) - 1)
= 2sin(x)cos(x) - sin(x)
Using the identity 2sin(x)cos(x) = sin(2x):
f''(x) = sin(2x) - sin(x)
Simplifying the second derivative:
f''(x) = 2sin(x)cos(x) - sin(x)
= sin(x)(2cos(x) - 1)
Evaluating the second derivative at the critical points:
f''(π/2) = sin(π/2)(2cos(π/2) - 1)
= 1(2(0) - 1)
= -1
f''(3π/2) = sin(3π/2)(2cos(3π/2) - 1)
= -1(2(0) - 1)
= 1
f''(0
The Fourier series expansion of a symmetric and even function, f(x) where 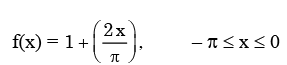
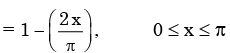 Will be
Will be - a)
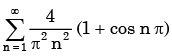
- b)
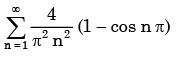
- c)

- d)
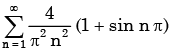
Correct answer is option 'B'. Can you explain this answer?
The Fourier series expansion of a symmetric and even function, f(x) where
Will be
a)
b)
c)
d)
|
|
Rhea Reddy answered |
f(x) is symmetric and even, it’s Fourier series contain only cosine term. Now.
Suppose C is the closed curve defined as the circle x2 + y2 = 1 with C oriented anti-clockwise. The value of ∮(xy2dx + x2ydy) over the curve C equals ________
Correct answer is between '-0.03,0.03'. Can you explain this answer?
Suppose C is the closed curve defined as the circle x2 + y2 = 1 with C oriented anti-clockwise. The value of ∮(xy2dx + x2ydy) over the curve C equals ________

|
Engineers Adda answered |
Concept:
Green’s theorem:
Let R be a closed bounded region in the xy plane whose boundary C consists of finitely many
smooth curves.
Let F1(x, y) & F(x, y) be functions that are continuous and have continuous partial
derivatives
∂F1 / ∂y and ∂F2 / ∂x. Then
∂F1 / ∂y and ∂F2 / ∂x. Then
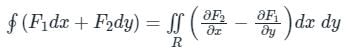
Analysis:
Given curve C: x2 + y2 = 1
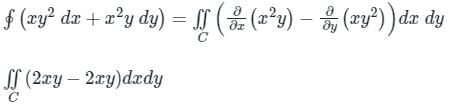
= 0
Mathematically, the functions in Green’s theorem will be- a)Continuous derivatives
- b)Discrete derivatives
- c)Continuous partial derivatives
- d)Discrete partial derivatives
Correct answer is option 'C'. Can you explain this answer?
Mathematically, the functions in Green’s theorem will be
a)
Continuous derivatives
b)
Discrete derivatives
c)
Continuous partial derivatives
d)
Discrete partial derivatives

|
Engineers Adda answered |
The Green’s theorem states that if L and M are functions of (x,y) in an open region containing D and having continuous partial derivatives then,
∫ (F dx + G dy) = ∫∫(dG/dx – dF/dy)dx dy, with path taken anticlockwise.
∫ (F dx + G dy) = ∫∫(dG/dx – dF/dy)dx dy, with path taken anticlockwise.
The value of the integral of the complex function 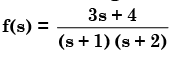 Along the path |s| = 3 is
Along the path |s| = 3 is - a)2πj
- b)4πj
- c)6πj
- d)8πj
Correct answer is option 'C'. Can you explain this answer?
The value of the integral of the complex function
Along the path |s| = 3 is
a)
2πj
b)
4πj
c)
6πj
d)
8πj

|
Cstoppers Instructors answered |
f (s) has singularities at s =−1, −2 which are inside the given circle
Using Cauchy’s integral theorem, the value of the integral (integration being taken in counter clockwise direction) 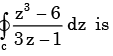
- a)
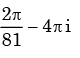
- b)

- c)
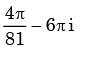
- d)1
Correct answer is option 'A'. Can you explain this answer?
Using Cauchy’s integral theorem, the value of the integral (integration being taken in counter clockwise direction) 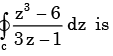
a)
b)
c)
d)
1
|
|
Yash Patel answered |
Here f (z) has a singularities at z i / 3
The residues of a complex function 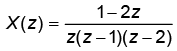 at its poles are
at its poles are - a)

- b)
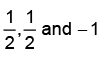
- c)
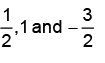
- d)
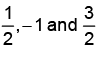
Correct answer is option 'C'. Can you explain this answer?
The residues of a complex function 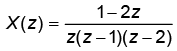 at its poles are
at its poles are
a)
b)
c)
d)
|
|
Avinash Sharma answered |
x(z) has simple poles at z = 0,1, 2.
Using Green’s theorem, the value of the integral 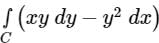 , where C is the square, cut from the first quadrant by the lines x = 1 and y = 1, will be.
, where C is the square, cut from the first quadrant by the lines x = 1 and y = 1, will be.- a)1
- b)1/2
- c)5/3
- d)3/2
Correct answer is option 'D'. Can you explain this answer?
Using Green’s theorem, the value of the integral 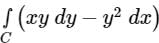 , where C is the square, cut from the first quadrant by the lines x = 1 and y = 1, will be.
, where C is the square, cut from the first quadrant by the lines x = 1 and y = 1, will be.
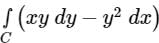 , where C is the square, cut from the first quadrant by the lines x = 1 and y = 1, will be.
, where C is the square, cut from the first quadrant by the lines x = 1 and y = 1, will be.a)
1
b)
1/2
c)
5/3
d)
3/2
|
|
Sanya Agarwal answered |
Concept:
If M(x,y), N(x,y), ∂N/∂y and ∂M/∂x be continuous functions over region R bounded by a simple closed curve c in x-y plane, then according to this theorem:
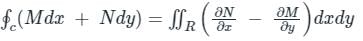
It is used to simplify the vector integration.
It gives the relation between the closed line and open surface integration.
Calculation:
Given:
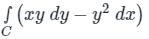
Comparing with the standard equation Mdx + Ndy; M = -y2 and N = xy.
∴ 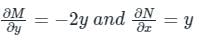
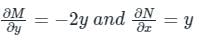
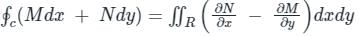
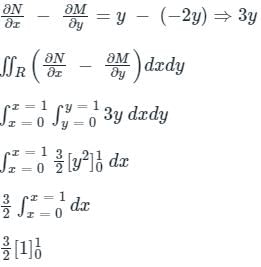
= 3/2
The following surface integral is to be evaluated over a sphere for the given steady vector field, F = xi + yj + zk defined with respect to a Cartesian coordinate system having i, j, and k as unit base vectors.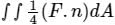 , Where S is the sphere, x2 + y2 + z2 = 1 and n is the outward unit normal vector to the sphere. The value of the surface integral is
, Where S is the sphere, x2 + y2 + z2 = 1 and n is the outward unit normal vector to the sphere. The value of the surface integral is- a)π
- b)2π
- c)
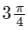
- d)4π
Correct answer is option 'A'. Can you explain this answer?
The following surface integral is to be evaluated over a sphere for the given steady vector field, F = xi + yj + zk defined with respect to a Cartesian coordinate system having i, j, and k as unit base vectors.
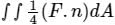 , Where S is the sphere, x2 + y2 + z2 = 1 and n is the outward unit normal vector to the sphere. The value of the surface integral is
, Where S is the sphere, x2 + y2 + z2 = 1 and n is the outward unit normal vector to the sphere. The value of the surface integral isa)
π
b)
2π
c)
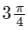
d)
4π

|
Pioneer Academy answered |
Concept:
Gauss divergence theorem:
It states that the surface integral of the normal component of a vector function 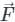 taken over a closed surface ‘S’ is equal to the volume integral of the divergence of that vector function
taken over a closed surface ‘S’ is equal to the volume integral of the divergence of that vector function 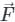 taken over a volume enclosed by the closed surface ‘S’.
taken over a volume enclosed by the closed surface ‘S’.
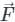 taken over a closed surface ‘S’ is equal to the volume integral of the divergence of that vector function
taken over a closed surface ‘S’ is equal to the volume integral of the divergence of that vector function 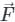 taken over a volume enclosed by the closed surface ‘S’.
taken over a volume enclosed by the closed surface ‘S’.
Calculation:
Given:
F = xi + yj + zk
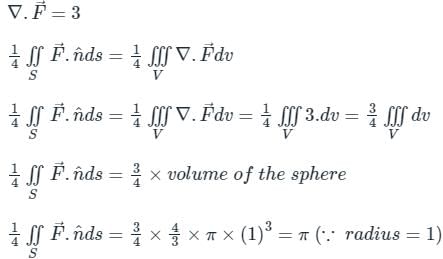
Stokes theorem:
It states that the line integral of a vector field 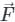 around any closed surface C is equal to the surface integral of the normal component of the curl of vector
around any closed surface C is equal to the surface integral of the normal component of the curl of vector 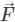 over an unclosed surface ‘S’.
over an unclosed surface ‘S’.
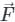 around any closed surface C is equal to the surface integral of the normal component of the curl of vector
around any closed surface C is equal to the surface integral of the normal component of the curl of vector 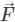 over an unclosed surface ‘S’.
over an unclosed surface ‘S’.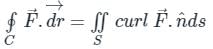
Green's theorem:
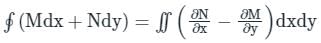
The value of 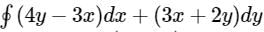 where ‘C’ is the curve passing through the point (0, √2) and satisfying the differential equation dy/dx = −2x/y is ________.
where ‘C’ is the curve passing through the point (0, √2) and satisfying the differential equation dy/dx = −2x/y is ________.
Correct answer is between '-5,-4'. Can you explain this answer?
The value of 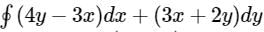 where ‘C’ is the curve passing through the point (0, √2) and satisfying the differential equation dy/dx = −2x/y is ________.
where ‘C’ is the curve passing through the point (0, √2) and satisfying the differential equation dy/dx = −2x/y is ________.
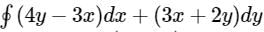 where ‘C’ is the curve passing through the point (0, √2) and satisfying the differential equation dy/dx = −2x/y is ________.
where ‘C’ is the curve passing through the point (0, √2) and satisfying the differential equation dy/dx = −2x/y is ________.

|
Engineers Adda answered |
Concept:
Green's theorem converts the line integral to a double integral.
Green's theorem transform the line integral in xy - plane to a surface integral on the same xy - plane
If P and Q are functions of (x, y) defined in an open region then
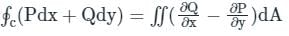
Application:
Given the differential equation is:
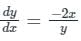
y dy = -2 xdx
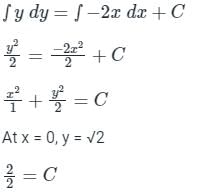
C = 1
∴ The equation of a curve is:
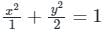
This is an ellipse.
On comparing with 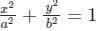 we get:
we get:
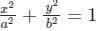 we get:
we get:a = 1 and b = √2
Now, the given integral is:
(4y – 3x)dx + (3x + 2y) dy
Here M = 4y – 3x and N = 3x + 2y
Applying Greens theorem, we convert the line integral to a double integral, i.e.

∴ The given integral becomes:
= 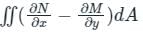
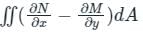
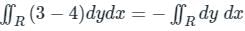
= - (Area under ellipse)
= 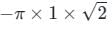
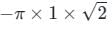
= 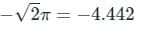
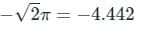
With a 1 unit change in b, what is the change in x in the solution of the system of equations x + y = 2, 1.01 x + 0.99 y = b? - a)Zero
- b)2 units
- c)50 units
- d)100 units
Correct answer is option 'C'. Can you explain this answer?
With a 1 unit change in b, what is the change in x in the solution of the system of equations x + y = 2, 1.01 x + 0.99 y = b?
a)
Zero
b)
2 units
c)
50 units
d)
100 units
|
|
Sahil Majumdar answered |
Given x + y = 2 …………….. (i)
1.01 x + 0.99 y = b …………….. (ii)
Multiply 0.99 is equation (i), and subtract from equation (ii), we get
The expression curl (grad f), where f is a scalar function, is - a)Equal to ∇2f
- b)Equal to div (grad f)
- c) A scalar of zero magnitude
- d)A vector of zero magnitude
Correct answer is option 'D'. Can you explain this answer?
The expression curl (grad f), where f is a scalar function, is
a)
Equal to ∇2f
b)
Equal to div (grad f)
c)
A scalar of zero magnitude
d)
A vector of zero magnitude
|
|
Gaurav Kapoor answered |
The expression curl (grad f), where f is a scalar function, is a vector of zero magnitude.
Explanation:
1. Curl and Gradient
To understand the expression curl (grad f), we need to first understand the concepts of curl and gradient.
- Curl: The curl of a vector field measures the rotation or circulation of the field at a particular point. It is denoted by curl(F) or ∇ × F, where ∇ is the del operator.
- Gradient: The gradient of a scalar function measures the rate of change or the slope of the function at a particular point. It is denoted by grad(f) or ∇f.
2. Curl of Gradient
Now, let's consider the expression curl (grad f), where f is a scalar function.
- First, we find the gradient of the scalar function f, which is given by grad(f) = ∇f. The gradient is a vector field.
- Next, we take the curl of the gradient, which is given by curl (grad f) or ∇ × (∇f).
3. Curl of Gradient of a Scalar Function
For any scalar function f, the curl of its gradient is always a vector of zero magnitude. This means that the curl (grad f) = 0.
- The reason for this is that the curl measures the rotation or circulation of a vector field. However, the gradient of a scalar function is a conservative vector field, which means it has zero curl.
- In other words, the gradient of a scalar function represents a field with no rotation or circulation. Therefore, taking the curl of such a field will always result in zero.
4. Conclusion
In conclusion, the expression curl (grad f), where f is a scalar function, is a vector of zero magnitude. This is because the gradient of a scalar function represents a field with no rotation or circulation, and taking the curl of such a field always results in zero.
Explanation:
1. Curl and Gradient
To understand the expression curl (grad f), we need to first understand the concepts of curl and gradient.
- Curl: The curl of a vector field measures the rotation or circulation of the field at a particular point. It is denoted by curl(F) or ∇ × F, where ∇ is the del operator.
- Gradient: The gradient of a scalar function measures the rate of change or the slope of the function at a particular point. It is denoted by grad(f) or ∇f.
2. Curl of Gradient
Now, let's consider the expression curl (grad f), where f is a scalar function.
- First, we find the gradient of the scalar function f, which is given by grad(f) = ∇f. The gradient is a vector field.
- Next, we take the curl of the gradient, which is given by curl (grad f) or ∇ × (∇f).
3. Curl of Gradient of a Scalar Function
For any scalar function f, the curl of its gradient is always a vector of zero magnitude. This means that the curl (grad f) = 0.
- The reason for this is that the curl measures the rotation or circulation of a vector field. However, the gradient of a scalar function is a conservative vector field, which means it has zero curl.
- In other words, the gradient of a scalar function represents a field with no rotation or circulation. Therefore, taking the curl of such a field will always result in zero.
4. Conclusion
In conclusion, the expression curl (grad f), where f is a scalar function, is a vector of zero magnitude. This is because the gradient of a scalar function represents a field with no rotation or circulation, and taking the curl of such a field always results in zero.
Find the greatest value of the directional derivatives of the function f = x2yz3 at (2, 1, -1) is
Correct answer is between '13.0,13.7'. Can you explain this answer?
Find the greatest value of the directional derivatives of the function f = x2yz3 at (2, 1, -1) is
|
|
Sanya Agarwal answered |
Concept:
The greatest value of directional derivative = |∇ ϕ|
Analysis:
f = x2yz3 (2, 1, -1)
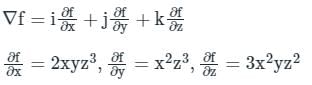
∇f = -4i - 4j + 12k

|Δ f| = 13.26
The minimum distance from the point (4, 2) to the parabola y2 = 8x is- a)√2
- b)2√2
- c)2
- d)3√2
Correct answer is option 'B'. Can you explain this answer?
The minimum distance from the point (4, 2) to the parabola y2 = 8x is
a)
√2
b)
2√2
c)
2
d)
3√2

|
Anshu Kumar answered |
Let the point closest to (4, 2) be (2t2,4)
The value of the integral of the function g(x, y) = 4x3 + 10y4 along the straight line segment from the point (0, 0) to the point (1, 2) in the x-y plane is - a)33
- b)35
- c)40
- d)56
Correct answer is option 'A'. Can you explain this answer?
The value of the integral of the function g(x, y) = 4x3 + 10y4 along the straight line segment from the point (0, 0) to the point (1, 2) in the x-y plane is
a)
33
b)
35
c)
40
d)
56
|
|
Rajat Basu answered |
The equation of the line passing through (0,0) and (1,2) is y = 2x
Given y x, y ) = 4x3+ 10y4 = 4x3 + 10(2x )4 = 4x3+ 160xy
Which of the following theorem convert line integral to surface integral?- a)Gauss divergence and Stoke’s theorem
- b)Stoke’s theorem only
- c)Green’ s theorem only
- d)Stoke’s and Green’s theorem
Correct answer is option 'D'. Can you explain this answer?
Which of the following theorem convert line integral to surface integral?
a)
Gauss divergence and Stoke’s theorem
b)
Stoke’s theorem only
c)
Green’ s theorem only
d)
Stoke’s and Green’s theorem

|
Nilesh Kapoor answered |
The correct answer is b) Gauss divergence and Stokes.
The function f(x) = |x+1| on the interval [-2, 0] - a)Continuous and differentiable
- b) Continuous on the integral but not differentiable at all points
- c) Neither continuous nor differentiable
- d)Differentiable but not continuous
Correct answer is option 'B'. Can you explain this answer?
The function f(x) = |x+1| on the interval [-2, 0]
a)
Continuous and differentiable
b)
Continuous on the integral but not differentiable at all points
c)
Neither continuous nor differentiable
d)
Differentiable but not continuous
|
|
Mrinalini Sharma answered |
f(x ) = x+ 1
f is continuous in [−2, 0]
but not differentiable at
x =−1 because we can draw
infinite number of tangents at x = −1
The directional derivative of ϕ = xy + yz + zx along the tangent to the curve at x = t, y = t2, z = t3 at P(1,1,1) is A/√14, then the value of A is:
Correct answer is '12'. Can you explain this answer?
The directional derivative of ϕ = xy + yz + zx along the tangent to the curve at x = t, y = t2, z = t3 at P(1,1,1) is A/√14, then the value of A is:

|
Mahesh Yadav answered |
To find the directional derivative of the function f(x,y,z) = xy + yz + zx, we need to find the gradient vector of f at the point P(1,1,1) and then take the dot product of the gradient vector with the tangent vector of the curve at P.
First, let's find the gradient vector of f:
∇f = (∂f/∂x, ∂f/∂y, ∂f/∂z)
= (y+z, x+z, x+y)
Now, let's find the tangent vector of the curve at P(1,1,1). We can do this by taking the derivative of each component of the curve with respect to t:
r(t) = (x(t), y(t), z(t))
= (t, t^2, t^3)
dr/dt = (dx/dt, dy/dt, dz/dt)
= (1, 2t, 3t^2)
At P(1,1,1), t = 1, so the tangent vector at P is:
dr/dt = (1, 2(1), 3(1)^2)
= (1, 2, 3)
Finally, we can find the directional derivative by taking the dot product of the gradient vector and the tangent vector:
Directional derivative = ∇f · dr/dt
= (y+z, x+z, x+y) · (1, 2, 3)
= (1+1, 1+1, 1+2)
= (2, 2, 3)
Therefore, the directional derivative of f = xy + yz + zx along the tangent to the curve at P(1,1,1) is (2, 2, 3).
First, let's find the gradient vector of f:
∇f = (∂f/∂x, ∂f/∂y, ∂f/∂z)
= (y+z, x+z, x+y)
Now, let's find the tangent vector of the curve at P(1,1,1). We can do this by taking the derivative of each component of the curve with respect to t:
r(t) = (x(t), y(t), z(t))
= (t, t^2, t^3)
dr/dt = (dx/dt, dy/dt, dz/dt)
= (1, 2t, 3t^2)
At P(1,1,1), t = 1, so the tangent vector at P is:
dr/dt = (1, 2(1), 3(1)^2)
= (1, 2, 3)
Finally, we can find the directional derivative by taking the dot product of the gradient vector and the tangent vector:
Directional derivative = ∇f · dr/dt
= (y+z, x+z, x+y) · (1, 2, 3)
= (1+1, 1+1, 1+2)
= (2, 2, 3)
Therefore, the directional derivative of f = xy + yz + zx along the tangent to the curve at P(1,1,1) is (2, 2, 3).
The directional derivative of 1/r in the direction of 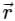 is
is- a)1/r2
- b)-1/r2
- c)1/r3
- d)-
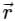 /r3
/r3
Correct answer is option 'B'. Can you explain this answer?
The directional derivative of 1/r in the direction of 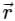 is
is
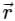 is
isa)
1/r2
b)
-1/r2
c)
1/r3
d)
-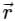 /r3
/r3
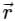 /r3
/r3

|
Pioneer Academy answered |
Concept:
Let f(r) be a function then directional derivative of the function f(r) is given by:
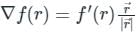
Calculation:
Given:
f(r) = 1/r
As we know that, if f(r) is a function then directional derivative of the function f(r)is given by:
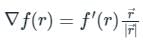
f(r) = 1/r
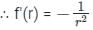
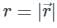
∵ 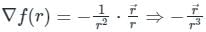
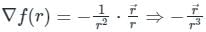
Here, we have to find the directional derivative of f(r) in the direction of 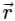 . It will be given by:
. It will be given by:
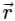 . It will be given by:
. It will be given by: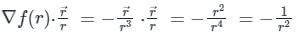
Chapter doubts & questions for Calculus - 6 Months Preparation for GATE Electrical 2025 is part of Electrical Engineering (EE) exam preparation. The chapters have been prepared according to the Electrical Engineering (EE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Calculus - 6 Months Preparation for GATE Electrical in English & Hindi are available as part of Electrical Engineering (EE) exam.
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
6 Months Preparation for GATE Electrical
795 videos|1417 docs|800 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup