All questions of Algorithms for Computer Science Engineering (CSE) Exam
Which one of the following hash functions on integers will distribute keys most uniformly over 10 buckets numbered 0 to 9 for i ranging from 0 to 2020?- a)h(i) =i2 mod 10
- b)h(i) =i3 mod 10
- c)h(i) = (11 ∗ i2) mod 10
- d)h(i) = (12 ∗ i) mod 10
Correct answer is option 'B'. Can you explain this answer?
Which one of the following hash functions on integers will distribute keys most uniformly over 10 buckets numbered 0 to 9 for i ranging from 0 to 2020?
a)
h(i) =i2 mod 10
b)
h(i) =i3 mod 10
c)
h(i) = (11 ∗ i2) mod 10
d)
h(i) = (12 ∗ i) mod 10
|
|
Ravi Singh answered |
Since mod 10 is used, the last digit matters. If you do cube all numbers from 0 to 9, you get following
Therefore all numbers from 0 to 2020 are equally divided in 10 buckets. If we make a table for square, we don't get equal distribution. In the following table. 1, 4, 6 and 9 are repeated, so these buckets would have more entries and buckets 2, 3, 7 and 8 would be empty.
Which of the following is not a stable sorting algorithm in its typical implementation.- a)Insertion Sort
- b)Merge Sort
- c)Quick Sort
- d)Bubble Sort
Correct answer is option 'C'. Can you explain this answer?
Which of the following is not a stable sorting algorithm in its typical implementation.
a)
Insertion Sort
b)
Merge Sort
c)
Quick Sort
d)
Bubble Sort
|
|
Anushka Khanna answered |
Explanation:
- A sorting algorithm is said to be stable if two objects with equal keys appear in the same order in sorted output as they appear in the input array to be sorted.
- Means, a sorting algorithm is called stable if two identical elements do not change the order during the process of sorting.
- Some sorting algorithms are stable by nature like Insertion sort, Merge Sort, Bubble Sort, etc. and some sorting algorithms are not, like Heap Sort, Quick Sort, etc.
You can study about Sorting Algorithms through the document:
Consider the following directed graph:  The number of different topological orderings of the vertices of the graph is _____________.
The number of different topological orderings of the vertices of the graph is _____________.
Correct answer is '6'. Can you explain this answer?
Consider the following directed graph:
The number of different topological orderings of the vertices of the graph is _____________.
|
|
Yash Patel answered |
Here Start with a and End with f.
a _ _ _ _ f
Blanks spaces are to be filled with b, c, d, e such that b comes before c, and d comes before e..
Number of ways to arrange b,c,d,e such that b comes before c and d comes before e. will be = 4!/(2!*2!) = 6
Number of ways to arrange b,c,d,e such that b comes before c and d comes before e. will be = 4!/(2!*2!) = 6
A networking company uses a compression technique to encode the message before transmitting over the network. Suppose the message contains the following characters with their frequency: Note : Each character in input message takes 1 byte. If the compression technique used is Huffman Coding, how many bits will be saved in the message?
Note : Each character in input message takes 1 byte. If the compression technique used is Huffman Coding, how many bits will be saved in the message?- a)224
- b)800
- c)576
- d)324
Correct answer is option 'C'. Can you explain this answer?
A networking company uses a compression technique to encode the message before transmitting over the network. Suppose the message contains the following characters with their frequency:
Note : Each character in input message takes 1 byte. If the compression technique used is Huffman Coding, how many bits will be saved in the message?
a)
224
b)
800
c)
576
d)
324

|
Crack Gate answered |
Total number of characters in the message = 100.
Each character takes 1 byte. So total number of bits needed = 800.
Each character takes 1 byte. So total number of bits needed = 800.
After Huffman Coding, the characters can be represented with:
f: 0
c: 100
d: 101
a: 1100
b: 1101
e: 111
f: 0
c: 100
d: 101
a: 1100
b: 1101
e: 111
Total number of bits needed = 224
Hence, number of bits saved = 800 - 224 = 576
See here for complete explanation and algorithm.
Hence, number of bits saved = 800 - 224 = 576
See here for complete explanation and algorithm.
Which sorting algorithm will take least time when all elements of input array are identical? Consider typical implementations of sorting algorithms.- a)Insertion Sort
- b)Heap Sort
- c)Merge Sort
- d)Selection Sort
Correct answer is option 'A'. Can you explain this answer?
Which sorting algorithm will take least time when all elements of input array are identical? Consider typical implementations of sorting algorithms.
a)
Insertion Sort
b)
Heap Sort
c)
Merge Sort
d)
Selection Sort
|
|
Dipika Chavan answered |
Explanation:
When all elements of the input array are identical, it means that the array is already sorted. In such a case, some sorting algorithms perform better than others.
Insertion Sort:
Insertion Sort is an efficient algorithm when it comes to sorting an already sorted array. The algorithm simply traverses the array once, comparing each element with its predecessor. Since all elements are already identical, the algorithm will just compare each element with its predecessor and find no difference, thus completing the sort in minimum time.
Heap Sort:
Heap Sort is a comparison-based sorting algorithm that uses a binary heap data structure to sort elements. In the case of an array with identical elements, it takes the same amount of time as any other comparison-based sorting algorithm.
Merge Sort:
Merge Sort is a divide-and-conquer algorithm that divides an array into two halves, sorts them separately, and then merges them back together. In the case of an array with identical elements, Merge Sort still needs to perform the divide and merge operations, which takes more time than Insertion Sort.
Selection Sort:
Selection Sort is a simple sorting algorithm that selects the smallest element from an unsorted array and swaps it with the first element, then selects the second smallest element and swaps it with the second element, and so on. In the case of an array with identical elements, Selection Sort will still perform the same number of swaps as in any other case, making it slower than Insertion Sort.
Therefore, Insertion Sort is the best sorting algorithm when all elements of the input array are identical.
When all elements of the input array are identical, it means that the array is already sorted. In such a case, some sorting algorithms perform better than others.
Insertion Sort:
Insertion Sort is an efficient algorithm when it comes to sorting an already sorted array. The algorithm simply traverses the array once, comparing each element with its predecessor. Since all elements are already identical, the algorithm will just compare each element with its predecessor and find no difference, thus completing the sort in minimum time.
Heap Sort:
Heap Sort is a comparison-based sorting algorithm that uses a binary heap data structure to sort elements. In the case of an array with identical elements, it takes the same amount of time as any other comparison-based sorting algorithm.
Merge Sort:
Merge Sort is a divide-and-conquer algorithm that divides an array into two halves, sorts them separately, and then merges them back together. In the case of an array with identical elements, Merge Sort still needs to perform the divide and merge operations, which takes more time than Insertion Sort.
Selection Sort:
Selection Sort is a simple sorting algorithm that selects the smallest element from an unsorted array and swaps it with the first element, then selects the second smallest element and swaps it with the second element, and so on. In the case of an array with identical elements, Selection Sort will still perform the same number of swaps as in any other case, making it slower than Insertion Sort.
Therefore, Insertion Sort is the best sorting algorithm when all elements of the input array are identical.
Which of the following statements is false?- a)Optimal binary search tree construction can be performed efficiently using dynamic programming
- b)Breadth-first search cannot be used to find connected components of a graph
- c)Given the prefix and postfix walks over a binary tree, the binary tree cannot be uniquely constructed.
- d)Depth-first search can be used to find connected components of a graph
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is false?
a)
Optimal binary search tree construction can be performed efficiently using dynamic programming
b)
Breadth-first search cannot be used to find connected components of a graph
c)
Given the prefix and postfix walks over a binary tree, the binary tree cannot be uniquely constructed.
d)
Depth-first search can be used to find connected components of a graph
|
|
Palak Saini answered |
(a) True.
(b) False.
(c) True.
(d) True.
(b) False.
(c) True.
(d) True.
What happens when a top-down approach of dynamic programming is applied to any problem?- a)It increases both, the time complexity and the space complexity
- b)It increases the space complexity and decreases the time complexity.
- c)It increases the time complexity and decreases the space complexity
- d)It decreases both, the time complexity and the space complexity
Correct answer is option 'B'. Can you explain this answer?
What happens when a top-down approach of dynamic programming is applied to any problem?
a)
It increases both, the time complexity and the space complexity
b)
It increases the space complexity and decreases the time complexity.
c)
It increases the time complexity and decreases the space complexity
d)
It decreases both, the time complexity and the space complexity
|
|
Ravi Singh answered |
As the mentioned approach uses the memoization technique it always stores the previously calculated values. Due to this, the time complexity is decreased but the space complexity is increased.
Consider a hash table with 100 slots. Collisions are resolved using chaining. Assuming simple uniform hashing, what is the probability that the first 3 slots are unfilled after the first 3 insertions?- a)(97 × 97 × 97)/1003
- b)(99 × 98 × 97)/1003
- c)(97 × 96 × 95)/1003
- d)(97 × 96 × 95)/(3! × 1003)
Correct answer is option 'A'. Can you explain this answer?
Consider a hash table with 100 slots. Collisions are resolved using chaining. Assuming simple uniform hashing, what is the probability that the first 3 slots are unfilled after the first 3 insertions?
a)
(97 × 97 × 97)/1003
b)
(99 × 98 × 97)/1003
c)
(97 × 96 × 95)/1003
d)
(97 × 96 × 95)/(3! × 1003)
|
|
Mayank Malik answered |
Simple Uniform hashing function is a hypothetical hashing function that evenly distributes items into the slots of a hash table. Moreover, each item to be hashed has an equal probability of being placed into a slot, regardless of the other elements already placed.
Probability that the first 3 slots are unfilled after the first 3 insertions =
(probability that first item doesn't go in any of the first 3 slots)*
(probability that second item doesn't go in any of the first 3 slots)*
(probability that third item doesn't go in any of the first 3 slots)
(probability that first item doesn't go in any of the first 3 slots)*
(probability that second item doesn't go in any of the first 3 slots)*
(probability that third item doesn't go in any of the first 3 slots)
= (97/100) * (97/100) * (97/100)
What is the size of the smallest MIS(Maximal Independent Set) of a chain of nine nodes?- a)5
- b)4
- c)3
- d)2
Correct answer is option 'C'. Can you explain this answer?
What is the size of the smallest MIS(Maximal Independent Set) of a chain of nine nodes?
a)
5
b)
4
c)
3
d)
2
|
|
Sounak Joshi answered |
A set of vertices is called independent set such that no two vertices in the set are adjacent. A maximal independent set (MIS) is an independent set which is not subset of any other independent set. The question is about smallest MIS. We can see in below diagram, the three highlighted vertices (2nd, 5th and 8th) form a maximal independent set (not subset of any other MIS) and smallest MIS.
0----0----0----0----0----0----0----0----0
Consider a hash function that distributes keys uniformly. The hash table size is 20. After hashing of how many keys will the probability that any new key hashed collides with an existing one exceed 0.5.- a)5
- b)6
- c)7
- d)10
Correct answer is option 'D'. Can you explain this answer?
Consider a hash function that distributes keys uniformly. The hash table size is 20. After hashing of how many keys will the probability that any new key hashed collides with an existing one exceed 0.5.
a)
5
b)
6
c)
7
d)
10
|
|
Ishaan Saini answered |
For each entry probability of collision is 1/20 {as possible total spaces =20, and an entry will go into only 1 place}
Say after inserting x values probability becomes ½
(1/20).x = ½
X=10
Say after inserting x values probability becomes ½
(1/20).x = ½
X=10
Which of the following standard algorithms is not a Greedy algorithm?- a)Dijkstra's shortest path algorithm
- b)Prim's algorithm
- c)Kruskal algorithm
- d)Huffman Coding
- e)Bellmen Ford Shortest path algorithm
Correct answer is option 'E'. Can you explain this answer?
Which of the following standard algorithms is not a Greedy algorithm?
a)
Dijkstra's shortest path algorithm
b)
Prim's algorithm
c)
Kruskal algorithm
d)
Huffman Coding
e)
Bellmen Ford Shortest path algorithm

|
Shivam Sharma answered |
The Bellman-Ford algorithm is a graph search algorithm that finds the shortest path between a given source vertex and all other vertices in the graph. This algorithm can be used on both weighted and unweighted graphs.
Like Dijkstra's shortest path algorithm, the Bellman-Ford algorithm is guaranteed to find the shortest path in a graph. Though it is slower than Dijkstra's algorithm, Bellman-Ford is capable of handling graphs that contain negative edge weights, so it is more versatile. It is worth noting that if there exists a negative cycle in the graph, then there is no shortest path. Going around the negative cycle an infinite number of times would continue to decrease the cost of the path (even though the path length is increasing). Because of this, Bellman-Ford can also detect negative cycles which is a useful feature.
What does it mean when we say that an algorithm X is asymptotically more efficient than Y?- a)X will be a better choice for all inputs
- b)X will be a better choice for all inputs except small inputs
- c)X will be a better choice for all inputs except large inputs
- d)Y will be a better choice for small inputs
Correct answer is option 'B'. Can you explain this answer?
What does it mean when we say that an algorithm X is asymptotically more efficient than Y?
a)
X will be a better choice for all inputs
b)
X will be a better choice for all inputs except small inputs
c)
X will be a better choice for all inputs except large inputs
d)
Y will be a better choice for small inputs
|
|
Sanya Agarwal answered |
In asymptotic analysis we consider growth of algorithm in terms of input size. An algorithm X is said to be asymptotically better than Y if X takes smaller time than y for all input sizes n larger than a value n0 where n0 > 0.
Consider a sequence F00 defined as : F00(0) = 1, F00(1) = 1 F00(n) = 10 ∗ F00(n – 1) + 100 F00(n – 2) for n ≥ 2 Then what shall be the set of values of the sequence F00 ?- a)(1, 110, 1200)
- b)(1, 110, 600, 1200)
- c)(1, 2, 55, 110, 600, 1200)
- d)(1, 55, 110, 600, 1200)
Correct answer is option 'A'. Can you explain this answer?
Consider a sequence F00 defined as : F00(0) = 1, F00(1) = 1 F00(n) = 10 ∗ F00(n – 1) + 100 F00(n – 2) for n ≥ 2 Then what shall be the set of values of the sequence F00 ?
a)
(1, 110, 1200)
b)
(1, 110, 600, 1200)
c)
(1, 2, 55, 110, 600, 1200)
d)
(1, 55, 110, 600, 1200)
|
|
Sanya Agarwal answered |
F00(0) = 1, F00(1) = 1 F00(n) = 10 ∗ F00(n – 1) + 100 F00(2) = 10 * F00(1) + 100 = 10 * 1 + 100 = 10 + 100 = 110 Similarly: F00(3) = 10 * F00(2) + 100 = 10 * 110 + 100 = 1100 + 100 = 1200 The sequence will be (1, 110, 1200).
So, (A) will be the answer.
Which of the following is true about Huffman Coding.- a)Huffman coding may become lossy in some cases
- b)Huffman Codes may not be optimal lossless codes in some cases
- c)In Huffman coding, no code is prefix of any other code.
- d)All of the above
Correct answer is option 'C'. Can you explain this answer?
Which of the following is true about Huffman Coding.
a)
Huffman coding may become lossy in some cases
b)
Huffman Codes may not be optimal lossless codes in some cases
c)
In Huffman coding, no code is prefix of any other code.
d)
All of the above
|
|
Maheshwar Saha answered |
Huffman Coding
Huffman coding is a lossless data compression algorithm that assigns variable-length codes to characters based on their frequency of occurrence in a given text. It is widely used in data compression applications, such as ZIP files and MP3 audio files.
True statement about Huffman Coding
The correct answer is option 'C', which states that "In Huffman coding, no code is prefix of any other code." This statement is true because of the following reasons:
Prefix Codes
In Huffman coding, the variable-length codes assigned to characters are called prefix codes. A prefix code is a code in which no code word is a prefix of any other code word. For example, consider the following codes:
A -> 0
B -> 10
C -> 110
D -> 111
These codes are prefix codes because no code word is a prefix of any other code word. For instance, the code for B (10) is not a prefix of the code for C (110).
Optimality of Huffman Codes
Huffman codes are optimal prefix codes, which means that they have the minimum average codeword length among all prefix codes that can be generated from the same frequency distribution. This optimality property of Huffman codes ensures that they provide the best possible compression ratio for a given text.
Losslessness of Huffman Coding
Huffman coding is a lossless data compression algorithm, which means that the original text can be recovered exactly from the compressed data. There is no loss of information in the encoding and decoding process.
Conclusion
In conclusion, the true statement about Huffman coding is that it generates prefix codes in which no code word is a prefix of any other code word. This property ensures the uniqueness of the codes and enables their efficient decoding. Huffman codes are optimal prefix codes that provide the best compression ratio for a given text, and they are lossless, which means that the original text can be recovered exactly from the compressed data.
Huffman coding is a lossless data compression algorithm that assigns variable-length codes to characters based on their frequency of occurrence in a given text. It is widely used in data compression applications, such as ZIP files and MP3 audio files.
True statement about Huffman Coding
The correct answer is option 'C', which states that "In Huffman coding, no code is prefix of any other code." This statement is true because of the following reasons:
Prefix Codes
In Huffman coding, the variable-length codes assigned to characters are called prefix codes. A prefix code is a code in which no code word is a prefix of any other code word. For example, consider the following codes:
A -> 0
B -> 10
C -> 110
D -> 111
These codes are prefix codes because no code word is a prefix of any other code word. For instance, the code for B (10) is not a prefix of the code for C (110).
Optimality of Huffman Codes
Huffman codes are optimal prefix codes, which means that they have the minimum average codeword length among all prefix codes that can be generated from the same frequency distribution. This optimality property of Huffman codes ensures that they provide the best possible compression ratio for a given text.
Losslessness of Huffman Coding
Huffman coding is a lossless data compression algorithm, which means that the original text can be recovered exactly from the compressed data. There is no loss of information in the encoding and decoding process.
Conclusion
In conclusion, the true statement about Huffman coding is that it generates prefix codes in which no code word is a prefix of any other code word. This property ensures the uniqueness of the codes and enables their efficient decoding. Huffman codes are optimal prefix codes that provide the best compression ratio for a given text, and they are lossless, which means that the original text can be recovered exactly from the compressed data.
Assume that a mergesort algorithm in the worst case takes 30 seconds for an input of size 64. Which of the following most closely approximates the maximum input size of a problem that can be solved in 6 minutes?- a)256
- b)512
- c)1024
- d)2048
Correct answer is option 'B'. Can you explain this answer?
Assume that a mergesort algorithm in the worst case takes 30 seconds for an input of size 64. Which of the following most closely approximates the maximum input size of a problem that can be solved in 6 minutes?
a)
256
b)
512
c)
1024
d)
2048
|
|
Yash Patel answered |
Time complexity of merge sort is Θ(nLogn)
c*64Log64 is 30
c*64*6 is 30
c is 5/64
c*64*6 is 30
c is 5/64
For time 6 minutes
5/64*nLogn = 6*60
nLogn = 72*64 = 512 * 9
n = 512.
5/64*nLogn = 6*60
nLogn = 72*64 = 512 * 9
n = 512.
Example 1:
Consider array has 4 elements and a searching element 16.
A[4]= {10, 16, 22, 25}
The number of iterations are required to search an element by using a binary search= T1Example 2:
Consider array has 4 elements and a searching element 22.
A[4]= {10, 16, 22, 25}
The number of iterations are required to search an element by using a binary search= T2
Note: Searching is successful.Q.Which of the following statement are true?- a)T1 = T2
- b)T1 < T2
- c)T1 >T2
- d)T2 < T1
Correct answer is option 'B'. Can you explain this answer?
Example 1:
Consider array has 4 elements and a searching element 16.
A[4]= {10, 16, 22, 25}
The number of iterations are required to search an element by using a binary search= T1
Consider array has 4 elements and a searching element 16.
A[4]= {10, 16, 22, 25}
The number of iterations are required to search an element by using a binary search= T1
Example 2:
Consider array has 4 elements and a searching element 22.
A[4]= {10, 16, 22, 25}
The number of iterations are required to search an element by using a binary search= T2
Note: Searching is successful.
Consider array has 4 elements and a searching element 22.
A[4]= {10, 16, 22, 25}
The number of iterations are required to search an element by using a binary search= T2
Note: Searching is successful.
Q.Which of the following statement are true?
a)
T1 = T2
b)
T1 < T2
c)
T1 >T2
d)
T2 < T1

|
Riverdale Learning Institute answered |
The correct answer is option 2.
Concept:
Binary Search:
A Binary Search is a sorting method used to find a specific member in a sorted array. Because binary search works only on sorted arrays, an array must be sorted before using binary search on it. As the number of iterations in the binary search reduces, it is a superior searching approach to the liner search technique.
Algorithm:
int binarySearch(int a[], int beg, int end, int K)
{
int mid;
if(end >= beg)
{ mid = (beg + end)/2;
if(a[mid] == K)
return mid+1;
else if(a[mid] < K)
return binarySearch(a, mid+1, end, K);
else
return binarySearch(a, beg, mid-1, K);
}
return -1;
}
Example 1:
The given data,
A[4]= {10, 16, 22, 25}
Searching element= K= 16
beg= 0
end = 3
mid = 3/2 = 1
if K with A[mid] and search is successful.
Hence the number iterations are =1.
Example 2:
The given data,
A[4]= {10, 16, 22, 25}
Searching element= K= 22
beg= 0
end = 3
mid = 3/2 = 1.
Compare 22 with A[1] is not found and K is greater than A[mid]. So call binarySearch(a, 1+1, 3, 2);
beg= 2
end = 3
mid = 5/2 = 2.
Compare 22 with A[2] is found.
Hence the number of iterations is = 2
Hence the correct answer is T1 < T2.
Concept:
Binary Search:
A Binary Search is a sorting method used to find a specific member in a sorted array. Because binary search works only on sorted arrays, an array must be sorted before using binary search on it. As the number of iterations in the binary search reduces, it is a superior searching approach to the liner search technique.
Algorithm:
int binarySearch(int a[], int beg, int end, int K)
{
int mid;
if(end >= beg)
{ mid = (beg + end)/2;
if(a[mid] == K)
return mid+1;
else if(a[mid] < K)
return binarySearch(a, mid+1, end, K);
else
return binarySearch(a, beg, mid-1, K);
}
return -1;
}
Example 1:
The given data,
A[4]= {10, 16, 22, 25}
Searching element= K= 16
beg= 0
end = 3
mid = 3/2 = 1
if K with A[mid] and search is successful.
Hence the number iterations are =1.
Example 2:
The given data,
A[4]= {10, 16, 22, 25}
Searching element= K= 22
beg= 0
end = 3
mid = 3/2 = 1.
Compare 22 with A[1] is not found and K is greater than A[mid]. So call binarySearch(a, 1+1, 3, 2);
beg= 2
end = 3
mid = 5/2 = 2.
Compare 22 with A[2] is found.
Hence the number of iterations is = 2
Hence the correct answer is T1 < T2.
What is recurrence for worst case of QuickSort and what is the time complexity in Worst case?- a)Recurrence is T(n) = T(n-2) + O(n) and time complexity is O(n^2)
- b)Recurrence is T(n) = T(n-1) + O(n) and time complexity is O(n^2)
- c)Recurrence is T(n) = 2T(n/2) + O(n) and time complexity is O(nLogn)
- d)Recurrence is T(n) = T(n/10) + T(9n/10) + O(n) and time complexity is O(nLogn)
Correct answer is option 'B'. Can you explain this answer?
What is recurrence for worst case of QuickSort and what is the time complexity in Worst case?
a)
Recurrence is T(n) = T(n-2) + O(n) and time complexity is O(n^2)
b)
Recurrence is T(n) = T(n-1) + O(n) and time complexity is O(n^2)
c)
Recurrence is T(n) = 2T(n/2) + O(n) and time complexity is O(nLogn)
d)
Recurrence is T(n) = T(n/10) + T(9n/10) + O(n) and time complexity is O(nLogn)
|
|
Harshitha Kaur answered |
The worst case of QuickSort occurs when the picked pivot is always one of the corner elements in sorted array. In worst case, QuickSort recursively calls one subproblem with size 0 and other subproblem with size (n-1). So recurrence is T(n) = T(n-1) + T(0) + O(n) The above expression can be rewritten as T(n) = T(n-1) + O(n) 1
void exchange(int *a, int *b)
{
int temp;
temp = *a;
*a = *b;
*b = temp;
}
int partition(int arr[], int si, int ei)
{
int x = arr[ei];
int i = (si - 1);
int j;
for (j = si; j <= ei - 1; j++)
{
if(arr[j] <= x)
{
i++;
exchange(&arr[i], &arr[j]);
}
}
exchange (&arr[i + 1], &arr[ei]);
return (i + 1);
}
/* Implementation of Quick Sort
arr[] --> Array to be sorted
si --> Starting index
ei --> Ending index
*/
void quickSort(int arr[], int si, int ei)
{
int pi; /* Partitioning index */
if(si < ei)
{
pi = partition(arr, si, ei);
quickSort(arr, si, pi - 1);
quickSort(arr, pi + 1, ei);
}
}
Given an unsorted array. The array has this property that every element in array is at most k distance from its position in sorted array where k is a positive integer smaller than size of array. Which sorting algorithm can be easily modified for sorting this array and what is the obtainable time complexity?- a)Insertion Sort with time complexity O(kn)
- b)Heap Sort with time complexity O(nLogk)
- c)Quick Sort with time complexity O(kLogk)
- d)Merge Sort with time complexity O(kLogk)
Correct answer is option 'B'. Can you explain this answer?
Given an unsorted array. The array has this property that every element in array is at most k distance from its position in sorted array where k is a positive integer smaller than size of array. Which sorting algorithm can be easily modified for sorting this array and what is the obtainable time complexity?
a)
Insertion Sort with time complexity O(kn)
b)
Heap Sort with time complexity O(nLogk)
c)
Quick Sort with time complexity O(kLogk)
d)
Merge Sort with time complexity O(kLogk)

|
Swara Dasgupta answered |
We can perform this in O(nlogK) time using heaps.
First, create a min-heap with first k+1 elements.Now, we are sure that the smallest element will be in this K+1 elements..Now,remove the smallest element from the min-heap(which is the root) and put it in the result array.Next,insert another element from the unsorted array into the mean-heap, now,the second smallest element will be in this..extract it from the mean-heap and continue this until no more elements are in the unsorted array.Next, use simple heap sort for the remaining elements.
Time Complexity---
O(k) to build the initial min-heap
O((n-k)logk) for remaining elements...
Thus we get O(nlogk)
Hence,B is the correct answer
First, create a min-heap with first k+1 elements.Now, we are sure that the smallest element will be in this K+1 elements..Now,remove the smallest element from the min-heap(which is the root) and put it in the result array.Next,insert another element from the unsorted array into the mean-heap, now,the second smallest element will be in this..extract it from the mean-heap and continue this until no more elements are in the unsorted array.Next, use simple heap sort for the remaining elements.
Time Complexity---
O(k) to build the initial min-heap
O((n-k)logk) for remaining elements...
Thus we get O(nlogk)
Hence,B is the correct answer
You have to sort 1 GB of data with only 100 MB of available main memory. Which sorting technique will be most appropriate?- a)Heap sort
- b)Merge sort
- c)Quick sort
- d)Insertion sort
Correct answer is option 'B'. Can you explain this answer?
You have to sort 1 GB of data with only 100 MB of available main memory. Which sorting technique will be most appropriate?
a)
Heap sort
b)
Merge sort
c)
Quick sort
d)
Insertion sort
|
|
Aditya Deshmukh answered |
Merge sort data can be sorted using external sorting which usses merge sort..
Exponentiation is a heavily used operation in public key cryptography. Which of the following options is the tightest upper bound on the number of multiplications required to compute 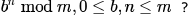
- a)
- b)
- c)
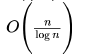
- d)
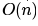
Correct answer is option 'A'. Can you explain this answer?
Exponentiation is a heavily used operation in public key cryptography. Which of the following options is the tightest upper bound on the number of multiplications required to compute 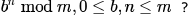
a)
b)
c)
d)

|
Yatharth Sant answered |
We can use divide and conquer paradigm here as follows:
int exp(b,n,m)
{
if(n == 0)
return 1;
if(n == 1)
return b % m;
else
{
int split = exp(b, n/2, m);
if(n%2)
return (((split * split) %m ) * n ) %m;
else
return (split * split ) % m;
}
}
Here Recurrence relation would be T(n) = T(n/2) + k. On solving it we will get T(n) = 0(logn)
Consider the following segment of C-code:int j, n;j = 1;while (j <= n) j = j * 2;- a) [log2 n] + 1
- b)n
- c)[log2 n]
- d)[log2 n] + 2
Correct answer is option 'A'. Can you explain this answer?
Consider the following segment of C-code:
int j, n;
j = 1;
while (j <= n)
j = j * 2;
a)
[log2 n] + 1
b)
n
c)
[log2 n]
d)
[log2 n] + 2
|
|
Swati Kaur answered |
The given C code segment is as follows:
```
int j, n;
j = 1;
while (j = n)
j = j * 2;
```
This code segment initializes two variables, `j` and `n`, and assigns the value 1 to `j`. It then enters a while loop that continues as long as the value of `j` is equal to the value of `n`. Within the loop, the value of `j` is multiplied by 2.
The correct answer to determine the time complexity of this code segment is option 'A' - [log2n] 1. Let's understand why this is the case.
1. Analysis of the code segment:
- The variable `j` is initially set to 1.
- The while loop condition checks if `j` is equal to `n`.
- If `j` is equal to `n`, `j` is multiplied by 2.
- The loop continues as long as `j` is equal to `n`.
2. Execution of the code segment:
- Since `j` is initialized as 1, the loop will execute at least once.
- In each iteration of the loop, `j` is multiplied by 2.
- Therefore, the value of `j` will keep increasing exponentially.
3. Termination condition:
- The loop will terminate when the value of `j` is no longer equal to `n`.
- Since `j` is increasing exponentially, it will eventually become larger than `n`, breaking the loop.
4. Time complexity analysis:
- The loop will execute until `j` becomes larger than `n`.
- The value of `j` in each iteration can be represented as 2^k, where k is the number of iterations.
- The loop will terminate when 2^k > n.
- Taking the logarithm base 2 on both sides of the inequality, we get k > log2n.
- Therefore, the loop will execute log2n + 1 times.
5. Conclusion:
- The time complexity of this code segment is O(log2n) because the loop executes log2n + 1 times, which can be approximated as O(log2n).
- Hence, the correct answer is option 'A' - [log2n] 1.
```
int j, n;
j = 1;
while (j = n)
j = j * 2;
```
This code segment initializes two variables, `j` and `n`, and assigns the value 1 to `j`. It then enters a while loop that continues as long as the value of `j` is equal to the value of `n`. Within the loop, the value of `j` is multiplied by 2.
The correct answer to determine the time complexity of this code segment is option 'A' - [log2n] 1. Let's understand why this is the case.
1. Analysis of the code segment:
- The variable `j` is initially set to 1.
- The while loop condition checks if `j` is equal to `n`.
- If `j` is equal to `n`, `j` is multiplied by 2.
- The loop continues as long as `j` is equal to `n`.
2. Execution of the code segment:
- Since `j` is initialized as 1, the loop will execute at least once.
- In each iteration of the loop, `j` is multiplied by 2.
- Therefore, the value of `j` will keep increasing exponentially.
3. Termination condition:
- The loop will terminate when the value of `j` is no longer equal to `n`.
- Since `j` is increasing exponentially, it will eventually become larger than `n`, breaking the loop.
4. Time complexity analysis:
- The loop will execute until `j` becomes larger than `n`.
- The value of `j` in each iteration can be represented as 2^k, where k is the number of iterations.
- The loop will terminate when 2^k > n.
- Taking the logarithm base 2 on both sides of the inequality, we get k > log2n.
- Therefore, the loop will execute log2n + 1 times.
5. Conclusion:
- The time complexity of this code segment is O(log2n) because the loop executes log2n + 1 times, which can be approximated as O(log2n).
- Hence, the correct answer is option 'A' - [log2n] 1.
In the following C function, let n ≥ mint gcd(n,m) {if (n%m == 0) return m; n = n%m;return gcd(m,n);
}How many recursive calls are made by this function?- a)
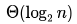
- b)
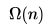
- c)
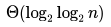
- d)
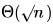
Correct answer is option 'A'. Can you explain this answer?
In the following C function, let n ≥ m
int gcd(n,m) {
if (n%m == 0) return m;
n = n%m;
return gcd(m,n);
}
}
How many recursive calls are made by this function?
a)
b)
c)
d)
|
|
Mita Mehta answered |
Worst case will arise when both n and m are consecutive Fibonacci numbers.
and nth Fibonacci number is 1.618n where 1.618 is the Golden ratio.
So, to find gcd(n,m), number of recursive calls will be θ(logn)
Consider the array A[]= {6,4,8,1,3} apply the insertion sort to sort the array . Consider the cost associated with each sort is 25 rupees , what is the total cost of the insertion sort when element 1 reaches the first position of the array?- a)50
- b)25
- c)75
- d)100
Correct answer is option 'A'. Can you explain this answer?
Consider the array A[]= {6,4,8,1,3} apply the insertion sort to sort the array . Consider the cost associated with each sort is 25 rupees , what is the total cost of the insertion sort when element 1 reaches the first position of the array?
a)
50
b)
25
c)
75
d)
100
|
|
Aditya Deshmukh answered |
When the element 1 reaches the first position of the array two comparisons are only required hence 25 * 2= 50 rupees.
*step 1: 4 6 8 1 3 .
*step 2: 1 4 6 8 3.
Let G be connected undirected graph of 100 vertices and 300 edges. The weight of a minimum spanning tree of G is 500. When the weight of each edge of G is increased by five, the weight of a minimum spanning tree becomes ________.- a)1000
- b)995
- c)2000
- d)1995
Correct answer is option 'B'. Can you explain this answer?
Let G be connected undirected graph of 100 vertices and 300 edges. The weight of a minimum spanning tree of G is 500. When the weight of each edge of G is increased by five, the weight of a minimum spanning tree becomes ________.
a)
1000
b)
995
c)
2000
d)
1995
|
|
Pooja Patel answered |
Since there are 100 vertices, there must be 99 edges in Minimum Spanning Tree (MST). When weight of every edge is increased by 5, the increment in weight of MST is = 99 * 5 = 495 So new weight of MST is 500 + 495 which is 995
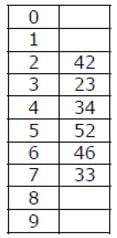 How many different insertion sequences of the key values using the same hash function and linear probing will result in the hash table shown above?
How many different insertion sequences of the key values using the same hash function and linear probing will result in the hash table shown above?
- a)10
- b)20
- c)30
- d)40
Correct answer is option 'C'. Can you explain this answer?

How many different insertion sequences of the key values using the same hash function and linear probing will result in the hash table shown above?
a)
10
b)
20
c)
30
d)
40

|
Shivam Sharma answered |
In a valid insertion sequence, the elements 42, 23 and 34 must appear before 52 and 33, and 46 must appear before 33.
Total number of different sequences = 3! x 5 = 30
In the above expression, 3! is for elements 42, 23 and 34 as they can appear in any order, and 5 is for element 46 as it can appear at 5 different places.
Arrange the following functions in increasing asymptotic order:
A. n1/3
B. en
C. n7/4
D. n log9n
E. 1.0000001n- a)A, D, C, E, B
- b)D, A, C, E, B
- c)A, C, D, E, B
- d)A, C, D, B, E
Correct answer is option 'A'. Can you explain this answer?
Arrange the following functions in increasing asymptotic order:
A. n1/3
B. en
C. n7/4
D. n log9n
E. 1.0000001n
A. n1/3
B. en
C. n7/4
D. n log9n
E. 1.0000001n
a)
A, D, C, E, B
b)
D, A, C, E, B
c)
A, C, D, E, B
d)
A, C, D, B, E
|
|
Deepika Choudhary answered |
Explanation:
To arrange the given functions in increasing asymptotic order, we need to compare their growth rates as n approaches infinity.
1. Constant function: 1.0000001n
This is a constant function, as it does not depend on the value of n. Therefore, its growth rate is O(1), which is the slowest possible growth rate.
2. Cube root function: n1/3
As n approaches infinity, the cube root of n grows slower than any positive power of n, but faster than any logarithmic function. Therefore, its growth rate is O(n1/3).
3. Logarithmic function: n log9n
As n approaches infinity, the logarithmic function grows slower than any positive power of n, but faster than any root function. However, the base of the logarithm does not affect its growth rate, so we can ignore the base 9. Therefore, its growth rate is O(n log n).
4. Power function: n7/4
As n approaches infinity, any positive power of n grows faster than any root or logarithmic function. Therefore, its growth rate is O(n7/4).
5. Exponential function: en
As n approaches infinity, the exponential function grows faster than any positive power of n, root function, or logarithmic function. Therefore, its growth rate is O(en).
Arranged order from slowest to fastest growth rate:
A. n1/3
D. n log9n
C. n7/4
E. en
B. 1.0000001n
Therefore, the correct order is option 'A': A, D, C, E, B.
To arrange the given functions in increasing asymptotic order, we need to compare their growth rates as n approaches infinity.
1. Constant function: 1.0000001n
This is a constant function, as it does not depend on the value of n. Therefore, its growth rate is O(1), which is the slowest possible growth rate.
2. Cube root function: n1/3
As n approaches infinity, the cube root of n grows slower than any positive power of n, but faster than any logarithmic function. Therefore, its growth rate is O(n1/3).
3. Logarithmic function: n log9n
As n approaches infinity, the logarithmic function grows slower than any positive power of n, but faster than any root function. However, the base of the logarithm does not affect its growth rate, so we can ignore the base 9. Therefore, its growth rate is O(n log n).
4. Power function: n7/4
As n approaches infinity, any positive power of n grows faster than any root or logarithmic function. Therefore, its growth rate is O(n7/4).
5. Exponential function: en
As n approaches infinity, the exponential function grows faster than any positive power of n, root function, or logarithmic function. Therefore, its growth rate is O(en).
Arranged order from slowest to fastest growth rate:
A. n1/3
D. n log9n
C. n7/4
E. en
B. 1.0000001n
Therefore, the correct order is option 'A': A, D, C, E, B.
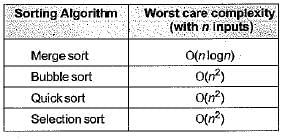
Which of the following sorting algorithms has the lowest worst-case complexity?- a)Merge Sort
- b)Bubble Sort
- c)Quick Sort
- d)Selection Sort
Correct answer is option 'A'. Can you explain this answer?
Which of the following sorting algorithms has the lowest worst-case complexity?
a)
Merge Sort
b)
Bubble Sort
c)
Quick Sort
d)
Selection Sort
|
|
Sanya Agarwal answered |
Worst case complexities for the above sorting algorithms are as follows: Merge Sort — nLogn Bubble Sort — n^2 Quick Sort — n^2 Selection Sort — n^2
How many times is the comparison i > = n performed in the following program?int i=85, n=5;main() {while (i >= n) { i=i-1; n=n+1;}
}- a)40
- b)41
- c)42
- d)43
Correct answer is option 'C'. Can you explain this answer?
How many times is the comparison i > = n performed in the following program?
int i=85, n=5;
main() {
while (i >= n) {
i=i-1;
n=n+1;
}
}
}
a)
40
b)
41
c)
42
d)
43
|
|
Sushant Malik answered |
It will start comparison from (85, 5), (84, 6), (83, 7) .............. (45, 45), (44, 46)
Hence total number of comparison will be (85-44) + 1 = 41 + 1 = 42
Hence total number of comparison will be (85-44) + 1 = 41 + 1 = 42
Consider the following C program segment: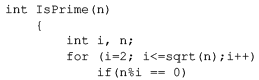
 Let T(n) denote number of times the for loop is executed by the program on input . Which of the following is TRUE?
Let T(n) denote number of times the for loop is executed by the program on input . Which of the following is TRUE?- a)
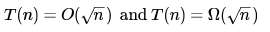
- b)
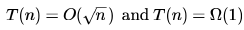
- c)
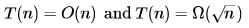
- d) None of the above
Correct answer is option 'B'. Can you explain this answer?
Consider the following C program segment:
Let T(n) denote number of times the for loop is executed by the program on input . Which of the following is TRUE?
a)
b)
c)
d)
None of the above
|
|
Avinash Sharma answered |
Worst Case : 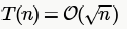
Best Case : When n is an even number body of for loop is executed only 1 time (due to "return 0" inside if) which is irrespective of 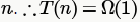
Randomized quicksort is an extension of quicksort where the pivot is chosen randomly. What is the worst case complexity of sorting n numbers using randomized quicksort?- a)O(n)
- b)O(n Log n)
- c)O(n2)
- d)O(n!)
Correct answer is option 'C'. Can you explain this answer?
Randomized quicksort is an extension of quicksort where the pivot is chosen randomly. What is the worst case complexity of sorting n numbers using randomized quicksort?
a)
O(n)
b)
O(n Log n)
c)
O(n2)
d)
O(n!)
|
|
Aravind Sengupta answered |
Randomized quicksort has expected time complexity as O(nLogn), but worst case time complexity remains same. In worst case the randomized function can pick the index of corner element every time.
A list of n string, each of length n, is sorted into lexicographic order using the merge-sort algorithm. The worst case running time of this computation is- a)O(nlogn)
- b)O(n2logn)
- c)O(n2+logn)
- d)O(n2)
Correct answer is option 'B'. Can you explain this answer?
A list of n string, each of length n, is sorted into lexicographic order using the merge-sort algorithm. The worst case running time of this computation is
a)
O(nlogn)
b)
O(n2logn)
c)
O(n2+logn)
d)
O(n2)

|
Shivam Sharma answered |
When we are sorting an array of n integers, Recurrence relation for Total number of comparisons involved will be,
T(n) = 2T(n/2) + (n) where (n) is the number of comparisons in order to merge 2 sorted subarrays of size n/2.
= (nlog2n)
Instead of integers whose comparison take O(1) time, we are given n strings. We can compare 2 strings in O(n) worst case. Therefore, Total number of comparisons now will be (n2log2n) where each comparison takes O(n) time now.
In general, merge sort makes (nlog2n) comparisons, and runs in (nlog2n) time if each comparison can be done in O(1) time.
To learn more about time complexity:
In the following table, the left column contains the names of standard graph algorithms and the right column contains the time complexities of the algorithms. Match each algorithm with its time complexity.1. Bellman-Ford algorithm
2. Kruskal’s algorithm
3. Floyd-Warshall algorithm
4. Topological sortingA : O(m log n)
B : O(n3)
C : O(nm)
D : O(n + m)- a)1→ C, 2 → A, 3 → B, 4 → D
- b)1→ B, 2 → D, 3 → C, 4 → A
- c)1→ C, 2 → D, 3 → A, 4 → B
- d)1→ B, 2 → A, 3 → C, 4 → D
Correct answer is option 'A'. Can you explain this answer?
In the following table, the left column contains the names of standard graph algorithms and the right column contains the time complexities of the algorithms. Match each algorithm with its time complexity.
1. Bellman-Ford algorithm
2. Kruskal’s algorithm
3. Floyd-Warshall algorithm
4. Topological sorting
2. Kruskal’s algorithm
3. Floyd-Warshall algorithm
4. Topological sorting
A : O(m log n)
B : O(n3)
C : O(nm)
D : O(n + m)
B : O(n3)
C : O(nm)
D : O(n + m)
a)
1→ C, 2 → A, 3 → B, 4 → D
b)
1→ B, 2 → D, 3 → C, 4 → A
c)
1→ C, 2 → D, 3 → A, 4 → B
d)
1→ B, 2 → A, 3 → C, 4 → D
|
|
Asha Das answered |
Explanation:
The time complexities of the given graph algorithms are as follows:
- Bellman-Ford algorithm: O(nm)
- Kruskal's algorithm: O(m log n)
- Floyd-Warshall algorithm: O(n^3)
- Topological sorting: O(n + m)
Matching the algorithms with their time complexities:
1. Bellman-Ford algorithm: O(nm)
2. Kruskal's algorithm: O(m log n)
3. Floyd-Warshall algorithm: O(n^3)
4. Topological sorting: O(n + m)
Matching the algorithms with their time complexities:
1. Bellman-Ford algorithm: O(nm) - matches with option C
2. Kruskal's algorithm: O(m log n) - matches with option A
3. Floyd-Warshall algorithm: O(n^3) - matches with option B
4. Topological sorting: O(n + m) - matches with option D
Therefore, the correct answer is option A: 1 C, 2 A, 3 B, 4 D.
The time complexities of the given graph algorithms are as follows:
- Bellman-Ford algorithm: O(nm)
- Kruskal's algorithm: O(m log n)
- Floyd-Warshall algorithm: O(n^3)
- Topological sorting: O(n + m)
Matching the algorithms with their time complexities:
1. Bellman-Ford algorithm: O(nm)
2. Kruskal's algorithm: O(m log n)
3. Floyd-Warshall algorithm: O(n^3)
4. Topological sorting: O(n + m)
Matching the algorithms with their time complexities:
1. Bellman-Ford algorithm: O(nm) - matches with option C
2. Kruskal's algorithm: O(m log n) - matches with option A
3. Floyd-Warshall algorithm: O(n^3) - matches with option B
4. Topological sorting: O(n + m) - matches with option D
Therefore, the correct answer is option A: 1 C, 2 A, 3 B, 4 D.
Consider a hash table of size seven, with starting index zero, and a hash function (3x + 4)mod7. Assuming the hash table is initially empty, which of the following is the contents of the table when the sequence 1, 3, 8, 10 is inserted into the table using closed hashing? Note that ‘_’ denotes an empty location in the table.- a)8, _, _, _, _, _, 10
- b)1, 8, 10, _, _, _, 3
- c)1, _, _, _, _, _,3
- d)1, 10, 8, _, _, _, 3
Correct answer is option 'B'. Can you explain this answer?
Consider a hash table of size seven, with starting index zero, and a hash function (3x + 4)mod7. Assuming the hash table is initially empty, which of the following is the contents of the table when the sequence 1, 3, 8, 10 is inserted into the table using closed hashing? Note that ‘_’ denotes an empty location in the table.
a)
8, _, _, _, _, _, 10
b)
1, 8, 10, _, _, _, 3
c)
1, _, _, _, _, _,3
d)
1, 10, 8, _, _, _, 3
|
|
Palak Khanna answered |
Let us put values 1, 3, 8, 10 in the hash of size 7. Initially, hash table is empty
The value of function (3x + 4)mod 7 for 1 is 0, so let us put the value at 0
The value of function (3x + 4)mod 7 for 3 is 6, so let us put the value at 6
The value of function (3x + 4)mod 7 for 8 is 0, but 0 is already occupied, let us put the value(8) at next available space(1)
The value of function (3x + 4)mod 7 for 10 is 6, but 6 is already occupied, let us put the value(10) at next available space(2)
Which of the following standard algorithms is not Dynamic Programming based.- a)Bellman–Ford Algorithm for single source shortest path
- b)Floyd Warshall Algorithm for all pairs shortest paths
- c)0-1 Knapsack problem
- d)Prim's Minimum Spanning Tree
Correct answer is option 'D'. Can you explain this answer?
Which of the following standard algorithms is not Dynamic Programming based.
a)
Bellman–Ford Algorithm for single source shortest path
b)
Floyd Warshall Algorithm for all pairs shortest paths
c)
0-1 Knapsack problem
d)
Prim's Minimum Spanning Tree
|
|
Amrutha Sharma answered |
Prims Minimum Spanning Tree
Prims Minimum Spanning Tree algorithm is not a Dynamic Programming based algorithm. Here's why:
Dynamic Programming Algorithms
- Dynamic Programming algorithms involve breaking down a complex problem into simpler subproblems and solving each subproblem only once, then storing the solutions to avoid redundant calculations.
- Common characteristics of Dynamic Programming algorithms include overlapping subproblems and optimal substructure.
Prims Minimum Spanning Tree Algorithm
- Prim's algorithm is a greedy algorithm used to find the minimum spanning tree of a connected, undirected graph.
- It starts with an arbitrary node and grows the spanning tree by adding the minimum weight edge at each step until all nodes are included.
- Unlike Dynamic Programming algorithms, Prim's algorithm does not involve breaking down the problem into subproblems or storing intermediate results to avoid recomputation.
Therefore, Prims Minimum Spanning Tree algorithm is not considered a Dynamic Programming based algorithm.
Prims Minimum Spanning Tree algorithm is not a Dynamic Programming based algorithm. Here's why:
Dynamic Programming Algorithms
- Dynamic Programming algorithms involve breaking down a complex problem into simpler subproblems and solving each subproblem only once, then storing the solutions to avoid redundant calculations.
- Common characteristics of Dynamic Programming algorithms include overlapping subproblems and optimal substructure.
Prims Minimum Spanning Tree Algorithm
- Prim's algorithm is a greedy algorithm used to find the minimum spanning tree of a connected, undirected graph.
- It starts with an arbitrary node and grows the spanning tree by adding the minimum weight edge at each step until all nodes are included.
- Unlike Dynamic Programming algorithms, Prim's algorithm does not involve breaking down the problem into subproblems or storing intermediate results to avoid recomputation.
Therefore, Prims Minimum Spanning Tree algorithm is not considered a Dynamic Programming based algorithm.
In the above question, which entry of the array X, if TRUE, implies that there is a subset whose elements sum to W?- a)X[1, W]
- b)X[n ,0]
- c)X[n, W]
- d)X[n -1, n]
Correct answer is option 'C'. Can you explain this answer?
In the above question, which entry of the array X, if TRUE, implies that there is a subset whose elements sum to W?
a)
X[1, W]
b)
X[n ,0]
c)
X[n, W]
d)
X[n -1, n]
|
|
Baishali Reddy answered |
If we get the entry X[n, W] as true then there is a subset of {a1, a2, .. an} that has sum as W.
Consider the array L = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]. Suppose you’re searching for the value 3 using binary search method. What is the value of the variable last after two iterations?- a)14
- b)2
- c)6
- d)3
Correct answer is option 'B'. Can you explain this answer?
Consider the array L = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]. Suppose you’re searching for the value 3 using binary search method. What is the value of the variable last after two iterations?
a)
14
b)
2
c)
6
d)
3
|
|
Sudhir Patel answered |
The starting values of first and last are 0 and 14 respectively.
The iterations are shown below:
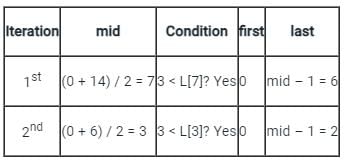
Therefore, the value of the variable last is 2 after the first two iterations.
Important points:
The iterations are shown below:

Therefore, the value of the variable last is 2 after the first two iterations.
Important points:
- The binary search method works on sorted arrays only.
- It checks the middle element with the search element. If it matches, the index is returned.
- Otherwise, if the search element is lesser than the middle element then the algorithm repeats the process in the left half of the array. Else, it searches in the right half of the array.
Following statement is true or false?
If we make following changes to Dijkstra, then it can be used to find the longest simple path, assume that the graph is acyclic.1) Initialize all distances as minus infinite instead of plus infinite.
2) Modify the relax condition in Dijkstra's algorithm to update distance of an adjacent v of the currently considered vertex u only if "dist[u]+graph[u][v] > dist[v]". In shortest path algo, the sign is opposite.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
Following statement is true or false?
If we make following changes to Dijkstra, then it can be used to find the longest simple path, assume that the graph is acyclic.
If we make following changes to Dijkstra, then it can be used to find the longest simple path, assume that the graph is acyclic.
1) Initialize all distances as minus infinite instead of plus infinite.
2) Modify the relax condition in Dijkstra's algorithm to update distance of an adjacent v of the currently considered vertex u only if "dist[u]+graph[u][v] > dist[v]". In shortest path algo, the sign is opposite.
2) Modify the relax condition in Dijkstra's algorithm to update distance of an adjacent v of the currently considered vertex u only if "dist[u]+graph[u][v] > dist[v]". In shortest path algo, the sign is opposite.
a)
True
b)
False
|
|
Shruti Tiwari answered |
In shortest path algo, we pick the minimum distance vertex from the set of vertices for which distance is not finalized yet. And we finalize the distance of the minimum distance vertex. For maximum distance problem, we cannot finalize the distance because there can be a longer path through not yet finalized vertices.
Consider the following functions:f(n) = 2^n
g(n) = n!
h(n) = n^lognQ. Which of the following statements about the asymptotic behavior of f(n), g(n), and h(n) is true?- a) f(n) = O(g(n)); g(n) = O(h(n))
- b)f(n) = Ω(g(n)); g(n) = O(h(n))
- c)g(n) = O(f(n)); h(n) = O(f(n))
- d)h(n) = O(f(n)); g(n) = Ω(f(n))
Correct answer is option 'D'. Can you explain this answer?
Consider the following functions:
f(n) = 2^n
g(n) = n!
h(n) = n^logn
g(n) = n!
h(n) = n^logn
Q. Which of the following statements about the asymptotic behavior of f(n), g(n), and h(n) is true?
a)
f(n) = O(g(n)); g(n) = O(h(n))
b)
f(n) = Ω(g(n)); g(n) = O(h(n))
c)
g(n) = O(f(n)); h(n) = O(f(n))
d)
h(n) = O(f(n)); g(n) = Ω(f(n))
|
|
Abhay Ghoshal answered |
According to order of growth: h(n) < f(n) < g(n) (g(n) is asymptotically greater than f(n) and f(n) is asymptotically greater than h(n) ) We can easily see above order by taking logs of the given 3 functions
lognlogn < n < log(n!) (logs of the given f(n), g(n) and h(n)).
Note that log(n!) = 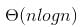
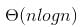
What is recurrence for worst case of QuickSort and what is the time complexity in Worst case?- a)Recurrence is T(n) = T(n-2) + O(n) and time complexity is O(n^2)
- b)Recurrence is T(n) = T(n-1) + O(n) and time complexity is O(n^2)
- c)Recurrence is T(n) = 2T(n/2) + O(n) and time complexity is O(nLogn)
- d)Recurrence is T(n) = T(n/10) + T(9n/10) + O(n) and time complexity is O(nLogn)
Correct answer is option 'B'. Can you explain this answer?
What is recurrence for worst case of QuickSort and what is the time complexity in Worst case?
a)
Recurrence is T(n) = T(n-2) + O(n) and time complexity is O(n^2)
b)
Recurrence is T(n) = T(n-1) + O(n) and time complexity is O(n^2)
c)
Recurrence is T(n) = 2T(n/2) + O(n) and time complexity is O(nLogn)
d)
Recurrence is T(n) = T(n/10) + T(9n/10) + O(n) and time complexity is O(nLogn)

|
Nabanita Saha answered |
The worst case of QuickSort occurs when the picked pivot is always one of the corner elements in sorted array. In worst case, QuickSort recursively calls one subproblem with size 0 and other subproblem with size (n-1). So recurrence is T(n) = T(n-1) + T(0) + O(n) The above expression can be rewritten as T(n) = T(n-1) + O(n) 1
void exchange(int *a, int *b)
{
int temp;
temp = *a;
*a = *b;
*b = temp;
}
{
int temp;
temp = *a;
*a = *b;
*b = temp;
}
int partition(int arr[], int si, int ei)
{
int x = arr[ei];
int i = (si - 1);
int j;
{
int x = arr[ei];
int i = (si - 1);
int j;
for (j = si; j <= ei - 1; j++)
{
if(arr[j] <= x)
{
i++;
exchange(&arr[i], &arr[j]);
}
}
{
if(arr[j] <= x)
{
i++;
exchange(&arr[i], &arr[j]);
}
}
exchange (&arr[i + 1], &arr[ei]);
return (i + 1);
}
return (i + 1);
}
/* Implementation of Quick Sort
arr[] --> Array to be sorted
si --> Starting index
ei --> Ending index
*/
void quickSort(int arr[], int si, int ei)
{
int pi; /* Partitioning index */
if(si < ei)
{
pi = partition(arr, si, ei);
quickSort(arr, si, pi - 1);
quickSort(arr, pi + 1, ei);
}
}
arr[] --> Array to be sorted
si --> Starting index
ei --> Ending index
*/
void quickSort(int arr[], int si, int ei)
{
int pi; /* Partitioning index */
if(si < ei)
{
pi = partition(arr, si, ei);
quickSort(arr, si, pi - 1);
quickSort(arr, pi + 1, ei);
}
}
Which one of the following algorithm design techniques is used in finding all pairs of shortest distances in a graph?- a)Dynamic programming
- b)Backtracking
- c)Greedy
- d)Divide and Conquer
Correct answer is option 'A'. Can you explain this answer?
Which one of the following algorithm design techniques is used in finding all pairs of shortest distances in a graph?
a)
Dynamic programming
b)
Backtracking
c)
Greedy
d)
Divide and Conquer
|
|
Palak Khanna answered |
Answer is A because floyd warshall algorithm used to find all shortest path which is a dynamic programming approach.
Consider the tree arcs of a BFS traversal from a source node W in an unweighted, connected, undirected graph. The tree T formed by the tree arcs is a data structure for computing- a)the shortest path between every pair of vertices.
- b)the shortest path W from to every vertex in the graph.
- c)the shortest paths from W to only those nodes that are leaves of T
- d)the longest path in the graph.
Correct answer is option 'B'. Can you explain this answer?
Consider the tree arcs of a BFS traversal from a source node W in an unweighted, connected, undirected graph. The tree T formed by the tree arcs is a data structure for computing
a)
the shortest path between every pair of vertices.
b)
the shortest path W from to every vertex in the graph.
c)
the shortest paths from W to only those nodes that are leaves of T
d)
the longest path in the graph.
|
|
Diya Chauhan answered |
BFS always having starting node. It does not calculate shortest path between every pair but it computes shorted path between W and any other vertex ..
Which of the following statements is correct with respect to insertion sort?*Online - can sort a list at runtime
*Stable - doesn't change the relative order of elements with equal keys.- a)Insertion sort is stable, online but not suited well for large number of elements.
- b)Insertion sort is unstable and online
- c)Insertion sort is online and can be applied to more than 100 elements
- d)Insertion sort is stable & online and can be applied to more than 100 elements
Correct answer is option 'A'. Can you explain this answer?
Which of the following statements is correct with respect to insertion sort?
*Online - can sort a list at runtime
*Stable - doesn't change the relative order of elements with equal keys.
*Stable - doesn't change the relative order of elements with equal keys.
a)
Insertion sort is stable, online but not suited well for large number of elements.
b)
Insertion sort is unstable and online
c)
Insertion sort is online and can be applied to more than 100 elements
d)
Insertion sort is stable & online and can be applied to more than 100 elements
|
|
Aditi Gupta answered |
Time taken by algorithm is good for small number of elements, but increases quadratically for large number of elements.
What is the time complexity of Huffman Coding?- a)O(N)
- b)O(NlogN)
- c)O(N(logN)^2)
- d)O(N^2)
Correct answer is option 'B'. Can you explain this answer?
What is the time complexity of Huffman Coding?
a)
O(N)
b)
O(NlogN)
c)
O(N(logN)^2)
d)
O(N^2)
|
|
Nilesh Saha answered |
O(nlogn) where n is the number of unique characters. If there are n nodes, extractMin() is called 2*(n – 1) times. extractMin() takes O(logn) time as it calles minHeapify(). So, overall complexity is O(nlogn). See here for more details of the algorithm.
You are asked to sort 15 randomly generated numbers. You should prefer- a)Bubble sort
- b)Selection sort
- c)Insertion sort
- d)Heap sort
Correct answer is option 'C'. Can you explain this answer?
You are asked to sort 15 randomly generated numbers. You should prefer
a)
Bubble sort
b)
Selection sort
c)
Insertion sort
d)
Heap sort
|
|
Aditi Gupta answered |
In-order traversal of a Binary Search Tree lists the nodes in ascending order.
Let A1, A2, A3, and A4 be four matrices of dimensions 10 x 5, 5 x 20, 20 x 10, and 10 x 5, respectively. The minimum number of scalar multiplications required to find the product A1A2A3A4 using the basic matrix multiplication method is- a)1500
- b)2000
- c)500
- d)100
Correct answer is option 'A'. Can you explain this answer?
Let A1, A2, A3, and A4 be four matrices of dimensions 10 x 5, 5 x 20, 20 x 10, and 10 x 5, respectively. The minimum number of scalar multiplications required to find the product A1A2A3A4 using the basic matrix multiplication method is
a)
1500
b)
2000
c)
500
d)
100
|
|
Sanya Agarwal answered |
We have many ways to do matrix chain multiplication because matrix multiplication is associative. In other words, no matter how we parenthesize the product, the result of the matrix chain multiplication obtained will remain the same. Here we have four matrices A1, A2, A3, and A4, we would have: ((A1A2)A3)A4 = ((A1(A2A3))A4) = (A1A2)(A3A4) = A1((A2A3)A4) = A1(A2(A3A4)). However, the order in which we parenthesize the product affects the number of simple arithmetic operations needed to compute the product, or the efficiency. Here, A1 is a 10 × 5 matrix, A2 is a 5 x 20 matrix, and A3 is a 20 x 10 matrix, and A4 is 10 x 5. If we multiply two matrices A and B of order l x m and m x n respectively,then the number of scalar multiplications in the multiplication of A and B will be lxmxn. Then, The number of scalar multiplications required in the following sequence of matrices will be : A1((A2A3)A4) = (5 x 20 x 10) + (5 x 10 x 5) + (10 x 5 x 5) = 1000 + 250 + 250 = 1500. All other parenthesized options will require number of multiplications more than 1500.
Which of the following statements is true?
1. As the number of entries in the hash table increases, the number of collisions increases.
2. Recursive program are efficient.
3. The worst time complexity of quick sort is O(n2).
4. Binary search implemented using a linked list is efficient- a)1 and 2
- b)2 and 3
- c)1 and 4
- d)1 and 3
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements is true?
1. As the number of entries in the hash table increases, the number of collisions increases.
2. Recursive program are efficient.
3. The worst time complexity of quick sort is O(n2).
4. Binary search implemented using a linked list is efficient
1. As the number of entries in the hash table increases, the number of collisions increases.
2. Recursive program are efficient.
3. The worst time complexity of quick sort is O(n2).
4. Binary search implemented using a linked list is efficient
a)
1 and 2
b)
2 and 3
c)
1 and 4
d)
1 and 3
|
|
Sagnik Singh answered |
Recursive programs take more time than the equivalent non-recursive version and so not efficient. This is because of the function call overhead.
In binary search, since every time the current list is probed at the middle, random access is preferred. Since linked list does not support random access, binary search implemented this way is inefficient.
In binary search, since every time the current list is probed at the middle, random access is preferred. Since linked list does not support random access, binary search implemented this way is inefficient.
Randomized quicksort is an extension of quicksort where the pivot is chosen randomly. What is the worst case complexity of sorting n numbers using randomized quicksort?- a)O(n)
- b)(nlogn)
- c)0(n2)
- d)0(n!)
Correct answer is option 'C'. Can you explain this answer?
Randomized quicksort is an extension of quicksort where the pivot is chosen randomly. What is the worst case complexity of sorting n numbers using randomized quicksort?
a)
O(n)
b)
(nlogn)
c)
0(n2)
d)
0(n!)
|
|
Subhankar Chawla answered |
Randomized quick sort worst case time complexity = O (n2).
Chapter doubts & questions for Algorithms - GATE Computer Science Engineering(CSE) 2026 Mock Test Series 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Algorithms - GATE Computer Science Engineering(CSE) 2026 Mock Test Series in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily