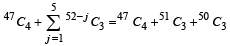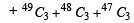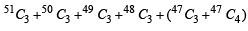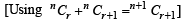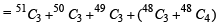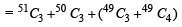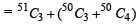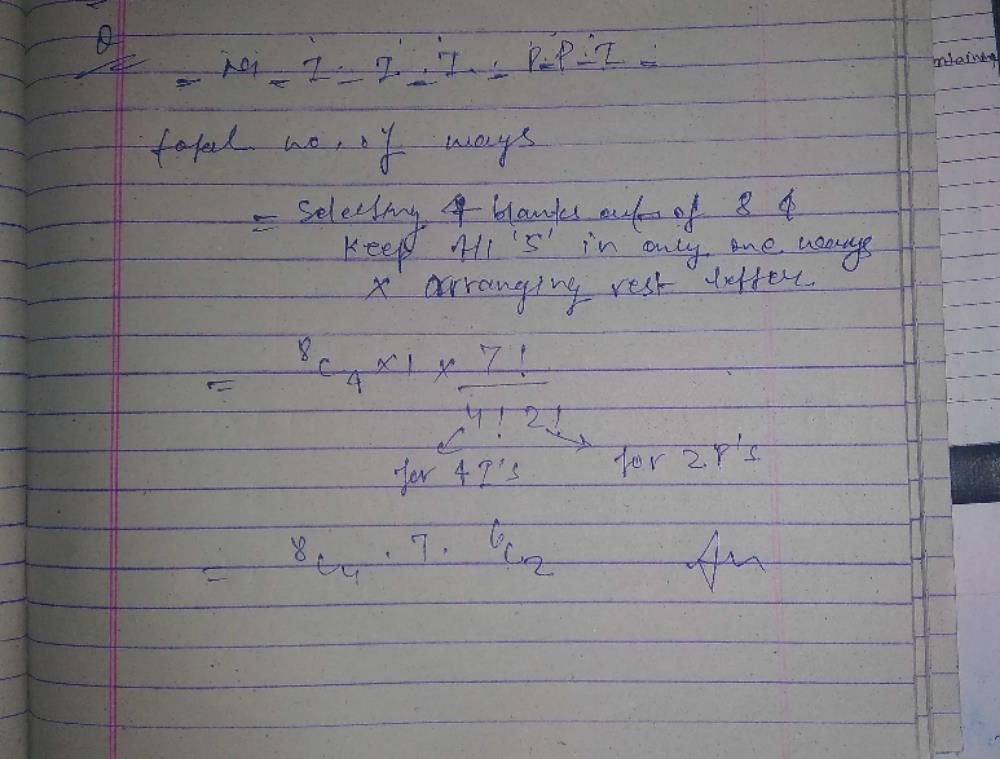All Exams >
JEE >
Maths 35 Year Past year Papers JEE Main & Advanced >
All Questions
All questions of Permutations and Combinations for JEE Exam
Total number of four digit odd numbers that can be formed using 0, 1, 2, 3, 5, 7 (using repetition allowed) are [2002]- a)216
- b)375
- c)400
- d)720
Correct answer is option 'D'. Can you explain this answer?
Total number of four digit odd numbers that can be formed using 0, 1, 2, 3, 5, 7 (using repetition allowed) are [2002]
a)
216
b)
375
c)
400
d)
720
|
|
Dishani Dey answered |
Required number of numbers = 5 x 6 x 6 x 4 = 36 x 20 = 720.
The number of seven digit i ntegers, with sum of the digits equal to 10 and formed by using the digits 1, 2 and 3 only, is (2009)- a)55
- b)66
- c)77
- d)88
Correct answer is option 'C'. Can you explain this answer?
The number of seven digit i ntegers, with sum of the digits equal to 10 and formed by using the digits 1, 2 and 3 only, is (2009)
a)
55
b)
66
c)
77
d)
88
|
|
Lavanya Menon answered |
We h ave to for m 7 digit n umber s, using th e digits 1, 2 and 3 only, such that the sum of the digits in a number = 10.
This can be done by taking 2, 2, 2, 1, 1, 1, 1, or by taking 2, 3, 1, 1, 1, 1, 1.
∴ Number of ways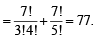
This can be done by taking 2, 2, 2, 1, 1, 1, 1, or by taking 2, 3, 1, 1, 1, 1, 1.
∴ Number of ways
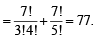
These are 10 points in a plane, out of these 6 are collinear, if N is the number of triangles formed by joining these points. then:[2012]- a)n ≤ 100
- b)100 < n ≤ 140
- c)140 < n ≤190
- d)n > 190
Correct answer is option 'A'. Can you explain this answer?
These are 10 points in a plane, out of these 6 are collinear, if N is the number of triangles formed by joining these points. then:[2012]
a)
n ≤ 100
b)
100 < n ≤ 140
c)
140 < n ≤190
d)
n > 190
|
|
Anaya Patel answered |
Number of required triangles
= 10C3 – 6C3
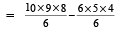 = 120 - 20 =100
= 120 - 20 =100The number of arrangements of the letters of the word BANANA in which the two N's do not appear adjacently is (2002S)- a)40
- b)60
- c)80
- d)100
Correct answer is option 'A'. Can you explain this answer?
The number of arrangements of the letters of the word BANANA in which the two N's do not appear adjacently is (2002S)
a)
40
b)
60
c)
80
d)
100
|
|
Abhijeet Chauhan answered |
Total number of ways of arranging the letters of the word BANANA is 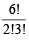 = 60 Number of words in which 2 N’s come together is
= 60 Number of words in which 2 N’s come together is 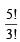 = 20
= 20
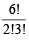 = 60 Number of words in which 2 N’s come together is
= 60 Number of words in which 2 N’s come together is 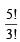 = 20
= 20Hence the required number = 60 – 20 = 40
Let Tn denote the number of triangles which can be formed using the vertices of a regular polygon of n sides. If Tn + 1 - Tn = 21, then n equals (2001S)- a)5
- b)7
- c)6
- d)4
Correct answer is option 'B'. Can you explain this answer?
Let Tn denote the number of triangles which can be formed using the vertices of a regular polygon of n sides. If Tn + 1 - Tn = 21, then n equals (2001S)
a)
5
b)
7
c)
6
d)
4
|
|
Rounak Unni answered |
Solution:
Given, Tn - 1 - Tn = 21
Let's try to find a general formula for Tn.
Consider a regular polygon of n sides. To form a triangle, we need to choose 3 vertices out of n vertices. The number of ways to choose 3 vertices out of n vertices is given by the combination formula.
Number of ways to choose 3 vertices out of n vertices = C(n, 3) = n!/[(n-3)!*3!]
Number of triangles that can be formed using the vertices of a regular polygon of n sides = Tn = C(n, 3)
Therefore, Tn = n!/[(n-3)!*3!]
Now, let's use this formula to solve the given equation.
Tn - 1 - Tn = 21
n!/[(n-4)!*3!] - n!/[(n-3)!*3!] = 21
n(n-3)/6 - (n-3)/2 = 21
Simplifying the above equation, we get
n^2 - 9n + 66 = 0
Solving the above quadratic equation, we get n = 6 or 3.
But n cannot be 3 as a polygon cannot have less than 3 sides.
Therefore, n = 6.
Hence, the correct option is (B) 7.
Given, Tn - 1 - Tn = 21
Let's try to find a general formula for Tn.
Consider a regular polygon of n sides. To form a triangle, we need to choose 3 vertices out of n vertices. The number of ways to choose 3 vertices out of n vertices is given by the combination formula.
Number of ways to choose 3 vertices out of n vertices = C(n, 3) = n!/[(n-3)!*3!]
Number of triangles that can be formed using the vertices of a regular polygon of n sides = Tn = C(n, 3)
Therefore, Tn = n!/[(n-3)!*3!]
Now, let's use this formula to solve the given equation.
Tn - 1 - Tn = 21
n!/[(n-4)!*3!] - n!/[(n-3)!*3!] = 21
n(n-3)/6 - (n-3)/2 = 21
Simplifying the above equation, we get
n^2 - 9n + 66 = 0
Solving the above quadratic equation, we get n = 6 or 3.
But n cannot be 3 as a polygon cannot have less than 3 sides.
Therefore, n = 6.
Hence, the correct option is (B) 7.
How many ways are there to arrange the letters in the word GARDEN with vowels in alphabetical order [2004]- a)480
- b)240
- c)360
- d)120
Correct answer is option 'C'. Can you explain this answer?
How many ways are there to arrange the letters in the word GARDEN with vowels in alphabetical order [2004]
a)
480
b)
240
c)
360
d)
120
|
|
Disha Mishra answered |
To find the number of ways to arrange the letters in the word GARDEN with vowels in alphabetical order, we can follow these steps:
Step 1: Identify the vowels in the word GARDEN
The vowels in the word GARDEN are A and E.
Step 2: Fix the positions of the vowels
Since we want the vowels to be in alphabetical order, we need to fix their positions in the arrangement. Let's assume we arrange the vowels in alphabetical order first.
Step 3: Arrange the remaining consonants
After fixing the positions of the vowels, we need to arrange the remaining consonants (G, R, and D) in the remaining positions.
Step 4: Calculate the number of arrangements
Step 2: Fix the positions of the vowels
Since the vowels A and E need to be in alphabetical order, we have three possible scenarios:
1. A _ E _ _ _ (A before E)
2. E _ A _ _ _ (E before A)
3. A _ _ E _ _ (A before E)
For each scenario, we need to calculate the number of ways to arrange the remaining consonants.
Step 3: Arrange the remaining consonants
After fixing the positions of the vowels, we have three remaining consonants (G, R, and D). We need to arrange them in the remaining positions.
For scenario 1 (A _ E _ _ _):
The first consonant can be any of the three remaining consonants (G, R, D).
The second consonant can be any of the two remaining consonants.
The third consonant can be the remaining consonant.
So, for scenario 1, there are 3 * 2 * 1 = 6 ways to arrange the consonants.
Similarly, for scenario 2 (E _ A _ _ _), there are also 6 ways to arrange the consonants.
For scenario 3 (A _ _ E _ _), there are also 6 ways to arrange the consonants.
Step 4: Calculate the number of arrangements
Now, we need to calculate the total number of arrangements by multiplying the number of ways to arrange the vowels and the number of ways to arrange the consonants.
For each scenario, there are 6 ways to arrange the consonants.
Since there are 3 scenarios, the total number of arrangements is 3 * 6 = 18.
Therefore, the correct answer is option C) 360.
Step 1: Identify the vowels in the word GARDEN
The vowels in the word GARDEN are A and E.
Step 2: Fix the positions of the vowels
Since we want the vowels to be in alphabetical order, we need to fix their positions in the arrangement. Let's assume we arrange the vowels in alphabetical order first.
Step 3: Arrange the remaining consonants
After fixing the positions of the vowels, we need to arrange the remaining consonants (G, R, and D) in the remaining positions.
Step 4: Calculate the number of arrangements
Step 2: Fix the positions of the vowels
Since the vowels A and E need to be in alphabetical order, we have three possible scenarios:
1. A _ E _ _ _ (A before E)
2. E _ A _ _ _ (E before A)
3. A _ _ E _ _ (A before E)
For each scenario, we need to calculate the number of ways to arrange the remaining consonants.
Step 3: Arrange the remaining consonants
After fixing the positions of the vowels, we have three remaining consonants (G, R, and D). We need to arrange them in the remaining positions.
For scenario 1 (A _ E _ _ _):
The first consonant can be any of the three remaining consonants (G, R, D).
The second consonant can be any of the two remaining consonants.
The third consonant can be the remaining consonant.
So, for scenario 1, there are 3 * 2 * 1 = 6 ways to arrange the consonants.
Similarly, for scenario 2 (E _ A _ _ _), there are also 6 ways to arrange the consonants.
For scenario 3 (A _ _ E _ _), there are also 6 ways to arrange the consonants.
Step 4: Calculate the number of arrangements
Now, we need to calculate the total number of arrangements by multiplying the number of ways to arrange the vowels and the number of ways to arrange the consonants.
For each scenario, there are 6 ways to arrange the consonants.
Since there are 3 scenarios, the total number of arrangements is 3 * 6 = 18.
Therefore, the correct answer is option C) 360.
Eight chairs are numbered 1 to 8. Two women and three men wish to occupy one chair each. First the women choose the chairs from amongst the chairs marked 1 to 4 ; and then the men select the chairs from amongst the remaining. The number of possible arrangements is (1982 - 2 Marks)- a)6 C3 x4C2
- b)4 P2 x 4P3
- c)4 C2 x 4P3
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
Eight chairs are numbered 1 to 8. Two women and three men wish to occupy one chair each. First the women choose the chairs from amongst the chairs marked 1 to 4 ; and then the men select the chairs from amongst the remaining. The number of possible arrangements is (1982 - 2 Marks)
a)
6 C3 x4C2
b)
4 P2 x 4P3
c)
4 C2 x 4P3
d)
none of these
|
|
Anand Kumar answered |
Two women can choose two chairs in 4C2 ways and arranged in factorial 2 .
After this no.of chairs left =6
3 men can choose 3 chairs out of 6 chairs in 6C3 and arranged in factorial 3.
therefore, required answer = 4P2 × 6P3
After this no.of chairs left =6
3 men can choose 3 chairs out of 6 chairs in 6C3 and arranged in factorial 3.
therefore, required answer = 4P2 × 6P3
A student is to answer 10 out of 13 questions in an examination such that he must choose at least 4 from the first five questions. The number of choices available to him is[2003]- a)346
- b)140
- c)196
- d)280
Correct answer is option 'C'. Can you explain this answer?
A student is to answer 10 out of 13 questions in an examination such that he must choose at least 4 from the first five questions. The number of choices available to him is[2003]
a)
346
b)
140
c)
196
d)
280
|
|
Charvi Chopra answered |
Problem:
A student is to answer 10 out of 13 questions in an examination such that he must choose at least 4 from the first five questions. The number of choices available to him is
Solution:
To find the number of choices available to the student, we need to consider two cases:
1. The student chooses exactly 4 questions from the first five questions.
2. The student chooses more than 4 questions from the first five questions.
Case 1: Choosing exactly 4 questions from the first five questions
To choose exactly 4 questions from the first five questions, we need to choose 4 questions from the first five and 6 questions from the remaining 8 questions. This can be done in C(5, 4) * C(8, 6) ways, where C(n, r) represents the number of combinations of choosing r items from a set of n items.
C(5, 4) = 5! / (4! * (5-4)!) = 5
C(8, 6) = 8! / (6! * (8-6)!) = 28
Therefore, the number of choices in this case is 5 * 28 = 140.
Case 2: Choosing more than 4 questions from the first five questions
To choose more than 4 questions from the first five questions, we can choose 5, 6, 7, or all 8 questions from the first five. For each of these cases, we need to choose the remaining questions from the remaining 8 questions.
Number of choices when choosing 5 questions from the first five:
C(5, 5) * C(8, 5) = 1 * 56 = 56
Number of choices when choosing 6 questions from the first five:
C(5, 6) * C(8, 4) = 0 * 70 = 0 (since we cannot choose 6 questions from a set of 5)
Number of choices when choosing 7 questions from the first five:
C(5, 7) * C(8, 3) = 0 * 56 = 0 (since we cannot choose 7 questions from a set of 5)
Number of choices when choosing all 8 questions from the first five:
C(5, 8) * C(8, 2) = 0 * 28 = 0 (since we cannot choose 8 questions from a set of 5)
Therefore, the number of choices in this case is 56.
Total number of choices:
The total number of choices available to the student is the sum of the choices in both cases.
Total number of choices = 140 + 56 = 196
Therefore, the correct answer is option C, 196.
A student is to answer 10 out of 13 questions in an examination such that he must choose at least 4 from the first five questions. The number of choices available to him is
Solution:
To find the number of choices available to the student, we need to consider two cases:
1. The student chooses exactly 4 questions from the first five questions.
2. The student chooses more than 4 questions from the first five questions.
Case 1: Choosing exactly 4 questions from the first five questions
To choose exactly 4 questions from the first five questions, we need to choose 4 questions from the first five and 6 questions from the remaining 8 questions. This can be done in C(5, 4) * C(8, 6) ways, where C(n, r) represents the number of combinations of choosing r items from a set of n items.
C(5, 4) = 5! / (4! * (5-4)!) = 5
C(8, 6) = 8! / (6! * (8-6)!) = 28
Therefore, the number of choices in this case is 5 * 28 = 140.
Case 2: Choosing more than 4 questions from the first five questions
To choose more than 4 questions from the first five questions, we can choose 5, 6, 7, or all 8 questions from the first five. For each of these cases, we need to choose the remaining questions from the remaining 8 questions.
Number of choices when choosing 5 questions from the first five:
C(5, 5) * C(8, 5) = 1 * 56 = 56
Number of choices when choosing 6 questions from the first five:
C(5, 6) * C(8, 4) = 0 * 70 = 0 (since we cannot choose 6 questions from a set of 5)
Number of choices when choosing 7 questions from the first five:
C(5, 7) * C(8, 3) = 0 * 56 = 0 (since we cannot choose 7 questions from a set of 5)
Number of choices when choosing all 8 questions from the first five:
C(5, 8) * C(8, 2) = 0 * 28 = 0 (since we cannot choose 8 questions from a set of 5)
Therefore, the number of choices in this case is 56.
Total number of choices:
The total number of choices available to the student is the sum of the choices in both cases.
Total number of choices = 140 + 56 = 196
Therefore, the correct answer is option C, 196.
Statement-1: The number of ways of distributing 10 identical balls in 4 distinct boxes such that no box is empty is 9C3 .Statement-2: The number of ways of choosing any 3 places from 9 different places is 9C3 . [2011]- a)Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
- b)Statement-1 is true, Statement-2 is false.
- c)Statement-1 is false, Statement-2 is true.
- d)Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
Correct answer is option 'D'. Can you explain this answer?
Statement-1: The number of ways of distributing 10 identical balls in 4 distinct boxes such that no box is empty is 9C3 .Statement-2: The number of ways of choosing any 3 places from 9 different places is 9C3 . [2011]
a)
Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
b)
Statement-1 is true, Statement-2 is false.
c)
Statement-1 is false, Statement-2 is true.
d)
Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
|
|
Nishtha Mishra answered |
Statement-1: The number of ways of distributing 10 identical balls in 4 distinct boxes such that no box is empty is 9C3.
Statement-2: The number of ways of choosing any 3 places from 9 different places is 9C3.
To evaluate the validity of the given statements, let's analyze each statement individually:
Statement-1:
The number of ways to distribute 10 identical balls in 4 distinct boxes such that no box is empty can be calculated using the concept of stars and bars.
In this scenario, we can represent the 10 identical balls as 10 stars (**********) and represent the 4 distinct boxes using 3 bars (|||). The balls before the first bar go into the first box, the balls between the first and second bar go into the second box, and so on.
For example, if we have the arrangement **|***|****|**, it means the first box has 2 balls, the second box has 3 balls, the third box has 4 balls, and the fourth box is empty.
The number of ways to arrange the stars and bars can be calculated using the formula for combinations. We have a total of 10 stars and 3 bars to arrange, so the number of ways is given by 13C3, which is equal to 286.
Therefore, Statement-1 is true.
Statement-2:
The number of ways to choose any 3 places from 9 different places can also be calculated using the concept of combinations.
We have a total of 9 different places, and we want to choose 3 of them. The number of ways to do this is given by 9C3, which is equal to 84.
Therefore, Statement-2 is true.
Explanation:
Statement-2 is a correct explanation for Statement-1 because the number of ways to distribute 10 identical balls in 4 distinct boxes such that no box is empty (286) is equal to the number of ways to choose any 3 places from 9 different places (84).
Hence, the correct answer is option 'D'.
Statement-2: The number of ways of choosing any 3 places from 9 different places is 9C3.
To evaluate the validity of the given statements, let's analyze each statement individually:
Statement-1:
The number of ways to distribute 10 identical balls in 4 distinct boxes such that no box is empty can be calculated using the concept of stars and bars.
In this scenario, we can represent the 10 identical balls as 10 stars (**********) and represent the 4 distinct boxes using 3 bars (|||). The balls before the first bar go into the first box, the balls between the first and second bar go into the second box, and so on.
For example, if we have the arrangement **|***|****|**, it means the first box has 2 balls, the second box has 3 balls, the third box has 4 balls, and the fourth box is empty.
The number of ways to arrange the stars and bars can be calculated using the formula for combinations. We have a total of 10 stars and 3 bars to arrange, so the number of ways is given by 13C3, which is equal to 286.
Therefore, Statement-1 is true.
Statement-2:
The number of ways to choose any 3 places from 9 different places can also be calculated using the concept of combinations.
We have a total of 9 different places, and we want to choose 3 of them. The number of ways to do this is given by 9C3, which is equal to 84.
Therefore, Statement-2 is true.
Explanation:
Statement-2 is a correct explanation for Statement-1 because the number of ways to distribute 10 identical balls in 4 distinct boxes such that no box is empty (286) is equal to the number of ways to choose any 3 places from 9 different places (84).
Hence, the correct answer is option 'D'.
In a shop there are five types of ice-creams available. A child buys six ice-creams.Statement-1 : The number of different ways the child can buy the six ice-creams is 10C5.Statement -2 : The number of different ways the child can buy the six ice-creams is equal to the number of different ways of arranging 6 A’s and 4 B’s in a row. [2008]- a)Statement -1 is false, Statement-2 is true
- b)Statement -1 is true, Statement-2 is true; Statement -2 is a correct explanation for Statement-1
- c)Statement -1 is true, Statement-2 is true; Statement -2 is not a correct explanation for Statement-1
- d)Statement -1 is true, Statement-2 is false
Correct answer is option 'A'. Can you explain this answer?
In a shop there are five types of ice-creams available. A child buys six ice-creams.Statement-1 : The number of different ways the child can buy the six ice-creams is 10C5.Statement -2 : The number of different ways the child can buy the six ice-creams is equal to the number of different ways of arranging 6 A’s and 4 B’s in a row. [2008]
a)
Statement -1 is false, Statement-2 is true
b)
Statement -1 is true, Statement-2 is true; Statement -2 is a correct explanation for Statement-1
c)
Statement -1 is true, Statement-2 is true; Statement -2 is not a correct explanation for Statement-1
d)
Statement -1 is true, Statement-2 is false
|
|
Mehul Kulkarni answered |
The given situation in statement 1 is equivalent to find the non negative integral solutions of the equation x1 + x2 + x3 + x4 + x5 = 6
which is coeff. of x6 in the expansion of (1 + x + x2 + x3 + .....∞)5
= coeff. of x6 in (1– x)–5
= coeff. of x6 in 1 + 5x +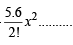
which is coeff. of x6 in the expansion of (1 + x + x2 + x3 + .....∞)5
= coeff. of x6 in (1– x)–5
= coeff. of x6 in 1 + 5x +
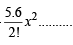
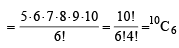
∴ Statement 1 is wrong.
Number of ways of arranging 6A’s and 4B’s in a row
Number of ways of arranging 6A’s and 4B’s in a row
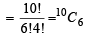 which is same as the number of ways the child can buy six icecreams.
which is same as the number of ways the child can buy six icecreams.∴ Statement 2 is true.
Assuming the balls to be identical except for difference in colours, the number of ways in which one or more balls can be selected from 10 white, 9 green and 7 black balls is : [2012]- a)880
- b)629
- c)630
- d)879
Correct answer is option 'D'. Can you explain this answer?
Assuming the balls to be identical except for difference in colours, the number of ways in which one or more balls can be selected from 10 white, 9 green and 7 black balls is : [2012]
a)
880
b)
629
c)
630
d)
879
|
|
Shreya Dasgupta answered |
Number of white balls = 10
Number of green balls = 9
Number of green balls = 9
an d Number of black balls = 7
∴ Required probability = (10 + 1) (9 + 1) ( 7 + 1) – 1 = 11.10.8 –1 = 879
∴ Required probability = (10 + 1) (9 + 1) ( 7 + 1) – 1 = 11.10.8 –1 = 879
[∵ The total number of ways of selecting one or more items from p identical items of one kind, q identical items of second kind; r identical items of third kind is ( p + 1) (q + 1) (r + 1) –1 ]
If nCr denotes the number of combination of n things taken r at a time, then the expression nCr +1 + nC r -1 + 2 x nCr equals[2003]- a) n+1Cr +1
- b) n+ 2 C r
- c) n+ 2Cr +1
- d) n+1Cr
Correct answer is option 'C'. Can you explain this answer?
If nCr denotes the number of combination of n things taken r at a time, then the expression nCr +1 + nC r -1 + 2 x nCr equals[2003]
a)
n+1Cr +1
b)
n+ 2 C r
c)
n+ 2Cr +1
d)
n+1Cr
|
|
Shruti Khanna answered |
If nCr denotes the number of combinations of n things taken r at a time, then the expression nCr * (nC r-1) * 2 * nCr equals
To solve this problem, we need to simplify the given expression step by step.
Step 1: Simplifying nCr * (nC r-1)
We know that nCr = n! / (r! * (n-r)!), where "!" denotes the factorial of a number.
By substituting the values, we get:
nC r-1 = n! / ((r-1)! * (n-r+1)!)
Multiplying nCr with nC r-1, we get:
nCr * nC r-1 = (n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r+1)!))
Step 2: Simplifying (n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r+1)!))
To simplify this expression further, we can notice that (n-r+1)! = (n-r)! * (n-r+1).
By substituting this value, we get:
(n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r+1)!)) = (n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r)! * (n-r+1)))
Step 3: Simplifying (n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r)! * (n-r+1))) * 2 * nCr
Multiplying the above expression with 2 * nCr, we get:
(n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r)! * (n-r+1))) * 2 * nCr = 2 * nCr * ((n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r)! * (n-r+1))))
Step 4: Simplifying 2 * nCr * ((n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r)! * (n-r+1))))
We can observe that (n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r)! * (n-r+1))) = n! * n! / (r! * (r-1)! * (n-r)! * (n-r)! * (n-r+1))
Simplifying further, we get:
2 * nCr * ((n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r)! * (n-r+1)))) = 2 * nCr * (n! * n! / (r! * (n-r)! * (r-1)! * (n-r)! * (n-r+1)))
Step
To solve this problem, we need to simplify the given expression step by step.
Step 1: Simplifying nCr * (nC r-1)
We know that nCr = n! / (r! * (n-r)!), where "!" denotes the factorial of a number.
By substituting the values, we get:
nC r-1 = n! / ((r-1)! * (n-r+1)!)
Multiplying nCr with nC r-1, we get:
nCr * nC r-1 = (n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r+1)!))
Step 2: Simplifying (n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r+1)!))
To simplify this expression further, we can notice that (n-r+1)! = (n-r)! * (n-r+1).
By substituting this value, we get:
(n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r+1)!)) = (n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r)! * (n-r+1)))
Step 3: Simplifying (n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r)! * (n-r+1))) * 2 * nCr
Multiplying the above expression with 2 * nCr, we get:
(n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r)! * (n-r+1))) * 2 * nCr = 2 * nCr * ((n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r)! * (n-r+1))))
Step 4: Simplifying 2 * nCr * ((n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r)! * (n-r+1))))
We can observe that (n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r)! * (n-r+1))) = n! * n! / (r! * (r-1)! * (n-r)! * (n-r)! * (n-r+1))
Simplifying further, we get:
2 * nCr * ((n! / (r! * (n-r)!)) * (n! / ((r-1)! * (n-r)! * (n-r+1)))) = 2 * nCr * (n! * n! / (r! * (n-r)! * (r-1)! * (n-r)! * (n-r+1)))
Step
Let Tn be the number of all possible triangles formed by joining vertices of an n-sided regular polygon. If Tn+1 – Tn = 10, then the value of n is : [JEE M 2013]- a)7
- b)5
- c)10
- d)8
Correct answer is option 'B'. Can you explain this answer?
Let Tn be the number of all possible triangles formed by joining vertices of an n-sided regular polygon. If Tn+1 – Tn = 10, then the value of n is : [JEE M 2013]
a)
7
b)
5
c)
10
d)
8
|
|
Vaibhav Mehta answered |
We know, Tn = nC3, Tn+1 = n+1C3
ATQ, Tn+1 – Tn = n+1C3 – nC3 = 10
⇒ nC2 = 10
⇒ n = 5.
ATQ, Tn+1 – Tn = n+1C3 – nC3 = 10
⇒ nC2 = 10
⇒ n = 5.
Number greater than 1000 but less than 4000 is formed using the digits 0, 1, 2, 3, 4 (repetition allowed). Their number is [2002]- a)125
- b)105
- c)375
- d)625
Correct answer is option 'C'. Can you explain this answer?
Number greater than 1000 but less than 4000 is formed using the digits 0, 1, 2, 3, 4 (repetition allowed). Their number is [2002]
a)
125
b)
105
c)
375
d)
625
|
|
Pranjal Saini answered |
Solution:
To form a number greater than 1000 and less than 4000, the thousands place must be either 1, 2, or 3.
Case 1: Thousands place is 1
In this case, the remaining three digits can be any of the five digits (0, 1, 2, 3, 4) with repetition allowed. Therefore, the number of such numbers is 5x5x5 = 125.
Case 2: Thousands place is 2
In this case, the remaining three digits can be any of the five digits (0, 1, 2, 3, 4) with repetition allowed. Therefore, the number of such numbers is 5x5x5 = 125.
Case 3: Thousands place is 3
In this case, the remaining three digits can be any of the five digits (0, 1, 2, 3, 4) with repetition allowed. Therefore, the number of such numbers is 5x5x5 = 125.
Therefore, the total number of such numbers is 125+125+125 = 375.
Hence, the correct option is (C) 375.
To form a number greater than 1000 and less than 4000, the thousands place must be either 1, 2, or 3.
Case 1: Thousands place is 1
In this case, the remaining three digits can be any of the five digits (0, 1, 2, 3, 4) with repetition allowed. Therefore, the number of such numbers is 5x5x5 = 125.
Case 2: Thousands place is 2
In this case, the remaining three digits can be any of the five digits (0, 1, 2, 3, 4) with repetition allowed. Therefore, the number of such numbers is 5x5x5 = 125.
Case 3: Thousands place is 3
In this case, the remaining three digits can be any of the five digits (0, 1, 2, 3, 4) with repetition allowed. Therefore, the number of such numbers is 5x5x5 = 125.
Therefore, the total number of such numbers is 125+125+125 = 375.
Hence, the correct option is (C) 375.
At an election , a voter may vote for an y number of candidates, not greater than the number to be elected. There are 10 candidates and 4 are of be selected, if a voter votes for at least one candidate, then the number of ways in which he can vote is [2006]- a)5040
- b)6210
- c)385
- d)1110
Correct answer is option 'C'. Can you explain this answer?
At an election , a voter may vote for an y number of candidates, not greater than the number to be elected. There are 10 candidates and 4 are of be selected, if a voter votes for at least one candidate, then the number of ways in which he can vote is [2006]
a)
5040
b)
6210
c)
385
d)
1110
|
|
Mihir Chaudhary answered |
10C1 + 10C2 + 10C3 + 10C4
= 10 + 45 + 120 + 210 = 385
= 10 + 45 + 120 + 210 = 385
A debate club consists of 6 girls and 4 boys. A team of 4 members is to be selected from this club including the selection of a captain (from among these 4 memoers) for the team. If the team has to include at most one boy, then the number of ways of selecting the team is (JEE Adv. 2016)- a)380
- b)320
- c)260
- d)95
Correct answer is option 'A'. Can you explain this answer?
A debate club consists of 6 girls and 4 boys. A team of 4 members is to be selected from this club including the selection of a captain (from among these 4 memoers) for the team. If the team has to include at most one boy, then the number of ways of selecting the team is (JEE Adv. 2016)
a)
380
b)
320
c)
260
d)
95
|
|
Anand Kumar answered |

Six cards and six envelopes are numbered 1, 2, 3, 4, 5, 6 and cards are to be placed in envelopes so that each envelope contains exactly one card and no card is placed in the envelope bearing the same number and moreover the card numbered 1 is always placed in envelope numbered 2. Then the number of ways it can be done is (JEE Adv. 2014)- a)264
- b)265
- c)53
- d)67
Correct answer is option 'C'. Can you explain this answer?
Six cards and six envelopes are numbered 1, 2, 3, 4, 5, 6 and cards are to be placed in envelopes so that each envelope contains exactly one card and no card is placed in the envelope bearing the same number and moreover the card numbered 1 is always placed in envelope numbered 2. Then the number of ways it can be done is (JEE Adv. 2014)
a)
264
b)
265
c)
53
d)
67
|
|
Janani Roy answered |
∵ Car d numbered 1 is always placed in envelope numbered 2, we can consider two cases.
Case I: Card numbered 2 is placed in envelope numbered 1.
Then it is dearrangement of 4 objects, which can be done in
Case I: Card numbered 2 is placed in envelope numbered 1.
Then it is dearrangement of 4 objects, which can be done in
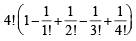 = 9 ways
= 9 waysCase II: Card numbered 2 is not placed in envelope numbered 1.
Then it is dearrangement of 5 objects, which can be done in
Then it is dearrangement of 5 objects, which can be done in
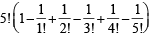 = 44 ways
= 44 ways∴ Total ways = 44 + 9 = 53
The number of integers greater than 6,000 that can be formed, using the digits 3, 5, 6, 7 and 8, without repetition, is : [JEE M 2015]- a)120
- b)72
- c)216
- d)192
Correct answer is option 'D'. Can you explain this answer?
The number of integers greater than 6,000 that can be formed, using the digits 3, 5, 6, 7 and 8, without repetition, is : [JEE M 2015]
a)
120
b)
72
c)
216
d)
192
|
|
Chirag Verma answered |
Four digits number can be arranged in 3 × 4! ways.
Five digits number can be arranged in 5! ways.
Number of integers = 3 × 4! + 5! = 192.
Five digits number can be arranged in 5! ways.
Number of integers = 3 × 4! + 5! = 192.
There are two urns. Urn A has 3 distinct red balls and urn B has 9 distinct blue balls. From each urn two balls are taken out at random and then transferred to the other. The number of ways in which this can be done is [2010]- a)36
- b)66
- c)108
- d)3
Correct answer is option 'C'. Can you explain this answer?
There are two urns. Urn A has 3 distinct red balls and urn B has 9 distinct blue balls. From each urn two balls are taken out at random and then transferred to the other. The number of ways in which this can be done is [2010]
a)
36
b)
66
c)
108
d)
3
|
|
Manisha Kumar answered |
Total number of ways = 3C2 x 9C2
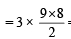 = 3 x 36 = 108
= 3 x 36 = 108The number of ways in which 6 men and 5 women can dine at a round table if no two women are to sit together is given by[2003]- a)7! × 5!
- b)6! × 5!
- c)30!
- d)5! × 4!
Correct answer is option 'B'. Can you explain this answer?
The number of ways in which 6 men and 5 women can dine at a round table if no two women are to sit together is given by[2003]
a)
7! × 5!
b)
6! × 5!
c)
30!
d)
5! × 4!
|
|
Megha Nair answered |
No. of ways in which 6 men can be arranged at a round table = (6 - 1)! = 5!
Now women can be arranged in 6 P5 = 6! Ways.
Total Number of ways = 6! × 5!
Now women can be arranged in 6 P5 = 6! Ways.
Total Number of ways = 6! × 5!
If the LCM of p, q is r2t4s2, where r, s, t are prime numbers and p, q are the positive integers then the number of ordered pair (p, q) is (2006 - 3M, –1)- a)252
- b)254
- c)225
- d)224
Correct answer is option 'C'. Can you explain this answer?
If the LCM of p, q is r2t4s2, where r, s, t are prime numbers and p, q are the positive integers then the number of ordered pair (p, q) is (2006 - 3M, –1)
a)
252
b)
254
c)
225
d)
224
|
|
Jithin Roy answered |
∵ r, s, t are prime numbers,
∴ Section of (p, q) can be done as follows
∴ Section of (p, q) can be done as follows
∴ r can be selected 1 + 1 + 3 = 5 ways
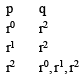
Similarly s and t can be selected in 9 and 5 ways respectivley.
∴ Total ways = 5 × 9 × 5 = 225
∴ Total ways = 5 × 9 × 5 = 225
If the letters of the word SACHIN are arranged in all possible ways and these words are written out as in dictionary, then the word SACHIN appears at serial number [2005]- a)601
- b)600
- c)603
- d)602
Correct answer is option 'A'. Can you explain this answer?
If the letters of the word SACHIN are arranged in all possible ways and these words are written out as in dictionary, then the word SACHIN appears at serial number [2005]
a)
601
b)
600
c)
603
d)
602
|
|
Gaurav Dasgupta answered |
Alphabetical order is A, C, H, I, N, S
No. of words starting with A – 5!
No. of words starting with C – 5!
No. of words starting with H – 5!
No. of words starting with I – 5!
No. of words starting with N – 5!
SACHIN – 1
∴ sachin appears at serial no 601
No. of words starting with A – 5!
No. of words starting with C – 5!
No. of words starting with H – 5!
No. of words starting with I – 5!
No. of words starting with N – 5!
SACHIN – 1
∴ sachin appears at serial no 601
The number of ways of distributing 8 identical balls in 3 distinct boxes so that none of the boxes is empty is [2004]- a)8C3
- b)21
- c)38
- d)5
Correct answer is option 'B'. Can you explain this answer?
The number of ways of distributing 8 identical balls in 3 distinct boxes so that none of the boxes is empty is [2004]
a)
8C3
b)
21
c)
38
d)
5
|
|
Devanshi Bajaj answered |
We know that the number of ways of distributing n identical items among r persons, when each one of them receives at least one item is n -1Cr -1
∴ The required number of ways
∴ The required number of ways
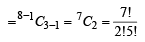
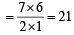
A five-digit numbers divisible by 3 is to be formed using the numerals 0, 1, 2, 3, 4 and 5, without repetition. The total number of ways this can be done is (1989 - 2 Marks)- a)216
- b)240
- c)600
- d)3125
Correct answer is option 'A'. Can you explain this answer?
A five-digit numbers divisible by 3 is to be formed using the numerals 0, 1, 2, 3, 4 and 5, without repetition. The total number of ways this can be done is (1989 - 2 Marks)
a)
216
b)
240
c)
600
d)
3125
|
|
Ram Mohith answered |
The condition for a number to be divisible by 3 is that the sum of individual digits must be divisible by 3. To form a five digit number (from the given numbers) which is divisible by 3 we can do it only with two set of numbers. They are {1,2,3,4,5} and {0,1,2,4,5}.
Case 1 : Using digits 1,2,3,4,5
In this case there is no restriction and the number of ways of arranging them is 5! = 120 ways
Case 2 : Using digits 0,1,2,4,5
In this case there is restriction that the first digit should not be zero.
The first place can be filled in 4 ways (any digit except 0). The second digit can be filled in 4 ways (any of the other 4 digits including 0). Similarly, the third, fourth, and fifth places can be filled in 3,2 and 1 ways respectively.
Number of ways = 4 x 4 x 3 x 2 x 1 = 96 ways
Total number of ways = 120 + 96 = 216 way
Case 1 : Using digits 1,2,3,4,5
In this case there is no restriction and the number of ways of arranging them is 5! = 120 ways
Case 2 : Using digits 0,1,2,4,5
In this case there is restriction that the first digit should not be zero.
The first place can be filled in 4 ways (any digit except 0). The second digit can be filled in 4 ways (any of the other 4 digits including 0). Similarly, the third, fourth, and fifth places can be filled in 3,2 and 1 ways respectively.
Number of ways = 4 x 4 x 3 x 2 x 1 = 96 ways
Total number of ways = 120 + 96 = 216 way
Ten different letters of an alphabet are given. Words with five letters are formed from these given letters. Then the number of words which have at least one letter repeated are (1982 - 2 Marks)- a)69760
- b)30240
- c)99748
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Ten different letters of an alphabet are given. Words with five letters are formed from these given letters. Then the number of words which have at least one letter repeated are (1982 - 2 Marks)
a)
69760
b)
30240
c)
99748
d)
none of these
|
|
Nandita Sharma answered |
Total number of words that can be formed using 5 letters out of 10 given different letters
= 10 × 10 × 10 × 10 × 10 (as letters can repeat)
= 1, 00, 000
Number of words that can be formed using 5 different letters out of 10 different letters
= 10P5 (none can repeat)
= 10 × 10 × 10 × 10 × 10 (as letters can repeat)
= 1, 00, 000
Number of words that can be formed using 5 different letters out of 10 different letters
= 10P5 (none can repeat)

∴ Number of words in which at least one letter is repeated
= total words–words with none of the letters repeated
= 1,00,000 – 30,240
= 69760
= total words–words with none of the letters repeated
= 1,00,000 – 30,240
= 69760
The total number of ways in which 5 balls of different colours can be distributed among 3 persons so that each person gets at least one ball is (2012)- a)75
- b)150
- c)210
- d)243
Correct answer is option 'B'. Can you explain this answer?
The total number of ways in which 5 balls of different colours can be distributed among 3 persons so that each person gets at least one ball is (2012)
a)
75
b)
150
c)
210
d)
243
|
|
Anirudh Malik answered |
∵ Each person gets at least one ball.
∴ 3 Per son s can have 5 balls in th e followin g systems
∴ 3 Per son s can have 5 balls in th e followin g systems
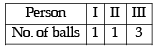
or
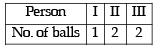
The number of ways to distribute the balls in first system =
5C1 x 4C1 x 3C3
5C1 x 4C1 x 3C3
Also 3, persons having 1, 1 and 3 balls can be arranged in 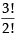 ways.
ways.
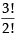 ways.
ways.∴ No. of ways to distribute 1, 1, 3 balls to the three persons
5C1 x 4C1 x 3C3 x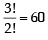
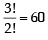
Similarly the total no. of ways to distribute 1, 2, 2 balls to the three persons = 5C1 x 4C2 x 2C2 x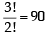
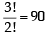
∴ The required number of ways = 60 + 90 = 150
A rectangle with sides of length (2m – 1) an d (2n – 1) units is divided into squares of unit length by drawing parallel lines as shown in the diagram, then the number of rectangles possible with odd side length s is (2005S)
- a)(m + n – 1)2
- b)4m+n–1
- c)m2n2
- d)m(m + 1)n(n + 1)
Correct answer is option 'C'. Can you explain this answer?
A rectangle with sides of length (2m – 1) an d (2n – 1) units is divided into squares of unit length by drawing parallel lines as shown in the diagram, then the number of rectangles possible with odd side length s is (2005S)

a)
(m + n – 1)2
b)
4m+n–1
c)
m2n2
d)
m(m + 1)n(n + 1)
|
|
Nabanita Chavan answered |
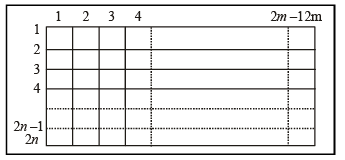
If we see the blocks in terms of lines then there are 2m vertical lines and 2n horizontal lines. To form the required rectangle we must select two horizontal lines, one even numbered (out of 2, 4, .....2n) and one odd numbered (out of 1, 3....2n–1) and similarly two vertical lines. The number of rectangles is
mC1 . mC1 . nC1 . nC1 = m2n2
mC1 . mC1 . nC1 . nC1 = m2n2
How many different nine digit numbers can be formed from the number 223355888 by rearranging its digits so that the odd digits occupy even positions ? (2000S)- a)16
- b)36
- c)60
- d)180
Correct answer is option 'C'. Can you explain this answer?
How many different nine digit numbers can be formed from the number 223355888 by rearranging its digits so that the odd digits occupy even positions ? (2000S)
a)
16
b)
36
c)
60
d)
180
|
|
Ram Mohith answered |
The 4 odd number (3,3,5,5) must be filled at 4 even positions.
Number of ways = (4!/2!2!) = 6 ways
The remaining 5 even numbers (2,2,8,8,8) must be filled at 5 odd positions.
Number of ways = (5!/2!3!) = 10 ways
Total number of ways = 6 x 10 = 60 ways
From 6 different novels and 3 different dictionaries,4 novels and 1 dictionary are to be selected and arranged in a row on a shelf so that the dictionary is always in the middle. Then the number of such arrangement is: [2009]- a)at least 500 but less than 750
- b)at least 750 but less than 1000
- c)at least 1000
- d)less than 500
Correct answer is option 'C'. Can you explain this answer?
From 6 different novels and 3 different dictionaries,4 novels and 1 dictionary are to be selected and arranged in a row on a shelf so that the dictionary is always in the middle. Then the number of such arrangement is: [2009]
a)
at least 500 but less than 750
b)
at least 750 but less than 1000
c)
at least 1000
d)
less than 500
|
|
Kritika Choudhary answered |
4 novels, out of 6 novels and 1 dictionary out of 3 can be selected in 6 C4 x 3C1 ways
Then 4 novels with one dictionary in the middle can be arranged in 4! ways.
∴ Total ways of arrangement = 6C4 x 3C1x 4! = 1080
Then 4 novels with one dictionary in the middle can be arranged in 4! ways.
∴ Total ways of arrangement = 6C4 x 3C1x 4! = 1080
If all the words (with or without meaning) having five letters, formed using the letters of the word SMALL and arranged as in a dictionary; then the position of the word SMALL is : [JEE M 2016]- a)52nd
- b)58th
- c)46th
- d)59th
Correct answer is option 'B'. Can you explain this answer?
If all the words (with or without meaning) having five letters, formed using the letters of the word SMALL and arranged as in a dictionary; then the position of the word SMALL is : [JEE M 2016]
a)
52nd
b)
58th
c)
46th
d)
59th
|
|
Sanchita Chavan answered |
ALLMS
No. of words starting with
No. of words starting with
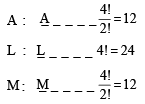
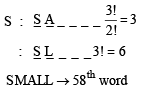
The set S = {1, 2, 3, ......., 12} is to be partitioned into three sets A , B, C of equal size. Thus A ∪ B ∪ C = S , A∩B =B∩C= A∩C= φ. The number of ways to partition S is [2007]- a)
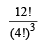
- b)
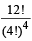
- c)
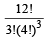
- d)
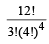
Correct answer is option 'A'. Can you explain this answer?
The set S = {1, 2, 3, ......., 12} is to be partitioned into three sets A , B, C of equal size. Thus A ∪ B ∪ C = S , A∩B =B∩C= A∩C= φ. The number of ways to partition S is [2007]
a)
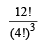
b)
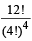
c)
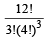
d)
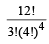
|
|
Soumya Nambiar answered |
Set S = {1, 2, 3, ...... 12}
A∪B∪C = S, A∩B =B∩C=A∩C= φ.
∴ The number of ways to partition
= 12C4 × 8C4 × 4C4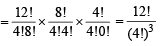
The letters of the word COCHIN are permuted and all the permutations are arranged in an alphabetical order as in an English dictionary. The number of words that appear before the word COCHIN is (2007 -3 marks)- a)360
- b)192
- c)96
- d)48
Correct answer is option 'C'. Can you explain this answer?
The letters of the word COCHIN are permuted and all the permutations are arranged in an alphabetical order as in an English dictionary. The number of words that appear before the word COCHIN is (2007 -3 marks)
a)
360
b)
192
c)
96
d)
48
|
|
Tulsi Kumari Tulsi Kumar answered |
The number of words starting with CC=4!
The number of words starting with CH=4!
The number of words starting with CI=4!
The number of words starting with CN=4!
COCHIN is the first word in the list of words beginning with CO.
∴ Number of words that appear before the words COCHIN =96
The number of words starting with CH=4!
The number of words starting with CI=4!
The number of words starting with CN=4!
COCHIN is the first word in the list of words beginning with CO.
∴ Number of words that appear before the words COCHIN =96
nCr–1 = 36, nCr = 84 and nCr + 1 = 126, then r is : (1979) - a)1
- b)2
- c)3
- d)None of these.
Correct answer is option 'C'. Can you explain this answer?
nCr–1 = 36, nCr = 84 and nCr + 1 = 126, then r is : (1979)
a)
1
b)
2
c)
3
d)
None of these.
|
|
Poulomi Gupta answered |
nCr -1 = 36, nCr = 84,nCr+1= 126
KEY CONCEPT : We know that
KEY CONCEPT : We know that
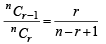
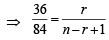
⇒ 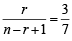
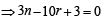 ....(1)
....(1)
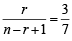
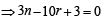 ....(1)
....(1)⇒ 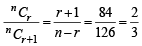
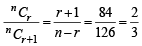
⇒ 2n – 5r – 3 = 0 ....(2)
Solving (1) and (2), we get n = 9 and r = 3.
Chapter doubts & questions for Permutations and Combinations - Maths 35 Year Past year Papers JEE Main & Advanced 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Permutations and Combinations - Maths 35 Year Past year Papers JEE Main & Advanced in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup

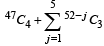 is equal to (1982 - 2 Marks)
is equal to (1982 - 2 Marks)