All Exams >
CA Foundation >
Quantitative Aptitude for CA Foundation >
All Questions
All questions of Chapter 3: Linear Inequalities for CA Foundation Exam
The solution of the inequality 8x + 6 < 12x + 14 is- a)(-2,2)
- b)(0,-2)
- c)(2, ∞)
- d)(-2,∞)
Correct answer is option 'D'. Can you explain this answer?
The solution of the inequality 8x + 6 < 12x + 14 is
a)
(-2,2)
b)
(0,-2)
c)
(2, ∞)
d)
(-2,∞)
|
Mrinalini Iyer answered |
There are different ways to express the solution of an inequality, but one common way is to write it in interval notation. To do this, we first isolate the variable on one side of the inequality:
8x - 6 ≤ 0
8x ≤ 6
x ≤ 6/8
x ≤ 3/4
This means that any value of x that is less than or equal to 3/4 makes the inequality true. We can represent this as the interval:
(-∞, 3/4]
Alternatively, we can write the solution using set-builder notation, which specifies the set of all x values that satisfy the inequality:
{x | x ≤ 3/4}
Either way, the solution indicates that x can be any number less than or equal to 3/4, including fractions, decimals, and negative numbers.
8x - 6 ≤ 0
8x ≤ 6
x ≤ 6/8
x ≤ 3/4
This means that any value of x that is less than or equal to 3/4 makes the inequality true. We can represent this as the interval:
(-∞, 3/4]
Alternatively, we can write the solution using set-builder notation, which specifies the set of all x values that satisfy the inequality:
{x | x ≤ 3/4}
Either way, the solution indicates that x can be any number less than or equal to 3/4, including fractions, decimals, and negative numbers.
For all integral values of x,|x - 4| x< 5- a)-1 ≤x≤5
- b)1 ≤x≤5
- c)-1 ≤ x ≤ 1
- d)x<5
Correct answer is option 'D'. Can you explain this answer?
For all integral values of x,
|x - 4| x< 5
a)
-1 ≤x≤5
b)
1 ≤x≤5
c)
-1 ≤ x ≤ 1
d)
x<5
|
Preeti Khanna answered |
At x = 0 inequality is satisfied, option (b) is rejected.
At x = 2, inequality is satisfied, option (c) is rejected.
At x = 5, LHS = RHS.
Thus, option (d) is correct.
The rules and regulations demand that the employer should employ not more than 5 experienced hands to 1 fresh one and this fact be expressed as- a)y ≥ x/5
- b)5y ≤ x
- c)5 y ≥ x
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The rules and regulations demand that the employer should employ not more than 5 experienced hands to 1 fresh one and this fact be expressed as
a)
y ≥ x/5
b)
5y ≤ x
c)
5 y ≥ x
d)
none of these
|
|
Simran Pillai answered |
The employer must maintain a ratio of 5 experienced employees to 1 fresh employee as per the rules and regulations.
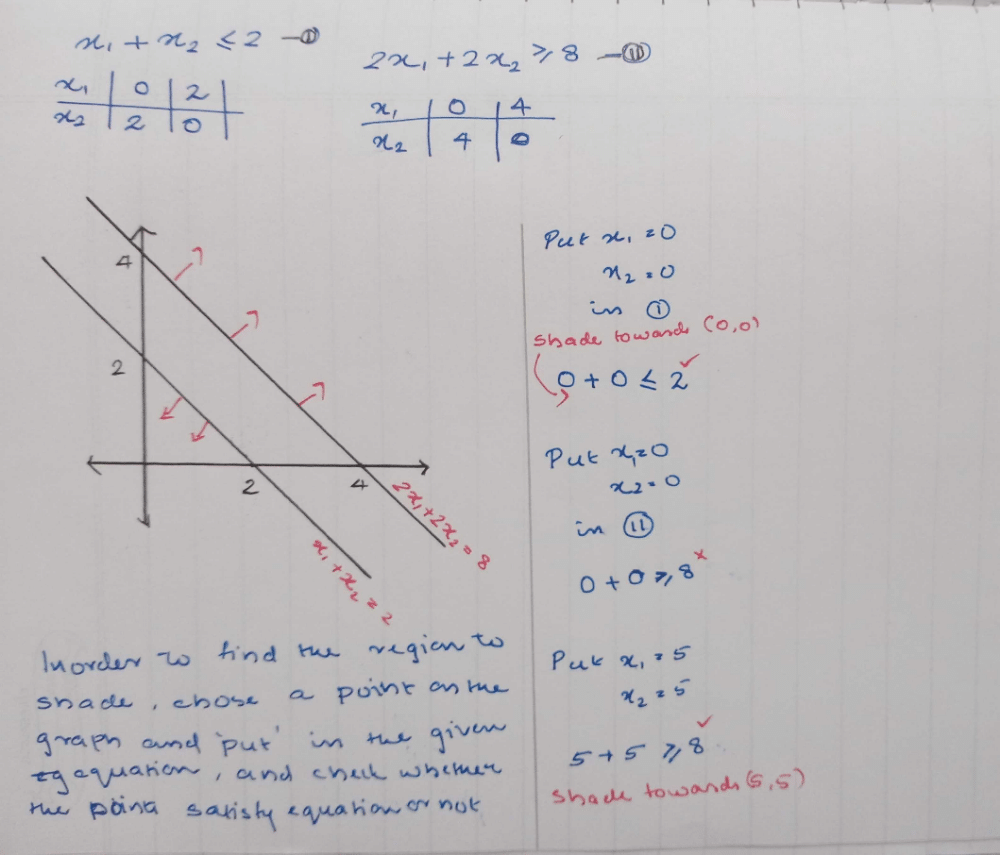
The shaded region represents: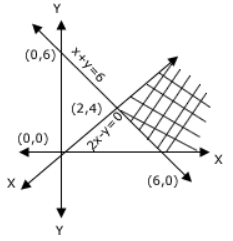
- a)x + y > 6, 2x - y > 0
- b) x + y < 6, 2x -y > 0
- c) x + y > 6, 2x -y < 0
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The shaded region represents:
a)
x + y > 6, 2x - y > 0
b)
x + y < 6, 2x -y > 0
c)
x + y > 6, 2x -y < 0
d)
None of these
|
Rashmi Chaurasia answered |
I think option c is correct because sheded is above the eqn x+y=6 than x+y>6and second sheded blow the eqn 2x - y=0than 2x-y< o="" so="" c="" is="" correct="" o="" so="" c="" is="" />
3x2 - 7x + 6 < 0- a)0.66 <x< 3
- b)-0.66 <x< 3
- c)-1 < x < 3
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
3x2 - 7x + 6 < 0
a)
0.66 <x< 3
b)
-0.66 <x< 3
c)
-1 < x < 3
d)
None of these
|
Avik Choudhury answered |
At x = 0, inequality is not satisfied.
Hence, options (b), (c) and (d) are rejected. At x = 2, inequality is not satisfied. Hence, option (a) is rejected.
Thus, option (d) is correct.
Hence, options (b), (c) and (d) are rejected. At x = 2, inequality is not satisfied. Hence, option (a) is rejected.
Thus, option (d) is correct.
By solving the inequality 3(a - 6) < 4 + a, the answer will be
- a)a < 9
- b)a < 12
- c)a < 13
- d)a < 11
Correct answer is option 'D'. Can you explain this answer?
By solving the inequality 3(a - 6) < 4 + a, the answer will be
a)
a < 9
b)
a < 12
c)
a < 13
d)
a < 11
|
|
Akshat Choudhary answered |
We cannot solve this inequality as it is incomplete. There must be a comparison operator (such as <,>, ≤, or ≥) to determine the relationship between the expression 3(a - 6) and some other value or expression.
x2 - 7x + 12 < | x - 4 |- a)x < 2
- b)x > 4
- c)2 < x < 4
- d)2 ≤ x ≤ 4
Correct answer is option 'C'. Can you explain this answer?
x2 - 7x + 12 < | x - 4 |
a)
x < 2
b)
x > 4
c)
2 < x < 4
d)
2 ≤ x ≤ 4
|
Harsh Jain answered |
At x = 0, inequality is not satisfied, option (a) is rejected.
At x = 5, inequality is not satisfied, option (b) is rejected.
At x = 2 inequality is not satisfied.
Options (d) are rejected.
Option (c) is correct.
At x = 2 inequality is not satisfied.
Options (d) are rejected.
Option (c) is correct.
On solving the inequalities 6x+ y ≥ 18, x+4y ≥ 12, 2x+y ≥ 10, we get following situation- a)(0,18), (12,0), (4,2) and (7,6)
- b)(3,0),(0,3),,(4,2) and (7,6)
- c)(5,0),(0,10),,(4,2) and (7,6)
- d)(0,18), (12,0),(4,2) ,(0,0) and (7,6)
Correct answer is option 'A'. Can you explain this answer?
On solving the inequalities 6x+ y ≥ 18, x+4y ≥ 12, 2x+y ≥ 10, we get following situation
a)
(0,18), (12,0), (4,2) and (7,6)
b)
(3,0),(0,3),,(4,2) and (7,6)
c)
(5,0),(0,10),,(4,2) and (7,6)
d)
(0,18), (12,0),(4,2) ,(0,0) and (7,6)
|
|
Ishan Goyal answered |
I'm sorry, but the inequality is incomplete. There is no inequality sign (such as <,>, ≤, or ≥) to indicate the relationship between 6x + y and some other value. Please provide more information or context so I can assist you better.
|x2 – 2x – 3| < 3x – 3- a)2 < x < 5
- b)–2 < x < 5
- c)x > 5
- d)1 < x < 3
Correct answer is option 'A'. Can you explain this answer?
|x2 – 2x – 3| < 3x – 3
a)
2 < x < 5
b)
–2 < x < 5
c)
x > 5
d)
1 < x < 3
|
Yash Patel answered |
x2 - 2x - 3 ≥ 0
(x-3) (x+1) ≥ 0
x belongs to (-∞,-3]∪[3,∞)
Therefore, x belongs to (-1,3)
=> x2 - 2x - 3 > 0
x2 - 2x - 3< 3x - 3
x2 - 5x < 0
x(x-5) < 0
x belongs to (0,5)........(1)
x2 - 2x - 3 < 0
x2 - 2x - 3 < 3x - 3
x2 + x - 6 > 0
(x+3)(x-2) > 0
x belongs to (-∞,-3]∪[2,∞)
x belongs to (2,3)........(2)
Taking intersection of (1) and (2)
we get,
x belongs to (2,5)
(x-3) (x+1) ≥ 0
x belongs to (-∞,-3]∪[3,∞)
Therefore, x belongs to (-1,3)
=> x2 - 2x - 3 > 0
x2 - 2x - 3< 3x - 3
x2 - 5x < 0
x(x-5) < 0
x belongs to (0,5)........(1)
x2 - 2x - 3 < 0
x2 - 2x - 3 < 3x - 3
x2 + x - 6 > 0
(x+3)(x-2) > 0
x belongs to (-∞,-3]∪[2,∞)
x belongs to (2,3)........(2)
Taking intersection of (1) and (2)
we get,
x belongs to (2,5)
If x, y and z are real numbers such that x + y + z = 5 and xy + yz + zx = 3, what is the largest value that x can have?- a)5/3
- b)13/3
- c)√19
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If x, y and z are real numbers such that x + y + z = 5 and xy + yz + zx = 3, what is the largest value that x can have?
a)
5/3
b)
13/3
c)
√19
d)
None of these
|
Upsc Rank Holders answered |
The given equations are x + y + z = 5 — (1) , xy + yz + zx = 3 — (2)
xy + yz + zx = 3
x(y + z) + yz = 3
⇒ x ( 5 - x ) +y ( 5 – x – y) = 3
⇒ -y2 - y(5 - x) - x2 + 5x = 3
⇒ y2 + y(x - 5) + (x2 - 5x + 3) = 0
The above equation should have real roots for y, => Determinant >= 0
⇒ y2 + y(x - 5) + (x2 - 5x + 3) = 0
The above equation should have real roots for y, => Determinant >= 0
⇒ b2 - 4ac0
⇒ (x - 5)2 - 4(x2 - 5x + 3) ≥ 0
⇒ 3x2 - 10x - 13 ≤ 0
⇒ -1 ≤ x ≤ 13/3
Hence maximum value x can take is 13/3, and the corresponding values for y,z are 1/3, 1/3
An employer recruits experienced (x) and fresh workmen (y) for his firm under the condition that he cannot employ more than 9 people. X and Y can be related by the inequality- a)x+y ≠ 9
- b)x+ y ≤ 9 x ≥ 0, y ≥ 0
- c)x+y ≥ 9 x ≥ 0, y ≥ 0
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
An employer recruits experienced (x) and fresh workmen (y) for his firm under the condition that he cannot employ more than 9 people. X and Y can be related by the inequality
a)
x+y ≠ 9
b)
x+ y ≤ 9 x ≥ 0, y ≥ 0
c)
x+y ≥ 9 x ≥ 0, y ≥ 0
d)
none of these
|
|
Mehul Ghoshal answered |
The inequality given is not complete. There is no inequality symbol specified. Assuming that the inequality is meant to be "x + y ≤ 9" (since the employer cannot employ more than 9 people), then:
- x represents the number of experienced workmen the employer recruits.
- y represents the number of fresh workmen the employer recruits.
The inequality "x + y ≤ 9" means that the sum of x and y cannot exceed 9, which is the maximum number of people the employer can hire. This also implies that x and y must be non-negative integers (since the employer cannot hire a fraction of a person).
- x represents the number of experienced workmen the employer recruits.
- y represents the number of fresh workmen the employer recruits.
The inequality "x + y ≤ 9" means that the sum of x and y cannot exceed 9, which is the maximum number of people the employer can hire. This also implies that x and y must be non-negative integers (since the employer cannot hire a fraction of a person).
If a, b, c and d are four positive real numbers such that abcd = 1, what is the minimum value of (1 + a)(1 + b)(1 + c)(1+ d)?- a)16
- b)1
- c)4
- d)18
Correct answer is option 'A'. Can you explain this answer?
If a, b, c and d are four positive real numbers such that abcd = 1, what is the minimum value of (1 + a)(1 + b)(1 + c)(1+ d)?
a)
16
b)
1
c)
4
d)
18
|
|
Upsc Rank Holders answered |
Since the product is constant, (a + b + c + d)/4 > = (abcd)1/4
We know that abcd = 1.
Therefore, a + b + c + d > = 4
(a + 1)(b + 1)(c + 1)(d + 1)
= 1 + a + b + c + d + ab + ac + ad + bc + bd + cd + abc + bed + cda + dab + abcd
We know that abcd = 1
Therefore, a = 1/bcd, b = 1/acd, c = 1/bda and d = 1/abc
Also, cd = 1/ab, bd = 1/ac, bc = 1/ad
The expression can be clubbed together as
1 + abcd + (a+1/a)+(b+1/b)+(c+1/c)+(d+1/d) + (ab+1/ab) + (ac+1/ac) + (ad +1/ad)
For any positive real number x, x + 1/x ≥ 2
Therefore, the least value that (a+1/a), (b+1/b).... (ad + 1/ad) can take is 2.
(a+1)(b+1)(c+1)(d+1) > 1 + 1 + 2 + 2 + 2 + 2 + 2 + 2 + 2
=> (a + 1)(b + 1)(c + 1)(d + 1) ≥ 16
The least value that the given expression can take is 16.
|x2 + x| – 5 < 0
- a)x < 0
- b)x > 0
- c)None of these
- d)All values of x
Correct answer is option 'C'. Can you explain this answer?
|x2 + x| – 5 < 0
a)
x < 0
b)
x > 0
c)
None of these
d)
All values of x
|
|
Sinjini Gupta answered |
At x = 0 inequality is satisfied.
Thus, options (a), (b), and (d) are rejected.
Option (c) is correct.
Thus, options (a), (b), and (d) are rejected.
Option (c) is correct.
On the average, experienced person does 5 units of work while a fresh one 3 units work daily but the employer have to maintain the output of at least 30 units of work per day. The situation can be expressed as. - a)5x + 3y ≤ 30
- b)5x + 3y ≥ 30
- c)5x + 3y = 30
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
On the average, experienced person does 5 units of work while a fresh one 3 units work daily but the employer have to maintain the output of at least 30 units of work per day. The situation can be expressed as.
a)
5x + 3y ≤ 30
b)
5x + 3y ≥ 30
c)
5x + 3y = 30
d)
None of these
|
Dhruv Mehra answered |
Let "x" and "y" be the number of experienced person and fresh workmen respectively.
Total number of units of work done by experienced person per day = 5x
Total number of units of work done by fresh one per day = 3y
Total number of units of work done by both experienced person and fresh one per day = 5x + 3y
As per the question, total number of units of work per day should be at least 30 units.
That is, total number of units of work (5x+3y) should be equal to 30 or more than 30.
So, we have 5x + 3y ≥ 30
Hence, option "C" is correct
Find the range of real values of x satisfying the inequalities 3x-2 > 7 and 4x - 13 > 15 - a)x > 3
- b)x > 7
- c)x < 7
- d)x < 3
Correct answer is option 'B'. Can you explain this answer?
Find the range of real values of x satisfying the inequalities 3x-2 > 7 and 4x - 13 > 15
a)
x > 3
b)
x > 7
c)
x < 7
d)
x < 3
|
|
Dhruv Mehra answered |
As, 3x - 2 > 7 => 3x > 9 => x > 3
and 4x - 13 > 15 => 4x > 28 => x > 7, 7 is greater than 3.
Therefore, x > 7.
The number of positive integer valued pairs (x, y), satisfying 4x – 17 y = 1 and x < 1000 is:- a)55
- b)57
- c)59
- d)58
Correct answer is option 'C'. Can you explain this answer?
The number of positive integer valued pairs (x, y), satisfying 4x – 17 y = 1 and x < 1000 is:
a)
55
b)
57
c)
59
d)
58
|
EduRev CLAT answered |
The integral values of x for which y is an integer are 13, 30, 47,……
The values are in the form 17n + 13, where n ≥ 0
17n + 13 < 1000
⇒ 17n < 987
⇒ n < 58.05
⇒ n can take values from 0 to 58
⇒ Number of values = 59
The number of integers n satisfying -n + 2 ≥ 0 and 2n ≥ 4 is- a)1
- b)0
- c)2
- d)3
Correct answer is option 'A'. Can you explain this answer?
The number of integers n satisfying -n + 2 ≥ 0 and 2n ≥ 4 is
a)
1
b)
0
c)
2
d)
3
|
Innovative Classes answered |
First inequality:
-n + 2 ≥ 0
-n ≥ -2
n ≤ 2
Second inequality:
2n ≥ 4
n ≥ 2
Only n = 2 satisfies both inequalities. So, there is only 1 integer that satisfies both the inequalities.
The correct option is A.
|x - 6| > x2 - 5x + 9- a)1 ≤ x < 3
- b)1 < x < 3
- c)2 < x < 5
- d)-3 < x < 1
Correct answer is option 'B'. Can you explain this answer?
|x - 6| > x2 - 5x + 9
a)
1 ≤ x < 3
b)
1 < x < 3
c)
2 < x < 5
d)
-3 < x < 1
|
Shail Jain answered |
At x = 2, inequality is satisfied.
At x = 0, inequality is not satisfied.
At x = 1, inequality is not satisfied but LHS = RHS. At x = 3, inequality is not satisfied but LHS = RHS. Thus, option (b) is correct.
Solve other questions of LOD I and LOD II in the same fashion.
At x = 0, inequality is not satisfied.
At x = 1, inequality is not satisfied but LHS = RHS. At x = 3, inequality is not satisfied but LHS = RHS. Thus, option (b) is correct.
Solve other questions of LOD I and LOD II in the same fashion.
The union forbids employer to employ less than two experienced person (x) to each, fresh person (y). This situation can be expressed as: - a)x ≤ y/2
- b)y ≤ x/2
- c)y ≥ x/2
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The union forbids employer to employ less than two experienced person (x) to each, fresh person (y). This situation can be expressed as:
a)
x ≤ y/2
b)
y ≤ x/2
c)
y ≥ x/2
d)
None of these
|
|
Akshat Choudhary answered |
≥ 2y
b)y ≥ 2x
c)2x ≥ y
d)y ≥ x/2
Answer: c) 2x ≥ y
b)y ≥ 2x
c)2x ≥ y
d)y ≥ x/2
Answer: c) 2x ≥ y
|x2 - 2x| < x- a)l < x < 3
- b)—1 < x < 3
- c)0 < x < 4
- d)x > 3
Correct answer is option 'A'. Can you explain this answer?
|x2 - 2x| < x
a)
l < x < 3
b)
—1 < x < 3
c)
0 < x < 4
d)
x > 3
|
Dishani Banerjee answered |
Method to Solve :
You can factor x^2+2x=0 as:
x(x+2)=0
Now, we can solve each term for 0:
x=0 - no other work needed,
and
x+2=0
x+2−2=0−2
x+0=−2
x=−2
x(x+2)=0
Now, we can solve each term for 0:
x=0 - no other work needed,
and
x+2=0
x+2−2=0−2
x+0=−2
x=−2
|x – 6| > x2 – 5x + 9- a)1 £ x < 3
- b)1 < x < 3
- c)2 < x < 5
- d)–3 < x < 1
Correct answer is option 'B'. Can you explain this answer?
|x – 6| > x2 – 5x + 9
a)
1 £ x < 3
b)
1 < x < 3
c)
2 < x < 5
d)
–3 < x < 1
|
|
Atharva Khanna answered |
At x = 2, inequality is satisfied.
At x = 0, inequality is not satisfied.
At x = 1, inequality is not satisfied but LHS = RHS.
At x = 3, inequality is not satisfied but LHS = RHS.
Thus, option (b) is correct.
Solve other questions of LOD I and LOD II in the same fashion.
At x = 0, inequality is not satisfied.
At x = 1, inequality is not satisfied but LHS = RHS.
At x = 3, inequality is not satisfied but LHS = RHS.
Thus, option (b) is correct.
Solve other questions of LOD I and LOD II in the same fashion.
On solving the inequalities 6x + y ≥ 18, x + 4y ≥ 12, 2x + y≤ 10, we get the following situation:- a)(0,18), (12,0), (4,2), &(7,6)
- b)(3,0),(0,3),(4,2),&(7,6)
- c)(5,0),(0,10),(4,2)&(7,6)
- d)(0,18),(12,0),(4,2),(0,0) and (7,6)
Correct answer is option 'A'. Can you explain this answer?
On solving the inequalities 6x + y ≥ 18, x + 4y ≥ 12, 2x + y≤ 10, we get the following situation:
a)
(0,18), (12,0), (4,2), &(7,6)
b)
(3,0),(0,3),(4,2),&(7,6)
c)
(5,0),(0,10),(4,2)&(7,6)
d)
(0,18),(12,0),(4,2),(0,0) and (7,6)
|
Ishleen Kohli answered |
Please give explanation ?
3x2 – 7x – 6 < 0- a)–0.66 < x < 3
- b)x < – 0.66 or x > 3
- c)3 < x < 7
- d)–2 < x < 2
Correct answer is option 'A'. Can you explain this answer?
3x2 – 7x – 6 < 0
a)
–0.66 < x < 3
b)
x < – 0.66 or x > 3
c)
3 < x < 7
d)
–2 < x < 2
|
|
Gargi Kulkarni answered |
At x = 0, inequality is satisfied. Hence, options (b) and (c) are rejected. x = 3 gives LHS = RHS.
and x = – 0.66 also does the same. Hence. roots of the equation are 3 and – 0.66.
Thus, option (a) is correct.
and x = – 0.66 also does the same. Hence. roots of the equation are 3 and – 0.66.
Thus, option (a) is correct.
3x2 - 7x + 4 ≤ 0- a)x > 0
- b)x < 0
- c)All x
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
3x2 - 7x + 4 ≤ 0
a)
x > 0
b)
x < 0
c)
All x
d)
None of these
|
|
Rajdeep Ghoshal answered |
At x = 0, inequality is not satisfied. Thus, option (c) is rejected. Also x = 0 is not a solution of the equation. Since, this is a continuous function, the solution cannot start from 0. Thus options (a) and (b) are not right. Further, we see that the given function is quadratic with real roots. Hence, option (d) is also rejected.
The Linear relationship between two variables in an inequality :- a)ax + by ≤ c
- b)ax + bxy ≤ c
- c)axy + by ≤ c
- d)none
Correct answer is option 'A'. Can you explain this answer?
The Linear relationship between two variables in an inequality :
a)
ax + by ≤ c
b)
ax + bxy ≤ c
c)
axy + by ≤ c
d)
none
|
|
Sinjini Gupta answered |
The linear relationship between two variables in an inequality can be expressed in the form of ax + by < c="" or="" ax="" +="" by="" /> c, where a, b and c are constants, and x and y are the two variables.
If ax + by < c,="" it="" means="" that="" the="" values="" of="" x="" and="" y="" that="" satisfy="" this="" inequality="" lie="" below="" the="" line="" represented="" by="" the="" equation="" ax="" +="" by="c." in="" other="" words,="" the="" region="" below="" the="" line="" is="" the="" solution="" set="" for="" the="" />
Similarly, if ax + by > c, it means that the values of x and y that satisfy this inequality lie above the line represented by the equation ax + by = c. In other words, the region above the line is the solution set for the inequality.
If ax + by < c,="" it="" means="" that="" the="" values="" of="" x="" and="" y="" that="" satisfy="" this="" inequality="" lie="" below="" the="" line="" represented="" by="" the="" equation="" ax="" +="" by="c." in="" other="" words,="" the="" region="" below="" the="" line="" is="" the="" solution="" set="" for="" the="" />
Similarly, if ax + by > c, it means that the values of x and y that satisfy this inequality lie above the line represented by the equation ax + by = c. In other words, the region above the line is the solution set for the inequality.
x2 – 14x – 15 > 0- a)x < –1
- b)15 < x
- c)Both (a) and (b)
- d)–1 < x < 15
Correct answer is option 'C'. Can you explain this answer?
x2 – 14x – 15 > 0
a)
x < –1
b)
15 < x
c)
Both (a) and (b)
d)
–1 < x < 15
|
|
Aditi Menon answered |
At x = 0 inequality is not satisfied. Thus option (d) is rejected.
x = –1 and x = 15 are the roots of the quadratic equation. Thus, option (c) is correct.
x = –1 and x = 15 are the roots of the quadratic equation. Thus, option (c) is correct.
Mary scored 200 marks in three tests. If average score of 60 is required then the lowest marks she must score for fourth test are- a)x gt; 40
- b)x gt; 50
- c)x gt; 60
- d)x gt; 70
Correct answer is option 'A'. Can you explain this answer?
Mary scored 200 marks in three tests. If average score of 60 is required then the lowest marks she must score for fourth test are
a)
x gt; 40
b)
x gt; 50
c)
x gt; 60
d)
x gt; 70
|
|
Aditi Joshi answered |
Given:
Mary scored 200 marks in three tests.
Average score of 60 is required.
To find:
The lowest marks she must score for the fourth test.
Solution:
Let the marks scored by Mary in the fourth test be x.
Total marks scored by Mary in four tests = 200 + x
Average score = (Total marks scored) / (Number of tests)
60 = (200 + x) / 4
240 = 200 + x
x = 40
Therefore, Mary must score at least 40 marks in the fourth test to maintain an average score of 60.
Answer: Option A, x > 40.
Mary scored 200 marks in three tests.
Average score of 60 is required.
To find:
The lowest marks she must score for the fourth test.
Solution:
Let the marks scored by Mary in the fourth test be x.
Total marks scored by Mary in four tests = 200 + x
Average score = (Total marks scored) / (Number of tests)
60 = (200 + x) / 4
240 = 200 + x
x = 40
Therefore, Mary must score at least 40 marks in the fourth test to maintain an average score of 60.
Answer: Option A, x > 40.
p, q and r are three non-negative integers such that p + q + r = 10. The maximum value of pq + qr + pr + pqr is- a)≥ 60 and < 70
- b)≥ 50 and < 60
- c)≥ 40 and < 50
- d)≥ 70 and < 80
Correct answer is option 'A'. Can you explain this answer?
p, q and r are three non-negative integers such that p + q + r = 10. The maximum value of pq + qr + pr + pqr is
a)
≥ 60 and < 70
b)
≥ 50 and < 60
c)
≥ 40 and < 50
d)
≥ 70 and < 80
|
S.S Career Academy answered |
The product of 2 numbers A and B is maximum when A = B.
If we cannot equate the numbers, then we have to try to minimize the difference between the numbers as much as possible.
pq will be maximum when p=q.
qr will be maximum when q=r.
qr will be maximum when r=p.
Therefore, p, q, and r should be as close to each other as possible.
We know that p,q,and r are integers and p + q + r = 10.
=> p,q, and r should be 3, 3, and 4 in any order.
Substituting the values in the expression, we get,
pq + qr + pr + pqr = 3*3 + 3*4 + 3*4 + 3*3*4
= 9 + 12 + 12 + 36
= 69
For x = 15, y = 10 and z = 9, find the value of le(x, min(y, x-z), le(9, 8, ma(x, y, z)).- a)5
- b)9
- c)12
- d)4
Correct answer is option 'B'. Can you explain this answer?
For x = 15, y = 10 and z = 9, find the value of le(x, min(y, x-z), le(9, 8, ma(x, y, z)).
a)
5
b)
9
c)
12
d)
4
|
|
EduRev CLAT answered |
Given expression can be reduced to
le(15, min(10,15-9) , le(9,8,12))
Or le(15,6,1) = 9
le(15, min(10,15-9) , le(9,8,12))
Or le(15,6,1) = 9
If x > 5 and y < -1, then which of the following statements is true?- a)(x + 4y) > 1
- b)x > -4y
- c)-4x < 5y
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
If x > 5 and y < -1, then which of the following statements is true?
a)
(x + 4y) > 1
b)
x > -4y
c)
-4x < 5y
d)
None of these
|
Damini jain answered |
If x = 5, then the equation y = 2x + 3 can be solved as follows:
y = 2(5) + 3
y = 10 + 3
y = 13
y = 2(5) + 3
y = 10 + 3
y = 13
Let a, b, c, d be four integers such that a + b + c + d = 4m + 1 where m is a positive integer. Given m, which one of the following is necessarily true?- a)The minimum possible value of a2 + b2 + c2 + d2 is 4m2 - 2m + 1
- b)The maximum possible value of a2 + b2 + c2 + d2 is 4m2 + 2m + 1
- c)The maximum possible value of a2 + b2 + c2 + d2 is 4m2 - 2m + 1
- d)The minimum possible value of a2 + b2 + c2 + d2 is 4m2 + 2m +1
Correct answer is option 'D'. Can you explain this answer?
Let a, b, c, d be four integers such that a + b + c + d = 4m + 1 where m is a positive integer. Given m, which one of the following is necessarily true?
a)
The minimum possible value of a2 + b2 + c2 + d2 is 4m2 - 2m + 1
b)
The maximum possible value of a2 + b2 + c2 + d2 is 4m2 + 2m + 1
c)
The maximum possible value of a2 + b2 + c2 + d2 is 4m2 - 2m + 1
d)
The minimum possible value of a2 + b2 + c2 + d2 is 4m2 + 2m +1
|
Mira patil answered |
Explanation:
Given that a, b, c, d are four integers such that a + b + c + d = 4m + 1, where m is a positive integer, we need to determine which of the given options is necessarily true regarding the minimum and maximum possible values of a^2 + b^2 + c^2 + d^2.
Minimum Possible Value:
To find the minimum possible value of a^2 + b^2 + c^2 + d^2, we need to minimize each of the integers a, b, c, and d. Since the minimum value of a single integer squared is 0, the minimum possible value of a^2 + b^2 + c^2 + d^2 occurs when each integer is 0.
Therefore, the minimum possible value of a^2 + b^2 + c^2 + d^2 is 0.
Maximum Possible Value:
To find the maximum possible value of a^2 + b^2 + c^2 + d^2, we need to maximize each of the integers a, b, c, and d. Since the maximum value of a single integer squared is infinity, there is no upper bound on the maximum possible value of a^2 + b^2 + c^2 + d^2.
Comparing with the Options:
Now let's compare the minimum and maximum possible values of a^2 + b^2 + c^2 + d^2 with the options given:
a) The minimum possible value of a^2 + b^2 + c^2 + d^2 is 4m^2 - 2m + 1
b) The maximum possible value of a^2 + b^2 + c^2 + d^2 is 4m^2 + 2m + 1
c) The maximum possible value of a^2 + b^2 + c^2 + d^2 is 4m^2 - 2m + 1
d) The minimum possible value of a^2 + b^2 + c^2 + d^2 is 4m^2 + 2m + 1
Comparing the options with our findings, we can see that option d) aligns with the minimum possible value of 0, which we determined earlier.
Therefore, the correct answer is option d) The minimum possible value of a^2 + b^2 + c^2 + d^2 is 4m^2 + 2m + 1.
Given that a, b, c, d are four integers such that a + b + c + d = 4m + 1, where m is a positive integer, we need to determine which of the given options is necessarily true regarding the minimum and maximum possible values of a^2 + b^2 + c^2 + d^2.
Minimum Possible Value:
To find the minimum possible value of a^2 + b^2 + c^2 + d^2, we need to minimize each of the integers a, b, c, and d. Since the minimum value of a single integer squared is 0, the minimum possible value of a^2 + b^2 + c^2 + d^2 occurs when each integer is 0.
Therefore, the minimum possible value of a^2 + b^2 + c^2 + d^2 is 0.
Maximum Possible Value:
To find the maximum possible value of a^2 + b^2 + c^2 + d^2, we need to maximize each of the integers a, b, c, and d. Since the maximum value of a single integer squared is infinity, there is no upper bound on the maximum possible value of a^2 + b^2 + c^2 + d^2.
Comparing with the Options:
Now let's compare the minimum and maximum possible values of a^2 + b^2 + c^2 + d^2 with the options given:
a) The minimum possible value of a^2 + b^2 + c^2 + d^2 is 4m^2 - 2m + 1
b) The maximum possible value of a^2 + b^2 + c^2 + d^2 is 4m^2 + 2m + 1
c) The maximum possible value of a^2 + b^2 + c^2 + d^2 is 4m^2 - 2m + 1
d) The minimum possible value of a^2 + b^2 + c^2 + d^2 is 4m^2 + 2m + 1
Comparing the options with our findings, we can see that option d) aligns with the minimum possible value of 0, which we determined earlier.
Therefore, the correct answer is option d) The minimum possible value of a^2 + b^2 + c^2 + d^2 is 4m^2 + 2m + 1.
x2 – 7x + 12 < |x – 4|- a)x < 2
- b)x > 4
- c)2 < x < 4
- d)2 £ x £ 4
Correct answer is option 'C'. Can you explain this answer?
x2 – 7x + 12 < |x – 4|
a)
x < 2
b)
x > 4
c)
2 < x < 4
d)
2 £ x £ 4
|
|
Prisha Shah answered |
At x = 0, inequality is not satisfied, option (a) is rejected.
At x = 5, inequality is not satisfied, option (b) is rejected.
At x = 2 inequality is not satisfied.
Options (d) are rejected.
Option (c) is correct
At x = 5, inequality is not satisfied, option (b) is rejected.
At x = 2 inequality is not satisfied.
Options (d) are rejected.
Option (c) is correct
Solution space of the inequalities 2x + y ≤ 10 and x - 7 ≤ 5:
(i) includes the origin.
(ii) includes the point (4,3)
which one is correct?- a)Only (i)
- b) Only (ii)
- c) Both (i) and (ii)
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
Solution space of the inequalities 2x + y ≤ 10 and x - 7 ≤ 5:
(i) includes the origin.
(ii) includes the point (4,3)
which one is correct?
(i) includes the origin.
(ii) includes the point (4,3)
which one is correct?
a)
Only (i)
b)
Only (ii)
c)
Both (i) and (ii)
d)
None of the above
|
|
Amrutha Goyal answered |
There is no specific inequality given in the question. Please provide the complete information so that the solution space can be determined.
x, y and z are three positive integers such that x > y > z. Which of the following is closest to the product xyz?- a)(x - 1)yz
- b)x(y - 1)z
- c)xy(z - 1)
- d)x(y + 1)z
Correct answer is option 'A'. Can you explain this answer?
x, y and z are three positive integers such that x > y > z. Which of the following is closest to the product xyz?
a)
(x - 1)yz
b)
x(y - 1)z
c)
xy(z - 1)
d)
x(y + 1)z
|
|
Innovative Classes answered |
The expressions in the four options can be expanded as
xyz-yz; xyz-xz; xyz-xy and xyz+xz
The closest value to xyz would be xyz-yz, as yz is the least value among yz, xz and xy.
Option a) is the correct answer.
What is the value of ma(10, 4, le((la10, 5, 3), 5, 3))?- a) 7
- b) 6.5
- c) 8
- d) 7.5
Correct answer is option 'B'. Can you explain this answer?
What is the value of ma(10, 4, le((la10, 5, 3), 5, 3))?
a)
7
b)
6.5
c)
8
d)
7.5
|
|
Innovative Classes answered |
Ma(10, 4, le((la10, 5, 3), 5, 3))
Or Ma(10, 4, le(8, 5, 3))
Or Ma(10, 4, 3)
Or 1/2(6 + 7) = 6.5
X2 - 14x - 15 > 0
- a)x < -1
- b)x > 15
- c)x < -1 and x > 15
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
X2 - 14x - 15 > 0
a)
x < -1
b)
x > 15
c)
x < -1 and x > 15
d)
None of these
|
Aarav Sharma answered |
The expression x^2 - 14x - 15 can be factored as (x - 15)(x + 1).
The union however forbids forbide him to employ less than 2 experiencedd person to each fresh person. This situation can be expressed as- a)x ≤ y/2
- b)y ≤ x/2
- c)y ≥ x/2
- d)x > 2y
Correct answer is option 'B'. Can you explain this answer?
The union however forbids forbide him to employ less than 2 experiencedd person to each fresh person. This situation can be expressed as
a)
x ≤ y/2
b)
y ≤ x/2
c)
y ≥ x/2
d)
x > 2y
|
|
Moumita Bajaj answered |
≥ 2y, where x represents the number of experienced workers and y represents the number of fresh workers that the employer hires.
A car manufacturing company manufactures cars of two types A and B. Model A requires 150 man-hours for assembling, 50 man-hours for painting and 10 man-hours for checking and testing. Model B requires 60 man-hours for assembling, 40 man-hours for painting and 20 man-hours for checking and testing. There are available 30 thousand man-hours for assembling, 13 thousand man-hours for checking and testing. Express the above situation using linear inequalities. Let the company manufacture x units of type A model of car and y units type B model of car. Then, the inequalities are:- a)5x+2y ≥ 1000; 5x + 4y ≥ 1300,x+2y ≤ 500; x ≥ 0, y ≥ 0,
- b)5x + 2y ≤ 1000, 5x+4y ≤ 13000,x+2y ≥ 500; x ≥ 0, y ≥ 0.
- c)5x+2y ≤ 1,000, 5x+4y ≤ 1300,x+2y ≤ 500; x≥ 0, y≥ 0.
- d)5x + 2y = 1000, 5x+4y ≥ 1300,x+2y = 500; x≥ 0, y ≥ 0.
Correct answer is option 'C'. Can you explain this answer?
A car manufacturing company manufactures cars of two types A and B. Model A requires 150 man-hours for assembling, 50 man-hours for painting and 10 man-hours for checking and testing. Model B requires 60 man-hours for assembling, 40 man-hours for painting and 20 man-hours for checking and testing. There are available 30 thousand man-hours for assembling, 13 thousand man-hours for checking and testing. Express the above situation using linear inequalities. Let the company manufacture x units of type A model of car and y units type B model of car. Then, the inequalities are:
a)
5x+2y ≥ 1000; 5x + 4y ≥ 1300,x+2y ≤ 500; x ≥ 0, y ≥ 0,
b)
5x + 2y ≤ 1000, 5x+4y ≤ 13000,x+2y ≥ 500; x ≥ 0, y ≥ 0.
c)
5x+2y ≤ 1,000, 5x+4y ≤ 1300,x+2y ≤ 500; x≥ 0, y≥ 0.
d)
5x + 2y = 1000, 5x+4y ≥ 1300,x+2y = 500; x≥ 0, y ≥ 0.
|
|
Vaishnavi Gupta answered |
1. Assembling constraint:
150x + 60y ≤ 30,000
This inequality represents the constraint that the total man-hours spent on assembling cars cannot exceed the available 30,000 man-hours.
2. Painting constraint:
50x + 40y ≤ M
The value of M is not given in the problem, but it represents the maximum number of man-hours available for painting cars. We cannot determine the value of M from the given information, so we leave it as an unknown constant.
3. Checking and testing constraint:
10x + 20y ≤ 13,000
This inequality represents the constraint that the total man-hours spent on checking and testing cars cannot exceed the available 13,000 man-hours.
4. Non-negative constraint:
x ≥ 0, y ≥ 0
This inequality represents the fact that the company cannot manufacture negative units of cars.
5. Integer constraint:
x, y ∈ ℤ
This inequality represents the fact that the company can only manufacture integer units of cars, and not fractional units.
Putting all the above inequalities together, we get the following set of linear inequalities:
150x + 60y ≤ 30,000
50x + 40y ≤ M
10x + 20y ≤ 13,000
x ≥ 0, y ≥ 0
x, y ∈ ℤ
150x + 60y ≤ 30,000
This inequality represents the constraint that the total man-hours spent on assembling cars cannot exceed the available 30,000 man-hours.
2. Painting constraint:
50x + 40y ≤ M
The value of M is not given in the problem, but it represents the maximum number of man-hours available for painting cars. We cannot determine the value of M from the given information, so we leave it as an unknown constant.
3. Checking and testing constraint:
10x + 20y ≤ 13,000
This inequality represents the constraint that the total man-hours spent on checking and testing cars cannot exceed the available 13,000 man-hours.
4. Non-negative constraint:
x ≥ 0, y ≥ 0
This inequality represents the fact that the company cannot manufacture negative units of cars.
5. Integer constraint:
x, y ∈ ℤ
This inequality represents the fact that the company can only manufacture integer units of cars, and not fractional units.
Putting all the above inequalities together, we get the following set of linear inequalities:
150x + 60y ≤ 30,000
50x + 40y ≤ M
10x + 20y ≤ 13,000
x ≥ 0, y ≥ 0
x, y ∈ ℤ
The longest side of a triangle is 3 times the shortest side, and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.- a)9 cm
- b)11 cm
- c)13 cm
- d)14 cm
Correct answer is option 'A'. Can you explain this answer?
The longest side of a triangle is 3 times the shortest side, and the third side is 2 cm shorter than the longest side. If the perimeter of the triangle is at least 61 cm, find the minimum length of the shortest side.
a)
9 cm
b)
11 cm
c)
13 cm
d)
14 cm
|
Freedom Institute answered |
Let x cm be the length of the shortest side of the triangle.
∴ According to the question, length of the longest side = 3x cm
Length of the third side = (3x – 2) cm
The least perimeter of the triangle = 61 cm (given)
Thus, x + 3x + (3x – 2) cm ≥ 61 cm
= 7x – 2 ≥ 61
= 7x ≥ 63
Dividing by 7 on both sides, we get;
= 7x/7 ≥ 63/7
= x ≥ 9
Hence, the minimum length of the shortest side will be 9 cm.
The union however forbids him to employ less than 2 experienced person to each fresh person. This situation can be expressed as- a)x ≤ y/2
- b)y ≤ x/2
- c)y ≥ x /2
- d)x > 2y
Correct answer is option 'B'. Can you explain this answer?
The union however forbids him to employ less than 2 experienced person to each fresh person. This situation can be expressed as
a)
x ≤ y/2
b)
y ≤ x/2
c)
y ≥ x /2
d)
x > 2y
|
Qudrat Chauhan answered |
The union however forbids him to employ less than 2 experienced person to each fresh person. 2y ≤ x. or x ≥ 2y.
A firm makes two types of products: Type A and Type B. The profit on product A is Rs. 20 each and that on product B is Rs. 30 each. Both types are processed on three machines M1, M2 and M3. The time required in hour by each product and total time available in hours per week on each machine are asa follows:
Machine Product A Product B Available Time
M1 3 3 36
M2 5 2 50
M3 2 6 60
The constraints can be formulated taking x1 = number of units A and x2 = number of unit of B as- a)x1 + x2 ≤ 12
5x1 + 2x2 ≤ 50
2x1 + 6x2 ≤ 60 - b)3x1 + 3x2 ≥ 36
5x1 + 2x2 ≤ 50
2x1 + 6x2 ≥ 60
x1 ≥ 0, x2 ≥ 0 - c)3x1 + 3x2 ≤ 36
5x1 + 2x2 ≤ 50
2x1 + 6x2 ≤ 60
x1 ≥ 0, x2 ≥ 0 - d)none of these
Correct answer is option 'C'. Can you explain this answer?
A firm makes two types of products: Type A and Type B. The profit on product A is Rs. 20 each and that on product B is Rs. 30 each. Both types are processed on three machines M1, M2 and M3. The time required in hour by each product and total time available in hours per week on each machine are asa follows:
Machine Product A Product B Available Time
M1 3 3 36
M2 5 2 50
M3 2 6 60
The constraints can be formulated taking x1 = number of units A and x2 = number of unit of B as
Machine Product A Product B Available Time
M1 3 3 36
M2 5 2 50
M3 2 6 60
The constraints can be formulated taking x1 = number of units A and x2 = number of unit of B as
a)
x1 + x2 ≤ 12
5x1 + 2x2 ≤ 50
2x1 + 6x2 ≤ 60
5x1 + 2x2 ≤ 50
2x1 + 6x2 ≤ 60
b)
3x1 + 3x2 ≥ 36
5x1 + 2x2 ≤ 50
2x1 + 6x2 ≥ 60
x1 ≥ 0, x2 ≥ 0
5x1 + 2x2 ≤ 50
2x1 + 6x2 ≥ 60
x1 ≥ 0, x2 ≥ 0
c)
3x1 + 3x2 ≤ 36
5x1 + 2x2 ≤ 50
2x1 + 6x2 ≤ 60
x1 ≥ 0, x2 ≥ 0
5x1 + 2x2 ≤ 50
2x1 + 6x2 ≤ 60
x1 ≥ 0, x2 ≥ 0
d)
none of these
|
|
Mehul Saini answered |
To formulate the constraints, we need to consider the time required by each product on each machine and the available time on each machine. Let x1 be the number of units of product A produced and x2 be the number of units of product B produced.
On machine M1:
The time required to process x1 units of A is 3x1 hours
The time required to process x2 units of B is 3x2 hours
The total time available is 36 hours
So, the constraint is: 3x1 + 3x2 ≤ 36
On machine M2:
The time required to process x1 units of A is 5x1 hours
The time required to process x2 units of B is 2x2 hours
The total time available is 50 hours
So, the constraint is: 5x1 + 2x2 ≤ 50
On machine M3:
The time required to process x1 units of A is 2x1 hours
The time required to process x2 units of B is 6x2 hours
The total time available is 60 hours
So, the constraint is: 2x1 + 6x2 ≤ 60
We also have the non-negativity constraints:
x1 ≥ 0 and x2 ≥ 0
The objective function is to maximize the total profit, which can be expressed as:
Z = 20x1 + 30x2
Therefore, the linear programming problem can be formulated as follows:
Maximize Z = 20x1 + 30x2
Subject to:
3x1 + 3x2 ≤ 36
5x1 + 2x2 ≤ 50
2x1 + 6x2 ≤ 60
x1 ≥ 0, x2 ≥ 0
On machine M1:
The time required to process x1 units of A is 3x1 hours
The time required to process x2 units of B is 3x2 hours
The total time available is 36 hours
So, the constraint is: 3x1 + 3x2 ≤ 36
On machine M2:
The time required to process x1 units of A is 5x1 hours
The time required to process x2 units of B is 2x2 hours
The total time available is 50 hours
So, the constraint is: 5x1 + 2x2 ≤ 50
On machine M3:
The time required to process x1 units of A is 2x1 hours
The time required to process x2 units of B is 6x2 hours
The total time available is 60 hours
So, the constraint is: 2x1 + 6x2 ≤ 60
We also have the non-negativity constraints:
x1 ≥ 0 and x2 ≥ 0
The objective function is to maximize the total profit, which can be expressed as:
Z = 20x1 + 30x2
Therefore, the linear programming problem can be formulated as follows:
Maximize Z = 20x1 + 30x2
Subject to:
3x1 + 3x2 ≤ 36
5x1 + 2x2 ≤ 50
2x1 + 6x2 ≤ 60
x1 ≥ 0, x2 ≥ 0
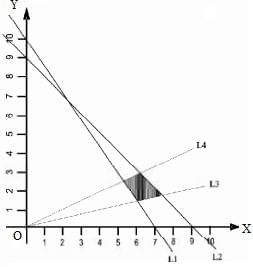
L1 : 5x + 3y = 30 L2 : x+y = 9 L3 : y = x/3 L4 : y = x/2 The common region (shaded part) shown in the diagram refers to- a)
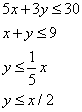
- b)
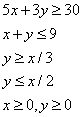
- c)
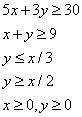
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
L1 : 5x + 3y = 30 L2 : x+y = 9 L3 : y = x/3 L4 : y = x/2 The common region (shaded part) shown in the diagram refers to
a)
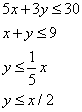
b)
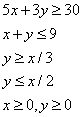
c)
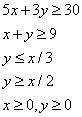
d)
None of these
|
|
Qudrat Chauhan answered |
The diagram shows the region which is common of the equations of inequality.
We will select one point from the shaded region and write the equations of inequalities.
Lets the consider the point (6, 2.5) and substitute in equations .
5x + 3y = 5(6) + 3(2.5) = 30 + 7.5 = 37.5 > 30
x + y = 6 + 2.5 = 8.5 < 9
x / 3 = 6/3 = 2 < 2.5 < y
So the answer is none of these.
We will select one point from the shaded region and write the equations of inequalities.
Lets the consider the point (6, 2.5) and substitute in equations .
5x + 3y = 5(6) + 3(2.5) = 30 + 7.5 = 37.5 > 30
x + y = 6 + 2.5 = 8.5 < 9
x / 3 = 6/3 = 2 < 2.5 < y
So the answer is none of these.
The rules and regulations demand that the employer should employ not more than 5 experienced hands to 1 fresh one and this fact can be expressed as- a)y ≥ x/5
- b)5y ≤ x
- c)5 y ≥ x
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The rules and regulations demand that the employer should employ not more than 5 experienced hands to 1 fresh one and this fact can be expressed as
a)
y ≥ x/5
b)
5y ≤ x
c)
5 y ≥ x
d)
none of these
|
|
Qudrat Chauhan answered |
The rules and regulations demand that the employer should employ not more than 5 experienced hands to 1 fresh one.
so 5y ≥ x .
so 5y ≥ x .
The shaded region represents:
- a)3x + 5y ≥ 15, 5x+2y ≥ 10, x, y ≥ 0
- b)3x + 5y ≤ 15, 5x+2y ≤ 10, x, y≥ 0
- c)3x+ 5y ≥ 15, 5x+2y ≥ 10, x, y, ≥ 0
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
The shaded region represents:
a)
3x + 5y ≥ 15, 5x+2y ≥ 10, x, y ≥ 0
b)
3x + 5y ≤ 15, 5x+2y ≤ 10, x, y≥ 0
c)
3x+ 5y ≥ 15, 5x+2y ≥ 10, x, y, ≥ 0
d)
None of these
|
|
Alok Mehta answered |
The feasible region determined by the system of constraints, 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, and y ≥ 0, are as follows:
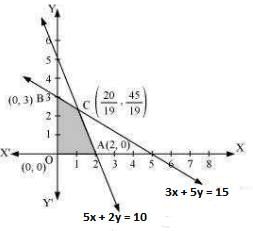
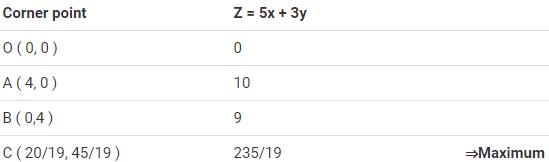
Therefore, at the point ( 20/19 , 45/19 ) the maximum value of Z is 235/19.
The corner points of the feasible region are O (0, 0), A (2, 0), B (0, 3), and C ( 20/19 , 45/19 ).
The values of Z at these corner points are as follows:
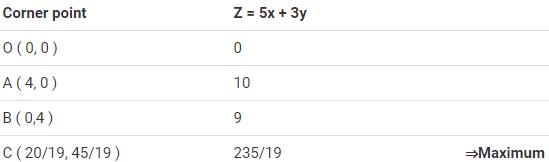
Therefore, at the point ( 20/19 , 45/19 ) the maximum value of Z is 235/19.
A dietitian wishes to mix together two kinds of food so that the vitamin content of the mixture is at least 9 units of vitamin A, 7 units of vitamin B, 10 units of vitamin C and 12 units of vitamin D. The vitamin content per Kg. of each food is shown below: A B C D Food I : 2 1 1 2 Food II: 1 1 2 3 Assuming x units of food I is to be mixed with y units of food II the situation can be expressed as- a)
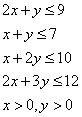
- b)
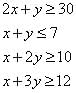
- c)
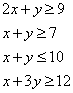
- d)
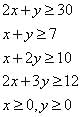
Correct answer is option 'D'. Can you explain this answer?
A dietitian wishes to mix together two kinds of food so that the vitamin content of the mixture is at least 9 units of vitamin A, 7 units of vitamin B, 10 units of vitamin C and 12 units of vitamin D. The vitamin content per Kg. of each food is shown below: A B C D Food I : 2 1 1 2 Food II: 1 1 2 3 Assuming x units of food I is to be mixed with y units of food II the situation can be expressed as
a)
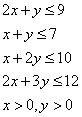
b)
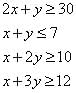
c)
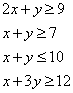
d)
|
|
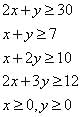
Qudrat Chauhan answered |
According the data given we get
2x + y ≥ 9, x + y ≥ 7 , x + 2y ≥ 10 and 2x + 3y ≥ 12, x≥ 0 and y ≥ 0
the correct the option is d.
2x + y ≥ 9, x + y ≥ 7 , x + 2y ≥ 10 and 2x + 3y ≥ 12, x≥ 0 and y ≥ 0
the correct the option is d.
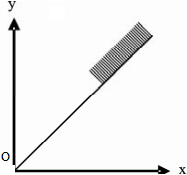
The graph to express the inequality y ≤ (½)x is indicated by- a)
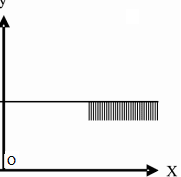
- b)
- c)
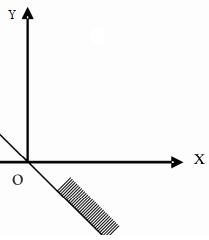
- d)
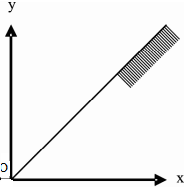
Correct answer is option 'D'. Can you explain this answer?
The graph to express the inequality y ≤ (½)x is indicated by
a)
b)
c)
d)
|
|
Qudrat Chauhan answered |
To plot the graph of y ≤ (½)x, first plote the graph of y =(½)x
It will be a straight line passing through (0 ,0) and (2, 1) .
The graph of inequality is the region satisfying the inequality.
So it is on one side of a line.
Now we will check any one point of one side , if it satisfy the inequality then the shading is done on that side or on the other side.
As the line passes through origin we can not check (0,0).
Let us check (2,0) , When x = 2, then y = 1. 0 < 1 , So (2,0) satisfy the inequality.
So shading must be towards the point . that is towards x axis.
It will be a straight line passing through (0 ,0) and (2, 1) .
The graph of inequality is the region satisfying the inequality.
So it is on one side of a line.
Now we will check any one point of one side , if it satisfy the inequality then the shading is done on that side or on the other side.
As the line passes through origin we can not check (0,0).
Let us check (2,0) , When x = 2, then y = 1. 0 < 1 , So (2,0) satisfy the inequality.
So shading must be towards the point . that is towards x axis.
Chapter doubts & questions for Chapter 3: Linear Inequalities - Quantitative Aptitude for CA Foundation 2025 is part of CA Foundation exam preparation. The chapters have been prepared according to the CA Foundation exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CA Foundation 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chapter 3: Linear Inequalities - Quantitative Aptitude for CA Foundation in English & Hindi are available as part of CA Foundation exam.
Download more important topics, notes, lectures and mock test series for CA Foundation Exam by signing up for free.
Quantitative Aptitude for CA Foundation
101 videos|276 docs|89 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup