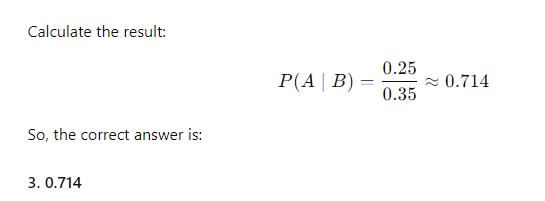All Exams >
CA Foundation >
Quantitative Aptitude for CA Foundation >
All Questions
All questions of Chapter 15: Probability for CA Foundation Exam
What is the chance of getting at least one defective item if 3 items are drawn randomly from a lot containing 6 items of which 2 are defective item?- a)0.30
- b)0.20
- c)0.80
- d)0.50
Correct answer is option 'C'. Can you explain this answer?
What is the chance of getting at least one defective item if 3 items are drawn randomly from a lot containing 6 items of which 2 are defective item?
a)
0.30
b)
0.20
c)
0.80
d)
0.50

|
Lakshmi Kaur answered |
Solution:
To find the probability of getting at least one defective item, we need to find the probability of getting 1, 2, or 3 defective items.
Probability of getting 1 defective item out of 3 drawn:
The first defective item can be drawn in 2C1 ways (selecting 1 item out of 2 defective items), and the remaining 2 non-defective items can be drawn in 4C2 ways (selecting 2 items out of 4 non-defective items). Therefore, the probability of getting 1 defective item is:
P(1) = (2C1 x 4C2) / 6C3 = (2 x 6) / 20 = 0.6
Probability of getting 2 defective items out of 3 drawn:
The two defective items can be drawn in 2C2 ways (selecting 2 items out of 2 defective items), and the remaining 1 non-defective item can be drawn in 4C1 ways (selecting 1 item out of 4 non-defective items). Therefore, the probability of getting 2 defective items is:
P(2) = (2C2 x 4C1) / 6C3 = (1 x 4) / 20 = 0.2
Probability of getting 3 defective items out of 3 drawn:
The three defective items can be drawn in 2C3 ways (selecting 3 items out of 2 defective items, which is not possible), so the probability of getting 3 defective items is 0.
Therefore, the probability of getting at least one defective item is:
P(at least 1) = P(1) + P(2) + P(3) = 0.6 + 0.2 + 0 = 0.8
Hence, the correct answer is option C, 0.8.
To find the probability of getting at least one defective item, we need to find the probability of getting 1, 2, or 3 defective items.
Probability of getting 1 defective item out of 3 drawn:
The first defective item can be drawn in 2C1 ways (selecting 1 item out of 2 defective items), and the remaining 2 non-defective items can be drawn in 4C2 ways (selecting 2 items out of 4 non-defective items). Therefore, the probability of getting 1 defective item is:
P(1) = (2C1 x 4C2) / 6C3 = (2 x 6) / 20 = 0.6
Probability of getting 2 defective items out of 3 drawn:
The two defective items can be drawn in 2C2 ways (selecting 2 items out of 2 defective items), and the remaining 1 non-defective item can be drawn in 4C1 ways (selecting 1 item out of 4 non-defective items). Therefore, the probability of getting 2 defective items is:
P(2) = (2C2 x 4C1) / 6C3 = (1 x 4) / 20 = 0.2
Probability of getting 3 defective items out of 3 drawn:
The three defective items can be drawn in 2C3 ways (selecting 3 items out of 2 defective items, which is not possible), so the probability of getting 3 defective items is 0.
Therefore, the probability of getting at least one defective item is:
P(at least 1) = P(1) + P(2) + P(3) = 0.6 + 0.2 + 0 = 0.8
Hence, the correct answer is option C, 0.8.
When 3 unbiased coins are tossed. The probability of obtaining 3 heads is- a)2/4
- b)¼
- c)¾
- d)0
Correct answer is option 'D'. Can you explain this answer?
When 3 unbiased coins are tossed. The probability of obtaining 3 heads is
a)
2/4
b)
¼
c)
¾
d)
0
|
|
Poonam Reddy answered |
Correct Answer :- d
Explanation :
Total no. Of outcomes: HHH, HHT, HTH, THH, TTH, THT, HTT, TTT
No. Outcomes of all heads: 1
Prob. Of all heads = no. Of outcomes of all heads/ total no. Of outcomes
i.e (1/8)
In a class 40 % students read Mathematics, 25 % Biology and 15 % both Mathematics and Biology. One student is select at random. The probability that he reads Mathematics if it is known that he reads Biology is- a)2/5
- b)3/5
- c)4/5
- d)none
Correct answer is option 'B'. Can you explain this answer?
In a class 40 % students read Mathematics, 25 % Biology and 15 % both Mathematics and Biology. One student is select at random. The probability that he reads Mathematics if it is known that he reads Biology is
a)
2/5
b)
3/5
c)
4/5
d)
none

|
Sonal Patel answered |
Given information:
- 40% of students read Mathematics.
- 25% of students read Biology.
- 15% of students read both Mathematics and Biology.
To find:
- The probability that a student reads Mathematics if it is known that he reads Biology.
Solution:
Step 1: Draw a Venn diagram representing the given information.
The rectangle represents the total number of students in the class. The circle on the left represents the number of students who read Mathematics, and the circle on the right represents the number of students who read Biology. The overlapping region represents the number of students who read both Mathematics and Biology.
Step 2: Calculate the number of students who read only Biology.
To do this, we subtract the number of students who read both Mathematics and Biology from the total number of students who read Biology.
Number of students who read only Biology = Total number of students who read Biology - Number of students who read both Mathematics and Biology
= 25% - 15%
= 10%
Step 3: Calculate the probability that a student reads Mathematics given that he reads Biology.
We can use Bayes' theorem to calculate this probability.
P(Mathematics | Biology) = P(Biology | Mathematics) * P(Mathematics) / P(Biology)
- P(Mathematics) = 40%
- P(Biology) = 25%
- P(Biology | Mathematics) = The probability that a student reads Biology given that he reads Mathematics. This can be calculated as follows:
P(Biology | Mathematics) = (Number of students who read both Mathematics and Biology) / (Total number of students who read Mathematics)
= 15% / 40%
= 3/8
Substituting these values into Bayes' theorem, we get:
P(Mathematics | Biology) = (3/8 * 40%) / 25%
= 3/5
Therefore, the probability that a student reads Mathematics given that he reads Biology is 3/5 or option B.
- 40% of students read Mathematics.
- 25% of students read Biology.
- 15% of students read both Mathematics and Biology.
To find:
- The probability that a student reads Mathematics if it is known that he reads Biology.
Solution:
Step 1: Draw a Venn diagram representing the given information.
The rectangle represents the total number of students in the class. The circle on the left represents the number of students who read Mathematics, and the circle on the right represents the number of students who read Biology. The overlapping region represents the number of students who read both Mathematics and Biology.
Step 2: Calculate the number of students who read only Biology.
To do this, we subtract the number of students who read both Mathematics and Biology from the total number of students who read Biology.
Number of students who read only Biology = Total number of students who read Biology - Number of students who read both Mathematics and Biology
= 25% - 15%
= 10%
Step 3: Calculate the probability that a student reads Mathematics given that he reads Biology.
We can use Bayes' theorem to calculate this probability.
P(Mathematics | Biology) = P(Biology | Mathematics) * P(Mathematics) / P(Biology)
- P(Mathematics) = 40%
- P(Biology) = 25%
- P(Biology | Mathematics) = The probability that a student reads Biology given that he reads Mathematics. This can be calculated as follows:
P(Biology | Mathematics) = (Number of students who read both Mathematics and Biology) / (Total number of students who read Mathematics)
= 15% / 40%
= 3/8
Substituting these values into Bayes' theorem, we get:
P(Mathematics | Biology) = (3/8 * 40%) / 25%
= 3/5
Therefore, the probability that a student reads Mathematics given that he reads Biology is 3/5 or option B.
The probability of winning of a person is 6/11 and at a result he gets Rs.77/= .The expectation of this person is
- a)Rs.35/=
- b)Rs.42/=
- c)Rs.58/=
- d)none
Correct answer is option 'B'. Can you explain this answer?
The probability of winning of a person is 6/11 and at a result he gets Rs.77/= .The expectation of this person is
a)
Rs.35/=
b)
Rs.42/=
c)
Rs.58/=
d)
none

|
Rajveer Jain answered |
Solution:
Given, probability of winning of a person = 6/11
Amount received by the person = Rs. 77/=
To find: Expectation of the person
Calculation:
The formula to find the expectation of a person is:
Expectation = (Amount received x Probability of winning) - (Amount lost x Probability of losing)
Here, the probability of losing = 1 - Probability of winning
= 1 - (6/11)
= 5/11
Substituting the given values in the formula, we get:
Expectation = (77 x 6/11) - (0 x 5/11)
= 42
Therefore, the expectation of the person is Rs.42/=. Hence, option B is the correct answer.
Conclusion:
The expectation of the person who wins with a probability of 6/11 and receives Rs.77/= is Rs.42/=.
Given, probability of winning of a person = 6/11
Amount received by the person = Rs. 77/=
To find: Expectation of the person
Calculation:
The formula to find the expectation of a person is:
Expectation = (Amount received x Probability of winning) - (Amount lost x Probability of losing)
Here, the probability of losing = 1 - Probability of winning
= 1 - (6/11)
= 5/11
Substituting the given values in the formula, we get:
Expectation = (77 x 6/11) - (0 x 5/11)
= 42
Therefore, the expectation of the person is Rs.42/=. Hence, option B is the correct answer.
Conclusion:
The expectation of the person who wins with a probability of 6/11 and receives Rs.77/= is Rs.42/=.
A box contains 2 red, 3 green and 2 blue balls. Two bails are drawn at random. What is the probability that none of the balls drawn is blue?- a)10/21
- b)11/21
- c)2/7
- d)5/7
Correct answer is option 'A'. Can you explain this answer?
A box contains 2 red, 3 green and 2 blue balls. Two bails are drawn at random. What is the probability that none of the balls drawn is blue?
a)
10/21
b)
11/21
c)
2/7
d)
5/7

|
Ruchi Mishra answered |
Given:
- Total number of balls = 2 red + 3 green + 2 blue = 7
- Two balls are drawn at random
To find:
- Probability that none of the balls drawn is blue
Solution:
Let's first find the total number of ways to draw 2 balls out of 7:
Total ways = 7C2 = (7 * 6) / (2 * 1) = 21
Now, let's find the number of ways to draw 2 balls such that none of them is blue:
Number of ways = 2C0 * 5C2 + 2C1 * 5C1 + 2C2 * 5C0
- 2C0 * 5C2 represents selecting 0 blue balls out of 2 and 2 green balls out of 3
- 2C1 * 5C1 represents selecting 1 blue ball out of 2 and 1 green ball out of 3 (or 1 red ball out of 2 and 1 green ball out of 3)
- 2C2 * 5C0 represents selecting 2 blue balls out of 2 and 0 green balls out of 3 (or 2 red balls out of 2 and 0 green balls out of 3)
Number of ways = (1 * 10) + (2 * 5) + (1 * 1) = 21
Therefore, the probability of drawing 2 balls such that none of them is blue = (Number of ways to draw 2 balls such that none of them is blue) / (Total ways) = 21/21 = 1
But, we need to find the probability that none of the balls drawn is blue. So, we subtract the probability of drawing 2 blue balls from 1:
Probability that none of the balls drawn is blue = 1 - (Probability of drawing 2 blue balls) = 1 - (Number of ways to draw 2 blue balls / Total ways)
Number of ways to draw 2 blue balls = 2C2 * 5C0 = 1
Probability of drawing 2 blue balls = 1/21
Therefore, Probability that none of the balls drawn is blue = 1 - (1/21) = 20/21
Hence, option A (10/21) is incorrect and the correct answer is option B (11/21).
- Total number of balls = 2 red + 3 green + 2 blue = 7
- Two balls are drawn at random
To find:
- Probability that none of the balls drawn is blue
Solution:
Let's first find the total number of ways to draw 2 balls out of 7:
Total ways = 7C2 = (7 * 6) / (2 * 1) = 21
Now, let's find the number of ways to draw 2 balls such that none of them is blue:
Number of ways = 2C0 * 5C2 + 2C1 * 5C1 + 2C2 * 5C0
- 2C0 * 5C2 represents selecting 0 blue balls out of 2 and 2 green balls out of 3
- 2C1 * 5C1 represents selecting 1 blue ball out of 2 and 1 green ball out of 3 (or 1 red ball out of 2 and 1 green ball out of 3)
- 2C2 * 5C0 represents selecting 2 blue balls out of 2 and 0 green balls out of 3 (or 2 red balls out of 2 and 0 green balls out of 3)
Number of ways = (1 * 10) + (2 * 5) + (1 * 1) = 21
Therefore, the probability of drawing 2 balls such that none of them is blue = (Number of ways to draw 2 balls such that none of them is blue) / (Total ways) = 21/21 = 1
But, we need to find the probability that none of the balls drawn is blue. So, we subtract the probability of drawing 2 blue balls from 1:
Probability that none of the balls drawn is blue = 1 - (Probability of drawing 2 blue balls) = 1 - (Number of ways to draw 2 blue balls / Total ways)
Number of ways to draw 2 blue balls = 2C2 * 5C0 = 1
Probability of drawing 2 blue balls = 1/21
Therefore, Probability that none of the balls drawn is blue = 1 - (1/21) = 20/21
Hence, option A (10/21) is incorrect and the correct answer is option B (11/21).
In a class 40 % students read Mathematics, 25 % Biology and 15 % both Mathematics and Biology. One student is select at random.The probability that he reads Biology if he reads Mathematics- a)7/8
- b)1/8
- c)3/8
- d)none
Correct answer is option 'C'. Can you explain this answer?
In a class 40 % students read Mathematics, 25 % Biology and 15 % both Mathematics and Biology. One student is select at random.The probability that he reads Biology if he reads Mathematics
a)
7/8
b)
1/8
c)
3/8
d)
none

|
Aditya Das answered |
Solution:
Given,
percentage of students who read Mathematics = 40%
percentage of students who read Biology = 25%
percentage of students who read both Mathematics and Biology = 15%
Let,
M = event that a student reads Mathematics
B = event that a student reads Biology
To find: Probability of reading Biology given that the student reads Mathematics i.e. P(B|M)
We know that,
P(B ∪ M) = P(B) + P(M) - P(B ∩ M) (where ∪ represents union and ∩ represents intersection)
Also,
P(B ∪ M) = 100% (as all students either read Mathematics or Biology or both)
Therefore,
P(B) + P(M) - P(B ∩ M) = 100%
25% + 40% - 15% = 50%
Now, we can use the formula of conditional probability to find P(B|M):
P(B|M) = P(B ∩ M) / P(M)
= 15% / 40%
= 3/8
Hence, the correct option is (c) 3/8.
Given,
percentage of students who read Mathematics = 40%
percentage of students who read Biology = 25%
percentage of students who read both Mathematics and Biology = 15%
Let,
M = event that a student reads Mathematics
B = event that a student reads Biology
To find: Probability of reading Biology given that the student reads Mathematics i.e. P(B|M)
We know that,
P(B ∪ M) = P(B) + P(M) - P(B ∩ M) (where ∪ represents union and ∩ represents intersection)
Also,
P(B ∪ M) = 100% (as all students either read Mathematics or Biology or both)
Therefore,
P(B) + P(M) - P(B ∩ M) = 100%
25% + 40% - 15% = 50%
Now, we can use the formula of conditional probability to find P(B|M):
P(B|M) = P(B ∩ M) / P(M)
= 15% / 40%
= 3/8
Hence, the correct option is (c) 3/8.
Probability of getting a head when two unbiased coins are tossed simultaneously is
- a)0.25
- b)0.5
- c)0.20
- d)0.75
Correct answer is option 'B'. Can you explain this answer?
Probability of getting a head when two unbiased coins are tossed simultaneously is
a)
0.25
b)
0.5
c)
0.20
d)
0.75

|
Srsps answered |
Favourable number of outcomes, getting one head ={HT, TH}
Total number of outcomes ={HH, HT, TH, TT}
Probability =2/4=1/2
Total number of outcomes ={HH, HT, TH, TT}
Probability =2/4=1/2
Out of the following values, which one is not possible in probability?- a)P(x) = 1
- b)∑ x P(x) = 3
- c)P(x) = 0.5
- d)P(x) = – 0.5
Correct answer is option 'D'. Can you explain this answer?
Out of the following values, which one is not possible in probability?
a)
P(x) = 1
b)
∑ x P(x) = 3
c)
P(x) = 0.5
d)
P(x) = – 0.5

|
Freedom Institute answered |
In probability P(x) is always greater than or equal to zero.
Two unbiased dice are thrown. The Expected value of the sum of numbers on the upper side is;- a)3.5
- b)7
- c)12
- d)6
Correct answer is option 'B'. Can you explain this answer?
Two unbiased dice are thrown. The Expected value of the sum of numbers on the upper side is;
a)
3.5
b)
7
c)
12
d)
6

|
Anuj Roy answered |
Solution:
When two dice are thrown, the possible outcomes can be represented by a sample space of 36 outcomes.
Let A be the event that the sum of the numbers on the upper side of the dice is k, where k = 2, 3, ..., 12.
Then, the probability of A is given by:
P(A) = number of outcomes in A / total number of outcomes
The number of outcomes in A can be determined by counting the number of ways that k can be obtained as the sum of two numbers on the dice. For example, if k = 7, there are six ways to obtain this sum:
1 + 6, 2 + 5, 3 + 4, 4 + 3, 5 + 2, 6 + 1
Therefore, the number of outcomes in A is:
number of outcomes in A = 6 if k = 7
number of outcomes in A = 5 if k = 6 or 8
number of outcomes in A = 4 if k = 5 or 9
number of outcomes in A = 3 if k = 4 or 10
number of outcomes in A = 2 if k = 3 or 11
number of outcomes in A = 1 if k = 2 or 12
The total number of outcomes is 36, so the probabilities of the events A are:
P(A=2) = 1/36
P(A=3) = 2/36
P(A=4) = 3/36
P(A=5) = 4/36
P(A=6) = 5/36
P(A=7) = 6/36
P(A=8) = 5/36
P(A=9) = 4/36
P(A=10) = 3/36
P(A=11) = 2/36
P(A=12) = 1/36
The expected value of the sum of the numbers on the upper side of the dice is given by:
E(X) = Σk P(X=k)
where k is the sum of the numbers on the upper side of the dice.
Using the probabilities calculated above, we can find that:
E(X) = 2×1/36 + 3×2/36 + 4×3/36 + 5×4/36 + 6×5/36 + 7×6/36 + 8×5/36 + 9×4/36 + 10×3/36 + 11×2/36 + 12×1/36
Simplifying this expression, we get:
E(X) = (2+3+4+5+6+7+8+9+10+11+12)/2
E(X) = 7
Therefore, the expected value of the sum of the numbers on the upper side of the dice is 7.
Hence, option B is the correct answer.
When two dice are thrown, the possible outcomes can be represented by a sample space of 36 outcomes.
Let A be the event that the sum of the numbers on the upper side of the dice is k, where k = 2, 3, ..., 12.
Then, the probability of A is given by:
P(A) = number of outcomes in A / total number of outcomes
The number of outcomes in A can be determined by counting the number of ways that k can be obtained as the sum of two numbers on the dice. For example, if k = 7, there are six ways to obtain this sum:
1 + 6, 2 + 5, 3 + 4, 4 + 3, 5 + 2, 6 + 1
Therefore, the number of outcomes in A is:
number of outcomes in A = 6 if k = 7
number of outcomes in A = 5 if k = 6 or 8
number of outcomes in A = 4 if k = 5 or 9
number of outcomes in A = 3 if k = 4 or 10
number of outcomes in A = 2 if k = 3 or 11
number of outcomes in A = 1 if k = 2 or 12
The total number of outcomes is 36, so the probabilities of the events A are:
P(A=2) = 1/36
P(A=3) = 2/36
P(A=4) = 3/36
P(A=5) = 4/36
P(A=6) = 5/36
P(A=7) = 6/36
P(A=8) = 5/36
P(A=9) = 4/36
P(A=10) = 3/36
P(A=11) = 2/36
P(A=12) = 1/36
The expected value of the sum of the numbers on the upper side of the dice is given by:
E(X) = Σk P(X=k)
where k is the sum of the numbers on the upper side of the dice.
Using the probabilities calculated above, we can find that:
E(X) = 2×1/36 + 3×2/36 + 4×3/36 + 5×4/36 + 6×5/36 + 7×6/36 + 8×5/36 + 9×4/36 + 10×3/36 + 11×2/36 + 12×1/36
Simplifying this expression, we get:
E(X) = (2+3+4+5+6+7+8+9+10+11+12)/2
E(X) = 7
Therefore, the expected value of the sum of the numbers on the upper side of the dice is 7.
Hence, option B is the correct answer.
The probability of a cricket term winning match at Kanpur is 2/5 and hosing match at Delhi is 1/7 what is the Probability of the term winning atleast one match?- a)3/35
- b)32/35
- c)18/35
- d)17/35
Correct answer is option 'B'. Can you explain this answer?
The probability of a cricket term winning match at Kanpur is 2/5 and hosing match at Delhi is 1/7 what is the Probability of the term winning atleast one match?
a)
3/35
b)
32/35
c)
18/35
d)
17/35

|
Freedom Institute answered |
B is correct.
Step-by-step explanation:
Probability( winning a match at Kanpur),P(WK) 
Probability( losing a match at Kanpur),P(LK)
Probability( losing a match at Delhi), P(LD)
Probability( winning a match at Delhi),P(WD)
The probability of the team winning at least one match,
P( team winning at least one match ) =1 - P(Losing both math)
Probability( losing a match at Kanpur),P(LK)
Probability( losing a match at Delhi), P(LD)
Probability( winning a match at Delhi),P(WD)
The probability of the team winning at least one match,
P( team winning at least one match ) =1 - P(Losing both math)
Hence, the probability of the team winning at least one match is 
A bag contains 12 balls which are numbered from 1 to 12. If a ball is selected at random, what is the probability that the number of the ball will be a multiple of 5 or 6 ?- a)0.30
- b)0.25
- c)0.20
- d)1/3
Correct answer is option 'D'. Can you explain this answer?
A bag contains 12 balls which are numbered from 1 to 12. If a ball is selected at random, what is the probability that the number of the ball will be a multiple of 5 or 6 ?
a)
0.30
b)
0.25
c)
0.20
d)
1/3

|
Meera Basak answered |
Solution:
Multiples of 5: 5, 10
Multiples of 6: 6, 12
The numbers which are multiple of 5 or 6 are: 5, 6, 10, 12
Total number of balls = 12
Therefore, the required probability is:
P(multiple of 5 or 6) = (number of favorable outcomes)/(total number of outcomes)
P(multiple of 5 or 6) = 4/12
P(multiple of 5 or 6) = 1/3
Therefore, the correct option is (d) 1/3.
Multiples of 5: 5, 10
Multiples of 6: 6, 12
The numbers which are multiple of 5 or 6 are: 5, 6, 10, 12
Total number of balls = 12
Therefore, the required probability is:
P(multiple of 5 or 6) = (number of favorable outcomes)/(total number of outcomes)
P(multiple of 5 or 6) = 4/12
P(multiple of 5 or 6) = 1/3
Therefore, the correct option is (d) 1/3.
For two events A and B, P(A ∪ B) = P(A) + P(A) only when- a)A and B are equally likely events
- b)A and B are exhaustive events
- c)A and B are mutually independent
- d)A and B are mutually exclusive
Correct answer is option 'D'. Can you explain this answer?
For two events A and B, P(A ∪ B) = P(A) + P(A) only when
a)
A and B are equally likely events
b)
A and B are exhaustive events
c)
A and B are mutually independent
d)
A and B are mutually exclusive

|
Srsps answered |
Definition: Two events are mutually exclusive (or disjoint) if they cannot occur at the same time. In other words, the occurrence of one event excludes the possibility of the other event occurring.
Hence, the intersection of both the events must be zero.
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
and as the intersection is 0 in mutually exclusive events
P(A ∪ B) = P(A) + P(B)
Hence, the intersection of both the events must be zero.
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
and as the intersection is 0 in mutually exclusive events
P(A ∪ B) = P(A) + P(B)
The odds against A solving a certain problem are 4 to 3 and the odds in favour of B solving the same problem are 7 to 5. What is the probability that the problem will be solved if they both try?- a)15/21
- b)16/21
- c)17/21
- d)13/21
Correct answer is option 'B'. Can you explain this answer?
The odds against A solving a certain problem are 4 to 3 and the odds in favour of B solving the same problem are 7 to 5. What is the probability that the problem will be solved if they both try?
a)
15/21
b)
16/21
c)
17/21
d)
13/21

|
Gowri Chakraborty answered |
Odds against Ram are 4:3 so probability that he will solve the problem is 3/7.
Odds in favor of Krishna are 7:5 so probability that he will solve it is 7/12
It will be solved means that either Ram or Krishna or both will be able to solve it.
P(A or B) = P(A) + P(B) - P(A and B) = 3/7 + 7/12 - (3/7)*(7/12) = 16/21
Values of a random variable are- a)always positive numbers.
- b)always positive real numbers.
- c)real numbers.
- d)natural numbers
Correct answer is option 'C'. Can you explain this answer?
Values of a random variable are
a)
always positive numbers.
b)
always positive real numbers.
c)
real numbers.
d)
natural numbers

|
Shanaya Dasgupta answered |
Explanation:
Random variable is a variable whose value is subject to variations due to chance, i.e., it is a variable whose value is determined by the outcome of a random event. The values of a random variable can be classified into four categories:
a) Always positive numbers: This is not always true for all random variables. For example, the outcome of a coin toss can be either heads or tails, which are not positive numbers.
b) Always positive real numbers: This is also not always true for all random variables. For example, the outcome of rolling a six-sided die can be any integer from 1 to 6, which are not necessarily positive real numbers.
c) Real numbers: This is the correct answer. The values of a random variable can be any real number. For example, the height of a person, the weight of an object, or the temperature in a room can all be random variables that take on real number values.
d) Natural numbers: This is not always true for all random variables. For example, the outcome of rolling a six-sided die can be any integer from 1 to 6, which are natural numbers, but the outcome of flipping a coin cannot be a natural number.
In conclusion, the values of a random variable can be any real number, which is option 'C'.
Random variable is a variable whose value is subject to variations due to chance, i.e., it is a variable whose value is determined by the outcome of a random event. The values of a random variable can be classified into four categories:
a) Always positive numbers: This is not always true for all random variables. For example, the outcome of a coin toss can be either heads or tails, which are not positive numbers.
b) Always positive real numbers: This is also not always true for all random variables. For example, the outcome of rolling a six-sided die can be any integer from 1 to 6, which are not necessarily positive real numbers.
c) Real numbers: This is the correct answer. The values of a random variable can be any real number. For example, the height of a person, the weight of an object, or the temperature in a room can all be random variables that take on real number values.
d) Natural numbers: This is not always true for all random variables. For example, the outcome of rolling a six-sided die can be any integer from 1 to 6, which are natural numbers, but the outcome of flipping a coin cannot be a natural number.
In conclusion, the values of a random variable can be any real number, which is option 'C'.
If all the values taken by a random variable are equal then- a)its expected value is zero
- b)its standard deviation is zero
- c)its standard deviation is positive
- d)its standard deviation is a real number
Correct answer is option 'B'. Can you explain this answer?
If all the values taken by a random variable are equal then
a)
its expected value is zero
b)
its standard deviation is zero
c)
its standard deviation is positive
d)
its standard deviation is a real number

|
Pranav Gupta answered |
Explanation:
A random variable is a variable whose possible values are numerical outcomes of a random phenomenon. If all the values taken by a random variable are equal, then the variable is a constant random variable.
a) its expected value is zero: Since all the values are equal, the expected value will be the same as those values. Therefore, the expected value will be the constant value itself, which is not zero in general.
b) its standard deviation is zero: The standard deviation of a random variable is a measure of the spread of its values. Since all the values are equal, there is no spread, and the standard deviation is zero.
c) its standard deviation is positive: This option is incorrect since the standard deviation cannot be positive if all the values are equal.
d) its standard deviation is a real number: This option is incorrect since every real number is a real number, and it does not provide any useful information.
Therefore, the correct answer is option B.
A random variable is a variable whose possible values are numerical outcomes of a random phenomenon. If all the values taken by a random variable are equal, then the variable is a constant random variable.
a) its expected value is zero: Since all the values are equal, the expected value will be the same as those values. Therefore, the expected value will be the constant value itself, which is not zero in general.
b) its standard deviation is zero: The standard deviation of a random variable is a measure of the spread of its values. Since all the values are equal, there is no spread, and the standard deviation is zero.
c) its standard deviation is positive: This option is incorrect since the standard deviation cannot be positive if all the values are equal.
d) its standard deviation is a real number: This option is incorrect since every real number is a real number, and it does not provide any useful information.
Therefore, the correct answer is option B.
The odds that a book will be favourable received by 3 independent received by 3 independent reviewers are 5 to 2, 4 to 3 and 4 to 4 respectively. What is the probability that out of 3 reviewers a majority will be favourable?- a)209/343
- b)209/434
- c)209/443
- d)209/350
Correct answer is option 'A'. Can you explain this answer?
The odds that a book will be favourable received by 3 independent received by 3 independent reviewers are 5 to 2, 4 to 3 and 4 to 4 respectively. What is the probability that out of 3 reviewers a majority will be favourable?
a)
209/343
b)
209/434
c)
209/443
d)
209/350

|
Gopal Sen answered |
To find the probability that a majority of the 3 reviewers will give a favorable review, we need to consider the different combinations of favorable and unfavorable reviews that can occur. Let's analyze each scenario:
1. All 3 reviewers give a favorable review:
The probability of this scenario is (5/7) * (4/7) * (4/8) = 80/343.
2. Two reviewers give a favorable review and one gives an unfavorable review:
We need to consider all possible combinations of 2 favorable and 1 unfavorable review. There are 3 ways this can happen:
- Favorable, Favorable, Unfavorable: (5/7) * (4/7) * (4/8) = 80/343
- Favorable, Unfavorable, Favorable: (5/7) * (3/7) * (4/8) = 60/343
- Unfavorable, Favorable, Favorable: (2/7) * (4/7) * (4/8) = 32/343
The total probability for this scenario is 80/343 + 60/343 + 32/343 = 172/343.
3. One reviewer gives a favorable review and two give an unfavorable review:
Again, we need to consider all possible combinations. There are 3 ways this can happen:
- Favorable, Unfavorable, Unfavorable: (5/7) * (3/7) * (4/8) = 60/343
- Unfavorable, Favorable, Unfavorable: (2/7) * (4/7) * (4/8) = 32/343
- Unfavorable, Unfavorable, Favorable: (2/7) * (3/7) * (4/8) = 24/343
The total probability for this scenario is 60/343 + 32/343 + 24/343 = 116/343.
4. All 3 reviewers give an unfavorable review:
The probability of this scenario is (2/7) * (3/7) * (4/8) = 24/343.
Adding up the probabilities for all scenarios where a majority of the reviewers give a favorable review, we get:
80/343 + 172/343 = 252/343.
Therefore, the probability that out of 3 reviewers a majority will be favorable is 252/343, which is approximately 0.734 or 73.4%. This corresponds to answer choice A: 209/343.
1. All 3 reviewers give a favorable review:
The probability of this scenario is (5/7) * (4/7) * (4/8) = 80/343.
2. Two reviewers give a favorable review and one gives an unfavorable review:
We need to consider all possible combinations of 2 favorable and 1 unfavorable review. There are 3 ways this can happen:
- Favorable, Favorable, Unfavorable: (5/7) * (4/7) * (4/8) = 80/343
- Favorable, Unfavorable, Favorable: (5/7) * (3/7) * (4/8) = 60/343
- Unfavorable, Favorable, Favorable: (2/7) * (4/7) * (4/8) = 32/343
The total probability for this scenario is 80/343 + 60/343 + 32/343 = 172/343.
3. One reviewer gives a favorable review and two give an unfavorable review:
Again, we need to consider all possible combinations. There are 3 ways this can happen:
- Favorable, Unfavorable, Unfavorable: (5/7) * (3/7) * (4/8) = 60/343
- Unfavorable, Favorable, Unfavorable: (2/7) * (4/7) * (4/8) = 32/343
- Unfavorable, Unfavorable, Favorable: (2/7) * (3/7) * (4/8) = 24/343
The total probability for this scenario is 60/343 + 32/343 + 24/343 = 116/343.
4. All 3 reviewers give an unfavorable review:
The probability of this scenario is (2/7) * (3/7) * (4/8) = 24/343.
Adding up the probabilities for all scenarios where a majority of the reviewers give a favorable review, we get:
80/343 + 172/343 = 252/343.
Therefore, the probability that out of 3 reviewers a majority will be favorable is 252/343, which is approximately 0.734 or 73.4%. This corresponds to answer choice A: 209/343.
There are three boxes with the following composition:Box I: 5 Red + 7 White + 6 Blue ballsBox II: 4 Red + 8 White + 6 Blue ballsBox III: 3 Red + 4 White + 2 Blue ballsIf one ball is drawn at random, then what is the probability that they would be of same colour?- a)89/729
- b)97/729
- c)82/729
- d)23/32
Correct answer is option 'A'. Can you explain this answer?
There are three boxes with the following composition:
Box I: 5 Red + 7 White + 6 Blue balls
Box II: 4 Red + 8 White + 6 Blue balls
Box III: 3 Red + 4 White + 2 Blue balls
If one ball is drawn at random, then what is the probability that they would be of same colour?
a)
89/729
b)
97/729
c)
82/729
d)
23/32

|
Ruchi Mishra answered |
Solution:
To find the probability that the ball drawn is of the same color, we need to find the probability of drawing a red ball or a white ball or a blue ball from any of the three boxes.
Probability of drawing a red ball:
Total red balls = 5 + 4 + 3 = 12
Total number of balls = 5 + 7 + 6 + 4 + 8 + 6 + 3 + 4 + 2 = 45
Therefore, the probability of drawing a red ball = 12/45 = 4/15
Probability of drawing a white ball:
Total white balls = 7 + 8 + 4 = 19
Total number of balls = 5 + 7 + 6 + 4 + 8 + 6 + 3 + 4 + 2 = 45
Therefore, the probability of drawing a white ball = 19/45
Probability of drawing a blue ball:
Total blue balls = 6 + 6 + 2 = 14
Total number of balls = 5 + 7 + 6 + 4 + 8 + 6 + 3 + 4 + 2 = 45
Therefore, the probability of drawing a blue ball = 14/45
Now, we need to find the probability of drawing a ball of the same color, which can be calculated as follows:
Probability of drawing a ball of the same color = Probability of drawing a red ball + Probability of drawing a white ball + Probability of drawing a blue ball
Probability of drawing a ball of the same color = 4/15 + 19/45 + 14/45
Probability of drawing a ball of the same color = 89/225
Simplifying the fraction, we get:
Probability of drawing a ball of the same color = 89/729
Therefore, the correct option is (a) 89/729.
To find the probability that the ball drawn is of the same color, we need to find the probability of drawing a red ball or a white ball or a blue ball from any of the three boxes.
Probability of drawing a red ball:
Total red balls = 5 + 4 + 3 = 12
Total number of balls = 5 + 7 + 6 + 4 + 8 + 6 + 3 + 4 + 2 = 45
Therefore, the probability of drawing a red ball = 12/45 = 4/15
Probability of drawing a white ball:
Total white balls = 7 + 8 + 4 = 19
Total number of balls = 5 + 7 + 6 + 4 + 8 + 6 + 3 + 4 + 2 = 45
Therefore, the probability of drawing a white ball = 19/45
Probability of drawing a blue ball:
Total blue balls = 6 + 6 + 2 = 14
Total number of balls = 5 + 7 + 6 + 4 + 8 + 6 + 3 + 4 + 2 = 45
Therefore, the probability of drawing a blue ball = 14/45
Now, we need to find the probability of drawing a ball of the same color, which can be calculated as follows:
Probability of drawing a ball of the same color = Probability of drawing a red ball + Probability of drawing a white ball + Probability of drawing a blue ball
Probability of drawing a ball of the same color = 4/15 + 19/45 + 14/45
Probability of drawing a ball of the same color = 89/225
Simplifying the fraction, we get:
Probability of drawing a ball of the same color = 89/729
Therefore, the correct option is (a) 89/729.
If A denotes that a student reads in a school and B denotes that he plays cricket, then- a)P(A ∩ B) = 1
- b)P(A ∪ B) = 1
- c)P(A ∩ B) = 0
- d)P(A) = P(B)
Correct answer is option 'C'. Can you explain this answer?
If A denotes that a student reads in a school and B denotes that he plays cricket, then
a)
P(A ∩ B) = 1
b)
P(A ∪ B) = 1
c)
P(A ∩ B) = 0
d)
P(A) = P(B)

|
Hrishikesh Mukherjee answered |
Probability of a student reading in school and playing cricket
To solve this problem, we need to understand the definitions of probability and set theory.
Probability: Probability is the measure of the likelihood of an event occurring.
Set theory: Set theory is the branch of mathematics that deals with the study of sets, which are collections of objects.
In this problem, we are given two events:
A: A student reads in a school
B: A student plays cricket
We need to find the probability of the event A and B occurring together.
Intersection of two events
The intersection of two events is the set of elements that belong to both events.
In set theory, the intersection of two sets A and B is denoted by A ∩ B.
For example, if A = {1, 2, 3} and B = {2, 3, 4}, then A ∩ B = {2, 3}.
Probability of intersection of two events
The probability of the intersection of two events A and B is denoted by P(A ∩ B).
P(A ∩ B) represents the probability that both A and B occur.
Formula:
P(A ∩ B) = P(A) * P(B|A)
where P(B|A) represents the probability of B occurring given that A has already occurred.
If A and B are independent events, then P(B|A) = P(B), and the formula reduces to:
P(A ∩ B) = P(A) * P(B)
Solution
In this problem, we are not given any information about the relationship between A and B.
Therefore, we cannot assume that they are independent events.
Since we do not have any information about the relationship between A and B, we cannot calculate the probability of their intersection.
Therefore, the correct answer is option C: P(A ∩ B) = 0.
To solve this problem, we need to understand the definitions of probability and set theory.
Probability: Probability is the measure of the likelihood of an event occurring.
Set theory: Set theory is the branch of mathematics that deals with the study of sets, which are collections of objects.
In this problem, we are given two events:
A: A student reads in a school
B: A student plays cricket
We need to find the probability of the event A and B occurring together.
Intersection of two events
The intersection of two events is the set of elements that belong to both events.
In set theory, the intersection of two sets A and B is denoted by A ∩ B.
For example, if A = {1, 2, 3} and B = {2, 3, 4}, then A ∩ B = {2, 3}.
Probability of intersection of two events
The probability of the intersection of two events A and B is denoted by P(A ∩ B).
P(A ∩ B) represents the probability that both A and B occur.
Formula:
P(A ∩ B) = P(A) * P(B|A)
where P(B|A) represents the probability of B occurring given that A has already occurred.
If A and B are independent events, then P(B|A) = P(B), and the formula reduces to:
P(A ∩ B) = P(A) * P(B)
Solution
In this problem, we are not given any information about the relationship between A and B.
Therefore, we cannot assume that they are independent events.
Since we do not have any information about the relationship between A and B, we cannot calculate the probability of their intersection.
Therefore, the correct answer is option C: P(A ∩ B) = 0.
A and B are two events such that P(A)= 1/3, P(B) = ¼, P(A+B)= 1/2, than P(B/A) is equal to- a)¼
- b)1/3
- c)1/2
- d)none
Correct answer is option 'A'. Can you explain this answer?
A and B are two events such that P(A)= 1/3, P(B) = ¼, P(A+B)= 1/2, than P(B/A) is equal to
a)
¼
b)
1/3
c)
1/2
d)
none

|
Mihir Banerjee answered |
Given, P(A) = 1/3, P(B), P(A ∩ B) = 1/2
We know that the conditional probability of B given A is given by:
P(B/A) = P(A ∩ B) / P(A)
Substituting the given values, we get:
P(B/A) = (1/2) / (1/3) = (1/2) x (3/1) = 3/2
But the probability of an event cannot be greater than 1. Therefore, option A is incorrect.
So, the correct answer is option D (none).
Explanation: It is not possible to calculate P(B/A) with the given information because we do not know the value of P(B ∩ A). We only know the value of P(A ∩ B) and not P(B ∩ A). Hence, none of the options given are correct.
We know that the conditional probability of B given A is given by:
P(B/A) = P(A ∩ B) / P(A)
Substituting the given values, we get:
P(B/A) = (1/2) / (1/3) = (1/2) x (3/1) = 3/2
But the probability of an event cannot be greater than 1. Therefore, option A is incorrect.
So, the correct answer is option D (none).
Explanation: It is not possible to calculate P(B/A) with the given information because we do not know the value of P(B ∩ A). We only know the value of P(A ∩ B) and not P(B ∩ A). Hence, none of the options given are correct.
A company employed 7 CA's, 6 MBA's and 3 Engineer's. In how many ways the company can form a committe, if the committee has two members of each type.- a)900
- b)1,000
- c)787
- d)945
Correct answer is option 'D'. Can you explain this answer?
A company employed 7 CA's, 6 MBA's and 3 Engineer's. In how many ways the company can form a committe, if the committee has two members of each type.
a)
900
b)
1,000
c)
787
d)
945

|
Jatin Mehta answered |
Given:
- 7 CAs
- 6 MBAs
- 3 Engineers
- Need to form a committee with 2 members of each type
To find: In how many ways can the committee be formed?
Solution:
We can choose 2 CAs out of 7 in 7C2 ways, i.e., 21 ways.
Similarly, we can choose 2 MBAs out of 6 in 6C2 ways, i.e., 15 ways.
And, we can choose 2 Engineers out of 3 in 3C2 ways, i.e., 3 ways.
Total number of ways to form the committee = 21 x 15 x 3 = 945
Therefore, the correct option is (d) 945.
- 7 CAs
- 6 MBAs
- 3 Engineers
- Need to form a committee with 2 members of each type
To find: In how many ways can the committee be formed?
Solution:
We can choose 2 CAs out of 7 in 7C2 ways, i.e., 21 ways.
Similarly, we can choose 2 MBAs out of 6 in 6C2 ways, i.e., 15 ways.
And, we can choose 2 Engineers out of 3 in 3C2 ways, i.e., 3 ways.
Total number of ways to form the committee = 21 x 15 x 3 = 945
Therefore, the correct option is (d) 945.
When unbiased coins are tossed. The probability of getting both heads or both tails is- a)½
- b)¾
- c)¼
- d)none
Correct answer is option 'A'. Can you explain this answer?
When unbiased coins are tossed. The probability of getting both heads or both tails is
a)
½
b)
¾
c)
¼
d)
none

|
Prasenjit Kapoor answered |
Probability of Getting Both Heads or Both Tails
Explanation:
When two unbiased coins are tossed, there are four possible outcomes:
- Head, Head
- Head, Tail
- Tail, Head
- Tail, Tail
Out of these four outcomes, only two outcomes have both heads or both tails:
- Head, Head
- Tail, Tail
Therefore, the probability of getting both heads or both tails is:
P(both heads or both tails) = P(Head, Head) + P(Tail, Tail)
Since the coins are unbiased, the probability of getting a head or a tail on a single coin toss is 1/2. Therefore, the probability of getting both heads or both tails is:
P(both heads or both tails) = P(Head, Head) + P(Tail, Tail) = 1/2 × 1/2 + 1/2 × 1/2 = 1/4 + 1/4 = 1/2
Hence, the correct answer is option 'A' - 1/2.
Explanation:
When two unbiased coins are tossed, there are four possible outcomes:
- Head, Head
- Head, Tail
- Tail, Head
- Tail, Tail
Out of these four outcomes, only two outcomes have both heads or both tails:
- Head, Head
- Tail, Tail
Therefore, the probability of getting both heads or both tails is:
P(both heads or both tails) = P(Head, Head) + P(Tail, Tail)
Since the coins are unbiased, the probability of getting a head or a tail on a single coin toss is 1/2. Therefore, the probability of getting both heads or both tails is:
P(both heads or both tails) = P(Head, Head) + P(Tail, Tail) = 1/2 × 1/2 + 1/2 × 1/2 = 1/4 + 1/4 = 1/2
Hence, the correct answer is option 'A' - 1/2.
Arun & Tarun appear for an interview for two vacancies. The probability of Arun's selection is 1/3 and that of Tarun's selection is 1/5. Find the probability that only one of them will be selected.
- a)2/5
- b)4/5
- c)6/5
- d)8/5
Correct answer is option 'A'. Can you explain this answer?
Arun & Tarun appear for an interview for two vacancies. The probability of Arun's selection is 1/3 and that of Tarun's selection is 1/5. Find the probability that only one of them will be selected.
a)
2/5
b)
4/5
c)
6/5
d)
8/5

|
Pallabi Khanna answered |
Can you please provide more context or information about who Arun is?
Two coins are tossed simultaneously. Find the probability of getting exactly one head.- a)3/4
- b)2/3
- c)1/4
- d)1/2
Correct answer is option 'D'. Can you explain this answer?
Two coins are tossed simultaneously. Find the probability of getting exactly one head.
a)
3/4
b)
2/3
c)
1/4
d)
1/2

|
Kamaljeet Kaur answered |
Total outcomes =(HH, HT, TH, TT) = 4
Favourable outcomes = (HT, TH) =2
Probability = 2/4=1/2
Favourable outcomes = (HT, TH) =2
Probability = 2/4=1/2
Let P be a probability function on S = {X1 , X2 , X3} if P(X1)= ¼ and P(X3) = 1/3 then P (X2) is equal to- a)5/12
- b)7/12
- c)3/4
- d)none
Correct answer is option 'A'. Can you explain this answer?
Let P be a probability function on S = {X1 , X2 , X3} if P(X1)= ¼ and P(X3) = 1/3 then P (X2) is equal to
a)
5/12
b)
7/12
c)
3/4
d)
none

|
Muskaan Tiwari answered |
Given information:
- S = {X1, X2, X3}
- P(X1) =
- P(X3) = 1/3
To find:
- P(X2)
Solution:
- As P is a probability function, the sum of probabilities of all elements in the sample space S must be 1.
- Therefore, P(X1) + P(X2) + P(X3) = 1
- Using the given values, we get:
+ + 1/3 = 1
+ = 2/3
- Therefore, P(X2) =
Answer:
- P(X2) =
- Option A, 5/12, is the correct answer.
- S = {X1, X2, X3}
- P(X1) =
- P(X3) = 1/3
To find:
- P(X2)
Solution:
- As P is a probability function, the sum of probabilities of all elements in the sample space S must be 1.
- Therefore, P(X1) + P(X2) + P(X3) = 1
- Using the given values, we get:
+ + 1/3 = 1
+ = 2/3
- Therefore, P(X2) =
Answer:
- P(X2) =
- Option A, 5/12, is the correct answer.
(Direction 1 - 40) Write down the correct answers. Each question carRies 1 mark.Q. Initially, probability was a branch of- a)Physics
- b)Statistics
- c)Mathematics
- d)Economics.
Correct answer is option 'C'. Can you explain this answer?
(Direction 1 - 40) Write down the correct answers. Each question carRies 1 mark.
Q. Initially, probability was a branch of
a)
Physics
b)
Statistics
c)
Mathematics
d)
Economics.

|
Freedom Institute answered |
Probability theory is the branch of Mathematics concerned with analysis of random phenomena.
Two unbiased coins are tossed. The probability of obtaining one head and one tail is
- a)¼
- b)2/4
- c)¾
- d)none
Correct answer is option 'B'. Can you explain this answer?
Two unbiased coins are tossed. The probability of obtaining one head and one tail is
a)
¼
b)
2/4
c)
¾
d)
none

|
Jyoti Nair answered |
Explanation:
When two unbiased coins are tossed, there are four possible outcomes: HH, HT, TH, and TT. Out of these, only two outcomes have one head and one tail: HT and TH.
Therefore, the probability of obtaining one head and one tail is the ratio of the number of favorable outcomes to the total number of possible outcomes.
Solution:
Number of favorable outcomes: 2 (HT and TH)
Total number of possible outcomes: 4 (HH, HT, TH, and TT)
Probability of obtaining one head and one tail:
= Number of favorable outcomes / Total number of possible outcomes
= 2 / 4
= 1/2
Hence, the correct answer is option B: 2/4.
When two unbiased coins are tossed, there are four possible outcomes: HH, HT, TH, and TT. Out of these, only two outcomes have one head and one tail: HT and TH.
Therefore, the probability of obtaining one head and one tail is the ratio of the number of favorable outcomes to the total number of possible outcomes.
Solution:
Number of favorable outcomes: 2 (HT and TH)
Total number of possible outcomes: 4 (HH, HT, TH, and TT)
Probability of obtaining one head and one tail:
= Number of favorable outcomes / Total number of possible outcomes
= 2 / 4
= 1/2
Hence, the correct answer is option B: 2/4.
Two coins are tossed simultaneously. What is the probability that the second coin would show a tail given that the first coin has shown a head?
- a)0.25
- b)0.50
- c)0.75
- d)0.125
Correct answer is option 'A'. Can you explain this answer?
Two coins are tossed simultaneously. What is the probability that the second coin would show a tail given that the first coin has shown a head?
a)
0.25
b)
0.50
c)
0.75
d)
0.125

|
Freedom Institute answered |
The sample space for two coins is {HH,HT,TH,TT}, n(S)=4
Favourable outcomes for the first coin head and second coin showing tail are HT, n(E)=1
Hence, the probability that the second coin would show a tail given that the first coin has shown a head is n(E)/n(S) = 1/4 = 0.25
The Theorem of Compound Probability states that for any two events A and B.- a)P(A ∩ B) = P(A) × P(B/A)
- b)P(A ∪ B) = P(A) × P(B/A)
- c)P(A ∪ B) = P(B) + P(B) – P(A ∩ B)
- d)P(A ∩ B) = P(A) × P(B)
Correct answer is option 'C'. Can you explain this answer?
The Theorem of Compound Probability states that for any two events A and B.
a)
P(A ∩ B) = P(A) × P(B/A)
b)
P(A ∪ B) = P(A) × P(B/A)
c)
P(A ∪ B) = P(B) + P(B) – P(A ∩ B)
d)
P(A ∩ B) = P(A) × P(B)

|
Sai Joshi answered |
Correct Answer :- C
Explanation : If two events, A and B, are mutually exclusive, then the probability that either A or B occurs is the sum of their probabilities.
For mutually inclusive events, P (A or B) = P(A) + P(B) - P(A and B).
Two broad divisions of probability are- a)Subjective probability and objective probability
- b)Deductive probability and non–deductive probability
- c)Statistical probability and Mathematical probability
- d)None of these.
Correct answer is option 'A'. Can you explain this answer?
Two broad divisions of probability are
a)
Subjective probability and objective probability
b)
Deductive probability and non–deductive probability
c)
Statistical probability and Mathematical probability
d)
None of these.

|
Gaurav Chatterjee answered |
Divisions of Probability
Probability refers to the measure of the likelihood or chance of an event occurring. It is categorized into two broad divisions:
1. Subjective Probability
Subjective probability refers to the measure of probability based on personal judgement or experience. It is based on personal opinions and cannot be measured objectively. It relies on the individual's beliefs, biases, and intuition. It is often used in situations where there is a lack of data or information.
2. Objective Probability
Objective probability refers to the measure of probability based on data and evidence. It is based on empirical evidence and can be measured objectively. It relies on mathematical computations and statistical analysis. It is often used in situations where there is a large amount of data or information available.
Conclusion
In conclusion, probability is divided into subjective and objective probability. Subjective probability is based on personal judgement and experience while objective probability is based on data and evidence.
Probability refers to the measure of the likelihood or chance of an event occurring. It is categorized into two broad divisions:
1. Subjective Probability
Subjective probability refers to the measure of probability based on personal judgement or experience. It is based on personal opinions and cannot be measured objectively. It relies on the individual's beliefs, biases, and intuition. It is often used in situations where there is a lack of data or information.
2. Objective Probability
Objective probability refers to the measure of probability based on data and evidence. It is based on empirical evidence and can be measured objectively. It relies on mathematical computations and statistical analysis. It is often used in situations where there is a large amount of data or information available.
Conclusion
In conclusion, probability is divided into subjective and objective probability. Subjective probability is based on personal judgement and experience while objective probability is based on data and evidence.
For a group of students, 30 %, 40% and 50% failed in Physics , Chemistry and at least one of the two subjects respectively. If an examinee is selected at random, what is the probability that he passed in Physics if it is known that he failed in Chemistry?- a)1/2
- b)1/3
- c)1/4
- d)1/6
Correct answer is option 'D'. Can you explain this answer?
For a group of students, 30 %, 40% and 50% failed in Physics , Chemistry and at least one of the two subjects respectively. If an examinee is selected at random, what is the probability that he passed in Physics if it is known that he failed in Chemistry?
a)
1/2
b)
1/3
c)
1/4
d)
1/6

|
Simran Pillai answered |
Let the total number of students = 100
Number of students failed in physics = 30% of 100 =30
Number of students failed in chemistry = 40% of 100 =40
Number of students failed at least one of the two subjects = 50% of 100 =50
We need to calculate

Following are the wages of 8 workers in rupees:50, 62, 40, 70, 45, 56, 32, 45If one of the workers is selected at random, what is the probability that his wage would be lower than the average wage?- a)0.625
- b)0.500
- c)0.375
- d)0.450
Correct answer is option 'B'. Can you explain this answer?
Following are the wages of 8 workers in rupees:
50, 62, 40, 70, 45, 56, 32, 45
If one of the workers is selected at random, what is the probability that his wage would be lower than the average wage?
a)
0.625
b)
0.500
c)
0.375
d)
0.450

|
Vaishnavi Gupta answered |
Given:
Wages of 8 workers in rupees:50, 62, 40, 70, 45, 56, 32, 45
To find:
Probability that a worker's wage would be lower than the average wage.
Solution:
Step 1: Calculate the average wage
Average wage = (50+62+40+70+45+56+32+45)/8
Average wage = 47.5
Step 2: Find the number of workers whose wage is lower than the average wage
Number of workers whose wage is lower than the average wage = 3 (out of 8)
Step 3: Calculate the probability
Probability = Number of workers whose wage is lower than the average wage / Total number of workers
Probability = 3/8
Probability = 0.5
Therefore, the probability that a worker's wage would be lower than the average wage is 0.5 or 50%. Hence, option B is the correct answer.
Wages of 8 workers in rupees:50, 62, 40, 70, 45, 56, 32, 45
To find:
Probability that a worker's wage would be lower than the average wage.
Solution:
Step 1: Calculate the average wage
Average wage = (50+62+40+70+45+56+32+45)/8
Average wage = 47.5
Step 2: Find the number of workers whose wage is lower than the average wage
Number of workers whose wage is lower than the average wage = 3 (out of 8)
Step 3: Calculate the probability
Probability = Number of workers whose wage is lower than the average wage / Total number of workers
Probability = 3/8
Probability = 0.5
Therefore, the probability that a worker's wage would be lower than the average wage is 0.5 or 50%. Hence, option B is the correct answer.
(Direction 16 - 38) Write down the correct answers. Each question carries 2 marks.Q.Two balls are drawn from a bag containing 5 white and 7 black balls at random. What is the probability that they would be of different colours? - a)35/66
- b)30/66
- c)12/66
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
(Direction 16 - 38) Write down the correct answers. Each question carries 2 marks.
Q.Two balls are drawn from a bag containing 5 white and 7 black balls at random. What is the probability that they would be of different colours?
a)
35/66
b)
30/66
c)
12/66
d)
None of these

|
Deepika Nambiar answered |
Solution:
Given, a bag contains 5 white and 7 black balls.
We need to find the probability of drawing two balls of different colours.
Total number of ways to draw two balls out of 12 balls = 12C2 = (12 × 11) / (2 × 1) = 66
Number of ways to draw two balls of different colours = Number of ways to draw one white and one black ball + Number of ways to draw one black and one white ball
= (5C1 × 7C1) + (7C1 × 5C1)
= (5 × 7) + (7 × 5)
= 35 + 35
= 70
Therefore, the probability of drawing two balls of different colours = Number of ways to draw two balls of different colours / Total number of ways to draw two balls
= 70 / 66
= 35 / 33
Hence, the correct option is (a) 35/66.
Given, a bag contains 5 white and 7 black balls.
We need to find the probability of drawing two balls of different colours.
Total number of ways to draw two balls out of 12 balls = 12C2 = (12 × 11) / (2 × 1) = 66
Number of ways to draw two balls of different colours = Number of ways to draw one white and one black ball + Number of ways to draw one black and one white ball
= (5C1 × 7C1) + (7C1 × 5C1)
= (5 × 7) + (7 × 5)
= 35 + 35
= 70
Therefore, the probability of drawing two balls of different colours = Number of ways to draw two balls of different colours / Total number of ways to draw two balls
= 70 / 66
= 35 / 33
Hence, the correct option is (a) 35/66.
Find the expected value of the following probability distribution

1/20- a)20.5
- b)21.5
- c)22.5
- d)24.5
Correct answer is option 'B'. Can you explain this answer?
Find the expected value of the following probability distribution

1/20
1/20
a)
20.5
b)
21.5
c)
22.5
d)
24.5

|
Qudrat Chauhan answered |
Check that these probabilities sum to 1:
3/20 + 1/5 + 1/2 + 1/10 + 1/20 = 1
3/20 + 1/5 + 1/2 + 1/10 + 1/20 = 1
Calculate the expected value E(X)
E(X) = (-20)(3/20) + (-10)(1/5) + 30(1/2) + 75(1/10) + 80(1/20)
= -3 + -2 + 15 + 7.5 + 4
= -5 + 15 + 7.5 + 4
= 21.5
= -3 + -2 + 15 + 7.5 + 4
= -5 + 15 + 7.5 + 4
= 21.5
Hence, the expected value of X is 21.5.
Two unbiased coins are tossed. The probability of obtaining at least one head is- a)¼
- b)2/4
- c)¾
- d)none
Correct answer is option 'C'. Can you explain this answer?
Two unbiased coins are tossed. The probability of obtaining at least one head is
a)
¼
b)
2/4
c)
¾
d)
none

|
Pathan Mahenoor answered |
Total outcomes = (HH,HT,TT,TH) = 4
atleast one head means 1 head or more
p(HT,TH,HH) = 3/4
atleast one head means 1 head or more
p(HT,TH,HH) = 3/4
If p : q are the odds in favour of an event, then the probability of that event is- a)p/q
- b)p/p+q
- c)q/p+q
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If p : q are the odds in favour of an event, then the probability of that event is
a)
p/q
b)
p/p+q
c)
q/p+q
d)
none of these
|
|
Rajat Patel answered |
Explanation:
Total number of cases=p+q
Favourable cases=p
Probability of that event is=p/(p+q)
For any two events A1, A2 letP(A1) = 2/3,P(A2) = 3/8 and P(A1 ∩ A2) =1/4 then A1, A2 are: - a)Mutually exclusive but not independent events
- b) Mutually exclusive and independent events
- c)Independent but not mutually exclusive
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
For any two events A1, A2 letP(A1) = 2/3,P(A2) = 3/8 and P(A1 ∩ A2) =1/4 then A1, A2 are:
a)
Mutually exclusive but not independent events
b)
Mutually exclusive and independent events
c)
Independent but not mutually exclusive
d)
None of these

|
Siddharth Sen answered |
To use Bayes' theorem, we need to first find P(A1 and B) and P(A2 and B). We can use the formula:
P(A and B) = P(A) * P(B|A)
where P(B|A) is the probability of event B given that event A has occurred.
For A1 and B:
P(A1 and B) = P(B|A1) * P(A1)
P(B|A1) is given as 1/2, since if A1 has occurred, then only half of the remaining cards can be black.
P(A1) is given as 2/3.
So, P(A1 and B) = (1/2) * (2/3) = 1/3.
For A2 and B:
P(A2 and B) = P(B|A2) * P(A2)
P(B|A2) is given as 3/7, since if A2 has occurred, then 3 of the remaining 7 cards are black.
P(A2) is given as 3/8.
So, P(A2 and B) = (3/7) * (3/8) = 9/56.
Now we can apply Bayes' theorem:
P(A1|B) = P(A1 and B) / P(B)
P(A2|B) = P(A2 and B) / P(B)
where P(B) is the probability of event B occurring, which is the sum of the probabilities of A1 and B and A2 and B:
P(B) = P(A1 and B) + P(A2 and B) = 1/3 + 9/56 = 25/56.
So,
P(A1|B) = (1/3) / (25/56) = 56/225
P(A2|B) = (9/56) / (25/56) = 9/25
Therefore, the probability that the card drawn is from deck 1 given that it is a black card is 56/225, and the probability that it is from deck 2 given that it is a black card is 9/25.
P(A and B) = P(A) * P(B|A)
where P(B|A) is the probability of event B given that event A has occurred.
For A1 and B:
P(A1 and B) = P(B|A1) * P(A1)
P(B|A1) is given as 1/2, since if A1 has occurred, then only half of the remaining cards can be black.
P(A1) is given as 2/3.
So, P(A1 and B) = (1/2) * (2/3) = 1/3.
For A2 and B:
P(A2 and B) = P(B|A2) * P(A2)
P(B|A2) is given as 3/7, since if A2 has occurred, then 3 of the remaining 7 cards are black.
P(A2) is given as 3/8.
So, P(A2 and B) = (3/7) * (3/8) = 9/56.
Now we can apply Bayes' theorem:
P(A1|B) = P(A1 and B) / P(B)
P(A2|B) = P(A2 and B) / P(B)
where P(B) is the probability of event B occurring, which is the sum of the probabilities of A1 and B and A2 and B:
P(B) = P(A1 and B) + P(A2 and B) = 1/3 + 9/56 = 25/56.
So,
P(A1|B) = (1/3) / (25/56) = 56/225
P(A2|B) = (9/56) / (25/56) = 9/25
Therefore, the probability that the card drawn is from deck 1 given that it is a black card is 56/225, and the probability that it is from deck 2 given that it is a black card is 9/25.
If an unbiased die is rolled once, the odds in favour of getting a point which is a multiple of 3 is- a)1:2
- b)2:1
- c)1:3
- d)3:1
Correct answer is option 'C'. Can you explain this answer?
If an unbiased die is rolled once, the odds in favour of getting a point which is a multiple of 3 is
a)
1:2
b)
2:1
c)
1:3
d)
3:1

|
Anu Kaur answered |
Total number =6
Getting a 'multiple of 3' = 2 . So, probability = 2/6 =1/3
Getting a 'multiple of 3' = 2 . So, probability = 2/6 =1/3
Given that for two events A and B, P(A)=3/5, P(B)=2/3 and P(A union B) =3/4, what is P(A|B)?- a)0.655
- b)13/60
- c)31/60
- d)0.775
Correct answer is option 'D'. Can you explain this answer?
Given that for two events A and B, P(A)=3/5, P(B)=2/3 and P(A union B) =3/4, what is P(A|B)?
a)
0.655
b)
13/60
c)
31/60
d)
0.775

|
Freedom Institute answered |
P(A|B) = P(A&B)/P(B)
So first we have to find P(A&B)
P(AUB) = P(A) + P(B) - P(A&B)3/4 = 3/5 + 2/3 - P(A&B)
Multiply through by 60
45 = 36 + 40 - 60P(A&B)
45 = 76 - 60P(A&B)
-31 = -60P(A&B)
31/60 = P(A&B)
Go back to
P(A|B) = P(A&B)/P(B)
P(A|B) = (31/60)/(2/3)
P(A|B) = (31/60)(3/2)
P(A|B) = 31/40 = 0.775
So first we have to find P(A&B)
P(AUB) = P(A) + P(B) - P(A&B)3/4 = 3/5 + 2/3 - P(A&B)
Multiply through by 60
45 = 36 + 40 - 60P(A&B)
45 = 76 - 60P(A&B)
-31 = -60P(A&B)
31/60 = P(A&B)
Go back to
P(A|B) = P(A&B)/P(B)
P(A|B) = (31/60)/(2/3)
P(A|B) = (31/60)(3/2)
P(A|B) = 31/40 = 0.775
If events A and B are independent and P(A)= 2/3 , P(B)= 3/5 then P(A+B)is equal to- a)13/15
- b)6/15
- c)1/15
- d)none
Correct answer is option 'A'. Can you explain this answer?
If events A and B are independent and P(A)= 2/3 , P(B)= 3/5 then P(A+B)is equal to
a)
13/15
b)
6/15
c)
1/15
d)
none

|
Deepika Desai answered |
Given:
- Events A and B are independent
- P(A)= 2/3
- P(B)= 3/5
To find:
- P(A ∩ B)
Approach:
- Use the formula for the probability of the intersection of independent events
- Substitute the given values
- Simplify the expression
Formula:
- P(A ∩ B) = P(A) * P(B)
Calculation:
- P(A ∩ B) = P(A) * P(B)
- P(A ∩ B) = (2/3) * (3/5)
- P(A ∩ B) = 6/15
- P(A ∩ B) = 2/5
Answer:
- The correct option is A) 13/15.
- Events A and B are independent
- P(A)= 2/3
- P(B)= 3/5
To find:
- P(A ∩ B)
Approach:
- Use the formula for the probability of the intersection of independent events
- Substitute the given values
- Simplify the expression
Formula:
- P(A ∩ B) = P(A) * P(B)
Calculation:
- P(A ∩ B) = P(A) * P(B)
- P(A ∩ B) = (2/3) * (3/5)
- P(A ∩ B) = 6/15
- P(A ∩ B) = 2/5
Answer:
- The correct option is A) 13/15.
The odds against A solving a certain problem are 4 to 3 and the odds in favour of B solving the same problem are 7 to 5. What is the probability that the problem will be solved if they both try?- a)15/21
- b)16/21
- c)17/21
- d)13/21
Correct answer is option 'B'. Can you explain this answer?
The odds against A solving a certain problem are 4 to 3 and the odds in favour of B solving the same problem are 7 to 5. What is the probability that the problem will be solved if they both try?
a)
15/21
b)
16/21
c)
17/21
d)
13/21

|
Meera Joshi answered |
**Given information:**
- Odds against A solving the problem are 4 to 3.
- Odds in favor of B solving the problem are 7 to 5.
**Understanding odds:**
Odds represent the likelihood of an event occurring. In this case, the odds are given as ratios. For example, odds against A solving the problem are 4 to 3 means that for every 4 times A fails to solve the problem, A succeeds 3 times.
**Calculating probabilities from odds:**
To calculate the probability from odds, we use the formula:
Probability = favorable outcomes / total outcomes
In this case, the favorable outcomes represent the number of times A or B can solve the problem, and the total outcomes represent all possible outcomes.
**Calculating the probability of A solving the problem:**
If the odds against A solving the problem are 4 to 3, it means that out of every 4+3=7 attempts, A succeeds 3 times. Therefore, the probability of A solving the problem can be calculated as:
Probability of A = 3 / 7
**Calculating the probability of B solving the problem:**
If the odds in favor of B solving the problem are 7 to 5, it means that out of every 7+5=12 attempts, B succeeds 7 times. Therefore, the probability of B solving the problem can be calculated as:
Probability of B = 7 / 12
**Calculating the probability of both A and B solving the problem:**
To calculate the probability that both A and B solve the problem, we multiply their individual probabilities:
Probability of both A and B = Probability of A * Probability of B
= (3 / 7) * (7 / 12)
= 21 / 84
= 1 / 4
**Simplifying the probability:**
To simplify the probability, we can divide both the numerator and denominator by their greatest common divisor, which is 1 in this case:
Probability of both A and B = 1 / 4
**Converting the probability to odds:**
To convert the probability to odds, we use the formula:
Odds = favorable outcomes : unfavorable outcomes
In this case, the favorable outcome is 1 (both A and B solving the problem) and the unfavorable outcome is 3 (A not solving the problem). Therefore, the odds in favor of both A and B solving the problem can be written as:
Odds in favor = 1 : 3
**Calculating the probability that the problem will be solved:**
The probability that the problem will be solved is the sum of the probabilities of A and B solving the problem, minus the probability of both A and B solving the problem (to avoid double counting):
Probability of problem solved = Probability of A + Probability of B - Probability of both A and B
= 3 / 7 + 7 / 12 - 1 / 4
= (36 + 49 - 21) / 84
= 64 / 84
= 16 / 21
Therefore, the probability that the problem will be solved if both A and B try is 16/21.
**Conclusion:**
The correct answer is option B) 16/21.
- Odds against A solving the problem are 4 to 3.
- Odds in favor of B solving the problem are 7 to 5.
**Understanding odds:**
Odds represent the likelihood of an event occurring. In this case, the odds are given as ratios. For example, odds against A solving the problem are 4 to 3 means that for every 4 times A fails to solve the problem, A succeeds 3 times.
**Calculating probabilities from odds:**
To calculate the probability from odds, we use the formula:
Probability = favorable outcomes / total outcomes
In this case, the favorable outcomes represent the number of times A or B can solve the problem, and the total outcomes represent all possible outcomes.
**Calculating the probability of A solving the problem:**
If the odds against A solving the problem are 4 to 3, it means that out of every 4+3=7 attempts, A succeeds 3 times. Therefore, the probability of A solving the problem can be calculated as:
Probability of A = 3 / 7
**Calculating the probability of B solving the problem:**
If the odds in favor of B solving the problem are 7 to 5, it means that out of every 7+5=12 attempts, B succeeds 7 times. Therefore, the probability of B solving the problem can be calculated as:
Probability of B = 7 / 12
**Calculating the probability of both A and B solving the problem:**
To calculate the probability that both A and B solve the problem, we multiply their individual probabilities:
Probability of both A and B = Probability of A * Probability of B
= (3 / 7) * (7 / 12)
= 21 / 84
= 1 / 4
**Simplifying the probability:**
To simplify the probability, we can divide both the numerator and denominator by their greatest common divisor, which is 1 in this case:
Probability of both A and B = 1 / 4
**Converting the probability to odds:**
To convert the probability to odds, we use the formula:
Odds = favorable outcomes : unfavorable outcomes
In this case, the favorable outcome is 1 (both A and B solving the problem) and the unfavorable outcome is 3 (A not solving the problem). Therefore, the odds in favor of both A and B solving the problem can be written as:
Odds in favor = 1 : 3
**Calculating the probability that the problem will be solved:**
The probability that the problem will be solved is the sum of the probabilities of A and B solving the problem, minus the probability of both A and B solving the problem (to avoid double counting):
Probability of problem solved = Probability of A + Probability of B - Probability of both A and B
= 3 / 7 + 7 / 12 - 1 / 4
= (36 + 49 - 21) / 84
= 64 / 84
= 16 / 21
Therefore, the probability that the problem will be solved if both A and B try is 16/21.
**Conclusion:**
The correct answer is option B) 16/21.
The probability of Girl getting scholarship is 0.6 and the same probability for Boy is 0.8. Find the probability that at least one of the categories getiing scholarship.
- a)0.32
- b)0.44
- c)0.52
- d)None of the above.
Correct answer is option 'C'. Can you explain this answer?
The probability of Girl getting scholarship is 0.6 and the same probability for Boy is 0.8. Find the probability that at least one of the categories getiing scholarship.
a)
0.32
b)
0.44
c)
0.52
d)
None of the above.

|
Malavika Basak answered |
Solution:
Given, the probability of a girl getting a scholarship is 0.6 and the probability of a boy getting a scholarship is 0.8.
Let A be the event that a girl gets a scholarship and B be the event that a boy gets a scholarship.
We need to find the probability that at least one of the categories is getting a scholarship, i.e., P(A∪B).
Using the formula for the probability of the union of two events, we have:
P(A∪B) = P(A) + P(B) - P(A∩B)
where P(A∩B) is the probability that both a girl and a boy get a scholarship.
Since the events A and B are independent (i.e., the probability of one event does not affect the probability of the other event), we have:
P(A∩B) = P(A) × P(B) = 0.6 × 0.8 = 0.48
Substituting the values in the above equation, we get:
P(A∪B) = 0.6 + 0.8 - 0.48 = 0.92
Hence, the probability that at least one of the categories is getting a scholarship is 0.92.
Therefore, the correct answer is option 'C'.
Given, the probability of a girl getting a scholarship is 0.6 and the probability of a boy getting a scholarship is 0.8.
Let A be the event that a girl gets a scholarship and B be the event that a boy gets a scholarship.
We need to find the probability that at least one of the categories is getting a scholarship, i.e., P(A∪B).
Using the formula for the probability of the union of two events, we have:
P(A∪B) = P(A) + P(B) - P(A∩B)
where P(A∩B) is the probability that both a girl and a boy get a scholarship.
Since the events A and B are independent (i.e., the probability of one event does not affect the probability of the other event), we have:
P(A∩B) = P(A) × P(B) = 0.6 × 0.8 = 0.48
Substituting the values in the above equation, we get:
P(A∪B) = 0.6 + 0.8 - 0.48 = 0.92
Hence, the probability that at least one of the categories is getting a scholarship is 0.92.
Therefore, the correct answer is option 'C'.
What is the probability of having at least one ‘six’ from 3 throws of a perfect die?- a)5/6
- b)(5/6)3
- c)1– (1/6)3
- d)1 – (5/6)3
Correct answer is option 'A'. Can you explain this answer?
What is the probability of having at least one ‘six’ from 3 throws of a perfect die?
a)
5/6
b)
(5/6)3
c)
1– (1/6)3
d)
1 – (5/6)3

|
Prashanth Datta answered |
Solution:
The probability of getting a six on a single throw of a perfect die is 1/6.
To find the probability of having at least one six from 3 throws of a perfect die, we can use the complementary probability approach.
Complementary Probability Approach:
The complementary probability of an event A is the probability of the event not occurring (i.e., 1 minus the probability of A).
Let B be the event of not getting a six in a single throw of a perfect die. Then, the probability of B is:
P(B) = 1 - 1/6 = 5/6
Now, let C be the event of not getting a six in any of the 3 throws of a perfect die. Then, the probability of C is:
P(C) = P(B) × P(B) × P(B) (since the throws are independent)
P(C) = (5/6) × (5/6) × (5/6) = (5/6)3
Finally, the probability of having at least one six from 3 throws of a perfect die is:
P(at least one six) = 1 - P(C) (using the complementary probability)
P(at least one six) = 1 - (5/6)3 ≈ 0.4213
Therefore, the correct answer is option 'A' (5/6).
The probability of getting a six on a single throw of a perfect die is 1/6.
To find the probability of having at least one six from 3 throws of a perfect die, we can use the complementary probability approach.
Complementary Probability Approach:
The complementary probability of an event A is the probability of the event not occurring (i.e., 1 minus the probability of A).
Let B be the event of not getting a six in a single throw of a perfect die. Then, the probability of B is:
P(B) = 1 - 1/6 = 5/6
Now, let C be the event of not getting a six in any of the 3 throws of a perfect die. Then, the probability of C is:
P(C) = P(B) × P(B) × P(B) (since the throws are independent)
P(C) = (5/6) × (5/6) × (5/6) = (5/6)3
Finally, the probability of having at least one six from 3 throws of a perfect die is:
P(at least one six) = 1 - P(C) (using the complementary probability)
P(at least one six) = 1 - (5/6)3 ≈ 0.4213
Therefore, the correct answer is option 'A' (5/6).
When unbiased coins are tossed. The probability of obtaining not more than 3 heads is- a)¾
- b)½
- c)1
- d)0
Correct answer is option 'C'. Can you explain this answer?
When unbiased coins are tossed. The probability of obtaining not more than 3 heads is
a)
¾
b)
½
c)
1
d)
0

|
Maheshwar Sharma answered |
Solution:
Given, unbiased coins are tossed.
We need to find the probability of obtaining not more than 3 heads.
Let us consider the possible outcomes when 4 coins are tossed:
- All tails: TTTT
- One head: HTTT, THTT, TTHT, TTTH
- Two heads: HHTT, HTHT, HTTH, THHT, THTH, TTHH
- Three heads: HHHT, HHTH, HTHH, THHH
- All heads: HHHH
Out of these possible outcomes, there are 4 outcomes where we obtain not more than 3 heads.
Therefore, the probability of obtaining not more than 3 heads = 4/16 = 1/4 = 0.25.
Hence, the correct answer is option 'C'.
Note: The probability of obtaining not more than 3 heads can also be calculated using the binomial distribution formula as follows:
P(X ≤ 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
where X is the number of heads obtained in 4 tosses of a coin.
Using the binomial distribution formula, we get:
P(X ≤ 3) = (4C0 * (1/2)^0 * (1/2)^4) + (4C1 * (1/2)^1 * (1/2)^3) + (4C2 * (1/2)^2 * (1/2)^2) + (4C3 * (1/2)^3 * (1/2)^1)
= (1 * 1 * 1/16) + (4 * 1/2 * 1/8) + (6 * 1/4 * 1/4) + (4 * 1/8 * 1/2)
= 1/16 + 1/4 + 3/16 + 1/8
= 1/4
Therefore, the probability of obtaining not more than 3 heads = 1/4 = 0.25.
Given, unbiased coins are tossed.
We need to find the probability of obtaining not more than 3 heads.
Let us consider the possible outcomes when 4 coins are tossed:
- All tails: TTTT
- One head: HTTT, THTT, TTHT, TTTH
- Two heads: HHTT, HTHT, HTTH, THHT, THTH, TTHH
- Three heads: HHHT, HHTH, HTHH, THHH
- All heads: HHHH
Out of these possible outcomes, there are 4 outcomes where we obtain not more than 3 heads.
Therefore, the probability of obtaining not more than 3 heads = 4/16 = 1/4 = 0.25.
Hence, the correct answer is option 'C'.
Note: The probability of obtaining not more than 3 heads can also be calculated using the binomial distribution formula as follows:
P(X ≤ 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
where X is the number of heads obtained in 4 tosses of a coin.
Using the binomial distribution formula, we get:
P(X ≤ 3) = (4C0 * (1/2)^0 * (1/2)^4) + (4C1 * (1/2)^1 * (1/2)^3) + (4C2 * (1/2)^2 * (1/2)^2) + (4C3 * (1/2)^3 * (1/2)^1)
= (1 * 1 * 1/16) + (4 * 1/2 * 1/8) + (6 * 1/4 * 1/4) + (4 * 1/8 * 1/2)
= 1/16 + 1/4 + 3/16 + 1/8
= 1/4
Therefore, the probability of obtaining not more than 3 heads = 1/4 = 0.25.
If probability of drawing a spade from a well-shuffled pack of playing cards is ¼ then the probability that of the card drawn from a well-shuffled pack of playing cards is ‘not a spade’ is
- a)1
- b)½
- c)¼
- d)¾
Correct answer is option 'D'. Can you explain this answer?
If probability of drawing a spade from a well-shuffled pack of playing cards is ¼ then the probability that of the card drawn from a well-shuffled pack of playing cards is ‘not a spade’ is
a)
1
b)
½
c)
¼
d)
¾

|
Ipsita Rane answered |
Probability of Drawing a Spade
The probability of drawing a spade from a well-shuffled pack of playing cards is given as:
P(spade) =
where n(spade) is the number of spades in the deck and n(total) is the total number of cards in the deck.
Probability of Not Drawing a Spade
To find the probability of not drawing a spade, we need to subtract the probability of drawing a spade from 1 (since the probability of an event happening plus the probability of it not happening equals 1). Therefore, the probability of not drawing a spade is:
P(not spade) = 1 - P(spade)
Substituting the value of P(spade) in the above equation, we get:
P(not spade) = 1 -
Simplifying the expression, we get:
P(not spade) =
Therefore, the correct answer is option 'D'
The probability of drawing a spade from a well-shuffled pack of playing cards is given as:
P(spade) =
where n(spade) is the number of spades in the deck and n(total) is the total number of cards in the deck.
Probability of Not Drawing a Spade
To find the probability of not drawing a spade, we need to subtract the probability of drawing a spade from 1 (since the probability of an event happening plus the probability of it not happening equals 1). Therefore, the probability of not drawing a spade is:
P(not spade) = 1 - P(spade)
Substituting the value of P(spade) in the above equation, we get:
P(not spade) = 1 -
Simplifying the expression, we get:
P(not spade) =
Therefore, the correct answer is option 'D'
Two dice are thrown at a time. The probability that ‘the difference of nos shown is 1’ is- a)11/18
- b)5/18
- c)7/18
- d)none
Correct answer is option 'B'. Can you explain this answer?
Two dice are thrown at a time. The probability that ‘the difference of nos shown is 1’ is
a)
11/18
b)
5/18
c)
7/18
d)
none

|
Himanshi Tapkir answered |
Correct option is A)
Possible outcomes on rolling two dices are 36
Out of the possible outcomes, chances of getting numbers with difference one are as follows : 2,1;3,2;4,3;5,4;6,5 and vice versa in each case.
⇒ Number of favourable outcomes =10
Probability = Favourable Outcomes ÷ Total Outcomes =3610=185
Possible outcomes on rolling two dices are 36
Out of the possible outcomes, chances of getting numbers with difference one are as follows : 2,1;3,2;4,3;5,4;6,5 and vice versa in each case.
⇒ Number of favourable outcomes =10
Probability = Favourable Outcomes ÷ Total Outcomes =3610=185
Probability of throwing an odd no with an ordinary six faced die is- a)1/2
- b)1
- c)–1/2
- d)0
Correct answer is option 'A'. Can you explain this answer?
Probability of throwing an odd no with an ordinary six faced die is
a)
1/2
b)
1
c)
–1/2
d)
0

|
Sahil Malik answered |
Probability of Throwing an Odd Number with an Ordinary Six-Faced Die
To understand the probability of throwing an odd number with an ordinary six-faced die, we need to first understand what is meant by a six-faced die.
Definition of a Six-Faced Die
A six-faced die is a cube-shaped object with each face representing a number from 1 to 6. When the die is rolled, the outcome is random and can be any number from 1 to 6.
Understanding Probability
Probability is the likelihood or chance of an event occurring. It is expressed as a fraction or a percentage. For example, if we toss a coin, the probability of getting heads is 1/2 or 50%.
Determining the Probability of Throwing an Odd Number
To determine the probability of throwing an odd number with an ordinary six-faced die, we need to first identify the number of odd numbers that can be thrown. The odd numbers that can be thrown with a six-faced die are 1, 3, and 5.
Next, we need to determine the total number of possible outcomes. With a six-faced die, the total number of possible outcomes is 6 (1, 2, 3, 4, 5, and 6).
Finally, we can determine the probability of throwing an odd number by dividing the number of odd numbers by the total number of possible outcomes.
Probability of throwing an odd number = Number of odd numbers / Total number of possible outcomes
Probability of throwing an odd number = 3 / 6
Probability of throwing an odd number = 1/2
Therefore, the correct answer is option 'A', which states that the probability of throwing an odd number with an ordinary six-faced die is 1/2.
To understand the probability of throwing an odd number with an ordinary six-faced die, we need to first understand what is meant by a six-faced die.
Definition of a Six-Faced Die
A six-faced die is a cube-shaped object with each face representing a number from 1 to 6. When the die is rolled, the outcome is random and can be any number from 1 to 6.
Understanding Probability
Probability is the likelihood or chance of an event occurring. It is expressed as a fraction or a percentage. For example, if we toss a coin, the probability of getting heads is 1/2 or 50%.
Determining the Probability of Throwing an Odd Number
To determine the probability of throwing an odd number with an ordinary six-faced die, we need to first identify the number of odd numbers that can be thrown. The odd numbers that can be thrown with a six-faced die are 1, 3, and 5.
Next, we need to determine the total number of possible outcomes. With a six-faced die, the total number of possible outcomes is 6 (1, 2, 3, 4, 5, and 6).
Finally, we can determine the probability of throwing an odd number by dividing the number of odd numbers by the total number of possible outcomes.
Probability of throwing an odd number = Number of odd numbers / Total number of possible outcomes
Probability of throwing an odd number = 3 / 6
Probability of throwing an odd number = 1/2
Therefore, the correct answer is option 'A', which states that the probability of throwing an odd number with an ordinary six-faced die is 1/2.
Chapter doubts & questions for Chapter 15: Probability - Quantitative Aptitude for CA Foundation 2025 is part of CA Foundation exam preparation. The chapters have been prepared according to the CA Foundation exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CA Foundation 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chapter 15: Probability - Quantitative Aptitude for CA Foundation in English & Hindi are available as part of CA Foundation exam.
Download more important topics, notes, lectures and mock test series for CA Foundation Exam by signing up for free.
Quantitative Aptitude for CA Foundation
101 videos|209 docs|89 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily