All Exams >
Electrical Engineering (EE) >
Network Theory (Electric Circuits) >
All Questions
All questions of Graph Theory for Electrical Engineering (EE) Exam
Consider the following circuits :
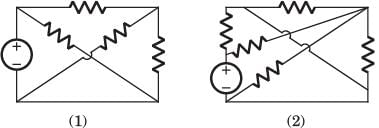
The planner circuits are- a)1 and 2
- b)2 and 3
- c)3 and 4
- d)4 and 1
Correct answer is option 'A'. Can you explain this answer?
Consider the following circuits :
The planner circuits are
The planner circuits are
a)
1 and 2
b)
2 and 3
c)
3 and 4
d)
4 and 1
|
Ravi Singh answered |
The circuit 1 and 2 are redrawn as below. 3 and 4 can not be redrawn on a plane without crossing other branch.
Consider the following statements1. The rows of the incidence matrix [A] represent the number of branches and the column of the matrix represents the number of nodes in the given graph.2. The algebraic sum of elements of all the columns is zero.3. The rank of the incidence matrix is (n–1) where n is the number of nodes.4. The determinant of the incidence matrix of a closed loop is equal to unity.Which of the above statements are correct?- a)1, 2 and 3 only
- b)2 and 3 only
- c)1, 3 and 4 only
- d)1, 2, 3 and 4
Correct answer is option 'B'. Can you explain this answer?
Consider the following statements
1. The rows of the incidence matrix [A] represent the number of branches and the column of the matrix represents the number of nodes in the given graph.
2. The algebraic sum of elements of all the columns is zero.
3. The rank of the incidence matrix is (n–1) where n is the number of nodes.
4. The determinant of the incidence matrix of a closed loop is equal to unity.
Which of the above statements are correct?
a)
1, 2 and 3 only
b)
2 and 3 only
c)
1, 3 and 4 only
d)
1, 2, 3 and 4
|
Zoya Sharma answered |
Incidence matrix:
- It is the matrix that gives a relation between the branches and nodes.
- The rows of the incidence matrix [A] represent the number of nodes and the column of the matrix represents the number of branches in the given graph.
- If there are ‘n’ number of rows in a given incidence matrix[A], that means in a graph there are ‘n’ number of nodes.
- Similarly, if there are ‘b’ number of columns in that given incidence matrix[A], that means in that graph there are ‘b’ number of branches.
- We can construct the incidence matrix for the directed graph. We can draw a graph with the help of the incidence matrix.
- The algebraic sum of elements of all the columns is zero.
- The rank of the incidence matrix is (n – 1).
- The determinant of the incidence matrix of a closed loop is zero.
Hence, Only statement I is correct.
If no two branches of the graph cross each other, then the graph is called?- a)directed graph
- b)undirected graph
- c)planar graph
- d)non-planar graph
Correct answer is option 'C'. Can you explain this answer?
If no two branches of the graph cross each other, then the graph is called?
a)
directed graph
b)
undirected graph
c)
planar graph
d)
non-planar graph
|
Bijoy Nair answered |
Planar Graph Explanation:
Planar graph is a type of graph in which no two branches cross each other. This property makes planar graphs particularly interesting and useful in various applications, such as circuit design, network analysis, and transportation planning.
Definition of Planar Graph:
A graph is called planar if it can be drawn on a plane in such a way that no two edges intersect except at their endpoints. In other words, the graph can be represented without any edge crossings.
Characteristics of Planar Graph:
1. No edge crossings: In a planar graph, no two edges cross each other, which means the edges do not intersect except at the vertices.
2. Embedded on a plane: The graph can be drawn on a flat surface (plane) without any edge crossings.
3. Regions: The plane divides into regions by the edges and vertices of the graph, forming a unique structure.
Importance of Planar Graphs:
1. Simplified visualization: Planar graphs offer a clear and easy-to-understand representation due to the absence of edge crossings.
2. Efficient algorithms: Many algorithms are designed specifically for planar graphs, taking advantage of their unique properties to achieve faster and more efficient computations.
3. Practical applications: Planar graphs are commonly used in various real-world scenarios, such as designing electronic circuits, mapping transportation networks, and analyzing social connections.
In conclusion, a graph is called a planar graph if its branches do not cross each other when represented on a plane. This property makes planar graphs valuable in different fields of study and practical applications.
In the following graph, the number of trees (P) and cutset (Q) are
- a)P = 2, Q = 2
- b)P = 2, Q = 6
- c)P = 4, Q = 6
- d)P = 4, Q = 10
Correct answer is option 'C'. Can you explain this answer?
In the following graph, the number of trees (P) and cutset (Q) are
a)
P = 2, Q = 2
b)
P = 2, Q = 6
c)
P = 4, Q = 6
d)
P = 4, Q = 10
|
|
Zoya Sharma answered |
Concept:
The tree is a connected subgraph that consists of all the nodes of the network but it does not consist of any closed path. So, we have drawn below the trees possible without forming any loop.
On other hand, cutsets are the same as a twig(tree branches).
Analysis:
Possible trees of the given graph is:
Therefore no. of trees possible P = 4.
Possible cut sets of the given graph are
No. of possible cut sets Q = 6
Two networks are said to be dual when- a)Their node equations are the same
- b)The loop equations of one network are analogous to the node equations of the other
- c)Their loop equations are the same
- d)The voltage sources of one network are the current sources of the other
Correct answer is option 'B'. Can you explain this answer?
Two networks are said to be dual when
a)
Their node equations are the same
b)
The loop equations of one network are analogous to the node equations of the other
c)
Their loop equations are the same
d)
The voltage sources of one network are the current sources of the other
|
Pooja Patel answered |
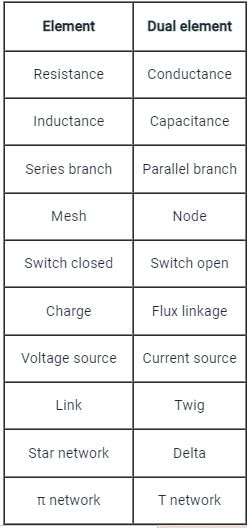
Duality:
- Two electrical networks are said to be dual networks if the mesh equations of one network are equal to the node equation of others.
- Identical behavior patterns observed between voltages and currents in two circuits illustrate the principle of duality.
- The dual networks are based on Kirchhoff Current Law and Kirchhoff Voltage Law.
Some important dual relations are given below.
Which network topology term got reference directions and marked on the edges of the graph by arrow heads?- a)Sub graph
- b)Node
- c)Vertex
- d)Oriented graph
Correct answer is option 'D'. Can you explain this answer?
Which network topology term got reference directions and marked on the edges of the graph by arrow heads?
a)
Sub graph
b)
Node
c)
Vertex
d)
Oriented graph
|
Pioneer Academy answered |
Oriented Graph:
- If all the branches of a graph are represented with arrows, then that graph is called a directed graph.
- These arrows indicate the direction of current flow in each branch. Hence, this graph is also called an oriented graph.
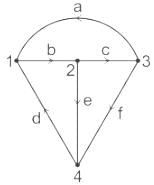
- In the above graph, the direction of the current flow is represented with an arrow in each branch. Hence, it is an oriented graph.
The number of branches incident at the node of a graph is called?- a)degree of the node
- b)order of the node
- c)status of the node
- d)number of the node
Correct answer is option 'A'. Can you explain this answer?
The number of branches incident at the node of a graph is called?
a)
degree of the node
b)
order of the node
c)
status of the node
d)
number of the node
|
Maulik Chatterjee answered |
Answer:
The number of branches incident at a node in a graph is called the degree of the node. It is a fundamental concept in graph theory and is used to describe the connectivity of a node in a graph. The degree of a node is defined as the number of edges that are connected to that node.
Explanation:
In a graph, nodes represent entities, and edges represent relationships or connections between these entities. The degree of a node is a measure of how many connections or branches are incident at that node.
Example:
Consider a simple graph with three nodes A, B, and C. If there are two edges connecting node A to node B and one edge connecting node A to node C, then the degree of node A would be 3. This means that there are three branches or edges incident at node A.
Significance:
The degree of a node provides important information about the connectivity of a graph. It can help determine the complexity of a network, identify important nodes or hubs, and analyze the flow of information or resources in a system.
Properties:
- In an undirected graph, the degree of a node is equal to the number of edges connected to that node.
- In a directed graph, the degree of a node is the sum of the in-degree (number of edges coming into the node) and the out-degree (number of edges going out from the node).
- The minimum degree of a node in a graph is 0, indicating that it is not connected to any other node.
- The maximum degree of a node in a graph is the number of nodes minus one, indicating that it is connected to all other nodes in the graph.
Conclusion:
In graph theory, the degree of a node is a fundamental concept that describes the connectivity of a node in a graph. It is defined as the number of branches or edges incident at that node. The degree of a node provides important information about the structure and connectivity of a graph and is used in various applications such as network analysis, social network analysis, and routing algorithms.
The number of branches incident at a node in a graph is called the degree of the node. It is a fundamental concept in graph theory and is used to describe the connectivity of a node in a graph. The degree of a node is defined as the number of edges that are connected to that node.
Explanation:
In a graph, nodes represent entities, and edges represent relationships or connections between these entities. The degree of a node is a measure of how many connections or branches are incident at that node.
Example:
Consider a simple graph with three nodes A, B, and C. If there are two edges connecting node A to node B and one edge connecting node A to node C, then the degree of node A would be 3. This means that there are three branches or edges incident at node A.
Significance:
The degree of a node provides important information about the connectivity of a graph. It can help determine the complexity of a network, identify important nodes or hubs, and analyze the flow of information or resources in a system.
Properties:
- In an undirected graph, the degree of a node is equal to the number of edges connected to that node.
- In a directed graph, the degree of a node is the sum of the in-degree (number of edges coming into the node) and the out-degree (number of edges going out from the node).
- The minimum degree of a node in a graph is 0, indicating that it is not connected to any other node.
- The maximum degree of a node in a graph is the number of nodes minus one, indicating that it is connected to all other nodes in the graph.
Conclusion:
In graph theory, the degree of a node is a fundamental concept that describes the connectivity of a node in a graph. It is defined as the number of branches or edges incident at that node. The degree of a node provides important information about the structure and connectivity of a graph and is used in various applications such as network analysis, social network analysis, and routing algorithms.
What will be the number of tie set currents in the given circuit?
- a)4
- b)3
- c)6
- d)1
Correct answer is option 'B'. Can you explain this answer?
What will be the number of tie set currents in the given circuit?
a)
4
b)
3
c)
6
d)
1
|
|
Pioneer Academy answered |
Concept:
Tie set matrix:
- It gives the relation between tie-set currents and branch currents.
- The rows of a matrix represent the tie-set currents.
- The columns of a matrix represent branches of the graph.
- The order of the tie set matrix is (B – N + 1) × b
- The rank of a tie-set matrix is (B – N + 1)
Application:
Circuit Diagram:
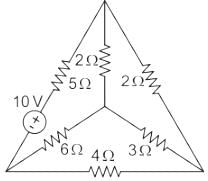
The above figure consists of 4 Nodes and 6 Branches
B = 6, N = 4
The rows of a matrix represent the tie-set currents = (B - N + 1)
= 6 - 4 + 1
= 3
Two labeled trees are isomorphic if ____________- a)graphs of the two trees are isomorphic
- b)the two trees have same label
- c)graphs of the two trees are isomorphic and the two trees have the same label
- d)graphs of the two trees are cyclic
Correct answer is option 'C'. Can you explain this answer?
Two labeled trees are isomorphic if ____________
a)
graphs of the two trees are isomorphic
b)
the two trees have same label
c)
graphs of the two trees are isomorphic and the two trees have the same label
d)
graphs of the two trees are cyclic
|
Raghav Majumdar answered |
Isomorphism in Labeled Trees
Labeled trees are trees in which each node is assigned a label or a value. Two labeled trees are isomorphic if they have the same structure and the same labels on the nodes. In other words, they are identical except for the labels assigned to the nodes.
Graph Isomorphism
Graph isomorphism is a concept in graph theory that describes when two graphs are structurally identical. A graph is a collection of vertices or nodes and edges that connect them. If two graphs have the same number of vertices and edges, and the edges connect the vertices in the same way, then they are isomorphic.
Isomorphism in Labeled Trees and Graphs
Labeled trees can be represented as graphs, where the nodes of the tree become vertices of the graph, and the edges of the tree become edges of the graph. Therefore, if two labeled trees are isomorphic, then their corresponding graphs are also isomorphic.
Answer Explanation
Option C is the correct answer because it includes both the conditions for isomorphism in labeled trees and graphs. Two labeled trees are isomorphic if their corresponding graphs are isomorphic and they have the same labels on the nodes. Therefore, option C combines both the necessary conditions for isomorphism in labeled trees and graphs, making it the correct choice.
Conclusion
In conclusion, isomorphism in labeled trees and graphs is a concept that requires both a structural match and identical node labels. Option C in this question combines both of these conditions, making it the correct answer.
Labeled trees are trees in which each node is assigned a label or a value. Two labeled trees are isomorphic if they have the same structure and the same labels on the nodes. In other words, they are identical except for the labels assigned to the nodes.
Graph Isomorphism
Graph isomorphism is a concept in graph theory that describes when two graphs are structurally identical. A graph is a collection of vertices or nodes and edges that connect them. If two graphs have the same number of vertices and edges, and the edges connect the vertices in the same way, then they are isomorphic.
Isomorphism in Labeled Trees and Graphs
Labeled trees can be represented as graphs, where the nodes of the tree become vertices of the graph, and the edges of the tree become edges of the graph. Therefore, if two labeled trees are isomorphic, then their corresponding graphs are also isomorphic.
Answer Explanation
Option C is the correct answer because it includes both the conditions for isomorphism in labeled trees and graphs. Two labeled trees are isomorphic if their corresponding graphs are isomorphic and they have the same labels on the nodes. Therefore, option C combines both the necessary conditions for isomorphism in labeled trees and graphs, making it the correct choice.
Conclusion
In conclusion, isomorphism in labeled trees and graphs is a concept that requires both a structural match and identical node labels. Option C in this question combines both of these conditions, making it the correct answer.
What are the properties of a tree in a network graph?1. It consists of all the nodes of the graph.2. If the graph has N number of nodes, the tree will have (N – 1) branches.3. There will be only one closed path in the tree.- a)1, 2 and 3
- b)1 and 3 only
- c)1 and 2 only
- d)2 and 3 only
Correct answer is option 'C'. Can you explain this answer?
What are the properties of a tree in a network graph?
1. It consists of all the nodes of the graph.
2. If the graph has N number of nodes, the tree will have (N – 1) branches.
3. There will be only one closed path in the tree.
a)
1, 2 and 3
b)
1 and 3 only
c)
1 and 2 only
d)
2 and 3 only
|
Anirban Gupta answered |
Understanding Tree Properties in Network Graphs
In network graphs, trees serve as vital structures with specific properties. Let’s break down the properties mentioned in the question to understand why option 'C' (1 and 2 only) is correct.
Property 1: All Nodes Included
- A tree is defined as a connected acyclic graph.
- This means that it includes all nodes present in the original graph while ensuring connectivity among them.
Property 2: Branches Count
- A crucial characteristic of a tree is that if it contains N nodes, it will have exactly (N - 1) branches (or edges).
- This is because adding one more edge would create a cycle, violating the tree's acyclic nature.
Property 3: Closed Paths
- A tree cannot contain any closed paths (cycles).
- The essence of a tree is that every pair of nodes is connected by exactly one path, ensuring that no closed loop exists.
Conclusion on Options
- Since property 3 states that a tree has only one closed path, which contradicts the definition of a tree, this property is incorrect.
- Hence, the correct properties are 1 and 2 only.
Final Answer
- The correct answer is indeed option C (1 and 2 only), as properties 1 and 2 accurately describe the nature of trees in network graphs, while property 3 is false.
In network graphs, trees serve as vital structures with specific properties. Let’s break down the properties mentioned in the question to understand why option 'C' (1 and 2 only) is correct.
Property 1: All Nodes Included
- A tree is defined as a connected acyclic graph.
- This means that it includes all nodes present in the original graph while ensuring connectivity among them.
Property 2: Branches Count
- A crucial characteristic of a tree is that if it contains N nodes, it will have exactly (N - 1) branches (or edges).
- This is because adding one more edge would create a cycle, violating the tree's acyclic nature.
Property 3: Closed Paths
- A tree cannot contain any closed paths (cycles).
- The essence of a tree is that every pair of nodes is connected by exactly one path, ensuring that no closed loop exists.
Conclusion on Options
- Since property 3 states that a tree has only one closed path, which contradicts the definition of a tree, this property is incorrect.
- Hence, the correct properties are 1 and 2 only.
Final Answer
- The correct answer is indeed option C (1 and 2 only), as properties 1 and 2 accurately describe the nature of trees in network graphs, while property 3 is false.
Considering the principle of duality, which of the following pair is INVALID dual pair?- a)Resistance and Conductance
- b)Impedance and Reactance
- c)Voltage and Current
- d)Inductance and Capacitance
Correct answer is option 'B'. Can you explain this answer?
Considering the principle of duality, which of the following pair is INVALID dual pair?
a)
Resistance and Conductance
b)
Impedance and Reactance
c)
Voltage and Current
d)
Inductance and Capacitance
|
Niharika Basu answered |
Invalid Dual Pair Explanation:
Resistance and Conductance are valid dual pairs in the principle of duality as they are reciprocals of each other. The same applies to Voltage and Current, as well as Inductance and Capacitance.
Impedance and Reactance:
- Impedance is a measure of the total opposition to current flow in an AC circuit, including resistance and reactance.
- Reactance, on the other hand, is the opposition to the change in current flow due to capacitance or inductance in the circuit.
- These two quantities are not reciprocals of each other and do not have a direct mathematical relationship that makes them a valid dual pair in the principle of duality.
Therefore, the invalid dual pair in the given options is Impedance and Reactance.
A polytree is called _______- a)directed acyclic graph
- b)directed cyclic graph
- c)bipartite graph
- d)connected graph
Correct answer is option 'A'. Can you explain this answer?
A polytree is called _______
a)
directed acyclic graph
b)
directed cyclic graph
c)
bipartite graph
d)
connected graph
|
Samarth Khanna answered |
Polytree:
A polytree is a special type of directed graph where there are no cycles, meaning there are no paths that start and end at the same node. In other words, it is a directed acyclic graph.
Directed Acyclic Graph (DAG):
A directed acyclic graph (DAG) is a finite directed graph with no directed cycles. This means that it is a graph in which the edges have a direction and there are no loops. Each node in a DAG can be reached from a starting node by following the directed edges, but there are no loops that would allow you to return to a node you have already visited.
Explanation:
- Polytree as a Directed Acyclic Graph: A polytree is a specific type of directed graph where there are no cycles. This means that it satisfies the definition of a directed acyclic graph (DAG). In a polytree, the edges have a direction and there are no loops or cycles.
- No Cycles in a Polytree: The absence of cycles in a polytree is an important property. It ensures that there is a well-defined flow of information or influence from one node to another without any feedback loops. This makes polytrees useful in various applications such as decision-making processes, hierarchical structures, and flow networks.
- Directed Edges in a Polytree: In a polytree, the edges have a direction. This means that there is a specific order or dependency between the nodes. The directed edges represent the flow of information, influence, or causality from one node to another.
- Example of a Polytree: Consider a simple example of a polytree. Let's say we have four nodes A, B, C, and D. There are directed edges from A to B, B to C, and C to D. This forms a polytree because there are no cycles. If there was an edge from D to A, it would create a cycle and the graph would not be a polytree.
- Importance of Polytree: Polytree structures have various applications in different domains. They can be used to represent decision trees, hierarchical relationships, dependencies in project management, information flow in computer networks, and more. The absence of cycles in a polytree ensures that there is a clear and unambiguous flow of information or influence between the nodes.
Conclusion:
In conclusion, a polytree is a directed acyclic graph (DAG) because it is a graph with directed edges and no cycles. The absence of cycles in a polytree ensures a well-defined flow of information or influence between the nodes, making it useful in various applications.
A polytree is a special type of directed graph where there are no cycles, meaning there are no paths that start and end at the same node. In other words, it is a directed acyclic graph.
Directed Acyclic Graph (DAG):
A directed acyclic graph (DAG) is a finite directed graph with no directed cycles. This means that it is a graph in which the edges have a direction and there are no loops. Each node in a DAG can be reached from a starting node by following the directed edges, but there are no loops that would allow you to return to a node you have already visited.
Explanation:
- Polytree as a Directed Acyclic Graph: A polytree is a specific type of directed graph where there are no cycles. This means that it satisfies the definition of a directed acyclic graph (DAG). In a polytree, the edges have a direction and there are no loops or cycles.
- No Cycles in a Polytree: The absence of cycles in a polytree is an important property. It ensures that there is a well-defined flow of information or influence from one node to another without any feedback loops. This makes polytrees useful in various applications such as decision-making processes, hierarchical structures, and flow networks.
- Directed Edges in a Polytree: In a polytree, the edges have a direction. This means that there is a specific order or dependency between the nodes. The directed edges represent the flow of information, influence, or causality from one node to another.
- Example of a Polytree: Consider a simple example of a polytree. Let's say we have four nodes A, B, C, and D. There are directed edges from A to B, B to C, and C to D. This forms a polytree because there are no cycles. If there was an edge from D to A, it would create a cycle and the graph would not be a polytree.
- Importance of Polytree: Polytree structures have various applications in different domains. They can be used to represent decision trees, hierarchical relationships, dependencies in project management, information flow in computer networks, and more. The absence of cycles in a polytree ensures that there is a clear and unambiguous flow of information or influence between the nodes.
Conclusion:
In conclusion, a polytree is a directed acyclic graph (DAG) because it is a graph with directed edges and no cycles. The absence of cycles in a polytree ensures a well-defined flow of information or influence between the nodes, making it useful in various applications.
A graph is said to be a directed graph if ________ of the graph has direction.- a)1 branch
- b)2 branches
- c)3 branches
- d)every branch
Correct answer is option 'D'. Can you explain this answer?
A graph is said to be a directed graph if ________ of the graph has direction.
a)
1 branch
b)
2 branches
c)
3 branches
d)
every branch
|
|
Pooja Patel answered |
If every branch of the graph has direction, then the graph is said to be a directed graph. If the graph does not have any direction then that graph is called undirected graph.
Consider the following statements regarding trees:1. A tree contains all the nodes of the graph.2. A tree shall contain any one of the loops.3. Every connected graph has at least one tree.Which of the above statements are correct?- a)1 and 2 only
- b)1 and 3 only
- c)2 and 3 only
- d)1, 2 and 3
Correct answer is option 'B'. Can you explain this answer?
Consider the following statements regarding trees:
1. A tree contains all the nodes of the graph.
2. A tree shall contain any one of the loops.
3. Every connected graph has at least one tree.
Which of the above statements are correct?
a)
1 and 2 only
b)
1 and 3 only
c)
2 and 3 only
d)
1, 2 and 3
|
Anjali Choudhury answered |
The Correct Answer is Option B: 1 and 3 only.
Explanation:
Let's analyze each statement one by one to determine their correctness.
Statement 1: A tree contains all the nodes of the graph.
This statement is correct. A tree is a type of graph that is connected and acyclic, which means it does not contain any loops or cycles. In a tree, every node is connected to every other node through a unique path. Therefore, all the nodes in a graph must be present in a tree.
Statement 2: A tree shall contain any one of the loops.
This statement is incorrect. As mentioned earlier, a tree is a graph without any loops or cycles. Therefore, a tree cannot contain any loops. If a graph contains a loop, it cannot be considered a tree.
Statement 3: Every connected graph has at least one tree.
This statement is correct. A connected graph is a graph in which there is a path between any two nodes. To form a tree from a connected graph, we need to remove some edges to eliminate any loops or cycles. By removing a minimum number of edges, we can obtain a tree that preserves the connectivity of the original graph. Therefore, every connected graph can be transformed into at least one tree.
Based on the analysis of each statement, we can conclude that statements 1 and 3 are correct, while statement 2 is incorrect. Thus, the correct answer is option B: 1 and 3 only.
Explanation:
Let's analyze each statement one by one to determine their correctness.
Statement 1: A tree contains all the nodes of the graph.
This statement is correct. A tree is a type of graph that is connected and acyclic, which means it does not contain any loops or cycles. In a tree, every node is connected to every other node through a unique path. Therefore, all the nodes in a graph must be present in a tree.
Statement 2: A tree shall contain any one of the loops.
This statement is incorrect. As mentioned earlier, a tree is a graph without any loops or cycles. Therefore, a tree cannot contain any loops. If a graph contains a loop, it cannot be considered a tree.
Statement 3: Every connected graph has at least one tree.
This statement is correct. A connected graph is a graph in which there is a path between any two nodes. To form a tree from a connected graph, we need to remove some edges to eliminate any loops or cycles. By removing a minimum number of edges, we can obtain a tree that preserves the connectivity of the original graph. Therefore, every connected graph can be transformed into at least one tree.
Based on the analysis of each statement, we can conclude that statements 1 and 3 are correct, while statement 2 is incorrect. Thus, the correct answer is option B: 1 and 3 only.
The maximum number of binary trees that can be formed with 4 unlabeled nodes is- a)10
- b)15
- c)14
- d)13
Correct answer is option 'C'. Can you explain this answer?
The maximum number of binary trees that can be formed with 4 unlabeled nodes is
a)
10
b)
15
c)
14
d)
13
|
|
Saumya Sen answered |
Solution:
To find the maximum number of binary trees that can be formed with 4 unlabeled nodes, we can use the formula for the number of binary trees with n nodes:
Number of binary trees = (2n)! / (n+1)!n!
where n is the number of nodes.
Using this formula, we can find the number of binary trees for n=4:
Number of binary trees = (2*4)! / (4+1)!4!
= 40320 / 120 * 24
= 14
Therefore, the maximum number of binary trees that can be formed with 4 unlabeled nodes is 14.
HTML Code:
To find the maximum number of binary trees that can be formed with 4 unlabeled nodes, we can use the formula for the number of binary trees with n nodes:
Number of binary trees = (2n)! / (n+1)!n!
where n is the number of nodes.
Using this formula, we can find the number of binary trees for n=4:
Number of binary trees = (2*4)! / (4+1)!4!
= 40320 / 120 * 24
= 14
Therefore, the maximum number of binary trees that can be formed with 4 unlabeled nodes is 14.
HTML Code:
Solution:
To find the maximum number of binary trees that can be formed with 4 unlabeled nodes, we can use the formula for the number of binary trees with n nodes:
- Number of binary trees = (2n)! / (n+1)!n!
- where n is the number of nodes.
Using this formula, we can find the number of binary trees for n=4:
- Number of binary trees = (2*4)! / (4+1)!4!
- = 40320 / 120 * 24
- = 14
Therefore, the maximum number of binary trees that can be formed with 4 unlabeled nodes is 14.
Number of twigs in a tree are? (where, n-number of nodes)- a)n
- b)n + 1
- c)n - 1
- d)n - 2
Correct answer is option 'C'. Can you explain this answer?
Number of twigs in a tree are? (where, n-number of nodes)
a)
n
b)
n + 1
c)
n - 1
d)
n - 2
|
|
Maulik Choudhury answered |
Explanation:
Number of Twigs in a Tree:
Twigs in a tree are the nodes that do not have any child nodes. In a tree structure, the number of twigs can be calculated using the formula n - 1, where n is the total number of nodes in the tree.
Calculation:
- Let's consider a tree with n nodes.
- In a tree, there is always 1 root node, which does not have a parent node.
- Therefore, the number of twigs in the tree will be equal to the total number of nodes minus 1.
- Hence, the formula to calculate the number of twigs in a tree is n - 1.
Therefore, the correct answer is option C - n - 1.
A connected network of N > 2 nodes has at most one branch directly connecting any pair of nodes. The graph of the network _____.- a)must have at least N branches for one or more closed paths to exist
- b)can have an unlimited number of branches
- c)can only have at most N branches
- d)can have a minimum number of branches not decided by N
Correct answer is option 'A'. Can you explain this answer?
A connected network of N > 2 nodes has at most one branch directly connecting any pair of nodes. The graph of the network _____.
a)
must have at least N branches for one or more closed paths to exist
b)
can have an unlimited number of branches
c)
can only have at most N branches
d)
can have a minimum number of branches not decided by N
|
Divya Nair answered |
Explanation:
Connected Network Constraints:
- A connected network of N nodes has at most one branch directly connecting any pair of nodes.
- This means that there can be multiple branches in the network, but only one branch can directly connect any pair of nodes.
Importance of Branches:
- For one or more closed paths to exist in a network, there must be at least N branches.
- Each branch creates a path between nodes, and in order to form a closed loop or path that connects all N nodes, there must be at least N branches.
Example:
- Consider a network with 3 nodes (N=3). If there is only 1 branch connecting all 3 nodes, there cannot be a closed loop or path that includes all nodes.
- However, if there are at least 3 branches in the network, different paths can be formed to create closed loops or paths that connect all nodes.
Conclusion:
- Therefore, the graph of the network must have at least N branches for one or more closed paths to exist.
- Having more branches can provide flexibility in creating different paths and connections within the network.
Connected Network Constraints:
- A connected network of N nodes has at most one branch directly connecting any pair of nodes.
- This means that there can be multiple branches in the network, but only one branch can directly connect any pair of nodes.
Importance of Branches:
- For one or more closed paths to exist in a network, there must be at least N branches.
- Each branch creates a path between nodes, and in order to form a closed loop or path that connects all N nodes, there must be at least N branches.
Example:
- Consider a network with 3 nodes (N=3). If there is only 1 branch connecting all 3 nodes, there cannot be a closed loop or path that includes all nodes.
- However, if there are at least 3 branches in the network, different paths can be formed to create closed loops or paths that connect all nodes.
Conclusion:
- Therefore, the graph of the network must have at least N branches for one or more closed paths to exist.
- Having more branches can provide flexibility in creating different paths and connections within the network.
If there are 4 branches, 3 nodes then number of links in a co-tree are?- a)2
- b)4
- c)6
- d)8
Correct answer is option 'A'. Can you explain this answer?
If there are 4 branches, 3 nodes then number of links in a co-tree are?
a)
2
b)
4
c)
6
d)
8
|
|
Pooja Patel answered |
Number of links = b - n + 1. Given number of branches = 4 and number of nodes = 3. On substituting in the equation, number of links in a co-tree = 4 – 3 + 1 = 2.
The tree elements are called __________- a)vertices
- b)nodes
- c)points
- d)edges
Correct answer is option 'B'. Can you explain this answer?
The tree elements are called __________
a)
vertices
b)
nodes
c)
points
d)
edges
|
|
Harsh Kulkarni answered |
Explanation:
In a tree data structure, the individual elements are known as nodes. The correct answer is option 'B' - nodes.
Nodes in a Tree:
- A tree is a hierarchical data structure that consists of nodes connected by edges.
- Each node in a tree can have zero or more child nodes.
- The nodes in a tree represent the elements of the data structure.
Characteristics of Nodes:
- Each node in a tree can have multiple children but only one parent (except for the root node, which has no parent).
- The nodes in a tree can be organized in a hierarchical manner, with one node being the parent of another node.
- The nodes in a tree are connected by edges, which represent the relationships between the nodes.
Vertices, Points, and Edges:
- While vertices, points, and edges are terminologies used in graph theory, they are not commonly used in the context of trees.
- In graph theory, vertices and nodes are often used interchangeably to refer to the elements of a graph.
- Points and edges are used to describe the connections between the vertices in a graph.
Conclusion:
- In the context of a tree data structure, the elements are called nodes.
- The nodes represent the individual elements of the tree, and they are connected by edges to form a hierarchical structure.
- Therefore, the correct answer is option 'B' - nodes.
In a tree data structure, the individual elements are known as nodes. The correct answer is option 'B' - nodes.
Nodes in a Tree:
- A tree is a hierarchical data structure that consists of nodes connected by edges.
- Each node in a tree can have zero or more child nodes.
- The nodes in a tree represent the elements of the data structure.
Characteristics of Nodes:
- Each node in a tree can have multiple children but only one parent (except for the root node, which has no parent).
- The nodes in a tree can be organized in a hierarchical manner, with one node being the parent of another node.
- The nodes in a tree are connected by edges, which represent the relationships between the nodes.
Vertices, Points, and Edges:
- While vertices, points, and edges are terminologies used in graph theory, they are not commonly used in the context of trees.
- In graph theory, vertices and nodes are often used interchangeably to refer to the elements of a graph.
- Points and edges are used to describe the connections between the vertices in a graph.
Conclusion:
- In the context of a tree data structure, the elements are called nodes.
- The nodes represent the individual elements of the tree, and they are connected by edges to form a hierarchical structure.
- Therefore, the correct answer is option 'B' - nodes.
The number of closed paths in a tree of the graph is:- a)3
- b)2
- c)0
- d)1
Correct answer is option 'C'. Can you explain this answer?
The number of closed paths in a tree of the graph is:
a)
3
b)
2
c)
0
d)
1
|
|
Maulik Choudhury answered |
Understanding Trees in Graph Theory
In graph theory, a tree is a special type of graph that has unique characteristics. Trees are widely used in various applications, especially in Electrical Engineering.
Key Characteristics of Trees:
- Acyclic Nature: Trees are defined as acyclic graphs, meaning they do not contain any cycles or closed paths.
- Connected Structure: A tree is connected, meaning there is a path between any two vertices. However, this connectivity does not lead to cycles.
- Vertices and Edges: A tree with 'n' vertices always has 'n-1' edges. This relationship contributes to the absence of cycles.
Closed Paths in Trees:
- Definition of Closed Paths: A closed path (or cycle) in a graph is a path that starts and ends at the same vertex without retracing any edges.
- Implication in Trees: Since trees are acyclic, they inherently have no closed paths. Each of the connections (edges) between vertices allows traversal without revisiting any edge.
Conclusion:
Given the definition and properties of trees, it is clear that:
- The number of closed paths in a tree is zero.
Thus, the correct answer to the question about the number of closed paths in a tree is option C) 0. This fundamental property of trees is crucial in understanding their structure and behavior in various applications, including network design and data organization in Electrical Engineering.
In graph theory, a tree is a special type of graph that has unique characteristics. Trees are widely used in various applications, especially in Electrical Engineering.
Key Characteristics of Trees:
- Acyclic Nature: Trees are defined as acyclic graphs, meaning they do not contain any cycles or closed paths.
- Connected Structure: A tree is connected, meaning there is a path between any two vertices. However, this connectivity does not lead to cycles.
- Vertices and Edges: A tree with 'n' vertices always has 'n-1' edges. This relationship contributes to the absence of cycles.
Closed Paths in Trees:
- Definition of Closed Paths: A closed path (or cycle) in a graph is a path that starts and ends at the same vertex without retracing any edges.
- Implication in Trees: Since trees are acyclic, they inherently have no closed paths. Each of the connections (edges) between vertices allows traversal without revisiting any edge.
Conclusion:
Given the definition and properties of trees, it is clear that:
- The number of closed paths in a tree is zero.
Thus, the correct answer to the question about the number of closed paths in a tree is option C) 0. This fundamental property of trees is crucial in understanding their structure and behavior in various applications, including network design and data organization in Electrical Engineering.
An undirected graph G which is connected and acyclic is called ____________- a)bipartite graph
- b)cyclic graph
- c)tree
- d)forest
Correct answer is option 'C'. Can you explain this answer?
An undirected graph G which is connected and acyclic is called ____________
a)
bipartite graph
b)
cyclic graph
c)
tree
d)
forest
|
|
Zoya Sharma answered |
An undirected graph G which is connected and acyclic is termed as a tree. G contains no cycles and if any edge is added to G a simple cycle is formed.
To construct the dual of a four-mesh network how many nodes are required?- a)4
- b)2
- c)3
- d)5
Correct answer is option 'D'. Can you explain this answer?
To construct the dual of a four-mesh network how many nodes are required?
a)
4
b)
2
c)
3
d)
5
|
|
Pooja Patel answered |
Concept:
Duality:
- Two electrical networks are said to be dual networks if the mesh equations of one network are equal to the node equation of others.
- Identical behavior patterns observed between voltages and currents in two circuits illustrate the principle of duality.
- The dual networks are based on Kirchhoff Current Law and Kirchhoff Voltage Law.
Nodal Analysis:
Nodal analysis is a method of analyzing networks with the help of KCL equations.
For a network of N nodes, the number of simultaneous equations to be solved to get the unknowns
= Number of KCL equations
= N - 1
Mesh Analysis:
Mesh analysis is a method of analyzing networks with the help of KVL equations.
For a network having N nodes and B branches, the number of simultaneous equations to be solved to get the unknowns
= Number of KVL equations
= number of independent loop equations
= B - N + 1
Application:
Given: KVL equations = 4,
Therefore, B - N + 1 = 4
B = 3 + N ........(1)
For duality of two networks,
Mesh equations of one network = nodal equations of other
Hence,
B - N + 1 = N - 1
N = B + 2 / 2 .....(2)
substitute (1) in (2)
N = N + 5 / 2
N = 5
If a graph consists of 5 nodes, then the number of twigs in the tree is?- a)1
- b)2
- c)3
- d)4
Correct answer is option 'D'. Can you explain this answer?
If a graph consists of 5 nodes, then the number of twigs in the tree is?
a)
1
b)
2
c)
3
d)
4
|
|
Pooja Patel answered |
Number of twigs = n-1. As given number of nodes are 5 then n = 5. On substituting in the equation, number of twigs = 5 -1 = 4.
If [A] Matrix is Incidence matrix then which one of the following is true?- a)|A| = 0 (For closed loop)
- b)Adj [A] / |A| = 0 (For closed loop)
- c)[A] = 1 (For closed loop)
- d)|A| = 1 (For closed loop)
Correct answer is option 'A'. Can you explain this answer?
If [A] Matrix is Incidence matrix then which one of the following is true?
a)
|A| = 0 (For closed loop)
b)
Adj [A] / |A| = 0 (For closed loop)
c)
[A] = 1 (For closed loop)
d)
|A| = 1 (For closed loop)
|
|
Raghav Nambiar answered |
Understanding the Incidence Matrix
An incidence matrix is a mathematical representation used in graph theory, particularly in electrical engineering for circuit analysis. Each row represents a node, and each column represents a branch of the network.
Closed Loop in Circuit Theory
In circuit theory, a closed loop refers to a continuous path in which a circuit returns to its original point. This is essential for the analysis of circuits, especially when applying Kirchhoff's laws.
Determinant of the Incidence Matrix
- The determinant of the incidence matrix, denoted as |A|, provides information about the properties of the graph.
- For a closed loop, the determinant of the incidence matrix is always equal to zero (|A| = 0).
Why |A| = 0 for Closed Loops?
- A closed loop indicates that there is a redundancy in the paths, meaning that the matrix does not have full rank.
- When a graph has a closed loop, there are linearly dependent rows in the incidence matrix, leading to a determinant of zero.
Conclusion
Thus, when evaluating the properties of an incidence matrix for a network with a closed loop, the correct assertion is that the determinant of the incidence matrix is zero.
Overall, the assertion that |A| = 0 for a closed loop is a fundamental concept in understanding the relationship between graphs and their matrix representations in electrical engineering.
An incidence matrix is a mathematical representation used in graph theory, particularly in electrical engineering for circuit analysis. Each row represents a node, and each column represents a branch of the network.
Closed Loop in Circuit Theory
In circuit theory, a closed loop refers to a continuous path in which a circuit returns to its original point. This is essential for the analysis of circuits, especially when applying Kirchhoff's laws.
Determinant of the Incidence Matrix
- The determinant of the incidence matrix, denoted as |A|, provides information about the properties of the graph.
- For a closed loop, the determinant of the incidence matrix is always equal to zero (|A| = 0).
Why |A| = 0 for Closed Loops?
- A closed loop indicates that there is a redundancy in the paths, meaning that the matrix does not have full rank.
- When a graph has a closed loop, there are linearly dependent rows in the incidence matrix, leading to a determinant of zero.
Conclusion
Thus, when evaluating the properties of an incidence matrix for a network with a closed loop, the correct assertion is that the determinant of the incidence matrix is zero.
Overall, the assertion that |A| = 0 for a closed loop is a fundamental concept in understanding the relationship between graphs and their matrix representations in electrical engineering.
If the number of branch in a network is b, the number of nodes is n and the number of dependent loop is l, then the number of independent node equations will be- a)n + l - 1
- b)b - 1
- c)b - n + 1
- d)n - 1
Correct answer is option 'D'. Can you explain this answer?
If the number of branch in a network is b, the number of nodes is n and the number of dependent loop is l, then the number of independent node equations will be
a)
n + l - 1
b)
b - 1
c)
b - n + 1
d)
n - 1
|
Alok Verma answered |
The number of independent node equation are n - 1.
The number of twigs and links in a connected network graph with 'n' nodes and 'b' branches are, respectively.- a)n - 2, b - n - 2
- b)n - 1, b - n + 1
- c)n, 2n - b
- d)2n, 2n - b
Correct answer is option 'B'. Can you explain this answer?
The number of twigs and links in a connected network graph with 'n' nodes and 'b' branches are, respectively.
a)
n - 2, b - n - 2
b)
n - 1, b - n + 1
c)
n, 2n - b
d)
2n, 2n - b
|
|
Pooja Patel answered |
Concept:
Tree: A tree is a sub graph of main graph which connects all the nodes without forming a closed loop.
For a graph with ‘n’ nodes, the rank of tree = n – 1
Any tree for a given graph can be constructed with (n–1) branches.
Twig: The branch of a tree is called as twig indicated by thick Line. Any tree with n nodes has (n – 1) twigs.
Co-tree: The set of branches in a graph other than tree branches form a co tree.
Link: The branch of a co tree is called link indicated by dotted Line.
For any graph with n nodes and b branches, the numbers of links is given by:
= b – n + 1
What is a star tree?- a)A tree having a single internal vertex and n-1 leaves
- b)A tree having n vertices arranged in a line
- c)A tree which has 0 or more connected subtrees
- d)A tree which contains n vertices and n-1 cycles
Correct answer is option 'A'. Can you explain this answer?
What is a star tree?
a)
A tree having a single internal vertex and n-1 leaves
b)
A tree having n vertices arranged in a line
c)
A tree which has 0 or more connected subtrees
d)
A tree which contains n vertices and n-1 cycles
|
|
Aaditya Choudhary answered |
A star tree is a tree having a single internal vertex and n-1 leaves.
A tree is a connected acyclic graph, meaning that it consists of a set of vertices and edges, where each edge connects two vertices and there are no cycles (loops) in the graph. In a tree, there is a unique path between any pair of vertices.
A star tree is a specific type of tree that has a distinctive shape resembling a star. It consists of a single internal vertex, also known as the center or hub, and n-1 leaves, which are the endpoints of the edges connected to the internal vertex. The internal vertex is connected to each of the leaves, but the leaves are not connected to each other.
Example:
Let's consider an example to illustrate a star tree. Suppose we have a star tree with 5 leaves. The tree will have 6 vertices in total - one internal vertex and five leaves.
Internal Vertex:
- The internal vertex is the center of the star tree.
- It has a degree of n-1, where n is the number of leaves.
- In this example, the internal vertex will have a degree of 4.
Leaves:
- The leaves are the endpoints of the edges connected to the internal vertex.
- Each leaf has a degree of 1, as it is connected only to the internal vertex.
- In this example, each of the five leaves will have a degree of 1.
Edges:
- The edges connect the internal vertex to each of the leaves.
- In this example, there will be five edges connecting the internal vertex to each of the leaves.
Properties of a star tree:
- A star tree has n vertices, where n is the number of leaves.
- It has n-1 edges, connecting the internal vertex to each of the leaves.
- The internal vertex has a degree of n-1, while the leaves have a degree of 1.
- The leaves are not connected to each other, only to the internal vertex.
Conclusion:
In summary, a star tree is a specific type of tree that consists of a single internal vertex and n-1 leaves. The internal vertex is connected to each of the leaves, and the leaves are not connected to each other. This structure gives the tree its distinctive star-like shape.
A tree is a connected acyclic graph, meaning that it consists of a set of vertices and edges, where each edge connects two vertices and there are no cycles (loops) in the graph. In a tree, there is a unique path between any pair of vertices.
A star tree is a specific type of tree that has a distinctive shape resembling a star. It consists of a single internal vertex, also known as the center or hub, and n-1 leaves, which are the endpoints of the edges connected to the internal vertex. The internal vertex is connected to each of the leaves, but the leaves are not connected to each other.
Example:
Let's consider an example to illustrate a star tree. Suppose we have a star tree with 5 leaves. The tree will have 6 vertices in total - one internal vertex and five leaves.
Internal Vertex:
- The internal vertex is the center of the star tree.
- It has a degree of n-1, where n is the number of leaves.
- In this example, the internal vertex will have a degree of 4.
Leaves:
- The leaves are the endpoints of the edges connected to the internal vertex.
- Each leaf has a degree of 1, as it is connected only to the internal vertex.
- In this example, each of the five leaves will have a degree of 1.
Edges:
- The edges connect the internal vertex to each of the leaves.
- In this example, there will be five edges connecting the internal vertex to each of the leaves.
Properties of a star tree:
- A star tree has n vertices, where n is the number of leaves.
- It has n-1 edges, connecting the internal vertex to each of the leaves.
- The internal vertex has a degree of n-1, while the leaves have a degree of 1.
- The leaves are not connected to each other, only to the internal vertex.
Conclusion:
In summary, a star tree is a specific type of tree that consists of a single internal vertex and n-1 leaves. The internal vertex is connected to each of the leaves, and the leaves are not connected to each other. This structure gives the tree its distinctive star-like shape.
For a network graph having its fundamental loop matrix Bf and its sub-matrices Bt and Bl corresponding to twigs and links, which of the following statements are correct?1) Bl is always an identity matrix.2) Bt is an identity matrix.3) Bf has rank of b – (n – 1), where b is the number of branches and n is the number of nodes of the graph.- a)1 and 2 only
- b)2 and 3 only
- c)1 and 3 only
- d)1, 2 and 3
Correct answer is option 'C'. Can you explain this answer?
For a network graph having its fundamental loop matrix Bf and its sub-matrices Bt and Bl corresponding to twigs and links, which of the following statements are correct?
1) Bl is always an identity matrix.
2) Bt is an identity matrix.
3) Bf has rank of b – (n – 1), where b is the number of branches and n is the number of nodes of the graph.
a)
1 and 2 only
b)
2 and 3 only
c)
1 and 3 only
d)
1, 2 and 3
|
|
Tanishq Majumdar answered |
Explanation:
Bl is always an identity matrix:
- The sub-matrix Bl corresponds to links, which represent the branches of the network graph.
- Each link in the network graph is independent of other links, hence the sub-matrix Bl will always be an identity matrix.
Bt is not an identity matrix:
- The sub-matrix Bt corresponds to twigs, which are sets of branches that form loops.
- Unlike links, twigs are not independent of each other, so the sub-matrix Bt will not be an identity matrix.
Bf has rank of b - (n - 1):
- The fundamental loop matrix Bf is a square matrix of size (b x b), where b is the number of branches in the network.
- The rank of Bf is equal to the number of linearly independent rows or columns in the matrix.
- For a connected network with n nodes, the rank of Bf is given by b - (n - 1), where n is the number of nodes.
Therefore, the correct statements are:
- 1 and 3 only.
Bl is always an identity matrix:
- The sub-matrix Bl corresponds to links, which represent the branches of the network graph.
- Each link in the network graph is independent of other links, hence the sub-matrix Bl will always be an identity matrix.
Bt is not an identity matrix:
- The sub-matrix Bt corresponds to twigs, which are sets of branches that form loops.
- Unlike links, twigs are not independent of each other, so the sub-matrix Bt will not be an identity matrix.
Bf has rank of b - (n - 1):
- The fundamental loop matrix Bf is a square matrix of size (b x b), where b is the number of branches in the network.
- The rank of Bf is equal to the number of linearly independent rows or columns in the matrix.
- For a connected network with n nodes, the rank of Bf is given by b - (n - 1), where n is the number of nodes.
Therefore, the correct statements are:
- 1 and 3 only.
What is a bipartite graph?- a)a graph which contains only one cycle
- b)a graph which consists of more than 3 number of vertices
- c)a graph which has odd number of vertices and even number of edges
- d)a graph which contains no cycles of odd length
Correct answer is option 'D'. Can you explain this answer?
What is a bipartite graph?
a)
a graph which contains only one cycle
b)
a graph which consists of more than 3 number of vertices
c)
a graph which has odd number of vertices and even number of edges
d)
a graph which contains no cycles of odd length
|
|
Harsh Kulkarni answered |
A bipartite graph is a type of graph in which the vertices can be divided into two disjoint sets such that all edges connect vertices from different sets. In other words, there are no edges that connect vertices within the same set.
Explanation:
- Bipartite graph definition:
- A bipartite graph G = (V, E) is a graph whose vertex set V can be partitioned into two sets V1 and V2 such that every edge in E connects a vertex from V1 to a vertex from V2.
- Example of a bipartite graph:
- A simple example of a bipartite graph is a graph representing the relationship between students and classes. Let's say we have a set of students (V1) and a set of classes (V2). An edge between a student and a class indicates that the student is enrolled in that class. In this case, all the edges will connect a student from V1 to a class from V2, satisfying the definition of a bipartite graph.
- No cycles of odd length:
- One important property of bipartite graphs is that they do not contain any cycles of odd length. This can be proven by contradiction. Assume we have a bipartite graph with a cycle of odd length. Since the cycle is of odd length, the number of edges in the cycle is also odd. But according to the definition of a bipartite graph, all edges connect vertices from different sets. Therefore, the number of edges in the cycle must be even, which contradicts our assumption.
- Why no cycles of odd length?
- The absence of cycles of odd length in bipartite graphs is related to the concept of colorability. Bipartite graphs can be colored with two colors such that no adjacent vertices have the same color. This is known as a 2-coloring. If a cycle of odd length exists in a bipartite graph, it would require three colors to color the vertices in the cycle without adjacent vertices having the same color. But since a bipartite graph can be 2-colored, the existence of a cycle of odd length would contradict the property of being bipartite.
In summary, a bipartite graph is a graph in which the vertices can be divided into two disjoint sets such that all edges connect vertices from different sets. Additionally, bipartite graphs do not contain cycles of odd length.
Explanation:
- Bipartite graph definition:
- A bipartite graph G = (V, E) is a graph whose vertex set V can be partitioned into two sets V1 and V2 such that every edge in E connects a vertex from V1 to a vertex from V2.
- Example of a bipartite graph:
- A simple example of a bipartite graph is a graph representing the relationship between students and classes. Let's say we have a set of students (V1) and a set of classes (V2). An edge between a student and a class indicates that the student is enrolled in that class. In this case, all the edges will connect a student from V1 to a class from V2, satisfying the definition of a bipartite graph.
- No cycles of odd length:
- One important property of bipartite graphs is that they do not contain any cycles of odd length. This can be proven by contradiction. Assume we have a bipartite graph with a cycle of odd length. Since the cycle is of odd length, the number of edges in the cycle is also odd. But according to the definition of a bipartite graph, all edges connect vertices from different sets. Therefore, the number of edges in the cycle must be even, which contradicts our assumption.
- Why no cycles of odd length?
- The absence of cycles of odd length in bipartite graphs is related to the concept of colorability. Bipartite graphs can be colored with two colors such that no adjacent vertices have the same color. This is known as a 2-coloring. If a cycle of odd length exists in a bipartite graph, it would require three colors to color the vertices in the cycle without adjacent vertices having the same color. But since a bipartite graph can be 2-colored, the existence of a cycle of odd length would contradict the property of being bipartite.
In summary, a bipartite graph is a graph in which the vertices can be divided into two disjoint sets such that all edges connect vertices from different sets. Additionally, bipartite graphs do not contain cycles of odd length.
If the incident matrix of a graph is given below. The corresponding graph is?
- a)
- b)
- c)
- d)
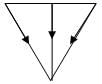
Correct answer is option 'B'. Can you explain this answer?
If the incident matrix of a graph is given below. The corresponding graph is?
a)
b)
c)
d)
|
Cstoppers Instructors answered |
For the given incidence matrix,
the corresponding graph is
considering the directions specified in the graph.
If one link fails, the entire network can be disabled in ______.- a)Mesh Topology
- b)Bus Topology
- c)Star Topology
- d)Bus and Ring Topology
Correct answer is option 'D'. Can you explain this answer?
If one link fails, the entire network can be disabled in ______.
a)
Mesh Topology
b)
Bus Topology
c)
Star Topology
d)
Bus and Ring Topology
|
|
Pioneer Academy answered |
Concept:
A single cable links all of the included nodes in a bus topology. The primary cable serves as the network's backbone. If the common cable breaks, the entire system will be brought to a halt.
Every device in a ring network has exactly two neighbors for communication purposes. It's called ring topology because it's shaped like a ring. Every computer in this topology is linked to another computer. A single computer failure can disrupt the entire network.
As a result, bus and ring topologies have difficulties, such as the possibility of the entire network being deactivated if one connection fails.
Hence the correct answer is Bus and Ring Topology.
Loops which contain only one link are independent are called?- a)open loops
- b)closed loops
- c)basic loops
- d)none of the mentioned
Correct answer is option 'C'. Can you explain this answer?
Loops which contain only one link are independent are called?
a)
open loops
b)
closed loops
c)
basic loops
d)
none of the mentioned
|
|
Zoya Sharma answered |
The addition of subsequent link forms one or more additional loops. Loops that contain only one link are independent are called basic loops.
If A represents incidence matrix, I represents branch current vectors, then?- a)AI = 1
- b)AI = 0
- c)AI = 2
- d)AI= 3
Correct answer is option 'B'. Can you explain this answer?
If A represents incidence matrix, I represents branch current vectors, then?
a)
AI = 1
b)
AI = 0
c)
AI = 2
d)
AI= 3
|
|
Pooja Patel answered |
If A represents incidence matrix, I represents branch current vectors, then the relation is AI= 0 that is its characteristic equation must be equated to zero
Following is not the property of a complete incidence matrix:- a)Algebraic sum of the column entries of an incidence matrix is zero
- b)The rank of a complete incidence matrix of a connected graph is (n - 1), where n is total number of nodes
- c)Order of a complete incidence matrix will be (n × b), where b is total number of branches and n is total number of nodes
- d)Determinant of the incidence matrix of a closed loop is not zero.
Correct answer is option 'D'. Can you explain this answer?
Following is not the property of a complete incidence matrix:
a)
Algebraic sum of the column entries of an incidence matrix is zero
b)
The rank of a complete incidence matrix of a connected graph is (n - 1), where n is total number of nodes
c)
Order of a complete incidence matrix will be (n × b), where b is total number of branches and n is total number of nodes
d)
Determinant of the incidence matrix of a closed loop is not zero.
|
|
Pooja Patel answered |
Incidence matrix:
- It is the matrix which gives relation between branches and nodes.
- The rows of matrix represent the number of nodes and the columns of matrix represents the numbers of branches.
- We can construct the incidence matrix for the directed graph. We can draw a graph with the help of incidence matrix.
- The algebraic sum of elements of all the columns is zero.
- The rank of incidence matrix is (n–1).
- The order of incidence matrix will be (n × b).
- The determinant of the incidence matrix of a closed loop is zero.
The elements of incidence matrix are given by [A] = [aij]n × b
Where aij = 1, if jth branch is incident at ith node and oriented away.
aij = -1, if jth branch is incident at ith node and oriented towards.
aij = 0, if jth branch is not incident at ith node
b is total number of branches
n is total number of nodes
Reduced incidence matrix:
- If one of the nodes in the given graph is considered as reference node, then that row can be neglected by writing incidence matrix is called as reduced incidence matrix.
- The order of reduced incidence matrix is (n – 1) × b.
- The Algebraic sum of some of the columns is not zero.
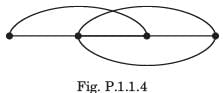
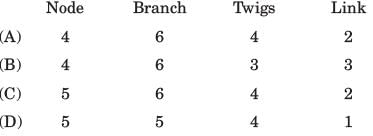
For the graph shown in fig. P.1.1.4 correct set is
- a)A
- b)B
- c)C
- d)D
Correct answer is option 'B'. Can you explain this answer?
For the graph shown in fig. P.1.1.4 correct set is
a)
A
b)
B
c)
C
d)
D
|
|
Meghana Gupta answered |
There are 4 node and 6 branches.
t = n - 1 = 3, l = b - n + 1 = 3
t = n - 1 = 3, l = b - n + 1 = 3
Consider the following with regards to graph as shown in the figure given below: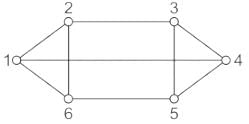
1. Regular graph2. Connected graph3. Complete graph4. Non-regular graphWhich of the above are correct?- a)1 and 4
- b)3 and 4
- c)2 and 3
- d)1 and 2
Correct answer is option 'D'. Can you explain this answer?
Consider the following with regards to graph as shown in the figure given below:
1. Regular graph
2. Connected graph
3. Complete graph
4. Non-regular graph
Which of the above are correct?
a)
1 and 4
b)
3 and 4
c)
2 and 3
d)
1 and 2
|
|
Pooja Patel answered |
Concept:
- A graph is said to be a regular graph if all nodes connected with other nodes in the same manner, otherwise the graph will be non-regular.
- A graph is said to be a connected graph, if at least one branch must present between any two nodes of the graph otherwise it will be an unconnected graph.
- A graph is said to be a complete graph if every node in the graph is connected with every other node in the graph.
Analysis:
A network graph is given as:
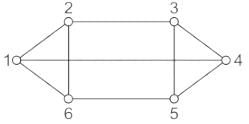
From the network graph above, we have:
Total nodes or vertex = 6
= (1, 2, 3, 4, 5, 6)
And Total edges or branches = 9
= (1 - 2), (2 - 3), (3 - 4), (4 - 5), (5 - 6), (6 - 1), (1 - 4), (2 - 6), (3 - 5)
- Since each node of the graph is connected via three other nodes. So it is a regular graph.
- i.e. for Node 1: Node 2, 4, 6 are connected from node-1
- for node-2: nodes 1, 6, 3 are connected from node 2, and so on.
- In the network graph, a defined path exists between every pair of nodes. So it is a connected graph.
- Since in the given network graph, every node is not connected with every other node. So it is not a complete graph.
- e.g. node 1 is not connected from node 3, 5
- node 2 is not connected from nodes 4, 5, and so on.
Branch current and loop current relation are expressed in matrix form as
where ij represent branch current and Ik loop current.
Q. The directed graph will be- a)
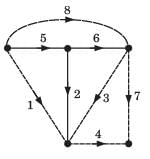
- b)
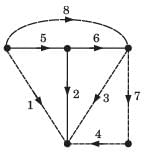
- c)
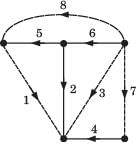
- d)
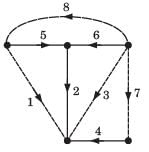
Correct answer is option 'B'. Can you explain this answer?
Branch current and loop current relation are expressed in matrix form as
where ij represent branch current and Ik loop current.
Q. The directed graph will be
where ij represent branch current and Ik loop current.
Q. The directed graph will be
a)
b)
c)
d)
|
|
Shanaya Mehta answered |
We know the branch current and loop current are related as
f-loop 1 include branch (2, 4, 6, 7) and direction of branch–2 is opposite to other (B only).
f-loop 1 include branch (2, 4, 6, 7) and direction of branch–2 is opposite to other (B only).
A network has 8 branches and 3 independent loops. How many nodes are there in the network?- a)6
- b)5
- c)11
- d)10
Correct answer is option 'A'. Can you explain this answer?
A network has 8 branches and 3 independent loops. How many nodes are there in the network?
a)
6
b)
5
c)
11
d)
10
|
|
Zoya Sharma answered |
Concept:
Nodal Analysis:
Nodal analysis is a method of analyzing network with the help of KCL equations.
For a network of N nodes, the number of simultaneous equations to be solved to get the unknowns
= Number of KCL equations
= N - 1
Mesh Analysis:
Mesh analysis is a method of analyzing network with the help of KVL equations.
For a network having N nodes and B branches, the number of simultaneous equations to be solved to get the unknowns
= Number of KVL equations
= number of independent loop equations
= B - N + 1
Calculation:
Given that, number of loops (l) = 3
Number of branches (b) = 8
In any network, number of independent loops,
l = b – n + 1
⇒ 3 = 8 – n + 1
⇒ n = 6
Branch current and loop current relation are expressed in matrix form as
where ij represent branch current and Ik loop current. The number of independent node equation are- a)4
- b)5
- c)6
- d)7
Correct answer is option 'A'. Can you explain this answer?
Branch current and loop current relation are expressed in matrix form as
where ij represent branch current and Ik loop current. The number of independent node equation are
where ij represent branch current and Ik loop current. The number of independent node equation are
a)
4
b)
5
c)
6
d)
7
|
|
Mayank Sengupta answered |
Number of branch = 8
Number of link = 4
Number of twigs = 8 - 4 = 4
Number of twigs =number of independent node equation.
Number of link = 4
Number of twigs = 8 - 4 = 4
Number of twigs =number of independent node equation.
Branch current and loop current relation are expressed in matrix form as
where ij represent branch current and Ik loop current.
Q. The rank of incidence matrix is- a)4
- b)5
- c)6
- d)8
Correct answer is option 'A'. Can you explain this answer?
Branch current and loop current relation are expressed in matrix form as
where ij represent branch current and Ik loop current.
Q. The rank of incidence matrix is
where ij represent branch current and Ik loop current.
Q. The rank of incidence matrix is
a)
4
b)
5
c)
6
d)
8
|
|
Sparsh Saini answered |
Number of branch b=8
Number of link l = 4
Number of twigs t = b - l = 4
rank of matrix = n - 1 = t = 4
Number of link l = 4
Number of twigs t = b - l = 4
rank of matrix = n - 1 = t = 4
Consider the graph given below. Which of the following is a not a tree to the graph?
- a)
- b)
- c)
- d)
Correct answer is option 'D'. Can you explain this answer?
Consider the graph given below. Which of the following is a not a tree to the graph?
a)
b)
c)
d)
|
|
Pooja Patel answered |
Tree is sub graph which consists of all node of original graph but no closed paths. So, ‘d’ is not a tree to the graph.
Which of the following is not true for tree and graph?- a)A tree is a graph
- b)A graph is a tree
- c)Tree can have a cycle
- d)Tree is a DAG
Correct answer is option 'C'. Can you explain this answer?
Which of the following is not true for tree and graph?
a)
A tree is a graph
b)
A graph is a tree
c)
Tree can have a cycle
d)
Tree is a DAG
|
|
Zoya Sharma answered |
Tree:
A tree is a connected subgraph of a connected graph containing all the nodes of the graph but containing no loops, i.e., there is a unique path between every pair of nodes.
The number of closed paths in a tree of the graph is zero. Therefore is not true for tree and graph.
Twig: The branches of the tree are called twigs.
Link: Those branches of the graph which are not in the tree.
Co-tree: All the links of a tree together constitute complement of the tree and is called co-tree, in which the number of branches is equal to b - (n - 1)
Where b is the number of branches of the graph.
Number of twigs: t = n - 1
Number of links: L = b - t = b – n + 1
If we want to represent a relation between number of link current and number of branch currents in a directional graph, we should use: - a)reduced incidence
- b)incidence
- c)tie set
- d)cutset
Correct answer is option 'C'. Can you explain this answer?
If we want to represent a relation between number of link current and number of branch currents in a directional graph, we should use:
a)
reduced incidence
b)
incidence
c)
tie set
d)
cutset
|
|
Pooja Patel answered |
Tie set matrix:
- It gives the relation between tie-set currents and branch currents.
- The rows of a matrix represent the tie-set currents.
- The columns of a matrix represent branches of the graph.
- The order of the tie set matrix is (B – N + 1) × b
- The rank of a tie-set matrix is (B – N + 1)
Cut-set matrix:
- It gives the relation between cut-set voltages and branch voltages.
- The rows of a matrix represent the cut-set voltages.
- The columns of a matrix represent the branches of the graph.
- The order of the cut-set matrix is (n – 1) × b.
- The rank of a cut-set matrix is (n – 1)
Incidence matrix:
- It is the matrix which gives relation between branches and nodes.
- The rows of matrix represent the number of nodes and the columns of matrix represents the numbers of branches.
- We can construct the incidence matrix for the directed graph. We can draw a graph with the help of incidence matrix.
- The algebraic sum of elements of all the columns is zero.
- The rank of incidence matrix is (n – 1).
- The order of incidence matrix will be (n × b).
- The determinant of the incidence matrix of a closed loop is zero.
Reduced incidence matrix:
- If one of the nodes in the given graph is considered as reference node, then that row can be neglected by writing incidence matrix is called as reduced incidence matrix.
- The order of reduced incidence matrix is (n – 1) × b.
- The Algebraic sum of some of the columns is not zero.
A loop which does not contain any other loop within it is called _________.- a)Mesh
- b)Super node
- c)Node
- d)Port
Correct answer is option 'A'. Can you explain this answer?
A loop which does not contain any other loop within it is called _________.
a)
Mesh
b)
Super node
c)
Node
d)
Port
|
|
Pooja Patel answered |
Node:
A point or junction where two or more circuit elements (resistor, capacitor, inductor, etc.) meet is called Node. In other words, a point of connection between two or more branches is known as a Node.
Supernode:
If a voltage source is connected between two non-reference nodes, then we combine the two nodes as to yield super node.
Branch:
That part or section of a circuit locate between two junctions is called the branch. In a branch, one or more elements can be connected, and they have two terminals.
Loop:
A closed path in a circuit where more than two meshes can occur is known as Loop i.e. there may be many meshes in a loop, but a mesh does not contain on one loop.
Mesh:
A closed-loop that contains no other loop within it or a path which does not contain other paths is called Mesh.
Super mesh:
If a current source is present at the common boundary of two meshes, then we create a super mesh by avoiding the current source and any element connected to it in series.
Note: The number of independent loops for a network with n nodes and b branches is = b - n + 1
The degree of a tree is the _____ degree of a node in the tree.- a)Maximum
- b)second minimum
- c)minimum
- d)second maximum
Correct answer is option 'A'. Can you explain this answer?
The degree of a tree is the _____ degree of a node in the tree.
a)
Maximum
b)
second minimum
c)
minimum
d)
second maximum
|
|
Zoya Sharma answered |
Concept:
Tree:
- A tree consists of nodes or vertices that store information and often are labeled by a number or a letter.
- A tree consists of directed edges or undirected edges or both.
- The number of subtrees of a node is called its degree.
- A leaf or a terminal node is a node of degree zero
- A node that is not a leaf is called an interior node or an internal node
The degree of a node is the number of its children. The degree of a tree is the maximum degree of any of its nodes.
Consider the following graphs
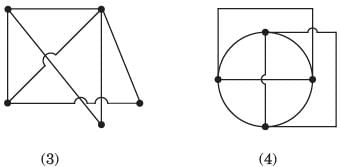
Non-planner graphs are- a)1 and 3
- b)4 only
- c)3 only
- d)3 and 4
Correct answer is option 'B'. Can you explain this answer?
Consider the following graphs
Non-planner graphs are
Non-planner graphs are
a)
1 and 3
b)
4 only
c)
3 only
d)
3 and 4
|
|
Suyash Joshi answered |
Other three circuits can be drawn on plane without crossing
Which one of the following property is correct for a red-black tree?- a)Every simple path from a node to a descendant leaf contains the same number of black nodes
- b)If a node is red, then one children is red and another is black
- c)If a node is red, then both its children are red
- d)Every leaf node (sentinel node) is red
Correct answer is option 'A'. Can you explain this answer?
Which one of the following property is correct for a red-black tree?
a)
Every simple path from a node to a descendant leaf contains the same number of black nodes
b)
If a node is red, then one children is red and another is black
c)
If a node is red, then both its children are red
d)
Every leaf node (sentinel node) is red
|
|
Zoya Sharma answered |
A red-black tree is a balanced binary search tree with the following properties:
- Every node is colored red or black.
- Every leaf is a NIL node and is colored black.
- If a node is red, then both its children are black.
- Every simple path from a node to a descendant leaf contains the same number of black nodes.
The incident matrix of a graph is given below:
The corresponding graph is- a)
- b)
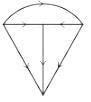
- c)
- d)
Correct answer is option 'B'. Can you explain this answer?
The incident matrix of a graph is given below:
The corresponding graph is
a)
b)
c)
d)
|
|
Zoya Sharma answered |
Concept:
- The no. of rows in an incident matrix determines the total no. of nodes present in a graph.
- The no. of columns in an incident matrix determines the total no. of branches present in a graph.
- The incoming arrow to a node is taken as -1.
- The outgoing arrow to a node is taken as +1.
Explanation:
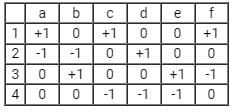
Following are the results from the above incident matrix:
No. of rows = 4 = Total no. of nodes
No. of columns = 6 = Total no. of branches
Node 1: Three outgoing arrows
Node 2: Two incoming and one outgoing arrow
Node 3: One incoming and two outgoing arrows
Node 4: Three incoming arrows
All the above conditions are fulfilled by option 2.
In which of the following network topologies, each device has a dedicated point-to-point link with only two devices on its either side and a signal is passed in one direction, from source to destination?- a)Mesh
- b)Ring
- c)Bus
- d)Star
Correct answer is option 'B'. Can you explain this answer?
In which of the following network topologies, each device has a dedicated point-to-point link with only two devices on its either side and a signal is passed in one direction, from source to destination?
a)
Mesh
b)
Ring
c)
Bus
d)
Star
|
|
Pooja Patel answered |
Concept:
Network topology:
Network topology refers to the manner in which the links and nodes of a network are arranged to relate to each other.
Ring Topology:
In a ring topology,each device a dedicated point-to-point line configuration only with the two device on either side of it. A signal is passed along the ring in one direction from devices to device,until it reaches its destination.
Hence the correct answer is ring.
Chapter doubts & questions for Graph Theory - Network Theory (Electric Circuits) 2025 is part of Electrical Engineering (EE) exam preparation. The chapters have been prepared according to the Electrical Engineering (EE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electrical Engineering (EE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Graph Theory - Network Theory (Electric Circuits) in English & Hindi are available as part of Electrical Engineering (EE) exam.
Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free.
Network Theory (Electric Circuits)
76 videos|152 docs|62 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily