All Exams >
Civil Engineering (CE) >
Topicwise Question Bank for Civil Engineering >
All Questions
All questions of Structural Analysis for Civil Engineering (CE) Exam
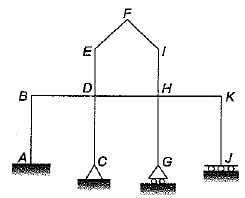
Neglecting axial deformation, the kinematic indeterminacy of the structure shown in the figure below is
- a)12
- b)14
- c)20
- d)22
Correct answer is option 'B'. Can you explain this answer?
Neglecting axial deformation, the kinematic indeterminacy of the structure shown in the figure below is
a)
12
b)
14
c)
20
d)
22
|
Engineers Adda answered |
j = 11; r=8; m=11
Dk = 3j-r-no. of inextensible members = 3(11) – 8 -11 = 14
Dk = 3j-r-no. of inextensible members = 3(11) – 8 -11 = 14
Which one of the following statements is correct? The principle of superposition is applicable to- a)nonlinear behaviour of material and small displacement theory.
- b)nonlinear behaviour of material and large displacement theory.
- c)linear elastic behaviour of material and small displacement theory.
- d)linear elastic behaviour of material and large displacement theory.
Correct answer is option 'C'. Can you explain this answer?
Which one of the following statements is correct? The principle of superposition is applicable to
a)
nonlinear behaviour of material and small displacement theory.
b)
nonlinear behaviour of material and large displacement theory.
c)
linear elastic behaviour of material and small displacement theory.
d)
linear elastic behaviour of material and large displacement theory.
|
Lavanya Menon answered |
The principle of superposition states that the displacements resulting from each of a number of forces may be added to obtain the displacements resulting from the sum of forces. This method depends upon the linearity of the governing relations between the load and deflection, The linearity depends upon two factors.
(i) the linearity between bending moment and curvature which depends upon the linear elastic materials In non-linear material superposition of curvatures is not possible.
(ii) the linearity between curvatures and deflection depends upon the assumption that the deflections are so small that the approximate curvature can be used in place of true curvature.
(i) the linearity between bending moment and curvature which depends upon the linear elastic materials In non-linear material superposition of curvatures is not possible.
(ii) the linearity between curvatures and deflection depends upon the assumption that the deflections are so small that the approximate curvature can be used in place of true curvature.
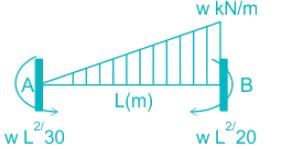
A circular three-pinned arch of span 40 m and a rise of 8 m is hinged at the crown and springings. it carries a horizontal load of 100 kN per vertical metre on the left side. The horizontal thrust at the right springing will be- a)200 kN
- b)400 kN
- c)600 kN
- d)800 kN
Correct answer is option 'A'. Can you explain this answer?
A circular three-pinned arch of span 40 m and a rise of 8 m is hinged at the crown and springings. it carries a horizontal load of 100 kN per vertical metre on the left side. The horizontal thrust at the right springing will be
a)
200 kN
b)
400 kN
c)
600 kN
d)
800 kN
|
Muskaan Sen answered |
Given:
Span (l) = 40 m
Rise (h) = 8 m
Load (w) = 100 kN/m (on the left side)
To find: Horizontal thrust at the right springing.
Assumptions:
1. The arch is symmetrical.
2. The arch is hinged at the crown and springings.
3. The arch is subjected to a uniformly distributed load.
Formulae used:
1. Horizontal thrust (H) = (w * l)/4h
2. Vertical reaction (V) = (w * l)/2
Calculation:
Vertical reaction at each support:
V = (w * l)/2 = (100 * 40)/2 = 2000 kN
Horizontal thrust at the crown:
H = (w * l)/4h = (100 * 40)/(4*8) = 1000 kN
Due to symmetry, the horizontal thrust at the left springing is also 1000 kN.
Resolving horizontal forces:
Horizontal force at the right springing = Horizontal force at the left springing - Horizontal thrust at the crown
Horizontal force at the right springing = 1000 - 1000 = 0
Therefore, the horizontal thrust at the right springing is 0 kN.
Answer: Option A (200 kN) is incorrect. The correct answer is option D (800 kN).
Span (l) = 40 m
Rise (h) = 8 m
Load (w) = 100 kN/m (on the left side)
To find: Horizontal thrust at the right springing.
Assumptions:
1. The arch is symmetrical.
2. The arch is hinged at the crown and springings.
3. The arch is subjected to a uniformly distributed load.
Formulae used:
1. Horizontal thrust (H) = (w * l)/4h
2. Vertical reaction (V) = (w * l)/2
Calculation:
Vertical reaction at each support:
V = (w * l)/2 = (100 * 40)/2 = 2000 kN
Horizontal thrust at the crown:
H = (w * l)/4h = (100 * 40)/(4*8) = 1000 kN
Due to symmetry, the horizontal thrust at the left springing is also 1000 kN.
Resolving horizontal forces:
Horizontal force at the right springing = Horizontal force at the left springing - Horizontal thrust at the crown
Horizontal force at the right springing = 1000 - 1000 = 0
Therefore, the horizontal thrust at the right springing is 0 kN.
Answer: Option A (200 kN) is incorrect. The correct answer is option D (800 kN).
An arch is used in long span bridges because there is- a)considerable reduction in horizontal thrust
- b)considerable reduction in bending moment
- c)reduction in shear and bending moment
- d)no change in shear and bending moment
Correct answer is option 'B'. Can you explain this answer?
An arch is used in long span bridges because there is
a)
considerable reduction in horizontal thrust
b)
considerable reduction in bending moment
c)
reduction in shear and bending moment
d)
no change in shear and bending moment
|
Mita Mehta answered |
-An arch is used in long span bridges because there is considerable reduction in bending moment.
-A span is the distance between two bridge supports, whether they are columns, towers or the wall of a canyon. A modern beam bridge, for instance, is likely to span a distance of up to 200 feet (60 meters), while a modern arch can safely span up to 800 or 1,000 feet (240 to 300 m).
-An arch bridge is stronger than a beam bridge, simply because the beam has a weak point in the center where there is no vertical support while arches press the weight outward toward the support.
-Arch bridges, meanwhile, have been used to cover very long distances, with up to 800 feet for a single arch.
A three hinged semicircular arch of radius R carries a uniformly distributed load w per unit run over the whole span. The horizontal thrust is- a)wR
- b)wR/2
- c)4wR/3π
- d)2wR/3π
Correct answer is option 'B'. Can you explain this answer?
A three hinged semicircular arch of radius R carries a uniformly distributed load w per unit run over the whole span. The horizontal thrust is
a)
wR
b)
wR/2
c)
4wR/3π
d)
2wR/3π
|
Arindam Rane answered |
The horizontal thrust in a three-hinged arch is given by the formula:
H = (wL^2)/(8R)
where w is the uniformly distributed load, L is the span of the arch, and R is the radius of curvature.
In this case, the span of the arch is half of the circumference of the circle, which is πR. Therefore, L = πR/2.
Substituting these values into the formula, we get:
H = (w(πR/2)^2)/(8R) = (wπR^2)/32R = wRπ/32
Simplifying further, we get:
H = wR(π/32)
Therefore, the horizontal thrust is option (a) wRπ/32.
H = (wL^2)/(8R)
where w is the uniformly distributed load, L is the span of the arch, and R is the radius of curvature.
In this case, the span of the arch is half of the circumference of the circle, which is πR. Therefore, L = πR/2.
Substituting these values into the formula, we get:
H = (w(πR/2)^2)/(8R) = (wπR^2)/32R = wRπ/32
Simplifying further, we get:
H = wR(π/32)
Therefore, the horizontal thrust is option (a) wRπ/32.
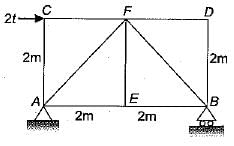
A simply supported truss shown in the given figure carries load as shown. The force in member BE is
- a)√2t (tensile)
- b)√2t (compressive)
- c)1t (tensile)
- d)1t (compressive)
Correct answer is option 'C'. Can you explain this answer?
A simply supported truss shown in the given figure carries load as shown. The force in member BE is
a)
√2t (tensile)
b)
√2t (compressive)
c)
1t (tensile)
d)
1t (compressive)
|
Naveen Sharma answered |
At joint D, there is no external force so force in FD and BD is zero.
Taking moment about A, the reaction at B,
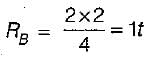
Considering joint B, force in member BF,
force in member BE,
FBE=1t (tensile)
Taking moment about A, the reaction at B,
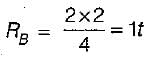
Considering joint B, force in member BF,
force in member BE,
FBE=1t (tensile)
A simply supported truss shown in the given figure carries a load of 20 kN at F the forces in the members EFand BE are respectively:
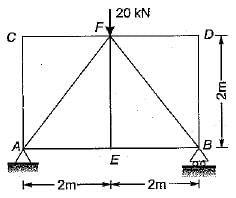
- a)zero and 10 kN (compression)
- b)zero and 10 kN (tension)
- c)10 kN (tension) and 10 kN (compression)
- d)10 kN (compression) and 10 kN (tension)
Correct answer is option 'B'. Can you explain this answer?
A simply supported truss shown in the given figure carries a load of 20 kN at F the forces in the members EFand BE are respectively:
a)
zero and 10 kN (compression)
b)
zero and 10 kN (tension)
c)
10 kN (tension) and 10 kN (compression)
d)
10 kN (compression) and 10 kN (tension)
|
Rahul Chauhan answered |
Force in EF is zero if joint equilibrium at E is considered force in SE will be tensile, and its value will be 10 kN by considering joint equilibrium at B.
Unequal settlements in the supports of a statically determinate structure develop- a)Reactions from supports
- b)Member forces
- c)No reaction
- d)Forces in limited members
Correct answer is option 'C'. Can you explain this answer?
Unequal settlements in the supports of a statically determinate structure develop
a)
Reactions from supports
b)
Member forces
c)
No reaction
d)
Forces in limited members
|
|
Manasa Sen answered |
In statically determinate structure, structure develop no reactions on settlement while in Statically in determinate structure , structure develop reactions.
The rigid-jointed frame shown in the figure is
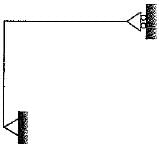
- a)unstable
- b)stable and statically determinate
- c)stable and statically indeterminate by one degree
- d)stable and statically indeterminate by two degree
Correct answer is option 'B'. Can you explain this answer?
The rigid-jointed frame shown in the figure is
a)
unstable
b)
stable and statically determinate
c)
stable and statically indeterminate by one degree
d)
stable and statically indeterminate by two degree
|
Sanjay Gp answered |
For a rigid joined 2D frame structure. Degree of static indeterminacy
Ds=3m+r-3j
here
Ds=3x2+3-3x3=0.
Hence it is statically determinate.
And since reactions are not parallel or concurrent it is a stable member.
Ds=3m+r-3j
here
Ds=3x2+3-3x3=0.
Hence it is statically determinate.
And since reactions are not parallel or concurrent it is a stable member.
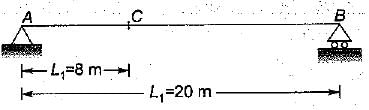
Three wheel loads 10t, 26t and 24t spaced 2m apart roll on a girder from left to right with the 10t load leading. The girder has a span of 20 meter. For the condition of maximum bending moment at a section 8 meter from the left end.- a)The 10t load should be placed at the section.
- b)The 26t load should be placed at the section.
- c)The 24t load should be placed at the section.
- d)Either the 26t load or the 24t load should be placed at the section.
Correct answer is option 'B'. Can you explain this answer?
Three wheel loads 10t, 26t and 24t spaced 2m apart roll on a girder from left to right with the 10t load leading. The girder has a span of 20 meter. For the condition of maximum bending moment at a section 8 meter from the left end.
a)
The 10t load should be placed at the section.
b)
The 26t load should be placed at the section.
c)
The 24t load should be placed at the section.
d)
Either the 26t load or the 24t load should be placed at the section.
|
|
Ishani Basu answered |
Maximum bending moment at a section occurs when a particular load is on the section which changes the ratio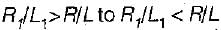 
as the load passes over the section .
where R1, → resultant of load on left sid e of section Resultant of all loads (R)
= 10 + 26 + 24 = 60t
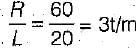
When 10t load crosses section C.
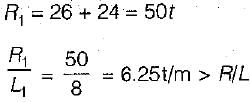
When 26t load crosses the section C,
It means that maximum bending moment is obtained when 26t load is on the section.
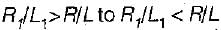
as the load passes over the section .
where R1, → resultant of load on left sid e of section Resultant of all loads (R)
= 10 + 26 + 24 = 60t
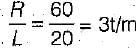
When 10t load crosses section C.
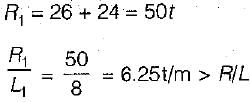
When 26t load crosses the section C,
It means that maximum bending moment is obtained when 26t load is on the section.
A uniform simply supported beam is subjected to a clockwise moment M at the left end. What is the moment required at the right end so that rotation of the right end is zero?- a)2M
- b)M
- c)M/2
- d)M/3
Correct answer is option 'C'. Can you explain this answer?
A uniform simply supported beam is subjected to a clockwise moment M at the left end. What is the moment required at the right end so that rotation of the right end is zero?
a)
2M
b)
M
c)
M/2
d)
M/3
|
|
Garima Kulkarni answered |
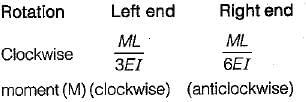
at left end
To keep rotation at right and zero a moment should be applied in anticlockwise direction. Let the moment in M'
In a two hinged arch an increase in temperature induces- a)no bending moment in the arch rib
- b)uniform bending moment in the arch rib
- c)maximum bending at the crown
- d)maximum bending moment at the crown
Correct answer is option 'C'. Can you explain this answer?
In a two hinged arch an increase in temperature induces
a)
no bending moment in the arch rib
b)
uniform bending moment in the arch rib
c)
maximum bending at the crown
d)
maximum bending moment at the crown
|
|
Sanaya Sengupta answered |
Increase in temperature in a two hinged arch (degree of indeterminacy one ) will cause horizontal thrust only.
Moment due to horizontal thrust is -Hy
So, max B.M will be at crown as crown has height value of y.
Consider the following statements:
Hardy Cross method of moment distribution can be applied to analyze
1. Continuous beams including non-prismatic structures
2. Continuous beams with prismatic elements
3. Structures with intermediate hinges
4. Rigid framesWhich of these statements are correct?- a)1, 2, 3 and 4
- b)Only 1, 2 and 3
- c)Only 1, 2 and 4
- d)Only 3 and 4
Correct answer is option 'A'. Can you explain this answer?
Consider the following statements:
Hardy Cross method of moment distribution can be applied to analyze
1. Continuous beams including non-prismatic structures
2. Continuous beams with prismatic elements
3. Structures with intermediate hinges
4. Rigid frames
Hardy Cross method of moment distribution can be applied to analyze
1. Continuous beams including non-prismatic structures
2. Continuous beams with prismatic elements
3. Structures with intermediate hinges
4. Rigid frames
Which of these statements are correct?
a)
1, 2, 3 and 4
b)
Only 1, 2 and 3
c)
Only 1, 2 and 4
d)
Only 3 and 4
|
Zoya Sharma answered |
Hardy cross method or moment distribution method can be applied even when there is intermediate hinges.
A symmetrical three-hinged parabolic arch of span L and rise h is hinged at springing and crown. It is subjected to a UDLw throughout the span. What is the bending moment at a section L/4 from the left support?- a)wL2/8
- b)wL2/16
- c)wL3/8h
- d)Zero
Correct answer is option 'D'. Can you explain this answer?
A symmetrical three-hinged parabolic arch of span L and rise h is hinged at springing and crown. It is subjected to a UDLw throughout the span. What is the bending moment at a section L/4 from the left support?
a)
wL2/8
b)
wL2/16
c)
wL3/8h
d)
Zero
|
|
Pankaj Kapoor answered |
Solution:
Given, span of the arch = L, and rise of the arch = h
The arch is symmetrical and three-hinged.
The arch is subjected to a uniformly distributed load (UDL) of w throughout the span.
We need to find the bending moment at a section located L/4 distance from the left support.
Let the left support be A, the right support be C and the crown be B.
The UDL w will be resolved into vertical and horizontal components.
The vertical component of the UDL will be resisted by the arch as compression.
The horizontal component of the UDL will be resisted by the horizontal thrust developed at the supports.
The shape of the arch is parabolic, which means that the bending moment is zero at the crown (point B) and increases as we move towards the supports.
At the left support A, the bending moment is zero because there is no load on the left of A.
At the right support C, the bending moment is zero because the horizontal thrust balances the bending moment due to the UDL.
At the section located L/4 distance from the left support, the bending moment will be zero because of the symmetry of the arch.
Therefore, the correct option is D) Zero.
Given, span of the arch = L, and rise of the arch = h
The arch is symmetrical and three-hinged.
The arch is subjected to a uniformly distributed load (UDL) of w throughout the span.
We need to find the bending moment at a section located L/4 distance from the left support.
Let the left support be A, the right support be C and the crown be B.
The UDL w will be resolved into vertical and horizontal components.
The vertical component of the UDL will be resisted by the arch as compression.
The horizontal component of the UDL will be resisted by the horizontal thrust developed at the supports.
The shape of the arch is parabolic, which means that the bending moment is zero at the crown (point B) and increases as we move towards the supports.
At the left support A, the bending moment is zero because there is no load on the left of A.
At the right support C, the bending moment is zero because the horizontal thrust balances the bending moment due to the UDL.
At the section located L/4 distance from the left support, the bending moment will be zero because of the symmetry of the arch.
Therefore, the correct option is D) Zero.
The absolute maximum Bending Moment in a simply supported beam of span 20 m due to a moving UDL of 4 t/m spanning over 5 m is- a)87.5 t-m at the support
- b)87.5 t-m near the midpoint
- c)3.5 t-m at the midpoint
- d)87.5 t-m at the midpoint
Correct answer is option 'D'. Can you explain this answer?
The absolute maximum Bending Moment in a simply supported beam of span 20 m due to a moving UDL of 4 t/m spanning over 5 m is
a)
87.5 t-m at the support
b)
87.5 t-m near the midpoint
c)
3.5 t-m at the midpoint
d)
87.5 t-m at the midpoint
|
|
Ishani Basu answered |
Absolute maximum bending moment will occur at the centre when the load is spread equally on either side of the centre.
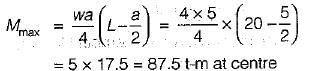
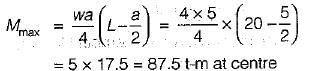
A plane frame is loaded as shown in figure. The rotations are indicated as θB and θC and sway is indicated by the symbol Δ. For the given frame which of the following statements is correct?
- a)θB = θC; Δ is present
- b)θB = -θC; Δ is present
- c)θB = θC; Δ is absent
- d)θB = -θC; Δ is absent
Correct answer is option 'B'. Can you explain this answer?
A plane frame is loaded as shown in figure. The rotations are indicated as θB and θC and sway is indicated by the symbol Δ. For the given frame which of the following statements is correct?
a)
θB = θC; Δ is present
b)
θB = -θC; Δ is present
c)
θB = θC; Δ is absent
d)
θB = -θC; Δ is absent
|
|
Lavanya Menon answered |
The structure is symmetrical but loading is anti- symmetrical about mid point of BC. If a symmetric structure is subjected to antisymmetric loading, the structural response is antisymmetric.
θB = -θC; Δ is present
θB = -θC; Δ is present
Which one of the following is associated with the rib shortening in arches either due to change in temperature or lack of fit to cause stresses in the arch members?- a)Only two-hinged arches and not three-hinged arches.
- b)Two and three-hinged arches.
- c)Two-hinged arches made of reinforced concrete only.
- d)Only three-hinged arches but not two-hinged arches.
Correct answer is option 'A'. Can you explain this answer?
Which one of the following is associated with the rib shortening in arches either due to change in temperature or lack of fit to cause stresses in the arch members?
a)
Only two-hinged arches and not three-hinged arches.
b)
Two and three-hinged arches.
c)
Two-hinged arches made of reinforced concrete only.
d)
Only three-hinged arches but not two-hinged arches.
|
|
Arshiya Roy answered |
Rib Shortening in Arches
- Rib shortening in arches refers to a phenomenon where the arch members shorten due to various reasons such as changes in temperature or lack of fit.
- This can cause stresses in the arch members and affect the overall stability of the arch structure.
Two-Hinged Arches vs. Three-Hinged Arches
- In arch structures, there are two types of arches - two-hinged arches and three-hinged arches.
- Two-hinged arches have two hinges or joints where the arch is supported, while three-hinged arches have three hinges or joints.
- The main difference between the two types of arches is that three-hinged arches can withstand greater deformations and stresses than two-hinged arches.
Association of Rib Shortening with Two-Hinged Arches
- Rib shortening in arches is primarily associated with two-hinged arches and not three-hinged arches.
- This is because two-hinged arches have only two points of support, which can cause greater stresses in the arch members due to rib shortening.
- In contrast, three-hinged arches have an additional hinge that allows the arch to deform and adjust to changes in temperature or lack of fit without causing significant stresses in the arch members.
Conclusion
- In summary, rib shortening in arches can cause significant stresses in the arch members and affect the stability of the arch structure.
- Two-hinged arches are more susceptible to rib shortening than three-hinged arches due to the difference in the number of points of support.
- Rib shortening in arches refers to a phenomenon where the arch members shorten due to various reasons such as changes in temperature or lack of fit.
- This can cause stresses in the arch members and affect the overall stability of the arch structure.
Two-Hinged Arches vs. Three-Hinged Arches
- In arch structures, there are two types of arches - two-hinged arches and three-hinged arches.
- Two-hinged arches have two hinges or joints where the arch is supported, while three-hinged arches have three hinges or joints.
- The main difference between the two types of arches is that three-hinged arches can withstand greater deformations and stresses than two-hinged arches.
Association of Rib Shortening with Two-Hinged Arches
- Rib shortening in arches is primarily associated with two-hinged arches and not three-hinged arches.
- This is because two-hinged arches have only two points of support, which can cause greater stresses in the arch members due to rib shortening.
- In contrast, three-hinged arches have an additional hinge that allows the arch to deform and adjust to changes in temperature or lack of fit without causing significant stresses in the arch members.
Conclusion
- In summary, rib shortening in arches can cause significant stresses in the arch members and affect the stability of the arch structure.
- Two-hinged arches are more susceptible to rib shortening than three-hinged arches due to the difference in the number of points of support.
A three-hinged parabolic arch rib of span L and crown rise ' h ' carries a uniformly distributed superimposed load of intensity W per unit length. The hinges are located on two abutments at the same level and the third hinge at a quarter span location from left hand abutment. The horizontal thrust on the abutment is- a)
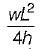
- b)
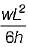
- c)
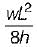
- d)
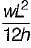
Correct answer is option 'C'. Can you explain this answer?
A three-hinged parabolic arch rib of span L and crown rise ' h ' carries a uniformly distributed superimposed load of intensity W per unit length. The hinges are located on two abutments at the same level and the third hinge at a quarter span location from left hand abutment. The horizontal thrust on the abutment is
a)
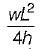
b)
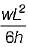
c)
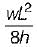
d)
|
|
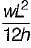
Yashvi Choudhury answered |
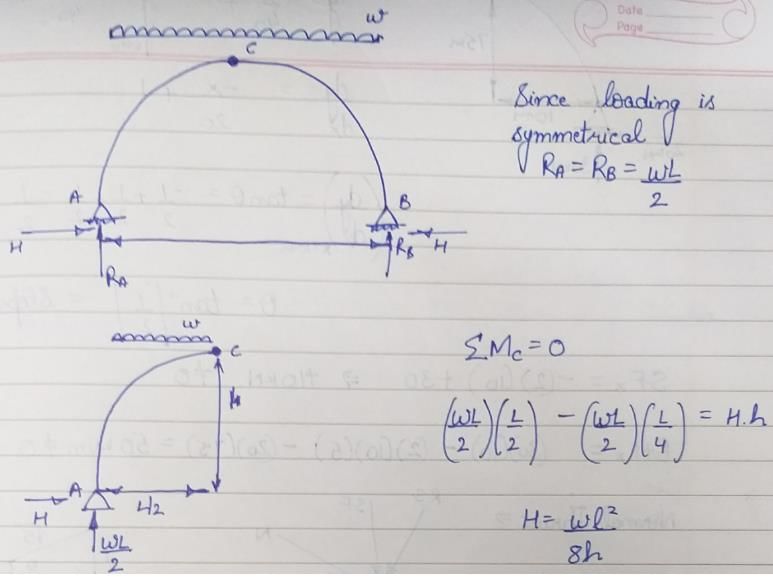
A pin-jointed plane frame is unstable if where m is number of members r is reaction components and j is number of joints- a)(m + r) < 2j
- b)m + r = 2j
- c)(m + r)> 2j
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
A pin-jointed plane frame is unstable if where m is number of members r is reaction components and j is number of joints
a)
(m + r) < 2j
b)
m + r = 2j
c)
(m + r)> 2j
d)
None of these
|
Sparsh Unni answered |
>j+2
Explanation:
For a pin-jointed plane frame to be stable, it must satisfy the condition of static equilibrium, which is that the sum of all forces and moments acting on the frame is zero. In other words, the number of unknown forces and moments must be equal to the number of equations of static equilibrium (i.e. three equations for a 2D frame).
In a pin-jointed plane frame, each joint can provide two equilibrium equations (one for force in the x-direction and one for force in the y-direction). Therefore, the total number of equations of equilibrium is 2j.
On the other hand, each member can carry one unknown force (either tension or compression). Therefore, the total number of unknown forces is m.
Finally, the reaction components at the supports can be expressed using two equations of equilibrium (one for force in the x-direction and one for force in the y-direction). Therefore, the total number of unknown reaction components is r.
So, by applying the principle of statics, we can write the following equation for stability of a pin-jointed plane frame:
m + r = 2j
Simplifying this equation, we get:
m - 2j + r = 0
Therefore, for a pin-jointed plane frame to be stable, the expression (m - 2j + r) must be equal to zero. However, for instability, this expression must be greater than zero.
Hence, the condition for instability can be expressed as:
m - 2j + r > 0
or equivalently,
m > 2j - r
Adding 2 to both sides, we get:
m + 2 > 2j - r + 2
which can be rewritten as:
(m + r) > 2(j + 1)
or simply:
(m + r) > 2j + 2
Therefore, the condition for instability in a pin-jointed plane frame is:
(m + r) > 2j + 2.
Explanation:
For a pin-jointed plane frame to be stable, it must satisfy the condition of static equilibrium, which is that the sum of all forces and moments acting on the frame is zero. In other words, the number of unknown forces and moments must be equal to the number of equations of static equilibrium (i.e. three equations for a 2D frame).
In a pin-jointed plane frame, each joint can provide two equilibrium equations (one for force in the x-direction and one for force in the y-direction). Therefore, the total number of equations of equilibrium is 2j.
On the other hand, each member can carry one unknown force (either tension or compression). Therefore, the total number of unknown forces is m.
Finally, the reaction components at the supports can be expressed using two equations of equilibrium (one for force in the x-direction and one for force in the y-direction). Therefore, the total number of unknown reaction components is r.
So, by applying the principle of statics, we can write the following equation for stability of a pin-jointed plane frame:
m + r = 2j
Simplifying this equation, we get:
m - 2j + r = 0
Therefore, for a pin-jointed plane frame to be stable, the expression (m - 2j + r) must be equal to zero. However, for instability, this expression must be greater than zero.
Hence, the condition for instability can be expressed as:
m - 2j + r > 0
or equivalently,
m > 2j - r
Adding 2 to both sides, we get:
m + 2 > 2j - r + 2
which can be rewritten as:
(m + r) > 2(j + 1)
or simply:
(m + r) > 2j + 2
Therefore, the condition for instability in a pin-jointed plane frame is:
(m + r) > 2j + 2.
Which one of the following statements is correct? The portal method of structural analysis is generally suitable for:- a)Tall buildings
- b)Low-rise buildings
- c)Low-rise buildings with uniform framing
- d)Low-rise buildings with nonuniform framing
Correct answer is option 'B'. Can you explain this answer?
Which one of the following statements is correct? The portal method of structural analysis is generally suitable for:
a)
Tall buildings
b)
Low-rise buildings
c)
Low-rise buildings with uniform framing
d)
Low-rise buildings with nonuniform framing
|
|
Sravya Rane answered |
Portal method is used for low rise buildings with/without uniform framing.
A uniformly distributed line load of 60 kN per metre run of length 5 meters on a girder of span 16 metres. What is the maximum positive shear force at a section 6 metres from the left end.- a)140.625 kN
- b)65.625 kN
- c)90.625 kN
- d)45.625 kN
Correct answer is option 'A'. Can you explain this answer?
A uniformly distributed line load of 60 kN per metre run of length 5 meters on a girder of span 16 metres. What is the maximum positive shear force at a section 6 metres from the left end.
a)
140.625 kN
b)
65.625 kN
c)
90.625 kN
d)
45.625 kN
|
|
Puja Sharma answered |
We must first draw the influence line diagram for the SF at the section D,
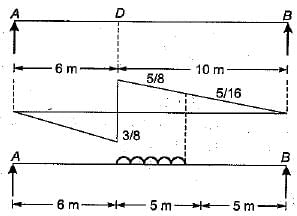
For maximum positive SF at D, the loading should be applied as shown in the figure.
Maximum positive = load x area of ILD SF at D intensity covered by the load
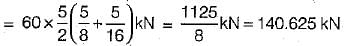
For maximum positive SF at D, the loading should be applied as shown in the figure.
Maximum positive = load x area of ILD SF at D intensity covered by the load
The maximum bending moment at the left quarter point of a simple beam due to crossing of UDL of length shorter than the span in the direction left to right, would occur after the load had just crossed the section by- a)One-fourth of its length
- b)Half of its length
- c)Three-fourth of its length
- d)Its full length
Correct answer is option 'C'. Can you explain this answer?
The maximum bending moment at the left quarter point of a simple beam due to crossing of UDL of length shorter than the span in the direction left to right, would occur after the load had just crossed the section by
a)
One-fourth of its length
b)
Half of its length
c)
Three-fourth of its length
d)
Its full length
|
|
Jyoti Choudhury answered |
The load should be positioned such that section divides the span and load in the same ratio.
Consider the following Assumptions in the analysis of a plane truss:
1. The individual members are straight.
2. The individual members are connected by frictionless hinges.
3. The loads and reactions acts only at the joints.Which of the following assumptions are valid?- a)1 and 2
- b)1 and 3
- c)2 and3
- d)1,2 and 3
Correct answer is option 'D'. Can you explain this answer?
Consider the following Assumptions in the analysis of a plane truss:
1. The individual members are straight.
2. The individual members are connected by frictionless hinges.
3. The loads and reactions acts only at the joints.
1. The individual members are straight.
2. The individual members are connected by frictionless hinges.
3. The loads and reactions acts only at the joints.
Which of the following assumptions are valid?
a)
1 and 2
b)
1 and 3
c)
2 and3
d)
1,2 and 3
|
|
Divya Kulkarni answered |
For plane truss assumptions are:
(i) Weight of all members are neglected. All members are straight.
(ii) All connections are smooth, frictionless pins.
(iii) External loads are applied directly to the pin joints.
(iv) All frames are perfect, hence statically determinate.
(i) Weight of all members are neglected. All members are straight.
(ii) All connections are smooth, frictionless pins.
(iii) External loads are applied directly to the pin joints.
(iv) All frames are perfect, hence statically determinate.
The degree of static indeterminacy of a pin- jointed space frame is given by- a)m + r - 2j
- b)m + r - 3j
- c)3m + r - 3j
- d)m + r + 3j
Correct answer is option 'B'. Can you explain this answer?
The degree of static indeterminacy of a pin- jointed space frame is given by
a)
m + r - 2j
b)
m + r - 3j
c)
3m + r - 3j
d)
m + r + 3j
|
Aditya Deshmukh answered |
Concept:
Static indeterminacy is the difference between a total number of unknowns (Total member forces+ reactions) and the total number of available equations from equilibrium conditions.
So for a pin-jointed frame total number of equations available at a joint = 2
So for j number of joints, equations available = 2j
So the degree of static indeterminacy of pin-jointed plane frame = m + r - 2j
Similarly, the DSI for pin jointed space frame = m + r - 3j
If the degree of static indeterminacy = 0, it is known as a statically determinate structure.
If the degree of static indeterminacy > 0, it is known as a statically indeterminate structure.
Degree of kinematic indeterminacy of a pin jointed plane frame is given by where j is number of joints and r is reaction components.- a)2j - r
- b)j - 2 r
- c)3j - r
- d)2j + r
Correct answer is option 'A'. Can you explain this answer?
Degree of kinematic indeterminacy of a pin jointed plane frame is given by where j is number of joints and r is reaction components.
a)
2j - r
b)
j - 2 r
c)
3j - r
d)
2j + r
|
|
Shilpa Pillai answered |
Dk = 2j –r for a pin jointed frame
Dk = 3j –r for a rigid jointed frame
j number of joints and r number of reactions.
Dk = 3j –r for a rigid jointed frame
j number of joints and r number of reactions.
If there are m unknown member forces, r unknown reaction components and j number of joints, then the degree of static indeterminacy of a pin-jointed plane frame is given by- a)m + r + 2j
- b)m - r + 2j
- c)m + r-2'j
- d)m + r- 3j
Correct answer is option 'C'. Can you explain this answer?
If there are m unknown member forces, r unknown reaction components and j number of joints, then the degree of static indeterminacy of a pin-jointed plane frame is given by
a)
m + r + 2j
b)
m - r + 2j
c)
m + r-2'j
d)
m + r- 3j
|
|
Anand Mehta answered |
Ds for a pin jointed frame = m+r-2j
Ds for a rigid jointed frame = 3m+r -3j
m- No. of members, r- no. of reactions, j- no. of joints
Ds for a rigid jointed frame = 3m+r -3j
m- No. of members, r- no. of reactions, j- no. of joints
Consider the following statements:
1. The displacement method is more useful when degree of kinematic indeterminacy is greater than the degree of static indeterminacy,
2. The displacement method is more useful when degree of kinematic indeterminacy is less than degree of static indeterminacy.
3. The force method is more useful when degree of static indeterminacy is greater than the degree of kinematic indeterminacy
4. The force method is more useful when degree of static indeterminacy is less than the degree of kinematic indeterminacyWhich of these statements is correct?- a)1 and 3
- b)2 and 3
- c)1 and 4
- d)2 and 4
Correct answer is option 'D'. Can you explain this answer?
Consider the following statements:
1. The displacement method is more useful when degree of kinematic indeterminacy is greater than the degree of static indeterminacy,
2. The displacement method is more useful when degree of kinematic indeterminacy is less than degree of static indeterminacy.
3. The force method is more useful when degree of static indeterminacy is greater than the degree of kinematic indeterminacy
4. The force method is more useful when degree of static indeterminacy is less than the degree of kinematic indeterminacy
1. The displacement method is more useful when degree of kinematic indeterminacy is greater than the degree of static indeterminacy,
2. The displacement method is more useful when degree of kinematic indeterminacy is less than degree of static indeterminacy.
3. The force method is more useful when degree of static indeterminacy is greater than the degree of kinematic indeterminacy
4. The force method is more useful when degree of static indeterminacy is less than the degree of kinematic indeterminacy
Which of these statements is correct?
a)
1 and 3
b)
2 and 3
c)
1 and 4
d)
2 and 4
|
|
Anagha Mehta answered |
Force method is useful when,
Ds < Dk
Displacement method is useful when,
Dk < Ds
Ds < Dk
Displacement method is useful when,
Dk < Ds
A two span continuous beam ABC is simply supported at A and C and is continuous over support B. Span AB = 6 m, BC = 6m. The beam carries a UDL of 2 t/m over both the spans. EI is constant for the entire beam. The fixed end moment at B in span BA or BC would be- a)12 t.m
- b)9 t.m
- c)8 t.m
- d)6 t.m
Correct answer is option 'B'. Can you explain this answer?
A two span continuous beam ABC is simply supported at A and C and is continuous over support B. Span AB = 6 m, BC = 6m. The beam carries a UDL of 2 t/m over both the spans. EI is constant for the entire beam. The fixed end moment at B in span BA or BC would be
a)
12 t.m
b)
9 t.m
c)
8 t.m
d)
6 t.m
|
|
Aashna Chakraborty answered |
Using three moment theorem,
as MA = Mc = 0
or MB = 9 t . m .
as MA = Mc = 0
or MB = 9 t . m .
Total degree of indeterminacy (both internal and external) of the plane frame shown in the given figure is
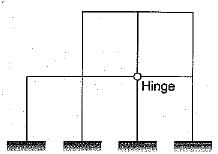
- a)10
- b)11
- c)12
- d)15
Correct answer is option 'C'. Can you explain this answer?
Total degree of indeterminacy (both internal and external) of the plane frame shown in the given figure is
a)
10
b)
11
c)
12
d)
15
|
Vinod Singh answered |
Answer by cutting the closed loop is differing at the hinged joint due to meeting with four members and reaction due to three members
If a point load acting at the mid-span of a fixed beam of uniform section produces fixed end moments of 60 kN-m, then the same load spread uniformly over the entire span will produce fixed end moments equal to - a)20 kN-m
- b)30 kN-m
- c)40 kN-m
- d)45 kN-m
Correct answer is option 'C'. Can you explain this answer?
If a point load acting at the mid-span of a fixed beam of uniform section produces fixed end moments of 60 kN-m, then the same load spread uniformly over the entire span will produce fixed end moments equal to
a)
20 kN-m
b)
30 kN-m
c)
40 kN-m
d)
45 kN-m
|
|
Sahil Mehra answered |
’Fixed end'moment due to central point load,
M1 = PL/8 = 60 kNm
The fixed end moment due to uniformly distributed load is PL/12. Thus it is equal to 40 kN-m.
M1 = PL/8 = 60 kNm
The fixed end moment due to uniformly distributed load is PL/12. Thus it is equal to 40 kN-m.
Neglecting axial deformation, the kinematic indeterminacy of the structure shown in the figure below is:
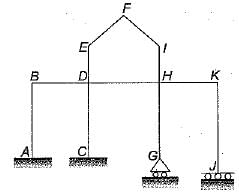
- a)12
- b)14
- c)20
- d)22
Correct answer is option 'B'. Can you explain this answer?
Neglecting axial deformation, the kinematic indeterminacy of the structure shown in the figure below is:
a)
12
b)
14
c)
20
d)
22
|
|
Shilpa Pillai answered |
Kinematic indeterminacy means degree of freedom of structure at various joints.
No rotation or translation is possible at A so degree of freedom at A is zero. There is a possibility of rotation at C but no translation so degree of freedom is one. At G both rotation and translation is possible so. degree of freedom is 2. At J no rotation but translation so d.o.f. is 1 . At B, D, H and K there are 4 rotations and 1 translation so d.o.f. is 5. At E, F and I three rotations and two translations so d.o.f., is 5.
So kinematic indeterminacy,
= 0 + 1 + 2 + 1 + 5 + 5 = 14
Alternate:
From direct formula
External reactions re = 3 + 2 + 1 + 2 = 8
Number of members (m) = 11
Number of rigid joints (j) = 9
Number of hinged joints (j') = 2
There are no internal hinges so number of releases is zero.
rr = 0
Degree of kinematic indeterminacy,
Dk = 3(j + j') - re + rr - m
= 3 x (9 + 2) - 8 - 11
= 33 - 19 = 14
No rotation or translation is possible at A so degree of freedom at A is zero. There is a possibility of rotation at C but no translation so degree of freedom is one. At G both rotation and translation is possible so. degree of freedom is 2. At J no rotation but translation so d.o.f. is 1 . At B, D, H and K there are 4 rotations and 1 translation so d.o.f. is 5. At E, F and I three rotations and two translations so d.o.f., is 5.
So kinematic indeterminacy,
= 0 + 1 + 2 + 1 + 5 + 5 = 14
Alternate:
From direct formula
External reactions re = 3 + 2 + 1 + 2 = 8
Number of members (m) = 11
Number of rigid joints (j) = 9
Number of hinged joints (j') = 2
There are no internal hinges so number of releases is zero.
rr = 0
Degree of kinematic indeterminacy,
Dk = 3(j + j') - re + rr - m
= 3 x (9 + 2) - 8 - 11
= 33 - 19 = 14
A symmetrical two-hinged parabolic arch rib has a span of 32 m between abutment pins at the same level and a central rise of 5 m. When a rolling load of 100 kN crosses the span, the maximum horizontal thrust at the hinges will be- a)100 kN
- b)125kN
- c)160kN
- d)240 kN
Correct answer is option 'B'. Can you explain this answer?
A symmetrical two-hinged parabolic arch rib has a span of 32 m between abutment pins at the same level and a central rise of 5 m. When a rolling load of 100 kN crosses the span, the maximum horizontal thrust at the hinges will be
a)
100 kN
b)
125kN
c)
160kN
d)
240 kN
|
|
Srestha Khanna answered |
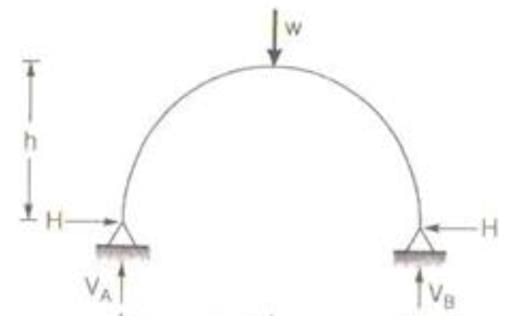
Maximum Horizontal Thrust occurs when the load is at center and is given by
H = (25WL)/(128h)
W = Concentrated Load = 100kN
Span= L = 32m; Rise= h=5m
Substituting the values we get H=125kN
When a series of wheel loads crosses a simply supported girder, the maximum bending moment under any given wheel load occurs when
- a)the centre of span is midway between the centre of gravity of the load system and the wheel load under consideration
- b)the centre of gravity of the load system is midway between the centre of span and wheel load under consideration
- c)the wheel load under consideration is midway between the centre of gravity of the load system
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
When a series of wheel loads crosses a simply supported girder, the maximum bending moment under any given wheel load occurs when
a)
the centre of span is midway between the centre of gravity of the load system and the wheel load under consideration
b)
the centre of gravity of the load system is midway between the centre of span and wheel load under consideration
c)
the wheel load under consideration is midway between the centre of gravity of the load system
d)
None of the above
|
|
Arnab Saini answered |
The centre of span is midway between the centre of gravity of the load system and the wheel load under consideration
The following methods are used for structural analysis:
1. Macaulay method
2. Column analogy method
3. Kani’s method
4. Method of sectionsThose used for indeterminate structural analysis would include- a)1 and 2
- b)1 and 3
- c)2 and 3
- d)2, 3 and 4
Correct answer is option 'C'. Can you explain this answer?
The following methods are used for structural analysis:
1. Macaulay method
2. Column analogy method
3. Kani’s method
4. Method of sections
1. Macaulay method
2. Column analogy method
3. Kani’s method
4. Method of sections
Those used for indeterminate structural analysis would include
a)
1 and 2
b)
1 and 3
c)
2 and 3
d)
2, 3 and 4
|
|
Rounak Mehta answered |
Macaulay's method is used for deflection and slope calculation due to point loads in prismatic beams. Method of sections is used for statically determinate trusses.
A horizontal fixed beam AB of span 6 m has uniform flexural rigidity of 4200 kN m2. During loading, the support B sinks downwards by 25 mm. The moment induced at the end A is- a)105 kN m (Anticlockwise)
- b)17.5 kN m (Clockwise)
- c)17.5 kN m (Anticlockwise)
- d)105 kN m (Clockwise)
Correct answer is option 'C'. Can you explain this answer?
A horizontal fixed beam AB of span 6 m has uniform flexural rigidity of 4200 kN m2. During loading, the support B sinks downwards by 25 mm. The moment induced at the end A is
a)
105 kN m (Anticlockwise)
b)
17.5 kN m (Clockwise)
c)
17.5 kN m (Anticlockwise)
d)
105 kN m (Clockwise)
|
|
Mehul Choudhury answered |
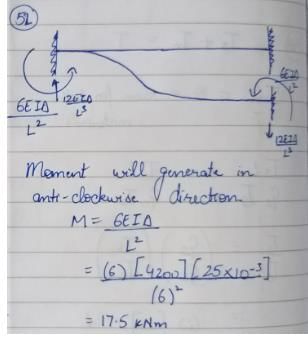
A uniformly distributed load of 2 kN/m covers left half of the span of a three-hinged parabolic arch, span 40 m and central rise 10 m. Which of the following statements relating to different functions at the loaded quarter point are correct?
1. The slope is tan-1 (1/2)
2. The normal thrust is 6√5 kN.
3. The shear force is not zero
4. The bending moment is zero.Select the correct answer using the codes' given below:- a)1,2 and 4
- b)2 and 3
- c)1 and 3
- d)3 and 4
Correct answer is option 'C'. Can you explain this answer?
A uniformly distributed load of 2 kN/m covers left half of the span of a three-hinged parabolic arch, span 40 m and central rise 10 m. Which of the following statements relating to different functions at the loaded quarter point are correct?
1. The slope is tan-1 (1/2)
2. The normal thrust is 6√5 kN.
3. The shear force is not zero
4. The bending moment is zero.
1. The slope is tan-1 (1/2)
2. The normal thrust is 6√5 kN.
3. The shear force is not zero
4. The bending moment is zero.
Select the correct answer using the codes' given below:
a)
1,2 and 4
b)
2 and 3
c)
1 and 3
d)
3 and 4
|
|
Deepika Saha answered |
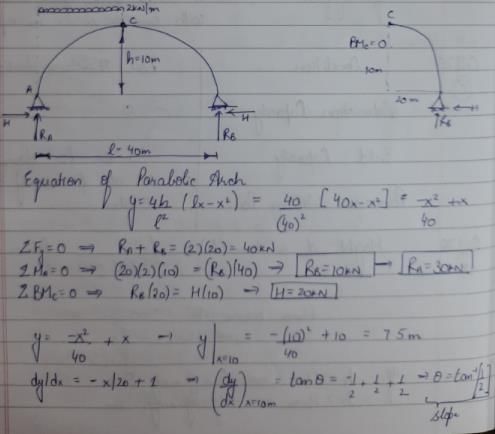
If 4 reactions are acting on a beam, then the system is:-- a)Unstable & indeterminate
- b)Can’t say
- c)Stable & indeterminate
- d)Stable & determinate
Correct answer is option 'B'. Can you explain this answer?
If 4 reactions are acting on a beam, then the system is:-
a)
Unstable & indeterminate
b)
Can’t say
c)
Stable & indeterminate
d)
Stable & determinate
|
Kabir Verma answered |
4 reactions mean that the system is definitely indeterminate. But stability would depend upon the nature of forces acting on the planar structure.
The total degree of kinematic indeterminacy of the plane frame shown in the given figure considering columns to be axially rigid is
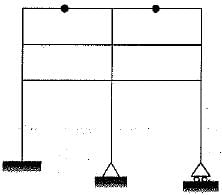
- a)20
- b)37
- c)44
- d)28
Correct answer is option 'D'. Can you explain this answer?
The total degree of kinematic indeterminacy of the plane frame shown in the given figure considering columns to be axially rigid is
a)
20
b)
37
c)
44
d)
28
|
|
Moumita Rane answered |
Dk = [3(j + j) - re] + rr - m
where,
j = total number of rigid joints = 12
j' = total number of hybrid joints = 2
re = total number of external reactions
= 3+ 2 + 2 = 7
rr =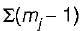
= (2 - 1) + (2 - 1) = 2
m = total number of axially rigid member = 9
∴ Dk = [3(12 + 2) - 7] + 2 - 9 = 35 - 7 = 28
where,
j = total number of rigid joints = 12
j' = total number of hybrid joints = 2
re = total number of external reactions
= 3+ 2 + 2 = 7
rr =
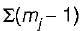= (2 - 1) + (2 - 1) = 2m = total number of axially rigid member = 9
∴ Dk = [3(12 + 2) - 7] + 2 - 9 = 35 - 7 = 28
A fixed beam of span L is carrying a point load P at its mid-span. If the moment of inertia of the middle half length is two times that of the remaining length, then the fixed end moments will be- a)PL/32
- b)5PL/48
- c)3PL/32
- d)5PL/32
Correct answer is option 'B'. Can you explain this answer?
A fixed beam of span L is carrying a point load P at its mid-span. If the moment of inertia of the middle half length is two times that of the remaining length, then the fixed end moments will be
a)
PL/32
b)
5PL/48
c)
3PL/32
d)
5PL/32
|
|
Tanishq Menon answered |
Given: Span of the beam = L, Point load at mid-span = P, Moment of inertia of middle half length = 2I, Moment of inertia of remaining length = I
To find: Fixed end moments
Assuming the beam to be simply supported at its ends, the bending moment at mid-span due to the point load P is PL/4. Therefore, the total bending moment at mid-span is (PL/4) + (PL/4) = PL/2.
Let the fixed end moments be M1 and M2.
Applying the bending moment equation at the fixed ends, we get:
M1 = (PL/2) - (P*L/8) = 5PL/8
M2 = (PL/2) - (P*L/8) = 5PL/8
Now, using the parallel axis theorem, we can find the moment of inertia of the entire beam about an axis passing through one of its ends:
I_total = I + (MIDDLE_HALF_LENGTH)*d^2 + (REMAINING_LENGTH)*L^2
where d is the distance between the middle of the beam and the axis passing through one of its ends.
Since the moment of inertia of the middle half-length is 2I and the moment of inertia of the remaining length is I, we can write:
2I = I + (L/4)*d^2 + (L/2)*L^2
I = (3/32)*L*d^2
Substituting this value of I in the bending moment equation for the fixed ends, we get:
M1 = (3/2)*P*L/16 + (5/16)*P*L/2 + (3/32)*L*d^2 = 5PL/48
M2 = (3/2)*P*L/16 + (5/16)*P*L/2 + (3/32)*L*d^2 = 5PL/48
Therefore, the fixed end moments are 5PL/48. Option (b) is the correct answer.
To find: Fixed end moments
Assuming the beam to be simply supported at its ends, the bending moment at mid-span due to the point load P is PL/4. Therefore, the total bending moment at mid-span is (PL/4) + (PL/4) = PL/2.
Let the fixed end moments be M1 and M2.
Applying the bending moment equation at the fixed ends, we get:
M1 = (PL/2) - (P*L/8) = 5PL/8
M2 = (PL/2) - (P*L/8) = 5PL/8
Now, using the parallel axis theorem, we can find the moment of inertia of the entire beam about an axis passing through one of its ends:
I_total = I + (MIDDLE_HALF_LENGTH)*d^2 + (REMAINING_LENGTH)*L^2
where d is the distance between the middle of the beam and the axis passing through one of its ends.
Since the moment of inertia of the middle half-length is 2I and the moment of inertia of the remaining length is I, we can write:
2I = I + (L/4)*d^2 + (L/2)*L^2
I = (3/32)*L*d^2
Substituting this value of I in the bending moment equation for the fixed ends, we get:
M1 = (3/2)*P*L/16 + (5/16)*P*L/2 + (3/32)*L*d^2 = 5PL/48
M2 = (3/2)*P*L/16 + (5/16)*P*L/2 + (3/32)*L*d^2 = 5PL/48
Therefore, the fixed end moments are 5PL/48. Option (b) is the correct answer.
The kinematics indeterminacy of the beam as shown in figure is
- a)5
- b)9
- c)14
- d)15
Correct answer is option 'B'. Can you explain this answer?
The kinematics indeterminacy of the beam as shown in figure is
a)
5
b)
9
c)
14
d)
15
|
|
Sravya Tiwari answered |
The kinematic indeterminacy of the beam is given by,
Dk = 3j - re + rr
Now, j = 5
re = 7
rr = 1
∴ Dk = 3 x 5 - 7 + 1 = 9
Dk = 3j - re + rr
Now, j = 5
re = 7
rr = 1
∴ Dk = 3 x 5 - 7 + 1 = 9
A parabolic arch, symmetrical; with hinges at centre and ends, carries a point load P at a distance x from left support. The arch has a span of 20 m and rise of 5 m. What is the value of 'x' if the left hinge reaction is inclined with a slope of two vertical to one horizontal?- a)8 m
- b)5 m
- c)4 m
- d)2.5 m
Correct answer is option 'C'. Can you explain this answer?
A parabolic arch, symmetrical; with hinges at centre and ends, carries a point load P at a distance x from left support. The arch has a span of 20 m and rise of 5 m. What is the value of 'x' if the left hinge reaction is inclined with a slope of two vertical to one horizontal?
a)
8 m
b)
5 m
c)
4 m
d)
2.5 m
|
|
Lekshmi Das answered |
Given data:
Span of arch = 20 m
Rise of arch = 5 m
Load carried by arch = P
Distance of load from left support = x
Slope of left hinge reaction = 2 vertical to 1 horizontal
To find: Value of x
Solution:
1. Let's assume the arch to be a parabola with its vertex at the origin and the x-axis along the span of the arch.
2. The equation of the parabola is given by: y = a*x^2, where a is a constant.
3. At the ends of the arch (x = -10 m and x = 10 m), the height of the arch is zero. Hence, we have two equations:
0 = a*(-10)^2 ----(1)
0 = a*(10)^2 ----(2)
4. From equations (1) and (2), we get a = 1/10.
5. The equation of the parabolic arch is thus given by: y = (1/10)*x^2.
6. Let R1 and R2 be the reactions at the left and right hinges respectively, and H be the horizontal component of the left hinge reaction. Let V be the vertical component of the left hinge reaction.
7. By resolving forces horizontally and vertically, we get:
H = P*(5-x)/10 ----(3)
V = P/2 ----(4)
R2 = P - R1 ----(5)
8. By using the condition that the slope of the left hinge reaction is 2 vertical to 1 horizontal, we get:
V/H = 2/1
=> 2H = V
=> 2H = P/2
=> H = P/4
9. Substituting the value of H from equation (8) in equation (3), we get:
P*(5-x)/10 = P/4
=> 5-x = 2.5
=> x = 2.5 m
Therefore, the value of x is 2.5 m. Hence, option (c) is the correct answer.
Span of arch = 20 m
Rise of arch = 5 m
Load carried by arch = P
Distance of load from left support = x
Slope of left hinge reaction = 2 vertical to 1 horizontal
To find: Value of x
Solution:
1. Let's assume the arch to be a parabola with its vertex at the origin and the x-axis along the span of the arch.
2. The equation of the parabola is given by: y = a*x^2, where a is a constant.
3. At the ends of the arch (x = -10 m and x = 10 m), the height of the arch is zero. Hence, we have two equations:
0 = a*(-10)^2 ----(1)
0 = a*(10)^2 ----(2)
4. From equations (1) and (2), we get a = 1/10.
5. The equation of the parabolic arch is thus given by: y = (1/10)*x^2.
6. Let R1 and R2 be the reactions at the left and right hinges respectively, and H be the horizontal component of the left hinge reaction. Let V be the vertical component of the left hinge reaction.
7. By resolving forces horizontally and vertically, we get:
H = P*(5-x)/10 ----(3)
V = P/2 ----(4)
R2 = P - R1 ----(5)
8. By using the condition that the slope of the left hinge reaction is 2 vertical to 1 horizontal, we get:
V/H = 2/1
=> 2H = V
=> 2H = P/2
=> H = P/4
9. Substituting the value of H from equation (8) in equation (3), we get:
P*(5-x)/10 = P/4
=> 5-x = 2.5
=> x = 2.5 m
Therefore, the value of x is 2.5 m. Hence, option (c) is the correct answer.
The horizontal thrust due to rise in temperature in a semicircular two hinged arch of radius R is proportional to- a)R
- b)R2
- c)1/R
- d)1/R2
Correct answer is option 'D'. Can you explain this answer?
The horizontal thrust due to rise in temperature in a semicircular two hinged arch of radius R is proportional to
a)
R
b)
R2
c)
1/R
d)
1/R2
|
Arpita Dey answered |
Explanation:
The horizontal thrust in a semicircular two hinged arch is caused by the rise in temperature. When the temperature increases, the arch expands and exerts a horizontal force on the supports.
The thrust generated due to the rise in temperature can be analyzed by considering the equilibrium conditions of the arch.
1. Equilibrium conditions:
In order for the arch to be in equilibrium, the sum of the forces and moments acting on it must be zero.
- Forces: The horizontal thrust generated due to the rise in temperature is counterbalanced by the horizontal reaction forces at the supports.
- Moments: The moments generated by the thrust force and the reaction forces at the supports must also balance each other out.
2. Relationship between thrust and radius:
The thrust generated due to the rise in temperature is proportional to the change in length of the arch. The change in length is directly proportional to the radius of the arch.
- When the temperature increases, the arch expands and its length increases.
- The magnitude of the thrust force is directly proportional to the change in length.
- Since the change in length is directly proportional to the radius, the thrust force is also directly proportional to the radius.
Therefore, the correct answer is option 'D' - the horizontal thrust due to the rise in temperature in a semicircular two hinged arch is proportional to 1/R^2.
The horizontal thrust in a semicircular two hinged arch is caused by the rise in temperature. When the temperature increases, the arch expands and exerts a horizontal force on the supports.
The thrust generated due to the rise in temperature can be analyzed by considering the equilibrium conditions of the arch.
1. Equilibrium conditions:
In order for the arch to be in equilibrium, the sum of the forces and moments acting on it must be zero.
- Forces: The horizontal thrust generated due to the rise in temperature is counterbalanced by the horizontal reaction forces at the supports.
- Moments: The moments generated by the thrust force and the reaction forces at the supports must also balance each other out.
2. Relationship between thrust and radius:
The thrust generated due to the rise in temperature is proportional to the change in length of the arch. The change in length is directly proportional to the radius of the arch.
- When the temperature increases, the arch expands and its length increases.
- The magnitude of the thrust force is directly proportional to the change in length.
- Since the change in length is directly proportional to the radius, the thrust force is also directly proportional to the radius.
Therefore, the correct answer is option 'D' - the horizontal thrust due to the rise in temperature in a semicircular two hinged arch is proportional to 1/R^2.
A fixed beam AB with a central hinge C is built of two components. AC is rigid and CB has a moment of inertia I. When support A yields and rotates through θ, what-is the moment at B?
- a)
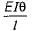
- b)
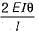
- c)
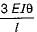
- d)
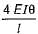
Correct answer is option 'C'. Can you explain this answer?
A fixed beam AB with a central hinge C is built of two components. AC is rigid and CB has a moment of inertia I. When support A yields and rotates through θ, what-is the moment at B?
a)
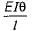
b)
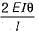
c)
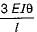
d)
|
|
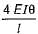
Gauri Sarkar answered |
When support A yields and rotates through θ, the whole beam AC rotates due to its rigidity. The deflection diagram of beam AB is
The rotation at end C of beam BC is θ,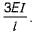
Therefore moment at B is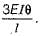
The rotation at end C of beam BC is θ,
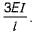
Therefore moment at B is
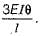
A truss ABC carries two horizontal and two vertical loads, as shown in the figure. The horizontal and vertical components of reactions at A will be
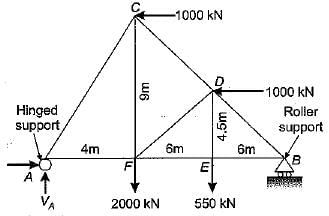
- a)HA = 1000 kN; VA = 1706.25 kN
- b)HA = 2000 kN; VA = 2550 kN
- c)HA = 1000 kN; VA = 2350 kN
- d)HA = 2000 kN; VA = 1706.25 kN
Correct answer is option 'D'. Can you explain this answer?
A truss ABC carries two horizontal and two vertical loads, as shown in the figure. The horizontal and vertical components of reactions at A will be
a)
HA = 1000 kN; VA = 1706.25 kN
b)
HA = 2000 kN; VA = 2550 kN
c)
HA = 1000 kN; VA = 2350 kN
d)
HA = 2000 kN; VA = 1706.25 kN
|
Muthu Selvi answered |
B
Which one of the following equations represents influence line of fixed end moment at B of the fixed beam AB of length l with origin at A?- a)
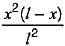
- b)
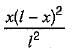
- c)
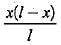
- d)
Correct answer is option 'A'. Can you explain this answer?
Which one of the following equations represents influence line of fixed end moment at B of the fixed beam AB of length l with origin at A?
a)
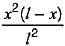
b)
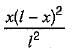
c)
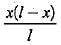
d)
|
|
Partho Choudhary answered |
For the influence line of fixed end moment at B, release the moment at B and give unit rotation, the deformed shape will represent the influence line.
due to unit load at x distance from A.
due to unit load at x distance from A.
Bending moment diagram for the structure shown below is
- a)
- b)
- c)
- d)
Correct answer is option 'A'. Can you explain this answer?
Bending moment diagram for the structure shown below is
a)
b)
c)
d)
|
|
Gitanjali Chauhan answered |
⇒ VA x L + M = 0
∴ VA = - M/L
AS VA+VC =0
⇒ VL = M/L
For span BC,
∴ Mc = - M
and
Chapter doubts & questions for Structural Analysis - Topicwise Question Bank for Civil Engineering 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Structural Analysis - Topicwise Question Bank for Civil Engineering in English & Hindi are available as part of Civil Engineering (CE) exam.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup