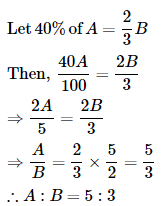All questions of Ratio & Proportion for UPSC CSE Exam
Can you explain the answer of this question below:According to the Boyle’s law, at a constant temperature, pressure of a definite mass of gas is inversely proportional to the volume. If the pressure is reduced by 20%, find the respective change in volume.
- A:
-33.33%
- B:
+25%
- C:
-25%
- D:
+33.33%
The answer is b.
According to the Boyle’s law, at a constant temperature, pressure of a definite mass of gas is inversely proportional to the volume. If the pressure is reduced by 20%, find the respective change in volume.
-33.33%
+25%
-25%
+33.33%
|
|
Ishan Chaudhary answered |
Point mutation involves- a)Change in single base pair
- b)Deletion
- c)Insertion
- d)Duplication
Correct answer is option 'A'. Can you explain this answer?

|
Honey answered |
Arun has a certain amount of money in the denomination of 1 rupee and 10 rupee notes . T he number of 1 rupee notes multiplied by the number of 10 rupee notes is equal to the total money (in rupees) that he has. What is the total number of ten rupee notes that he can have?- a)11
- b)13
- c)15
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
|
|
Dhruv Verma answered |
The sum of three numbers is 98. If the ratio of the first to second is 2 :3 and that of the second to the third is 5 : 8, then the second number is:- a)20
- b)30
- c)48
- d)58
Correct answer is option 'B'. Can you explain this answer?
|
|
Aarav Sharma answered |
- The sum of three numbers is 98.
- The ratio of the first number to the second number is 2:3.
- The ratio of the second number to the third number is 5:8.
**Let's solve the problem step by step:**
**Step 1:**
Let's assume the three numbers as follows:
- The first number = 2x
- The second number = 3x
- The third number = 8y
**Step 2:**
According to the given information, the sum of the three numbers is 98. Therefore, we can write the equation as:
2x + 3x + 8y = 98
**Step 3:**
Simplifying the equation, we get:
5x + 8y = 98
**Step 4:**
Now, we need to find the values of x and y in order to find the second number.
**Step 5:**
According to the given information, the ratio of the second number to the third number is 5:8. Therefore, we can write the equation as:
3x/8y = 5/8
**Step 6:**
Cross-multiplying the equation, we get:
24x = 40y
**Step 7:**
Simplifying the equation, we get:
3x = 5y
**Step 8:**
Now, we have two equations:
5x + 8y = 98
3x = 5y
**Step 9:**
Substituting the value of 3x from the second equation into the first equation, we get:
5(5y/3) + 8y = 98
25y/3 + 8y = 98
(25y + 24y)/3 = 98
49y/3 = 98
49y = 294
y = 294/49
y = 6
**Step 10:**
Substituting the value of y into the second equation, we get:
3x = 5(6)
3x = 30
x = 30/3
x = 10
**Step 11:**
Now, we can find the second number:
The second number = 3x = 3 * 10 = 30
Therefore, the correct answer is option **B) 30**.
Two-fifth of Anil’s salary is equal of Bhuvan’s salary and seven -ninth of Bhuvan’s salary is equal to Chandra’s salary. The sum of the salary of all of them is Rs 770. Which of the following is the salary of each?- a)300, 225, 250
- b)500, 425, 375
- c)450, 180, 140
- d)520, 610, 475
Correct answer is option 'C'. Can you explain this answer?
|
|
Anaya Patel answered |
A metal trader buys 2 kinds of silver foils, the ratio of their prices being 1:4. He sells the alloy at Rs 90 per kg so that he can make a profit of 20%. If the ratio of their quantities present in a alloy is 6:1 respectively, find the purchase price of the foil present in lesser quantity.
- a)Rs 52.5
- b)Rs 55
- c)Rs 47.5
- d)Rs 45
Correct answer is option 'A'. Can you explain this answer?

|
Arya Roy answered |

Anand and Bhavana have a few one rupee, 50 paise and 25 paise coins each. The total amount with each of them is Rs 5. The number of coins of two of the three types of coins that Anand has are equal and same is the case for the coins that Bhavana has. If Anand has the maximum possible total number of coins, then find the maximum possible total number of coins that Bhavana can have given that she has fewer coins than Anand.- a)16
- b)12
- c)10
- d)9
Correct answer is option 'B'. Can you explain this answer?
|
|
Nandita Kaur answered |
Can you explain the answer of this question below:The difference between the two positive numbers is 10 and the ratio between them is 5:3. Find the product of the two numbers.
- A:
375
- B:
325
- C:
275
- D:
125
The answer is a.
The difference between the two positive numbers is 10 and the ratio between them is 5:3. Find the product of the two numbers.
375
325
275
125

|
Subham Basu answered |
The ratio of the number of boys and girls in a college is 7 : 8. If the percentage increase in the number of boys and girls be 20% and 10% respectively, what will be the new ratio?- a)8 : 9
- b)17 : 18
- c)21 : 22
- d)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
|
|
Ravi Singh answered |
An alloy of manganese, tin and bronze contains 90% bronze, 7% manganese and 3% tin. A second alloy of bronze and tin is melted with the first and the mixture contains 85% of bronze, 5% of manganese and 10% of tin. What is the percentage of bronze in the second alloy?- a)67.5%
- b)72.5%
- c)77.5%
- d)82.5%
Correct answer is 'B'. Can you explain this answer?

|
Sameer Rane answered |
In a bag, there are coins of 25 p, 10 p and 5 p in the ratio of 1 : 2 : 3. If there is Rs. 30 in all, how many 5 p coins are there?- a)50
- b)100
- c)150
- d)200
Correct answer is option 'C'. Can you explain this answer?

|
Gowri Chakraborty answered |
Can you explain the answer of this question below:A and B invest Rs 12,000 and Rs 16,000 respectively in a business. At the year-end, they share the profit in the ratio of 3:1. If A has invested his capital for the whole year, for how many months B has invested his capital?
- A:
4 months
- B:
3 months
- C:
6 months
- D:
8 months
The answer is b.
A and B invest Rs 12,000 and Rs 16,000 respectively in a business. At the year-end, they share the profit in the ratio of 3:1. If A has invested his capital for the whole year, for how many months B has invested his capital?
4 months
3 months
6 months
8 months
|
|
Saranya Kaur answered |
Gandhiji owns cows, some black and some white. He finds that 4 black cows and 3 white cows gave the same amount of milk in 5 days as 3 black cows and 5 white cows gave in 4 days. What is the ratio of milk given by a black cow in a day to that given by a white cow in a day?- a)8 : 5
- b)5 : 8
- c)3 : 5
- d)5 : 3
Correct answer is option 'B'. Can you explain this answer?

|
Janhavi Nambiar answered |
The sum of four numbers is 253. The ratio of the first number to the second number is 2:3. The ratio of the second number to the third number is 5:6. The ratio of the third number to the fourth number is 8:9. What is the average of the second number and the third number?- a)72
- b)132
- c)60
- d)66
Correct answer is option 'D'. Can you explain this answer?
|
|
Anaya Patel answered |
2nd no.= B , 3rd no.= C , 4th no. = D
A: B =2:3
A/B = 2/3
x/B =2/3
B= 3x/2
B:C=5:6
(3x/2)/ C= 5/6
C=( 6×3x)/2×5= 9x/5
C= 9x/5
C:D= 8:9
9x/5/ D = 8/9
D= (9x×9)/8×5= 81x/40
D= 81x/40
A+B+C+D= 253. (GIVEN)
x+ 3x/2+9x/5+81x/40
Lcm = 40
(40x+ 60x+ 72x+81x)/40= 253
253x= 253×40
X= (253×40)/253= 40
Ist no.(A)= X= 40
2no.(B)= 3x/2=( 3 × 40)/2= 60
3rd no.(C)= 9x/5 = (9×40)/5= 72
4th no.(D)= 81x/40=( 81×40/)/40= 81
Average of numbers= sum of observations/ total no.of observations
Average of 2nd no. & 3rd no.= (60+72)/2= 132/2= 66
Four numbers in the ratio of 1:3:4:7 add up to give a sum of 75. Find the value of the biggest number.- a)42
- b)35
- c)49
- d)63
Correct answer is option 'B'. Can you explain this answer?
|
|
Kavya Saxena answered |
15x = 75
x = 75/15
x = 5
So, 1x = 1*5 = 5
3x = 3*5 = 15
4x = 4*5 = 20
7x = 7*5 = 35
Can you explain the answer of this question below:Two number are in the ratio 3 : 5. If 9 is subtracted from each, the new numbers are in the ratio 12 : 23. The smaller number is:
- A:
27
- B:
33
- C:
49
- D:
55
The answer is B.
Two number are in the ratio 3 : 5. If 9 is subtracted from each, the new numbers are in the ratio 12 : 23. The smaller number is:
27
33
49
55
|
|
Sagar Sharma answered |
The ratio of two numbers is 3:5
After subtracting 9 from each number, the new ratio is 12:23
Let's assume the two numbers in the original ratio are 3x and 5x.
Ratio of the new numbers:
(3x-9) : (5x-9) = 12 : 23
Cross-multiplying, we get:
12(5x-9) = 23(3x-9)
Simplifying the equation:
60x - 108 = 69x - 207
-9x = -99
x = 11
Finding the smaller number:
Smaller number = 3x = 3 * 11 = 33
Therefore, the smaller number is 33, which corresponds to option 'B'.
The salaries A, B, C are in the ratio 2 : 3 : 5. If the increments of 15%, 10% and 20% are allowed respectively in their salaries, then what will be new ratio of their salaries?- a)3 : 3 : 10
- b)10 : 11 : 20
- c)23 : 33 : 60
- d)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
|
|
Kavya Saxena answered |
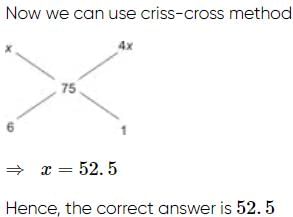
Salaries of Ravi and Sumit are in the ratio 2 : 3. If the 'salary of each' one of them is increased by Rs. 4000, the new ratio becomes 40 : 57. What is Sumit's present salary?
- a)Rs. 17,000
- b)Rs. 20,000
- c)Rs. 25,500
- d)Rs. 38,000
Correct answer is option 'D'. Can you explain this answer?

|
Sameer Rane answered |
Bidhan is planning to buy a bike worth Rs 35,000, provided his brother agrees to lend him 3/2 times the money. Bidhan contributes and the financer provides 3 times the brother’s contribution. How much does Bidhan’s brother contribute?- a)5,000
- b)7,500
- c)10,000
- d)7,000
Correct answer is option 'B'. Can you explain this answer?
|
|
Nikita Singh answered |
If 0.75 : x :: 5 : 8, then x is equal to:- a)1.12
- b)1.2
- c)1.25
- d)1.30
Correct answer is option 'B'. Can you explain this answer?
|
|
Aarav Sharma answered |
Step 1: Set up the proportion
0.75 : x :: 5 : 8
Step 2: Cross-multiply
0.75 * 8 = x * 5
Step 3: Solve for "x"
6 = 5x
Step 4: Divide both sides by 5
x = 6 / 5
Step 5: Simplify the fraction
x = 1.2
Therefore, the value of "x" in the proportion 0.75 : x :: 5 : 8 is equal to 1.2.
Summary:
To find the value of "x" in the given proportion, we set up the proportion and cross-multiply. Then we solve for "x" by dividing both sides of the equation. In this case, the value of "x" is equal to 1.2.
The sum of the ages of the 4 members of Sinha family is 140 years. 5 years ago the ages of the 4 members Nishu, Vicky, Mrs Sinha and Mr Sinha were in the ratio of 2 : 3 : 7 : 8 . After how many years would Nishu be as old as the present age of his mother?- a)10yrs
- b)17yrs
- c)30 yrs
- d)32 yrs
Correct answer is option 'C'. Can you explain this answer?
|
|
Lavanya Menon answered |
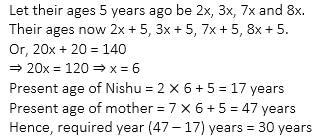
Two numbers are in the ratio 2:5. If 6 is added to both, their ratio changes to 4:7. What is the larger number?- a)6
- b)12
- c)15
- d)21
Correct answer is option 'C'. Can you explain this answer?
|
|
Mihir Mehta answered |
We have two numbers in the ratio 2:5. Let's denote these numbers as:
- First Number = 2x
- Second Number = 5x
After adding 6 to both numbers, their ratio changes to 4:7.
Setting Up the Equation
When we add 6 to both numbers, we can express the new situation as:
- New First Number = 2x + 6
- New Second Number = 5x + 6
According to the problem, the new ratio is:
(2x + 6) / (5x + 6) = 4/7
Cross-Multiplying to Solve
To eliminate the fraction, we can cross-multiply:
7(2x + 6) = 4(5x + 6)
This simplifies to:
14x + 42 = 20x + 24
Rearranging the Equation
Next, we rearrange it to isolate x:
14x - 20x = 24 - 42
This gives us:
-6x = -18
Thus, we find:
x = 3
Finding the Numbers
Now that we have x, we can find the original numbers:
- First Number = 2x = 2(3) = 6
- Second Number = 5x = 5(3) = 15
Conclusion
The larger number is:
- 15
Thus, the correct answer is option 'C'.
A and B invested Rs 12,000 and Rs 18,000 respectively in a business for the whole year. At the year-end, there was a total profit of Rs 2,000. What is the share of A in the profit?- a)Rs 800
- b)Rs 1,200
- c)Rs 1,600
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
|
|
Advait Saini answered |
A and B have invested different amounts in a business:
- A's investment: Rs 12,000
- B's investment: Rs 18,000
Total Investment
- Total investment by both A and B = Rs 12,000 + Rs 18,000 = Rs 30,000
Profit Distribution
The total profit at the year-end is Rs 2,000. The profit is shared based on the ratio of their investments.
Calculating the Ratio
- A's investment = Rs 12,000
- B's investment = Rs 18,000
- Ratio of A’s investment to B’s investment = 12,000 : 18,000
To simplify:
- Divide both sides by 6
- A : B = 2 : 3
Finding A's Share in Profit
To determine A's share in the profit, we first calculate the total parts in the ratio. The total parts = 2 (for A) + 3 (for B) = 5 parts.
Next, we find out how much each part is worth:
- Value of each part = Total Profit / Total Parts = Rs 2,000 / 5 = Rs 400
Now, we can calculate A's share:
- A's share = 2 parts * Value of each part = 2 * Rs 400 = Rs 800
Conclusion
Thus, A's share in the profit is Rs 800, which corresponds to option 'A'.
Anil started a manufacturing unit with a certain amount of money. After a few months, Dheeraj became his partner, contributing three times of what Anil had contributed. At the end of the year, each was entitled to half the total profit. If Anil started the unit in January, then when did Dheeraj join as a partner?- a)August
- b)September
- c)July
- d)October
Correct answer is option 'B'. Can you explain this answer?

|
Shraddha Dasgupta answered |

In a fort there are 1600 soldiers fighting a battle against their enemy. On a particular day after their morning meal the balance provision inside the fort is only sufficient for 12 days at the rate of 1.2 kg per day. If by the evening 400 soldiers die then for how many days will the provision be sufficient for remaining men at the rate of 1.6 kg per day. (Assume soldiers eat either in morning or in evening).- a)10
- b)8
- c)18
- d)12
Correct answer is option 'D'. Can you explain this answer?
|
|
Alok Verma answered |
= (1600) (12) (1.2)
Total number of soldiers left at the end of the day 1200
Now we have to calculate that for how long is available provision enough for the left-out soldiers
(1200) (x) (1.6)
(1600) (12) (1.2) = (1200) (x) (1.6)
Solving it for the value of x
We get x = 12
The provision is sufficient for 1200 soldiers for 12 days.
Read the passage below and solve the questions based on it.
A book having pages between 4,000 and 5,000 is divided into four parts, each part being divided into chapters. The total number of pages in each of the four parts is the same. The ratio of the chapters across all the parts is 6:5:10:14. The number of chapters in the fourth part is 70
Q.What is the total number of pages in the book?
- a)4,000
- b)4,800
- c)4,200
- d)4,600
Correct answer is option 'C'. Can you explain this answer?
A book having pages between 4,000 and 5,000 is divided into four parts, each part being divided into chapters. The total number of pages in each of the four parts is the same. The ratio of the chapters across all the parts is 6:5:10:14. The number of chapters in the fourth part is 70

|
Palak Yadav answered |
► Now in D there are 70 chapters
Therefore, A:B:C:D = 30:25:50:70 [ Multiplying Each by 5 ]
L.C.M of 30, 25, 50, 70 is 1050
So each part should have 1050 pages.
So total pages = 4 x 1050 = 4200 ans.
Ajay started a business by investing Rs5000. After 3 years, Binoy joined by investing Rs3000 whereas Ajay withdrew 1/5th of his capital. At the end of 12 years, they received a profit of Rs 52,000. What is Ajay’s share of profit?- a)18,000
- b)24,000
- c)34,000
- d)36,000
Correct answer is option 'C'. Can you explain this answer?

|
Upsc Rank Holders answered |
Ratio or profit 5000 × 3 + 4000 × 9 : 3000 × 9 = 51 : 27 = 17 : 9
Ajay’s share = 17/26 × 52,000 = 34,000
Can you explain the answer of this question below:Two cogged wheels of which one has 32 cogs and other 54 cogs, work into each other. If the latter turns 80 times in three quarter of a minute, how often does the other turn in 8 seconds? (Assume equal size cogs and equi-spaced).
- A:
24
- B:
16
- C:
32
- D:
8
The answer is a.
Two cogged wheels of which one has 32 cogs and other 54 cogs, work into each other. If the latter turns 80 times in three quarter of a minute, how often does the other turn in 8 seconds? (Assume equal size cogs and equi-spaced).
24
16
32
8

|
Dhruv Mehra answered |
In a garrison of 3600 men, the provisions were sufficient for 20 days at the rate of 1.5 kg per man per day. If x more men joined, the provisions would be sufficient for 12 days at the rate of 2 kg per man per day. Find x.- a)600
- b)800
- c)900
- d)720
Correct answer is option 'C'. Can you explain this answer?
|
|
Rhea Reddy answered |
The total quantity of food is = 3600(20) (1.5) kg ----------1
Now the available food will be consumed by (3600+x) men
(3600+x) (12) (2) kg --------------2
1 = 2
Solving both the equations
3600(20) (1.5) = (3600+x) (12) (2)
108000 = 86400 + 24x
21600 = 24x
X = 900
900 more men joined the garrison.
A man has rs.480 in the denominations of one-rupee notes, five-rupee notes and ten-rupee notes. The number of notes of each denomination is equal. What is the total number of notes that he has ?- a)100
- b)50
- c)78
- d)90
Correct answer is option 'D'. Can you explain this answer?
|
|
Aisha Gupta answered |
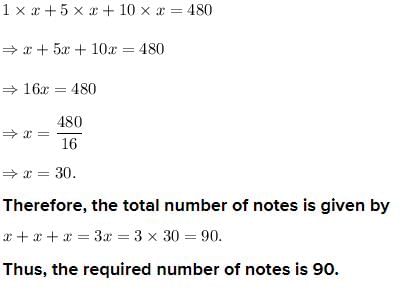
Two numbers are 30% and 20% less than a third number respectively. The ratio of first two numbers is:- a)7 : 6
- b)3 : 2
- c)7 : 8
- d)8 : 7
Correct answer is option 'C'. Can you explain this answer?

|
Capstone Ias Learning answered |
A is proportional to B. B is inversely proportional to C. C is proportional to the square of D. D is directly proportional to the cube root of E. Assuming positive integers, if A increases then E- a)Increases
- b)Decreases
- c)Cannot say
- d)Could increase or decrease
Correct answer is option 'B'. Can you explain this answer?

|
Akanksha Datta answered |
Three friends A, B and C started a venture with capitals in the ratio of 4:1:15. At the end of every quarter A halves his capital, while B doubles his capital and C leaves his capital untouched. This process is repeated till the end of the year. If at the end of the year B ’ s share of the profit is Rs 22,000, what is the total profit?
- a)Rs 88,000
- b)Rs 1,10,000
- c)Rs 2,25,000
- d)Rs 1,21,000
Correct answer is option 'D'. Can you explain this answer?

|
Bhavya Saha answered |
If A : B is 2 : 3, C : B is 3 : 4 and D : C is 4 : 5 then what is A : B : C : D?- a)40 : 60 : 45 : 36
- b)24 : 36 : 48 : 60
- c)40 : 45 : 60 : 36
- d)24 : 48 : 60 : 36
Correct answer is option 'A'. Can you explain this answer?

|
Master Training Institute answered |
Read the passage below and solve the questions based on it.
There are certain number of apples, guavas and oranges in a basket. The number of each variety is more than one. The ratio of the number of apples to the number of guavas is equal to the ratio of the number of guavas lo the number of oranges.Q.If the total number of fruits is 61, then find the number of guavas.- a)16
- b)20
- c)25
- d)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
There are certain number of apples, guavas and oranges in a basket. The number of each variety is more than one. The ratio of the number of apples to the number of guavas is equal to the ratio of the number of guavas lo the number of oranges.
|
|
Aarav Sharma answered |
- Let the number of apples be represented by A
- Let the number of guavas be represented by G
- Let the number of oranges be represented by O
- We know that A:G = G:O
Total number of fruits:
- The total number of fruits is given as 61
- Therefore, A + G + O = 61
Finding the number of guavas:
- We need to find the number of guavas, which is represented by G
- Since we know that A:G = G:O, we can write this as A/G = G/O
- Cross-multiplying, we get A*O = G*G
- We also know that A + G + O = 61
- Substituting A*O = G*G, we get G*G + G + G*O = 61G
- Simplifying, we get G^2 + G*O - 61G = 0
- Using the quadratic formula, we get G = 20 or G = 41
- Since the number of each variety is more than one, we can eliminate G = 41
- Therefore, the number of guavas is 20
Answer:
- Therefore, the correct option is (b) 20
In what ratio must be 40% acid solution and 70% acid solution mixed in order to get 50% acid solution?- a)1 : 2
- b)2 : 1
- c)1 : 3
- d)3 : 1
Correct answer is option 'B'. Can you explain this answer?

|
S.S Career Academy answered |
70 – 50 = 20
50 – 40 = 10
Ratio = 20:10 = 2:1
P works twice as fast as Q, whereas P and Q together can work three times as fast as R. If P, Q and R together work on a job, in what ratio should they share the earnings?- a)2:1:1
- b)4:2:1
- c)4:3:2
- d)4:2:3
Correct answer is option 'A'. Can you explain this answer?

|
Akanksha Datta answered |
Hence, earning should be distributed in the ratio of their efficiency, i.e., 2 : 1 : 1.
A bottle contains 10 litres of Milk. 2 litres of Milk is taken out of it and replaced by same quantity of Water. Again 2 litres of the mixture is taken out and replaced by same quantity of Water. What is the ratio of quantity of water to that of Milk in the final mixture?- a)16 : 19
- b)9 : 16
- c)5 : 4
- d)4 : 5
Correct answer is option 'B'. Can you explain this answer?
|
|
Maya Choudhary answered |
- Start with 10 litres of milk in the bottle.
First Replacement
- 2 litres of milk is removed:
- Remaining milk = 10 - 2 = 8 litres
- Add 2 litres of water:
- Total mixture = 8 litres of milk + 2 litres of water = 10 litres
Concentration After First Replacement
- Concentration of milk after first replacement:
- Milk = 8 litres
- Water = 2 litres
Second Replacement
- Take out 2 litres of the mixture (which contains both milk and water):
- The ratio of milk to water in the mixture = 8:2 or 4:1
- Total parts = 5 (4 parts milk + 1 part water)
- Amount of milk in 2 litres taken out:
- Milk taken out = (4/5) * 2 = 1.6 litres
- Amount of water in 2 litres taken out:
- Water taken out = (1/5) * 2 = 0.4 litres
Final Quantities
- Remaining milk = 8 - 1.6 = 6.4 litres
- Remaining water = 2 - 0.4 = 1.6 litres
- Add 2 litres of water to the mixture:
- Total water = 1.6 + 2 = 3.6 litres
Final Ratio of Water to Milk
- Final quantities:
- Milk = 6.4 litres
- Water = 3.6 litres
- Ratio of water to milk:
- Water : Milk = 3.6 : 6.4
- Simplifying this gives = 9 : 16
Correct Answer
- The final ratio of quantity of water to that of milk in the mixture is 9 : 16. Thus, the correct option is b.
A man has 25 paise, 50 paise and 1 Rupee coins. There are 220 coins in all and the total amount is 160. If there are thrice as many 1 Rupee coins as there are 25 paise coins, then what is the number of 50 paise coins?- a)60
- b)80
- c)100
- d)120
Correct answer is option 'A'. Can you explain this answer?
|
|
Aarav Sharma answered |
Total number of coins = 220
Total amount = 160
Let the number of 25 paise coins be x
Let the number of 50 paise coins be y
Let the number of 1 Rupee coins be z
Equations:
1. x + y + z = 220 (Total number of coins)
2. 0.25x + 0.5y + z = 160 (Total amount)
Given that there are thrice as many 1 Rupee coins as there are 25 paise coins:
3. z = 3x
Substituting equation 3 in equation 1, we get:
x + y + 3x = 220
4x + y = 220
Substituting equation 3 and equation 2 in equation 1, we get:
0.25x + 0.5y + 3x = 160
3.25x + 0.5y = 160
Solving equations 4 and 5 simultaneously, we get:
x = 20
y = 60
z = 60
Therefore, the number of 50 paise coins is 60. Hence, the correct answer is option A.
The first, second and third class fares between two railway stations, Patna and Lucknow were 10:8:3 and the number of first, second and third class passengers between the two stations was is 3:4:10. If total sales of the ticket is Rs 16,100, find the money obtained by the sales of second class tickets.- a)Rs 5,250
- b)Rs 5,600
- c)Rs 6,400
- d)Rs 6,650
Correct answer is option 'B'. Can you explain this answer?
|
|
Aarav Sharma answered |
Given information:
- The ratio of first, second, and third class fares between Patna and Lucknow is 10:8:3.
- The ratio of first, second, and third class passengers between the two stations is 3:4:10.
- The total sales of tickets is Rs 16,100.
Step 1: Calculate the total ratio of fares.
The total ratio of fares can be found by adding up the individual ratios: 10 + 8 + 3 = 21.
Step 2: Calculate the proportion of each fare.
To find the proportion of each fare, divide each individual fare ratio by the total ratio of fares:
First class fare proportion = 10/21
Second class fare proportion = 8/21
Third class fare proportion = 3/21
Step 3: Calculate the total sales from each fare.
To find the total sales from each fare, multiply the total sales by the proportion of each fare:
Total sales from first class fare = (10/21) * Rs 16,100
Total sales from second class fare = (8/21) * Rs 16,100
Total sales from third class fare = (3/21) * Rs 16,100
Step 4: Calculate the money obtained by the sales of second class tickets.
From step 3, we can see that the total sales from second class fare is:
Total sales from second class fare = (8/21) * Rs 16,100
Simplifying this expression, we get:
Total sales from second class fare = Rs 5,600
Therefore, the money obtained by the sales of second class tickets is Rs 5,600, which corresponds to option B.
Chapter doubts & questions for Ratio & Proportion - CSAT Preparation 2025 is part of UPSC CSE exam preparation. The chapters have been prepared according to the UPSC CSE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for UPSC CSE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.

Contact Support
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
Forgot Password
within 7 days!