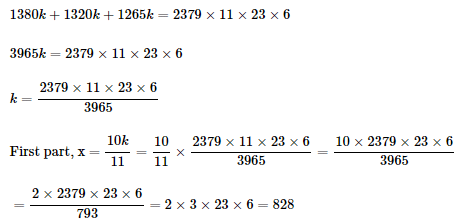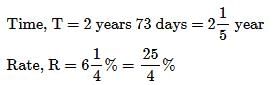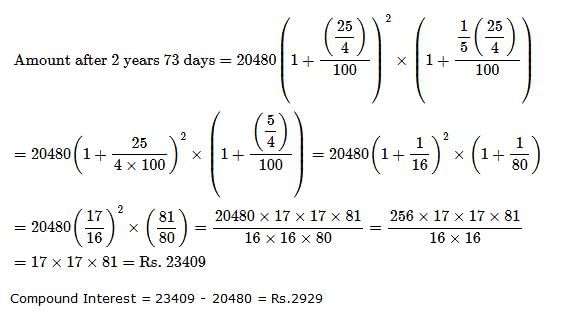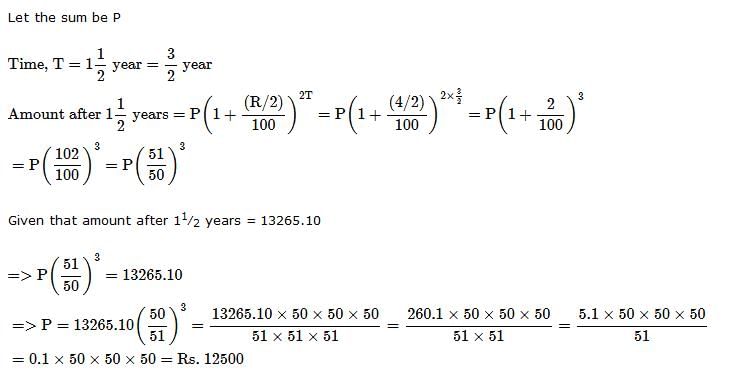All Exams >
UPSC >
CSAT Preparation >
All Questions
All questions of Interest (Simple & Compound) for UPSC CSE Exam
Can you explain the answer of this question below:A sum of money amounts to Rs.9800 after 5 years and Rs.12005 after 8 years at the same rate of simple interest. The rate of interest per annum is- A:15%
- B:12%
- C:8%
- D:5%
The answer is B.

|
Arya Roy answered |
We can get SI of 3 years = 12005 - 9800 = 2205
SI for 5 years = (2205/3)*5 = 3675 [so that we can get principal amount after deducting SI]
Principal = 12005 - 3675 = 6125
So Rate = (100*3675)/(6125*5) = 12%
If the simple interest on a certain sum of money after 25/8 years is 1/4 of the principal, what is the rate of interest per annum?
- a)6%
- b)4%
- c)8%
- d)12%
Correct answer is option 'C'. Can you explain this answer?
If the simple interest on a certain sum of money after 25/8 years is 1/4 of the principal, what is the rate of interest per annum?
a)
6%
b)
4%
c)
8%
d)
12%
|
|
Rahul Mehta answered |
Take P=x
given T=25/8
& I=1/4x
w.k.t I=PTR/100
1/4x =x*25/8*R/100
R = 8%
given T=25/8
& I=1/4x
w.k.t I=PTR/100
1/4x =x*25/8*R/100
R = 8%
A sum of money at simple interest amounts to Rs. 815 in 3 years and to Rs. 854 in 4 years. The sum is :- a)Rs. 700
- b)Rs. 690
- c)Rs. 650
- d)Rs. 698
Correct answer is option 'D'. Can you explain this answer?
a)
Rs. 700
b)
Rs. 690
c)
Rs. 650
d)
Rs. 698

|
Dhruv Mehra answered |
S.I. for 1 year = Rs. (854 - 815) = Rs. 39.
S.I. for 3 years = Rs.(39 * 3) = Rs. 117.
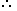 Principal = Rs. (815 - 117) = Rs. 698.
Principal = Rs. (815 - 117) = Rs. 698.A bank offers 5% compound interest calculated on half-yearly basis. A customer deposits Rs. 1600 each on 1st January and 1st July of a year. At the end of the year, the amount he would have gained by way of interest is:
- a)Rs. 120
- b)Rs. 121
- c)Rs. 123
- d)Rs. 122
Correct answer is option 'B'. Can you explain this answer?
A bank offers 5% compound interest calculated on half-yearly basis. A customer deposits Rs. 1600 each on 1st January and 1st July of a year. At the end of the year, the amount he would have gained by way of interest is:
a)
Rs. 120
b)
Rs. 121
c)
Rs. 123
d)
Rs. 122

|
Ishani Rane answered |

The difference between simple interest and compound on Rs. 900 for one year at 10% per annum reckoned half-yearly is: - a)Rs. 3
- b)Rs. 2.25
- c)Rs. 4.5
- d)Rs. 4
Correct answer is option 'B'. Can you explain this answer?
a)
Rs. 3
b)
Rs. 2.25
c)
Rs. 4.5
d)
Rs. 4
|
|
Maheshwar Banerjee answered |

Hence Option B is correct
For Complete syllabus of Quant for CAT click on the link given below:
Simple interest on a certain sum of money for 4 years at 5% per annum is half the compound interest on Rs. 3000 for 2 years at 10% per annum. The sum placed on simple interest is: - a)Rs.1575
- b)Rs. 2200
- c)Rs. 1200
- d)Rs. 1625
Correct answer is option 'A'. Can you explain this answer?
a)
Rs.1575
b)
Rs. 2200
c)
Rs. 1200
d)
Rs. 1625

|
KS Coaching Center answered |
C.I = P[(1 + r/100)n - 1]
C.I = 3000[(1 + 0.10)2 - 1]
= 3000(1.21 - 1)
⇒ 3000 * 0.21
⇒ 630
S.I = 630/2
⇒ 315
As we know that, P = (SI * 100)/(R * T)
⇒ (315 * 100)/(4 * 5)
⇒ 1575
C.I = 3000[(1 + 0.10)2 - 1]
= 3000(1.21 - 1)
⇒ 3000 * 0.21
⇒ 630
S.I = 630/2
⇒ 315
As we know that, P = (SI * 100)/(R * T)
⇒ (315 * 100)/(4 * 5)
⇒ 1575
An automobile financier claims to be lending money at simple interest, but he includes the interest every six months for calculating the principal. If he is charging an interest of 10%, the effective rate of interest becomes:- a)10%
- b)10.25%
- c)10.5%
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
a)
10%
b)
10.25%
c)
10.5%
d)
None of these

|
Master Training Institute answered |
B is the correct option. Solution
6 months interest will be 5%
next 6 months interest will be 5%
percentage effect = 5 + 5 +25/100
= 10.25 Ans
6 months interest will be 5%
next 6 months interest will be 5%
percentage effect = 5 + 5 +25/100
= 10.25 Ans
A lends Rs. 1500 to B and a certain sum to C at the same time at 8% per annum simple interest. If after 4 years, A altogether receives Rs. 1400 as interest from B and C, then the sum lent to C is A.
- a)Rs.2875
- b)Rs.1885
- c)Rs.2245
- d)Rs.2615
Correct answer is option 'A'. Can you explain this answer?
A lends Rs. 1500 to B and a certain sum to C at the same time at 8% per annum simple interest. If after 4 years, A altogether receives Rs. 1400 as interest from B and C, then the sum lent to C is A.
a)
Rs.2875
b)
Rs.1885
c)
Rs.2245
d)
Rs.2615

|
EduRev SSC CGL answered |
A is the correct option.
Simple interest on the total money lent at
8% FOR 4 YEARS = 1400
Total money lent
= 100/8 × 1400/4 =4375
Therefore, money lent to C
= 4375- 1400 = 2875
Simple interest on the total money lent at
8% FOR 4 YEARS = 1400
Total money lent
= 100/8 × 1400/4 =4375
Therefore, money lent to C
= 4375- 1400 = 2875
Arun took a loan of Rs. 1400 with simple interest for as many years as the rate of interest. If he paid Rs.686 as interest at the end of the loan period, what was the rate of interest?- a)8%
- b)6%
- c)4%
- d)7%
Correct answer is option 'D'. Can you explain this answer?
a)
8%
b)
6%
c)
4%
d)
7%
|
|
Meghana Mishra answered |
Simple Interest (SI) = P N R / 100
P is the Principal loan amount = Rs.1400
N is the number of years of deposit
R is the rate of interest
It is given that the loan period is as many years as the rate of interest.
So, N = R
Interest at the end of the loan period (SI ) = Rs.686
So,
686 = 1400 * R * R /100
R^2 = 686*100 /1400
R^2 = 49
R = 7%
What will be the compound interest on a sum of Rs. 40,000 after 3 years at the rate of 11 p.c.p.a.? - a)Rs. 14705.24
- b)Rs. 14602.25
- c)Rs. 14822.26
- d)Rs. 14322.10
Correct answer is option 'A'. Can you explain this answer?
a)
Rs. 14705.24
b)
Rs. 14602.25
c)
Rs. 14822.26
d)
Rs. 14322.10
|
|
Rhea Reddy answered |
Amount after 3 years = P(1 + R/100)T
=> 40000(1 + 11/100)3
=> 40000(111/100)3
=> 40000[(111*111*111)/(100*100*100)]
=> (4*111*111*111)/100
=> 54705.24
Compound Interest = 54705.24 - 40000
= Rs. 14705.24
=> 40000(1 + 11/100)3
=> 40000(111/100)3
=> 40000[(111*111*111)/(100*100*100)]
=> (4*111*111*111)/100
=> 54705.24
Compound Interest = 54705.24 - 40000
= Rs. 14705.24
The least number of complete years in which a sum of money put out at 20% compound interest will be more than doubled is- a)5
- b)4
- c)6
- d)2
Correct answer is option 'B'. Can you explain this answer?
a)
5
b)
4
c)
6
d)
2
|
|
Anaya Patel answered |
P [1 + (r/100)]n > 2P
⇒ P [1 + (20/100)]n > 2P
[1 + (2/10) ]n > 2
[12 / 10]n > 2
[6/5]n > 2
{6/5 * 6/5 * 6/5 * 6/5} > 2
∴ n = 4
⇒ P [1 + (20/100)]n > 2P
[1 + (2/10) ]n > 2
[12 / 10]n > 2
[6/5]n > 2
{6/5 * 6/5 * 6/5 * 6/5} > 2
∴ n = 4
Can you explain the answer of this question below:Mr. Thomas invested an amount of Rs. 13,900 divided in two different schemes A and B at the simple interest rate of 14% p.a. and 11% p.a. respectively. If the total amount of simple interest earned in 2 years be Rs. 3508, what was the amount invested in Scheme B?- A:Rs. 6400
- B:Rs. 7200
- C:Rs. 6500
- D:Rs. 7500
The answer is A.
A:
Rs. 6400
B:
Rs. 7200
C:
Rs. 6500
D:
Rs. 7500

|
Pallabi Deshpande answered |
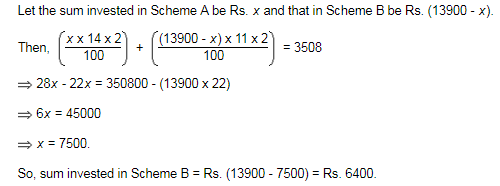
A sum of Rs. 14,000 amounts to Rs. 22,400 in 12 years at the rate of simple interest. What is the rate of interest?- a)7%
- b)6%
- c)5%
- d)4%
Correct answer is option 'C'. Can you explain this answer?
a)
7%
b)
6%
c)
5%
d)
4%

|
Aspire Academy answered |
Amount = 22400, P = 14000, T = 12yrs
SI = 22400 - 14000
= 8400
Rate = (8400*100)/(12*14000)
= 5%
SI = 22400 - 14000
= 8400
Rate = (8400*100)/(12*14000)
= 5%
A man took loan from a bank at the rate of 8% p.a. simple interest. After 4 years he had to pay Rs. 6200 interest only for the period. The principal amount borrowed by him was:- a)Rs.17322
- b)Rs.20245
- c)Rs.18230
- d)Rs.19375
Correct answer is option 'D'. Can you explain this answer?
a)
Rs.17322
b)
Rs.20245
c)
Rs.18230
d)
Rs.19375

|
Ishani Rane answered |
Principal(P) = ?
Time(T) = 4 years
Simple Interest(SI) = Rs.6200
R = 8%
P = 100 * SI/RT = 100 * 6200/8*4 = Rs.19375
A sum amounts to Rs. 882 in 2 years at 5% compound interest. The sum is - a)Rs. 800
- b)Rs. 822
- c)Rs. 840
- d)Rs. 816
Correct answer is option 'A'. Can you explain this answer?
a)
Rs. 800
b)
Rs. 822
c)
Rs. 840
d)
Rs. 816
|
|
Kavya Saxena answered |
Compound interest = Amount -Principal
Amount = P(1 + R/100)N
882 = P(1+5/100)2
= 882 × 20/21 × 20/21
P = 800
Amount = P(1 + R/100)N
882 = P(1+5/100)2
= 882 × 20/21 × 20/21
P = 800
The compound interest on Rs. 30,000 at 7% per annum is Rs. 4347. The period (in years) is: - a)1
- b)2
- c)3
- d)3.5
Correct answer is option 'B'. Can you explain this answer?
a)
1
b)
2
c)
3
d)
3.5

|
Raghavendra Sharma answered |
Amount = Rs. (30000 + 4347) = Rs. 34347.
Let the time be n years.
Then, 30000 (1 + 7/100)^n = 34347
= (107/100)^n = 34347/30000 = 11449/10000 = (107/100)^2
n = 2 years.
Suresh for 2 years invested Rs. 500 in SBI. He also invested Rs. 300 in ICICI for 4 years. At the end he received Rs. 220 from both banks as simple interest. What must have been rate of interest? (assuming the rate of interest for both banks is same)- a) 10%
- b) 12%
- c) 11%
- d) 5.5%
Correct answer is option 'A'. Can you explain this answer?
Suresh for 2 years invested Rs. 500 in SBI. He also invested Rs. 300 in ICICI for 4 years. At the end he received Rs. 220 from both banks as simple interest. What must have been rate of interest? (assuming the rate of interest for both banks is same)
a)
10%
b)
12%
c)
11%
d)
5.5%
|
|
Yash Patel answered |

A certain amount earns simple interest of Rs. 1750 after 7 years. Had the interest been 2% more, how much more interest would it have earned?
- a)Rs. 35
- b)Rs. 245
- c)Rs. 350
- d)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
A certain amount earns simple interest of Rs. 1750 after 7 years. Had the interest been 2% more, how much more interest would it have earned?
a)
Rs. 35
b)
Rs. 245
c)
Rs. 350
d)
Cannot be determined
|
|
Nitesh Verma answered |
I think data given in this question in not sufficient to solved it.
because we want atleast any one thing to solve this.( principle amount or rate of interest)
because we want atleast any one thing to solve this.( principle amount or rate of interest)
The compound interest on a certain sum for 2 years at 10% per annum is Rs. 525. The simple interest on the same sum for double the time at half the rate percent per annum is: - a)Rs. 500
- b)Rs. 400
- c)Rs. 450
- d)Rs. 600
Correct answer is option 'A'. Can you explain this answer?
a)
Rs. 500
b)
Rs. 400
c)
Rs. 450
d)
Rs. 600
|
|
Aarav Sharma answered |
Given data:
Compound Interest = Rs. 525
Rate of Interest = 10%
Time = 2 years
To find:
Simple Interest for double the time at half the rate of interest
Solution:
Let the principal amount be P.
Using the formula for compound interest, we have:
P(1 + 10/100)^2 - P = 525
Simplifying the above equation, we get:
P = 4500
Now, we need to find the simple interest for double the time at half the rate of interest.
New time = 4 years (double the time)
New rate of interest = 5% (half of 10%)
Using the formula for simple interest, we have:
SI = (P * R * T) / 100
SI = (4500 * 5 * 4) / 100
SI = Rs. 900
Therefore, the simple interest for double the time at half the rate of interest is Rs. 900, which is not one of the given options. However, we need to note that the question is asking for the simple interest on the same sum, which means we need to use the same principal amount of Rs. 4500.
If we calculate the simple interest for 2 years at 5%, we get:
SI = (4500 * 5 * 2) / 100
SI = Rs. 450
Hence, the correct answer is option A, Rs. 500.
Compound Interest = Rs. 525
Rate of Interest = 10%
Time = 2 years
To find:
Simple Interest for double the time at half the rate of interest
Solution:
Let the principal amount be P.
Using the formula for compound interest, we have:
P(1 + 10/100)^2 - P = 525
Simplifying the above equation, we get:
P = 4500
Now, we need to find the simple interest for double the time at half the rate of interest.
New time = 4 years (double the time)
New rate of interest = 5% (half of 10%)
Using the formula for simple interest, we have:
SI = (P * R * T) / 100
SI = (4500 * 5 * 4) / 100
SI = Rs. 900
Therefore, the simple interest for double the time at half the rate of interest is Rs. 900, which is not one of the given options. However, we need to note that the question is asking for the simple interest on the same sum, which means we need to use the same principal amount of Rs. 4500.
If we calculate the simple interest for 2 years at 5%, we get:
SI = (4500 * 5 * 2) / 100
SI = Rs. 450
Hence, the correct answer is option A, Rs. 500.
If the simple interest on a sum of money for 2 years at 5% per annum is Rs. 60, what is the compound interest on the same at the same rate and for the same time?
- a)Rs. 63.5
- b)Rs. 62
- c)Rs. 61.5
- d)Rs. 64
Correct answer is option 'C'. Can you explain this answer?
If the simple interest on a sum of money for 2 years at 5% per annum is Rs. 60, what is the compound interest on the same at the same rate and for the same time?
a)
Rs. 63.5
b)
Rs. 62
c)
Rs. 61.5
d)
Rs. 64

|
Venky Dhawan answered |
Since SI = 60
SI = P×R×T/ 100
which is P = 60×100/2×5 = 200
P = 600
CI= 600(1+5/100)^2
= 600(21/20)^2
= 600(1.025) = 661.5 which is amount
so sum = 600-661 = 61.5(C)
SI = P×R×T/ 100
which is P = 60×100/2×5 = 200
P = 600
CI= 600(1+5/100)^2
= 600(21/20)^2
= 600(1.025) = 661.5 which is amount
so sum = 600-661 = 61.5(C)
Arun invested an amount of Rs. 2000 in a fixed deposit scheme for 2 years at compound interest rate 4 p.c.p.a. How much amount will Arun get on maturity of the fixed deposit?
- a)2034.2
- b)2163.2
- c)2232.4
- d)2412.0
Correct answer is option 'B'. Can you explain this answer?
Arun invested an amount of Rs. 2000 in a fixed deposit scheme for 2 years at compound interest rate 4 p.c.p.a. How much amount will Arun get on maturity of the fixed deposit?
a)
2034.2
b)
2163.2
c)
2232.4
d)
2412.0

|
Monica A answered |
20,000*(104/100)² = 21632...(principle + Interest = Amount)...since it is fixed deposit, we receive amount after maturity
The effective annual rate of interest corresponding to a nominal rate of 6% per annum payable half-yearly is: - a)6.07%
- b)6.08%
- c)6.06%
- d)6.09%
Correct answer is option 'D'. Can you explain this answer?
a)
6.07%
b)
6.08%
c)
6.06%
d)
6.09%

|
Krithika Sengupta answered |
Amount of Rs. 100 for 1 year
when compounded half-yearly = Rs.[100*(1+3/100)^2]=Rs.106.09
Effective rate=(106.09-100)%=6.09%
What annual payment will discharge a debt of Rs. 6450 due in 5 years at 10% per annum?
- a)Rs.1075
- b)Rs.1050
- c)Rs.1100
- d)Rs.1025
Correct answer is option 'A'. Can you explain this answer?
What annual payment will discharge a debt of Rs. 6450 due in 5 years at 10% per annum?
a)
Rs.1075
b)
Rs.1050
c)
Rs.1100
d)
Rs.1025

|
Dhruv Mehra answered |
Installment for first year = x
Installment for second year = 1.10x
Installment for third year = 1.20x
Installment for third year = 1.30x
Installment for final year = 1.40x
Total amount to be paid = (1 + 1.10 + 1.20 + 1.30 + 1.40) × x = 6450
∴ x = 6450 / 6 = 1075
A sum of Rs. 10 is lend to be returned in 11 monthly instalments of Rs. 1 each, interest being simple. The rate of interest charged is:
- a)10%
- b)22%
- c)
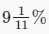
- d)
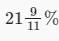
Correct answer is option 'D'. Can you explain this answer?
A sum of Rs. 10 is lend to be returned in 11 monthly instalments of Rs. 1 each, interest being simple. The rate of interest charged is:
a)
10%
b)
22%
c)
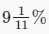
d)
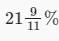

|
Pallabi Deshpande answered |
Given :
A sum of Rs. 10 is lend to be returned in 11 monthly instalments of Rs . 1 each interest being simple
Formula used :
Simple interest = P × R× T /100
Principal(P), Rate(R) and Time(T)
Calculation :
Let the rate of interest be R% per annum
⇒ Amount to be paid (if paid at the end of 11 months)
⇒ 10 + [10 × R × (11/12) / 100] = 10 + (11R/120)
⇒ Total effective payment = (Rs. 1 + interest on Rs. 1 for 10 months) + (Rs. 1 + interest on Rs. 1 for 9 months) + .... +(Rs. 1 + interest on Rs. 1 for 1 months) + Rs. 1
⇒ (1 + 1 × R × (10/12) / 100) + (1 + 1 × R × (9/12) / 100) + .... + (1 + 1 × R × (1/12) / 100) + 1
⇒ (1 + 10R/1200) + (1 + 9R/1200) + .... + (1 + R/1200) + 1
⇒ 11 + R(1 + 2 + .... + 10)/1200
⇒ 11 + R(10 × 11 / 2)/1200
⇒ 11 + R(10 × 11 / 2)/1200
⇒ 11 + 11R/240
Now we have,
⇒ 10 + 11R/120 = 11 + 11R/240
⇒ 11R/240 = 1
⇒ R = 240/11 = 21× 9/11%
∴ Rate of interest is 21(9/11)%
If a sum of Rs. 9 is lent to be paid back in 10 equal monthly installments of re. 1 each, then the rate of interest is
- a)11.33%
- b)11%
- c)266.67%
- d)33.33%
Correct answer is option 'D'. Can you explain this answer?
If a sum of Rs. 9 is lent to be paid back in 10 equal monthly installments of re. 1 each, then the rate of interest is
a)
11.33%
b)
11%
c)
266.67%
d)
33.33%

|
Manoj Ghosh answered |
Let's try to understand the problem step by step.
A sum of Rs. 9 is lent to be paid back in 10 equal monthly installments of Re. 1 each.
This means that the borrower is paying back Re. 1 per month for 10 months.
Now, let's calculate the interest paid in each installment.
1. In the first month, the borrower still owes Rs. 9, so no interest is paid.
2. In the second month, the borrower has already paid Re. 1, so he now owes Rs. 8. The interest paid would be on Rs. 8.
3. In the third month, the borrower has paid Rs. 2, so he now owes Rs. 7. The interest paid would be on Rs. 7.
4. This continues until the 10th month when the borrower has paid Rs. 9 and owes nothing.
Now let's calculate the total interest paid over the 10 months.
Total Interest Paid = (Interest on Rs. 8) + (Interest on Rs. 7) + ... + (Interest on Re. 1)
Let's assume the rate of interest is "R" percent per month.
Total Interest Paid = (8 * R) + (7 * R) + ... + (1 * R)
Now, we know that the total amount paid is Rs. 10 (10 installments of Re. 1 each), and the total amount lent is Rs. 9. So, the total interest paid is Rs. 1.
1 = (8 * R) + (7 * R) + ... + (1 * R)
Now we can simplify the equation:
1 = R * (8 + 7 + 6 + 5 + 4 + 3 + 2 + 1)
1 = R * 36
Now, let's find the value of R (the rate of interest per month):
R = 1/36
Since we need to calculate the rate of interest in percentage, we multiply R by 100:
R (%) = (1/36) * 100 = 2.78%
Now, we have the monthly rate of interest. To find the annual rate of interest, we multiply the monthly rate by 12:
Annual Rate of Interest = 2.78% * 12 = 33.33%
A sum of Rs. 9 is lent to be paid back in 10 equal monthly installments of Re. 1 each.
This means that the borrower is paying back Re. 1 per month for 10 months.
Now, let's calculate the interest paid in each installment.
1. In the first month, the borrower still owes Rs. 9, so no interest is paid.
2. In the second month, the borrower has already paid Re. 1, so he now owes Rs. 8. The interest paid would be on Rs. 8.
3. In the third month, the borrower has paid Rs. 2, so he now owes Rs. 7. The interest paid would be on Rs. 7.
4. This continues until the 10th month when the borrower has paid Rs. 9 and owes nothing.
Now let's calculate the total interest paid over the 10 months.
Total Interest Paid = (Interest on Rs. 8) + (Interest on Rs. 7) + ... + (Interest on Re. 1)
Let's assume the rate of interest is "R" percent per month.
Total Interest Paid = (8 * R) + (7 * R) + ... + (1 * R)
Now, we know that the total amount paid is Rs. 10 (10 installments of Re. 1 each), and the total amount lent is Rs. 9. So, the total interest paid is Rs. 1.
1 = (8 * R) + (7 * R) + ... + (1 * R)
Now we can simplify the equation:
1 = R * (8 + 7 + 6 + 5 + 4 + 3 + 2 + 1)
1 = R * 36
Now, let's find the value of R (the rate of interest per month):
R = 1/36
Since we need to calculate the rate of interest in percentage, we multiply R by 100:
R (%) = (1/36) * 100 = 2.78%
Now, we have the monthly rate of interest. To find the annual rate of interest, we multiply the monthly rate by 12:
Annual Rate of Interest = 2.78% * 12 = 33.33%
The difference between simple and compound interests compounded annually on a certain sum of money for 2 years at 4% per annum is Re. 1. The sum is: - a)Rs.600
- b)Rs.645
- c)Rs.525
- d)Rs.625
Correct answer is option 'D'. Can you explain this answer?
a)
Rs.600
b)
Rs.645
c)
Rs.525
d)
Rs.625

|
Arya Roy answered |
sum = Rs.x
C.I = [x(1+4/100)^2-x] = (676/625x-x) = 51/625
S.I = (x*4*2)/100 = 2x/25
x = 625
A lent Rs. 5000 to B for 2 years and Rs. 3000 to C for 4 years on simple interest at the same rate of interest and received Rs. 2200 in all from both of them as interest. The rate of interest per annum is:
- a)5%
- b)10%
- c)7%
- d)8%
Correct answer is option 'B'. Can you explain this answer?
A lent Rs. 5000 to B for 2 years and Rs. 3000 to C for 4 years on simple interest at the same rate of interest and received Rs. 2200 in all from both of them as interest. The rate of interest per annum is:
a)
5%
b)
10%
c)
7%
d)
8%
|
|
Aisha Gupta answered |
Let the rate of interest be x% per annum.
For the loan to B:
Simple interest = (5000)(2)(x)/100 = 100x
For the loan to C:
Simple interest = (3000)(4)(x)/100 = 120x
Total simple interest received = 100x + 120x = 220x
Given, 220x = 2200
x = 10
Therefore, the rate of interest per annum is 10%.
For the loan to B:
Simple interest = (5000)(2)(x)/100 = 100x
For the loan to C:
Simple interest = (3000)(4)(x)/100 = 120x
Total simple interest received = 100x + 120x = 220x
Given, 220x = 2200
x = 10
Therefore, the rate of interest per annum is 10%.
A sum of Rs. 725 is lent in the beginning of a year at a certain rate of interest. After 8 months, a sum of Rs. 362.50 more is lent but at the rate twice the former. At the end of the year, Rs. 33.50 is earned as interest from both the loans. What was the original rate of interest?- a)5%
- b)3.46%
- c)4.5%
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
a)
5%
b)
3.46%
c)
4.5%
d)
None of these

|
Ishani Rane answered |
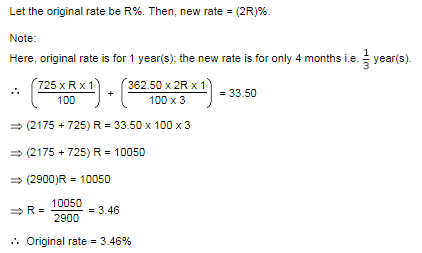
Chapter doubts & questions for Interest (Simple & Compound) - CSAT Preparation 2025 is part of UPSC CSE exam preparation. The chapters have been prepared according to the UPSC CSE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for UPSC CSE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Interest (Simple & Compound) - CSAT Preparation in English & Hindi are available as part of UPSC CSE exam.
Download more important topics, notes, lectures and mock test series for UPSC CSE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup