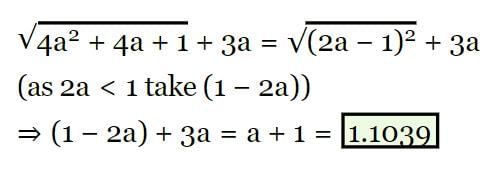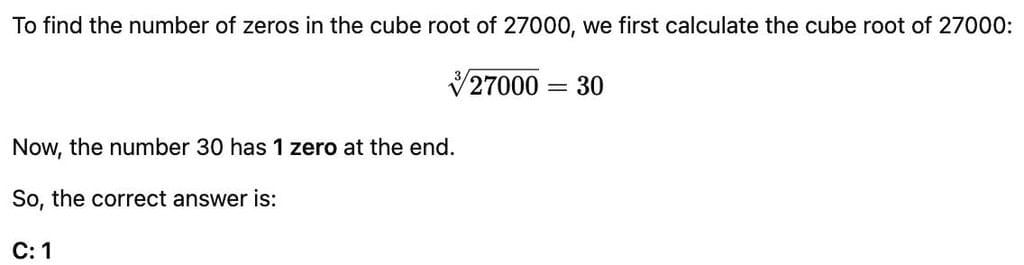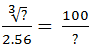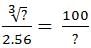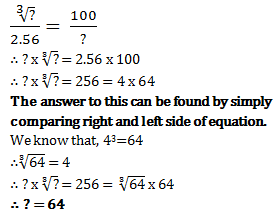All Exams >
UPSC >
CSAT Preparation >
All Questions
All questions of Square Roots and Cube Roots for UPSC CSE Exam
36 x K is a perfect cube number, then K = ______a)6b)5c)4d)3Correct answer is option 'A'. Can you explain this answer?
|
|
Kavya Saxena answered |
6×6=36 and 36×6=216, which is the cube of 6.
Which of the following is a perfect square number?
- a)222222
- b)23453
- c)1681
- d)1057
Correct answer is option 'C'. Can you explain this answer?
Which of the following is a perfect square number?
a)
222222
b)
23453
c)
1681
d)
1057

|
Shashwat Singh answered |
The answer is 1681 because it is the only number which has it's last digit as a number which a perfect square can have . 9×9=81 the last digit is 1.
Find the perfect square number between 30 and 40.
- a)36
- b)49
- c)25
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
Find the perfect square number between 30 and 40.
a)
36
b)
49
c)
25
d)
none of these
|
|
Amita Verma answered |
Since, 1 x 1 = 1
2 x 2 = 4
3 x 3 = 9
4 x 4 = 16
5 x 5 = 25
6 x 6 = 36
7 x 7 = 49
Thus, 36 is a perfact square number between 30 and 40.
Which of the following would end with digit 1?- a)1232
- b)1612
- c)772
- d)822
Correct answer is 'B'. Can you explain this answer?
Which of the following would end with digit 1?
a)
1232
b)
1612
c)
772
d)
822

|
Sneha Singh answered |
Option B is correct because the unit digit of 161 is 1 and if unit digit of any digit ends with 1 the its square will also end with 1.
Without doing any calculation, find the numbers which are surely perfect squares.- a)441
- b)408
- c)153
- d)257
Correct answer is option 'A'. Can you explain this answer?
Without doing any calculation, find the numbers which are surely perfect squares.
a)
441
b)
408
c)
153
d)
257

|
KS Coaching Center answered |
The perfect squares have 0,1,2,4,5,6 or 9 at their units place.
Therefore153,257 and 408 are surely not perfect squares.
Therefore153,257 and 408 are surely not perfect squares.
Without adding, find the sum. 1 + 3 + 5 + 7 + 9- a)16
- b)36
- c)9
- d)25
Correct answer is option 'D'. Can you explain this answer?
Without adding, find the sum. 1 + 3 + 5 + 7 + 9
a)
16
b)
36
c)
9
d)
25

|
Lakesway Classes answered |
Here, we have to find the sum of first five odd natural numbers.
Therefore, 1 + 3 + 5 + 7 + 9 = (5)2 = 25
Ones place digit in the cube of 5832 is ______.- a)5
- b)7
- c)2
- d)8
Correct answer is option 'D'. Can you explain this answer?
Ones place digit in the cube of 5832 is ______.
a)
5
b)
7
c)
2
d)
8

|
Shiksha Academy answered |
A number ending with 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 0 then it's cube ends with 1 , 8 , 7 , 4 , 5 , 6 , 3 , 2 , 0 respectively
⇒ One's digit of 5832= 2
⇒ Cube of 2=23 = 8
⇒ Cube of 2=23 = 8
So, the one's digit of cube of 5832=8
A natural number is said to be a perfect cube, if it is the cube of some ________.- a)cube number
- b)square numbers
- c)natural number
- d)none of these
Correct answer is 'C'. Can you explain this answer?
A natural number is said to be a perfect cube, if it is the cube of some ________.
a)
cube number
b)
square numbers
c)
natural number
d)
none of these
|
|
Kavya Saxena answered |
A natural number is said to be a perfect cube if it is the cube of some natural number.
Example
8 = 2 x 2 x 2
8 = 2 3
8 is the perfect cube because it is a cube of 2 which is a natural number.
But 12 is not a perfect cube because it is not a cube of any natural numbers.
Example
8 = 2 x 2 x 2
8 = 2 3
8 is the perfect cube because it is a cube of 2 which is a natural number.
But 12 is not a perfect cube because it is not a cube of any natural numbers.
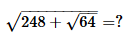
- a)21
- b)14
- c)12
- d)16
Correct answer is option 'D'. Can you explain this answer?
a)
21
b)
14
c)
12
d)
16
|
|
Krishna Iyer answered |
= [√248+√64]
= √248+8
= √256
= 16
= √248+8
= √256
= 16
What is smallest number with which 5400 may be multiplied so that the product is perfect cube? - a) 5
- b) 3
- c) 4
- d) 6
Correct answer is option 'A'. Can you explain this answer?
What is smallest number with which 5400 may be multiplied so that the product is perfect cube?
a)
5
b)
3
c)
4
d)
6

|
Devanshi Ahuja answered |
Find prime factors of 5400
5400=2×3×3×3×2×2×5×5
If we group them in the group of 3
5400=(2×2×2)×(3×3×3)×5×5
Here to make group of 3 for 5
We have to multiply 5400 by 5.
What is the cube of double of ‘a’?- a)16a3
- b)2a
- c)8a3
- d)4a2
Correct answer is option 'C'. Can you explain this answer?
What is the cube of double of ‘a’?
a)
16a3
b)
2a
c)
8a3
d)
4a2
|
|
Vivek Rana answered |
Double of a here a+a=2a
So cube of (2a)³=8a³
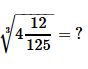
- a)1
- b)
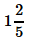
- c)
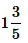
- d)
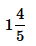
Correct answer is option 'C'. Can you explain this answer?
a)
1
b)
c)
d)

|
Wizius Careers answered |
Cube root of (512)/125
= 8/5
Convert it into mixed fraction, we get
= 1 3/5
= 8/5
Convert it into mixed fraction, we get
= 1 3/5
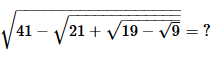
- a)3
- b)4
- c)5
- d)6
Correct answer is option 'D'. Can you explain this answer?
a)
3
b)
4
c)
5
d)
6
|
|
Alok Verma answered |
√41-√21+√19-√9
= √41-√21+√19-3
=√41-√21+√16
=√41-√21+4
=√41-√25
=√41-5
=√36
=6
= √41-√21+√19-3
=√41-√21+√16
=√41-√21+4
=√41-√25
=√41-5
=√36
=6
What is the least perfect square which is divisible by each of 21, 36 and 66?- a)213444
- b)214434
- c)214344
- d)231444
Correct answer is option 'A'. Can you explain this answer?
What is the least perfect square which is divisible by each of 21, 36 and 66?
a)
213444
b)
214434
c)
214344
d)
231444
|
|
Alok Verma answered |
LCM of 21, 36, 66 = 2772
i.e., all multiples of 2772 are divisible by 21, 36 and 66
Prime factorization of 2772 is,
2772 = 2 × 2 × 3 × 3 × 7 × 11
i.e., to make it a perfect square, we have to multiply it by 7 and 11
Hence, required number = 2772 × 7 × 11 = 213444
i.e., all multiples of 2772 are divisible by 21, 36 and 66
Prime factorization of 2772 is,
2772 = 2 × 2 × 3 × 3 × 7 × 11
i.e., to make it a perfect square, we have to multiply it by 7 and 11
Hence, required number = 2772 × 7 × 11 = 213444
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Squares and Square Roots, Class 8, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic.Q.Which of the following is a perfect square number?- a)222222
- b)23453
- c)1681
- d)1057
Correct answer is 'C'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Squares and Square Roots, Class 8, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic.
Q.
Which of the following is a perfect square number?
a)
222222
b)
23453
c)
1681
d)
1057

|
Sanjana Bose answered |
A number is a perfect square (or a square number) if its square root is an integer; that is to say, it is the product of an integer with itself. Here, the square root of 1681 is 41.
Therefore, the square root of 1681 is an integer, and as a consequence 1681 is a perfect square.
As a consequence, 41 is the square root of 1681.
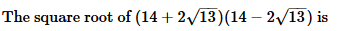
- a)8
- b)9
- c)10
- d)12
Correct answer is option 'D'. Can you explain this answer?
a)
8
b)
9
c)
10
d)
12
|
|
Avinash Sharma answered |
As we know that (a²-b²) = (a+b) (a-b)
Therefore 14² - 2²x13 = 144.
So √144 = 12.
Therefore 14² - 2²x13 = 144.
So √144 = 12.
The least perfect square, which is divisible by each of 21, 36 and 66 is:- a)213444
- b)214344
- c)214434
- d)231444
Correct answer is option 'A'. Can you explain this answer?
The least perfect square, which is divisible by each of 21, 36 and 66 is:
a)
213444
b)
214344
c)
214434
d)
231444

|
Ishani Rane answered |
L.C.M of 21,36,66=2772
Now, 2772=2*2*3*3*7*11
Hence to make it a perfect square , it must be multiplied by 7*11
∴ The required number is 2^2*3^3*7^2*11^2
= 213444
The cube of an even number is always ____________.- a)odd number
- b)even number
- c)prime number
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The cube of an even number is always ____________.
a)
odd number
b)
even number
c)
prime number
d)
none of these

|
Biswa Ranjan Parida Pari answered |
Because multiplication of even number is always even.
for ex 2³=2.2.2=8
for ex 2³=2.2.2=8
Express 63 as the sum of odd numbers.- a)31 + 33 + 35 + 37 + 39 + 41 + 43
- b)31 + 33 + 35 + 37 + 39 + 41
- c)31 + 33 + 35 + 37 + 39 + 41 + 43 + 45
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
Express 63 as the sum of odd numbers.
a)
31 + 33 + 35 + 37 + 39 + 41 + 43
b)
31 + 33 + 35 + 37 + 39 + 41
c)
31 + 33 + 35 + 37 + 39 + 41 + 43 + 45
d)
none of these
|
|
Pooja Shah answered |
We know,
⇒ 31 + 33 + 35 + 37 + 39 + 41 = 216
And the cube of 6 is also 216
⇒ 6 × 6 × 6 = 216
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Squares and Square Roots, Class 8, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic.Q.Which of the following is a perfect square number?- a)222222
- b)23453
- c)1681
- d)1057
Correct answer is option 'C'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for chapter Squares and Square Roots, Class 8, Mathematics . You can practice these practice quizzes as per your speed and improvise the topic.
Q.
Which of the following is a perfect square number?
a)
222222
b)
23453
c)
1681
d)
1057
|
|
Kavya Saxena answered |
The answer is 1681 because it is the only number which has it's last digit as a number which a perfect square can have . 9×9=81 the last digit is 1.
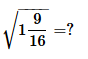
- a)
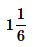
- b)

- c)
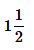
- d)
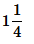
Correct answer is option 'D'. Can you explain this answer?
a)
b)
c)
d)

|
S.c.bhardwaj answered |
((1×16+9)÷16)*1/2=(25÷16)*1/2=5/4=1 1/4
How many numbers lie between square of 12 and 13- a)22
- b)23
- c)24
- d)25
Correct answer is option 'C'. Can you explain this answer?
How many numbers lie between square of 12 and 13
a)
22
b)
23
c)
24
d)
25
|
|
Rhea Reddy answered |
122 = 12*12 = 144
132 = 13*13 = 169
Now numbers are between144 and 169 are:
145, 146, 147,.............168
Total number = 24
So total numbers lies between 144 and 169 is 24
By which smallest natural number 392 must be multiplied so as to make the product a perfect cube ?- a)2
- b)14
- c)7
- d)49
Correct answer is option 'C'. Can you explain this answer?
By which smallest natural number 392 must be multiplied so as to make the product a perfect cube ?
a)
2
b)
14
c)
7
d)
49

|
Rohini Seth answered |
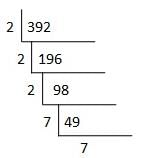
392 = 2 × 2 × 2 × 7 × 7
Hence the number should be multiplied by 7 to make it a perfect cube.
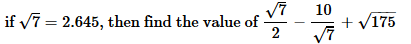
- a)7.22
- b)8.92
- c)6.72
- d)10.77
Correct answer is option 'D'. Can you explain this answer?
a)
7.22
b)
8.92
c)
6.72
d)
10.77
|
|
Dia Mehta answered |
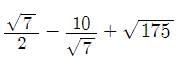
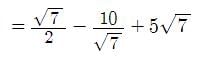
=
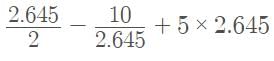
= 1.3225 - 3.78071 + 13.225
= 10.76679 ≈ 10.77
729 is the value of _______________.- a)83
- b)93
- c)63
- d)43
Correct answer is option 'B'. Can you explain this answer?
729 is the value of _______________.
a)
83
b)
93
c)
63
d)
43
|
|
Rhea Kaur answered |
To determine the value of 729, we need to examine the options given in the question and choose the correct one.
Let's analyze each option:
a) 83: This option does not seem to be related to the number 729. The digits in 729 do not match the digits in 83.
b) 93: This option also does not seem to be related to the number 729. Again, the digits in 729 do not match the digits in 93.
c) 63: This option does not seem to be related to the number 729 either. The digits in 729 do not match the digits in 63.
d) 43: This option does not seem to be related to the number 729. Once again, the digits in 729 do not match the digits in 43.
Therefore, none of the options provided correspond to the value of 729. As a result, the correct answer is not given in the options provided.
In conclusion, the given options are incorrect, and there is no correct answer provided for the value of 729.
Let's analyze each option:
a) 83: This option does not seem to be related to the number 729. The digits in 729 do not match the digits in 83.
b) 93: This option also does not seem to be related to the number 729. Again, the digits in 729 do not match the digits in 93.
c) 63: This option does not seem to be related to the number 729 either. The digits in 729 do not match the digits in 63.
d) 43: This option does not seem to be related to the number 729. Once again, the digits in 729 do not match the digits in 43.
Therefore, none of the options provided correspond to the value of 729. As a result, the correct answer is not given in the options provided.
In conclusion, the given options are incorrect, and there is no correct answer provided for the value of 729.
Can you explain the answer of this question below:The numbers 1, 8, 27... are ____________.
- A:
negative numbers
- B:
cube numbers
- C:
square numbers
- D:
none of these
The answer is B.
The numbers 1, 8, 27... are ____________.
negative numbers
cube numbers
square numbers
none of these

|
Saranya Khanna answered |
1×1×1 =1
2×2×2 = 8
3×3×3 = 27
4×4×4 = 64
5×5×5 = 125
What will be the unit digit of ∛216- a)3
- b)6
- c)4
- d)2
Correct answer is option 'B'. Can you explain this answer?
What will be the unit digit of ∛216
a)
3
b)
6
c)
4
d)
2

|
Humaira Tabassum answered |
We can find it by Prime Factorization method
³√216 = 2×2×2×3×3×3
= 2 and 3 are making triplets i.e. 2 and 3
= 2×3 = 6 Thus, we can say that 6 i.e option 'B' is correct.
If 5278 is squared, then what will be at unit place?- a)4
- b)7
- c)6
- d)8
Correct answer is option 'A'. Can you explain this answer?
If 5278 is squared, then what will be at unit place?
a)
4
b)
7
c)
6
d)
8
|
|
Ankita Shah answered |
Understanding the Unit Place of a Square
To determine the unit place of the square of a number, we only need to focus on the unit digit of that number.
Step-by-Step Process
1. Identify the Unit Digit
The number given is 5278. The unit digit is 8.
2. Square the Unit Digit
Now, we calculate the square of the unit digit:
8 * 8 = 64.
3. Find the Unit Digit of the Result
The unit digit of 64 is 4.
Conclusion
Thus, when 5278 is squared, the unit place of the result is 4. Therefore, the correct answer is option 'A'.
Key Points to Remember
- Only the unit digit affects the unit place when squaring a number.
- The process involves squaring the unit digit and then extracting the unit digit from the squared result.
- For 5278, focusing on the unit digit (8) leads to the conclusion that the unit place of 5278 squared is 4.
To determine the unit place of the square of a number, we only need to focus on the unit digit of that number.
Step-by-Step Process
1. Identify the Unit Digit
The number given is 5278. The unit digit is 8.
2. Square the Unit Digit
Now, we calculate the square of the unit digit:
8 * 8 = 64.
3. Find the Unit Digit of the Result
The unit digit of 64 is 4.
Conclusion
Thus, when 5278 is squared, the unit place of the result is 4. Therefore, the correct answer is option 'A'.
Key Points to Remember
- Only the unit digit affects the unit place when squaring a number.
- The process involves squaring the unit digit and then extracting the unit digit from the squared result.
- For 5278, focusing on the unit digit (8) leads to the conclusion that the unit place of 5278 squared is 4.
Which of the following is a perfect cube ?- a)125
- b)135
- c)145
- d)115
Correct answer is option 'A'. Can you explain this answer?
Which of the following is a perfect cube ?
a)
125
b)
135
c)
145
d)
115
|
|
Athul Sen answered |
Identifying a Perfect Cube
A perfect cube is a number that can be expressed as the product of three identical factors. For example, 27 is a perfect cube because it can be expressed as 3 x 3 x 3. To determine whether a number is a perfect cube, we need to find the cube root of that number. Here, we are given four options, and we can use the cube root method to identify the perfect cube.
Solution
a) 125
The cube root of 125 is 5. Since 125 can be expressed as 5 x 5 x 5, it is a perfect cube. Therefore, option A is the correct answer.
b) 135
The cube root of 135 is approximately 5.5. Since 5.5 is not a whole number, 135 is not a perfect cube.
c) 145
The cube root of 145 is approximately 5.7. Since 5.7 is not a whole number, 145 is not a perfect cube.
d) 115
The cube root of 115 is approximately 4.8. Since 4.8 is not a whole number, 115 is not a perfect cube.
Therefore, the only perfect cube among the given options is 125, which is option A.
A perfect cube is a number that can be expressed as the product of three identical factors. For example, 27 is a perfect cube because it can be expressed as 3 x 3 x 3. To determine whether a number is a perfect cube, we need to find the cube root of that number. Here, we are given four options, and we can use the cube root method to identify the perfect cube.
Solution
a) 125
The cube root of 125 is 5. Since 125 can be expressed as 5 x 5 x 5, it is a perfect cube. Therefore, option A is the correct answer.
b) 135
The cube root of 135 is approximately 5.5. Since 5.5 is not a whole number, 135 is not a perfect cube.
c) 145
The cube root of 145 is approximately 5.7. Since 5.7 is not a whole number, 145 is not a perfect cube.
d) 115
The cube root of 115 is approximately 4.8. Since 4.8 is not a whole number, 115 is not a perfect cube.
Therefore, the only perfect cube among the given options is 125, which is option A.
The cube of an odd number is always __________.- a)odd number
- b)even number
- c)prime number
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The cube of an odd number is always __________.
a)
odd number
b)
even number
c)
prime number
d)
none of these
|
|
Isha Desai answered |
The cube of a natural odd number is always odd.
For natural numbers, we know,
odd x odd = odd
odd x even = even
even x even = even.
So, cube of a natural odd number is
odd x odd x odd
= odd x odd
= odd.
Eg.: Cube of an odd number 3 is 27, which is also odd.
For natural numbers, we know,
odd x odd = odd
odd x even = even
even x even = even.
So, cube of a natural odd number is
odd x odd x odd
= odd x odd
= odd.
Eg.: Cube of an odd number 3 is 27, which is also odd.
Chapter doubts & questions for Square Roots and Cube Roots - CSAT Preparation 2025 is part of UPSC CSE exam preparation. The chapters have been prepared according to the UPSC CSE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for UPSC CSE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Square Roots and Cube Roots - CSAT Preparation in English & Hindi are available as part of UPSC CSE exam.
Download more important topics, notes, lectures and mock test series for UPSC CSE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup





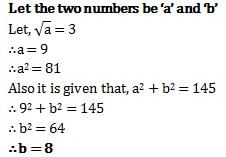
 is :
is :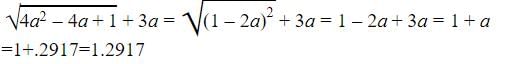

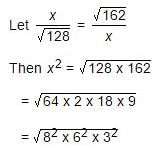
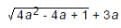 is:
is: