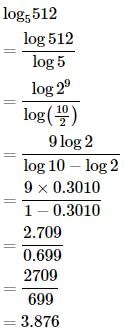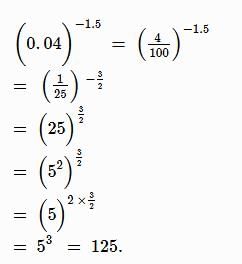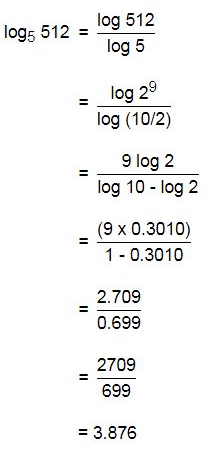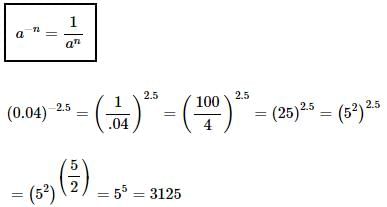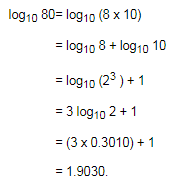All Exams >
UPSC >
CSAT Preparation >
All Questions
All questions of Surds, Indices and Logarithms for UPSC CSE Exam
(256)0.16 x (256)0.09 = ?- a)4
- b)16
- c)64
- d)256.25
Correct answer is option 'A'. Can you explain this answer?
(256)0.16 x (256)0.09 = ?
a)
4
b)
16
c)
64
d)
256.25
|
Naroj Boda answered |
⇒ (256)0.16 x (256)0.09 = (256)(0.16 + 0.09)
= (256)0.25
= (256)(25 / 100)
= (256)(1 / 4)
= (44)(1 / 4)
= 44(1 / 4)
= 41
= 4
= (256)(25 / 100)
= (256)(1 / 4)
= (44)(1 / 4)
= 44(1 / 4)
= 41
= 4
If 3(x - y) = 27 and 3(x + y) = 243, then x is equal to:- a)0
- b)2
- c)4
- d)6
Correct answer is option 'C'. Can you explain this answer?
If 3(x - y) = 27 and 3(x + y) = 243, then x is equal to:
a)
0
b)
2
c)
4
d)
6
|
Yash Patel answered |
⇒ 3x - y = 27 = 33 ⇔ x - y = 3 ....(i)
⇒ 3x + y = 243 = 35 ⇔ x + y = 5 ....(ii)
On solving (i) and (ii), we get x = 4.
Given that 100.48 = x, 100.70 = y and xz = y2, then the value of z is close to:- a)1.45
- b)1.88
- c)2.9
- d)3.7
Correct answer is option 'C'. Can you explain this answer?
Given that 100.48 = x, 100.70 = y and xz = y2, then the value of z is close to:
a)
1.45
b)
1.88
c)
2.9
d)
3.7
|
KS Coaching Center answered |
⇒ xz = y2 ⇔ 10(0.48 z) = 10(2 x 0.70) = 101.40
⇒ 0.48 z = 1.40
⇒ z = 140 / 48 = 35 / 12 = 2.9(approx.)
⇒ 0.48 z = 1.40
⇒ z = 140 / 48 = 35 / 12 = 2.9(approx.)
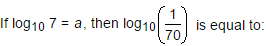
- a)- (1 + a)
- b)(1 + a)-1
- c)
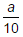
- d)
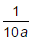
Correct answer is option 'A'. Can you explain this answer?
a)
- (1 + a)
b)
(1 + a)-1
c)
d)
|
Dia Mehta answered |
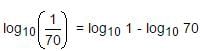
⇒ - log10 (7 x 10)
⇒ - (log10 7 + log10 10)
⇒ - (a + 1)
⇒ - (log10 7 + log10 10)
⇒ - (a + 1)
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for "Surds and Indices" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations. (17)3.5 x (17)? = 178- a)2.29
- b)2.75
- c)4.25
- d)4.5
Correct answer is option 'D'. Can you explain this answer?
Practice Quiz or MCQ (Multiple Choice Questions) with solutions are available for Practice, which would help you prepare for "Surds and Indices" under Quantitative Aptitude. You can practice these practice quizzes as per your speed and improvise the topic. The same topic is covered under various competitive examinations like - CAT, GMAT, Bank PO, SSC and other competitive examinations.
(17)3.5 x (17)? = 178
a)
2.29
b)
2.75
c)
4.25
d)
4.5
|
Divey Sethi answered |
Let (17)3.5 x (17)x = 178
Then, (17)3.5 + x = 178
∴ 3.5 + x = 8
⇒ x = (8 - 3.5)
⇒ x = 4.5
Then, (17)3.5 + x = 178
∴ 3.5 + x = 8
⇒ x = (8 - 3.5)
⇒ x = 4.5
The value of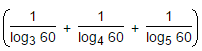 
is: - a)0
- b)1
- c)5
- d)60
Correct answer is option 'B'. Can you explain this answer?
The value of 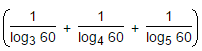is:
is:a)
0
b)
1
c)
5
d)
60
|
Shalini Patel answered |
Given expression = 1/log60 3 + 1/log60 4 + 1/log60 5
= log60 (3 x 4 x 5)
= log60 60
= 1.
= log60 (3 x 4 x 5)
= log60 60
= 1.
If 5a = 3125, then the value of 5(a - 3) is:- a)25
- b)125
- c)625
- d)1625
Correct answer is option 'A'. Can you explain this answer?
If 5a = 3125, then the value of 5(a - 3) is:
a)
25
b)
125
c)
625
d)
1625
|
Ravi Singh answered |
⇒ 5a = 3125 ⇔ 5a = 55
⇒ a = 5.
∴ 5(a - 3) = 5(5 - 3) = 52 = 25.
⇒ a = 5.
∴ 5(a - 3) = 5(5 - 3) = 52 = 25.
1/(1 + x(b - a) + x(c - a)) + 1/(1 + x(a - b) + x(c - b)) + 1/(1 + x(b - c) +x(a - c) ) = ?
- a)0
- b)1
- c)xa - b - c
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
1/(1 + x(b - a) + x(c - a)) + 1/(1 + x(a - b) + x(c - b)) + 1/(1 + x(b - c) +x(a - c) ) = ?
a)
0
b)
1
c)
xa - b - c
d)
None of these
|
|
Rhea Reddy answered |
Given Exp:
1/(1 + xb / xa + xc / xa) + 1/(1 + xa / xb + xc / xb) + 1/(1 + xb / xc +xa / xc)
1/(1 + xb / xa + xc / xa) + 1/(1 + xa / xb + xc / xb) + 1/(1 + xb / xc +xa / xc)
= xa/(xa + xb + xc ) + xb/(xa + xb + xc ) + xc/(xa + xb + xc )
= (xa + xb + xc ) / (xa + xb + xc )
= 1.
= (xa + xb + xc ) / (xa + xb + xc )
= 1.
if log 2 = 0.30103 and log 3 = 0.4771, find the number of digits in (648)5.- a)15
- b)14
- c)13
- d)12
Correct answer is option 'A'. Can you explain this answer?
if log 2 = 0.30103 and log 3 = 0.4771, find the number of digits in (648)5.
a)
15
b)
14
c)
13
d)
12
|
Ishani Rane answered |
log(648)^5
= 5 log(648)
= 5 log(81 x 8)
= 5[log(81) + log(8)]
=5 [log(34) + log(23)]
=5[4log(3) + 3log(2)]
= 5[4 x 0.4771 + 3 x 0.30103]
= 5(1.9084 + 0.90309)
= 5 x 2.81149
approx. = 14.05
ie, log(648)^5 = 14.05 (approx.)
ie, its characteristic = 14
Hence, number of digits in (648)5 = 14+1 = 15
Which of the following statements is not correct?
- a)log10 10 = 1
- b)log (2 + 3) = log (2 x 3)
- c)log10 1 = 0
- d)log (1 + 2 + 3) = log 1 + log 2 + log 3
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is not correct?
a)
log10 10 = 1
b)
log (2 + 3) = log (2 x 3)
c)
log10 1 = 0
d)
log (1 + 2 + 3) = log 1 + log 2 + log 3
|
Prince Chaudhary answered |
According to logarithm rule . option B is never correct
If log 27 = 1.431, then the value of log 9 is:- a)0.934
- b)0.945
- c)0.954
- d)0.958
Correct answer is option 'C'. Can you explain this answer?
If log 27 = 1.431, then the value of log 9 is:
a)
0.934
b)
0.945
c)
0.954
d)
0.958
|
Gowri Chakraborty answered |
Log 27 = 1.431
log (33 ) = 1.431
3 log 3 = 1.431
log 3 = 0.477
log 9 = log(32 ) = 2 log 3 = (2 x 0.477) = 0.954.
If m and n are whole numbers and mn = 196, what is the value of (m - 3)(n+1) ?- a)2744
- b)1
- c)121
- d)1331
Correct answer is option 'D'. Can you explain this answer?
If m and n are whole numbers and mn = 196, what is the value of (m - 3)(n+1) ?
a)
2744
b)
1
c)
121
d)
1331
|
Cstoppers Instructors answered |
mn = 196
We know that 142 = 196
Hence we can take m = 14 and n = 2
(m - 3)(n+1) = (14 - 3)(2+1) = 113 = 1331
We know that 142 = 196
Hence we can take m = 14 and n = 2
(m - 3)(n+1) = (14 - 3)(2+1) = 113 = 1331
If log10 5 + log10 (5x + 1) = log10 (x + 5) + 1, then x is equal to:- a)1
- b)3
- c)5
- d)10
Correct answer is option 'B'. Can you explain this answer?
If log10 5 + log10 (5x + 1) = log10 (x + 5) + 1, then x is equal to:
a)
1
b)
3
c)
5
d)
10
|
Aarav Sharma answered |
Given: log105 log10(5x 1) = log10(x 5) 1
To find: value of x
Solution:
Step 1: Simplify the given equation using logarithmic rules
log105 log10(5x 1) = log10(x 5) 1
log10(5) + log10(log10(5x 1)) = log10(x 5) 1
log10(log10(5x 1)) = log10(x 5) log10(5) 1
log10(log10(5x 1)) = log10(5x x 25) log10(5)
log10(log10(5x 1)) = log10(4x 25)
log10(5x 1) = 10^(log10(4x 25))
5x 1 = 4x 25
x = 24/1
x = 24
Step 2: Check the answer
log105 log10(5x 1) = log10(x 5) 1
log105 log10(5(24) 1) = log10(24 5) 1
log105 log10(119) = log10(29) 1
0.69897 2.07555 = 1.46240
2.77452 = 1.46240 (not true)
Therefore, the answer is not correct.
Step 3: Check the options
We can see that the correct answer is option 'B' which is 3.
Let's substitute x = 3 in the given equation and check:
log105 log10(5x 1) = log10(x 5) 1
log105 log10(5(3) 1) = log10(3 5) 1
0.69897 0.77815 = 0.77815
1.47712 = 1.47712 (true)
Therefore, the correct answer is option 'B' which is 3.
To find: value of x
Solution:
Step 1: Simplify the given equation using logarithmic rules
log105 log10(5x 1) = log10(x 5) 1
log10(5) + log10(log10(5x 1)) = log10(x 5) 1
log10(log10(5x 1)) = log10(x 5) log10(5) 1
log10(log10(5x 1)) = log10(5x x 25) log10(5)
log10(log10(5x 1)) = log10(4x 25)
log10(5x 1) = 10^(log10(4x 25))
5x 1 = 4x 25
x = 24/1
x = 24
Step 2: Check the answer
log105 log10(5x 1) = log10(x 5) 1
log105 log10(5(24) 1) = log10(24 5) 1
log105 log10(119) = log10(29) 1
0.69897 2.07555 = 1.46240
2.77452 = 1.46240 (not true)
Therefore, the answer is not correct.
Step 3: Check the options
We can see that the correct answer is option 'B' which is 3.
Let's substitute x = 3 in the given equation and check:
log105 log10(5x 1) = log10(x 5) 1
log105 log10(5(3) 1) = log10(3 5) 1
0.69897 0.77815 = 0.77815
1.47712 = 1.47712 (true)
Therefore, the correct answer is option 'B' which is 3.
(6)6.5 × (36)4.5 ÷ (216)4.5 = (6)?- a)1
- b)2
- c)4
- d)6
Correct answer is option 'B'. Can you explain this answer?
(6)6.5 × (36)4.5 ÷ (216)4.5 = (6)?
a)
1
b)
2
c)
4
d)
6
|
Uday Nambiar answered |
(6)6.5 × (36)4.5 ÷ (216)4.5
= (6)6.5 × [(6)2]4.5 ÷ [(6)3]4.5
= (6)6.5 × (6)9 ÷ (6)13.5
= (6)(6.5 + 9 - 13.5)
= (6)2
= (6)6.5 × [(6)2]4.5 ÷ [(6)3]4.5
= (6)6.5 × (6)9 ÷ (6)13.5
= (6)(6.5 + 9 - 13.5)
= (6)2
if log 2 = 0.30103, the number of digits in 2128 is- a)38
- b)39
- c)40
- d)41
Correct answer is option 'B'. Can you explain this answer?
if log 2 = 0.30103, the number of digits in 2128 is
a)
38
b)
39
c)
40
d)
41
|
Milan Nair answered |
log(2128) = 128log(2) = 128 × 0.30103 ≈ 38.4
ie, its characteristic = 38
Hence, number of digits in 2128 = 38+1 = 39
ie, its characteristic = 38
Hence, number of digits in 2128 = 38+1 = 39
If log(64)= 1.806, log(16) = ?- a) 1.204
- b)0.903
- c)1.806
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
If log(64)= 1.806, log(16) = ?
a)
1.204
b)
0.903
c)
1.806
d)
None of these
|
|
Gowri Chakraborty answered |
log(64)= 1.806
=> log(4^3) = 1.806
=> 3log(4) = 1.806
⇒log(4) = 1.806/3
log(16) = log (4^2) = 2log(4) = 2*1.806/3 = 2*0.062 = 1.204
10222 ÷ 10220 = ?- a)10
- b)100
- c)1000
- d)10000
Correct answer is option 'B'. Can you explain this answer?
10222 ÷ 10220 = ?
a)
10
b)
100
c)
1000
d)
10000
|
Sagar Sharma answered |
10222 is a positive integer.
(0.04)-2.5 = ?- a)125
- b)2
- c)4
- d)6
Correct answer is option 'C'. Can you explain this answer?
(0.04)-2.5 = ?
a)
125
b)
2
c)
4
d)
6
|
Moumita Das answered |
Ans.
Option (c)
If log 2 = 0.3010 and log 3 = 0.4771, What is the value of log51024?- a)4.31
- b)3.88
- c)3.91
- d)2.97
Correct answer is option 'A'. Can you explain this answer?
If log 2 = 0.3010 and log 3 = 0.4771, What is the value of log51024?
a)
4.31
b)
3.88
c)
3.91
d)
2.97
|
|
Gowri Chakraborty answered |
log 5 1024= log1024/log5 = log ( 2^10)/log(10/2)=10log(2)/log10−log2
=10*0.3010/1−0.3010 = 3.01/0.699 = 3010/699 = 4.31
(25)7.5 x (5)2.5 ÷ (125)1.5 = 5?
- a)8.5
- b)13
- c)16
- d)17.5
Correct answer is option 'B'. Can you explain this answer?
(25)7.5 x (5)2.5 ÷ (125)1.5 = 5?
a)
8.5
b)
13
c)
16
d)
17.5
|
|
Alok Verma answered |
Let (25)7.5 x (5)2.5 ÷ (125)1.5 = 5x.
Then, (52)7.5 x 52.5 / (53) 1.5 = 5x
Then, (52)7.5 x 52.5 / (53) 1.5 = 5x
⇒ (52)7.5 x 52.5 / (5)3 x 1.5 = 5x
⇒ 515 x 52.5 / 54.5 = 5x
⇒ 5x = 5(15 + 2.5 - 4.5)
⇒ 5x = 513
∴ x = 13.
⇒ 515 x 52.5 / 54.5 = 5x
⇒ 5x = 5(15 + 2.5 - 4.5)
⇒ 5x = 513
∴ x = 13.
If log10 2 = 0.3010, then log2 10 is equal to:- a)
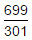
- b)
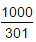
- c)0.3010
- d)0.6990
Correct answer is 'B'. Can you explain this answer?
If log10 2 = 0.3010, then log2 10 is equal to:
a)
b)
c)
0.3010
d)
0.6990
|
Aman Jha answered |
Log10 2=1/log2 10 therefore 0.3010=1/log2 10 log2 10=1/0.3010 so log2 10 = 1000/301
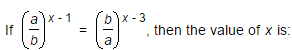
- a)
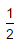
- b)1
- c)2
- d)
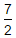
Correct answer is option 'C'. Can you explain this answer?
a)
b)
1
c)
2
d)
|
|
Aarav Sharma answered |
To solve the equation (a / b)x - 1 = (b / a)x - 3, we can start by simplifying both sides of the equation.
Step 1: Simplify the left side of the equation
(a / b)x - 1 = (b / a)x - 3
Multiply both sides of the equation by b to eliminate the fraction:
a^x - b = (b^2 / a)x - 3b
Step 2: Simplify the right side of the equation
(b / a)x - 3 = (b^2 / a)x - 3
Multiply both sides of the equation by a to eliminate the fraction:
ab^x - 3a = b^2x - 3a
Step 3: Combine like terms
a^x - b = ab^x - 3a
Rearrange the terms:
a^x - ab^x = b - 3a
Step 4: Factor out common terms
a^x(1 - b) = b - 3a
Step 5: Divide both sides of the equation by (1 - b)
a^x = (b - 3a) / (1 - b)
Step 6: Simplify the right side of the equation
a^x = (-3a + b) / (b - 1)
Step 7: Take the logarithm of both sides of the equation
log(a^x) = log((-3a + b) / (b - 1))
Step 8: Apply logarithmic properties
x log(a) = log((-3a + b) / (b - 1))
Step 9: Divide both sides of the equation by log(a)
x = log((-3a + b) / (b - 1)) / log(a)
At this point, we have obtained an expression for x in terms of a and b. To determine the specific value of x, we need to know the values of a and b. Without this information, we cannot calculate the exact value of x.
However, if we are given values for a and b, we can substitute them into the equation to find the value of x. In this case, the correct answer is option C, but we need to know the specific values of a and b to confirm this.
Step 1: Simplify the left side of the equation
(a / b)x - 1 = (b / a)x - 3
Multiply both sides of the equation by b to eliminate the fraction:
a^x - b = (b^2 / a)x - 3b
Step 2: Simplify the right side of the equation
(b / a)x - 3 = (b^2 / a)x - 3
Multiply both sides of the equation by a to eliminate the fraction:
ab^x - 3a = b^2x - 3a
Step 3: Combine like terms
a^x - b = ab^x - 3a
Rearrange the terms:
a^x - ab^x = b - 3a
Step 4: Factor out common terms
a^x(1 - b) = b - 3a
Step 5: Divide both sides of the equation by (1 - b)
a^x = (b - 3a) / (1 - b)
Step 6: Simplify the right side of the equation
a^x = (-3a + b) / (b - 1)
Step 7: Take the logarithm of both sides of the equation
log(a^x) = log((-3a + b) / (b - 1))
Step 8: Apply logarithmic properties
x log(a) = log((-3a + b) / (b - 1))
Step 9: Divide both sides of the equation by log(a)
x = log((-3a + b) / (b - 1)) / log(a)
At this point, we have obtained an expression for x in terms of a and b. To determine the specific value of x, we need to know the values of a and b. Without this information, we cannot calculate the exact value of x.
However, if we are given values for a and b, we can substitute them into the equation to find the value of x. In this case, the correct answer is option C, but we need to know the specific values of a and b to confirm this.
Which of the following statements is not correct?- a)log10 10 = 1
- b)log (2 + 3) = log (2 x 3)
- c)log10 1 = 0
- d)log (1 + 2 + 3) = log 1 + log 2 + log 3
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is not correct?
a)
log10 10 = 1
b)
log (2 + 3) = log (2 x 3)
c)
log10 1 = 0
d)
log (1 + 2 + 3) = log 1 + log 2 + log 3
|
Bank Exams India answered |
- Since loga a = 1, so log10 10 = 1.
- log (2 + 3) = log 5 and log (2 x 3) = log 6 = log 2 + log 3
∴ log (2 + 3) ≠ log (2 x 3) - Since loga 1 = 0. so logio 1 = 0.
- log (1 + 2 + 3) = log 6
log (1 x 2 x 3) = log 1 + log 2 + log 3=log (6).
So. option (b) is incorrect.
Chapter doubts & questions for Surds, Indices and Logarithms - CSAT Preparation 2025 is part of UPSC CSE exam preparation. The chapters have been prepared according to the UPSC CSE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for UPSC CSE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Surds, Indices and Logarithms - CSAT Preparation in English & Hindi are available as part of UPSC CSE exam.
Download more important topics, notes, lectures and mock test series for UPSC CSE Exam by signing up for free.
CSAT Preparation
205 videos|264 docs|136 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup