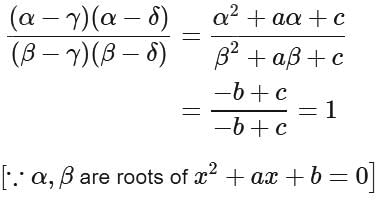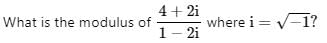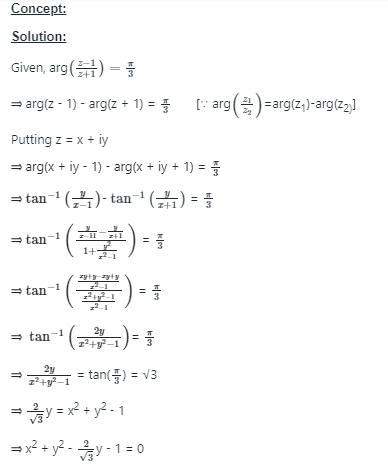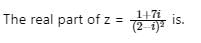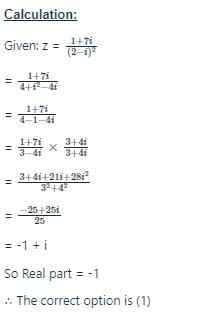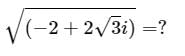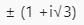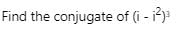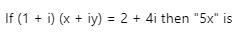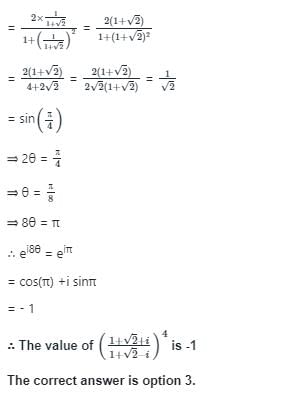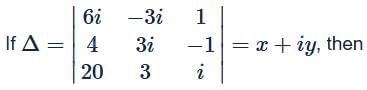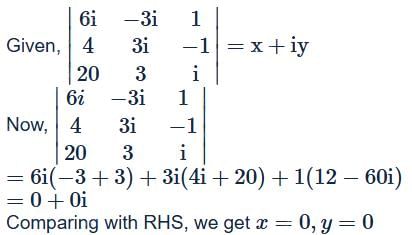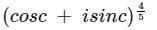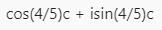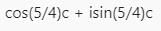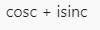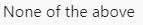All Exams >
JEE >
Mathematics (Maths) for JEE Main & Advanced >
All Questions
All questions of Complex Numbers and Quadratic Equation for JEE Exam
Imaginary part of −i(3i + 2) isa)−2b)2c)3d)−3Correct answer is option 'A'. Can you explain this answer?
|
|
Geetika Shah answered |
(-i)(3i) +2(-i) =-3(i^2)-2i =-3(-1)-2i =3-2i since i=√-1 =3+(-2)i comparing with a+bi,we get b=(-2)
Write in the simplest form: (i)-997- a)-i
- b)1
- c)-1
- d)i
Correct answer is 'A'. Can you explain this answer?
Write in the simplest form: (i)-997
a)
-i
b)
1
c)
-1
d)
i

|
Muskaan Mishra answered |
I^-997= 1/i^997, 1/(i^4)^249 × i, since i^4 = 1, i^4/i= i^3= -i
Find the reciprocal (or multiplicative inverse) of -2 + 5i - a)
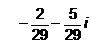
- b)
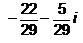
- c)
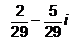
- d)
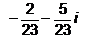
Correct answer is option 'A'. Can you explain this answer?
Find the reciprocal (or multiplicative inverse) of -2 + 5i
a)
b)
c)
d)
|
|
Gaurav Kumar answered |
-2 + 5i
multiplicative inverse of -2 + 5i is
1/(-2+5i)
= 1/(-2+5i) * ((-2-5i)/(-2-5i))
= -2-5i/(-2)^2 -(5i)^2
= -2-5i/4-(-25)
= -2-5i/4+25
= -2-5i/29
= -2/29 -5i/29
multiplicative inverse of -2 + 5i is
1/(-2+5i)
= 1/(-2+5i) * ((-2-5i)/(-2-5i))
= -2-5i/(-2)^2 -(5i)^2
= -2-5i/4-(-25)
= -2-5i/4+25
= -2-5i/29
= -2/29 -5i/29
Find the real numbers x and y such that : (x + iy)(3 + 2i) = 1 + i- a)
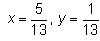
- b)
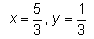
- c)
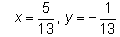
- d)
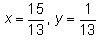
Correct answer is option 'A'. Can you explain this answer?
Find the real numbers x and y such that : (x + iy)(3 + 2i) = 1 + i
a)
b)
c)
d)
|
|
Suresh Iyer answered |
(x + iy)(3 + 2i) = (1 + i)
x + iy = (1 + i)/(3 + 2i)
x + iy = [(1 + i) * (3 - 2i)] / [(3 + 2i)*(3 - 2i)]
x + iy = (3 + 3i - 2i + 2) / [(3)2 + (2)2]
x + iy = (5 + i)/[ 9 + 4]
= (5 + i) / 13
=> 13x + 13iy = 5+i
13x = 5 13y = 1
x = 5/13 y = 1/13
x + iy = (1 + i)/(3 + 2i)
x + iy = [(1 + i) * (3 - 2i)] / [(3 + 2i)*(3 - 2i)]
x + iy = (3 + 3i - 2i + 2) / [(3)2 + (2)2]
x + iy = (5 + i)/[ 9 + 4]
= (5 + i) / 13
=> 13x + 13iy = 5+i
13x = 5 13y = 1
x = 5/13 y = 1/13
Express the following in standard form : 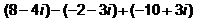
- a)3+3i
- b)2 + 2i
- c)1 + 2i
- d)0 + 2i
Correct answer is option 'D'. Can you explain this answer?
Express the following in standard form : 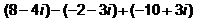
a)
3+3i
b)
2 + 2i
c)
1 + 2i
d)
0 + 2i
|
|
Gaurav Kumar answered |
(8 - 4i) - (-2 - 3i) + (-10 + 3i)
=> 8 - 4i + 2 + 3i-10 + 3i
=> 8 + 2 - 10 - 4i + 3i + 3i =>0 + 2i
=> 8 - 4i + 2 + 3i-10 + 3i
=> 8 + 2 - 10 - 4i + 3i + 3i =>0 + 2i
Find the real numbers x and y such that :a)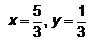 b)
b)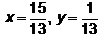 c)
c)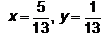 d)
d)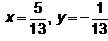 Correct answer is option 'c'. Can you explain this answer?
Correct answer is option 'c'. Can you explain this answer?
|
|
Hansa Sharma answered |
(x + iy) (3 + 2i)
= 3x + 2xi + 3iy + 3i*y = 1+i
= 3x-2y + i(2x+3y) = 1+i
= 3x-2y-1 = 0 ; 2x + 3y -1 = 0
on equating real and imaginary parts on both sides
on solving two equations
x= 5/13 ; y = 1/13
= 3x + 2xi + 3iy + 3i*y = 1+i
= 3x-2y + i(2x+3y) = 1+i
= 3x-2y-1 = 0 ; 2x + 3y -1 = 0
on equating real and imaginary parts on both sides
on solving two equations
x= 5/13 ; y = 1/13
Express the following in standard form :
- a)
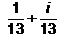
- b)
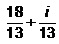
- c)
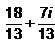
- d)

Correct answer is option 'B'. Can you explain this answer?
Express the following in standard form :
a)
b)
c)
d)
|
|
Pooja Shah answered |
first write above equation in complex number format , ie using iota
(3-4i) / (2-3i)*(2+3i) / (2+3i) = (6+9i-8i+12) / 13=(18/13)+(i/13)
(3-4i) / (2-3i)*(2+3i) / (2+3i) = (6+9i-8i+12) / 13=(18/13)+(i/13)
If z1 = 2 + i, z2 = 1 + 3i, then Re ( z1 - z2) =- a)ι
- b)1
- c)2 ι
- d)2
Correct answer is option 'B'. Can you explain this answer?
If z1 = 2 + i, z2 = 1 + 3i, then Re ( z1 - z2) =
a)
ι
b)
1
c)
2 ι
d)
2
|
|
Aditi Basu answered |
1
To find Re(z1 - z2), we first need to subtract z2 from z1:
z1 - z2 = (2i) - (1 + 3i) = 1 - i
Now, to find the real part of this complex number, we simply take the real component, which is 1. Therefore, Re(z1 - z2) = 1.
To find Re(z1 - z2), we first need to subtract z2 from z1:
z1 - z2 = (2i) - (1 + 3i) = 1 - i
Now, to find the real part of this complex number, we simply take the real component, which is 1. Therefore, Re(z1 - z2) = 1.
If S is the set of all real x such that 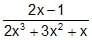 is positive, then S contains
is positive, then S contains- a)(– ∞, –3/2)
- b)(–3/2, 1/4)
- c)(–1/4, 1/2)
- d)(–1/2, 3)
Correct answer is option 'A'. Can you explain this answer?
If S is the set of all real x such that 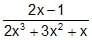 is positive, then S contains
is positive, then S contains
a)
(– ∞, –3/2)
b)
(–3/2, 1/4)
c)
(–1/4, 1/2)
d)
(–1/2, 3)
|
|
Rishi Raj answered |
Here we go:We get the roots (1/2), 0, -1, and (-1/... more2).
If (1 – p) is root of quadratic equation x2 + px + (1 – p) = 0, then its roots are- a)0, 1
- b)–1, 1
- c)0, –1
- d)–1, 2
Correct answer is option 'C'. Can you explain this answer?
If (1 – p) is root of quadratic equation x2 + px + (1 – p) = 0, then its roots are
a)
0, 1
b)
–1, 1
c)
0, –1
d)
–1, 2
|
|
Anand Kumar answered |
Put (1-p) In the given equation and solve for p.
after solving it u will have two values of p
now, for the solution put values p one by one in (1-p)
after solving it u will have two values of p
now, for the solution put values p one by one in (1-p)
The set of all solutions of the inequality 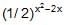 < 1/4 contains the set
< 1/4 contains the set- a) (–¥, 0)
- b)(–¥, 1)
- c) (1, ¥)
- d) (3, ¥)
Correct answer is option 'D'. Can you explain this answer?
The set of all solutions of the inequality 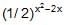 < 1/4 contains the set
< 1/4 contains the set
a)
(–¥, 0)
b)
(–¥, 1)
c)
(1, ¥)
d)
(3, ¥)
|
|
Hansa Sharma answered |
(1/2)(x2 - 2x) < (1/4)
(1/2)(x2 - 2x) < (1/2)2
x2 − 2x > 2......(as after multiplicative inverse sign of inequality changes)
x2 − 2x − 2 > 0
x2 - 2x + 1 - 3 >
(x-1)2 - 3 > 0
(x-1)2 > 3
So for the above to hold good both the expression must be positive or both must be negative. After finding the solution the range of the solution will be
either x > 3
(3,¥)
(1/2)(x2 - 2x) < (1/2)2
x2 − 2x > 2......(as after multiplicative inverse sign of inequality changes)
x2 − 2x − 2 > 0
x2 - 2x + 1 - 3 >
(x-1)2 - 3 > 0
(x-1)2 > 3
So for the above to hold good both the expression must be positive or both must be negative. After finding the solution the range of the solution will be
either x > 3
(3,¥)
Numbers of values of k for which roots of equation x2 − 3x + k = 0 lie in the interval (0,1) is- a)only one
- b)no value
- c)finite but more than one
- d)k ≤ 9/4
Correct answer is option 'B'. Can you explain this answer?
Numbers of values of k for which roots of equation x2 − 3x + k = 0 lie in the interval (0,1) is
a)
only one
b)
no value
c)
finite but more than one
d)
k ≤ 9/4

|
Pragati Choudhury answered |
Understanding the Quadratic Equation
The given quadratic equation is x² - 3x + k = 0. We need to determine the values of k for which the roots of this equation lie within the interval (0,1).
Condition for Roots in Interval (0,1)
For the roots of a quadratic equation ax² + bx + c = 0 to lie in an interval (a, b), the following conditions must be satisfied:
1. Sum of Roots: The sum of the roots (r1 + r2) = -b/a should be greater than 0 and less than 2.
2. Product of Roots: The product of the roots (r1 * r2) = c/a should be greater than 0.
In our case:
- Sum of Roots: r1 + r2 = 3
- Product of Roots: r1 * r2 = k
Analyzing the Conditions
1. Sum of Roots: Since 3 is not in the interval (0, 2), the first condition fails. This implies that the roots cannot both be positive and less than 1.
2. Product of Roots: For the product k to be positive, k must be greater than 0. However, this doesn’t help as the sum condition already invalidates the possibility of the roots lying in (0,1).
Conclusion
Given that the sum of the roots is fixed at 3, which does not allow both roots to lie within (0,1), we conclude that:
- There are no values of k that satisfy the conditions for the roots to lie in the interval (0,1).
Thus, the correct answer is option B: no value.
The given quadratic equation is x² - 3x + k = 0. We need to determine the values of k for which the roots of this equation lie within the interval (0,1).
Condition for Roots in Interval (0,1)
For the roots of a quadratic equation ax² + bx + c = 0 to lie in an interval (a, b), the following conditions must be satisfied:
1. Sum of Roots: The sum of the roots (r1 + r2) = -b/a should be greater than 0 and less than 2.
2. Product of Roots: The product of the roots (r1 * r2) = c/a should be greater than 0.
In our case:
- Sum of Roots: r1 + r2 = 3
- Product of Roots: r1 * r2 = k
Analyzing the Conditions
1. Sum of Roots: Since 3 is not in the interval (0, 2), the first condition fails. This implies that the roots cannot both be positive and less than 1.
2. Product of Roots: For the product k to be positive, k must be greater than 0. However, this doesn’t help as the sum condition already invalidates the possibility of the roots lying in (0,1).
Conclusion
Given that the sum of the roots is fixed at 3, which does not allow both roots to lie within (0,1), we conclude that:
- There are no values of k that satisfy the conditions for the roots to lie in the interval (0,1).
Thus, the correct answer is option B: no value.
If difference between the roots ofthe equation x2 – kx + 8 = 0 is 4 then the value of K is: - a)0
- b)±4
- c)±8√3
- d)±4√3
Correct answer is option 'D'. Can you explain this answer?
If difference between the roots ofthe equation x2 – kx + 8 = 0 is 4 then the value of K is:
a)
0
b)
±4
c)
±8√3
d)
±4√3

|
Nipuns Institute answered |
let α, β are roots of x2 – kx + 8 = 0
∴ α + β = -b/a = −(−k)/1 = k & α. β = c/a = 8/1 = 8
(α – β)2 = (α + β)2 – 4αβ = 42
⇒ k2 – 4 × 8 = 16
or k2 = 48 ⇒ k = ±√16×3 ⇒ k = ±4√3
(d) is correct.
∴ α + β = -b/a = −(−k)/1 = k & α. β = c/a = 8/1 = 8
(α – β)2 = (α + β)2 – 4αβ = 42
⇒ k2 – 4 × 8 = 16
or k2 = 48 ⇒ k = ±√16×3 ⇒ k = ±4√3
(d) is correct.
If the roots of the equation kx2 – 3x -1= 0 are the reciprocal of the roots of the equation x2 + 3x – 4 = 0 then K =- a)4
- b)-4
- c)3
- d)-3
Correct answer is option 'A'. Can you explain this answer?
If the roots of the equation kx2 – 3x -1= 0 are the reciprocal of the roots of the equation x2 + 3x – 4 = 0 then K =
a)
4
b)
-4
c)
3
d)
-3

|
KP Classes answered |
∵ x2 + 3x – 4 = 0
or; x2 – 4x + x – 4 = 0
or; x(x – 4) + 1(x – 4) = 0
or; (x – 4)(x + 1) = 0
x = 4; -1
Eqn. having roots 1/2 & 1/−1 = 1/4 & – 1 is.
or x2 – (1/4 – 1) + 1/4(-1) = 0
or x2 + 3/4x – 1/4 = 0
Multiplying by 4 ; we get
4x2 + 3x -1 = 0
Comparing it with kx2 + 3x -1 = 0
We get K = 4
Tricks : Eqn. having roots the reciprocal of the roots of ax2 + bx + c = 0 is cx2 + bx +a = 0 i.e. 1st and last term interchanges.
or; x2 – 4x + x – 4 = 0
or; x(x – 4) + 1(x – 4) = 0
or; (x – 4)(x + 1) = 0
x = 4; -1
Eqn. having roots 1/2 & 1/−1 = 1/4 & – 1 is.
or x2 – (1/4 – 1) + 1/4(-1) = 0
or x2 + 3/4x – 1/4 = 0
Multiplying by 4 ; we get
4x2 + 3x -1 = 0
Comparing it with kx2 + 3x -1 = 0
We get K = 4
Tricks : Eqn. having roots the reciprocal of the roots of ax2 + bx + c = 0 is cx2 + bx +a = 0 i.e. 1st and last term interchanges.
If coefficients of the equation ax2 + bx + c = 0, a < 0 are real and roots of the equation are non–real complex and a + c + b < 0, then- a)4a + c < 2b
- b)4a + c> 2b
- c)4a + c = 2b
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
If coefficients of the equation ax2 + bx + c = 0, a < 0 are real and roots of the equation are non–real complex and a + c + b < 0, then
a)
4a + c < 2b
b)
4a + c> 2b
c)
4a + c = 2b
d)
none of these

|
Arindam Unni answered |
Method to Solve
Puting x=-1
a-b+c
but
a+c<b or a+c-b<0
hence f(x)<0 for all real values of x
therefore
putting x=-2
we get f(X)=4a+c-2b<0
or 4a+c<2b
a-b+c
but
a+c<b or a+c-b<0
hence f(x)<0 for all real values of x
therefore
putting x=-2
we get f(X)=4a+c-2b<0
or 4a+c<2b
The value of p and q(p ≠ 0,q ≠ 0) for which p, q are the roots of the equation x2 + px + q = 0 are- a)p = 1,q = 2
- b)p = −1,q = 2
- c)p = −1, q = −2
- d)p = 1,q = −2
Correct answer is option 'D'. Can you explain this answer?
The value of p and q(p ≠ 0,q ≠ 0) for which p, q are the roots of the equation x2 + px + q = 0 are
a)
p = 1,q = 2
b)
p = −1,q = 2
c)
p = −1, q = −2
d)
p = 1,q = −2

|
Maulik Verma answered |
Understanding the Equation
The roots of the quadratic equation x² + px + q = 0 can be derived using Vieta's formulas, which state that for a quadratic equation ax² + bx + c = 0, if r₁ and r₂ are the roots, then:
- r₁ + r₂ = -b/a
- r₁ * r₂ = c/a
In this case, we have:
- p + q = -p (from the coefficient of x)
- pq = q (from the constant term)
Setting Up the Equations
From Vieta's formulas, we can rewrite the relationships:
1. p + q = -p
2. pq = q
Now, let's simplify these equations.
Solving the First Equation
From the first equation:
- p + q = -p
- 2p + q = 0
- q = -2p
Solving the Second Equation
From the second equation:
- pq = q (since q ≠ 0, we can divide both sides by q)
- p = 1 (as long as q is not zero)
Finding the Values of p and q
Substituting p = 1 into q = -2p:
- q = -2(1) = -2
Thus, we find:
- p = 1
- q = -2
Conclusion
The correct values for p and q that satisfy the equation x² + px + q = 0, while ensuring p and q are non-zero, are:
- p = 1
- q = -2
Therefore, the correct answer is option D: p = 1, q = -2.
The roots of the quadratic equation x² + px + q = 0 can be derived using Vieta's formulas, which state that for a quadratic equation ax² + bx + c = 0, if r₁ and r₂ are the roots, then:
- r₁ + r₂ = -b/a
- r₁ * r₂ = c/a
In this case, we have:
- p + q = -p (from the coefficient of x)
- pq = q (from the constant term)
Setting Up the Equations
From Vieta's formulas, we can rewrite the relationships:
1. p + q = -p
2. pq = q
Now, let's simplify these equations.
Solving the First Equation
From the first equation:
- p + q = -p
- 2p + q = 0
- q = -2p
Solving the Second Equation
From the second equation:
- pq = q (since q ≠ 0, we can divide both sides by q)
- p = 1 (as long as q is not zero)
Finding the Values of p and q
Substituting p = 1 into q = -2p:
- q = -2(1) = -2
Thus, we find:
- p = 1
- q = -2
Conclusion
The correct values for p and q that satisfy the equation x² + px + q = 0, while ensuring p and q are non-zero, are:
- p = 1
- q = -2
Therefore, the correct answer is option D: p = 1, q = -2.
If the roots of the equation x2 – 15x2 + kx – 45 = 0 are in A.P., find value of k:- a)56
- b)59
- c)-56
- d)-59
Correct answer is option 'B'. Can you explain this answer?
If the roots of the equation x2 – 15x2 + kx – 45 = 0 are in A.P., find value of k:
a)
56
b)
59
c)
-56
d)
-59

|
KP Classes answered |
∵ Roots are in A.R
Let roots are a – d; a; a + d
So, (a – d)+a + (a + d) = 15
or; 3a = 15
or; a = 5
And Product of roots
(a – d ). a . (a + d ) = 45
or (5 – d);5. (5 + d) = 45
or 25 – d2 = 9
or; d2 = 25 – 9 = 16
or; d = √16 = 4
Hence; roots are
a – d, a, a + d = 5 – 4; 5; 5 + 4
= 1; 5 ; 9.
The value of K
= Sum of product of two roots in a order
= (1 × 5) + (5 × 9) + (9 × 1)
= 5 + 45 + 9 = 59
(b) is correct.
Let roots are a – d; a; a + d
So, (a – d)+a + (a + d) = 15
or; 3a = 15
or; a = 5
And Product of roots
(a – d ). a . (a + d ) = 45
or (5 – d);5. (5 + d) = 45
or 25 – d2 = 9
or; d2 = 25 – 9 = 16
or; d = √16 = 4
Hence; roots are
a – d, a, a + d = 5 – 4; 5; 5 + 4
= 1; 5 ; 9.
The value of K
= Sum of product of two roots in a order
= (1 × 5) + (5 × 9) + (9 × 1)
= 5 + 45 + 9 = 59
(b) is correct.
If (x + iy)1/3 = a + ib, then x/a + y/b = K(a2 − b2), then the value of K is- a)1
- b)2
- c)4
- d)3
Correct answer is option 'C'. Can you explain this answer?
If (x + iy)1/3 = a + ib, then x/a + y/b = K(a2 − b2), then the value of K is
a)
1
b)
2
c)
4
d)
3

|
Bhavana Chavan answered |
Understanding the Problem
To solve the equation (x + iy)^(1/3) = a + ib, we need to analyze the expressions and establish the relationship between the variables involved.
Cube Root of a Complex Number
1. The cube root of a complex number can be expressed in terms of polar coordinates.
2. For (x + iy), we represent it as r(cos θ + i sin θ), where r is the modulus, and θ is the argument.
3. The cube root gives us:
- a = r^(1/3) cos(θ/3)
- b = r^(1/3) sin(θ/3)
Expressing x and y
1. From the expressions for a and b, we can express x and y in terms of a and b.
2. By using:
- x = a^3 - 3ab^2
- y = 3a^2b - b^3
Substituting Values
1. The equation x/a + y/b can be simplified:
- x/a = (a^3 - 3ab^2)/a = a^2 - 3b^2
- y/b = (3a^2b - b^3)/b = 3a^2 - b^2
2. Therefore, combining these gives:
- x/a + y/b = (a^2 - 3b^2) + (3a^2 - b^2) = 4a^2 - 4b^2 = 4(a^2 - b^2)
Identifying K
1. From the expression x/a + y/b = K(a^2 - b^2), we can see that K must equal 4.
2. Hence, the value of K is 4.
Conclusion
The correct answer is option 'C', which is 4. This derivation is crucial in understanding the relationship between the cube roots of complex numbers and their components.
To solve the equation (x + iy)^(1/3) = a + ib, we need to analyze the expressions and establish the relationship between the variables involved.
Cube Root of a Complex Number
1. The cube root of a complex number can be expressed in terms of polar coordinates.
2. For (x + iy), we represent it as r(cos θ + i sin θ), where r is the modulus, and θ is the argument.
3. The cube root gives us:
- a = r^(1/3) cos(θ/3)
- b = r^(1/3) sin(θ/3)
Expressing x and y
1. From the expressions for a and b, we can express x and y in terms of a and b.
2. By using:
- x = a^3 - 3ab^2
- y = 3a^2b - b^3
Substituting Values
1. The equation x/a + y/b can be simplified:
- x/a = (a^3 - 3ab^2)/a = a^2 - 3b^2
- y/b = (3a^2b - b^3)/b = 3a^2 - b^2
2. Therefore, combining these gives:
- x/a + y/b = (a^2 - 3b^2) + (3a^2 - b^2) = 4a^2 - 4b^2 = 4(a^2 - b^2)
Identifying K
1. From the expression x/a + y/b = K(a^2 - b^2), we can see that K must equal 4.
2. Hence, the value of K is 4.
Conclusion
The correct answer is option 'C', which is 4. This derivation is crucial in understanding the relationship between the cube roots of complex numbers and their components.
Find the positive value of k for which the equations : x2 + kx + 64 = 0 and x2 – 8x + k = 0 will have real roots:- a)12
- b)16
- c)18
- d)22
Correct answer is option 'B'. Can you explain this answer?
Find the positive value of k for which the equations : x2 + kx + 64 = 0 and x2 – 8x + k = 0 will have real roots:
a)
12
b)
16
c)
18
d)
22

|
Srishti Kaur answered |
Understanding the Problem
To determine the positive value of k for which both equations:
1. x² + kx + 64 = 0
2. x² - 8x + k = 0
will have real roots, we need to analyze the discriminant of each quadratic equation.
Discriminant Condition
The discriminant (D) of a quadratic equation ax² + bx + c = 0 is given by the formula:
D = b² - 4ac
For the roots to be real, D must be greater than or equal to zero (D ≥ 0).
Applying the Discriminant to Both Equations
1. For the first equation (x² + kx + 64 = 0):
- Here, a = 1, b = k, c = 64.
- D₁ = k² - 4(1)(64) = k² - 256.
Set the discriminant greater than or equal to zero:
- k² - 256 ≥ 0
- This simplifies to k² ≥ 256
- Therefore, k ≥ 16 or k ≤ -16. Since we need the positive value, we have k ≥ 16.
2. For the second equation (x² - 8x + k = 0):
- Here, a = 1, b = -8, c = k.
- D₂ = (-8)² - 4(1)(k) = 64 - 4k.
Again, set the discriminant greater than or equal to zero:
- 64 - 4k ≥ 0
- This simplifies to 64 ≥ 4k
- Thus, k ≤ 16.
Finding the Value of k
Combining the results from both equations:
- From the first equation: k ≥ 16
- From the second equation: k ≤ 16
The only value satisfying both conditions is k = 16.
Conclusion
Thus, the positive value of k for which both equations have real roots is:
16 (Option B)
To determine the positive value of k for which both equations:
1. x² + kx + 64 = 0
2. x² - 8x + k = 0
will have real roots, we need to analyze the discriminant of each quadratic equation.
Discriminant Condition
The discriminant (D) of a quadratic equation ax² + bx + c = 0 is given by the formula:
D = b² - 4ac
For the roots to be real, D must be greater than or equal to zero (D ≥ 0).
Applying the Discriminant to Both Equations
1. For the first equation (x² + kx + 64 = 0):
- Here, a = 1, b = k, c = 64.
- D₁ = k² - 4(1)(64) = k² - 256.
Set the discriminant greater than or equal to zero:
- k² - 256 ≥ 0
- This simplifies to k² ≥ 256
- Therefore, k ≥ 16 or k ≤ -16. Since we need the positive value, we have k ≥ 16.
2. For the second equation (x² - 8x + k = 0):
- Here, a = 1, b = -8, c = k.
- D₂ = (-8)² - 4(1)(k) = 64 - 4k.
Again, set the discriminant greater than or equal to zero:
- 64 - 4k ≥ 0
- This simplifies to 64 ≥ 4k
- Thus, k ≤ 16.
Finding the Value of k
Combining the results from both equations:
- From the first equation: k ≥ 16
- From the second equation: k ≤ 16
The only value satisfying both conditions is k = 16.
Conclusion
Thus, the positive value of k for which both equations have real roots is:
16 (Option B)
Find the condition that one root is double the of ax2 + bx + c = 0- a)2b2 = 3ac
- b)b2 = 3ac
- c)2b2 = 9ac
- d)None
Correct answer is option 'C'. Can you explain this answer?
Find the condition that one root is double the of ax2 + bx + c = 0
a)
2b2 = 3ac
b)
b2 = 3ac
c)
2b2 = 9ac
d)
None

|
Nipun Tuteja answered |
Let 1st root = 1
Then 2nd root = 2
The Eqn. is x2 – (1 + 2) + 1 × 2 = 0
or x2 – 3x + 2 = 0
Comparing it with ax2 + bx + c = 0 we get;
a = 1; b = -3 ; c = 2
Go by choices (GBC)
(a) 2b2 = 3ac
2.(-3)2 =3.1.2 (False)
(c) 2b2 =9.ac
2. (-3)2 = 9.1.2
⇒ 18 = 18 (True)
Hence, Option (c) is (true)
Then 2nd root = 2
The Eqn. is x2 – (1 + 2) + 1 × 2 = 0
or x2 – 3x + 2 = 0
Comparing it with ax2 + bx + c = 0 we get;
a = 1; b = -3 ; c = 2
Go by choices (GBC)
(a) 2b2 = 3ac
2.(-3)2 =3.1.2 (False)
(c) 2b2 =9.ac
2. (-3)2 = 9.1.2
⇒ 18 = 18 (True)
Hence, Option (c) is (true)
If a ∈ R and a1, a2, a3……,an ∈ R then (x − a1)2 + (x − a2)2 +…+ (x − an)2 assumes its least value at x=- a)a1 + a2 + …… + an
- b)2(a1 + a2 + a3 +…… + an)
- c)n(a1 + a2 + …… + an)
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
If a ∈ R and a1, a2, a3……,an ∈ R then (x − a1)2 + (x − a2)2 +…+ (x − an)2 assumes its least value at x=
a)
a1 + a2 + …… + an
b)
2(a1 + a2 + a3 +…… + an)
c)
n(a1 + a2 + …… + an)
d)
none of these

|
Nipun Tuteja answered |
We have
(x − a1)2 + (x − a2)2 +….. +(x − an)2 = nx2 − 2x(a1 + a2 + …. + an) + (a21 + a22 + ….. + a2n)
Clearly, y = nx2 − 2x (a1 + a2 + …… + an) + (a21 + a22 + …….. + a2n) represents a parabola which opens upward. So, it attains its minimum value at the vertex i.e. at
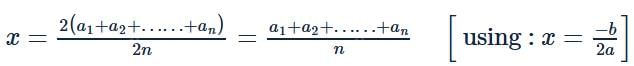
(x − a1)2 + (x − a2)2 +….. +(x − an)2 = nx2 − 2x(a1 + a2 + …. + an) + (a21 + a22 + ….. + a2n)
Clearly, y = nx2 − 2x (a1 + a2 + …… + an) + (a21 + a22 + …….. + a2n) represents a parabola which opens upward. So, it attains its minimum value at the vertex i.e. at
Consider y = 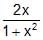 , where x is real, then the range of expression y2 + y – 2 is
, where x is real, then the range of expression y2 + y – 2 is- a)[–1, 1]
- b)[0, 1]
- c) [–9/4, 0]
- d) [–9/4, 1]
Correct answer is option 'C'. Can you explain this answer?
Consider y = 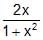 , where x is real, then the range of expression y2 + y – 2 is
, where x is real, then the range of expression y2 + y – 2 is
a)
[–1, 1]
b)
[0, 1]
c)
[–9/4, 0]
d)
[–9/4, 1]

|
Sravya Banerjee answered |
Ans.
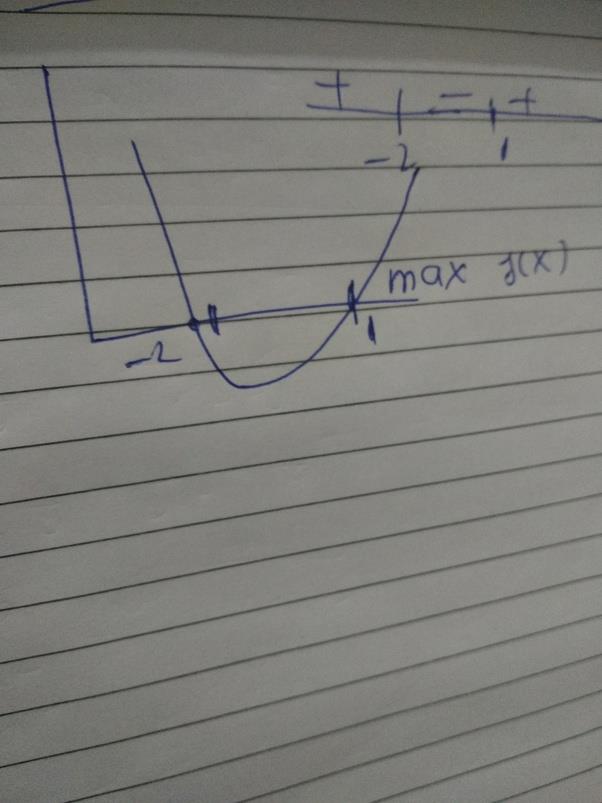
Option (C)
Here y=2x/(1+x^2)
Make sense
So multiply both side by (1+x^2)
a quadritic equation will form in
which cofficent
of x^2 will be y and that of x will be 2
And constant will be 2
For x to be real
D greater than or equal to zero
So
D=2^2–4y^2≥0
now
Y^2–1≥0
(y-1)(y+1)≥0
Solving inequaties
Y will be in[-1,1]
Now the given exp is
y^2y-2
Or by factorization
(y+2)(y-1)
Now the give exp will increase as in grap
Max will be at x=1 which equals 0 as domain is restricated
And min will be at -b/2a which equals -1/2
Or minimum value will be -D/4a which equals 9/4
If the roots of the equation 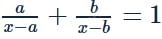 are equal in magnitude and opposite in sign, then
are equal in magnitude and opposite in sign, then- a)a − b = 0
- b)a + b = 1
- c)a − b = 1
- d)a + b = 0
Correct answer is option 'D'. Can you explain this answer?
If the roots of the equation 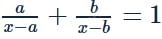 are equal in magnitude and opposite in sign, then
are equal in magnitude and opposite in sign, then
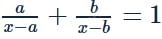 are equal in magnitude and opposite in sign, then
are equal in magnitude and opposite in sign, thena)
a − b = 0
b)
a + b = 1
c)
a − b = 1
d)
a + b = 0

|
Nipuns Institute answered |
The given equation can be written as x2 − 2(a + b)x + 3ab = 0
Since roots are equal in magnitude and opposite in sign.
∴ Sum of roots =0
∴a + b = 0
Since roots are equal in magnitude and opposite in sign.
∴ Sum of roots =0
∴a + b = 0
Chapter doubts & questions for Complex Numbers and Quadratic Equation - Mathematics (Maths) for JEE Main & Advanced 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Complex Numbers and Quadratic Equation - Mathematics (Maths) for JEE Main & Advanced in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup

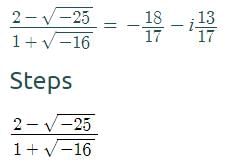
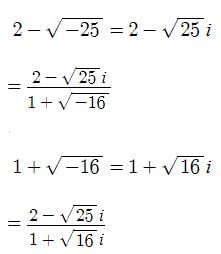
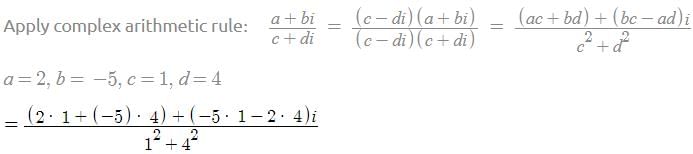
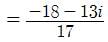

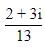
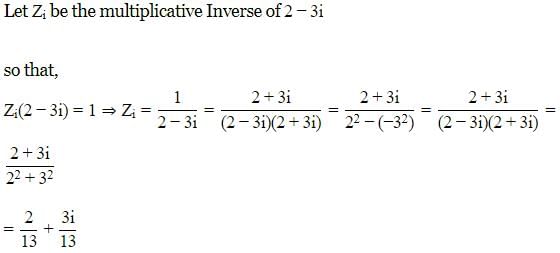


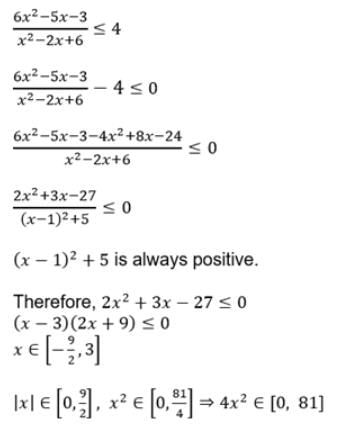

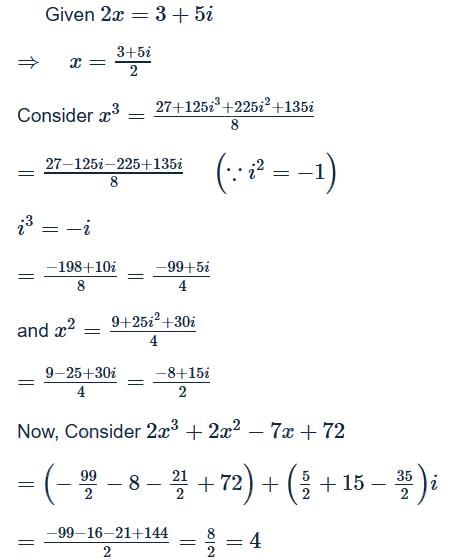
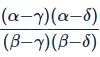 is independent of:
is independent of: