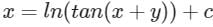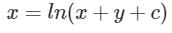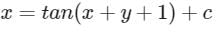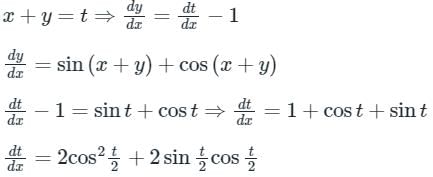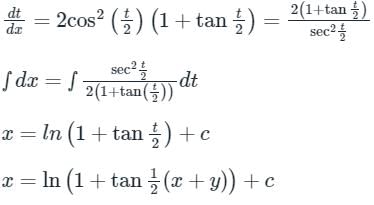All Exams >
Civil Engineering (CE) >
Engineering Mathematics >
All Questions
All questions of Differential Equations for Civil Engineering (CE) Exam
The following differential equation has 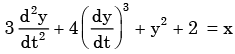 a)degree = 2, order = 1b)degree = 1, order = 2 c)degree = 4, order = 3 d)degree = 2, order = 3Correct answer is option 'B'. Can you explain this answer?
a)degree = 2, order = 1b)degree = 1, order = 2 c)degree = 4, order = 3 d)degree = 2, order = 3Correct answer is option 'B'. Can you explain this answer?
|
|
Anmol Basu answered |
Order of highest derivative = 2
Hence, most appropriate answer is (b)
Hence, most appropriate answer is (b)
The general solution of (x2 D2 – xD), y= 0 is :
- a) y = C1 + C2 ex
- b) y = C1 + C2 x2
- c)y = C1 x + C2 x2
- d)y = C1 + C2 x
Correct answer is option 'C'. Can you explain this answer?
The general solution of (x2 D2 – xD), y= 0 is :
a)
y = C1 + C2 ex
b)
y = C1 + C2 x2
c)
y = C1 x + C2 x2
d)
y = C1 + C2 x
|
|
Akshara Rane answered |
+ 4xD + 3y = 0) can be found by assuming a solution of the form y = e^(mx).
Substituting this into the differential equation gives:
x^2(m^2)e^(mx) + 4xme^(mx) + 3e^(mx) = 0
Dividing through by e^(mx) gives:
m^2x^2 + 4mx + 3 = 0
This is a quadratic equation in m, which can be solved using the quadratic formula:
m = (-4x ± √(16x^2 - 4(3)(x^2))) / (2x^2)
Simplifying this gives:
m = (-2 ± √1) / x
m1 = -1/x, m2 = -3/x
Therefore, the general solution is a linear combination of the two solutions:
y = c1e^(-x) + c2e^(-3x)
where c1 and c2 are arbitrary constants determined by initial or boundary conditions.
Substituting this into the differential equation gives:
x^2(m^2)e^(mx) + 4xme^(mx) + 3e^(mx) = 0
Dividing through by e^(mx) gives:
m^2x^2 + 4mx + 3 = 0
This is a quadratic equation in m, which can be solved using the quadratic formula:
m = (-4x ± √(16x^2 - 4(3)(x^2))) / (2x^2)
Simplifying this gives:
m = (-2 ± √1) / x
m1 = -1/x, m2 = -3/x
Therefore, the general solution is a linear combination of the two solutions:
y = c1e^(-x) + c2e^(-3x)
where c1 and c2 are arbitrary constants determined by initial or boundary conditions.
Which of the following is not a standard method for finding the solutions for differential equations?- a)Variable Separable
- b)Homogenous Equation
- c)Orthogonal Method
- d)Bernoulli’s Equation
Correct answer is option 'C'. Can you explain this answer?
Which of the following is not a standard method for finding the solutions for differential equations?
a)
Variable Separable
b)
Homogenous Equation
c)
Orthogonal Method
d)
Bernoulli’s Equation
|
|
Sanya Agarwal answered |
The following are the different standard methods used in finding the solution of a differential equation:
- Variable Separable
- Homogenous Equation
- Non-homogenous Equation reducible to Homogenous Equation
- Exact Differential Equation
- Non-exact Differential Equation that can be made exact with the help of integrating factors
- Linear First Order Equation
- Bernoulli’s Equation
Which of the following equations cannot be solved by using the method of separation of variables?- a)Laplace Equation
- b)Helmholtz Equation
- c)Alpha Equation
- d)Biharmonic Equation
Correct answer is option 'C'. Can you explain this answer?
Which of the following equations cannot be solved by using the method of separation of variables?
a)
Laplace Equation
b)
Helmholtz Equation
c)
Alpha Equation
d)
Biharmonic Equation
|
|
Sanya Agarwal answered |
The method of separation of variables is used to solve a wide range of linear partial differential equations with boundary and initial conditions, such as:
- Heat equation
- Wave equation
- Laplace equation
- Helmholtz equation
- Biharmonic equation
The general solution of the differential equation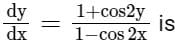
- a)tan y − cot x = c(c is a constant
- b)tan x − cot y = c(c is a constant)
- c)tan y + cot x = c(c is a constant)
- d)tan x + cot Y = c(c is a constant)
Correct answer is option 'C'. Can you explain this answer?
The general solution of the differential equation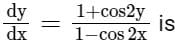
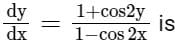
a)
tan y − cot x = c(c is a constant
b)
tan x − cot y = c(c is a constant)
c)
tan y + cot x = c(c is a constant)
d)
tan x + cot Y = c(c is a constant)

|
Pioneer Academy answered |
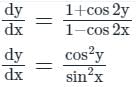
sec2ydy = cosec2x.dx
tan y = −cot x + c
tan y + cot x = c
A function n(x) satisfies the differential equation 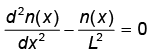 where L is a constant. The boundary conditions are: n(0)=K and n(∞)= 0. The solution to this equation is
where L is a constant. The boundary conditions are: n(0)=K and n(∞)= 0. The solution to this equation is - a)n(x) = K exp(x/L)
- b)n(x) = K exp( x / √L )
- c)n(x) = K2 exp(-x/L)
- d)n(x) = K exp( -x/L)
Correct answer is option 'D'. Can you explain this answer?
A function n(x) satisfies the differential equation 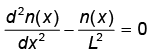 where L is a constant. The boundary conditions are: n(0)=K and n(∞)= 0. The solution to this equation is
where L is a constant. The boundary conditions are: n(0)=K and n(∞)= 0. The solution to this equation is
a)
n(x) = K exp(x/L)
b)
n(x) = K exp( x / √L )
c)
n(x) = K2 exp(-x/L)
d)
n(x) = K exp( -x/L)
|
|
Sanvi Kapoor answered |
For finite solution c1 = 0
What is the area common to the circles r = a and r = 2a cos θ? - a)0.524 a2
- b)0.614 a2
- c)1.047 a2
- d)1.228 a2
Correct answer is option 'D'. Can you explain this answer?
What is the area common to the circles r = a and r = 2a cos θ?
a)
0.524 a2
b)
0.614 a2
c)
1.047 a2
d)
1.228 a2

|
Srishti Chopra answered |
Area common to circles r = a
And r = 2a cos θ is 1.228 a2
The solution of dy/dx = y2 with initial value y(0) = 1 is bounded in the interval - a)−∞ ≤ x ≤ ∞
- b)−∞ ≤ x ≤ 1
- c)x < 1, x > 1
- d)−2 ≤ x ≤ 2
Correct answer is option 'C'. Can you explain this answer?
The solution of dy/dx = y2 with initial value y(0) = 1 is bounded in the interval
a)
−∞ ≤ x ≤ ∞
b)
−∞ ≤ x ≤ 1
c)
x < 1, x > 1
d)
−2 ≤ x ≤ 2
|
|
Sanya Agarwal answered |
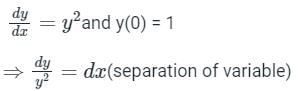
⇒ from the Integrating the equation, we get
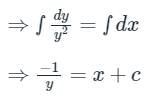
⇒ at x = 0, y = 1, hence -1/1 = c ⇒ c = -1
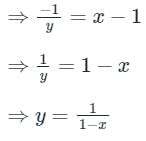
x ≠ 1, at (x = 1) y will be undefined
x > 1, x < 1
The solutions of the equation 3yy’ + 4x = 0 represents a:- a)Family of circles
- b)Family of ellipses
- c)Family of Parabolas
- d)Family of hyperbolas
Correct answer is option 'B'. Can you explain this answer?
The solutions of the equation 3yy’ + 4x = 0 represents a:
a)
Family of circles
b)
Family of ellipses
c)
Family of Parabolas
d)
Family of hyperbolas

|
Vertex Academy answered |
3yy’ + 4x = 0
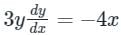
3ydy = - 4x dx
On integration both the sides:
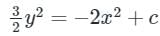
Where c is the constant of integration.
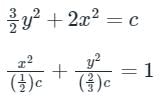
Thus, the solution of given differential equation represents the family of Ellipses.
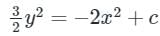
Where c is the constant of integration.
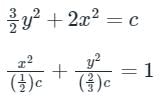
Thus, the solution of given differential equation represents the family of Ellipses.
Consider the following differential equation: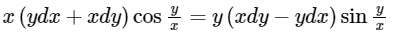 Which of the following is the solution of the above equation (c is an arbitrary constant)?
Which of the following is the solution of the above equation (c is an arbitrary constant)?- a)
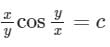
- b)
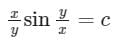
- c)
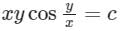
- d)
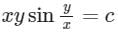
Correct answer is option 'C'. Can you explain this answer?
Consider the following differential equation:
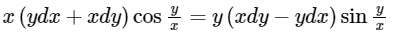
Which of the following is the solution of the above equation (c is an arbitrary constant)?
a)
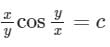
b)
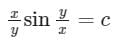
c)
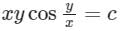
d)
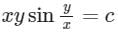

|
Engineers Adda answered |
Given differential eqaution is,
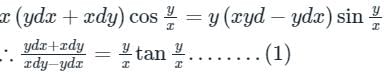
Let, y = v × x
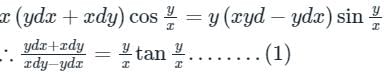
Let, y = v × x
dy = vdx + xdv
By substituting values of Y and dY in equation 1, we get
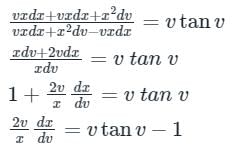
Integrating both sides
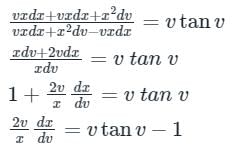
Integrating both sides
2 log x = log |sec v| - log v + log c
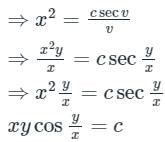
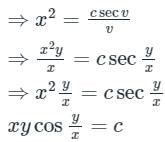
The differential equation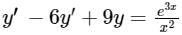 is solving by the method of variation of parameters, where the complementary function is given by- y = c1y1(x) + c2y2(x)
is solving by the method of variation of parameters, where the complementary function is given by- y = c1y1(x) + c2y2(x)- a)The value of y1(x) = e3x
- b)The value of y2(x) = e3x
- c)The value of y2(x) = xe3x
- d)
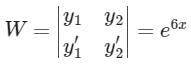
Correct answer is option 'D'. Can you explain this answer?
The differential equation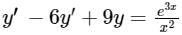 is solving by the method of variation of parameters, where the complementary function is given by- y = c1y1(x) + c2y2(x)
is solving by the method of variation of parameters, where the complementary function is given by- y = c1y1(x) + c2y2(x)
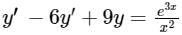 is solving by the method of variation of parameters, where the complementary function is given by- y = c1y1(x) + c2y2(x)
is solving by the method of variation of parameters, where the complementary function is given by- y = c1y1(x) + c2y2(x)a)
The value of y1(x) = e3x
b)
The value of y2(x) = e3x
c)
The value of y2(x) = xe3x
d)
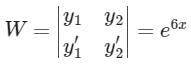

|
Engineers Adda answered |
Concept:
Calculation:

Calculation:
Given:
(D2 – 6D + 9)y = e3x/x2
Auxiliary equation is
(D2 – 6D + 9) = 0
⇒ (D – 3)2 = 0
C.F. = (C1 + C2x) e3x
C.F = C1(e3x) + C2(xe3x)


Every Cauchy sequence is- a)Unbounded
- b)Bounded
- c)Infinite
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Every Cauchy sequence is
a)
Unbounded
b)
Bounded
c)
Infinite
d)
None of these
|
|
Sanya Agarwal answered |
Basic properties of Cauchy sequences:
(i) Every convergent sequence is a Cauchy sequence,
(ii) Every Cauchy sequence of real (or complex) numbers is bounded,
(iii) If in a metric space, a Cauchy sequence possessing a convergent subsequence with limit is itself convergent and has the same limit.
∴ Every Cauchy sequence is bounded
A solution which does not contain any arbitrary constants is called a general solution.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
A solution which does not contain any arbitrary constants is called a general solution.
a)
True
b)
False
|
|
Sanya Agarwal answered |
The solution of a partial differential equation obtained by eliminating the arbitrary constants is called a general solution.
Which of the following is a type of Iterative method of solving non-linear equations?- a)Graphical method
- b)Interpolation method
- c)Trial and Error methods
- d)Direct Analytical methods
Correct answer is option 'B'. Can you explain this answer?
Which of the following is a type of Iterative method of solving non-linear equations?
a)
Graphical method
b)
Interpolation method
c)
Trial and Error methods
d)
Direct Analytical methods

|
Poulomi Patel answered |
Interpolation method
The interpolation method is a type of iterative method used for solving non-linear equations. It involves the use of interpolation techniques to approximate the solution of the equation.
Iterative methods
Iterative methods are a class of numerical methods used to solve equations by making an initial guess and then refining it through a series of iterations until a desired level of accuracy is achieved. These methods are particularly useful for solving non-linear equations, where direct analytical methods may not be feasible.
Interpolation
Interpolation is a mathematical technique used to estimate unknown values based on known data points. It involves constructing a function that passes through the given data points and then using this function to approximate the value of the unknown variable.
Application in solving non-linear equations
In the context of solving non-linear equations, the interpolation method can be used to approximate the solution by constructing an interpolating function that passes through two known points and then finding the value of the unknown variable at the intersection of this function with the x-axis.
Steps in the interpolation method
1. Choose two initial guesses for the unknown variable, x.
2. Evaluate the function at the two initial guesses to obtain corresponding function values, f(x1) and f(x2).
3. Use interpolation techniques, such as linear interpolation or polynomial interpolation, to construct an interpolating function that passes through the points (x1, f(x1)) and (x2, f(x2)).
4. Find the value of x where the interpolating function intersects the x-axis, which represents an approximation of the solution to the non-linear equation.
5. Repeat steps 2-4 until the desired level of accuracy is achieved.
Advantages of the interpolation method
- It is a simple and intuitive method.
- It does not require knowledge of the derivative of the function.
- It can be easily implemented using computer software or calculators.
- It provides a systematic approach to approximate the solution of non-linear equations.
In conclusion, the interpolation method is a type of iterative method commonly used for solving non-linear equations. It involves constructing an interpolating function based on two initial guesses and using this function to approximate the solution. This method is advantageous due to its simplicity and ease of implementation.
The interpolation method is a type of iterative method used for solving non-linear equations. It involves the use of interpolation techniques to approximate the solution of the equation.
Iterative methods
Iterative methods are a class of numerical methods used to solve equations by making an initial guess and then refining it through a series of iterations until a desired level of accuracy is achieved. These methods are particularly useful for solving non-linear equations, where direct analytical methods may not be feasible.
Interpolation
Interpolation is a mathematical technique used to estimate unknown values based on known data points. It involves constructing a function that passes through the given data points and then using this function to approximate the value of the unknown variable.
Application in solving non-linear equations
In the context of solving non-linear equations, the interpolation method can be used to approximate the solution by constructing an interpolating function that passes through two known points and then finding the value of the unknown variable at the intersection of this function with the x-axis.
Steps in the interpolation method
1. Choose two initial guesses for the unknown variable, x.
2. Evaluate the function at the two initial guesses to obtain corresponding function values, f(x1) and f(x2).
3. Use interpolation techniques, such as linear interpolation or polynomial interpolation, to construct an interpolating function that passes through the points (x1, f(x1)) and (x2, f(x2)).
4. Find the value of x where the interpolating function intersects the x-axis, which represents an approximation of the solution to the non-linear equation.
5. Repeat steps 2-4 until the desired level of accuracy is achieved.
Advantages of the interpolation method
- It is a simple and intuitive method.
- It does not require knowledge of the derivative of the function.
- It can be easily implemented using computer software or calculators.
- It provides a systematic approach to approximate the solution of non-linear equations.
In conclusion, the interpolation method is a type of iterative method commonly used for solving non-linear equations. It involves constructing an interpolating function based on two initial guesses and using this function to approximate the solution. This method is advantageous due to its simplicity and ease of implementation.
Which of the following is the property of error function?- a)erf (0) = 1
- b)erf (∞) = 1
- c)erf (0) = ∞
- d)erf (∞) = 0
Correct answer is option 'B'. Can you explain this answer?
Which of the following is the property of error function?
a)
erf (0) = 1
b)
erf (∞) = 1
c)
erf (0) = ∞
d)
erf (∞) = 0
|
|
Sanvi Kapoor answered |
Error Function is given by, 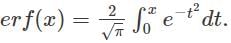
Some of its properties are:
erf (0) = 0
erf (∞) = 1
erf (-x) = -erf(x)
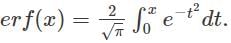
Some of its properties are:
erf (0) = 0
erf (∞) = 1
erf (-x) = -erf(x)
Let \(f\left( x \right) = \;\left\{ {\begin{array}{*{20}{c}} { - π }&{if\;}&{ - π
be a periodic function of period 2π. The coefficient of sin 5x in the Fourier series expansion of f(x) in the interval [-π, π] is- a)4/5
- b)5/4
- c)4/3
- d)3/4
Correct answer is option 'A'. Can you explain this answer?
Let \(f\left( x \right) = \;\left\{ {\begin{array}{*{20}{c}} { - π }&{if\;}&{ - π
be a periodic function of period 2π. The coefficient of sin 5x in the Fourier series expansion of f(x) in the interval [-π, π] is
be a periodic function of period 2π. The coefficient of sin 5x in the Fourier series expansion of f(x) in the interval [-π, π] is
a)
4/5
b)
5/4
c)
4/3
d)
3/4
|
|
Sanvi Kapoor answered |
Concept:
Let f(x) is a periodic function defined in (C, C + 2L) with period 2L, then the Fourier series of f(x) is
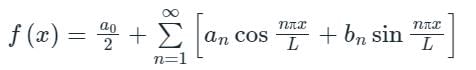
Where the Fourier series coefficients a0, an, and bn are given by

Let f(x) is a periodic function defined in (C, C + 2L) with period 2L, then the Fourier series of f(x) is
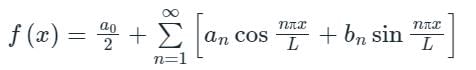
Where the Fourier series coefficients a0, an, and bn are given by

- If f(x) is an odd function, then only bn exists where a0 and bn are zero.
- If f(x) is an even function, then both a0 and an exists where bn is zero.
Calculation:
\(f\left( x \right) = \;\left\{ {\begin{array}{*{20}{c}} { - π }&{if\;}&{ - π
Fundamental period = 2π
The given function is an odd function and hence only bn exists.
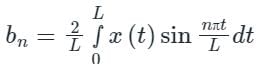
Here L = 2π
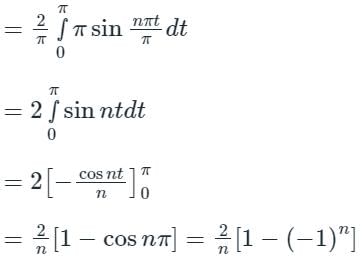
Now, the Fourier series of f(x) is,
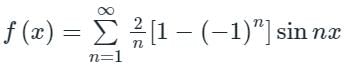
The coefficient of sin 5x = b5
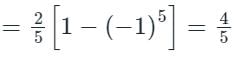
\(f\left( x \right) = \;\left\{ {\begin{array}{*{20}{c}} { - π }&{if\;}&{ - π
Fundamental period = 2π
The given function is an odd function and hence only bn exists.
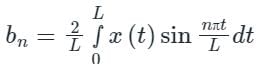
Here L = 2π
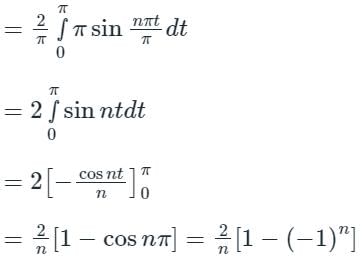
Now, the Fourier series of f(x) is,
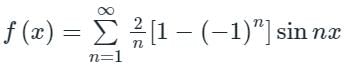
The coefficient of sin 5x = b5
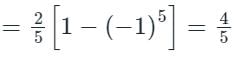
One dimensional wave equation is- a)
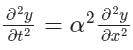
- b)

- c)
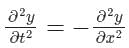
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
One dimensional wave equation is
a)
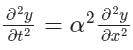
b)

c)
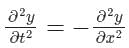
d)
None of these

|
Pioneer Academy answered |
Concept:
Wave equation:
It is a second-order linear partial differential equation for the description of waves (like mechanical waves).
The Partial Differential equation is given as,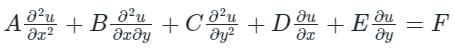
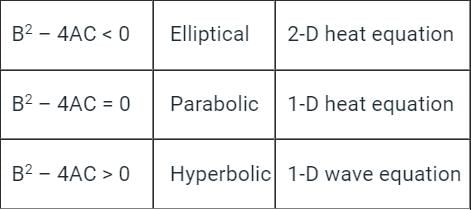
For One-Dimensional equation,
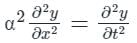
where, A = α2, B = 0, C = -1
Put all the values in equation (1)
∴ 0 - 4 (α2)(-1)
4α2 > 0.
So, this is a one-dimensional wave equation.
Additional Information
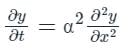
having A = α2, B = 0, C = 0
Put all the values in equation (1), we get
0 - 4(α2)(0) = 0, therefore it shows parabolic function.
So, this is a one-dimensional heat equation.
having A = 1, B = 0, C = 1
Put all the values in equation (1), we get 0 - 4(1)(1) = -4, therefore it shows elliptical function.
So, this is a two-dimensional heat equation.
Wave equation:
It is a second-order linear partial differential equation for the description of waves (like mechanical waves).
The Partial Differential equation is given as,
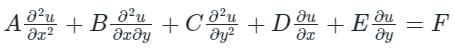

For One-Dimensional equation,
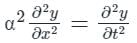
where, A = α2, B = 0, C = -1
Put all the values in equation (1)
∴ 0 - 4 (α2)(-1)
4α2 > 0.
So, this is a one-dimensional wave equation.
Additional Information
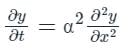
having A = α2, B = 0, C = 0
Put all the values in equation (1), we get
0 - 4(α2)(0) = 0, therefore it shows parabolic function.
So, this is a one-dimensional heat equation.
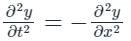
having A = 1, B = 0, C = 1
Put all the values in equation (1), we get 0 - 4(1)(1) = -4, therefore it shows elliptical function.
So, this is a two-dimensional heat equation.
Consider the differential equation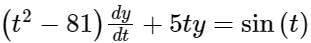 with y(1) = 2π. There exists a unique solution for this differential equation when t belongs to the interval
with y(1) = 2π. There exists a unique solution for this differential equation when t belongs to the interval- a)(–2, 2)
- b)(–10, 10)
- c)(–10, 2)
- d)(0, 10)
Correct answer is option 'A'. Can you explain this answer?
Consider the differential equation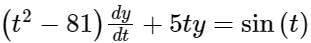 with y(1) = 2π. There exists a unique solution for this differential equation when t belongs to the interval
with y(1) = 2π. There exists a unique solution for this differential equation when t belongs to the interval
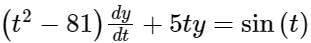 with y(1) = 2π. There exists a unique solution for this differential equation when t belongs to the interval
with y(1) = 2π. There exists a unique solution for this differential equation when t belongs to the intervala)
(–2, 2)
b)
(–10, 10)
c)
(–10, 2)
d)
(0, 10)
|
|
Sanya Agarwal answered |
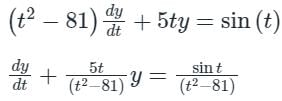
It is in the standard form of first order linear equation.
Integrating factor
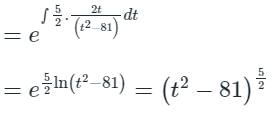
Solution of differential equation is:
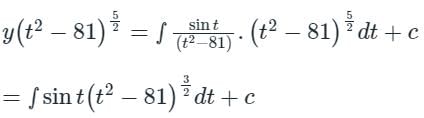
If t = ±9, solution doesn’t exist.

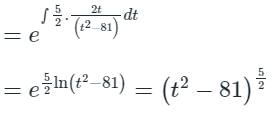
Solution of differential equation is:
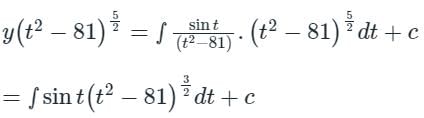
If t = ±9, solution doesn’t exist.
Hence t ≠ ±9.
From the options, (-2, 2) doesn’t consists of ±9, hence, (-2, 2) is the correct.
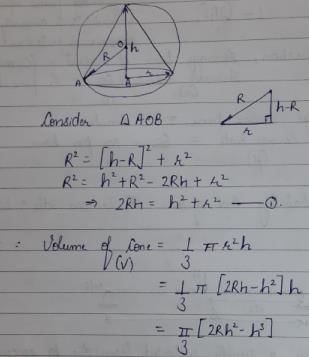
The expression 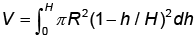 for the volume of a cone is equal to
for the volume of a cone is equal to- a)
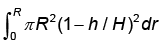
- b)
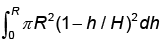
- c)
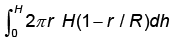
- d)
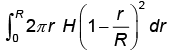
Correct answer is option 'D'. Can you explain this answer?
The expression 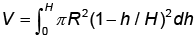 for the volume of a cone is equal to
for the volume of a cone is equal to
a)
b)
c)
d)
|
|
Nitin Joshi answered |
Choices (a) and (b) be correct because
for the volume of a cone is equal to
Which one of the following is the general solution of the first order differential equation dy/dx = (x + y − 1)2, where x, y are real?- a)y = 1 + x + tan–1 (x + c), where c is a constant.
- b)y = 1 + x + tan(x + c), where c is a constant.
- c)y = 1 – x + tan–1 (x + c), where c is a constant.
- d)y = 1 – x + tan(x + c), where c is a constant.
Correct answer is option 'D'. Can you explain this answer?
Which one of the following is the general solution of the first order differential equation dy/dx = (x + y − 1)2, where x, y are real?
a)
y = 1 + x + tan–1 (x + c), where c is a constant.
b)
y = 1 + x + tan(x + c), where c is a constant.
c)
y = 1 – x + tan–1 (x + c), where c is a constant.
d)
y = 1 – x + tan(x + c), where c is a constant.

|
Meghana Desai answered |
General Solution of the First Order Differential Equation
To find the general solution of the first order differential equation dy/dx = (x + y - 1)^2, we can rewrite the equation as:
dy/(x + y - 1)^2 = dx
Integrating both sides, we get:
Integration of the Differential Equation
∫ dy/(x + y - 1)^2 = ∫ dx
Substitute u = x + y - 1
Let u = x + y - 1. Then, du = dx + dy. Substituting these into the integral, we have:
∫ du/u^2 = ∫ dx
Integrate both sides
Integrating both sides, we get:
-1/u = x + C
where C is the constant of integration.
Substitute back y = u - x + 1
Substitute u = x + y - 1 back into the equation, we get:
-1/(x + y - 1) = x + C
Solving for y, we get:
y = 1 - x + tan(x + C)
Final General Solution
Therefore, the general solution of the first order differential equation dy/dx = (x + y - 1)^2 is:
y = 1 - x + tan(x + C), where C is a constant.
So, the correct answer is option 'D'.
The following partial differential equation is defined for u:u (x, y)
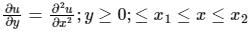
The set auxiliary conditions necessary to solve the equation uniquely, is - a)three initial conditions
- b)three boundary conditions
- c)two initial conditions and one boundary condition
- d)one initial conditions and two boundary conditions
Correct answer is option 'D'. Can you explain this answer?
The following partial differential equation is defined for u:u (x, y)
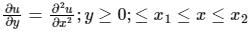
The set auxiliary conditions necessary to solve the equation uniquely, is
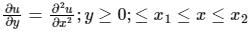
The set auxiliary conditions necessary to solve the equation uniquely, is
a)
three initial conditions
b)
three boundary conditions
c)
two initial conditions and one boundary condition
d)
one initial conditions and two boundary conditions

|
Pioneer Academy answered |
Given:

∵ y ≥ 0 ⇒ It can be replaced with ‘t’.
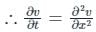
This is a 1-D Heat equation. It measures temperature distribution in a uniform rod.
The general solution is u = f(x, t)
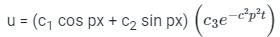
Auxiliary solutions include both initial and boundary conditions.
(1) Number of initial conditions = Highest order of time derivative in partial differential = 1
(2) The number of boundary conditions:
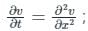 To solve this partial differential equation, it needs to be integrated twice that will introduce two arbitrary constants.
To solve this partial differential equation, it needs to be integrated twice that will introduce two arbitrary constants.
Hence 2 boundary conditions and 1 initial condition are required to solve this Partial differential equation.

∵ y ≥ 0 ⇒ It can be replaced with ‘t’.
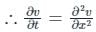
This is a 1-D Heat equation. It measures temperature distribution in a uniform rod.
The general solution is u = f(x, t)
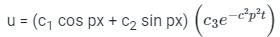
Auxiliary solutions include both initial and boundary conditions.
(1) Number of initial conditions = Highest order of time derivative in partial differential = 1
(2) The number of boundary conditions:
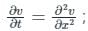 To solve this partial differential equation, it needs to be integrated twice that will introduce two arbitrary constants.
To solve this partial differential equation, it needs to be integrated twice that will introduce two arbitrary constants.Hence 2 boundary conditions and 1 initial condition are required to solve this Partial differential equation.
A particle undergoes forced vibrations according to the law xn(t) + 25x(t) = 21 sin t. If the particle starts from rest at t = 0, find the displacement at any time t > 0. - a)

- b)
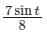
- c)
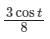
- d)
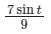
Correct answer is option 'B'. Can you explain this answer?
A particle undergoes forced vibrations according to the law xn(t) + 25x(t) = 21 sin t. If the particle starts from rest at t = 0, find the displacement at any time t > 0.
a)

b)
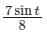
c)
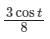
d)
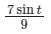
|
|
Sanya Agarwal answered |
Concept:
The solution of the linear differential equation is of the form:
y = C.F + P.I
where C.F is the complementary function and P.I is the particular integral.
The 2nd order linear differential equation in the symbolic form is represented as:
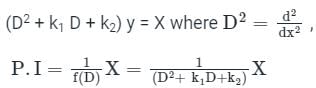
When X = Sin(ax)
f(-a2) is calculated by replacing D2 with a2 in f(D)
In the case of a forced damped system, the vibration equation:
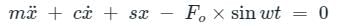 The solution of x is (CF + PI)
The solution of x is (CF + PI)Where CF is complimentary function and PI is particular integral
But after some time CF becomes zero.
∴ x = P.I
Calculation:
Given:
xn(t) + 25x(t) = 21 sin t
The above equation can be written as:
D2 + 25x = 21 × Sin (t)
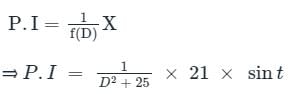
Here, a = 1, So putting -a2 = D2 = -1 in the above equation

∴ The displacement at any time t > 0 = 

Solve the following equation:
yexydx + (xexy + 2y)dy = 0- a)xexy + 2y2 = c
- b)xexy + y2 = c
- c)exy + 2y2 = c
- d)exy + y2 = c
Correct answer is option 'D'. Can you explain this answer?
Solve the following equation:
yexydx + (xexy + 2y)dy = 0
yexydx + (xexy + 2y)dy = 0
a)
xexy + 2y2 = c
b)
xexy + y2 = c
c)
exy + 2y2 = c
d)
exy + y2 = c
|
|
Sanya Agarwal answered |
The given equation is in the form of
M dx + N dy = 0
Here M = y exy
N = (x exy + 2y)


Hence the differential equation is an exact equation.
The solution is
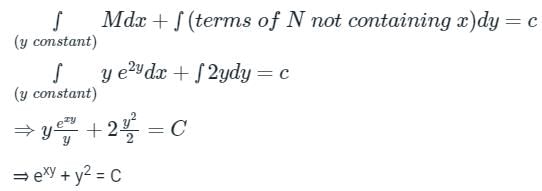
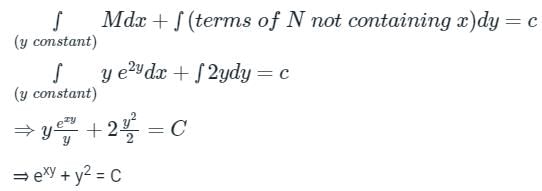
Find the particular solution of the differential equation
- a)
- b)
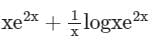
- c)

- d)
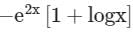
Correct answer is option 'D'. Can you explain this answer?
Find the particular solution of the differential equation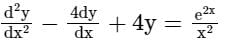
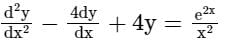
a)
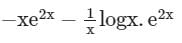
b)
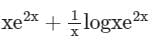
c)

d)
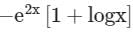

|
Engineers Adda answered |
Given differential equation is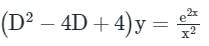
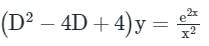
auxiliary equation is (D − 2)2 = 0 ⇒ D = 2, 2
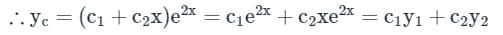
This problem can be solved by using the method of variation of parameters. Then
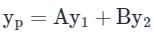
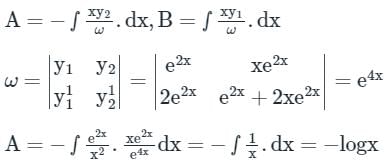
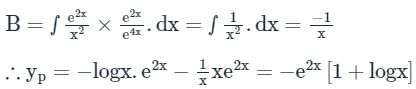
Given 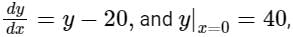 the value of y at x = 2 is ________ (round off to nearest integer) (Important - Enter only the numerical value in the answer)
the value of y at x = 2 is ________ (round off to nearest integer) (Important - Enter only the numerical value in the answer)
Correct answer is between '162,170'. Can you explain this answer?
Given 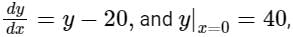 the value of y at x = 2 is ________ (round off to nearest integer) (Important - Enter only the numerical value in the answer)
the value of y at x = 2 is ________ (round off to nearest integer) (Important - Enter only the numerical value in the answer)
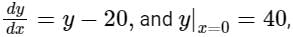 the value of y at x = 2 is ________ (round off to nearest integer) (Important - Enter only the numerical value in the answer)
the value of y at x = 2 is ________ (round off to nearest integer) (Important - Enter only the numerical value in the answer)|
|
Sanya Agarwal answered |
Given the differential equation is,
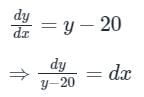
By integrating with respect to ‘x’, we get
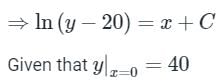
⇒ ln(20) = C
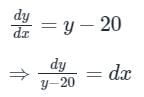
By integrating with respect to ‘x’, we get
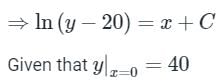
⇒ ln(20) = C
Now, the differential equation becomes

At x = 2, y = 20 (e2 + 1) = 167.78

At x = 2, y = 20 (e2 + 1) = 167.78
Cauchy’s linear differential equation 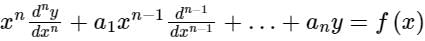 can be reduced to a linear differential equation with constant coefficient by using substitution
can be reduced to a linear differential equation with constant coefficient by using substitution- a)x = ez
- b)y = ez
- c)z = ex
- d)z = ey
Correct answer is option 'A'. Can you explain this answer?
Cauchy’s linear differential equation 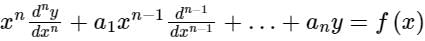 can be reduced to a linear differential equation with constant coefficient by using substitution
can be reduced to a linear differential equation with constant coefficient by using substitution
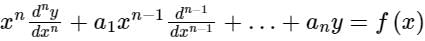 can be reduced to a linear differential equation with constant coefficient by using substitution
can be reduced to a linear differential equation with constant coefficient by using substitutiona)
x = ez
b)
y = ez
c)
z = ex
d)
z = ey

|
Gate Gurus answered |
Concept:
Any linear equation of the following form:
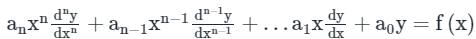 is considered as Cauchy’s differential equation. The equation has variable coefficients so its solution becomes tedious but we can convert the above equation into the linear differential equation with constant coefficients
is considered as Cauchy’s differential equation. The equation has variable coefficients so its solution becomes tedious but we can convert the above equation into the linear differential equation with constant coefficientsBy taking,
log x = z or x = ez
Proof:
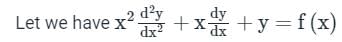
log x = z
Taking differentiation on both sides we get,
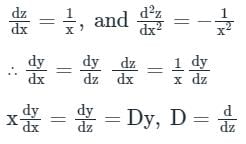
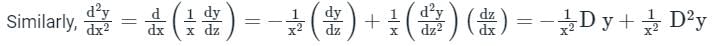

Now, it can be solved by finding C.F and P.I just like we solve linear differential equations with constant coefficients.
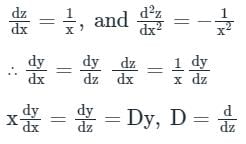
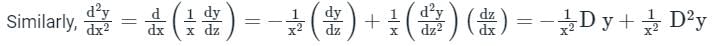

Now, it can be solved by finding C.F and P.I just like we solve linear differential equations with constant coefficients.
General solution of the Cauchy-Euler equation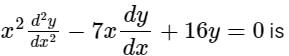
- a)y = c1x2 + c2x4
- b)y = c1x2 + c2x-4
- c)y = (c1 + c2 In x) x4
- d)y = c1x4 + c2x-4 In x
Correct answer is option 'C'. Can you explain this answer?
General solution of the Cauchy-Euler equation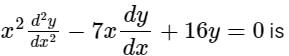
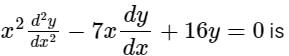
a)
y = c1x2 + c2x4
b)
y = c1x2 + c2x-4
c)
y = (c1 + c2 In x) x4
d)
y = c1x4 + c2x-4 In x

|
Gate Gurus answered |
Concept:
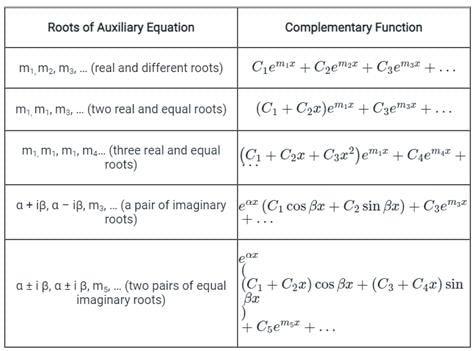
For different roots of the auxiliary equation, the solution (complementary function) of the differential equation is as shown below.
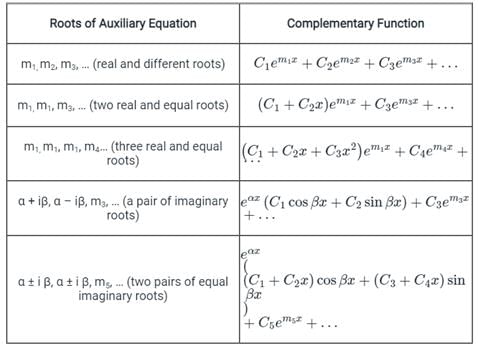
Calculation:

Calculation:
Given:

Put x = et

Put x = et
⇒ t = ln x
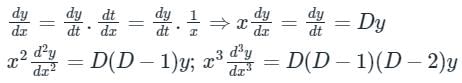
Now, the above differential equation becomes
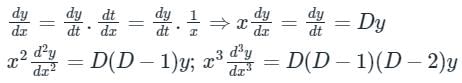
Now, the above differential equation becomes
D(D – 1)y – 7Dy + 16y = 0
⇒ D2y – Dy – 7Dy + 16y = 0
⇒ (D2 – 8D + 16)y = 0
Auxiliary equation:
(D2 – 8 D + 16) = 0
⇒ D = 4
The solutions for the above roots of auxiliary equations are:
y(t) = (c1 + c2 t) e4t
⇒ y(x) = (c1 + c2 ln x) x4
The Wronskian of the differential equation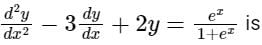
- a)ex
- b)-e3x
- c)e2x
- d)e5x
Correct answer is option 'B'. Can you explain this answer?
The Wronskian of the differential equation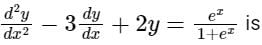
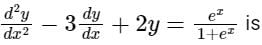
a)
ex
b)
-e3x
c)
e2x
d)
e5x
|
|
Sanya Agarwal answered |
If the given differential equation is in the form, y'' + py' + qy = x
Where, p, q, x are functions of x.
Then Wronskian is,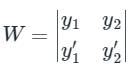
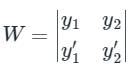
Here, y1 and y2 are the solutions of y'' + py' + qy = 0
Given differential equation is,
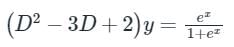
Auxiliary equation is,
D2 – 3D + 2 = 0
⇒ D = 1, 2
C.F. = c1 e2x + c2 ex
y1 = e2x, y2 = ex
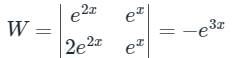
Consider the initial value problem below. The value of y at x = In 2, (rounded off to 3 decimal places) is dy/dx = 2x - y, y(0) = 1 (Important - Enter only the numerical value in the answer)
Correct answer is between '0.8774,0.8952'. Can you explain this answer?
Consider the initial value problem below. The value of y at x = In 2, (rounded off to 3 decimal places) is dy/dx = 2x - y, y(0) = 1 (Important - Enter only the numerical value in the answer)
|
|
Sanvi Kapoor answered |
Concept:
The standard form of a first-order linear differential equation is,
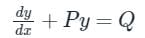
Where P and Q are the functions of x.
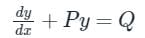
Where P and Q are the functions of x.
Integrating factor, IF = e∫Pdx
Now, the solution for the above differential equation is,
y(IF) = ∫IF.Qdx
Calculation:
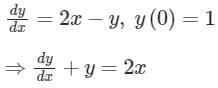
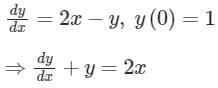
By comparing the above differential equation with the standard differential equation,
P = 1, Q = 2x
Integrating factor, IF = e∫Pdx = e∫1dx = ex
Now, the solution is
y(ex) = ∫ex(2x)dx
yex = 2(xex − ex) + C
⇒ y = 2(x − 1) + Ce−x
y(0) = 1
⇒ 1 = 2 (0 – 1) + C
⇒ C = 3
Now, the solution becomes
y = 2x – 2 + 3e-x
At x = ln 2,
y = 2 ln 2 – 2 + 3 (0.5) = 0.8862
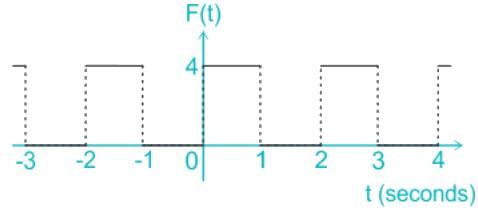
F(t) is a periodic square wave function as shown. It takes only two values, 4 and 0, and stays at each of these values for 1 second before changing. What is the constant term in the Fourier series expansion of F(t)?
- a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
F(t) is a periodic square wave function as shown. It takes only two values, 4 and 0, and stays at each of these values for 1 second before changing. What is the constant term in the Fourier series expansion of F(t)?


a)
1
b)
2
c)
3
d)
4

|
Pioneer Academy answered |
Concept:
Fourier Series is defined as
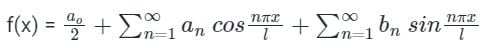

Calculation:
Given:
f(t) is an even periodic function, Since
f(-t) = f(t)
The constant term in the Fourier series is: ao/2
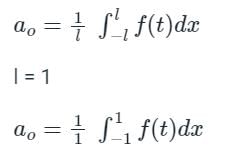
Since the function is not continious, we need to break the integral according to interval
from -1 to 0, f(t) = 0,
from 0 to 1, f(t) = 4
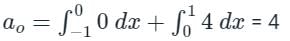
The constant term is:
a0/2 = 4/2 = 2
Mistake Points
Avoid using the integral property of even function because the given function f(t) is not continuous. Though the function given is an even periodic function but it is not continuous
Fourier Series is defined as
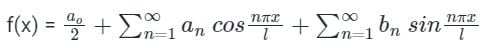

Calculation:
Given:
f(t) is an even periodic function, Since
f(-t) = f(t)
The constant term in the Fourier series is: ao/2
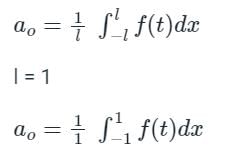
Since the function is not continious, we need to break the integral according to interval
from -1 to 0, f(t) = 0,
from 0 to 1, f(t) = 4
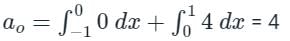
The constant term is:
a0/2 = 4/2 = 2
Mistake Points
Avoid using the integral property of even function because the given function f(t) is not continuous. Though the function given is an even periodic function but it is not continuous
The solution to the differential equation f’’(x)+4f’(x)+4f(x)=0 is - a)f1(x) = e-2x
- b)f1(x) = e2x, f2(x) = e-2x
- c)f1(x) = e-2x, f2(x) = xe-2x
- d)f1(x) = e-2x, f2(x) = e-x
Correct answer is option 'C'. Can you explain this answer?
The solution to the differential equation f’’(x)+4f’(x)+4f(x)=0 is
a)
f1(x) = e-2x
b)
f1(x) = e2x, f2(x) = e-2x
c)
f1(x) = e-2x, f2(x) = xe-2x
d)
f1(x) = e-2x, f2(x) = e-x
|
|
Anshu Patel answered |
Let y(x) = emx (m ≠ 0)be the trial soln .Auxiliary equation. m2 + 4m+ 4 = 0 ⇒(m+ 2)2 = 0
In particular, when A =1,B =1,then f(x) = (1 + x)e−2x
= e−2x + xe−2x
Solve: (x2D2 - 4xD + 6)y = x2
where D = d/dx - a)y = c1 x2 + c2 x2 - x2 logx2
- b)y = c1 x2 + c2 x3 - xlogx2
- c)y = c1 x2 + c2 x3 - x2logx2
- d)y = c1 x2 + c2 x2 - x logx2
Correct answer is option 'C'. Can you explain this answer?
Solve: (x2D2 - 4xD + 6)y = x2
where D = d/dx
where D = d/dx
a)
y = c1 x2 + c2 x2 - x2 logx2
b)
y = c1 x2 + c2 x3 - xlogx2
c)
y = c1 x2 + c2 x3 - x2logx2
d)
y = c1 x2 + c2 x2 - x logx2

|
Raghavendra Dasgupta answered |
To solve the given differential equation, we substitute the value of D in terms of d/dx and rearrange the equation to isolate y.
Given: (x^2D^2 - 4xD + 6)y = x^2
We are given that D = d/dx, so substituting this in the equation, we get:
(x^2(d/dx)^2 - 4x(d/dx) + 6)y = x^2
Simplifying the equation further, we have:
(x^2(d^2y/dx^2) - 4x(dy/dx) + 6)y = x^2
Expanding the equation, we get:
x^2(d^2y/dx^2)y - 4x(dy/dx)y + 6y = x^2
Rearranging the terms, we have:
x^2(d^2y/dx^2)y - 4x(dy/dx)y + (6y - x^2) = 0
Now, we can see that this is a homogeneous linear differential equation. So, let's assume y = x^m and substitute it in the equation.
(x^2d^2/dx^2)(x^m) - 4(xd/dx)(x^m) + (6x^m - x^2) = 0
Differentiating y = x^m twice, we get:
m(m-1)x^m-2 - 4m(x^m-1) + (6x^m - x^2) = 0
Expanding and combining like terms, we have:
m(m-1)x^m-2 - 4mx^m-1 + 6x^m - x^2 = 0
Now, let's divide the entire equation by x^m-2 to simplify further:
m(m-1) - 4mx + 6x^2/x^m-2 - x^2/x^m-2 = 0
Simplifying, we have:
m(m-1) - 4mx + 6x^2/x^2 - x^2/x^2 = 0
m(m-1) - 4mx + 6x^2 - x^2 = 0
m^2 - m - 4mx + 5x^2 = 0
Now, we can equate the coefficients of the like powers of x to get the values of m:
m^2 - m = 0 (coefficient of x^0)
-4m + 5 = 0 (coefficient of x^2)
Solving these equations, we get:
m = 0 or m = 1
m = 5/4
Therefore, the general solution to the differential equation is:
y = c1x^0 + c2x^1 + c3x^(5/4)
Simplifying further, we have:
y = c1 + c2x + c3x^(5/4)
This matches with the option C, which states that y = c1x^2 + c2x^3 - x^2log(x^2).
Hence, the correct answer is option C.
Given: (x^2D^2 - 4xD + 6)y = x^2
We are given that D = d/dx, so substituting this in the equation, we get:
(x^2(d/dx)^2 - 4x(d/dx) + 6)y = x^2
Simplifying the equation further, we have:
(x^2(d^2y/dx^2) - 4x(dy/dx) + 6)y = x^2
Expanding the equation, we get:
x^2(d^2y/dx^2)y - 4x(dy/dx)y + 6y = x^2
Rearranging the terms, we have:
x^2(d^2y/dx^2)y - 4x(dy/dx)y + (6y - x^2) = 0
Now, we can see that this is a homogeneous linear differential equation. So, let's assume y = x^m and substitute it in the equation.
(x^2d^2/dx^2)(x^m) - 4(xd/dx)(x^m) + (6x^m - x^2) = 0
Differentiating y = x^m twice, we get:
m(m-1)x^m-2 - 4m(x^m-1) + (6x^m - x^2) = 0
Expanding and combining like terms, we have:
m(m-1)x^m-2 - 4mx^m-1 + 6x^m - x^2 = 0
Now, let's divide the entire equation by x^m-2 to simplify further:
m(m-1) - 4mx + 6x^2/x^m-2 - x^2/x^m-2 = 0
Simplifying, we have:
m(m-1) - 4mx + 6x^2/x^2 - x^2/x^2 = 0
m(m-1) - 4mx + 6x^2 - x^2 = 0
m^2 - m - 4mx + 5x^2 = 0
Now, we can equate the coefficients of the like powers of x to get the values of m:
m^2 - m = 0 (coefficient of x^0)
-4m + 5 = 0 (coefficient of x^2)
Solving these equations, we get:
m = 0 or m = 1
m = 5/4
Therefore, the general solution to the differential equation is:
y = c1x^0 + c2x^1 + c3x^(5/4)
Simplifying further, we have:
y = c1 + c2x + c3x^(5/4)
This matches with the option C, which states that y = c1x^2 + c2x^3 - x^2log(x^2).
Hence, the correct answer is option C.
What is the complete solution for the equation x (y - z) p + y (z - x) q = z (x - y)?- a)ϕ (x + y + z, xyz) = 0
- b)ϕ (x + 2y + z, xz) = 0
- c)ϕ (2x + y + z, xyz) = 0
- d)ϕ (x + y + z, xy) = 0
Correct answer is option 'A'. Can you explain this answer?
What is the complete solution for the equation x (y - z) p + y (z - x) q = z (x - y)?
a)
ϕ (x + y + z, xyz) = 0
b)
ϕ (x + 2y + z, xz) = 0
c)
ϕ (2x + y + z, xyz) = 0
d)
ϕ (x + y + z, xy) = 0

|
Nilesh Kapoor answered |
To solve the equation x(y - z)p y(z - x)q = z(x - y), we need to simplify the equation and find the values of x, y, and z that satisfy the equation.
Given equation: x(y - z)p y(z - x)q = z(x - y)
Simplifying the equation:
xy^2p - xz^2p + y^2zq - yx^2q = zx - zy
xy^2p - xz^2p + y^2zq - yx^2q - zx + zy = 0
Now let's break down the options and see which one satisfies the equation:
a) (x y z, xyz) = 0
This option suggests that the values of x, y, and z multiplied together should be equal to zero. However, this condition does not ensure that the given equation is satisfied. Therefore, option 'A' is not the correct solution.
b) (x 2y z, xz) = 0
This option suggests that the values of x and z multiplied together should be equal to zero. Again, this condition does not guarantee that the equation is satisfied. Therefore, option 'B' is not the correct solution.
c) (2x y z, xyz) = 0
This option suggests that the values of 2x, y, and z multiplied together should be equal to zero. Similar to the previous options, this condition does not lead to the solution of the equation. Therefore, option 'C' is not the correct solution.
d) (x y z, xy) = 0
This option suggests that the values of x, y, and z multiplied by xy should be equal to zero. However, this condition does not satisfy the equation. Therefore, option 'D' is not the correct solution.
Therefore, the correct solution for the equation x(y - z)p y(z - x)q = z(x - y) is option 'A', which states that (x y z, xyz) = 0.
Given equation: x(y - z)p y(z - x)q = z(x - y)
Simplifying the equation:
xy^2p - xz^2p + y^2zq - yx^2q = zx - zy
xy^2p - xz^2p + y^2zq - yx^2q - zx + zy = 0
Now let's break down the options and see which one satisfies the equation:
a) (x y z, xyz) = 0
This option suggests that the values of x, y, and z multiplied together should be equal to zero. However, this condition does not ensure that the given equation is satisfied. Therefore, option 'A' is not the correct solution.
b) (x 2y z, xz) = 0
This option suggests that the values of x and z multiplied together should be equal to zero. Again, this condition does not guarantee that the equation is satisfied. Therefore, option 'B' is not the correct solution.
c) (2x y z, xyz) = 0
This option suggests that the values of 2x, y, and z multiplied together should be equal to zero. Similar to the previous options, this condition does not lead to the solution of the equation. Therefore, option 'C' is not the correct solution.
d) (x y z, xy) = 0
This option suggests that the values of x, y, and z multiplied by xy should be equal to zero. However, this condition does not satisfy the equation. Therefore, option 'D' is not the correct solution.
Therefore, the correct solution for the equation x(y - z)p y(z - x)q = z(x - y) is option 'A', which states that (x y z, xyz) = 0.
If we use the Fourier transform  to solve the partial differential equation
to solve the partial differential equation  in the half-plane {(x, y) : -∞ < x < ∞, 0 < y < ∞} the Fourier modes ϕk(y) depend on y as yα and yβ. The values of α and β are
in the half-plane {(x, y) : -∞ < x < ∞, 0 < y < ∞} the Fourier modes ϕk(y) depend on y as yα and yβ. The values of α and β are - a)

- b)

- c)

- d)
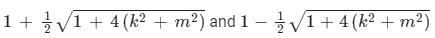
Correct answer is option 'C'. Can you explain this answer?
If we use the Fourier transform  to solve the partial differential equation
to solve the partial differential equation  in the half-plane {(x, y) : -∞ < x < ∞, 0 < y < ∞} the Fourier modes ϕk(y) depend on y as yα and yβ. The values of α and β are
in the half-plane {(x, y) : -∞ < x < ∞, 0 < y < ∞} the Fourier modes ϕk(y) depend on y as yα and yβ. The values of α and β are
 to solve the partial differential equation
to solve the partial differential equation  in the half-plane {(x, y) : -∞ < x < ∞, 0 < y < ∞} the Fourier modes ϕk(y) depend on y as yα and yβ. The values of α and β are
in the half-plane {(x, y) : -∞ < x < ∞, 0 < y < ∞} the Fourier modes ϕk(y) depend on y as yα and yβ. The values of α and β are a)

b)

c)

d)
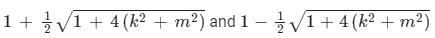

|
Pioneer Academy answered |
The Fourier transform, 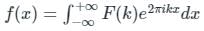
CALCULATION:
We have;
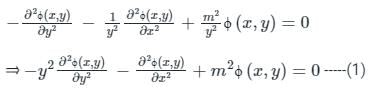
Now take the derivative of ϕ(x, y) we have;
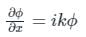
Again derivative we have;
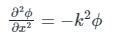
Now putting these values in equation 1) we have;
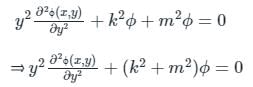
Now, by applying Cauchy's differential equation we have;
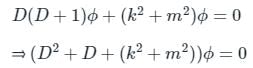
Again solving we have;
The roots are written as;
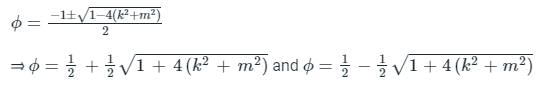
Hence option 3) is the correct answer.
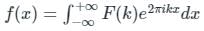
CALCULATION:
We have;
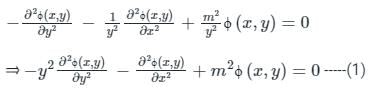
Now take the derivative of ϕ(x, y) we have;
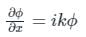
Again derivative we have;
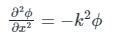
Now putting these values in equation 1) we have;
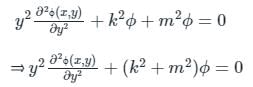
Now, by applying Cauchy's differential equation we have;
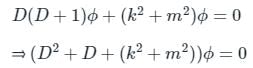
Again solving we have;
The roots are written as;
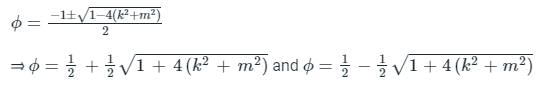
Hence option 3) is the correct answer.
The Fourier series expansion of x3 in the interval −1 ≤ x < 1 with periodic continuation has- a)only sine terms
- b)only cosine terms
- c)both sine and cosine terms
- d)only sine terms and a non-zero constant
Correct answer is option 'A'. Can you explain this answer?
The Fourier series expansion of x3 in the interval −1 ≤ x < 1 with periodic continuation has
a)
only sine terms
b)
only cosine terms
c)
both sine and cosine terms
d)
only sine terms and a non-zero constant
|
|
Sanya Agarwal answered |
f(x) = x3
find f(x) is even or odd
put x = -x
f(-x) = - x3
f(x) = -f(-x) hence it is odd function
for odd function, ao = an = 0
Fourier Series for odd function has only bn term
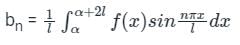
Hence only sine terms are left in Fourier expansion of x3
Additional Information
Fourier Series
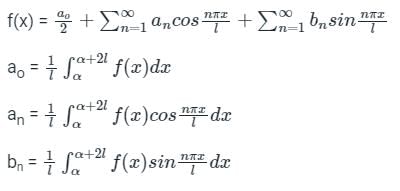
find f(x) is even or odd
put x = -x
f(-x) = - x3
f(x) = -f(-x) hence it is odd function
for odd function, ao = an = 0
Fourier Series for odd function has only bn term
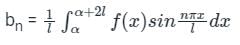
Hence only sine terms are left in Fourier expansion of x3
Additional Information
Fourier Series
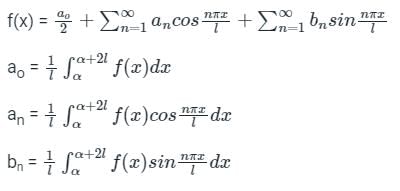
The solution of differential equation dx – (x + y + 1) dy = 0 is- a)(x + y + 2) ey = C
- b)(x – y - 2) ey = C
- c)(x + y + 2) e-y = C
- d)(x – y + 2) ey = C
Correct answer is option 'C'. Can you explain this answer?
The solution of differential equation dx – (x + y + 1) dy = 0 is
a)
(x + y + 2) ey = C
b)
(x – y - 2) ey = C
c)
(x + y + 2) e-y = C
d)
(x – y + 2) ey = C

|
Vertex Academy answered |
Given differential equation is,
dx – (x + y + 1) dy = 0
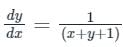
Put (x + y + 1) = t
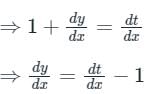
Now, the differential equation becomes
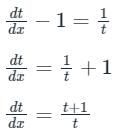
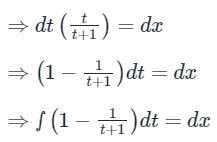
⇒ t - In (t + 1) = x + C1
⇒ (x + y + 1) – In (x + y + 2) = x + C1
⇒ y + 1 – C1 = In (x + y + 2)
⇒ In (x + y + 2) = y + k
⇒ (x + y + 2) = ey+k
⇒ (x + y + 2) e
= C
The solution of differential equation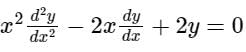 will be ___________, where c1 and c2 are arbitrary constants.
will be ___________, where c1 and c2 are arbitrary constants.- a)y = c1x + c2x2
- b)y = c1 log x + c2x
- c)y = c1 + c2x
- d)y = c1x2 + c2x3
Correct answer is option 'A'. Can you explain this answer?
The solution of differential equation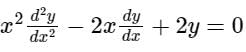 will be ___________, where c1 and c2 are arbitrary constants.
will be ___________, where c1 and c2 are arbitrary constants.
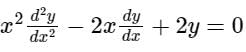 will be ___________, where c1 and c2 are arbitrary constants.
will be ___________, where c1 and c2 are arbitrary constants.a)
y = c1x + c2x2
b)
y = c1 log x + c2x
c)
y = c1 + c2x
d)
y = c1x2 + c2x3

|
Gate Gurus answered |
Concept:
Linear differential equations with variable coefficients can be reduced to linear differential equations with constant coefficients by suitable substitutions.
Euler Cauchy Homogeneous linear equation:
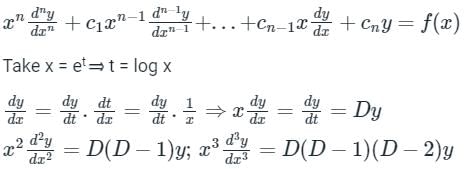
Calculation:
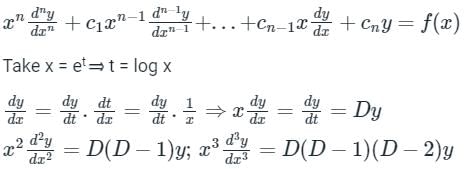
Calculation:
Given:
Euler Cauchy equation:
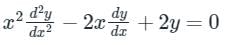
Now, the above differential equation becomes
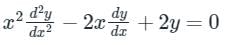
Now, the above differential equation becomes
D (D – 1) y – 2 D y + 2 y = 0
⇒ D2 y – D y – 2 D y + 2 y = 0
⇒ (D2 – 3 D + 2) y = 0
Auxiliary equation:
(D2 – 3 D + 2) = 0
⇒ (D - 2) (D - 1) = 0
⇒ D = 2, 1
Now the roots are real and different, and the general solution of given equation is
y = c1 e2t + c2 et
⇒ y = c1x + c2x2
Solve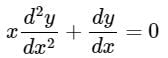 Which of the following is the solution of above equation, when x = 0?
Which of the following is the solution of above equation, when x = 0?- a)Can be any constant
- b)Undefined
- c)Zero
- d)1
Correct answer is option 'B'. Can you explain this answer?
Solve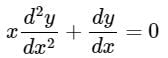
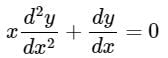
Which of the following is the solution of above equation, when x = 0?
a)
Can be any constant
b)
Undefined
c)
Zero
d)
1
|
|
Sanya Agarwal answered |
Concept:
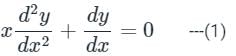
The given equation is multiplied with x to make it a equation of Cauchy Euler type.
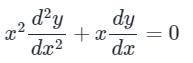
The given equation is of Cauchy Euler type. Cauchy Euler equation is homogenous linear equation with variable coefficient.
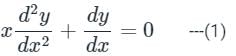
The given equation is multiplied with x to make it a equation of Cauchy Euler type.
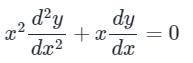
The given equation is of Cauchy Euler type. Cauchy Euler equation is homogenous linear equation with variable coefficient.
They can be reduced to linear equations with constant coefficients
Calculation:
Given:
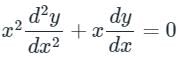
Put x = et
log x = t
The given equation is written as
[x2D2 + xD]y = 0 ---(1)
Put xD = D’, x2D2 = D’(D’ - 1)
[D’(D’ - 1) + D’]y = 0
D’2 y = 0
The auxiliary equation is D’2 = 0
The roots of this equation are 0, 0
C.F = (At + B) e0t
y = (At + B)
Put t = log x
y = A log x + B
At x = 0; y is undefined as log 0 is undefined.
Which of the following is an example of non-linear differential equation?- a)y = mx + c
- b)x + x’ = 0
- c)x + x2 = 0
- d)x” + 2x = 0
Correct answer is option 'C'. Can you explain this answer?
Which of the following is an example of non-linear differential equation?
a)
y = mx + c
b)
x + x’ = 0
c)
x + x2 = 0
d)
x” + 2x = 0
|
|
Sanya Agarwal answered |
For a differential equation to be linear the dependent variable should be of first degree. Since in equation x+x2=0, x2 is not a first power, it is not an example of linear differential equation.
What are the conditions called which are required for a signal to fulfil to be represented as Fourier series?- a)Dirichlet’s conditions
- b)Gibbs phenomenon
- c)Fourier conditions
- d)Fourier phenomenon
Correct answer is option 'A'. Can you explain this answer?
What are the conditions called which are required for a signal to fulfil to be represented as Fourier series?
a)
Dirichlet’s conditions
b)
Gibbs phenomenon
c)
Fourier conditions
d)
Fourier phenomenon
|
|
Sanya Agarwal answered |
When the Dirichlet’s conditions are satisfied, then only for a signal, the fourier series exist. Fourier series is of two types- trigonometric series and exponential series.
Singular solution of a differential equation is one that cannot be obtained from the general solution gotten by the usual method of solving the differential equation.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
Singular solution of a differential equation is one that cannot be obtained from the general solution gotten by the usual method of solving the differential equation.
a)
True
b)
False
|
|
Sanya Agarwal answered |
A differential equation is said to have a singular solution if in all points in the domain of the equation the uniqueness of the solution is violated. Hence, this solution cannot be obtained from the general solution.
The solution of the differential equation (dy/dx) = ky, y(0) = c is- a)x = ce-ky
- b)x = kecy
- c)y = cekx
- d)y = ce-kx
Correct answer is option 'C'. Can you explain this answer?
The solution of the differential equation (dy/dx) = ky, y(0) = c is
a)
x = ce-ky
b)
x = kecy
c)
y = cekx
d)
y = ce-kx

|
Alok Iyer answered |
Solution:
The given differential equation is
(dy/dx) = ky
To solve this differential equation, we can separate the variables by moving all terms involving y to one side and all terms involving x to the other side:
(dy/y) = k(dx)
Next, we can integrate both sides of the equation. The integral of (dy/y) is ln|y|, and the integral of k(dx) is kx + C, where C is the constant of integration:
ln|y| = kx + C
To eliminate the absolute value, we can exponentiate both sides of the equation:
e^(ln|y|) = e^(kx + C)
This simplifies to:
|y| = e^(kx) * e^C
Since e^C is a constant, we can replace it with another constant, let's say A:
|y| = Ae^(kx)
Now, we can consider two cases for the absolute value:
Case 1: y > 0
In this case, the absolute value can be removed:
y = Ae^(kx)
Case 2: y < />
In this case, the absolute value becomes a negative sign:
-y = Ae^(kx)
Multiplying both sides by -1, we get:
y = -Ae^(kx)
Combining both cases, we can write the solution as:
y = Ce^(kx)
where C = A if y > 0, and C = -A if y < />
Given that y(0) = c, we can substitute this initial condition into the solution:
c = Ce^(k*0)
Since e^0 = 1, this simplifies to:
c = C
Therefore, the constant C is equal to c. Substituting this back into the solution, we get:
y = ce^(kx)
Hence, the correct solution to the given differential equation is option 'C': y = ce^(kx).
The given differential equation is
(dy/dx) = ky
To solve this differential equation, we can separate the variables by moving all terms involving y to one side and all terms involving x to the other side:
(dy/y) = k(dx)
Next, we can integrate both sides of the equation. The integral of (dy/y) is ln|y|, and the integral of k(dx) is kx + C, where C is the constant of integration:
ln|y| = kx + C
To eliminate the absolute value, we can exponentiate both sides of the equation:
e^(ln|y|) = e^(kx + C)
This simplifies to:
|y| = e^(kx) * e^C
Since e^C is a constant, we can replace it with another constant, let's say A:
|y| = Ae^(kx)
Now, we can consider two cases for the absolute value:
Case 1: y > 0
In this case, the absolute value can be removed:
y = Ae^(kx)
Case 2: y < />
In this case, the absolute value becomes a negative sign:
-y = Ae^(kx)
Multiplying both sides by -1, we get:
y = -Ae^(kx)
Combining both cases, we can write the solution as:
y = Ce^(kx)
where C = A if y > 0, and C = -A if y < />
Given that y(0) = c, we can substitute this initial condition into the solution:
c = Ce^(k*0)
Since e^0 = 1, this simplifies to:
c = C
Therefore, the constant C is equal to c. Substituting this back into the solution, we get:
y = ce^(kx)
Hence, the correct solution to the given differential equation is option 'C': y = ce^(kx).
Chapter doubts & questions for Differential Equations - Engineering Mathematics 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Differential Equations - Engineering Mathematics in English & Hindi are available as part of Civil Engineering (CE) exam.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Engineering Mathematics
65 videos|122 docs|94 tests
|
Signup to see your scores go up within 7 days!
Study with 1000+ FREE Docs, Videos & Tests
10M+ students study on EduRev

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup