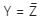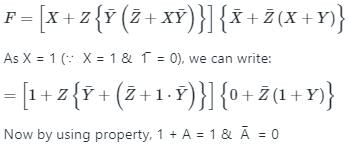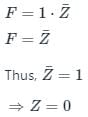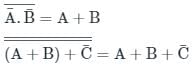All Exams >
Electronics and Communication Engineering (ECE) >
Digital Circuits >
All Questions
All questions of Boolean Algebra for Electronics and Communication Engineering (ECE) Exam
If the Boolean expression P̅Q + QR + PR is minimized, the expression becomes:- a)P̅Q + QR
- b)P̅Q + PR
- c)QR + PR
- d)P̅Q + QR + PR
Correct answer is option 'B'. Can you explain this answer?
If the Boolean expression P̅Q + QR + PR is minimized, the expression becomes:
a)
P̅Q + QR
b)
P̅Q + PR
c)
QR + PR
d)
P̅Q + QR + PR
|
|
Sudhir Patel answered |
Concept:
Consensus Law is one of the most powerful theorems used in digital electronics for the minimization of Boolean function or equation either in the successive reduction method or in the K-Map method.
Statement:
Consensus Law is one of the most powerful theorems used in digital electronics for the minimization of Boolean function or equation either in the successive reduction method or in the K-Map method.
Statement:
- The consensus theorem states that the consensus term of a disjunction is defined when the terms in function are reciprocals to each other (such as A and A̅).
- The consensus theorem is defined in two statements (normal form and it's dual). They are
- AB + ĀC+BC = AB+ĀC
- (A+B)(Ā+C)(B+C) = (A+B)( Ā+C)
Calculation:
Y = P̅Q + QR + PR
Y = P̅Q + PR + QR (P̅ + P)
Y = P̅Q + PR + QRP̅ + QRP
Y = P̅Q(1 + R) + PR(1 + Q)
Y = P̅Q + PR where (1 + A = 1) according to Boolean algebra.
Y = P̅Q + QR + PR
Y = P̅Q + PR + QR (P̅ + P)
Y = P̅Q + PR + QRP̅ + QRP
Y = P̅Q(1 + R) + PR(1 + Q)
Y = P̅Q + PR where (1 + A = 1) according to Boolean algebra.
Given below are two statements:
Statement I: A two-input OR gate and a two-input AND gate have similar inputs. but outputs may be the same or different.
Statement II: An AND gate has inputs A and B. The input B is always low, the state of input A can affect the output.
In the light of the above statements, choose the correct answer from the options given below:- a)Both Statement I and Statement II are true.
- b)Both Statement I and Statement II are false.
- c)Statement I is true but Statement II is false.
- d)Statement I is false but Statement II is true.
Correct answer is option 'B'. Can you explain this answer?
Given below are two statements:
Statement I: A two-input OR gate and a two-input AND gate have similar inputs. but outputs may be the same or different.
Statement II: An AND gate has inputs A and B. The input B is always low, the state of input A can affect the output.
In the light of the above statements, choose the correct answer from the options given below:
Statement I: A two-input OR gate and a two-input AND gate have similar inputs. but outputs may be the same or different.
Statement II: An AND gate has inputs A and B. The input B is always low, the state of input A can affect the output.
In the light of the above statements, choose the correct answer from the options given below:
a)
Both Statement I and Statement II are true.
b)
Both Statement I and Statement II are false.
c)
Statement I is true but Statement II is false.
d)
Statement I is false but Statement II is true.

|
Amit Kumar answered |
It's answer is wrong
answer will be C
answer will be C
Simplify the following expression.
Y = AB + A(B + C) + B(B + C)- a)Y = A + B + C
- b)Y = B + AC
- c)Y = A + BC
- d)Y = AB + C
Correct answer is option 'B'. Can you explain this answer?
Simplify the following expression.
Y = AB + A(B + C) + B(B + C)
Y = AB + A(B + C) + B(B + C)
a)
Y = A + B + C
b)
Y = B + AC
c)
Y = A + BC
d)
Y = AB + C

|
EduRev GATE answered |
Analysis:
Y = AB + A(B + C) + B(B + C)
= AB + AB + AC + B + BC
Since AB + AB = AB, we get:
Y = AB + AC + B (1 + C)
Since 1 + X (any variable) = X, we get:
Y = AB + AC + B
Y = B(1 + A) + AC
Y = B + AC
Y = AB + A(B + C) + B(B + C)
= AB + AB + AC + B + BC
Since AB + AB = AB, we get:
Y = AB + AC + B (1 + C)
Since 1 + X (any variable) = X, we get:
Y = AB + AC + B
Y = B(1 + A) + AC
Y = B + AC
DeMorgan’s theorem states that _________- a)(AB)’ = A’ + B’
- b)(A + B)’ = A’ * B
- c)A’ + B’ = A’B’
- d)(AB)’ = A’ + B
Correct answer is option 'A'. Can you explain this answer?
DeMorgan’s theorem states that _________
a)
(AB)’ = A’ + B’
b)
(A + B)’ = A’ * B
c)
A’ + B’ = A’B’
d)
(AB)’ = A’ + B
|
|
Nayanika Deshpande answered |
DeMorgan's laws are a set of rules that relate the logical operators "not", "and", and "or". These laws provide a way to simplify logical expressions and determine the relationship between negations of logical statements.
DeMorgan's first law states that the negation of a conjunction (logical "and") is equivalent to the disjunction (logical "or") of the negations of the individual statements. In other words:
¬(A ∧ B) = ¬A ∨ ¬B
This means that if the statement "A and B" is false, then either "A" is false or "B" is false (or both).
DeMorgan's second law states that the negation of a disjunction (logical "or") is equivalent to the conjunction (logical "and") of the negations of the individual statements. In other words:
¬(A ∨ B) = ¬A ∧ ¬B
This means that if the statement "A or B" is false, then both "A" and "B" must be false.
These laws can be used to simplify logical expressions by applying the negations to individual statements and converting between conjunctions and disjunctions. They are particularly useful when working with complex logical expressions or when proving logical equivalences.
DeMorgan's first law states that the negation of a conjunction (logical "and") is equivalent to the disjunction (logical "or") of the negations of the individual statements. In other words:
¬(A ∧ B) = ¬A ∨ ¬B
This means that if the statement "A and B" is false, then either "A" is false or "B" is false (or both).
DeMorgan's second law states that the negation of a disjunction (logical "or") is equivalent to the conjunction (logical "and") of the negations of the individual statements. In other words:
¬(A ∨ B) = ¬A ∧ ¬B
This means that if the statement "A or B" is false, then both "A" and "B" must be false.
These laws can be used to simplify logical expressions by applying the negations to individual statements and converting between conjunctions and disjunctions. They are particularly useful when working with complex logical expressions or when proving logical equivalences.
Simplify Y = AB’ + (A’ + B)C.- a)AB’ + C
- b)AB + AC
- c)A’B + AC’
- d)AB + A
Correct answer is option 'A'. Can you explain this answer?
Simplify Y = AB’ + (A’ + B)C.
a)
AB’ + C
b)
AB + AC
c)
A’B + AC’
d)
AB + A
|
|
Sudhir Patel answered |
Y = AB’ + (A’ + B)C = AB’ + (AB’)’C = (AB’ + C)( AB’ + AB’) = (AB’ + C).1 = (AB’ + C).
The minterm expansion of f (P, Q, R) = PQ + QR̅ + PR̅ is- a)m2 + m4 + m6 + m7
- b)m0 + m1 + m6 + m7
- c)m2 + m3 + m4 + m5
- d)m0 + m1 + m3 + m7
Correct answer is option 'A'. Can you explain this answer?
The minterm expansion of f (P, Q, R) = PQ + QR̅ + PR̅ is
a)
m2 + m4 + m6 + m7
b)
m0 + m1 + m6 + m7
c)
m2 + m3 + m4 + m5
d)
m0 + m1 + m3 + m7

|
EduRev GATE answered |
F(P, Q, R) = PQ + QR' + PR'
= PQ (R + R') + (P + P')QR' + P(Q + Q')R'
= PQR + PQR' + PQR' + P'QR' + PQR' + PQ'R'
= PQR + PQR' + P'QR' + PQ'R'
= m7 + m6 + m2 + m4
= m2 + m4 + m6 + m7
= PQ (R + R') + (P + P')QR' + P(Q + Q')R'
= PQR + PQR' + PQR' + P'QR' + PQR' + PQ'R'
= PQR + PQR' + P'QR' + PQ'R'
= m7 + m6 + m2 + m4
= m2 + m4 + m6 + m7
The minterm expansion of f (P, Q, R) = PQ + QR̅ + PR̅ is- a)m2 + m4 + m6 + m7
- b)m0 + m1 + m6 + m7
- c)m2 + m3 + m4 + m5
- d)m0 + m1 + m3 + m7
Correct answer is option 'A'. Can you explain this answer?
The minterm expansion of f (P, Q, R) = PQ + QR̅ + PR̅ is
a)
m2 + m4 + m6 + m7
b)
m0 + m1 + m6 + m7
c)
m2 + m3 + m4 + m5
d)
m0 + m1 + m3 + m7

|
Starcoders answered |
F(P, Q, R) = PQ + QR' + PR'
= PQ (R + R') + (P + P')QR' + P(Q + Q')R'
= PQR + PQR' + PQR' + P'QR' + PQR' + PQ'R'
= PQR + PQR' + P'QR' + PQ'R'
= m7 + m6 + m2 + m4
= m2 + m4 + m6 + m7
= PQ (R + R') + (P + P')QR' + P(Q + Q')R'
= PQR + PQR' + PQR' + P'QR' + PQR' + PQ'R'
= PQR + PQR' + P'QR' + PQ'R'
= m7 + m6 + m2 + m4
= m2 + m4 + m6 + m7
Select the Boolean function(s) equivalent to x + yz, where x, y, and z are Boolean variables, and + denotes logical OR operation.- a)x + z + xy
- b)(x + y)(x + z)
- c)x + xy + yz
- d)x + xz + xy
Correct answer is option 'B,C'. Can you explain this answer?
Select the Boolean function(s) equivalent to x + yz, where x, y, and z are Boolean variables, and + denotes logical OR operation.
a)
x + z + xy
b)
(x + y)(x + z)
c)
x + xy + yz
d)
x + xz + xy
|
|
Swati Saha answered |
Equivalent Boolean functions for x yz
To find the equivalent Boolean functions for the expression x yz, where x, y, and z are Boolean variables, we need to apply the rules of Boolean algebra. The expression x yz denotes the logical OR operation between x and yz.
Boolean Algebra Rules:
1. x + 0 = x (Identity Law)
2. x + 1 = 1 (Domination Law)
3. x + x' = 1 (Complement Law)
4. x + x = x (Idempotent Law)
5. x + y = y + x (Commutative Law)
6. x + (y + z) = (x + y) + z (Associative Law)
7. x + xy = x (Absorption Law)
8. x + x'y = x + y (Consensus Law)
Applying Boolean Algebra:
Given expression: x yz
We can break down the expression into two parts: x and yz. We need to find the equivalent Boolean functions for each part separately.
1. x:
- Since x is already a Boolean variable, the equivalent Boolean function for x is x itself.
2. yz:
- We can simplify yz using the distributive law: yz = (y + z)(y + z').
- Applying the identity law and the complement law, we can further simplify the expression:
yz = (y + z)(y + z') = yy + zy + yz + zz' = y + zy + yz + 0 = y + zy + yz.
Equivalent Boolean functions:
Using the above simplifications, we can express the given expression x yz as the sum of the equivalent Boolean functions for x and yz:
x yz = x + y + zy + yz.
Options:
The options given are:
a) x z xy
b) (x y)(x z)
c) x xy yz
d) x xz xy
Correct options:
From the above simplification, we can see that the equivalent Boolean functions for x yz are x + y + zy + yz.
Option B: (x y)(x z)
- This option is equivalent to xx + yx + xz + yz, which is not the same as x + y + zy + yz.
- Therefore, option B is not correct.
Option C: x xy yz
- This option is equivalent to x + xy + yz, which is the same as x + y + zy + yz.
- Therefore, option C is correct.
Therefore, the correct options are B and C.
To find the equivalent Boolean functions for the expression x yz, where x, y, and z are Boolean variables, we need to apply the rules of Boolean algebra. The expression x yz denotes the logical OR operation between x and yz.
Boolean Algebra Rules:
1. x + 0 = x (Identity Law)
2. x + 1 = 1 (Domination Law)
3. x + x' = 1 (Complement Law)
4. x + x = x (Idempotent Law)
5. x + y = y + x (Commutative Law)
6. x + (y + z) = (x + y) + z (Associative Law)
7. x + xy = x (Absorption Law)
8. x + x'y = x + y (Consensus Law)
Applying Boolean Algebra:
Given expression: x yz
We can break down the expression into two parts: x and yz. We need to find the equivalent Boolean functions for each part separately.
1. x:
- Since x is already a Boolean variable, the equivalent Boolean function for x is x itself.
2. yz:
- We can simplify yz using the distributive law: yz = (y + z)(y + z').
- Applying the identity law and the complement law, we can further simplify the expression:
yz = (y + z)(y + z') = yy + zy + yz + zz' = y + zy + yz + 0 = y + zy + yz.
Equivalent Boolean functions:
Using the above simplifications, we can express the given expression x yz as the sum of the equivalent Boolean functions for x and yz:
x yz = x + y + zy + yz.
Options:
The options given are:
a) x z xy
b) (x y)(x z)
c) x xy yz
d) x xz xy
Correct options:
From the above simplification, we can see that the equivalent Boolean functions for x yz are x + y + zy + yz.
Option B: (x y)(x z)
- This option is equivalent to xx + yx + xz + yz, which is not the same as x + y + zy + yz.
- Therefore, option B is not correct.
Option C: x xy yz
- This option is equivalent to x + xy + yz, which is the same as x + y + zy + yz.
- Therefore, option C is correct.
Therefore, the correct options are B and C.
A function (A, B, C) defined by three boolean variables A, B, and C when expressed as the sum of products is given by:
F = A̅.B̅.C̅ + A̅.B.C̅ + A.B̅.C̅
where, A̅, B̅, and C̅ are the complements of the respective variables. The product of sums (POS) form of the function F is- a)F = (A + B + C) . (A + B̅ + C) . (A̅ + B + C)
- b)F = (A̅ + B̅ + C̅) . (A̅ + B + C̅) + (A + B̅ + C̅)
- c)F = (A + B + C̅) . (A + B̅ + C̅) . (A̅ + B + C̅) . (A̅ + B̅ + C) . (A̅ + B̅ + C̅)
- d)F = (A̅ + B̅ + C) . (A̅ + B + C) . (A + B̅ + C) . (A + B + C̅) . (A + B + C)
Correct answer is option 'C'. Can you explain this answer?
A function (A, B, C) defined by three boolean variables A, B, and C when expressed as the sum of products is given by:
F = A̅.B̅.C̅ + A̅.B.C̅ + A.B̅.C̅
where, A̅, B̅, and C̅ are the complements of the respective variables. The product of sums (POS) form of the function F is
F = A̅.B̅.C̅ + A̅.B.C̅ + A.B̅.C̅
where, A̅, B̅, and C̅ are the complements of the respective variables. The product of sums (POS) form of the function F is
a)
F = (A + B + C) . (A + B̅ + C) . (A̅ + B + C)
b)
F = (A̅ + B̅ + C̅) . (A̅ + B + C̅) + (A + B̅ + C̅)
c)
F = (A + B + C̅) . (A + B̅ + C̅) . (A̅ + B + C̅) . (A̅ + B̅ + C) . (A̅ + B̅ + C̅)
d)
F = (A̅ + B̅ + C) . (A̅ + B + C) . (A + B̅ + C) . (A + B + C̅) . (A + B + C)
|
|
Qiana Iyer answered |
Explanation:
In the given question, the function F is defined by three boolean variables A, B, and C. The function is expressed as the sum of products, which means it is represented as a logical expression using the AND operator (.) and the OR operator (+).
The given expression is: F = A.B.C A.B.C A.B.C
To convert this expression into the product of sums (POS) form, we need to use the De Morgan's theorem and distribute the negation (complement) over the terms.
The De Morgan's theorem states that the complement of the product of terms is equal to the sum of the complements of the individual terms.
Conversion steps:
1. Apply De Morgan's theorem to the given expression to distribute the negation over the terms.
F = (A + B + C) . (A + B + C) . (A + B + C)
2. Simplify the expression by removing the redundant terms.
F = (A + B + C) . (A + B + C)
3. Apply the distributive property to expand the expression.
F = A.A + A.B + A.C + B.A + B.B + B.C + C.A + C.B + C.C
4. Simplify the expression by removing the redundant terms.
F = A + B + C
Therefore, the product of sums (POS) form of the function F is F = (A + B + C).
Answer:
The correct answer is option 'C': F = (A + B + C) . (A + B + C) . (A + B + C)
In the given question, the function F is defined by three boolean variables A, B, and C. The function is expressed as the sum of products, which means it is represented as a logical expression using the AND operator (.) and the OR operator (+).
The given expression is: F = A.B.C A.B.C A.B.C
To convert this expression into the product of sums (POS) form, we need to use the De Morgan's theorem and distribute the negation (complement) over the terms.
The De Morgan's theorem states that the complement of the product of terms is equal to the sum of the complements of the individual terms.
Conversion steps:
1. Apply De Morgan's theorem to the given expression to distribute the negation over the terms.
F = (A + B + C) . (A + B + C) . (A + B + C)
2. Simplify the expression by removing the redundant terms.
F = (A + B + C) . (A + B + C)
3. Apply the distributive property to expand the expression.
F = A.A + A.B + A.C + B.A + B.B + B.C + C.A + C.B + C.C
4. Simplify the expression by removing the redundant terms.
F = A + B + C
Therefore, the product of sums (POS) form of the function F is F = (A + B + C).
Answer:
The correct answer is option 'C': F = (A + B + C) . (A + B + C) . (A + B + C)
(A + B)(A’ * B’) = ?- a)1
- b)0
- c)AB
- d)AB’
Correct answer is option 'B'. Can you explain this answer?
(A + B)(A’ * B’) = ?
a)
1
b)
0
c)
AB
d)
AB’
|
|
Maitri Chakraborty answered |
Understanding the Expression
To solve the expression \((A + B)(A' * B')\), we need to break it down using Boolean algebra rules.
Definitions of Terms
- A': The complement of A (not A).
- B': The complement of B (not B).
- A + B: The logical OR operation between A and B.
- A' * B': The logical AND operation between the complements of A and B.
Breaking Down the Expression
1. First Component: \(A + B\)
- This component will evaluate to true (1) if either A or B (or both) are true.
2. Second Component: \(A' * B'\)
- This component will evaluate to true (1) only if both A and B are false (0).
Combining the Components
Now, we need to analyze the overall expression \((A + B)(A' * B')\):
- The expression will be true (1) if both components are true.
- However, for \(A' * B'\) to be true, both A and B must be 0, which means \(A + B\) will be false (0).
Conclusion
- Therefore, the expression \((A + B)(A' * B')\) can never be true because:
- If \(A + B = 1\), then \(A' * B' = 0\).
- If \(A + B = 0\), then \(A' * B' = 1\) is true.
Thus, the entire expression evaluates to 0.
Final Answer
The correct answer is option b) 0.
To solve the expression \((A + B)(A' * B')\), we need to break it down using Boolean algebra rules.
Definitions of Terms
- A': The complement of A (not A).
- B': The complement of B (not B).
- A + B: The logical OR operation between A and B.
- A' * B': The logical AND operation between the complements of A and B.
Breaking Down the Expression
1. First Component: \(A + B\)
- This component will evaluate to true (1) if either A or B (or both) are true.
2. Second Component: \(A' * B'\)
- This component will evaluate to true (1) only if both A and B are false (0).
Combining the Components
Now, we need to analyze the overall expression \((A + B)(A' * B')\):
- The expression will be true (1) if both components are true.
- However, for \(A' * B'\) to be true, both A and B must be 0, which means \(A + B\) will be false (0).
Conclusion
- Therefore, the expression \((A + B)(A' * B')\) can never be true because:
- If \(A + B = 1\), then \(A' * B' = 0\).
- If \(A + B = 0\), then \(A' * B' = 1\) is true.
Thus, the entire expression evaluates to 0.
Final Answer
The correct answer is option b) 0.
How many different Boolean functions of n variables are there?- a)n2n
- b)2n
- c)nn2
- d)22n
Correct answer is option 'D'. Can you explain this answer?
How many different Boolean functions of n variables are there?
a)
n2n
b)
2n
c)
nn2
d)
22n

|
Starcoders answered |
Any variable 'a' can have 2 value i.e, 0 or 1.
For 'n' variables there are 2n entries in the truth table.
And each output of any particular row in the truth table can be 0 or 1.
Hence, we have 22n different Boolean functions with n variables.
Let's understand with the help of an example -
Let's say there are 2 variables a, and b: n = 2
There are 22 entries in the truth table, and each entry can be 0 or 1
So, we have 222 = 16 different Boolean functions with 2 variables.
For 'n' variables there are 2n entries in the truth table.
And each output of any particular row in the truth table can be 0 or 1.
Hence, we have 22n different Boolean functions with n variables.
Let's understand with the help of an example -
Let's say there are 2 variables a, and b: n = 2
There are 22 entries in the truth table, and each entry can be 0 or 1
So, we have 222 = 16 different Boolean functions with 2 variables.
Identify the number of prime implicants and essential prime implicants for the function
f(A, B, C, D) = Σ m(0, 1, 4, 6, 7, 8, 10, 14, 15)
(where m represents min terms)- a)7, 2
- b)6, 2
- c)7, 1
- d)6, 1
Correct answer is option 'A'. Can you explain this answer?
Identify the number of prime implicants and essential prime implicants for the function
f(A, B, C, D) = Σ m(0, 1, 4, 6, 7, 8, 10, 14, 15)
(where m represents min terms)
f(A, B, C, D) = Σ m(0, 1, 4, 6, 7, 8, 10, 14, 15)
(where m represents min terms)
a)
7, 2
b)
6, 2
c)
7, 1
d)
6, 1
|
|
Megha Bajaj answered |
This function is missing, could you please provide the function?
In K-map reduction for 4-variables POS expression, the cell with address 0000 indicates:- a)ABCD
- b)A + B + C + D
- c)A̅B̅C̅D̅
- d)A̅ + B̅ + C̅ + D̅
Correct answer is option 'B'. Can you explain this answer?
In K-map reduction for 4-variables POS expression, the cell with address 0000 indicates:
a)
ABCD
b)
A + B + C + D
c)
A̅B̅C̅D̅
d)
A̅ + B̅ + C̅ + D̅
|
|
Inaya Reddy answered |
Explanation:
K-map Reduction for 4-variables POS Expression
- In K-map reduction for 4-variables POS expression, the cell with address 0000 represents the condition where none of the variables are present in the expression.
- Each cell in the K-map corresponds to a specific combination of input variables, where '1' represents the presence of the corresponding variable and '0' represents the absence of the variable.
- For a 4-variable K-map, the cells are arranged in a 2x2 grid where each cell corresponds to a unique combination of input variables.
- The cell with address 0000 indicates that none of the variables (A, B, C, D) are present in the expression, which simplifies to a constant '1' in the POS expression.
- Therefore, the correct interpretation of the cell with address 0000 in the K-map reduction for 4-variables POS expression is A + B + C + D, as all variables are absent in this case.
Conclusion
- Understanding the significance of each cell in the K-map is essential for simplifying Boolean expressions using the Karnaugh map method.
- The cell with address 0000 in a 4-variable K-map represents the condition where none of the variables are present in the expression, simplifying to A + B + C + D.
K-map Reduction for 4-variables POS Expression
- In K-map reduction for 4-variables POS expression, the cell with address 0000 represents the condition where none of the variables are present in the expression.
- Each cell in the K-map corresponds to a specific combination of input variables, where '1' represents the presence of the corresponding variable and '0' represents the absence of the variable.
- For a 4-variable K-map, the cells are arranged in a 2x2 grid where each cell corresponds to a unique combination of input variables.
- The cell with address 0000 indicates that none of the variables (A, B, C, D) are present in the expression, which simplifies to a constant '1' in the POS expression.
- Therefore, the correct interpretation of the cell with address 0000 in the K-map reduction for 4-variables POS expression is A + B + C + D, as all variables are absent in this case.
Conclusion
- Understanding the significance of each cell in the K-map is essential for simplifying Boolean expressions using the Karnaugh map method.
- The cell with address 0000 in a 4-variable K-map represents the condition where none of the variables are present in the expression, simplifying to A + B + C + D.
Logical expression (A+B) (A+C) is equal to- a)A + B + C
- b)A + B.C
- c)A.B + A.C
- d)A.B.C
Correct answer is option 'B'. Can you explain this answer?
Logical expression (A+B) (A+C) is equal to
a)
A + B + C
b)
A + B.C
c)
A.B + A.C
d)
A.B.C
|
|
Saanvi Joshi answered |
Explanation:
Given Expression: (A + B) (A + C)
Expanding the expression:
(A + B) (A + C) = A(A + C) + B(A + C)
= A.A + A.C + B.A + B.C
= A + AC + BA + BC
= A + AC + AB + BC
= A(1 + C) + B(C)
= A + AC + BC
Final Simplified Expression: A + B.C
Therefore, the logical expression (A + B) (A + C) is equal to A + B.C.
Given Expression: (A + B) (A + C)
Expanding the expression:
(A + B) (A + C) = A(A + C) + B(A + C)
= A.A + A.C + B.A + B.C
= A + AC + BA + BC
= A + AC + AB + BC
= A(1 + C) + B(C)
= A + AC + BC
Final Simplified Expression: A + B.C
Therefore, the logical expression (A + B) (A + C) is equal to A + B.C.
Given F1 = Π M (0, 4, 5, 6) and F2 = Π M (0, 3, 4, 6, 7). The maxterm expansion for F1F2 is given by:- a)Π M (3, 5, 7)
- b)Π M (1, 2)
- c)Π M (0, 3, 4, 5, 6, 7)
- d)Π M (0, 3, 5, 7)
Correct answer is option 'C'. Can you explain this answer?
Given F1 = Π M (0, 4, 5, 6) and F2 = Π M (0, 3, 4, 6, 7). The maxterm expansion for F1F2 is given by:
a)
Π M (3, 5, 7)
b)
Π M (1, 2)
c)
Π M (0, 3, 4, 5, 6, 7)
d)
Π M (0, 3, 5, 7)
|
|
Jiya Bhatia answered |
The question is incomplete as it does not provide any information about what F1 represents. Please provide more information or clarify the question.
The Boolean equation X = [(A + B̅) (B + C)] B can be simplified to- a)X = A̅B
- b)X = AB̅
- c)X = AB
- d)X = A̅ B̅
Correct answer is option 'C'. Can you explain this answer?
The Boolean equation X = [(A + B̅) (B + C)] B can be simplified to
a)
X = A̅B
b)
X = AB̅
c)
X = AB
d)
X = A̅ B̅
|
|
Sudhir Patel answered |
X = [(A + B̅) (B + C)] B
= (AB + AC + 0 + B̅C)B
= AB + ABC
= AB(1 + C)
= AB
= (AB + AC + 0 + B̅C)B
= AB + ABC
= AB(1 + C)
= AB
Consider a Boolean gate (D) where the output Y is related to the inputs A and B as, Y = A + B̅, where + denotes logical OR operation. The Boolean inputs ‘0’ and ‘1’ are also available separately. Using instances of only D gates and inputs ‘0’ and ‘1’, __________ (select the correct option(s)).- a)NAND logic can be implemented
- b)OR logic cannot be implemented
- c)NOR logic can be implemented
- d)AND logic cannot be implemented
Correct answer is option 'A,C'. Can you explain this answer?
Consider a Boolean gate (D) where the output Y is related to the inputs A and B as, Y = A + B̅, where + denotes logical OR operation. The Boolean inputs ‘0’ and ‘1’ are also available separately. Using instances of only D gates and inputs ‘0’ and ‘1’, __________ (select the correct option(s)).
a)
NAND logic can be implemented
b)
OR logic cannot be implemented
c)
NOR logic can be implemented
d)
AND logic cannot be implemented
|
|
Pritam Chavan answered |
A and B can take on two possible values each: 0 (False) or 1 (True).
When A=0 and B=0, Y=0 OR 0 = 0.
When A=0 and B=1, Y=0 OR 1 = 1.
When A=1 and B=0, Y=1 OR 0 = 1.
When A=1 and B=1, Y=1 OR 1 = 1.
Therefore, the output Y is always 1 (True) except when both inputs A and B are 0 (False).
When A=0 and B=0, Y=0 OR 0 = 0.
When A=0 and B=1, Y=0 OR 1 = 1.
When A=1 and B=0, Y=1 OR 0 = 1.
When A=1 and B=1, Y=1 OR 1 = 1.
Therefore, the output Y is always 1 (True) except when both inputs A and B are 0 (False).
The expression for Absorption law is given by _________- a)A + AB = A
- b)A + AB = B
- c)AB + AA’ = A
- d)A + B = B + A
Correct answer is option 'A'. Can you explain this answer?
The expression for Absorption law is given by _________
a)
A + AB = A
b)
A + AB = B
c)
AB + AA’ = A
d)
A + B = B + A
|
|
Sudhir Patel answered |
The expression for Absorption Law is given by: A+AB = A.
Proof: A + AB = A(1+B) = A (Since 1 + B = 1 as per 1’s Property).
Proof: A + AB = A(1+B) = A (Since 1 + B = 1 as per 1’s Property).
Simplify the following Boolean function in sum of minterm:
F(A, B, C, D) = Σ(0, 6, 8, 13, 14)
d (A, B, C, D) = Σ(2, 4, 10)
where, d stands for don't care condition- a)B̅D̅ + C̅D̅ + ABC̅D̅
- b)B̅D̅ + C̅D̅ + A̅BC̅D
- c)BD̅ + CD̅ + ABC̅
- d)B̅D̅ + CD̅ + ABC̅D
Correct answer is option 'D'. Can you explain this answer?
Simplify the following Boolean function in sum of minterm:
F(A, B, C, D) = Σ(0, 6, 8, 13, 14)
d (A, B, C, D) = Σ(2, 4, 10)
where, d stands for don't care condition
F(A, B, C, D) = Σ(0, 6, 8, 13, 14)
d (A, B, C, D) = Σ(2, 4, 10)
where, d stands for don't care condition
a)
B̅D̅ + C̅D̅ + ABC̅D̅
b)
B̅D̅ + C̅D̅ + A̅BC̅D
c)
BD̅ + CD̅ + ABC̅
d)
B̅D̅ + CD̅ + ABC̅D

|
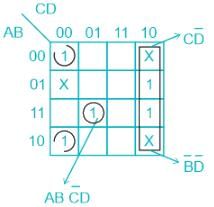
Imtiaz Ahmad answered |
- we are given the boolean function
- we need to simplify the function in the sum of minterms
- we will use the K-Map to simplify the function
- the K-Map is a very useful tool to simplify long boolean expressions into simplified form in a very systematic approach
From the K-Map we get
- F(A, B, C, D) = Σ(0, 6, 8, 13, 14)
- d (A, B, C, D) = Σ(2, 4, 10)
The output of logic circuit given below represents _______ gate.
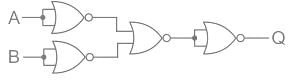
- a)OR
- b)NOR
- c)AND
- d)NAND
Correct answer is option 'D'. Can you explain this answer?
The output of logic circuit given below represents _______ gate.


a)
OR
b)
NOR
c)
AND
d)
NAND

|
EduRev GATE answered |
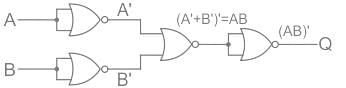
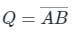
Output expression Q is equivalent to NAND gate.
Four statements are given below. Identify the correct statement.- a)XOR is universal gate
- b)XNOR is a basic gate
- c)XOR is derived gate
- d)XOR is a basic gate
Correct answer is option 'C'. Can you explain this answer?
Four statements are given below. Identify the correct statement.
a)
XOR is universal gate
b)
XNOR is a basic gate
c)
XOR is derived gate
d)
XOR is a basic gate
|
|
Sudhir Patel answered |
- AND, OR, NOT gates are the basic gates.
- The logic gates which are derived from the basic gates like AND, OR, NOT gates are known as derived gates. NAND, NOR, XOR, and XNOR are the derived gates.
- A universal gate is a gate which can implement any Boolean function without need to use any other gate type. The NAND and NOR gates are universal gates.
The Boolean expression AB + AC̅ + BC simplifies to- a)BC + AC̅
- b)AB + AC̅ + B
- c)AB + AC̅
- d)AB + BC
Correct answer is option 'A'. Can you explain this answer?
The Boolean expression AB + AC̅ + BC simplifies to
a)
BC + AC̅
b)
AB + AC̅ + B
c)
AB + AC̅
d)
AB + BC
|
|
Mayank Sen answered |
Explanation:
The given Boolean expression is AB • AC • BC.
To simplify this expression, we can use Boolean algebra rules and laws.
Distributive Law:
The Distributive Law states that AB + AC = A(B + C). Similarly, AB • AC = A • (B • C).
Using the Distributive Law:
AB • AC • BC = A • (B • C) • BC
Associative Law:
The Associative Law states that A • (B • C) = (A • B) • C.
Using the Associative Law:
A • (B • C) • BC = (A • B) • C • BC
Identity Law:
The Identity Law states that A • 1 = A and A + 0 = A.
Using the Identity Law:
(A • B) • C • BC = (A • B) • C • BC • 1
Commutative Law:
The Commutative Law states that AB = BA and A + B = B + A.
Using the Commutative Law:
(A • B) • C • BC • 1 = (A • B) • BC • C • 1
Identity Law:
Again, using the Identity Law, BC • C • 1 = BC.
Final Simplification:
Therefore, the simplified Boolean expression is (A • B) • BC.
Explanation of the Correct Answer:
The correct answer is option 'A' which is BC • AC. This is the correct simplification of the given Boolean expression AB • AC • BC.
The given Boolean expression is AB • AC • BC.
To simplify this expression, we can use Boolean algebra rules and laws.
Distributive Law:
The Distributive Law states that AB + AC = A(B + C). Similarly, AB • AC = A • (B • C).
Using the Distributive Law:
AB • AC • BC = A • (B • C) • BC
Associative Law:
The Associative Law states that A • (B • C) = (A • B) • C.
Using the Associative Law:
A • (B • C) • BC = (A • B) • C • BC
Identity Law:
The Identity Law states that A • 1 = A and A + 0 = A.
Using the Identity Law:
(A • B) • C • BC = (A • B) • C • BC • 1
Commutative Law:
The Commutative Law states that AB = BA and A + B = B + A.
Using the Commutative Law:
(A • B) • C • BC • 1 = (A • B) • BC • C • 1
Identity Law:
Again, using the Identity Law, BC • C • 1 = BC.
Final Simplification:
Therefore, the simplified Boolean expression is (A • B) • BC.
Explanation of the Correct Answer:
The correct answer is option 'A' which is BC • AC. This is the correct simplification of the given Boolean expression AB • AC • BC.
According to boolean law: A + 1 = ?- a)1
- b)A
- c)0
- d)A’
Correct answer is option 'A'. Can you explain this answer?
According to boolean law: A + 1 = ?
a)
1
b)
A
c)
0
d)
A’
|
|
Neha Kumar answered |
According to boolean law, A * 1 = A.
A = a1a0 and B = b1b0 are two 2-bit unsigned binary numbers. If F(a1, a0, b1, b0) is a Boolean function such that F = 1 only when A > B, and F = 0 otherwise, then F can be minimized to the form ______- a)a1b̅1 + a1a0b̅0
- b)a1b̅1 + a1a0b̅0 + a0b̅0b̅1
- c)a1a0b̅0 + a0b̅0b̅1
- d)a1b̅1 + a1a0b̅0 + a0b̅0b1
Correct answer is option 'B'. Can you explain this answer?
A = a1a0 and B = b1b0 are two 2-bit unsigned binary numbers. If F(a1, a0, b1, b0) is a Boolean function such that F = 1 only when A > B, and F = 0 otherwise, then F can be minimized to the form ______
a)
a1b̅1 + a1a0b̅0
b)
a1b̅1 + a1a0b̅0 + a0b̅0b̅1
c)
a1a0b̅0 + a0b̅0b̅1
d)
a1b̅1 + a1a0b̅0 + a0b̅0b1

|
Aniket Ghoshal answered |
Understanding the Problem
To determine when A (a1a0) is greater than B (b1b0), we need to analyze the possible values of these 2-bit unsigned binary numbers. The possible values range from 0 (00) to 3 (11).
Truth Table Creation
We'll construct a truth table to evaluate F(a1, a0, b1, b0):
| a1 | a0 | b1 | b0 | F (A > B) |
|----|----|----|----|-----------|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Minimization of F
From the truth table, we can summarize the conditions for F = 1:
- When A = 2 (A = 10) and B = 0, 1.
- When A = 3 (A = 11) and B = 0, 1, 2.
This can be represented as:
- a1b1 (A is greater than B when a1 is 1 and b1 is 0)
- a1a0b0 (A is greater than B when A has a0 = 1 and B has b0 = 0)
Thus, the minimized form of F is:
F = a1b1 + a1a0b0 + a0b0b1
Conclusion
The correct answer is option 'B': a1b1 + a1a0b0 + a0b0b1, which accurately represents the conditions under which A is greater than B.
To determine when A (a1a0) is greater than B (b1b0), we need to analyze the possible values of these 2-bit unsigned binary numbers. The possible values range from 0 (00) to 3 (11).
Truth Table Creation
We'll construct a truth table to evaluate F(a1, a0, b1, b0):
| a1 | a0 | b1 | b0 | F (A > B) |
|----|----|----|----|-----------|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Minimization of F
From the truth table, we can summarize the conditions for F = 1:
- When A = 2 (A = 10) and B = 0, 1.
- When A = 3 (A = 11) and B = 0, 1, 2.
This can be represented as:
- a1b1 (A is greater than B when a1 is 1 and b1 is 0)
- a1a0b0 (A is greater than B when A has a0 = 1 and B has b0 = 0)
Thus, the minimized form of F is:
F = a1b1 + a1a0b0 + a0b0b1
Conclusion
The correct answer is option 'B': a1b1 + a1a0b0 + a0b0b1, which accurately represents the conditions under which A is greater than B.
In Boolean algebra, (A.A̅) + A = ?- a)A
- b)0
- c)A̅
- d)1
Correct answer is option 'A'. Can you explain this answer?
In Boolean algebra, (A.A̅) + A = ?
a)
A
b)
0
c)
A̅
d)
1
|
|
Harshad Chakraborty answered |
Explanation:
- Boolean algebra is a branch of algebra in which variables are represented by binary values (0 or 1).
- Here, the variable A is multiplied with itself, which gives A.A = A2.
- Now, we need to multiply A2 with A, which gives A2.A = A.A.A = A3.
- Since the value of A can only be 0 or 1, A multiplied by itself or any other value will always be equal to A.
- Therefore, A.A = A and A3 = A.A.A = A.
- Hence, (A.A) A = A A = A2.A = A3 = A.
- Therefore, the correct answer is option 'A'.
A(A + B) = ?- a)AB
- b)1
- c)(1 + AB)
- d)A
Correct answer is option 'D'. Can you explain this answer?
A(A + B) = ?
a)
AB
b)
1
c)
(1 + AB)
d)
A
|
|
Sudhir Patel answered |
A(A + B) = AA + AB (By Distributive Property) = A + AB (A.A = A By Commutative Property) = A(1 + B) = A*1 (1 + B = 1 by 1’s Property) = A.
Complement of the expression A’B + CD’ is _________- a)(A’ + B)(C’ + D)
- b)(A + B’)(C’ + D)
- c)(A + B’)(C + D’)
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Complement of the expression A’B + CD’ is _________
a)
(A’ + B)(C’ + D)
b)
(A + B’)(C’ + D)
c)
(A + B’)(C + D’)
d)
None of these
|
|
Tanvi Chopra answered |
The complement of the expression A is the opposite of A. It is everything that is not included in A. In set theory, the complement of a set A is denoted by A'. For example, if A is the set of all even numbers less than 10, then A' is the set of all odd numbers less than 10. Similarly, if A is the set of all people who own a car, then A' is the set of all people who do not own a car.
Which one of the following gives the simplified sum of products expression for the Boolean function F = m0 + m2 + m3 + m5, where m0, m2, m3 and m5 are minterms corresponding to the inputs A, B and C and A as the MSB and C as the LSB?- a)
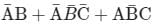
- b)
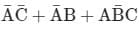
- c)
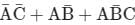
- d)
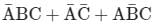
Correct answer is option 'B'. Can you explain this answer?
Which one of the following gives the simplified sum of products expression for the Boolean function F = m0 + m2 + m3 + m5, where m0, m2, m3 and m5 are minterms corresponding to the inputs A, B and C and A as the MSB and C as the LSB?
a)
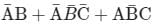
b)
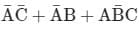
c)
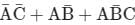
d)
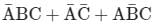

|
Abhijeet Kumar answered |
Why option 'a' is wrong?
The basic gates are:- a)AND, NOR and NOT gate
- b)AND, OR and NOT gate
- c)AND and NOT gate
- d)OR and NOT gate
Correct answer is option 'B'. Can you explain this answer?
The basic gates are:
a)
AND, NOR and NOT gate
b)
AND, OR and NOT gate
c)
AND and NOT gate
d)
OR and NOT gate
|
|
Sudhir Patel answered |
- AND, OR, NOT gates are the basic gates.
- The logic gates which are derived from the basic gates like AND, OR, NOT gates are known as derived gates. NAND, NOR, XOR, and XNOR are the derived gates.
- A universal gate is a gate which can implement any Boolean function without need to use any other gate type. The NAND and NOR gates are universal gates.
The Boolean expression 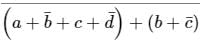 simplifies to
simplifies to- a)1
- b)
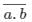
- c)a.b
- d)0
Correct answer is option 'D'. Can you explain this answer?
The Boolean expression 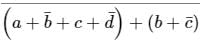 simplifies to
simplifies to
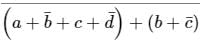 simplifies to
simplifies toa)
1
b)
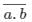
c)
a.b
d)
0

|
Imtiaz Ahmad answered |
De Morgan’s law states that:
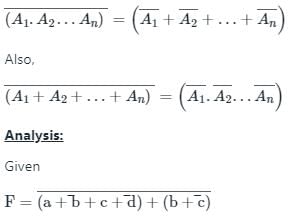
Applying the De-Morgans theorem in the above function F
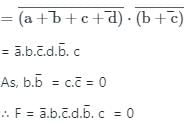
Hence option (4) is correct.
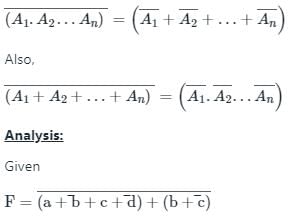
Applying the De-Morgans theorem in the above function F
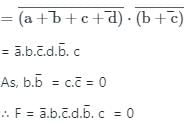
Hence option (4) is correct.
Simplification of the function 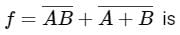
- a)AB
- b)A + B
- c)A̅ B̅
- d)
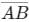
Correct answer is option 'D'. Can you explain this answer?
Simplification of the function 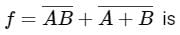
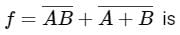
a)
AB
b)
A + B
c)
A̅ B̅
d)
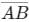
|
|
Sudhir Patel answered |
Concept:
De Morgan’s law states that:
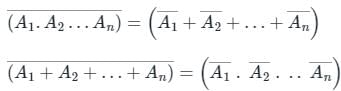
De Morgan’s law states that:
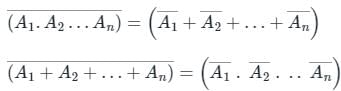
Application:
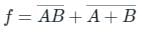
This can be written as:
f = A̅ + B̅ + A̅ B̅
f = A̅ (1 + B̅) + B̅
f = A̅ + B̅
Again using De-Morgan's property, we get:
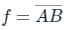
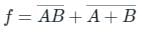
This can be written as:
f = A̅ + B̅ + A̅ B̅
f = A̅ (1 + B̅) + B̅
f = A̅ + B̅
Again using De-Morgan's property, we get:
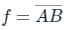
The expression for the truth table given below in POS form is given by:
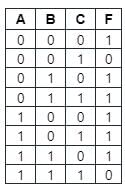
- a)AB'C + ABC'
- b)(A + B + C')(A' + B' + C')
- c)A'B'C + ABC
- d)(A + B' + C')(A' + B' + C')
Correct answer is option 'B'. Can you explain this answer?
The expression for the truth table given below in POS form is given by:


a)
AB'C + ABC'
b)
(A + B + C')(A' + B' + C')
c)
A'B'C + ABC
d)
(A + B' + C')(A' + B' + C')

|
Starcoders answered |
Minterm:
A minterm is a Boolean expression resulting in 1 for the output of a single cell, and 0s for all other cells in a Karnaugh map, or truth table.
0 is represented by A̅ or A'
1 is represented by A
Maxterm:
A maxterm is a Boolean expression resulting in a 0 for the output of a single cell expression, and 1s for all other cells in the Karnaugh map, or truth table.
0 is represented by A
1 is represented by A̅ or A'
Calculation:
The given Truth Table is:
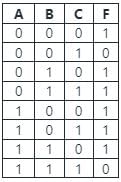
In POS form we consider only terms with 0 in output.
F = (A + B + C̅)(A̅ + B̅ + C̅)
Hence option (2) is the correct answer.
A minterm is a Boolean expression resulting in 1 for the output of a single cell, and 0s for all other cells in a Karnaugh map, or truth table.
0 is represented by A̅ or A'
1 is represented by A
Maxterm:
A maxterm is a Boolean expression resulting in a 0 for the output of a single cell expression, and 1s for all other cells in the Karnaugh map, or truth table.
0 is represented by A
1 is represented by A̅ or A'
Calculation:
The given Truth Table is:

In POS form we consider only terms with 0 in output.
F = (A + B + C̅)(A̅ + B̅ + C̅)
Hence option (2) is the correct answer.
The output Y of the logic circuit given below is:-
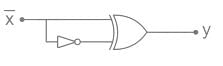
- a)1
- b)0
- c)X
- d)X̅
Correct answer is option 'A'. Can you explain this answer?
The output Y of the logic circuit given below is:-


a)
1
b)
0
c)
X
d)
X̅
|
|
Sudhir Patel answered |
XOR GATE
Symbol:
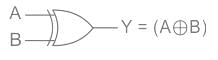
Truth Table:
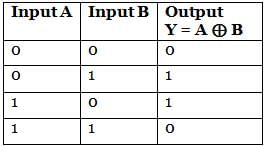
Symbol:

Truth Table:

Output Equation: 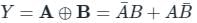
Key Points:
1) If B is always High, the output is the inverted value of the other input A, i.e. A̅.
1) The output is low when both the inputs are the same.
2) The output is high when both the inputs are different.
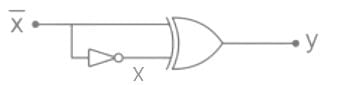
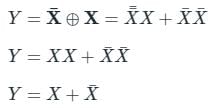
Y = 1
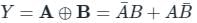
Key Points:
1) If B is always High, the output is the inverted value of the other input A, i.e. A̅.
1) The output is low when both the inputs are the same.
2) The output is high when both the inputs are different.

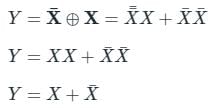
Y = 1
Which one of the following gives the simplified sum of products expression for the Boolean function F = m0 + m2 + m3 + m5, where m0, m2, m3 and m5 are minterms corresponding to the inputs A, B and C and A as the MSB and C as the LSB?- a)
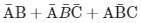
- b)
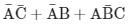
- c)
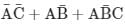
- d)
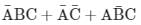
Correct answer is option 'B'. Can you explain this answer?
Which one of the following gives the simplified sum of products expression for the Boolean function F = m0 + m2 + m3 + m5, where m0, m2, m3 and m5 are minterms corresponding to the inputs A, B and C and A as the MSB and C as the LSB?
a)
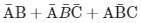
b)
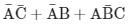
c)
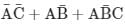
d)
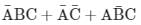

|
Starcoders answered |
F = ∑m (0, 2, 3, 5)
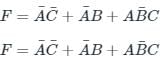

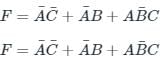
In Boolean algebra A + (B.C) = ?- a)A.(B + C)
- b)A.B + A.C
- c)A.B + C
- d)(A + B).(A + C)
Correct answer is option 'D'. Can you explain this answer?
In Boolean algebra A + (B.C) = ?
a)
A.(B + C)
b)
A.B + A.C
c)
A.B + C
d)
(A + B).(A + C)

|
Imtiaz Ahmad answered |
Logic: From the option we will find the question.
(A+B) (A+C) = A.A + A.C + B.A + B.C
Since A.A = A, the above expression becomes:
= A + A.C + A.B + B.C
= A(1 + C + B) + B.C
Since 1 + any variable = 1, the above expression becomes:
= A + B.C
(A+B) (A+C) = A + B.C
(A+B) (A+C) = A.A + A.C + B.A + B.C
Since A.A = A, the above expression becomes:
= A + A.C + A.B + B.C
= A(1 + C + B) + B.C
Since 1 + any variable = 1, the above expression becomes:
= A + B.C
(A+B) (A+C) = A + B.C
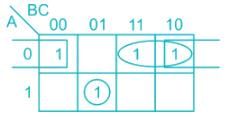
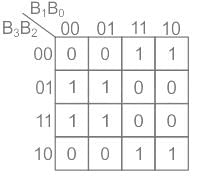
Write the simplified equation for the given K-Map.
- a)
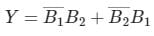
- b)
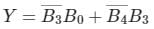
- c)
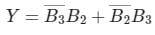
- d)
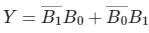
Correct answer is option 'A'. Can you explain this answer?
Write the simplified equation for the given K-Map.


a)
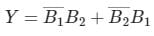
b)
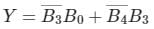
c)
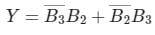
d)
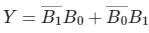
|
|
Sudhir Patel answered |
Concept:
K-map:
K-map:
- K-map (Karnaugh Map) is a pictorial method used to minimize Boolean expression without having to use Boolean Algebra theorems and equation manipulation.
- K-map can be thought of as a special version of a truth table.
- Using K-map, expression with two to four variables are easily minimized.
- K-maps are also referred to as 2D truth tables as each K-map is nothing but a different format of representing the values present in a one-dimensional truth table.
- To simplify a logic expression with two inputs, we require a K-map with 4 cells (= 22)
- Similarly, a logic expression with four inputs we require a K-map with 16 cells (= 24)
- Each cell within K-map has a definite place value which is obtained by using on encoding technique known as Gray code.
- For n-variable K-map, with 2n cells, try to group 2n cells first, then for 2n-1 cells, next for 2n-2 cells, and so on until the group contains only 2° cells ie. Isolated bits (if any)
- Also remember, the number of cells in a group must be equal to an integer power to 2 i.e. 1, 2, 4, 8, ...
Calculation:
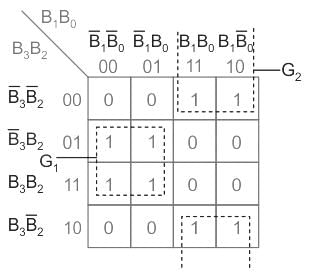
→ There are no 16 bits group, no 8-bits group, but there are 2-four bits group
→ Eliminate the variables for which the corresponding hit appears within the group as both 0 and 1.

→ There are no 16 bits group, no 8-bits group, but there are 2-four bits group
→ Eliminate the variables for which the corresponding hit appears within the group as both 0 and 1.
- Group 1 → B̅1 B2
- Group 2 → B1 B̅2
→ Therefore in SOP form (sum of products) output
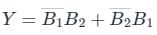
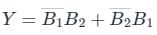
The simplified SOP (Sum of Product) form of the Boolean expression (P + Q̅ + R̅)⋅(P + Q̅ + R)⋅(P + Q + R̅) is- a)(P̅.Q + R̅)
- b)(P + Q̅.R̅)
- c)(P̅.Q + R)
- d)(P.Q + R)
Correct answer is option 'B'. Can you explain this answer?
The simplified SOP (Sum of Product) form of the Boolean expression (P + Q̅ + R̅)⋅(P + Q̅ + R)⋅(P + Q + R̅) is
a)
(P̅.Q + R̅)
b)
(P + Q̅.R̅)
c)
(P̅.Q + R)
d)
(P.Q + R)

|
Starcoders answered |
Some laws of Boolean Algebra:
Distributive Law:
Distributive Law:
- P +QR = (P + Q).(P + R)
- P(Q + R) = PQ + PR
Inverse Law:
- PP̅ =0
- P + P̅ =1
F = (P + Q̅ + R̅)⋅(P + Q̅ + R)⋅(P + Q + R̅)
F= ((P + Q̅) + R̅.R)(P + Q + R̅)
F = (P + Q̅)(P + Q + R̅)
F = P + Q̅.(Q + R̅)
F = P + Q̅R̅
F= ((P + Q̅) + R̅.R)(P + Q + R̅)
F = (P + Q̅)(P + Q + R̅)
F = P + Q̅.(Q + R̅)
F = P + Q̅R̅
The equivalence of given expression x + x'y with Boolean theorem is ____.- a)x
- b)x+y
- c)x'
- d)0
Correct answer is option 'B'. Can you explain this answer?
The equivalence of given expression x + x'y with Boolean theorem is ____.
a)
x
b)
x+y
c)
x'
d)
0

|
Starcoders answered |
To solve X+X'Y
Use X.1 = X,
= X.1 + X'Y
Use 1 + Y = 1
= X(1 + Y) + X'Y
= X + XY + X'Y
= X + Y(X + X')
Use X + X' = 1
= X + Y.1
Use Y.1 = Y
= X + Y
Hence answer is X+Y.
Use X.1 = X,
= X.1 + X'Y
Use 1 + Y = 1
= X(1 + Y) + X'Y
= X + XY + X'Y
= X + Y(X + X')
Use X + X' = 1
= X + Y.1
Use Y.1 = Y
= X + Y
Hence answer is X+Y.
The complement of the expression
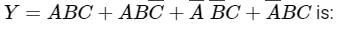
- a)
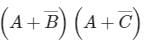
- b)
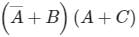
- c)
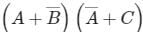
- d)
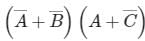
Correct answer is option 'D'. Can you explain this answer?
The complement of the expression
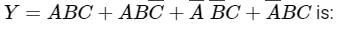
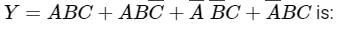
a)
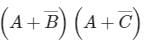
b)
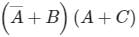
c)
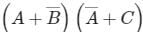
d)
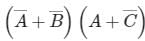
|
|
Sudhir Patel answered |
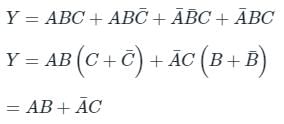
To find the complement of Y.
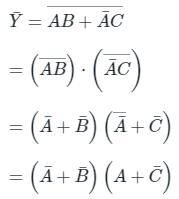
Which of the following expressions is in the Sum-Of-Products (SOP) form?- a)(A + B)(C + D)
- b)(A)-B (CD)
- c)AB (CD)
- d)AB + CD
Correct answer is option 'D'. Can you explain this answer?
Which of the following expressions is in the Sum-Of-Products (SOP) form?
a)
(A + B)(C + D)
b)
(A)-B (CD)
c)
AB (CD)
d)
AB + CD

|
Imtiaz Ahmad answered |
Sum of Product:
SOP is an abbreviation for Sum of Product. Sum of product form is a Boolean algebra statement in which distinct product terms of inputs are added together. This product is not an arithmetic multiply, but rather a Boolean logical AND, with the Sum being a Boolean logical OR.
SOP gives a minterm of a logical expression.
Example:
F= XY+YZ+ XZ
The above expression can be written like,
F= X.Y+Y.Z+ X.Z
F= (X) and (Y) or (Y) and (Z) or (X) and (Z)
In minterms X takes as '1' and X' takes 0 similarly same conventions follow for all variables.
XY= 110 (m6) and 111 (m7)
YZ= 011 (m3) and 111 (m7)
ZX= 101 (m5) and 111 (m7)
Min terms are, F= Σ(3,5,6,7)
Product of sum:
POS is an abbreviation for Product of Sum. Product of sum form is a Boolean algebra statement in which distinct product terms of inputs are multiplied together. This Sum is a Boolean logical OR, with the product being a Boolean logical AND.
POS gives a maxterm of a logical expression.
Example:
F= (X+Y). (Y+Z). (X+Z)
The above expression can be written like,
F= X+Y). (Y+Z). (X+Z)
F= (X) or (Y) and (Y) or (Z) and (X) or (Z)
In max terms X takes as '0' and X' takes '1' similarly same conventions follow for all variables.
X+Y= 000 (M0), 001 (M1)
Y+Z=000 (M0), 100 (M4)
Z+X=000 (M0), 010 (M2)
Max terms are, F= Σ(0, 1, 2,4)
Option 1:(A + B)(C + D)
False, It is in product of sum.
Option 2:(A)-B (CD)
False, It is not in POS and SOP.
Option 3: AB (CD)
False, It is not in POS and SOP.
Option 4: AB + CD
True, It is a correct form Sum of Product. It is Boolean logical AND, with the Sum being a Boolean logical OR.
Hence the correct answer is AB+CD.
SOP is an abbreviation for Sum of Product. Sum of product form is a Boolean algebra statement in which distinct product terms of inputs are added together. This product is not an arithmetic multiply, but rather a Boolean logical AND, with the Sum being a Boolean logical OR.
SOP gives a minterm of a logical expression.
Example:
F= XY+YZ+ XZ
The above expression can be written like,
F= X.Y+Y.Z+ X.Z
F= (X) and (Y) or (Y) and (Z) or (X) and (Z)
In minterms X takes as '1' and X' takes 0 similarly same conventions follow for all variables.
XY= 110 (m6) and 111 (m7)
YZ= 011 (m3) and 111 (m7)
ZX= 101 (m5) and 111 (m7)
Min terms are, F= Σ(3,5,6,7)
Product of sum:
POS is an abbreviation for Product of Sum. Product of sum form is a Boolean algebra statement in which distinct product terms of inputs are multiplied together. This Sum is a Boolean logical OR, with the product being a Boolean logical AND.
POS gives a maxterm of a logical expression.
Example:
F= (X+Y). (Y+Z). (X+Z)
The above expression can be written like,
F= X+Y). (Y+Z). (X+Z)
F= (X) or (Y) and (Y) or (Z) and (X) or (Z)
In max terms X takes as '0' and X' takes '1' similarly same conventions follow for all variables.
X+Y= 000 (M0), 001 (M1)
Y+Z=000 (M0), 100 (M4)
Z+X=000 (M0), 010 (M2)
Max terms are, F= Σ(0, 1, 2,4)
Option 1:(A + B)(C + D)
False, It is in product of sum.
Option 2:(A)-B (CD)
False, It is not in POS and SOP.
Option 3: AB (CD)
False, It is not in POS and SOP.
Option 4: AB + CD
True, It is a correct form Sum of Product. It is Boolean logical AND, with the Sum being a Boolean logical OR.
Hence the correct answer is AB+CD.
In boolean algebra, the OR operation is performed by which properties?- a)Associative properties
- b)Commutative properties
- c)Distributive properties
- d)All of the Mentioned
Correct answer is option 'D'. Can you explain this answer?
In boolean algebra, the OR operation is performed by which properties?
a)
Associative properties
b)
Commutative properties
c)
Distributive properties
d)
All of the Mentioned
|
|
Sudhir Patel answered |
The expression for Associative property is given by A+(B+C) = (A+B)+C & A*(B*C) = (A*B)*C.
The expression for Commutative property is given by A+B = B+A & A*B = B*A.
The expression for Distributive property is given by A+BC=(A+B)(A+C) & A(B+C) = AB+AC.
The expression for Commutative property is given by A+B = B+A & A*B = B*A.
The expression for Distributive property is given by A+BC=(A+B)(A+C) & A(B+C) = AB+AC.
In the following circuit determine the output F as sum of minterms
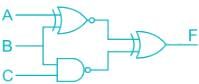
- a)∑ (2, 4, 6)
- b)∑ (0, 1, 6, 7)
- c)∑ (0, 1, 2, 4, 5, 6)
- d)∑ (2, 4, 5, 7)
Correct answer is option 'D'. Can you explain this answer?
In the following circuit determine the output F as sum of minterms


a)
∑ (2, 4, 6)
b)
∑ (0, 1, 6, 7)
c)
∑ (0, 1, 2, 4, 5, 6)
d)
∑ (2, 4, 5, 7)

|
Imtiaz Ahmad answered |
Canonical form: Any Boolean function that expressed as a sum of minterms or as a product of max terms is said to be in its canonical form.
There are two types of canonical forms:
SOP:
Sum of products or sum of minterms
In SOP (sum of product) form, a minterm is represented by 1.
Example of SOP: XY + X’Y’
POS:
Product of sums or product of max terms
In POS (product of sum) form, a maxterm is represented by 0.
Example of POS: (X+Y) (X’+Y’)
Calculation:
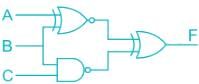
F(A, B, C) = ∑ (2, 4, 5, 7)
There are two types of canonical forms:
SOP:
Sum of products or sum of minterms
In SOP (sum of product) form, a minterm is represented by 1.
Example of SOP: XY + X’Y’
POS:
Product of sums or product of max terms
In POS (product of sum) form, a maxterm is represented by 0.
Example of POS: (X+Y) (X’+Y’)
Calculation:


F(A, B, C) = ∑ (2, 4, 5, 7)
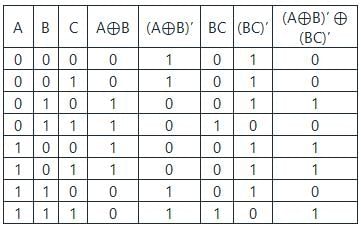
The Boolean SOP expression obtained from the truth table is:
- a)ABC'+A'BC
- b)AB'C+ABC'
- c)A'B'C+ABC'
- d)A'BC'+AB'C
Correct answer is option 'C'. Can you explain this answer?
The Boolean SOP expression obtained from the truth table is:


a)
ABC'+A'BC
b)
AB'C+ABC'
c)
A'B'C+ABC'
d)
A'BC'+AB'C

|
Starcoders answered |
We can minimize the Boolean expression/truth table of ‘n’ variable using a K-map in which 2n cells are present.
Steps to solve expression using K-map:
Steps to solve expression using K-map:
- Select the K-map according to the number of variables (Cells = 2n)
- Identify maxterm or minterm as given as per the problem.
- For SOP, put 1’s in blocks of K-map respective to the minterms.
- For POS, put 0’s in blocks of K-map respective to the max terms.
- To minimize, make rectangular groups containing total terms in power of two (like 1, 2, 4, 8..).
- From the groups made in step-5, find the product terms & add them for SOP form.
Calculation:
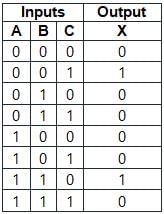
The truth table given is:
The 3 – variable K-map corresponding to the given truth table is drawn with 23 = 8 (cells) as shown:
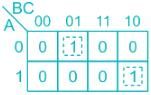
By making a group of 1’s,
Output (X) = A̅ B̅ C + A B C̅
The truth table given is:

The 3 – variable K-map corresponding to the given truth table is drawn with 23 = 8 (cells) as shown:

By making a group of 1’s,
Output (X) = A̅ B̅ C + A B C̅
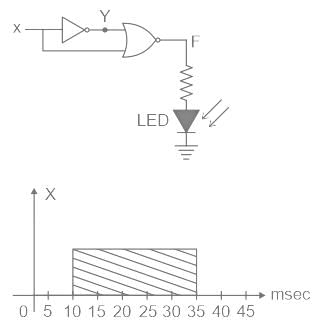
For the given digital circuit. NOT gate is having a time delay of 5 msec. Find for which time range the LED will glow up.
X input is logic 1 for 10 msec to 35msec as shown in the figure. (logic 1 is considered as 5 V and logic 0 as 0 V)
- a)10- 15msec
- b)20- 25msec
- c)30- 35msec
- d)35- 40msec
Correct answer is option 'D'. Can you explain this answer?
For the given digital circuit. NOT gate is having a time delay of 5 msec. Find for which time range the LED will glow up.
X input is logic 1 for 10 msec to 35msec as shown in the figure. (logic 1 is considered as 5 V and logic 0 as 0 V)

X input is logic 1 for 10 msec to 35msec as shown in the figure. (logic 1 is considered as 5 V and logic 0 as 0 V)

a)
10- 15msec
b)
20- 25msec
c)
30- 35msec
d)
35- 40msec
|
|
Sudhir Patel answered |
output F = (X + Y)'
waveforms are given as
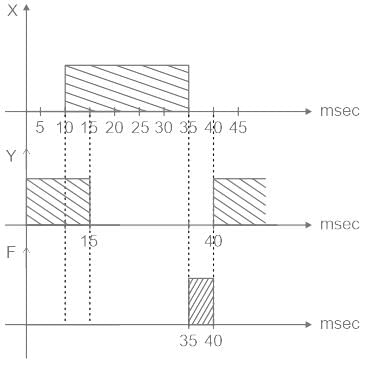
As we can see for the time 35msec to 40msec output F is logic 1 (5 V)
waveforms are given as

As we can see for the time 35msec to 40msec output F is logic 1 (5 V)
Which of the following is equivalent to the Boolean function X + XY?- a)0
- b)Y
- c)X
- d)1
Correct answer is option 'C'. Can you explain this answer?
Which of the following is equivalent to the Boolean function X + XY?
a)
0
b)
Y
c)
X
d)
1

|
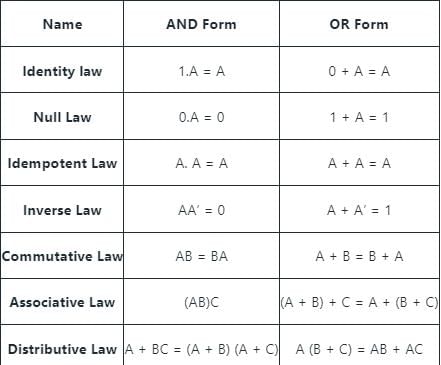
Starcoders answered |
All Boolean algebra laws are shown below
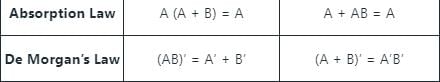
The given Boolean function can be simplified as :
Z = X + XY
Z = X (1 + Y)
Z = X

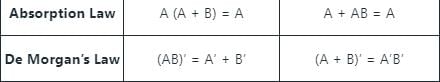
The given Boolean function can be simplified as :
Z = X + XY
Z = X (1 + Y)
Z = X
Find the output Boolean function for the logic circuit.
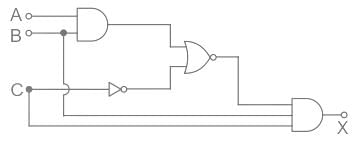
- a)X = ABC
- b)X = A̅BC
- c)X = A̅ B̅ C
- d)X = A̅ BC̅
Correct answer is option 'B'. Can you explain this answer?
Find the output Boolean function for the logic circuit.


a)
X = ABC
b)
X = A̅BC
c)
X = A̅ B̅ C
d)
X = A̅ BC̅
|
|
Sudhir Patel answered |

After simplification, we get
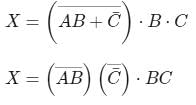
∵ De Morgan’s law:
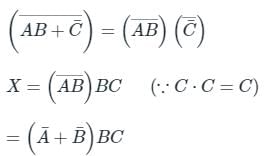
∵ De Morgan’s law:
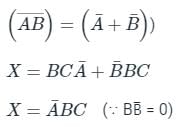
Chapter doubts & questions for Boolean Algebra - Digital Circuits 2025 is part of Electronics and Communication Engineering (ECE) exam preparation. The chapters have been prepared according to the Electronics and Communication Engineering (ECE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Electronics and Communication Engineering (ECE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Boolean Algebra - Digital Circuits in English & Hindi are available as part of Electronics and Communication Engineering (ECE) exam.
Download more important topics, notes, lectures and mock test series for Electronics and Communication Engineering (ECE) Exam by signing up for free.
Digital Circuits
76 videos|175 docs|70 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup


 then
then