All questions of Mensuration for Mechanical Engineering Exam
A circular wire of radius 56 cm is cut and bent in the form of a rectangle whose sides are in the ratio of 6:5. The smaller side of the rectangle is- a)70cm
- b)75cm
- c)80cm
- d)85cm
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A circular wire of radius 56 cm is cut and bent in the form of a rectangle whose sides are in the ratio of 6:5. The smaller side of the rectangle is
a)
70cm
b)
75cm
c)
80cm
d)
85cm
e)
None of these
|
|
Preeti Khanna answered |
The perimeter of the circle, that is, the rectangle is,
P=2πr = 2 * 22/7 * 56 =16×22 cm.
Let us assume the actual length and breadth of the rectangle be, 6xand 5x
So perimeter will be,
P=2(6x+5x)=22x
16×22=22x
X=16.
The smaller side or breadth =5x=80cm
P=2πr = 2 * 22/7 * 56 =16×22 cm.
Let us assume the actual length and breadth of the rectangle be, 6xand 5x
So perimeter will be,
P=2(6x+5x)=22x
16×22=22x
X=16.
The smaller side or breadth =5x=80cm
Smallest side of a right angled triangle is 13 cm less than the side of a square of perimeter 72 cm. Second largest side of the right angled triangle is 2 cm less than the length of the rectangle of area 112 cm² and breadth 8 cm. What is the largest side of the right angled triangle?- a)20 cm
- b)12 cm
- c)10 cm
- d)13 cm
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
Smallest side of a right angled triangle is 13 cm less than the side of a square of perimeter 72 cm. Second largest side of the right angled triangle is 2 cm less than the length of the rectangle of area 112 cm² and breadth 8 cm. What is the largest side of the right angled triangle?
a)
20 cm
b)
12 cm
c)
10 cm
d)
13 cm
e)
None of these

|
Naroj Boda answered |
Side of square = 72/4 = 18 cm
Smallest side of the right angled triangle = 18 – 13 = 5 cm
Length of rectangle = 112/8 = 14 cm
Second side of the right angled triangle = 14 – 2 = 12 cm
Hypotenuse of the right angled triangle = √(25 + 144) = 13cm
Smallest side of the right angled triangle = 18 – 13 = 5 cm
Length of rectangle = 112/8 = 14 cm
Second side of the right angled triangle = 14 – 2 = 12 cm
Hypotenuse of the right angled triangle = √(25 + 144) = 13cm
A hemispherical bowl of diameter 16cm is full of ice cream. Each student in a class is served exactly 4 scoops of ice cream. If the hemispherical scoop is having a radius of 2cm, then ice cream is served to how many students?- a)16
- b)32
- c)64
- d)128
- e)None
Correct answer is option 'A'. Can you explain this answer?
A hemispherical bowl of diameter 16cm is full of ice cream. Each student in a class is served exactly 4 scoops of ice cream. If the hemispherical scoop is having a radius of 2cm, then ice cream is served to how many students?
a)
16
b)
32
c)
64
d)
128
e)
None
|
|
Rajeev Kumar answered |
2/3*π*8³ = n*4*2/3*π*2³
n = 16
n = 16
The ratio between the sides of a room is 3:2. The cost of white washing the ceiling of the room at 5 Rs per square metre is Rs. 2500 and the cost of papering the walls at Rs. 2 per square metre is Rs. 960. The height of the room is?- a)4.8 m
- b)6.5 m
- c)3.5 m
- d)8.5 m
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
The ratio between the sides of a room is 3:2. The cost of white washing the ceiling of the room at 5 Rs per square metre is Rs. 2500 and the cost of papering the walls at Rs. 2 per square metre is Rs. 960. The height of the room is?
a)
4.8 m
b)
6.5 m
c)
3.5 m
d)
8.5 m
e)
None of these
|
|
Aryan Khanna answered |
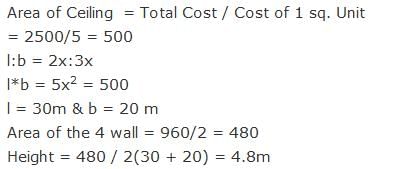
A deer and a rabbit can complete a full round on a circular track in 9 minutes and 5 minutes respectively. P, Q, R and S are the four consecutive points on the circular track which are equidistant from each other. P is opposite to R and Q is opposite to S. After how many minutes will they meet together for the first time at the starting point, when both have started simultaneously from the same point in same direction?- a)15 minutes
- b)25 minutes
- c)35 minutes
- d)45 minutes
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A deer and a rabbit can complete a full round on a circular track in 9 minutes and 5 minutes respectively. P, Q, R and S are the four consecutive points on the circular track which are equidistant from each other. P is opposite to R and Q is opposite to S. After how many minutes will they meet together for the first time at the starting point, when both have started simultaneously from the same point in same direction?
a)
15 minutes
b)
25 minutes
c)
35 minutes
d)
45 minutes
e)
None of these

|
Naroj Boda answered |
Time taken by a deer to complete one round = 9 minutes
Time taken by a rabbit to complete one round = 5 minutes
They meet together for the first time at the starting point = LCM of 9 and 5 = 45 minutes.
Time taken by a rabbit to complete one round = 5 minutes
They meet together for the first time at the starting point = LCM of 9 and 5 = 45 minutes.
The area of the Circular garden is 88704 m². Outside the garden a road of 7m width laid around it. What would be the cost of laying road at Rs. 2/m².- a)Rs.7546
- b)Rs.10036
- c)Rs.11092
- d)Rs.15092
- e)Rs.16086
Correct answer is option 'D'. Can you explain this answer?
The area of the Circular garden is 88704 m². Outside the garden a road of 7m width laid around it. What would be the cost of laying road at Rs. 2/m².
a)
Rs.7546
b)
Rs.10036
c)
Rs.11092
d)
Rs.15092
e)
Rs.16086

|
KS Coaching Center answered |
88704 = 22/7*r
r =168
Outer radius = 168+7 = 175
Outer area = 22/7*175 2 = 96250
Road area = 96250 – 88704 = 7546
Cost = 7546*2 = 15092
r =168
Outer radius = 168+7 = 175
Outer area = 22/7*175 2 = 96250
Road area = 96250 – 88704 = 7546
Cost = 7546*2 = 15092
A smaller triangle is having three sides. Another big triangle is having sides exactly double the sides of the smaller triangle. Then what is the ratio of Area of Smaller triangle to Area of the Bigger triangle?- a)1:2
- b)2:1
- c)1:4
- d)4:1
- e)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
A smaller triangle is having three sides. Another big triangle is having sides exactly double the sides of the smaller triangle. Then what is the ratio of Area of Smaller triangle to Area of the Bigger triangle?
a)
1:2
b)
2:1
c)
1:4
d)
4:1
e)
Cannot be determined

|
Cstoppers Instructors answered |
Smaller triangle sides = a, b, c
Area= √s(s-a) (s-b) (s-c);
s=a+b+c/2
= √(a+b+c)(b+c-a)(a+c- b)(a+b-c)/4
Bigger triangle =2a, 2b, 2c
Area = √(a+b+c)(b+c-a)(a+c- b)(a+b-c)
Ratio = 1:4
Area= √s(s-a) (s-b) (s-c);
s=a+b+c/2
= √(a+b+c)(b+c-a)(a+c- b)(a+b-c)/4
Bigger triangle =2a, 2b, 2c
Area = √(a+b+c)(b+c-a)(a+c- b)(a+b-c)
Ratio = 1:4
A well with 28 m inside diameter is dug out 18 m deep. The earth taken out of it has been evenly spread all around it to a width of 21 m to form an embarkment. Find the height of the embarkment.- a)3 m
- b)8 m
- c)9 m
- d)6 m
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A well with 28 m inside diameter is dug out 18 m deep. The earth taken out of it has been evenly spread all around it to a width of 21 m to form an embarkment. Find the height of the embarkment.
a)
3 m
b)
8 m
c)
9 m
d)
6 m
e)
None of these

|
Future Foundation Institute answered |
22/7[(R2) – (r2)] * h = 22/7(7*7*18)
[(352) – (72)]h = 14 * 14 * 18
(42*28)h = 14*14*18
h = 3 m
[(352) – (72)]h = 14 * 14 * 18
(42*28)h = 14*14*18
h = 3 m
A cylindrical cistern whose diameter is 14 cm is partly filled with water. If a rectangular block of iron 22 cm in length, 18 cm in breadth and 7 cm in thickness is wholly immersed in water, by how many cm will the water level rise?- a)10 cm
- b)18 cm
- c)12 cm
- d)16 cm
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A cylindrical cistern whose diameter is 14 cm is partly filled with water. If a rectangular block of iron 22 cm in length, 18 cm in breadth and 7 cm in thickness is wholly immersed in water, by how many cm will the water level rise?
a)
10 cm
b)
18 cm
c)
12 cm
d)
16 cm
e)
None of these

|
Cstoppers Instructors answered |
Volume of the Rectangular Block = 22 * 18 * 7
Radius of the Cistern = 7 cm
Area of the Cylinder = π * r² * h = 22/7 * 7 * 7 * h
22/7 * 7 * 7 * h = 22 * 18 * 7; h = 18 cm
Radius of the Cistern = 7 cm
Area of the Cylinder = π * r² * h = 22/7 * 7 * 7 * h
22/7 * 7 * 7 * h = 22 * 18 * 7; h = 18 cm
A hollow cylindrical tube is made of plastic is 4 cm thick. If the external diameter is 18 cm and length of the tube is 59cm, then find the volume of the plastic?- a)10380 cm³
- b)10384 cm³
- c)10440 cm³
- d)10444 cm³
- e)None
Correct answer is option 'B'. Can you explain this answer?
A hollow cylindrical tube is made of plastic is 4 cm thick. If the external diameter is 18 cm and length of the tube is 59cm, then find the volume of the plastic?
a)
10380 cm³
b)
10384 cm³
c)
10440 cm³
d)
10444 cm³
e)
None
|
|
Preeti Khanna answered |
R = 9, r =5
V =22/7*59(9 2 -5 2) = 10384
V =22/7*59(9 2 -5 2) = 10384
A room has floor size of 15*6sq cm. What is the height of the room , if the sum of the areas of the base and roof is equal to the sum of the areas of the four walls ?- a)1.12cm
- b)3.24cm
- c)4.29cm
- d)2.5cm
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A room has floor size of 15*6sq cm. What is the height of the room , if the sum of the areas of the base and roof is equal to the sum of the areas of the four walls ?
a)
1.12cm
b)
3.24cm
c)
4.29cm
d)
2.5cm
e)
None of these

|
Bank Exams India answered |
lb+lb = lh+hb+lh+hb
2lb = 2h(l+b)
h = lb/l+b
h=15*6/15+6 = 4.29 cm
2lb = 2h(l+b)
h = lb/l+b
h=15*6/15+6 = 4.29 cm
The biggest possible circle is inscribed in rectangle of length 10 m and breadth 7 m. Then the area of circle is?- a)35.8 m2
- b)36.5 m2
- c)30.5 m2
- d)38.5 m2
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
The biggest possible circle is inscribed in rectangle of length 10 m and breadth 7 m. Then the area of circle is?
a)
35.8 m2
b)
36.5 m2
c)
30.5 m2
d)
38.5 m2
e)
None of these
|
|
Preeti Khanna answered |
Radius = Breadth /2 = 7/2 = 3.5
Area = 22*3.5*3.5/7 = 269.5/7 = 38.5 m2
Area = 22*3.5*3.5/7 = 269.5/7 = 38.5 m2
A cylindrical tub of radius 10 cm contains water up to a depth of 25cm. A spherical iron ball is dropped into the tub and thus the level of water is raised by 5cm. What is the radius of the iron ball(approximate) ?- a)19
- b)15
- c)14
- d)17
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A cylindrical tub of radius 10 cm contains water up to a depth of 25cm. A spherical iron ball is dropped into the tub and thus the level of water is raised by 5cm. What is the radius of the iron ball(approximate) ?
a)
19
b)
15
c)
14
d)
17
e)
None of these
|
|
Nikita Singh answered |
Volume of the ball = volume of the raised water
4*22*r3 /3*7 = 22*100*5
r3 = 11000*3*7/88 = 2625
r = 13.79 or 14
4*22*r3 /3*7 = 22*100*5
r3 = 11000*3*7/88 = 2625
r = 13.79 or 14
A deer and a rabbit can complete a full round on a circular track in 9 minutes and 5 minutes respectively. P, Q, R and S are the four consecutive points on the circular track which are equidistant from each other. P is opposite to R and Q is opposite to S. After how many minutes will they meet together for the first time, when both have started simultaneously from the same point in same direction(in min)?- a)15/4
- b)45/4
- c)35/4
- d)25/4
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A deer and a rabbit can complete a full round on a circular track in 9 minutes and 5 minutes respectively. P, Q, R and S are the four consecutive points on the circular track which are equidistant from each other. P is opposite to R and Q is opposite to S. After how many minutes will they meet together for the first time, when both have started simultaneously from the same point in same direction(in min)?
a)
15/4
b)
45/4
c)
35/4
d)
25/4
e)
None of these
|
|
Kavya Saxena answered |
Circumference of the track = LCM of 9 and 5 = 45 m.
Ratio of time of deer and rabbit = 9 : 5
Ratio of speed of deer and rabbit = 5 : 9
Relative Speed = 4 m/min
They meet together for the first time at the starting point = 45/4 min
Ratio of time of deer and rabbit = 9 : 5
Ratio of speed of deer and rabbit = 5 : 9
Relative Speed = 4 m/min
They meet together for the first time at the starting point = 45/4 min
The perimeter of a rectangle and a square is 80 cm each. If the difference between their areas is 100 cm. Find the sides of the rectangle.- a)30cm, 10cm
- b)40cm, 15cm
- c)25cm, 10cm
- d)20cm, 30cm
- e)None of the Above
Correct answer is option 'A'. Can you explain this answer?
The perimeter of a rectangle and a square is 80 cm each. If the difference between their areas is 100 cm. Find the sides of the rectangle.
a)
30cm, 10cm
b)
40cm, 15cm
c)
25cm, 10cm
d)
20cm, 30cm
e)
None of the Above
|
|
Hasan Jawad answered |
Non of the above
In a rectangle the ratio of the length and breadth is 3:2. If each of the length and breadth is increased by 3m their ratio becomes 10:7. The area of the original rectangle in m² is?- a)384
- b)486
- c)346
- d)476
- e)None of the Above
Correct answer is option 'B'. Can you explain this answer?
In a rectangle the ratio of the length and breadth is 3:2. If each of the length and breadth is increased by 3m their ratio becomes 10:7. The area of the original rectangle in m² is?
a)
384
b)
486
c)
346
d)
476
e)
None of the Above

|
Praveen Raj Mehata answered |

Circumference of a circle A is 22/7 times perimeter of a square. Area of the square is 441 cm². What is the area of another circle B whose diameter is half the radius of the circle A(in cm²)?- a)354.5
- b)346.5
- c)316.5
- d)312.5
- e)None of the Above
Correct answer is option 'B'. Can you explain this answer?
Circumference of a circle A is 22/7 times perimeter of a square. Area of the square is 441 cm². What is the area of another circle B whose diameter is half the radius of the circle A(in cm²)?
a)
354.5
b)
346.5
c)
316.5
d)
312.5
e)
None of the Above
|
|
Anshul Singh answered |
Area of square=441 cm2
i.e. (side)2=441 cm2
side=21cm
Circumference of circle A=2πr
Perimeter of square(p)=4*side=(4*21)cm=84cm
According to question,
Circumference of A=22/7 of p
i.e. 2πr=(22/7)*84
2(22/7)*r=(22/7)*84
2r=84
r=42cm
let radius of B be 'R',
Diameter of B=(1/2) of radius of A
Diameter of B=(1/2)*42=21cm
R=(21/2)cm
Area of Circle B=πR2
=(22/7)*(21/2)*(21/2)cm2
hence on calculating the above solution we
get that area of circle B=346.5
i.e. option b).
thanking you if you understand it so plzzz follow me.
i.e. (side)2=441 cm2
side=21cm
Circumference of circle A=2πr
Perimeter of square(p)=4*side=(4*21)cm=84cm
According to question,
Circumference of A=22/7 of p
i.e. 2πr=(22/7)*84
2(22/7)*r=(22/7)*84
2r=84
r=42cm
let radius of B be 'R',
Diameter of B=(1/2) of radius of A
Diameter of B=(1/2)*42=21cm
R=(21/2)cm
Area of Circle B=πR2
=(22/7)*(21/2)*(21/2)cm2
hence on calculating the above solution we
get that area of circle B=346.5
i.e. option b).
thanking you if you understand it so plzzz follow me.
If each side pair of opposite sides of a square is increased by 20 m, the ratio of the length and breadth of the rectangular so formed becomes 5:3. The area of the old square is?- a)990m²
- b)900m²
- c)930m²
- d)945m²
- e)None of the Above
Correct answer is option 'B'. Can you explain this answer?
If each side pair of opposite sides of a square is increased by 20 m, the ratio of the length and breadth of the rectangular so formed becomes 5:3. The area of the old square is?
a)
990m²
b)
900m²
c)
930m²
d)
945m²
e)
None of the Above
|
|
Anaya Patel answered |
(x+20) / x = 5 / 3
3x + 60 = 5x
x = 30m; Area = 900m²
3x + 60 = 5x
x = 30m; Area = 900m²
The length of a rectangle wall is 3/2 times of its height. If the area of the wall is 600m². What is the sum of the length and height of the wall?- a)40
- b)60
- c)50
- d)70
- e)None of the Above
Correct answer is option 'C'. Can you explain this answer?
The length of a rectangle wall is 3/2 times of its height. If the area of the wall is 600m². What is the sum of the length and height of the wall?
a)
40
b)
60
c)
50
d)
70
e)
None of the Above

|
Akash Pandey answered |
length = 2x
height = 3x
Area of the wall = 3x * 2x = 6x² = 600
x = 10; Sum of the length and height of the wall = 50
height = 3x
Area of the wall = 3x * 2x = 6x² = 600
x = 10; Sum of the length and height of the wall = 50
The perimeter of a square is equal to twice the perimeter of a rectangle of length 10 cm and breadth 4 cm. What is the circumference of a semi-circle whose diameter is equal to the side of the square?- a)38 cm
- b)23 cm
- c)46 cm
- d)36 cm
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
The perimeter of a square is equal to twice the perimeter of a rectangle of length 10 cm and breadth 4 cm. What is the circumference of a semi-circle whose diameter is equal to the side of the square?
a)
38 cm
b)
23 cm
c)
46 cm
d)
36 cm
e)
None of these

|
KS Coaching Center answered |
Perimeter of square = 2(l + b)
= 2 * 2(10 + 4) = 2 * 28 = 56 cm
Side of square = 56/4 = 14 cm
Radius of semi circle = 14/2 = 7cm
Circumference of the semi-circle = 22/7 * 7 + 14 = 36 cm
= 2 * 2(10 + 4) = 2 * 28 = 56 cm
Side of square = 56/4 = 14 cm
Radius of semi circle = 14/2 = 7cm
Circumference of the semi-circle = 22/7 * 7 + 14 = 36 cm
The width of a rectangular piece of land is 1/4 th of its length. If the perimeter of the piece of land is 320 m its length is?- a)140 m
- b)128 m
- c)120 m
- d)156 m
- e)124 m
Correct answer is option 'B'. Can you explain this answer?
The width of a rectangular piece of land is 1/4 th of its length. If the perimeter of the piece of land is 320 m its length is?
a)
140 m
b)
128 m
c)
120 m
d)
156 m
e)
124 m
|
|
Yash Patel answered |
length = l ; breadth = l/4
2(l + b) = 320
2(l + l/4) = 320
l = 320 * 4/10 = 128m
2(l + b) = 320
2(l + l/4) = 320
l = 320 * 4/10 = 128m
Smallest side of a right angled triangle is 6 cm less than the side of a square of perimeter 60 cm. Second largest side of the right angled triangle is 4 cm less than the length of rectangle of area 80 sq. cm and breadth 5 cm. What is the largest side of the right angled triangle?- a)10cm
- b)9cm
- c)12cm
- d)15cm
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
Smallest side of a right angled triangle is 6 cm less than the side of a square of perimeter 60 cm. Second largest side of the right angled triangle is 4 cm less than the length of rectangle of area 80 sq. cm and breadth 5 cm. What is the largest side of the right angled triangle?
a)
10cm
b)
9cm
c)
12cm
d)
15cm
e)
None of these
|
|
Yash Patel answered |
Side of 1st square = 60/4 = 15 cm.
Smallest side of right angled triangle= 15 −6 = 9 cm.
Length of 2nd rectangle = 80/5 = 16 cm.
Second largest side of the 1strectangle = 16−4 = 12 cm.
Largest side = hypotenuse=√92+122=15cm
Smallest side of right angled triangle= 15 −6 = 9 cm.
Length of 2nd rectangle = 80/5 = 16 cm.
Second largest side of the 1strectangle = 16−4 = 12 cm.
Largest side = hypotenuse=√92+122=15cm
The area of a rectangle is equal to the area of a square whose diagonal is 12√2 metre. The difference between the length and the breadth of the rectangle is 7 metre. What is the perimeter of rectangle ? (in metre).- a)68 metre
- b)50 metre
- c)62 metre
- d)64 metre
- e)None of the Above
Correct answer is option 'B'. Can you explain this answer?
The area of a rectangle is equal to the area of a square whose diagonal is 12√2 metre. The difference between the length and the breadth of the rectangle is 7 metre. What is the perimeter of rectangle ? (in metre).
a)
68 metre
b)
50 metre
c)
62 metre
d)
64 metre
e)
None of the Above
|
|
Anaya Patel answered |
d = a√2
12√2 = a√2
a = 12
l * b = a² = (12²) = 144
l – b = 7 ; l = b + 7
(b + 7)*(b) = 144
b² + 7b – 144 = 0
b = 9; l = 16
2(l + b) = 2(16 + 9) = 50m
12√2 = a√2
a = 12
l * b = a² = (12²) = 144
l – b = 7 ; l = b + 7
(b + 7)*(b) = 144
b² + 7b – 144 = 0
b = 9; l = 16
2(l + b) = 2(16 + 9) = 50m
A right circular cone is placed over a cylinder of the same radius. Now the combined structure is painted on all sides. Then they are separated now the ratio of area painted on Cylinder to Cone is 3:1. What is the height of Cylinder if the height of Cone is 4 m and radius is 3 m?- a)5 m
- b)6 m
- c)8 m
- d)10 m
- e)Cannot be determined
Correct answer is 'B'. Can you explain this answer?
A right circular cone is placed over a cylinder of the same radius. Now the combined structure is painted on all sides. Then they are separated now the ratio of area painted on Cylinder to Cone is 3:1. What is the height of Cylinder if the height of Cone is 4 m and radius is 3 m?
a)
5 m
b)
6 m
c)
8 m
d)
10 m
e)
Cannot be determined

|
Machine Experts answered |
Cylinder painted area = 2πrh+πr²
Cone painted area = πrl
2h+r/√ (r² +h1² ) = 3:1
h = 6
Cone painted area = πrl
2h+r/√ (r² +h1² ) = 3:1
h = 6
A rectangular field is to be fenced on three sides leaving a side of 30 feet uncovered. If the area of the field is 720 sq. feet, how many feet of fencing will be required?- a)65
- b)78
- c)82
- d)89
- e)None of the Above
Correct answer is option 'B'. Can you explain this answer?
A rectangular field is to be fenced on three sides leaving a side of 30 feet uncovered. If the area of the field is 720 sq. feet, how many feet of fencing will be required?
a)
65
b)
78
c)
82
d)
89
e)
None of the Above
|
|
Kavya Saxena answered |
L = 30; lb = 720;
B= 24 ft
Length of fencing = l + 2b = 30 + 48 = 78 ft
B= 24 ft
Length of fencing = l + 2b = 30 + 48 = 78 ft
One of the adjacent sides of a rectangular courtyard is 5m and its diagonal measures 13 m long. What is the area of the courtyard?- a)60m²
- b)40m²
- c)50m²
- d)30m²
- e)None of the Above
Correct answer is option 'A'. Can you explain this answer?
One of the adjacent sides of a rectangular courtyard is 5m and its diagonal measures 13 m long. What is the area of the courtyard?
a)
60m²
b)
40m²
c)
50m²
d)
30m²
e)
None of the Above
|
|
Ravi Singh answered |
Another side = √[(13)² – (5)²] = 12m
Area = 12 * 5 = 60m²
Area = 12 * 5 = 60m²
What is the radius of the circle whose area is equal to the sum of the areas of two circles whose radii are 20 cm and 21 cm?- a)27m
- b)28m
- c)29m
- d)25m
- e)15m
Correct answer is option 'C'. Can you explain this answer?
What is the radius of the circle whose area is equal to the sum of the areas of two circles whose radii are 20 cm and 21 cm?
a)
27m
b)
28m
c)
29m
d)
25m
e)
15m
|
|
Alok Verma answered |
πR² = πr1² + πr2²
πR² = π(r1² + r2²)
R² = (400 + 441)
R = 29
πR² = π(r1² + r2²)
R² = (400 + 441)
R = 29
If the radius of cylinder is doubled, but height is reduced by 50%. What is the percentage change in volume?- a)100%
- b)150%
- c)125%
- d)175%
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
If the radius of cylinder is doubled, but height is reduced by 50%. What is the percentage change in volume?
a)
100%
b)
150%
c)
125%
d)
175%
e)
None of these
|
|
Nikita Singh answered |
R1/R2 = R/2R & H1/H2 = H/H/2
Original Volume = πr²h
New Volume = π(2r)²h/2
Change in Volume = (2 – 1)/1 * 100 = 100
Original Volume = πr²h
New Volume = π(2r)²h/2
Change in Volume = (2 – 1)/1 * 100 = 100
The ratio between the perimeter and the breadth of a rectangle is 5:1. If the area of the rectangle is 294 square cm, what is the length of the rectangle?- a)12 cm
- b)15 cm
- c)19 cm
- d)21 cm
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
The ratio between the perimeter and the breadth of a rectangle is 5:1. If the area of the rectangle is 294 square cm, what is the length of the rectangle?
a)
12 cm
b)
15 cm
c)
19 cm
d)
21 cm
e)
None of these
|
|
Kavya Saxena answered |
Perimeter=2*(l+b)
Perimeter/breadth = 5/1
2*(l+b)/b = 5/1
2l+2b = 5b
l= 3/2 b.
Area =l*b= 294 sq. units.
3/2 * b2 = 294
b=14
l= 21
Perimeter/breadth = 5/1
2*(l+b)/b = 5/1
2l+2b = 5b
l= 3/2 b.
Area =l*b= 294 sq. units.
3/2 * b2 = 294
b=14
l= 21
The length of a rectangle is 3/5th of the side of a square. The radius of a circle is equal to side of the square. The circumference of the circle is 132 cm. What is the area of the rectangle, if the breadth of the rectangle is 15 cm?- a)112 cm²
- b)149 cm²
- c)189 cm²
- d)Cannot be determined
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
The length of a rectangle is 3/5th of the side of a square. The radius of a circle is equal to side of the square. The circumference of the circle is 132 cm. What is the area of the rectangle, if the breadth of the rectangle is 15 cm?
a)
112 cm²
b)
149 cm²
c)
189 cm²
d)
Cannot be determined
e)
None of these

|
KS Coaching Center answered |
Circumference of the circle = 132
2πR = 132; R = 21 cm
Side of square = 21 cm
Length of the rectangle = 3/5 * 21 = 63/5
Area of the rectangle = 63/5 * 15 = 189 cm²
2πR = 132; R = 21 cm
Side of square = 21 cm
Length of the rectangle = 3/5 * 21 = 63/5
Area of the rectangle = 63/5 * 15 = 189 cm²
A ladder is resting with one end in contact with the top of the wall of height 15m and the other end of the ground is at a distance 8m from the wall. The length of the ladder is?- a)17m
- b)18m
- c)16m
- d)15m
- e)10m
Correct answer is option 'A'. Can you explain this answer?
A ladder is resting with one end in contact with the top of the wall of height 15m and the other end of the ground is at a distance 8m from the wall. The length of the ladder is?
a)
17m
b)
18m
c)
16m
d)
15m
e)
10m

|
Shailendra Singh answered |
Hypotenuse = √(base)² + (altitude)²
√(8)² + (15)² = √289 = 17m
√(8)² + (15)² = √289 = 17m
Two roads each 10m wide has been made running perpendicularly to each other inside a rectangular field of dimension 90m X 50m. What is the cost of spreading pebbles over them at the rate of Rs.8 per m².?- a)10400
- b)15400
- c)17500
- d)20600
- e)None of the Above
Correct answer is option 'A'. Can you explain this answer?
Two roads each 10m wide has been made running perpendicularly to each other inside a rectangular field of dimension 90m X 50m. What is the cost of spreading pebbles over them at the rate of Rs.8 per m².?
a)
10400
b)
15400
c)
17500
d)
20600
e)
None of the Above
|
|
Ravi Singh answered |
Area of Roads = (l + b – w) * w
Area of Roads = (90 + 50 – 10) * 10 = 1300m²
Cost = 1300 * 8 = 10400
Area of Roads = (90 + 50 – 10) * 10 = 1300m²
Cost = 1300 * 8 = 10400
The length of a plot is four times its breath. A playground measuring 400 square meters occupies one fourth of the total area of a plot. What is the length of the plot in meter.?- a)20
- b)30
- c)60
- d)40
- e)80
Correct answer is option 'E'. Can you explain this answer?
The length of a plot is four times its breath. A playground measuring 400 square meters occupies one fourth of the total area of a plot. What is the length of the plot in meter.?
a)
20
b)
30
c)
60
d)
40
e)
80
|
|
Aarav Sharma answered |
To solve this problem, we need to use the given information to find the length of the plot. Let's break down the information step by step:
1. The length of a plot is four times its breadth: Let's assume the breadth of the plot is 'x'. According to the given information, the length of the plot would be 4x.
2. A playground occupies one fourth of the total area of the plot: The area of the playground is given as 400 square meters. Since the playground occupies one fourth of the total area of the plot, we can calculate the total area of the plot by multiplying the area of the playground by 4. So, the total area of the plot would be 400 * 4 = 1600 square meters.
3. Now, we can use the total area of the plot to find the length. The formula to calculate the area of a rectangle is length * breadth. We know that the area of the plot is 1600 square meters and the length is 4x. Substituting these values into the formula, we get:
4x * x = 1600
4. Simplifying the equation, we have:
4x^2 = 1600
5. Dividing both sides of the equation by 4, we get:
x^2 = 400
6. Taking the square root of both sides, we get:
x = √400
7. Simplifying the square root, we have:
x = 20
8. Since the length of the plot is four times its breadth, we have:
Length = 4x = 4 * 20 = 80 meters
Therefore, the length of the plot is 80 meters. The correct answer is option E.
1. The length of a plot is four times its breadth: Let's assume the breadth of the plot is 'x'. According to the given information, the length of the plot would be 4x.
2. A playground occupies one fourth of the total area of the plot: The area of the playground is given as 400 square meters. Since the playground occupies one fourth of the total area of the plot, we can calculate the total area of the plot by multiplying the area of the playground by 4. So, the total area of the plot would be 400 * 4 = 1600 square meters.
3. Now, we can use the total area of the plot to find the length. The formula to calculate the area of a rectangle is length * breadth. We know that the area of the plot is 1600 square meters and the length is 4x. Substituting these values into the formula, we get:
4x * x = 1600
4. Simplifying the equation, we have:
4x^2 = 1600
5. Dividing both sides of the equation by 4, we get:
x^2 = 400
6. Taking the square root of both sides, we get:
x = √400
7. Simplifying the square root, we have:
x = 20
8. Since the length of the plot is four times its breadth, we have:
Length = 4x = 4 * 20 = 80 meters
Therefore, the length of the plot is 80 meters. The correct answer is option E.
A rectangular ground 16m long and 10m breadth. It has a gravel path 2.5m wide all around it on the outside. What is the area of the path?- a)159 m²
- b)155 m²
- c)187 m²
- d)183 m²
- e)None of the Above
Correct answer is option 'B'. Can you explain this answer?
A rectangular ground 16m long and 10m breadth. It has a gravel path 2.5m wide all around it on the outside. What is the area of the path?
a)
159 m²
b)
155 m²
c)
187 m²
d)
183 m²
e)
None of the Above
|
|
Sagar Sharma answered |
To find the area of the path, we need to subtract the area of the inner rectangle (without the path) from the area of the outer rectangle (with the path).
The area of the outer rectangle is given by the length multiplied by the breadth:
Area of outer rectangle = 16m * 10m = 160m²
The area of the inner rectangle is the length and breadth reduced by twice the width of the path on each side:
Length of inner rectangle = 16m - 2(2.5m) = 16m - 5m = 11m
Breadth of inner rectangle = 10m - 2(2.5m) = 10m - 5m = 5m
Area of inner rectangle = 11m * 5m = 55m²
Therefore, the area of the path is:
Area of path = Area of outer rectangle - Area of inner rectangle
Area of path = 160m² - 55m²
Area of path = 105m²
So the area of the path is 105 square meters.
The area of the outer rectangle is given by the length multiplied by the breadth:
Area of outer rectangle = 16m * 10m = 160m²
The area of the inner rectangle is the length and breadth reduced by twice the width of the path on each side:
Length of inner rectangle = 16m - 2(2.5m) = 16m - 5m = 11m
Breadth of inner rectangle = 10m - 2(2.5m) = 10m - 5m = 5m
Area of inner rectangle = 11m * 5m = 55m²
Therefore, the area of the path is:
Area of path = Area of outer rectangle - Area of inner rectangle
Area of path = 160m² - 55m²
Area of path = 105m²
So the area of the path is 105 square meters.
In a rectangle the ratio of the length and breadth is 3:2. If each of the length and breadth is increased by 4m their ratio becomes 10:7. The area of the original rectangle in m² is?- a)384
- b)486
- c)546
- d)864
- e)None of the Above
Correct answer is option 'D'. Can you explain this answer?
In a rectangle the ratio of the length and breadth is 3:2. If each of the length and breadth is increased by 4m their ratio becomes 10:7. The area of the original rectangle in m² is?
a)
384
b)
486
c)
546
d)
864
e)
None of the Above
|
|
Sagar Sharma answered |
Understanding the Problem
To find the area of the original rectangle, we start by acknowledging the given ratios and conditions.
Step 1: Define Variables
- Let the length of the rectangle be 3x and the breadth be 2x, based on the ratio of 3:2.
Step 2: Set Up the Equation
- According to the problem, when both length and breadth are increased by 4m, the new ratio becomes 10:7.
- This can be expressed as:
(3x + 4) / (2x + 4) = 10 / 7
Step 3: Cross-Multiply and Simplify
- Cross-multiplying gives:
7(3x + 4) = 10(2x + 4)
- Expanding both sides results in:
21x + 28 = 20x + 40
Step 4: Solve for x
- Rearranging yields:
21x - 20x = 40 - 28
x = 12
Step 5: Calculate Length and Breadth
- Plugging x back into our expressions:
Length = 3x = 36m
Breadth = 2x = 24m
Step 6: Find the Area
- The area of the rectangle is calculated as:
Area = Length × Breadth = 36m × 24m = 864m²
Conclusion
The area of the original rectangle is 864m², confirming that the correct answer is option 'D'.
To find the area of the original rectangle, we start by acknowledging the given ratios and conditions.
Step 1: Define Variables
- Let the length of the rectangle be 3x and the breadth be 2x, based on the ratio of 3:2.
Step 2: Set Up the Equation
- According to the problem, when both length and breadth are increased by 4m, the new ratio becomes 10:7.
- This can be expressed as:
(3x + 4) / (2x + 4) = 10 / 7
Step 3: Cross-Multiply and Simplify
- Cross-multiplying gives:
7(3x + 4) = 10(2x + 4)
- Expanding both sides results in:
21x + 28 = 20x + 40
Step 4: Solve for x
- Rearranging yields:
21x - 20x = 40 - 28
x = 12
Step 5: Calculate Length and Breadth
- Plugging x back into our expressions:
Length = 3x = 36m
Breadth = 2x = 24m
Step 6: Find the Area
- The area of the rectangle is calculated as:
Area = Length × Breadth = 36m × 24m = 864m²
Conclusion
The area of the original rectangle is 864m², confirming that the correct answer is option 'D'.
The length of a wall is 5/4 times of its height. If the area of wall will be 500m². What is the sum of the length and height of the wall?- a)55m
- b)45m
- c)40m
- d)50m
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The length of a wall is 5/4 times of its height. If the area of wall will be 500m². What is the sum of the length and height of the wall?
a)
55m
b)
45m
c)
40m
d)
50m
e)
None of these
|
|
Sagar Sharma answered |
Let's assume the height of the wall is "h".
The length of the wall will be 5/4 times the height, which is (5/4)h.
The area of the wall is calculated by multiplying the length and height:
Area = Length × Height
500 = (5/4)h × h
To solve for h, we can multiply both sides of the equation by 4/5:
(4/5) × 500 = (4/5) × (5/4)h × h
400 = h^2
Taking the square root of both sides, we find:
h = √400
h = 20
Therefore, the height of the wall is 20m.
The length of the wall can be found by multiplying the height by 5/4:
Length = (5/4) × 20
Length = 25
So, the length of the wall is 25m.
The length of the wall will be 5/4 times the height, which is (5/4)h.
The area of the wall is calculated by multiplying the length and height:
Area = Length × Height
500 = (5/4)h × h
To solve for h, we can multiply both sides of the equation by 4/5:
(4/5) × 500 = (4/5) × (5/4)h × h
400 = h^2
Taking the square root of both sides, we find:
h = √400
h = 20
Therefore, the height of the wall is 20m.
The length of the wall can be found by multiplying the height by 5/4:
Length = (5/4) × 20
Length = 25
So, the length of the wall is 25m.
A cylindrical tank of diameter 14 cm is full of water. If 9 litres of water is drawn off, the water level in the tank will drop by- a)230.6 cm
- b)223.5 cm
- c)233.8 cm
- d)238.3 cm
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A cylindrical tank of diameter 14 cm is full of water. If 9 litres of water is drawn off, the water level in the tank will drop by
a)
230.6 cm
b)
223.5 cm
c)
233.8 cm
d)
238.3 cm
e)
None of these
|
|
Sagar Sharma answered |
Given:
Diameter of cylindrical tank = 14 cm
Volume of water drawn off = 9 litres
To find:
The drop in water level in the tank
Formula:
The volume of a cylinder = πr²h, where r is the radius and h is the height.
Calculation:
1. Convert the volume of water drawn off from litres to cubic centimeters:
1 liter = 1000 cubic centimeters
So, 9 litres = 9 * 1000 = 9000 cubic centimeters
2. Find the radius of the cylindrical tank:
The diameter of the tank is given as 14 cm.
Radius (r) = Diameter / 2 = 14 / 2 = 7 cm
3. Let the initial water level in the tank be h1 and the final water level after drawing off 9 litres of water be h2.
4. The initial volume of water in the tank = πr²h1
The final volume of water in the tank = πr²h2
5. According to the problem, the initial volume of water in the tank is equal to the final volume plus the volume of water drawn off:
πr²h1 = πr²h2 + 9000
6. Since the tank has a constant cross-sectional area, we can cancel out the πr² terms:
h1 = h2 + 9000
7. We are asked to find the drop in water level, which is the difference between the initial and final water levels:
Drop in water level = h1 - h2 = (h2 + 9000) - h2 = 9000
8. Therefore, the drop in water level in the tank is 9000 cm or 233.8 cm.
Hence, the correct answer is option (c) 233.8 cm.
Diameter of cylindrical tank = 14 cm
Volume of water drawn off = 9 litres
To find:
The drop in water level in the tank
Formula:
The volume of a cylinder = πr²h, where r is the radius and h is the height.
Calculation:
1. Convert the volume of water drawn off from litres to cubic centimeters:
1 liter = 1000 cubic centimeters
So, 9 litres = 9 * 1000 = 9000 cubic centimeters
2. Find the radius of the cylindrical tank:
The diameter of the tank is given as 14 cm.
Radius (r) = Diameter / 2 = 14 / 2 = 7 cm
3. Let the initial water level in the tank be h1 and the final water level after drawing off 9 litres of water be h2.
4. The initial volume of water in the tank = πr²h1
The final volume of water in the tank = πr²h2
5. According to the problem, the initial volume of water in the tank is equal to the final volume plus the volume of water drawn off:
πr²h1 = πr²h2 + 9000
6. Since the tank has a constant cross-sectional area, we can cancel out the πr² terms:
h1 = h2 + 9000
7. We are asked to find the drop in water level, which is the difference between the initial and final water levels:
Drop in water level = h1 - h2 = (h2 + 9000) - h2 = 9000
8. Therefore, the drop in water level in the tank is 9000 cm or 233.8 cm.
Hence, the correct answer is option (c) 233.8 cm.
What is the radius of the circle whose area is equal to the sum of the areas of two circles whose radii are 20 cm and 21 cm?- a)27m
- b)28m
- c)29m
- d)25m
- e)15m
Correct answer is option 'C'. Can you explain this answer?
What is the radius of the circle whose area is equal to the sum of the areas of two circles whose radii are 20 cm and 21 cm?
a)
27m
b)
28m
c)
29m
d)
25m
e)
15m
|
|
Rhea Reddy answered |
πR² = πr1² + πr2²
πR² = π(r1² + r2²)
R² = (400 + 441)
R = 29
πR² = π(r1² + r2²)
R² = (400 + 441)
R = 29
The radius of a circle is 4 m. What is the radius of another circle whose area is 16 times of that first?- a)16 m
- b)64 m
- c)256 m
- d)400 m
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
The radius of a circle is 4 m. What is the radius of another circle whose area is 16 times of that first?
a)
16 m
b)
64 m
c)
256 m
d)
400 m
e)
None of these
|
|
Aisha Gupta answered |
Ratio of areas = (ratio of radii)²
16/1 = (ratio of radii)²
ratio of radii = 4/1
The required radius = 16 m
16/1 = (ratio of radii)²
ratio of radii = 4/1
The required radius = 16 m
A hollow cylindrical tube open at both ends is made of plastic 4 cm thick. If the external diameter be 54 cm and the length of the tube be 490 cm, find the volume of plastic.- a)320000 cm³
- b)340000 cm³
- c)306300 cm³
- d)308000 cm³
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A hollow cylindrical tube open at both ends is made of plastic 4 cm thick. If the external diameter be 54 cm and the length of the tube be 490 cm, find the volume of plastic.
a)
320000 cm³
b)
340000 cm³
c)
306300 cm³
d)
308000 cm³
e)
None of these
|
|
Alok Verma answered |
External Radius = 27; Internal Radius = 23
Volume of Plastic =πh(R² – r²) = 22/7 * 490(27² – 23²) = 308000 cm³
Volume of Plastic =πh(R² – r²) = 22/7 * 490(27² – 23²) = 308000 cm³
If each side pair of opposite sides of a square is increased by 10m, the ratio of the length and breadth of the rectangular so formed becomes 5:3. The area of the old square is?- a)290m²
- b)225m²
- c)230m²
- d)245m²
- e)None of the Above
Correct answer is option 'B'. Can you explain this answer?
If each side pair of opposite sides of a square is increased by 10m, the ratio of the length and breadth of the rectangular so formed becomes 5:3. The area of the old square is?
a)
290m²
b)
225m²
c)
230m²
d)
245m²
e)
None of the Above
|
|
Rajeev Kumar answered |
(x+10) / x = 5 / 3
3x + 30 = 5x
x = 15m; Area = 225m²
3x + 30 = 5x
x = 15m; Area = 225m²
The length of a park is four times of its breadth. A playground whose area is 1600 m² covers 1/4th part of the park. The length of the park is?- a)108 m
- b)140 m
- c)120 m
- d)160 m
- e)180 m
Correct answer is option 'D'. Can you explain this answer?
The length of a park is four times of its breadth. A playground whose area is 1600 m² covers 1/4th part of the park. The length of the park is?
a)
108 m
b)
140 m
c)
120 m
d)
160 m
e)
180 m
|
|
Sagar Sharma answered |
The area of a rectangle is given by the formula A = length * breadth.
Let's assume the breadth of the park is x meters.
According to the problem, the length of the park is four times its breadth, so the length is 4x meters.
The area of the park is given as 1600 square meters, so we can write the equation:
1600 = 4x * x
Simplifying the equation:
1600 = 4x^2
Dividing both sides by 4:
400 = x^2
Taking the square root of both sides:
x = ±20
Since the breadth cannot be negative, we take the positive value:
x = 20 meters
Therefore, the breadth of the park is 20 meters and the length is 4 times the breadth, which is 4*20 = 80 meters.
Let's assume the breadth of the park is x meters.
According to the problem, the length of the park is four times its breadth, so the length is 4x meters.
The area of the park is given as 1600 square meters, so we can write the equation:
1600 = 4x * x
Simplifying the equation:
1600 = 4x^2
Dividing both sides by 4:
400 = x^2
Taking the square root of both sides:
x = ±20
Since the breadth cannot be negative, we take the positive value:
x = 20 meters
Therefore, the breadth of the park is 20 meters and the length is 4 times the breadth, which is 4*20 = 80 meters.
The perimeter of a rectangular field is 120 m and the difference between its two adjacent sides is 40 m. The sides of the square field whose area is equal to this rectangular field is?- a)15√3
- b)10√3
- c)15√5
- d)10√5
- e)None of the Above
Correct answer is option 'D'. Can you explain this answer?
The perimeter of a rectangular field is 120 m and the difference between its two adjacent sides is 40 m. The sides of the square field whose area is equal to this rectangular field is?
a)
15√3
b)
10√3
c)
15√5
d)
10√5
e)
None of the Above
|
|
Ravi Singh answered |
Perimeter of rectangle = 2(l + b) = 120
l + b = 60m — (1)
l – b = 40m –(2)
From (1) and (2)
l = 50 m; b = 10m
Area of rectangle = 500m² = Area of Square
Side of a square = 10√5
l + b = 60m — (1)
l – b = 40m –(2)
From (1) and (2)
l = 50 m; b = 10m
Area of rectangle = 500m² = Area of Square
Side of a square = 10√5
10 cylindrical pillars of a building have to be painted. The diameter of each pillar is 70 cm and the height is 4m. What is the cost of painting at the rate of Rs. 10 per square metre?- a)790
- b)850
- c)880
- d)920
- e)None of the Above
Correct answer is option 'C'. Can you explain this answer?
10 cylindrical pillars of a building have to be painted. The diameter of each pillar is 70 cm and the height is 4m. What is the cost of painting at the rate of Rs. 10 per square metre?
a)
790
b)
850
c)
880
d)
920
e)
None of the Above
|
|
Faizan Khan answered |
CSA of 10 cyc= 10*2πrh
= 2 * 22/7 * 35/100 * 4
= 44*35*4/(700)
= 10*176*35/700
= 176*35 /70
Cost = 10*176*35/70
= 880rs
= 2 * 22/7 * 35/100 * 4
= 44*35*4/(700)
= 10*176*35/700
= 176*35 /70
Cost = 10*176*35/70
= 880rs
If the side of the square is increased by 30%, then how much % does its area get increased?- a)59%
- b)69%
- c)79%
- d)49%
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
If the side of the square is increased by 30%, then how much % does its area get increased?
a)
59%
b)
69%
c)
79%
d)
49%
e)
None of these
|
|
Alok Verma answered |
Area of the plot = 1.3 * 1.3 = 1.69 = 69%
If the ratio of radius two Cylinders A and B are in the ratio of 2:1 and their heights are in the ratio of 2:1 respectively. The ratio of their total surface areas of Cylinder A to B is?- a)2:1
- b)1:2
- c)1:4
- d)4:1
- e)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
If the ratio of radius two Cylinders A and B are in the ratio of 2:1 and their heights are in the ratio of 2:1 respectively. The ratio of their total surface areas of Cylinder A to B is?
a)
2:1
b)
1:2
c)
1:4
d)
4:1
e)
Cannot be determined
|
|
Sagar Sharma answered |
Given:
Ratio of radii of Cylinder A and Cylinder B = 2:1
Ratio of heights of Cylinder A and Cylinder B = 2:1
To find:
Ratio of total surface areas of Cylinder A to Cylinder B
Solution:
Let's assume the radius of Cylinder A as 2x and the radius of Cylinder B as x. Similarly, let's assume the height of Cylinder A as 2h and the height of Cylinder B as h.
Calculating the surface area of Cylinder A:
The total surface area of a cylinder is given by the formula:
Surface area = 2πrh + 2πr²
Substituting the values of radius and height of Cylinder A:
Surface area of Cylinder A = 2π(2x)(2h) + 2π(2x)²
Simplifying the expression:
Surface area of Cylinder A = 8πxh + 8πx² = 8π(xh + x²)
Calculating the surface area of Cylinder B:
Substituting the values of radius and height of Cylinder B:
Surface area of Cylinder B = 2π(x)(h) + 2π(x)²
Simplifying the expression:
Surface area of Cylinder B = 2πxh + 2πx²
Calculating the ratio of surface areas:
Ratio of surface areas of Cylinder A to Cylinder B = (Surface area of Cylinder A) / (Surface area of Cylinder B)
= (8π(xh + x²)) / (2πxh + 2πx²)
= 4(xh + x²) / (xh + x²)
= 4
Therefore, the ratio of the total surface areas of Cylinder A to Cylinder B is 4:1.
Answer:
The correct answer is option D) 4:1.
Ratio of radii of Cylinder A and Cylinder B = 2:1
Ratio of heights of Cylinder A and Cylinder B = 2:1
To find:
Ratio of total surface areas of Cylinder A to Cylinder B
Solution:
Let's assume the radius of Cylinder A as 2x and the radius of Cylinder B as x. Similarly, let's assume the height of Cylinder A as 2h and the height of Cylinder B as h.
Calculating the surface area of Cylinder A:
The total surface area of a cylinder is given by the formula:
Surface area = 2πrh + 2πr²
Substituting the values of radius and height of Cylinder A:
Surface area of Cylinder A = 2π(2x)(2h) + 2π(2x)²
Simplifying the expression:
Surface area of Cylinder A = 8πxh + 8πx² = 8π(xh + x²)
Calculating the surface area of Cylinder B:
Substituting the values of radius and height of Cylinder B:
Surface area of Cylinder B = 2π(x)(h) + 2π(x)²
Simplifying the expression:
Surface area of Cylinder B = 2πxh + 2πx²
Calculating the ratio of surface areas:
Ratio of surface areas of Cylinder A to Cylinder B = (Surface area of Cylinder A) / (Surface area of Cylinder B)
= (8π(xh + x²)) / (2πxh + 2πx²)
= 4(xh + x²) / (xh + x²)
= 4
Therefore, the ratio of the total surface areas of Cylinder A to Cylinder B is 4:1.
Answer:
The correct answer is option D) 4:1.
One side of rectangular ground is 8m and its diagonal is 17m. Find the area of ground?- a)150
- b)140
- c)130
- d)120
- e)None of the Above
Correct answer is option 'D'. Can you explain this answer?
One side of rectangular ground is 8m and its diagonal is 17m. Find the area of ground?
a)
150
b)
140
c)
130
d)
120
e)
None of the Above
|
|
Alok Verma answered |
d = √(l² + b²)
17 = √(l² + 8²)
l² = 17² – 8² ⇒ l = 289 – 64 = 225
l = 15 Area = 15 * 8 = 120m²
17 = √(l² + 8²)
l² = 17² – 8² ⇒ l = 289 – 64 = 225
l = 15 Area = 15 * 8 = 120m²
Chapter doubts & questions for Mensuration - RRB JE Mock Test Series for Mechanical Engineering (ME) 2026 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Mensuration - RRB JE Mock Test Series for Mechanical Engineering (ME) 2026 in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup











