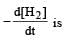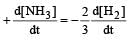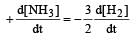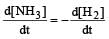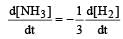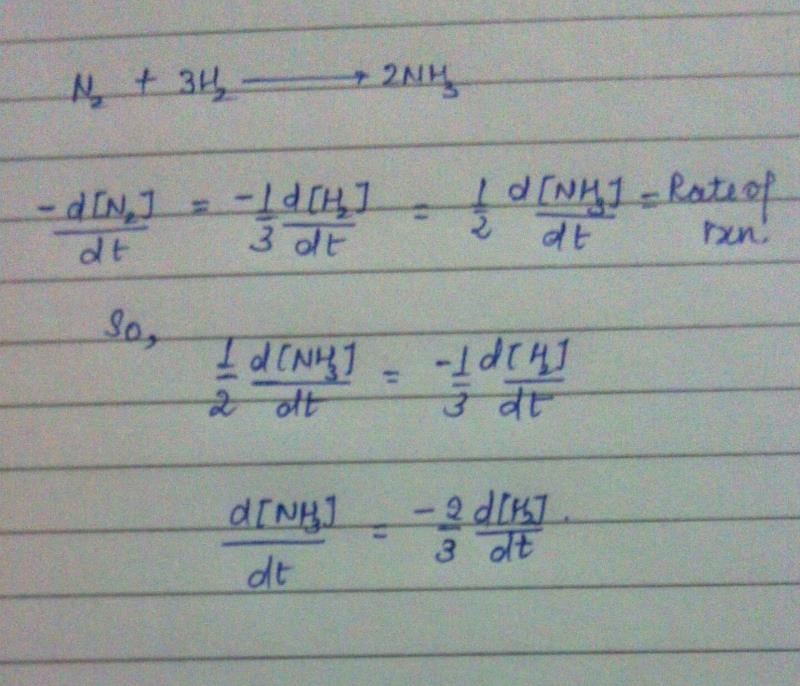All Exams >
NEET >
NEET Past Year Papers >
All Questions
All questions of Chemical Kinetics for NEET Exam
The rate constants k1 and k2 for two different reactions are 1016 . e–2000/T and 1015 . e–1000/T, respectively. The temperature at which k1 = k2 is :- a)1000 K
- b)
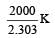
- c)2000 K
- d)
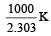
Correct answer is option 'D'. Can you explain this answer?
The rate constants k1 and k2 for two different reactions are 1016 . e–2000/T and 1015 . e–1000/T, respectively. The temperature at which k1 = k2 is :
a)
1000 K
b)
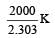
c)
2000 K
d)
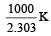
|
|
Priya Menon answered |
Given, 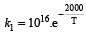
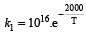
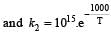
when k1 and k2 are equal at any temperature T, we have
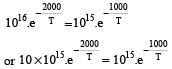
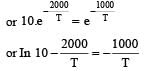
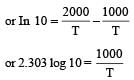
or 2.303 ×1×T=1000 [∴ log 10= 1]

A reaction is 50% completed in 2 hours and 75% completed in 4 hours. The order of reaction is [NEET Kar. 2013]- a)0
- b)1
- c)2
- d)3
Correct answer is option 'B'. Can you explain this answer?
A reaction is 50% completed in 2 hours and 75% completed in 4 hours. The order of reaction is [NEET Kar. 2013]
a)
0
b)
1
c)
2
d)
3

|
Naveen Menon answered |
For a first order reaction, t75% = 2 × t50%
During the kinetic study of the reaction, 2A + B → C + D, following results were obtained:
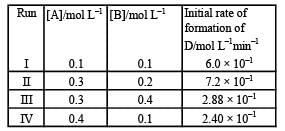 Based on the above data which one of the following is correct? [2010]
Based on the above data which one of the following is correct? [2010]
- a)rate = k [A]2 [B]
- b)rate = k[A] [B]
- c)rate = k [A]2 [B]2
- d)rate = k [A] [B]2
Correct answer is option 'D'. Can you explain this answer?
During the kinetic study of the reaction, 2A + B → C + D, following results were obtained:

Based on the above data which one of the following is correct? [2010]
a)
rate = k [A]2 [B]
b)
rate = k[A] [B]
c)
rate = k [A]2 [B]2
d)
rate = k [A] [B]2

|
Krish Khanna answered |
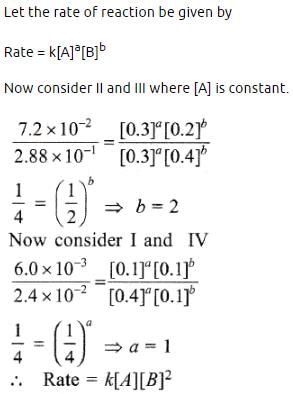
A reaction having equal energies of activation for forward and reverse reaction has : [NEET 2013]- a)ΔG = 0
- b)ΔH = 0
- c)ΔH = ΔG = ΔS = 0
- d)ΔS = 0
Correct answer is option 'B'. Can you explain this answer?
A reaction having equal energies of activation for forward and reverse reaction has : [NEET 2013]
a)
ΔG = 0
b)
ΔH = 0
c)
ΔH = ΔG = ΔS = 0
d)
ΔS = 0

|
Jatin Dasgupta answered |
A) A high equilibrium constant
b) A low equilibrium constant
c) No equilibrium constant
d) A negative equilibrium constant
The correct answer is: c) No equilibrium constant
b) A low equilibrium constant
c) No equilibrium constant
d) A negative equilibrium constant
The correct answer is: c) No equilibrium constant
The rate of the reaction  can be written in three ways :
can be written in three ways :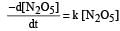
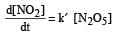
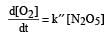 The relationship between k and k' and between k and k"are :[2011 M]
The relationship between k and k' and between k and k"are :[2011 M]- a)k' = 2k ; k' = k
- b)k' = 2k ; k" = k/2
- c)k' = 2k ; k" = 2k
- d)k' = k ; k" = k
Correct answer is option 'B'. Can you explain this answer?
The rate of the reaction 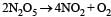 can be written in three ways :
can be written in three ways :
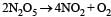 can be written in three ways :
can be written in three ways :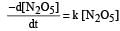
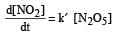
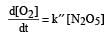
The relationship between k and k' and between k and k"are :
[2011 M]
a)
k' = 2k ; k' = k
b)
k' = 2k ; k" = k/2
c)
k' = 2k ; k" = 2k
d)
k' = k ; k" = k
|
|
Pooja Shah answered |
Rate of disappearance of reactants = Rate of appearance of products

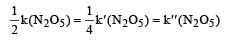
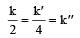
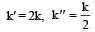
For a reaction between A and B the order with respect to A is 2 and the order with respect to B is 3. The concentrations of both A and B are doubled, the rate will increase by a factor of: [NEET Kar. 2013]- a)10
- b)12
- c)16
- d)32
Correct answer is option 'D'. Can you explain this answer?
For a reaction between A and B the order with respect to A is 2 and the order with respect to B is 3. The concentrations of both A and B are doubled, the rate will increase by a factor of: [NEET Kar. 2013]
a)
10
b)
12
c)
16
d)
32

|
Abhijeet Goyal answered |
Rate = k[A]2[B]3 when concentrations of both A and B are doubled then rate = k[2A]2[2B]3 = 32 k[A]2[B]3
∴ rate will increase by a factor of 32.
∴ rate will increase by a factor of 32.
For the reaction A + B → products, it is observed that: [2009]
(1) On doubling the initial concentration of A only, the rate of reaction is also doubled and
(2) On doubling the initial concentrations of both A and B, there is a change by a factor of 8 in the rate of the reaction.
The rate of this reaction is given by: - a)rate = k [A] [B]2
- b)rate = k [A]2 [B]2
- c)rate = k [A] [B]
- d)rate = k [A]2 [B]
Correct answer is option 'A'. Can you explain this answer?
For the reaction A + B → products, it is observed that: [2009]
(1) On doubling the initial concentration of A only, the rate of reaction is also doubled and
(2) On doubling the initial concentrations of both A and B, there is a change by a factor of 8 in the rate of the reaction.
The rate of this reaction is given by:
(1) On doubling the initial concentration of A only, the rate of reaction is also doubled and
(2) On doubling the initial concentrations of both A and B, there is a change by a factor of 8 in the rate of the reaction.
The rate of this reaction is given by:
a)
rate = k [A] [B]2
b)
rate = k [A]2 [B]2
c)
rate = k [A] [B]
d)
rate = k [A]2 [B]

|
Nilotpal Gupta answered |
When concentration A is doubled, rate is doubled. Hence order with respect to A is one.
When concentrations of both A and B are doubled, rate increases by 8 times hence order with respect to B is 2.
∴ rate = k [A]1 [B]2
Total order = 1 + 2 = 3
When concentrations of both A and B are doubled, rate increases by 8 times hence order with respect to B is 2.
∴ rate = k [A]1 [B]2
Total order = 1 + 2 = 3
In a reaction, A + B → Product, rate is doubled when the concentration of B is doubled, and rate increases by a factor of 8 when the concentrations of both the reactants (A and B) are doubled rate, law for the reaction can be written as : [2012]- a)Rate = k[A][B]2
- b)Rate = k[A]2 [B]2
- c)Rate = k[A] [B]
- d)Rate = k[A]2 B]
Correct answer is option 'D'. Can you explain this answer?
In a reaction, A + B → Product, rate is doubled when the concentration of B is doubled, and rate increases by a factor of 8 when the concentrations of both the reactants (A and B) are doubled rate, law for the reaction can be written as : [2012]
a)
Rate = k[A][B]2
b)
Rate = k[A]2 [B]2
c)
Rate = k[A] [B]
d)
Rate = k[A]2 B]

|
Sushant Goyal answered |
According to statement given in the question, it is clear that r ∝ [A]2 and r ∝ [B]
That means order of reaction with respect to B is 1 and w.r.t A is 2
Hence, Rate = k[A]2[B]1
That means order of reaction with respect to B is 1 and w.r.t A is 2
Hence, Rate = k[A]2[B]1
A chemical reaction is catalyzed by a catalyst X.Hence X [1995]- a)reduces enthalpy of the reaction
- b)decreases rate constant of the reaction
- c)increases activation energy of the reaction
- d)does not affect equilibrium constant of the reaction
Correct answer is option 'D'. Can you explain this answer?
A chemical reaction is catalyzed by a catalyst X.Hence X [1995]
a)
reduces enthalpy of the reaction
b)
decreases rate constant of the reaction
c)
increases activation energy of the reaction
d)
does not affect equilibrium constant of the reaction

|
Prashanth Dasgupta answered |
A catalyst affects equally both forward and backward reactions, therefore it does not affect equilibrium constant of reaction.
Select the rate law that corresponds to data shown for the following reaction [1994]
- a)rate = k [B]3
- b)rate = k [B]4
- c)rate = k [A] [B]3
- d)rate = k [A]2 [B]2
Correct answer is option 'A'. Can you explain this answer?
Select the rate law that corresponds to data shown for the following reaction [1994]

a)
rate = k [B]3
b)
rate = k [B]4
c)
rate = k [A] [B]3
d)
rate = k [A]2 [B]2

|
Palak Khanna answered |
From data 1 and 3, it is clear that keeping (B) const, When [A] is doubled, rate remains unaffected. Hence rate is independent of [A]. from 1 and 4, keeping [A] constant, when [B] is doubled, rate become 8 times. Hence [rate ∝ [ B]3].
A substance 'A' decomposes by a first or der reaction starting initially with [A] = 2.00 m and after 200 min, [A] becomes 0.15 m. For this reaction t1/2 is [1995]- a)53.72 min
- b)50.49 min
- c)48.45 min
- d)46.45 min
Correct answer is option 'A'. Can you explain this answer?
A substance 'A' decomposes by a first or der reaction starting initially with [A] = 2.00 m and after 200 min, [A] becomes 0.15 m. For this reaction t1/2 is [1995]
a)
53.72 min
b)
50.49 min
c)
48.45 min
d)
46.45 min
|
|
Ananya Das answered |
Given initial concentration (a) = 2.00 m; Time taken (t) = 200 min and final concentration (a – x) = 0.15 m. For a first order reation rate constant,
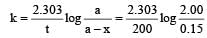
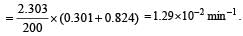
Further
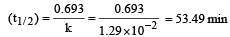
The reaction A → B follows first order kinetics.The time taken for 0.8 mole of A to produce 0.6 mole of B is 1 hour. What is the time taken for conversion of 0.9 mole of A to produce 0.675 mole of B?[2003]- a)2 hours
- b)1 hour
- c)0.5 hour
- d)0.25 hour
Correct answer is option 'B'. Can you explain this answer?
The reaction A → B follows first order kinetics.The time taken for 0.8 mole of A to produce 0.6 mole of B is 1 hour. What is the time taken for conversion of 0.9 mole of A to produce 0.675 mole of B?[2003]
a)
2 hours
b)
1 hour
c)
0.5 hour
d)
0.25 hour

|
Krish Patel answered |
A → B For a first order reaction given a = 0.8 mol, (a – x) = 0.8 – 0.6 = 0.2
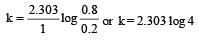
again a = 0.9, a – x = 0.9 – 0.675 = 0.225
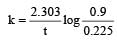
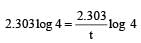
Hence t = 1 hour
Half life of a first order reaction is 4 s and the initial concentration of the reactants is 0.12 M.The concentration of the reactant left after 16 s is [1999]- a)0.0075 M
- b)0.06 M
- c)0.03 M
- d)0.015 M
Correct answer is option 'A'. Can you explain this answer?
Half life of a first order reaction is 4 s and the initial concentration of the reactants is 0.12 M.The concentration of the reactant left after 16 s is [1999]
a)
0.0075 M
b)
0.06 M
c)
0.03 M
d)
0.015 M

|
Nayanika Reddy answered |
t1/2 = 4 s T = 16
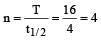
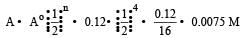
where Å = initial concentration & A = concentration left after time t
For a first order reaction A → B th e reaction rate at reactant concentration of 0.01 M is found to be 2.0 x 10-5 mol L-1 S-1. The half life period of the reaction is [2 00 5]- a)30 s
- b)220 s
- c)300 s
- d)347 s
Correct answer is option 'D'. Can you explain this answer?
For a first order reaction A → B th e reaction rate at reactant concentration of 0.01 M is found to be 2.0 x 10-5 mol L-1 S-1. The half life period of the reaction is [2 00 5]
a)
30 s
b)
220 s
c)
300 s
d)
347 s
|
|
Ameya Yadav answered |
A first-order reaction is a type of chemical reaction in which the rate of reaction is directly proportional to the concentration of one reactant. Mathematically, it can be represented by the following equation:
Rate = k[A]
Where Rate is the rate of reaction, k is the rate constant, and [A] is the concentration of reactant A.
The integrated rate law for a first-order reaction is given by:
ln([A]t/[A]0) = -kt
Where [A]t is the concentration of reactant A at time t, [A]0 is the initial concentration of reactant A, k is the rate constant, and t is the time.
In a first-order reaction, the half-life (t1/2) is constant and independent of the initial concentration of reactant A. The half-life can be calculated using the equation:
t1/2 = ln(2)/k
Overall, a first-order reaction is characterized by a decreasing concentration of reactant A over time, with the rate of reaction proportional to the concentration of A.
Rate = k[A]
Where Rate is the rate of reaction, k is the rate constant, and [A] is the concentration of reactant A.
The integrated rate law for a first-order reaction is given by:
ln([A]t/[A]0) = -kt
Where [A]t is the concentration of reactant A at time t, [A]0 is the initial concentration of reactant A, k is the rate constant, and t is the time.
In a first-order reaction, the half-life (t1/2) is constant and independent of the initial concentration of reactant A. The half-life can be calculated using the equation:
t1/2 = ln(2)/k
Overall, a first-order reaction is characterized by a decreasing concentration of reactant A over time, with the rate of reaction proportional to the concentration of A.
In a zero-order reaction for every 10° rise of temperature, the rate is doubled. If the temperature is increased from 10°C to 100°C, the rate of the reaction will become : [2012]- a)256 times
- b)512 times
- c)64 times
- d)128 times
Correct answer is option 'B'. Can you explain this answer?
In a zero-order reaction for every 10° rise of temperature, the rate is doubled. If the temperature is increased from 10°C to 100°C, the rate of the reaction will become : [2012]
a)
256 times
b)
512 times
c)
64 times
d)
128 times
|
|
Sounak Mukherjee answered |
In a zero-order reaction, the rate of the reaction does not depend on the concentration of the reactants. The reaction proceeds at a constant rate over time.
For every 10 units of time that pass, the concentration of the reactant will decrease by the same amount. This is because the rate of the reaction is constant and independent of the reactant concentration.
For example, if the initial concentration of the reactant is 100 units, after 10 units of time, the concentration will decrease to 90 units. After another 10 units of time, the concentration will decrease to 80 units, and so on.
This behavior is characteristic of zero-order reactions, where the rate is determined solely by the reaction mechanism and is not influenced by the concentration of the reactants.
For every 10 units of time that pass, the concentration of the reactant will decrease by the same amount. This is because the rate of the reaction is constant and independent of the reactant concentration.
For example, if the initial concentration of the reactant is 100 units, after 10 units of time, the concentration will decrease to 90 units. After another 10 units of time, the concentration will decrease to 80 units, and so on.
This behavior is characteristic of zero-order reactions, where the rate is determined solely by the reaction mechanism and is not influenced by the concentration of the reactants.
Activation energy of a chemical reaction can be determined by [1998]- a)evaluating rate constant at standard temperature
- b)evaluating velocities of reaction at two different temperatures
- c)evaluating rate constants at two different temperatures
- d)changing concentration of reactants
Correct answer is option 'C'. Can you explain this answer?
Activation energy of a chemical reaction can be determined by [1998]
a)
evaluating rate constant at standard temperature
b)
evaluating velocities of reaction at two different temperatures
c)
evaluating rate constants at two different temperatures
d)
changing concentration of reactants
|
|
Nabanita Pillai answered |
The activation energy of a chemical reaction is the minimum amount of energy required for the reactant molecules to undergo a chemical transformation and form products. It is an important parameter that determines the rate at which a reaction occurs.
To determine the activation energy of a chemical reaction, one method is to evaluate the rate constants at two different temperatures. This is the correct answer (option C) because it is based on the Arrhenius equation, which describes the relationship between the rate constant and temperature.
Here is a detailed explanation of why evaluating rate constants at two different temperatures helps determine the activation energy of a chemical reaction:
1. Arrhenius equation:
The Arrhenius equation is given by:
k = A * e^(-Ea/RT)
Where:
- k is the rate constant of the reaction,
- A is the pre-exponential factor or frequency factor,
- Ea is the activation energy,
- R is the gas constant, and
- T is the temperature in Kelvin.
2. Effect of temperature on rate constant:
According to the Arrhenius equation, the rate constant of a reaction is exponentially dependent on the temperature. As the temperature increases, the rate constant also increases.
3. Evaluating rate constants at two different temperatures:
By measuring the rate constants at two different temperatures, we can set up two equations using the Arrhenius equation. Let's assume the rate constants at temperature T1 and T2 are k1 and k2, respectively.
Using the Arrhenius equation for k1:
k1 = A * e^(-Ea/RT1)
Using the Arrhenius equation for k2:
k2 = A * e^(-Ea/RT2)
4. Taking the ratio:
Dividing the equation for k1 by the equation for k2 gives:
k1/k2 = (A * e^(-Ea/RT1)) / (A * e^(-Ea/RT2))
k1/k2 = e^((Ea/R)*((1/T2) - (1/T1)))
5. Simplifying the equation:
Taking the natural logarithm of both sides of the equation, we get:
ln(k1/k2) = (Ea/R)*((1/T2) - (1/T1))
6. Determining the activation energy:
By rearranging the equation, we can solve for Ea:
Ea = R * ((1/T2) - (1/T1)) * ln(k1/k2)
7. Conclusion:
By evaluating the rate constants at two different temperatures and using the Arrhenius equation, we can determine the activation energy of a chemical reaction. This method allows us to calculate the activation energy without directly measuring the reaction rate at different temperatures.
To determine the activation energy of a chemical reaction, one method is to evaluate the rate constants at two different temperatures. This is the correct answer (option C) because it is based on the Arrhenius equation, which describes the relationship between the rate constant and temperature.
Here is a detailed explanation of why evaluating rate constants at two different temperatures helps determine the activation energy of a chemical reaction:
1. Arrhenius equation:
The Arrhenius equation is given by:
k = A * e^(-Ea/RT)
Where:
- k is the rate constant of the reaction,
- A is the pre-exponential factor or frequency factor,
- Ea is the activation energy,
- R is the gas constant, and
- T is the temperature in Kelvin.
2. Effect of temperature on rate constant:
According to the Arrhenius equation, the rate constant of a reaction is exponentially dependent on the temperature. As the temperature increases, the rate constant also increases.
3. Evaluating rate constants at two different temperatures:
By measuring the rate constants at two different temperatures, we can set up two equations using the Arrhenius equation. Let's assume the rate constants at temperature T1 and T2 are k1 and k2, respectively.
Using the Arrhenius equation for k1:
k1 = A * e^(-Ea/RT1)
Using the Arrhenius equation for k2:
k2 = A * e^(-Ea/RT2)
4. Taking the ratio:
Dividing the equation for k1 by the equation for k2 gives:
k1/k2 = (A * e^(-Ea/RT1)) / (A * e^(-Ea/RT2))
k1/k2 = e^((Ea/R)*((1/T2) - (1/T1)))
5. Simplifying the equation:
Taking the natural logarithm of both sides of the equation, we get:
ln(k1/k2) = (Ea/R)*((1/T2) - (1/T1))
6. Determining the activation energy:
By rearranging the equation, we can solve for Ea:
Ea = R * ((1/T2) - (1/T1)) * ln(k1/k2)
7. Conclusion:
By evaluating the rate constants at two different temperatures and using the Arrhenius equation, we can determine the activation energy of a chemical reaction. This method allows us to calculate the activation energy without directly measuring the reaction rate at different temperatures.
The rate of the reaction 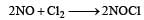 is given by the rate equation rate = k [NO]2 [Cl2] [2010] The value of the rate constant can be increased by:
is given by the rate equation rate = k [NO]2 [Cl2] [2010] The value of the rate constant can be increased by:- a)increasing the concentration of NO.
- b)increasing the temperature.
- c)increasing the concentration of the Cl2
- d)doing all of these
Correct answer is option 'B'. Can you explain this answer?
The rate of the reaction 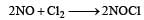 is given by the rate equation rate = k [NO]2 [Cl2] [2010] The value of the rate constant can be increased by:
is given by the rate equation rate = k [NO]2 [Cl2] [2010] The value of the rate constant can be increased by:
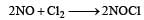 is given by the rate equation rate = k [NO]2 [Cl2] [2010] The value of the rate constant can be increased by:
is given by the rate equation rate = k [NO]2 [Cl2] [2010] The value of the rate constant can be increased by:a)
increasing the concentration of NO.
b)
increasing the temperature.
c)
increasing the concentration of the Cl2
d)
doing all of these

|
Swara Desai answered |
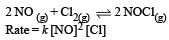
The value of rate constant can be increased by increasing the temperature.
∴ Correct choice : (b)
∴ Correct choice : (b)
In a reversible reaction the energy of activation of the forward reaction is 50 kcal. The energy of activation for the reverse reaction will be [1996]- a)< 50 kcal
- b)either greater than or less than 50 kcal
- c)50 kcal
- d)> 50 kcal
Correct answer is option 'B'. Can you explain this answer?
In a reversible reaction the energy of activation of the forward reaction is 50 kcal. The energy of activation for the reverse reaction will be [1996]
a)
< 50 kcal
b)
either greater than or less than 50 kcal
c)
50 kcal
d)
> 50 kcal

|
Anirudh Datta answered |
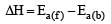
Thus energy of activation for reverse reaction depend upon whether reaction is exothermic or endothermic If reaction is exothermic, ΔH = +ve Ea(b) > Ea(f) If reaction is endothermic ΔH =+ve Ea(b) < Ea(f )
The rate of reaction depends upon the [1995]- a)volume
- b)force
- c)pressure
- d)conc. of reactants
Correct answer is option 'D'. Can you explain this answer?
The rate of reaction depends upon the [1995]
a)
volume
b)
force
c)
pressure
d)
conc. of reactants

|
Akshat Chavan answered |
The rate of a reaction is the speed at which the reactants are converted into products.
It depends upon the concentration of reactants. e.g for the reaction
It depends upon the concentration of reactants. e.g for the reaction
If the rate of the reaction is equal to the rate constant, the order of the reaction is [2003]- a)3
- b)0
- c)1
- d)2
Correct answer is option 'B'. Can you explain this answer?
If the rate of the reaction is equal to the rate constant, the order of the reaction is [2003]
a)
3
b)
0
c)
1
d)
2
|
|
Madhurima Mishra answered |
Rate of Reaction and Rate Constant
Rate of Reaction:
The rate of a chemical reaction is a measure of how quickly reactants are converted into products. It is determined by the change in concentration of the reactants or products over a given period of time. The rate of reaction can be expressed as the rate at which the concentration of a reactant decreases or the rate at which the concentration of a product increases.
Rate Constant:
The rate constant, denoted as k, is a proportionality constant that relates the rate of reaction to the concentrations of the reactants. It is specific to a particular reaction at a given temperature and is independent of reactant concentrations. The rate constant is determined experimentally and is often used to determine the order of a reaction.
Order of Reaction:
The order of a reaction is the sum of the exponents in the rate equation. It represents how the rate of reaction is affected by changes in the concentration of the reactants. The order can be zero, first, second, or any other positive or negative integer.
Explanation of the Answer:
In this question, it is given that the rate of the reaction is equal to the rate constant. This implies that the rate equation for the reaction can be written as:
rate = k[A]^x[B]^y
where [A] and [B] are the concentrations of the reactants, and x and y are the orders of the reaction with respect to A and B, respectively.
Since the rate of reaction is equal to the rate constant, the rate equation simplifies to:
rate = k
Comparing this with the general rate equation, we can conclude that the order of the reaction is zero. This means that the rate of the reaction is independent of the concentrations of the reactants.
Therefore, the correct answer is option 'B' which states that the order of the reaction is 0.
Rate of Reaction:
The rate of a chemical reaction is a measure of how quickly reactants are converted into products. It is determined by the change in concentration of the reactants or products over a given period of time. The rate of reaction can be expressed as the rate at which the concentration of a reactant decreases or the rate at which the concentration of a product increases.
Rate Constant:
The rate constant, denoted as k, is a proportionality constant that relates the rate of reaction to the concentrations of the reactants. It is specific to a particular reaction at a given temperature and is independent of reactant concentrations. The rate constant is determined experimentally and is often used to determine the order of a reaction.
Order of Reaction:
The order of a reaction is the sum of the exponents in the rate equation. It represents how the rate of reaction is affected by changes in the concentration of the reactants. The order can be zero, first, second, or any other positive or negative integer.
Explanation of the Answer:
In this question, it is given that the rate of the reaction is equal to the rate constant. This implies that the rate equation for the reaction can be written as:
rate = k[A]^x[B]^y
where [A] and [B] are the concentrations of the reactants, and x and y are the orders of the reaction with respect to A and B, respectively.
Since the rate of reaction is equal to the rate constant, the rate equation simplifies to:
rate = k
Comparing this with the general rate equation, we can conclude that the order of the reaction is zero. This means that the rate of the reaction is independent of the concentrations of the reactants.
Therefore, the correct answer is option 'B' which states that the order of the reaction is 0.
In the reaction [2009] 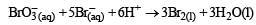 The rate of appearance of bromine (Br2) is related to rate of disappearance of bromide ions as following:
The rate of appearance of bromine (Br2) is related to rate of disappearance of bromide ions as following:- a)
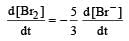
- b)
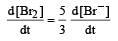
- c)
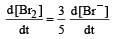
- d)
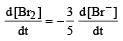
Correct answer is option 'D'. Can you explain this answer?
In the reaction [2009]
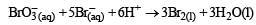
The rate of appearance of bromine (Br2) is related to rate of disappearance of bromide ions as following:
a)
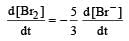
b)
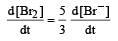
c)
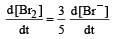
d)
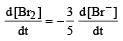

|
Palak Khanna answered |
Rate of disappearance of Br–
= rate of appearance of Br2
= rate of appearance of Br2
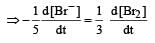

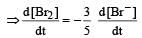
What is the activation energy for a reaction if its rate doubles when the temperature is raised from 20°C to 35°C? (R = 8.314 J mol–1 K–1) [NEET 2013]- a)269 kJ mol–1
- b)34.7 kJ mol–1
- c)15.1 kJ mol–1
- d)342 kJ mol–1
Correct answer is option 'B'. Can you explain this answer?
What is the activation energy for a reaction if its rate doubles when the temperature is raised from 20°C to 35°C? (R = 8.314 J mol–1 K–1) [NEET 2013]
a)
269 kJ mol–1
b)
34.7 kJ mol–1
c)
15.1 kJ mol–1
d)
342 kJ mol–1

|
Anand Jain answered |
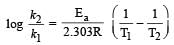
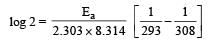
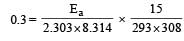
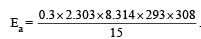
= 34673 J mole-1
= 34.7 J mole-1
= 34.7 J mole-1
In a reaction, A + B → Product, rate is doubled when the concentration of B is doubled, and rate increases by a factor of 8 when the concentrations of both the reactants (A and B) are doubled, rate law for the reaction can be written as - a)Rate = k[A] [B]
- b)Rate = k[A]2[B]
- c)Rate = k[A][B]2
- d)Rate = k[A]2[B]2
Correct answer is option 'B'. Can you explain this answer?
In a reaction, A + B → Product, rate is doubled when the concentration of B is doubled, and rate increases by a factor of 8 when the concentrations of both the reactants (A and B) are doubled, rate law for the reaction can be written as
a)
Rate = k[A] [B]
b)
Rate = k[A]2[B]
c)
Rate = k[A][B]2
d)
Rate = k[A]2[B]2
|
|
Mansi Nair answered |
\\
For the reaction  the value of rate of disappearance of N2O5 is given as 6.25 × 10–3 mol L–1s–1. The rate of formation of NO2 and O2 is given respectively as : [2010]
the value of rate of disappearance of N2O5 is given as 6.25 × 10–3 mol L–1s–1. The rate of formation of NO2 and O2 is given respectively as : [2010]- a)6.25 × 10–3 mol L–1s–1 and 6.25 × 10–3 mol L–1s–1
- b)1.25 × 10–2 mol L–1s–1 and 3.125 × 10–3 mol L–1s–1
- c)6.25 × 10–3 mol L–1s–1 and 3.125 × 10–3 mol L–1s–1
- d)1.25 × 10–2 mol L–1s–1 and 6.25 × 10–3 mol L–1s–1
Correct answer is option 'B'. Can you explain this answer?
For the reaction  the value of rate of disappearance of N2O5 is given as 6.25 × 10–3 mol L–1s–1. The rate of formation of NO2 and O2 is given respectively as : [2010]
the value of rate of disappearance of N2O5 is given as 6.25 × 10–3 mol L–1s–1. The rate of formation of NO2 and O2 is given respectively as : [2010]
 the value of rate of disappearance of N2O5 is given as 6.25 × 10–3 mol L–1s–1. The rate of formation of NO2 and O2 is given respectively as : [2010]
the value of rate of disappearance of N2O5 is given as 6.25 × 10–3 mol L–1s–1. The rate of formation of NO2 and O2 is given respectively as : [2010]a)
6.25 × 10–3 mol L–1s–1 and 6.25 × 10–3 mol L–1s–1
b)
1.25 × 10–2 mol L–1s–1 and 3.125 × 10–3 mol L–1s–1
c)
6.25 × 10–3 mol L–1s–1 and 3.125 × 10–3 mol L–1s–1
d)
1.25 × 10–2 mol L–1s–1 and 6.25 × 10–3 mol L–1s–1

|
Smruti Sucharita answered |
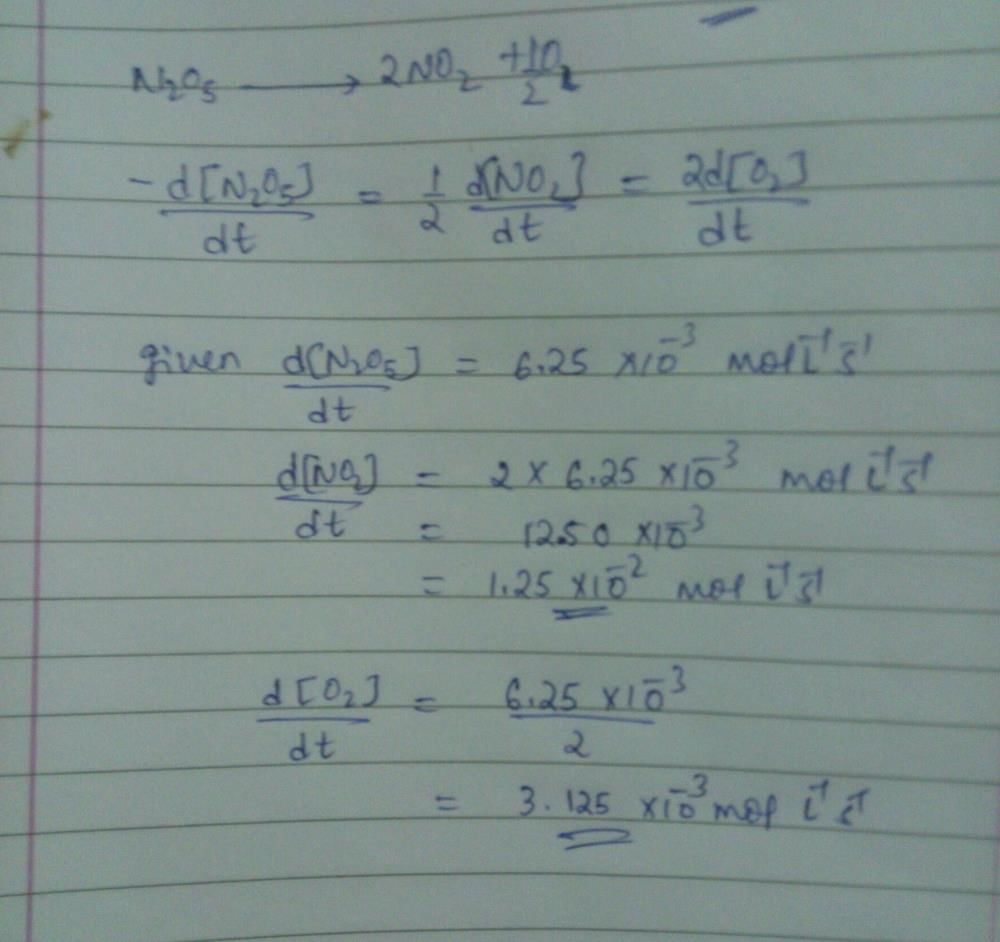
For the reaction 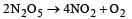 rate and rate constant are 1.02 × 10–4 mol lit–1 sec–1 and 3.4 × 10–5 sec–1 respectively then concentration of N2O5 at that time will be [2001]
rate and rate constant are 1.02 × 10–4 mol lit–1 sec–1 and 3.4 × 10–5 sec–1 respectively then concentration of N2O5 at that time will be [2001]- a)1.732M
- b)3M
- c)3.4 × 105M
- d)1.02 × 10–4M
Correct answer is option 'B'. Can you explain this answer?
For the reaction 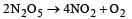 rate and rate constant are 1.02 × 10–4 mol lit–1 sec–1 and 3.4 × 10–5 sec–1 respectively then concentration of N2O5 at that time will be [2001]
rate and rate constant are 1.02 × 10–4 mol lit–1 sec–1 and 3.4 × 10–5 sec–1 respectively then concentration of N2O5 at that time will be [2001]
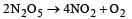 rate and rate constant are 1.02 × 10–4 mol lit–1 sec–1 and 3.4 × 10–5 sec–1 respectively then concentration of N2O5 at that time will be [2001]
rate and rate constant are 1.02 × 10–4 mol lit–1 sec–1 and 3.4 × 10–5 sec–1 respectively then concentration of N2O5 at that time will be [2001]a)
1.732M
b)
3M
c)
3.4 × 105M
d)
1.02 × 10–4M

|
Sarthak Saini answered |
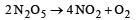
from the unit of rate constant it is clear that the reaction follow first order kinetics. Hence by rate law equation,
r = k [N2O5] where r = 1.02 × 10–4,
k = 3.4 × 10–5 1.02 × 10–4 = 3.4 × 10–5 [N2O5]
[N2O5] = 3M
r = k [N2O5] where r = 1.02 × 10–4,
k = 3.4 × 10–5 1.02 × 10–4 = 3.4 × 10–5 [N2O5]
[N2O5] = 3M
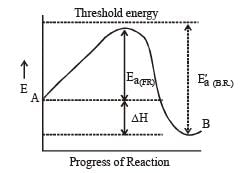
The activation energy for a simple chemical reaction A → B is Ea in forward direction. The activation energy for reverse reaction [2003]- a)Is always double of Ea
- b)Is negative of Ea
- c)Is always less than Ea
- d)Can be less than or more than Ea
Correct answer is option 'D'. Can you explain this answer?
The activation energy for a simple chemical reaction A → B is Ea in forward direction. The activation energy for reverse reaction [2003]
a)
Is always double of Ea
b)
Is negative of Ea
c)
Is always less than Ea
d)
Can be less than or more than Ea

|
Pooja Choudhary answered |
The activation energy of reverse reaction will depend upon whether the forward reaction is exothermic or endothermic.
As ΔH = Ea (forward reaction) – Ea(backward reaction)
For exothermic reaction
As ΔH = Ea (forward reaction) – Ea(backward reaction)
For exothermic reaction
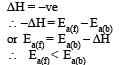
for endothermic reaction
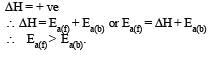
If 60% of a first order reaction was completed in 60 minutes, 50% of the same reaction would be completed in aproximately [2007]- a)45 minutes
- b)60 minutes
- c)40 minutes
- d)50 minutes (log 4 = 0.60, log 5 = 0.69)
Correct answer is option 'A'. Can you explain this answer?
If 60% of a first order reaction was completed in 60 minutes, 50% of the same reaction would be completed in aproximately [2007]
a)
45 minutes
b)
60 minutes
c)
40 minutes
d)
50 minutes (log 4 = 0.60, log 5 = 0.69)
|
|
Aditya Yadav answered |
For a first order reaction
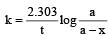
when t = 60 and x = 60%
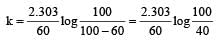
Now,
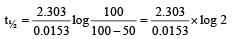
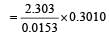 = 45.31 min.
= 45.31 min.For an exothermic reaction, the energy of activation of the reactants is [1994]- a)equal to the energy of activation of products
- b)less than the energy of activation of products
- c)greater than the energy of activation of products
- d)Sometimes greater and sometimes less than that of the products
Correct answer is option 'B'. Can you explain this answer?
For an exothermic reaction, the energy of activation of the reactants is [1994]
a)
equal to the energy of activation of products
b)
less than the energy of activation of products
c)
greater than the energy of activation of products
d)
Sometimes greater and sometimes less than that of the products

|
Snehal Shah answered |
Ea(Forward) + ΔH = Ea(back word)
For Exothermic reaction, ΔH = –ve and
∴ activation energy of reactant is less than the energy of activation of products.
For Exothermic reaction, ΔH = –ve and
∴ activation energy of reactant is less than the energy of activation of products.
The rate of a first order reaction is 1.5 × 10–2 mol L–1 min–1 at 0.5 M concentration of the reactant.The half life of the reaction is [2004]- a)0.383 min
- b)23.1 min
- c)8.73 min
- d)7.53 min
Correct answer is option 'B'. Can you explain this answer?
The rate of a first order reaction is 1.5 × 10–2 mol L–1 min–1 at 0.5 M concentration of the reactant.The half life of the reaction is [2004]
a)
0.383 min
b)
23.1 min
c)
8.73 min
d)
7.53 min

|
Shounak Nair answered |
For a first order reaction, A → products
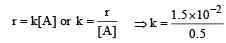
= 3 × 10–2
Further, 

The reaction of hydrogenandiodine monochloride is given as: [2007]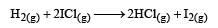 The reaction is of first order with respect to H2(g) and ICI(g), following mechanisms were proposed.
The reaction is of first order with respect to H2(g) and ICI(g), following mechanisms were proposed.
Mechanism A: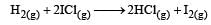 Mechanism B:
Mechanism B: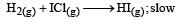
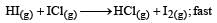 Which of the above mechanism(s) can be consistent with the given information about the reaction?
Which of the above mechanism(s) can be consistent with the given information about the reaction?- a)A and B both
- b)neither A nor B
- c)A only
- d)B only
Correct answer is option 'D'. Can you explain this answer?
The reaction of hydrogenandiodine monochloride is given as: [2007]
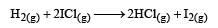
The reaction is of first order with respect to H2(g) and ICI(g), following mechanisms were proposed.
Mechanism A:
Mechanism A:
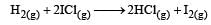
Mechanism B:
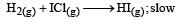
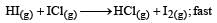
Which of the above mechanism(s) can be consistent with the given information about the reaction?
a)
A and B both
b)
neither A nor B
c)
A only
d)
B only

|
Sarthak Saini answered |
As the slowest step is the rate determining step thus the mechanism B will be more consistent with the given information also because it involve one molecule of H2 and one molecule of ICl it can expressed as r = k [H2][ICl] Which shows that the reaction is first order w.r.t. both H2 & ICl.
For the reaction 2A + B → 3C + D which of the following does not express the reaction rate ? [2006]- a)
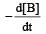
- b)
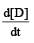
- c)
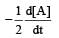
- d)
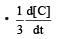
Correct answer is option 'D'. Can you explain this answer?
For the reaction 2A + B → 3C + D which of the following does not express the reaction rate ? [2006]
a)
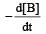
b)
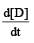
c)
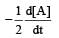
d)
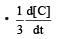

|
Nagendra Swamy answered |
For reaction aA+bB gives rise to cC+dD
formula is
-1/a = -1/b = 1/c = 1/d
formula is
-1/a = -1/b = 1/c = 1/d
Which one of the following statements for the order of a reaction is incorrect ? [2011]- a)Order can be determined only experimentally.
- b)Order is not influenced by stoichiometric coefficient of the reactants.
- c)Order of reaction is sum of power to the concentration terms of reactants to express the rate of reaction.
- d)Order of reaction is always whole number.
Correct answer is option 'D'. Can you explain this answer?
Which one of the following statements for the order of a reaction is incorrect ? [2011]
a)
Order can be determined only experimentally.
b)
Order is not influenced by stoichiometric coefficient of the reactants.
c)
Order of reaction is sum of power to the concentration terms of reactants to express the rate of reaction.
d)
Order of reaction is always whole number.

|
Arya Nair answered |
order of reaction may be zero, whole number or fractional.
For the reaction, 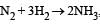 , [2009]
, [2009]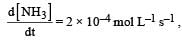 the value of
the value of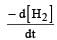 would be dt:
would be dt:- a)4 × 10–4 mol L–1 s–1
- b)6 × 10–4 mol L–1 s–1
- c)1 × 10–4 mol L–1 s–1
- d)3 × 10–4 mol L–1 s–1
Correct answer is option 'D'. Can you explain this answer?
For the reaction, 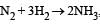 , [2009]
, [2009]
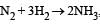 , [2009]
, [2009]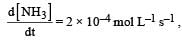 the value of
the value of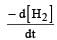 would be dt:
would be dt:a)
4 × 10–4 mol L–1 s–1
b)
6 × 10–4 mol L–1 s–1
c)
1 × 10–4 mol L–1 s–1
d)
3 × 10–4 mol L–1 s–1

|
Akshat Chavan answered |
Rate of disappearance of H2 = rate of formation of NH3.
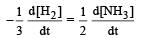
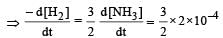
= 3 ×10 –4 mol L–1s –1
The unit of rate constant for a zero order reaction is [2011 M]- a)mol L–1 s–1
- b)L mol–1 s–1
- c)L2 mol–2 s–1
- d)s–1
Correct answer is option 'A'. Can you explain this answer?
The unit of rate constant for a zero order reaction is [2011 M]
a)
mol L–1 s–1
b)
L mol–1 s–1
c)
L2 mol–2 s–1
d)
s–1

|
Arya Khanna answered |
Rate = K(A)0 Unit of K = mol L–1 sec–1
 , rate of reaction
, rate of reaction 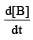 is equal to
is equal to- a)

- b)
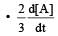
- c)
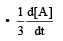
- d)
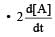
Correct answer is option 'B'. Can you explain this answer?
 , rate of reaction
, rate of reaction 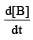 is equal to
is equal toa)

b)
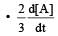
c)
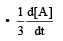
d)
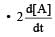

|
Prashanth Dasgupta answered |
 Rate of appearance of B is equal to rate of disappearance of A.
Rate of appearance of B is equal to rate of disappearance of A.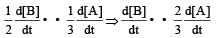
The temperature dependence of rate constant (k) of a chemical reaction is written in terms of Arrhenius equation, 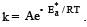 . Activation energy
. Activation energy 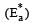 of the reaction can be calculated by plotting [2003]
of the reaction can be calculated by plotting [2003]- a)
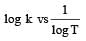
- b)k vs T
- c)
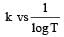
- d)
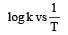
Correct answer is option 'D'. Can you explain this answer?
The temperature dependence of rate constant (k) of a chemical reaction is written in terms of Arrhenius equation, 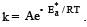 . Activation energy
. Activation energy 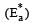 of the reaction can be calculated by plotting [2003]
of the reaction can be calculated by plotting [2003]
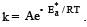 . Activation energy
. Activation energy 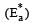 of the reaction can be calculated by plotting [2003]
of the reaction can be calculated by plotting [2003]a)
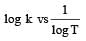
b)
k vs T
c)
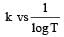
d)
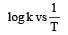

|
Mrosmick Mani answered |
D cz A nd R is const so, logk directly proportional to Ea/T
When a biochemical reaction is carried out in laboratory in the absence of enzyme then rate of reaction obtained is 10–6 times, then activation energy of reaction in the presence of enzyme is- a)
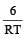 [2001]
[2001] - b)Different from Ea obtained in laboratory
- c)P is required
- d)Can't say anything
Correct answer is option 'B'. Can you explain this answer?
When a biochemical reaction is carried out in laboratory in the absence of enzyme then rate of reaction obtained is 10–6 times, then activation energy of reaction in the presence of enzyme is
a)
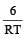 [2001]
[2001]b)
Different from Ea obtained in laboratory
c)
P is required
d)
Can't say anything

|
Nilotpal Gupta answered |
The presence of enzyme (catalyst) increases the speed of reaction by lowering the energy barrier, i.e. a new path is followed with lower activation energy.
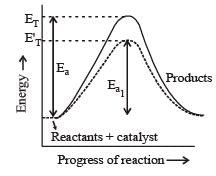
Here ET is the threshold energy.
Ea and Ea1 is energy of activation of reaction in absence and presence of catalyst respectively.
Ea and Ea1 is energy of activation of reaction in absence and presence of catalyst respectively.
The bromination of acetone that occurs in acid solution is represented by this equation. [2008]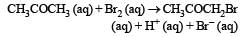 These kinetic data were obtained for given reaction concentrations.Initial Concentrations, M
These kinetic data were obtained for given reaction concentrations.Initial Concentrations, M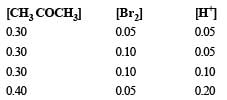 Initial rate, disappearance of Br2, Ms–15.7×10–5
Initial rate, disappearance of Br2, Ms–15.7×10–5
5.7 × 10–5
1.2 × 10–4
3.1 × 10–4Base on these data, the rate equations is:- a)Rate = k[CH3COCH3][H+]
- b)Rate = k [CH = COCH3][Br2]
- c)Rate = k [CH3 COCH3] [Br2] [H+]2
- d)Rate = k [CH3COCH3][Br2] [H+]
Correct answer is option 'A'. Can you explain this answer?
The bromination of acetone that occurs in acid solution is represented by this equation. [2008]
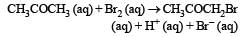
These kinetic data were obtained for given reaction concentrations.
Initial Concentrations, M

Initial rate, disappearance of Br2, Ms–1
5.7×10–5
5.7 × 10–5
1.2 × 10–4
3.1 × 10–4
5.7 × 10–5
1.2 × 10–4
3.1 × 10–4
Base on these data, the rate equations is:
a)
Rate = k[CH3COCH3][H+]
b)
Rate = k [CH = COCH3][Br2]
c)
Rate = k [CH3 COCH3] [Br2] [H+]2
d)
Rate = k [CH3COCH3][Br2] [H+]

|
Anand Jain answered |
Rewriting the given data for the reaction
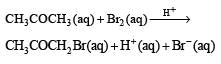

Actually this reaction is autocatalyzed and involves complex calculation for concentration terms.
We can look at the above results in a simple way to find the dependence of reaction rate (i.e. rate of disappearance of Br2).
From data (1) and (2) in which concentration of CH3COCH3 and H+ remain unchanged and only the concentration of Br2 is doubled, there is no change in rate of reaction. It means the rate of reaction is independent of concentration of Br2.
Again from (2) and (3) in which (CH3CO CH3) and (Br2) remain constant but H+ increases from 0.05 M to 0.10 i.e. doubled, the rate of reaction changes from 5.7×10–5 to 1.2 × 10–4 (or 12 × 10–5), thus it also becomes almost doubled. It shows that rate of reaction is directly proportional to [H+].
From (3) and (4), the rate should have doubled due to increase in conc of [H+] from 0.10 M to 0.20 M but the rate has changed from 1.2× 10–4 to 3.1×10–4. This is due to change in concentration of CH3 CO CH3 from 0.30 M to 0.40 M. Thus the rate is directly proportional to [CH3 COCH3].
We now get rate = k [CH3COCH3]1[Br2]0[H+]1
= k [CH3COCH3][H+].
We can look at the above results in a simple way to find the dependence of reaction rate (i.e. rate of disappearance of Br2).
From data (1) and (2) in which concentration of CH3COCH3 and H+ remain unchanged and only the concentration of Br2 is doubled, there is no change in rate of reaction. It means the rate of reaction is independent of concentration of Br2.
Again from (2) and (3) in which (CH3CO CH3) and (Br2) remain constant but H+ increases from 0.05 M to 0.10 i.e. doubled, the rate of reaction changes from 5.7×10–5 to 1.2 × 10–4 (or 12 × 10–5), thus it also becomes almost doubled. It shows that rate of reaction is directly proportional to [H+].
From (3) and (4), the rate should have doubled due to increase in conc of [H+] from 0.10 M to 0.20 M but the rate has changed from 1.2× 10–4 to 3.1×10–4. This is due to change in concentration of CH3 CO CH3 from 0.30 M to 0.40 M. Thus the rate is directly proportional to [CH3 COCH3].
We now get rate = k [CH3COCH3]1[Br2]0[H+]1
= k [CH3COCH3][H+].
 , it would be a zero order reaction when[2002]
, it would be a zero order reaction when[2002]- a)the rate of reaction is proportional to square of concentration of A
- b)the rate of reaction remains same at any concentration of A
- c)the rate remains unchanged at any concentration of B and C
- d)the rate of reaction doubles if concentration of B is increased to double
Correct answer is option 'B'. Can you explain this answer?
 , it would be a zero order reaction when[2002]
, it would be a zero order reaction when[2002]a)
the rate of reaction is proportional to square of concentration of A
b)
the rate of reaction remains same at any concentration of A
c)
the rate remains unchanged at any concentration of B and C
d)
the rate of reaction doubles if concentration of B is increased to double

|
Soumya Ahuja answered |
For reaction  If it is zero order reaction r = k [A]0, i.e the rate remains same at any concentration of 'A'. i.e independent upon concentration of A.
If it is zero order reaction r = k [A]0, i.e the rate remains same at any concentration of 'A'. i.e independent upon concentration of A.
 If it is zero order reaction r = k [A]0, i.e the rate remains same at any concentration of 'A'. i.e independent upon concentration of A.
If it is zero order reaction r = k [A]0, i.e the rate remains same at any concentration of 'A'. i.e independent upon concentration of A.Chapter doubts & questions for Chemical Kinetics - NEET Past Year Papers 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chemical Kinetics - NEET Past Year Papers in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup


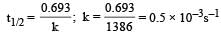

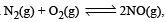 , the equilibrium constant is K1. The equilibrium constant is K2 for the reaction [2011]
, the equilibrium constant is K1. The equilibrium constant is K2 for the reaction [2011] 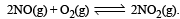 .What is K for the reaction
.What is K for the reaction 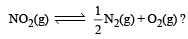


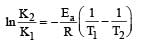
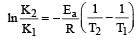
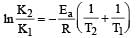
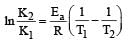

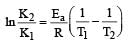
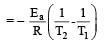
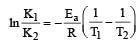
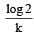
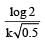
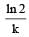
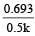

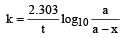
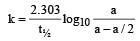
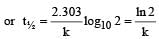
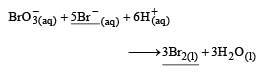
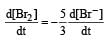
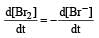
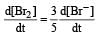
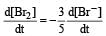

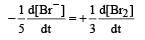
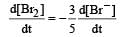
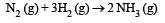 The equality relationship between
The equality relationship between 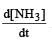 and
and