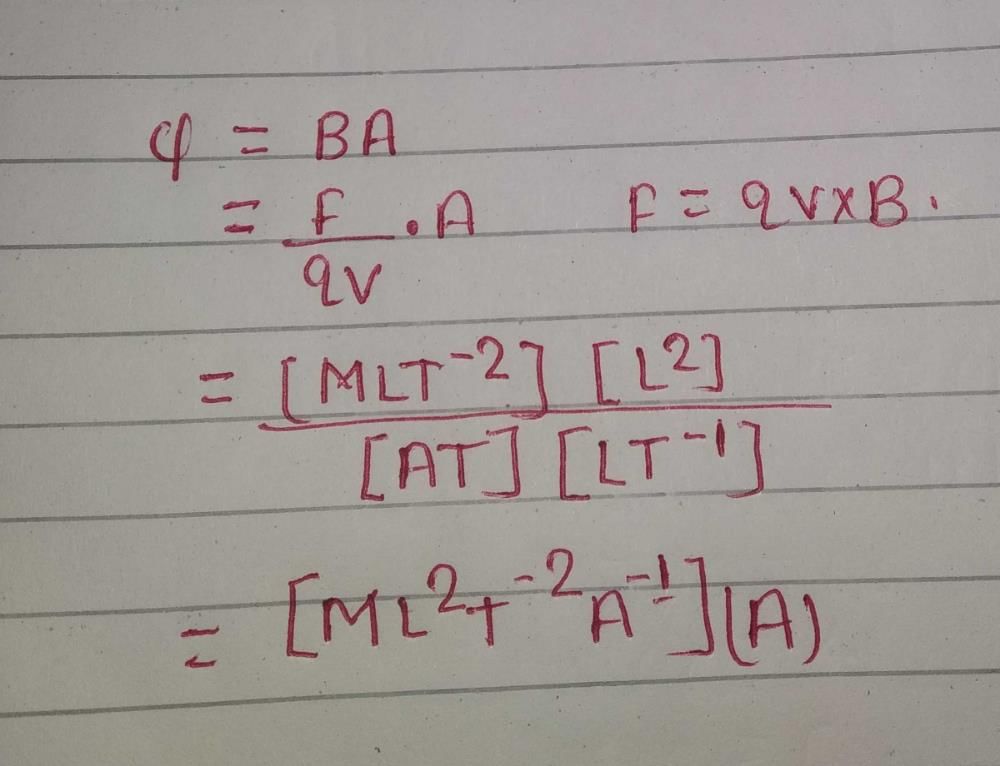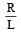All Exams >
NEET >
NEET Past Year Papers >
All Questions
All questions of Units and Measurements for NEET Exam
If the dimensions of a physical quantity are given by Ma Lb Tc, then the physical quantity will be:
- a)Velocity if a = 1, b = 0, c = – 1
- b)Acceleration if a = 1, b = 1, c = – 2
- c)Force if a = -1, b = 1, c = – 2
- d)Pressure if a = 1, b = - 1, c = - 2
Correct answer is option 'D'. Can you explain this answer?
If the dimensions of a physical quantity are given by Ma Lb Tc, then the physical quantity will be:
a)
Velocity if a = 1, b = 0, c = – 1
b)
Acceleration if a = 1, b = 1, c = – 2
c)
Force if a = -1, b = 1, c = – 2
d)
Pressure if a = 1, b = - 1, c = - 2
|
Anitosh Dash answered |
For velocity a=0 b=1 and c=-1
for acceleration a=0 b=2 and c=-2
for force a=1 b=1 and c=-2
for pressure= F/A a=1 b=-1 and c=-2
for acceleration a=0 b=2 and c=-2
for force a=1 b=1 and c=-2
for pressure= F/A a=1 b=-1 and c=-2
The density of material in CGS system of units is 4g/cm3. In a system of units in which unit of length is 10 cm and unit of mass is 100 g, the value of density of material will be [2011M]- a)0.4
- b)40
- c)400
- d)0.04
Correct answer is option 'B'. Can you explain this answer?
The density of material in CGS system of units is 4g/cm3. In a system of units in which unit of length is 10 cm and unit of mass is 100 g, the value of density of material will be [2011M]
a)
0.4
b)
40
c)
400
d)
0.04
|
Ananya Das answered |
In CGS system,
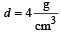
The unit of mass is 100g and unit of length is 10 cm, so
density =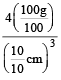 
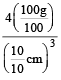
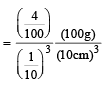
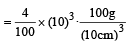
= 40 unit
The dimensions of universal gravitational constant are [1992, 2004]- a)M–2 L2 T–1
- b)M–1 L3 T–2
- c)M L2 T–1
- d)M–2 L3 T–2
Correct answer is option 'B'. Can you explain this answer?
The dimensions of universal gravitational constant are [1992, 2004]
a)
M–2 L2 T–1
b)
M–1 L3 T–2
c)
M L2 T–1
d)
M–2 L3 T–2
|
Pankaj Datta answered |
L3 T-2(b)M-1 L3 T-2(c)M-2 L3 T-2(d)M L3 T-2
The correct answer is (b) M-1 L3 T-2.
Universal gravitational constant, denoted by G, is defined as the proportionality constant in the law of universal gravitation. According to this law, the force of attraction between two point masses is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
Therefore, the dimensions of G can be derived by equating the dimensions of force, mass, and distance in the above equation.
Dimensions of force = M L T-2
Dimensions of mass = M
Dimensions of distance = L
Substituting these values in the equation, we get:
M L T-2 = G (M2/L2)
On simplifying, we get:
G = M-1 L3 T-2
Hence, the dimensions of universal gravitational constant are M-1 L3 T-2.
The correct answer is (b) M-1 L3 T-2.
Universal gravitational constant, denoted by G, is defined as the proportionality constant in the law of universal gravitation. According to this law, the force of attraction between two point masses is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
Therefore, the dimensions of G can be derived by equating the dimensions of force, mass, and distance in the above equation.
Dimensions of force = M L T-2
Dimensions of mass = M
Dimensions of distance = L
Substituting these values in the equation, we get:
M L T-2 = G (M2/L2)
On simplifying, we get:
G = M-1 L3 T-2
Hence, the dimensions of universal gravitational constant are M-1 L3 T-2.
The dimensional formula of torque is [1989]- a)[ML2T–2]
- b)[MLT–2]
- c)[ML–1T–2]
- d)[ML–2T–2]
Correct answer is option 'A'. Can you explain this answer?
The dimensional formula of torque is [1989]
a)
[ML2T–2]
b)
[MLT–2]
c)
[ML–1T–2]
d)
[ML–2T–2]
|
Aman Sharma answered |
ζ = [Force × distance] = [MLT–2] [L] = ML2T–2
In a particular system, the unit of length, mass and time are chosen to be 10 cm, 10 g and 0.1 s respectively. The unit of force in this system will be equivalen t to [1994]- a)0.1 N
- b)1 N
- c)10 N
- d)100 N
Correct answer is option 'A'. Can you explain this answer?
In a particular system, the unit of length, mass and time are chosen to be 10 cm, 10 g and 0.1 s respectively. The unit of force in this system will be equivalen t to [1994]
a)
0.1 N
b)
1 N
c)
10 N
d)
100 N
|
Arnav Iyer answered |
[F] = MLT–2 = (10g) (10 cm) (0.1s)–2
= (10–2 kg) (10–1m) (10–1s)–2 = 10–1N.
= (10–2 kg) (10–1m) (10–1s)–2 = 10–1N.
The frequency of vibr ation f of a mass m suspended from a spring of spring constant k is given by a relation of the type f = c mx ky, where c is a dimensionless constant. The values of x and y are [1990]- a)
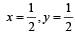
- b)
- c)
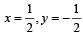
- d)
Correct answer is option 'D'. Can you explain this answer?
The frequency of vibr ation f of a mass m suspended from a spring of spring constant k is given by a relation of the type f = c mx ky, where c is a dimensionless constant. The values of x and y are [1990]
a)
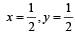
b)
c)
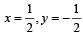
d)
|
Rhea Sarkar answered |
f = c mx ky; Spring constant k = force/length. [M0L0T–1] = [Mx (MT–2)y] =[ Mx + y T–2y]
⇒ x+y = 0, -2y = -1 or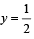 
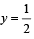
Therefore, x = -
If the error in the measurement of radius of a sphere is 2%, then the error in the determination of volume of the sphere will be: [2008]- a)4%
- b)6%
- c)8%
- d)2%
Correct answer is option 'B'. Can you explain this answer?
If the error in the measurement of radius of a sphere is 2%, then the error in the determination of volume of the sphere will be: [2008]
a)
4%
b)
6%
c)
8%
d)
2%
|
Arpita Tiwari answered |
Error in the measurement of radius of a sphere = 2%
Volume of the sphere =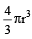 
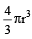
∴ Error in the volume =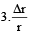 
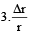
= 3 × 2% = 6%
If C and R denote capacitance and resistance, the dimensional formula of CR is [1988]- a)[M0L0T1]
- b)[M0L0T0]
- c)[M0L0T–1]
- d)not expressible in terms of M,L,T.
Correct answer is option 'A'. Can you explain this answer?
If C and R denote capacitance and resistance, the dimensional formula of CR is [1988]
a)
[M0L0T1]
b)
[M0L0T0]
c)
[M0L0T–1]
d)
not expressible in terms of M,L,T.
|
Nayanika Reddy answered |
CR = [M -1 L-2 T 4 A 2 ][M1 L2 T -3 A -2 ] = [T] = [M0 L0 T1]
The dimensional formula for angular momentum is[1988]- a)[M0L2T–2]
- b)[ML2T–1]
- c)[MLT–1]
- d)[ML2T–2]
Correct answer is option 'B'. Can you explain this answer?
The dimensional formula for angular momentum is[1988]
a)
[M0L2T–2]
b)
[ML2T–1]
c)
[MLT–1]
d)
[ML2T–2]
|
Abhiram Nair answered |
[Angular momentum ] = [Momentum of inertia] × [Angular velocity] = ML2 × T–1
= ML2T–1
= ML2T–1
The dimensional formula of pressure is [1990]- a)[MLT–2]
- b)[ML–1T2]
- c)[ML–1T–2]
- d)[MLT2]
Correct answer is option 'C'. Can you explain this answer?
The dimensional formula of pressure is [1990]
a)
[MLT–2]
b)
[ML–1T2]
c)
[ML–1T–2]
d)
[MLT2]
|
|
Arpita Tiwari answered |
[Pressure] = [Force] / [Area]
= ML–1T–2According to Newton, the viscous force acting between liquid layers of area A and velocity gradient ΔV/ΔZ is given by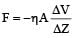
where η is constant called coefficient of viscosity. The dimensional formula of η is [1990]
- a)ML–2T–2
- b)M0L0T0
- c)ML2T–2
- d)ML–1T–1
Correct answer is option 'D'. Can you explain this answer?
According to Newton, the viscous force acting between liquid layers of area A and velocity gradient ΔV/ΔZ is given by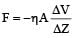 where η is constant called coefficient of viscosity. The dimensional formula of η is [1990]
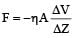where η is constant called coefficient of viscosity. The dimensional formula of η is [1990] a)
ML–2T–2
b)
M0L0T0
c)
ML2T–2
d)
ML–1T–1
|
Prashanth Dasgupta answered |
Substitute the dimension al formula of F, A, ΔV and ΔZ on both sides and find that for η.
P represents radiation pressure, crepresents speed of light and Q represents radiation energy striking unit area per sec. The non zero integers x, y, z such that Px Qy cz is dimensionless are [1992]
- a)x = 1, y = 1, z = 1
- b)x = – 1, y = 1, z = 1
- c)x = 1, y = – 1, z = 1
- d)x = 1, y = 1, z = – 1
Correct answer is option 'C'. Can you explain this answer?
P represents radiation pressure, crepresents speed of light and Q represents radiation energy striking unit area per sec. The non zero integers x, y, z such that Px Qy cz is dimensionless are [1992]
a)
x = 1, y = 1, z = 1
b)
x = – 1, y = 1, z = 1
c)
x = 1, y = – 1, z = 1
d)
x = 1, y = 1, z = – 1
|
Snehal Shah answered |
The ratio of the dimension of Planck’s constant and that of the moment of inertia is the dimension of [2005]- a)time
- b)frequency
- c)angular momentum
- d)velocity
Correct answer is option 'B'. Can you explain this answer?
The ratio of the dimension of Planck’s constant and that of the moment of inertia is the dimension of [2005]
a)
time
b)
frequency
c)
angular momentum
d)
velocity
|
|
Rohan Pillai answered |
The Planck length is approximately 1.616229 x 10^-35 meters, and the Planck time is approximately 5.39116 x 10^-44 seconds.
The ratio of the Planck length to the Planck time can be calculated as:
(1.616229 x 10^-35 m) / (5.39116 x 10^-44 s) = 2.998 x 10^8 m/s
This ratio represents the speed of light in a vacuum, which is a fundamental constant in physics.
The ratio of the Planck length to the Planck time can be calculated as:
(1.616229 x 10^-35 m) / (5.39116 x 10^-44 s) = 2.998 x 10^8 m/s
This ratio represents the speed of light in a vacuum, which is a fundamental constant in physics.
Which two of the following five physical parameters have the same dimensions?
(A) Energy density [2008]
(B) Refractive index
(C) Dielectric constant
(D) Young’s modulus
(E) Magnetic field- a)(B) and (D)
- b)(C) and (E)
- c)(A) and (D)
- d)(A) and (E)
Correct answer is option 'C'. Can you explain this answer?
Which two of the following five physical parameters have the same dimensions?
(A) Energy density [2008]
(B) Refractive index
(C) Dielectric constant
(D) Young’s modulus
(E) Magnetic field
(A) Energy density [2008]
(B) Refractive index
(C) Dielectric constant
(D) Young’s modulus
(E) Magnetic field
a)
(B) and (D)
b)
(C) and (E)
c)
(A) and (D)
d)
(A) and (E)
|
Meghana Dey answered |
Understanding Physical Parameters
In this problem, we need to identify which two physical parameters have the same dimensions. Let's break down each option:
Energy Density
- Energy density is defined as energy per unit volume.
- Its dimensions can be expressed as [Energy]/[Volume].
- Energy has dimensions of ML²T⁻², and volume has dimensions of L³.
- Thus, the dimensions of energy density are ML⁻¹T⁻².
Refractive Index
- The refractive index is a dimensionless quantity.
- It is the ratio of the speed of light in vacuum to the speed of light in a medium.
- Therefore, it has no dimensions.
Dielectric Constant
- The dielectric constant is also dimensionless.
- It represents the ability of a medium to store electrical energy in an electric field.
- Like the refractive index, it has no dimensions.
Young's Modulus
- Young's modulus is a measure of the stiffness of a material.
- It is defined as stress/strain.
- Stress has dimensions of ML⁻¹T⁻² and strain is dimensionless.
- Thus, the dimensions of Young's modulus are also ML⁻¹T⁻².
Magnetic Field
- The magnetic field (B) has dimensions of force per unit charge per unit velocity.
- Its dimensions can be expressed as [MLT⁻²]/[Q][L/T] = MLT⁻²Q⁻¹.
Conclusion
From the analysis, we find:
- Energy density and Young's modulus both share the dimensions of ML⁻¹T⁻².
- Options (B) and (C) are dimensionless, while (E) has different dimensions.
Thus, the correct answer is option C: (A) and (D), as they both have the same dimensions.
In this problem, we need to identify which two physical parameters have the same dimensions. Let's break down each option:
Energy Density
- Energy density is defined as energy per unit volume.
- Its dimensions can be expressed as [Energy]/[Volume].
- Energy has dimensions of ML²T⁻², and volume has dimensions of L³.
- Thus, the dimensions of energy density are ML⁻¹T⁻².
Refractive Index
- The refractive index is a dimensionless quantity.
- It is the ratio of the speed of light in vacuum to the speed of light in a medium.
- Therefore, it has no dimensions.
Dielectric Constant
- The dielectric constant is also dimensionless.
- It represents the ability of a medium to store electrical energy in an electric field.
- Like the refractive index, it has no dimensions.
Young's Modulus
- Young's modulus is a measure of the stiffness of a material.
- It is defined as stress/strain.
- Stress has dimensions of ML⁻¹T⁻² and strain is dimensionless.
- Thus, the dimensions of Young's modulus are also ML⁻¹T⁻².
Magnetic Field
- The magnetic field (B) has dimensions of force per unit charge per unit velocity.
- Its dimensions can be expressed as [MLT⁻²]/[Q][L/T] = MLT⁻²Q⁻¹.
Conclusion
From the analysis, we find:
- Energy density and Young's modulus both share the dimensions of ML⁻¹T⁻².
- Options (B) and (C) are dimensionless, while (E) has different dimensions.
Thus, the correct answer is option C: (A) and (D), as they both have the same dimensions.
The dimensions of (μ0ε0)–1/2 are : [2012M]- a)[L1/2T–1/2]
- b)[L–1T]
- c)[LT–1]
- d)[L1/2T1/2]
Correct answer is option 'C'. Can you explain this answer?
The dimensions of (μ0ε0)–1/2 are : [2012M]
a)
[L1/2T–1/2]
b)
[L–1T]
c)
[LT–1]
d)
[L1/2T1/2]
|
Soumya Ahuja answered |
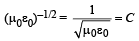: speed of lightwhere ε0 = permittivity of free space
μ0 = permeability of free space
So dimension LT–1
Dimensions of resistance in an electrical circuit, in terms of dimension of mass M, of length L, of time T and of current I, would be [2007]- a)ML2T–2
- b)ML2T–1I–1
- c)ML2T–3I–2
- d)ML2T–3I–1
Correct answer is option 'C'. Can you explain this answer?
Dimensions of resistance in an electrical circuit, in terms of dimension of mass M, of length L, of time T and of current I, would be [2007]
a)
ML2T–2
b)
ML2T–1I–1
c)
ML2T–3I–2
d)
ML2T–3I–1
|
|
Palak Basak answered |
The dimensions of resistance in an electrical circuit can be derived using Ohm's Law, which states that resistance (R) is equal to voltage (V) divided by current (I):
R = V/I
The dimensions of voltage can be represented as [ML2T-3I-1] (mass, length, time, and current), and the dimensions of current can be represented as [I] (current).
Therefore, the dimensions of resistance can be determined by dividing the dimensions of voltage by the dimensions of current:
[R] = [ML2T-3I-1] / [I]
Simplifying this expression:
[R] = [ML2T-3]
Therefore, the dimensions of resistance in an electrical circuit, in terms of mass (M), length (L), time (T), and current (I), would be a) ML2T.
R = V/I
The dimensions of voltage can be represented as [ML2T-3I-1] (mass, length, time, and current), and the dimensions of current can be represented as [I] (current).
Therefore, the dimensions of resistance can be determined by dividing the dimensions of voltage by the dimensions of current:
[R] = [ML2T-3I-1] / [I]
Simplifying this expression:
[R] = [ML2T-3]
Therefore, the dimensions of resistance in an electrical circuit, in terms of mass (M), length (L), time (T), and current (I), would be a) ML2T.
In an experiment four quantities a, b, c and d are measured with percentage error 1%, 2%, 3% and 4% respectively. Quantity P is calculated as follows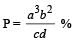 
error in P is [NEET 2013]- a)10%
- b)7%
- c)4%
- d)14%
Correct answer is option 'D'. Can you explain this answer?
In an experiment four quantities a, b, c and d are measured with percentage error 1%, 2%, 3% and 4% respectively. Quantity P is calculated as follows 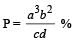error in P is [NEET 2013]
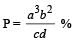error in P is [NEET 2013]a)
10%
b)
7%
c)
4%
d)
14%
|
|
Abhiram Nair answered |
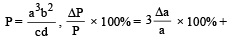
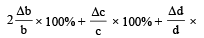100%.= 3 × 1% + 2 × 2% + 3% + 4% = 14%
The velocity v of a particle at time t is given by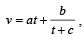
where a, b and c are constant.The dimensions of a, b and c are respectively [2006]- a)L2, T and LT2
- b)LT2, LT and L
- c)L, LT and T2
- d)LT–2, L and T
Correct answer is option 'D'. Can you explain this answer?
The velocity v of a particle at time t is given by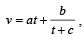 where a, b and c are constant.The dimensions of a, b and c are respectively [2006]
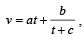where a, b and c are constant.The dimensions of a, b and c are respectively [2006]a)
L2, T and LT2
b)
LT2, LT and L
c)
L, LT and T2
d)
LT–2, L and T
|
|
Raza Great answered |
V=at+b/t+c
As c is added to t, ∴ [c]=[T]
[at]=[LT^−1] or, [a]=[LT-^1]/[T]= [LT−^2]
[b]/[T]= [LT−^1] ∴[b]=[L].
As c is added to t, ∴ [c]=[T]
[at]=[LT^−1] or, [a]=[LT-^1]/[T]= [LT−^2]
[b]/[T]= [LT−^1] ∴[b]=[L].
Which of the following is a dimensional constan t? [1995]- a)Refractive index
- b)Poisson s ratio
- c)Relative density
- d)Gravitational constant
Correct answer is option 'D'. Can you explain this answer?
Which of the following is a dimensional constan t? [1995]
a)
Refractive index
b)
Poisson s ratio
c)
Relative density
d)
Gravitational constant
|
|
Kusum answered |
Gravitational constant also known as universal gravitational constant has a symbol G and has a dimension [M-¹L³T-²] while others are dimensionless constant.
The dimension of 
where ε0 is permittivity of free space and E is electric field, is:[2010]- a)ML2 T–2
- b)ML–1T–2
- c)ML2T–1
- d)MLT–1
Correct answer is option 'B'. Can you explain this answer?
The dimension of where ε0 is permittivity of free space and E is electric field, is:[2010]
where ε0 is permittivity of free space and E is electric field, is:[2010]a)
ML2 T–2
b)
ML–1T–2
c)
ML2T–1
d)
MLT–1
|
Surbhi Das answered |
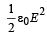represents energy density i.e., energy per unit volume.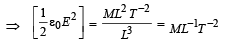
Of the following quantities, which one has dimension different from the remaining three? [1989]- a)Energy per unit volume
- b)Force per unit area
- c)Product of voltage and charge per unit volume
- d)Angular momentum.
Correct answer is option 'D'. Can you explain this answer?
Of the following quantities, which one has dimension different from the remaining three? [1989]
a)
Energy per unit volume
b)
Force per unit area
c)
Product of voltage and charge per unit volume
d)
Angular momentum.
|
Swara Desai answered |
For angular momentum, the dimensional formula is ML2T–1. For other three, it is ML2T–2.
The percentage errors in the measurement of mass and speed are 2% and 3% respectively.The error in kinetic energy obtained by measuring mass and speed will be [1995]- a)12 %
- b)10 %
- c)8 %
- d)2 %
Correct answer is option 'C'. Can you explain this answer?
The percentage errors in the measurement of mass and speed are 2% and 3% respectively.The error in kinetic energy obtained by measuring mass and speed will be [1995]
a)
12 %
b)
10 %
c)
8 %
d)
2 %
|
Aashna Rane answered |
Given information:
- Percentage error in mass measurement = 2%
- Percentage error in speed measurement = 3%
To find:
- The error in kinetic energy obtained by measuring mass and speed.
Solution:
Formula for kinetic energy:
The formula for kinetic energy (KE) is given by:
KE = (1/2)mv²
where:
- KE is the kinetic energy,
- m is the mass,
- v is the speed.
Error in kinetic energy:
The error in kinetic energy can be calculated using the formula for relative error. The relative error is given by:
Relative error = (error in quantity) / (actual quantity)
Error in mass:
Given that the percentage error in mass measurement is 2%, the error in mass can be calculated as:
Error in mass = (2/100) * mass
Error in speed:
Given that the percentage error in speed measurement is 3%, the error in speed can be calculated as:
Error in speed = (3/100) * speed
Error in kinetic energy:
To find the error in kinetic energy, we need to calculate the derivative of the kinetic energy formula with respect to both mass and speed:
dKE/dm = (1/2) * v²
dKE/dv = m * v
Using the formula for relative error, the error in kinetic energy can be calculated as:
Error in kinetic energy = [(dKE/dm) * (error in mass)] + [(dKE/dv) * (error in speed)]
Substituting the calculated values:
Error in kinetic energy = [(1/2) * v² * (2/100) * mass] + [m * v * (3/100) * speed]
Error in kinetic energy = (1/100) * (v² * mass + 3 * m * v * speed)
Calculating the percentage error:
To find the percentage error, we need to divide the error in kinetic energy by the actual kinetic energy and multiply by 100:
Percentage error = (Error in kinetic energy / Actual kinetic energy) * 100
Since we do not know the actual kinetic energy, we cannot calculate the exact percentage error. However, we can simplify the equation for the error in kinetic energy:
Percentage error = (1/100) * (v² * mass + 3 * m * v * speed) / Actual kinetic energy * 100
From the equation, we can see that the percentage error depends on the actual kinetic energy. Without knowing the actual kinetic energy, we cannot determine the exact percentage error. Therefore, the answer cannot be determined without additional information.
A certain body weighs 22.42 gm an d h as a measured volume of 4.7 cc. The possible error in the measurement of mass and volume are 0.01 gm and 0.1 cc. Then maximum error in the den sity will be [1991]- a)22 %
- b)2 %
- c)0.2 %
- d)0.02 %
Correct answer is option 'B'. Can you explain this answer?
A certain body weighs 22.42 gm an d h as a measured volume of 4.7 cc. The possible error in the measurement of mass and volume are 0.01 gm and 0.1 cc. Then maximum error in the den sity will be [1991]
a)
22 %
b)
2 %
c)
0.2 %
d)
0.02 %
|
Krish Chakraborty answered |
D = M/V
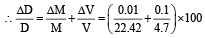=2 %The pair of quantities having same dimensions is [NEET Kar. 2013]- a)Young’s modulus and energy
- b)impulse and surface tension
- c)angular momentum and work
- d)work and torque
Correct answer is option 'D'. Can you explain this answer?
The pair of quantities having same dimensions is [NEET Kar. 2013]
a)
Young’s modulus and energy
b)
impulse and surface tension
c)
angular momentum and work
d)
work and torque
|
|
Arnav Iyer answered |
Work = Force × displacement Torque = Force × force arm
= mass × acceleration × length
= [M] × [LT–2] × [L] = [M L2T–2]
The density of a cube is measured by measuring its mass and length of its sides. If the maximum error in the measurement of mass and length are 4% and 3% respectively, the maximum error in the measurement of den sity will be [1996]- a)7%
- b)9%
- c)12%
- d)13%
Correct answer is option 'D'. Can you explain this answer?
The density of a cube is measured by measuring its mass and length of its sides. If the maximum error in the measurement of mass and length are 4% and 3% respectively, the maximum error in the measurement of den sity will be [1996]
a)
7%
b)
9%
c)
12%
d)
13%
|
Abhishek Choudhary answered |
Density =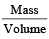 
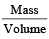
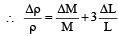
% error in density = % error in Mass + 3 (% error in length]
= 4 + 3(3) = 13%
= 4 + 3(3) = 13%
urpentine oil is flowing through a tube of length l and radius r. The pressure difference between the two ends of the tube is P. The viscosity of oil is given by 
where v is the velocity of oil at a distance a from the axis of the tube. The dimensions of η are- a)[M0L0T0]
- b)[MLT–1]
- c)[ML2T–2]
- d)[ML–1T–1]
Correct answer is option 'D'. Can you explain this answer?
urpentine oil is flowing through a tube of length l and radius r. The pressure difference between the two ends of the tube is P. The viscosity of oil is given by where v is the velocity of oil at a distance a from the axis of the tube. The dimensions of η are
where v is the velocity of oil at a distance a from the axis of the tube. The dimensions of η area)
[M0L0T0]
b)
[MLT–1]
c)
[ML2T–2]
d)
[ML–1T–1]
|
Aniket Chawla answered |
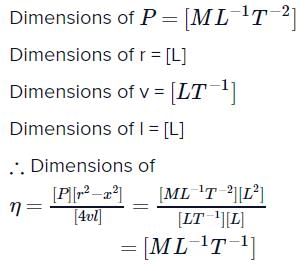
The dimensions of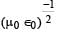 
are [2011]- a)[L1/2 T–1/2]
- b)[L–1 T]
- c)[L T–1]
- d)[L–1/2 T1/2]
Correct answer is option 'C'. Can you explain this answer?
The dimensions of 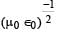are [2011]
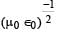are [2011]a)
[L1/2 T–1/2]
b)
[L–1 T]
c)
[L T–1]
d)
[L–1/2 T1/2]
|
Shounak Nair answered |
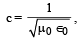, so, dimensions are [LTT–1].The dimensions of Planck’s constant are same as- a)energy
- b)power [2001]
- c)momentum
- d)angular momentum
Correct answer is option 'D'. Can you explain this answer?
The dimensions of Planck’s constant are same as
a)
energy
b)
power [2001]
c)
momentum
d)
angular momentum
|
Raghav Khanna answered |
We know that E = hv
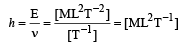
Angular momentum = Iω
= [ML2][T–1] = [ML2T–1]
= [ML2][T–1] = [ML2T–1]
Chapter doubts & questions for Units and Measurements - NEET Past Year Papers 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Units and Measurements - NEET Past Year Papers in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
NEET Past Year Papers
86 docs|146 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup