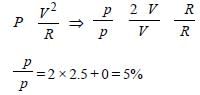All Exams >
NEET >
NEET Past Year Papers >
All Questions
All questions of Current Electricity for NEET Exam
A wire of resistance 12 Ωm-1 is bent to form a complete circle of radius 10 cm. The resistance between its two diametrically opposite point, A and B as shown in the figure, is [2009]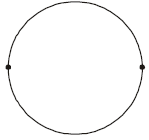
- a)3Ω
- b)6π Ω
- c)6Ω
- d)0. 6π Ω
Correct answer is option 'D'. Can you explain this answer?
A wire of resistance 12 Ωm-1 is bent to form a complete circle of radius 10 cm. The resistance between its two diametrically opposite point, A and B as shown in the figure, is [2009]
a)
3Ω
b)
6π Ω
c)
6Ω
d)
0. 6π Ω
|
|
Ram Mohith answered |
The two halves (or semicircles) are in parallel combination.
Length of each part is πr = π(0.1) m
Resistance of each part = 12(0.1π) = 1.2π
We know that when two equal resistance are kept in parallel the equivalent resistance will be half of any one resistance. So, the equivalent resistance between A and B is 0.6π
Length of each part is πr = π(0.1) m
Resistance of each part = 12(0.1π) = 1.2π
We know that when two equal resistance are kept in parallel the equivalent resistance will be half of any one resistance. So, the equivalent resistance between A and B is 0.6π
Consider the following two statements:
(a) Kirchhoff's junction law follows from the conservation of charge.
(b) Kirchhoff's loop law follows from the conservation of energy.Which of the following is correct? [2010]- a)Both (a) and (b) are wrong
- b)(a) is correct and (b) is wrong
- c)(a) is wrong and (b) is correct
- d)Both (a) and (b) are correct
Correct answer is option 'D'. Can you explain this answer?
Consider the following two statements:
(a) Kirchhoff's junction law follows from the conservation of charge.
(b) Kirchhoff's loop law follows from the conservation of energy.
(a) Kirchhoff's junction law follows from the conservation of charge.
(b) Kirchhoff's loop law follows from the conservation of energy.
Which of the following is correct? [2010]
a)
Both (a) and (b) are wrong
b)
(a) is correct and (b) is wrong
c)
(a) is wrong and (b) is correct
d)
Both (a) and (b) are correct
|
Nayanika Reddy answered |
Junction law follows from conservation
of charge and loop law is the conservation
of energy
of charge and loop law is the conservation
of energy
The total power dissipated in watts in the circuit shown here is [2007]
- a)40
- b)54
- c)4
- d)16
Correct answer is option 'B'. Can you explain this answer?
The total power dissipated in watts in the circuit shown here is [2007]
a)
40
b)
54
c)
4
d)
16
|
Ashwini Khanna answered |
The resistance of 6Ω and 3Ω are in parallel in the given circuit, their equivalent resistance is
In the circuit shown in the figure, if the potential at point A is taken to be zero, the potential at point B is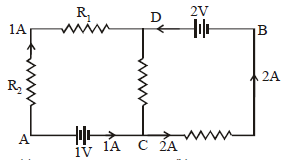
- a)–1V
- b)+ 2V
- c)–2V
- d)+ 1V
Correct answer is option 'D'. Can you explain this answer?
In the circuit shown in the figure, if the potential at point A is taken to be zero, the potential at point B is
a)
–1V
b)
+ 2V
c)
–2V
d)
+ 1V
|
Riya Banerjee answered |
Current from D to C = 1A
∴ VD – VC = 2 × 1 = 2V
VA = 0 ∴ VC = 1V, ∴ VD – VC = 2
⇒VD – 1 = 2 ∴ VD = 3V
∴ VD – VB = 2 ∴ 3 – VB = 2 ∴ VB = 1V
∴ VD – VC = 2 × 1 = 2V
VA = 0 ∴ VC = 1V, ∴ VD – VC = 2
⇒VD – 1 = 2 ∴ VD = 3V
∴ VD – VB = 2 ∴ 3 – VB = 2 ∴ VB = 1V
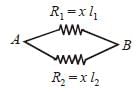
A ring is made of a wire having a resistance R0 = 12 Ω. Find the points A and B as shown in the figure, at which a current carrying conductor should be connected so that the resistance R of the sub-circuit between these points is equal to 8/3 Ω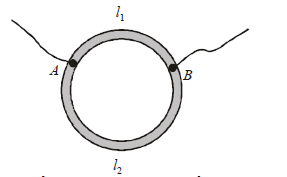
- a)
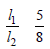
- b)
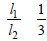
- c)
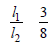
- d)
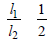
Correct answer is option 'D'. Can you explain this answer?
A ring is made of a wire having a resistance R0 = 12 Ω. Find the points A and B as shown in the figure, at which a current carrying conductor should be connected so that the resistance R of the sub-circuit between these points is equal to 8/3 Ω
a)
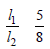
b)
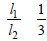
c)
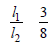
d)
|
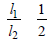
Geetika Shah answered |
Let x is the resistance per unit length then
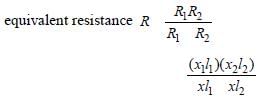
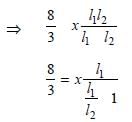
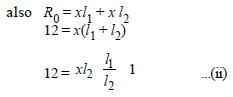
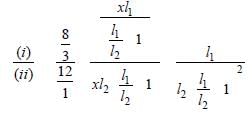
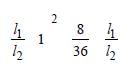
(y2 + 1 + 2y) × 8/36 y (where y l1/l2
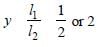
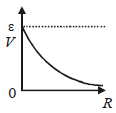
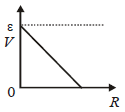
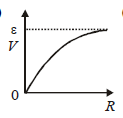
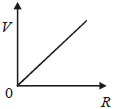
A student measures the terminal potentialdifference (V) of a cell (of emf E and internalresistance r) as a function of the current (I)flowing through it. The slope and intercept, ofthe graph between V and I, then, respectively,equal: [2009]- a)– r and E
- b)r and – E
- c)– E and r
- d)E and – r
Correct answer is option 'A'. Can you explain this answer?
A student measures the terminal potentialdifference (V) of a cell (of emf E and internalresistance r) as a function of the current (I)flowing through it. The slope and intercept, ofthe graph between V and I, then, respectively,equal: [2009]
a)
– r and E
b)
r and – E
c)
– E and r
d)
E and – r
|
Madhavan Patel answered |
The slope of the graph between V and I represents the internal resistance of the cell, r. This is because according to Ohm's Law, V = E - Ir, where E is the emf of the cell. Rearranging this equation, we get Ir = E - V, which shows that the current I is directly proportional to the difference between the emf and the terminal potential difference. Therefore, the slope of the graph is equal to the internal resistance, r.
The intercept of the graph represents the emf of the cell, E. This is because when the current I is zero, the equation V = E - Ir simplifies to V = E, meaning that the terminal potential difference is equal to the emf. Therefore, the intercept of the graph is equal to the emf, E.
The intercept of the graph represents the emf of the cell, E. This is because when the current I is zero, the equation V = E - Ir simplifies to V = E, meaning that the terminal potential difference is equal to the emf. Therefore, the intercept of the graph is equal to the emf, E.
See the electric circuit shown in the figure.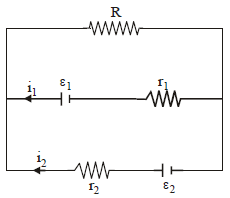
Which of the following equations is a correct equation for it? [2009]- a)ε2 – i2 r2 – ε1 – i1 r1 = 0
- b)-ε2 – (i1 + i2) R+ i2 r2 = 0
- c)ε1 – (i1 + i2) R + i1 r1 = 0
- d)ε1 – (i1 + i2) R– i1 r1 = 0
Correct answer is option 'D'. Can you explain this answer?
See the electric circuit shown in the figure.
Which of the following equations is a correct equation for it? [2009]
a)
ε2 – i2 r2 – ε1 – i1 r1 = 0
b)
-ε2 – (i1 + i2) R+ i2 r2 = 0
c)
ε1 – (i1 + i2) R + i1 r1 = 0
d)
ε1 – (i1 + i2) R– i1 r1 = 0
|
Shanaya Rane answered |
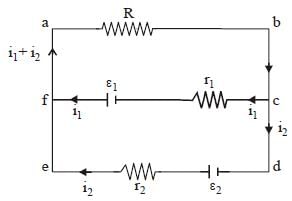
Applying Kirchhoff ’s rule in loop abcfa
ε1 – (i1 + i2) R – i1 r1 = 0.
ε1 – (i1 + i2) R – i1 r1 = 0.
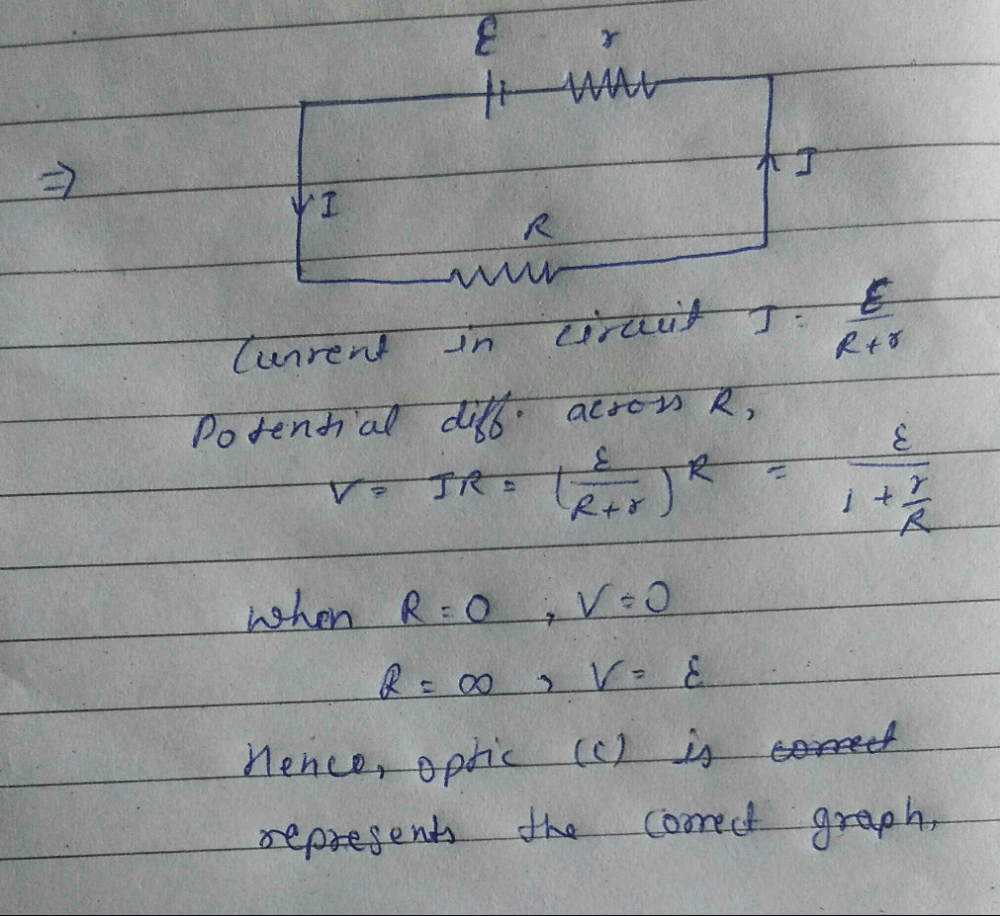
A cell can be balanced against 110 cm and 100cm of potentiometer wire, respectively with andwithout being short circuited through aresistance of 10Ω. Its internal resistance is [2008]- a)1.0 ohm
- b)0.5 ohm
- c)2.0 ohm
- d)zero
Correct answer is option 'A'. Can you explain this answer?
A cell can be balanced against 110 cm and 100cm of potentiometer wire, respectively with andwithout being short circuited through aresistance of 10Ω. Its internal resistance is [2008]
a)
1.0 ohm
b)
0.5 ohm
c)
2.0 ohm
d)
zero
|
Krish Khanna answered |
Here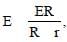 
hence the lengths 110 cm
and 100 cm are interchanged.
Without being short-circuited through R,
only the battery E is balanced.
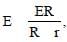hence the lengths 110 cmand 100 cm are interchanged.
Without being short-circuited through R,
only the battery E is balanced.
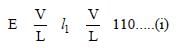
When R is connected across E, Ri, V/L, l2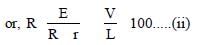
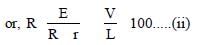
Dividing (i) by (ii), we get
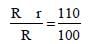
or, 100 R + 100 r = 110 R
or, 10 R = 100 r
or, 10 R = 100 r
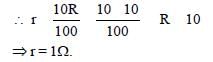
A milli voltmeter of 25 milli volt range is to beconverted into an ammeter of 25 ampere range.The value (in ohm) of necessary shunt will be :[2012]- a)0.001
- b)0.01
- c)1
- d)0.05
Correct answer is option 'A'. Can you explain this answer?
A milli voltmeter of 25 milli volt range is to beconverted into an ammeter of 25 ampere range.The value (in ohm) of necessary shunt will be :[2012]
a)
0.001
b)
0.01
c)
1
d)
0.05
|
Rohan Unni answered |
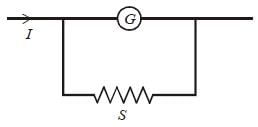
Galvanometer is converted into ammeter,
by connected a shunt, in parallel with it.
by connected a shunt, in parallel with it.
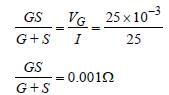
Here S << G so
S = 0.001 Ω
S = 0.001 Ω
Three resistances P, Q, R each of 2Ω and anunknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistanceof 6Ω is connected in parallel to S the bridgegets balanced. What is the value of S? [2007]- a)3Ω
- b)6Ω
- c)1Ω
- d)2Ω
Correct answer is option 'A'. Can you explain this answer?
Three resistances P, Q, R each of 2Ω and anunknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistanceof 6Ω is connected in parallel to S the bridgegets balanced. What is the value of S? [2007]
a)
3Ω
b)
6Ω
c)
1Ω
d)
2Ω
|
Moumita Khanna answered |
A balanced wheatstone bridge simply
requires
requires
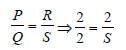
Therefore, S should be 2Ω.
A resistance of 6Ω is connected in parallel.
In parallel combination,
A resistance of 6Ω is connected in parallel.
In parallel combination,
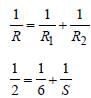
The resistance of an ammeter is 13 Ω and itsscale is graduated for a current upto 100 amps.After an additional shunt has been connectedto this ammeter it becomes possible to measurecurrents upto 750 amperes by this meter. Thevalue of shunt-resistance is [2007]- a)2 Ω
- b)0.2 Ω
- c)2 k Ω
- d)20 Ω
Correct answer is option 'A'. Can you explain this answer?
The resistance of an ammeter is 13 Ω and itsscale is graduated for a current upto 100 amps.After an additional shunt has been connectedto this ammeter it becomes possible to measurecurrents upto 750 amperes by this meter. Thevalue of shunt-resistance is [2007]
a)
2 Ω
b)
0.2 Ω
c)
2 k Ω
d)
20 Ω
|
Vaibhav Basu answered |
We know
In producing chlorine by electrolysis 100 kWpower at 125 V is being consumed. How muchchlorine per minute is liberated? (E.C.E. ofchlorine is 0.367×10–6 kg / C) [2010]- a)1.76 × 10–3 kg
- b)9.67 × 10. kg
- c)17.61 × 10–3 kg
- d)3.67 × 10–3 kg
Correct answer is option 'C'. Can you explain this answer?
In producing chlorine by electrolysis 100 kWpower at 125 V is being consumed. How muchchlorine per minute is liberated? (E.C.E. ofchlorine is 0.367×10–6 kg / C) [2010]
a)
1.76 × 10–3 kg
b)
9.67 × 10. kg
c)
17.61 × 10–3 kg
d)
3.67 × 10–3 kg
|
Srishti Chavan answered |
Calculation:
Given:
Power = 100 kW = 100,000 W
Voltage = 125 V
Charge of 1 mole of electrons (1 F) = 96500 C
E.C.E. of chlorine = 0.367 × 10⁻⁶ kg / C
Step 1: Calculate the charge consumed
Power (P) = Voltage (V) × Current (I)
Current (I) = P / V = 100,000 W / 125 V = 800 A
Step 2: Calculate the charge consumed per second
Charge (Q) = Current (I) × Time (t)
As power is given in kW and we need to find the amount per minute, convert time to seconds.
Time (t) = 1 minute = 60 seconds
Charge per second = 800 A × 60 s = 48,000 C
Step 3: Calculate the amount of chlorine liberated per second
Amount of chlorine liberated per second = E.C.E. of chlorine × Charge per second
= 0.367 × 10⁻⁶ kg / C × 48,000 C
= 17.616 × 10⁻³ kg
Step 4: Calculate the amount of chlorine liberated per minute
Amount of chlorine liberated per minute = Amount per second × 60
= 17.616 × 10⁻³ kg/s × 60 s
= 17.616 × 10⁻³ kg/min
= 17.61 × 10⁻³ kg/min
Therefore, the amount of chlorine liberated per minute is 17.61 × 10⁻³ kg, which is option C.
Given:
Power = 100 kW = 100,000 W
Voltage = 125 V
Charge of 1 mole of electrons (1 F) = 96500 C
E.C.E. of chlorine = 0.367 × 10⁻⁶ kg / C
Step 1: Calculate the charge consumed
Power (P) = Voltage (V) × Current (I)
Current (I) = P / V = 100,000 W / 125 V = 800 A
Step 2: Calculate the charge consumed per second
Charge (Q) = Current (I) × Time (t)
As power is given in kW and we need to find the amount per minute, convert time to seconds.
Time (t) = 1 minute = 60 seconds
Charge per second = 800 A × 60 s = 48,000 C
Step 3: Calculate the amount of chlorine liberated per second
Amount of chlorine liberated per second = E.C.E. of chlorine × Charge per second
= 0.367 × 10⁻⁶ kg / C × 48,000 C
= 17.616 × 10⁻³ kg
Step 4: Calculate the amount of chlorine liberated per minute
Amount of chlorine liberated per minute = Amount per second × 60
= 17.616 × 10⁻³ kg/s × 60 s
= 17.616 × 10⁻³ kg/min
= 17.61 × 10⁻³ kg/min
Therefore, the amount of chlorine liberated per minute is 17.61 × 10⁻³ kg, which is option C.
A galvanometer of resistance 50 Ω is connectedto battery of 3V along with a resistance of 2950 Ωin series. A full scale deflection of 30 divisions isobtained in the galvanometer. In order to reducethis deflection to 20 divisions, the resistance inseries should be [2008]- a)5050 Ω
- b)5550 Ω
- c)6050 Ω
- d)4450 Ω
Correct answer is option 'D'. Can you explain this answer?
A galvanometer of resistance 50 Ω is connectedto battery of 3V along with a resistance of 2950 Ωin series. A full scale deflection of 30 divisions isobtained in the galvanometer. In order to reducethis deflection to 20 divisions, the resistance inseries should be [2008]
a)
5050 Ω
b)
5550 Ω
c)
6050 Ω
d)
4450 Ω
|
Nilanjan Chakraborty answered |
Total internal resistance = (50+2950)Ω
= 3000 Ω
Emf of the cell, ε = 3V
= 3000 Ω
Emf of the cell, ε = 3V
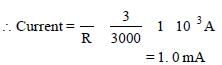
Current for full scale deflection of 30
divisions is 1.0 mA.
∴ Current for a deflection of 20 divisions
divisions is 1.0 mA.
∴ Current for a deflection of 20 divisions
Let the resistance be x Ω. Then
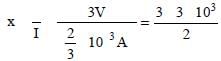
= 4500 Ω
But the resistance of the galvanometer
is 50Ω
∴ Resistance to be added
= (4500 –50) Ω= 4450 Ω
But the resistance of the galvanometer
is 50Ω
∴ Resistance to be added
= (4500 –50) Ω= 4450 Ω
A steady current of 1.5 amp flows through acopper voltameter for 10 minutes. If the electrochemical equivalent of copper is30 × 10–5 g coulomb–1, the mass of copperdeposited on the electrode will be [2007]- a)0.50 g
- b)0.67 g
- c)0.27 g
- d)0.40 g.
Correct answer is option 'C'. Can you explain this answer?
A steady current of 1.5 amp flows through acopper voltameter for 10 minutes. If the electrochemical equivalent of copper is30 × 10–5 g coulomb–1, the mass of copperdeposited on the electrode will be [2007]
a)
0.50 g
b)
0.67 g
c)
0.27 g
d)
0.40 g.
|
Arya Khanna answered |
We have, m = ZIt
where, Z is the electrochemical equivalent
of copper.
⇒ m = 30 x10-5 x1.5 x10 x 60
= 0.27 gm.
where, Z is the electrochemical equivalent
of copper.
⇒ m = 30 x10-5 x1.5 x10 x 60
= 0.27 gm.
The thermo e.m.f E in volts of a certain thermocouple is found to vary with temperature difference θ in °C between the two junctions according to the relation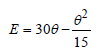
The neutral temperature for the thermocouplewill be- a)30° C
- b)450° C
- c)400 ° C
- d)225° C
Correct answer is option 'D'. Can you explain this answer?
The thermo e.m.f E in volts of a certain thermocouple is found to vary with temperature difference θ in °C between the two junctions according to the relation
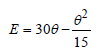
The neutral temperature for the thermocouplewill be
a)
30° C
b)
450° C
c)
400 ° C
d)
225° C
|
Rajeev Sharma answered |
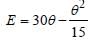
For neutral temperature,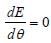 
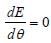
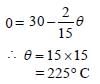
Hence, neutral temperature is 225°C.
The rate of increase of thermo–e.m.f. withtemperature at the neutral temperature of athermocouple [2011]- a)is positive
- b)is zero
- c)depends upon the choice of the twomaterials of the thermocouple
- d)is negative
Correct answer is option 'B'. Can you explain this answer?
The rate of increase of thermo–e.m.f. withtemperature at the neutral temperature of athermocouple [2011]
a)
is positive
b)
is zero
c)
depends upon the choice of the twomaterials of the thermocouple
d)
is negative
|
Jatin Chakraborty answered |
We have,
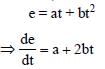
At neutral temperature,
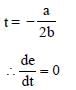
Two rods are joined end to end, as shown. Both have a cross-sectional area of 0.01 cm2. Each is 1 meter long. One rod is of copper with a resistivity of 1.7 × 10–6 ohm-centimeter, the other is of iron with a resistivity of 10–5 ohmcentimeter. [NEET Kar. 2013]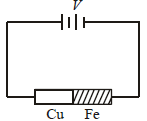
How much voltage is required to produce a current of 1 ampere in the rods?- a)0.117 V
- b)0.00145 V
- c)0.0145 V
- d)1.7 × 10–6 V
Correct answer is option 'A'. Can you explain this answer?
Two rods are joined end to end, as shown. Both have a cross-sectional area of 0.01 cm2. Each is 1 meter long. One rod is of copper with a resistivity of 1.7 × 10–6 ohm-centimeter, the other is of iron with a resistivity of 10–5 ohmcentimeter. [NEET Kar. 2013]
How much voltage is required to produce a current of 1 ampere in the rods?
a)
0.117 V
b)
0.00145 V
c)
0.0145 V
d)
1.7 × 10–6 V
|
Sarthak Saini answered |
Copper rod and iron rod are joined in series.
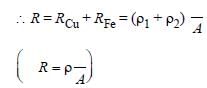
From ohm’s law V = RI
= (1.7 × 10–6 × 10–2 + 10–5 × 10–2) ÷ 0.01 × 10–4 volt
= 0.117 volt ( I = 1A)
= 0.117 volt ( I = 1A)
The internal resistance of a 2.1 V cell which givesa current of 0.2 A through a resistance of 10 Ω is[NEET 2013]- a)0.5 Ω
- b)0.8 Ω
- c)1.0 Ω
- d)0.2 Ω
Correct answer is option 'A'. Can you explain this answer?
The internal resistance of a 2.1 V cell which givesa current of 0.2 A through a resistance of 10 Ω is[NEET 2013]
a)
0.5 Ω
b)
0.8 Ω
c)
1.0 Ω
d)
0.2 Ω
|
Abhiram Nair answered |
Given : emf ε = 2.1 V
I = 0.2 A, R = 10Ω
Internal resistance r = ?
From formula.
ε – Ir = V = IR
2.1 – 0.2r = 0.2 × 10
2.1 – 0.2 r = 2 or 0.2 r = 0.1
I = 0.2 A, R = 10Ω
Internal resistance r = ?
From formula.
ε – Ir = V = IR
2.1 – 0.2r = 0.2 × 10
2.1 – 0.2 r = 2 or 0.2 r = 0.1
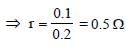
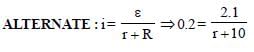
⇒ 2.1 = 0.2r +2 ⇒ r = 1/2 = 0.5Ω
A wire of a certain material is stretched slowlyby ten per cent. Its new resistance and specificresistance become respectively: [2008]- a)1.2 times, 1.3 times
- b)1.21 times, same
- c)both remain the same
- d)1.1 times, 1.1 times
Correct answer is option 'B'. Can you explain this answer?
A wire of a certain material is stretched slowlyby ten per cent. Its new resistance and specificresistance become respectively: [2008]
a)
1.2 times, 1.3 times
b)
1.21 times, same
c)
both remain the same
d)
1.1 times, 1.1 times
|
Dipanjan Mehta answered |
Resistance of a wire is given by R l/a
If the length is increased by 10% then new
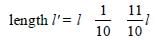
In that case, area of cross-section of wire
would decrease by 10%
∴ New area of cross-section
would decrease by 10%
∴ New area of cross-section
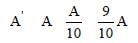
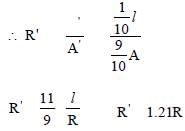
Thus the new resistance increases by 1.21
times. The specific resistance (resistivity)
remains unchanged as it depends on the
nature of the material of the wire.
times. The specific resistance (resistivity)
remains unchanged as it depends on the
nature of the material of the wire.
A 12 cm wire is given a shape of a right angled triangle ABC having sides 3 cm, 4 cm and 5 cm as shown in the figure. The resistance between two ends (AB, BC, CA) of the respective sides are measured one by one by a multi-meter. The resistances will be in the ratio of [NEET Kar. 2013]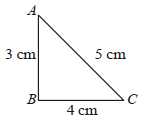
- a)3 : 4 : 5
- b)9 : 16 : 25
- c)27 : 32 : 35
- d)21 : 24 : 25
Correct answer is option 'C'. Can you explain this answer?
A 12 cm wire is given a shape of a right angled triangle ABC having sides 3 cm, 4 cm and 5 cm as shown in the figure. The resistance between two ends (AB, BC, CA) of the respective sides are measured one by one by a multi-meter. The resistances will be in the ratio of [NEET Kar. 2013]
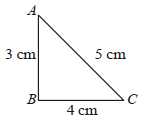
a)
3 : 4 : 5
b)
9 : 16 : 25
c)
27 : 32 : 35
d)
21 : 24 : 25
|
|
Dipanjan Mehta answered |
Resistance is directly proportional to length
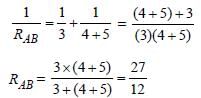
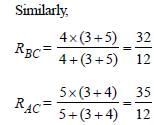
∴ RAB : RBC : RAC = 27 : 32 : 35
In the circuit shown, if a conducting wire is connected between points A and B, the current in this wire will [2006]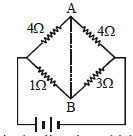
- a)flow in the direction which will be decidedby the value of V
- b)be zero
- c)flow from B to A
- d)flow from A to B
Correct answer is option 'C'. Can you explain this answer?
In the circuit shown, if a conducting wire is connected between points A and B, the current in this wire will [2006]
a)
flow in the direction which will be decidedby the value of V
b)
be zero
c)
flow from B to A
d)
flow from A to B
|
Kajal Bose answered |
Current will flow from B to A
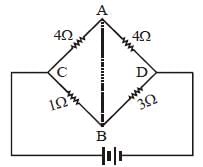
Potential drop over the resistance CA will be
more due to higher value of resistance. So
potential at A will be less as compared with at
B. Hence, current will flow from B to A.
more due to higher value of resistance. So
potential at A will be less as compared with at
B. Hence, current will flow from B to A.
Ten identical cells connected in series areneeded to heat a wire of length one meter andradius ‘r’ by 10ºC in time ‘t’. How many cells willbe required to heat the wire of length two meterof the same radius by the same temperature intime ‘t’? [NEET Kar. 2013]- a)10
- b)20
- c)30
- d)40
Correct answer is option 'B'. Can you explain this answer?
Ten identical cells connected in series areneeded to heat a wire of length one meter andradius ‘r’ by 10ºC in time ‘t’. How many cells willbe required to heat the wire of length two meterof the same radius by the same temperature intime ‘t’? [NEET Kar. 2013]
a)
10
b)
20
c)
30
d)
40
|
|
Nilanjan Chakraborty answered |
Resistance is directly proportionl to length
of the wire. As length is doubled so mass is
doubled and resistance is doubled.
We have
of the wire. As length is doubled so mass is
doubled and resistance is doubled.
We have
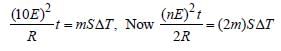
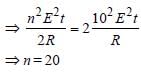
If power dissipated in the 9-Ω resistor in the circuit shown is 36 watt, the potential difference across the 2-Ω resistor is [2011]
- a)4 volt
- b)8 volt
- c)10 volt
- d)2 volt
Correct answer is option 'C'. Can you explain this answer?
If power dissipated in the 9-Ω resistor in the circuit shown is 36 watt, the potential difference across the 2-Ω resistor is [2011]
a)
4 volt
b)
8 volt
c)
10 volt
d)
2 volt
|
Anand Jain answered |
We have,
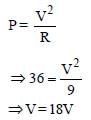
Current passing through the 9Ω resistor is
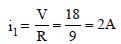
The 9Ω and 6Ω resistors are in parallel,
therefore
therefore
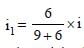
where i is the current delivered by the
battery.
battery.
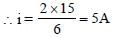
Thus, potential difference across 2Ω
resistor is
V = iR
= 5 × 2
= 10V
resistor is
V = iR
= 5 × 2
= 10V
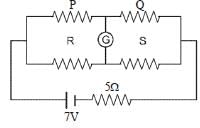
The resistance of the four arms P, Q, R and S in a Wheatstone’s bridge are 10 ohm, 30 ohm, 30 ohm and 90 ohm, respectively. The e.m.f. and internal resistance of the cell are 7 volt and 5 ohmrespectively. If the galvanometer resistance is50 ohm, the current drawn from the cell will be [NEET 2013]- a)0.2 A
- b)0.1 A
- c)2. 0 A
- d)1. 0 A
Correct answer is option 'A'. Can you explain this answer?
The resistance of the four arms P, Q, R and S in a Wheatstone’s bridge are 10 ohm, 30 ohm, 30 ohm and 90 ohm, respectively. The e.m.f. and internal resistance of the cell are 7 volt and 5 ohmrespectively. If the galvanometer resistance is50 ohm, the current drawn from the cell will be [NEET 2013]
a)
0.2 A
b)
0.1 A
c)
2. 0 A
d)
1. 0 A
|
Maheshwar Saini answered |
Given : V = 7 V
r = 5Ω
r = 5Ω
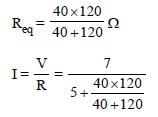
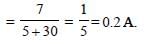
A current of 3 amp flows through the 2Ω resistor shown in the circuit. The power dissipated in the 5-Ω resistor is: [2008]
- a)4 watt
- b)2 watt
- c)1 watt
- d)5 watt
Correct answer is option 'D'. Can you explain this answer?
A current of 3 amp flows through the 2Ω resistor shown in the circuit. The power dissipated in the 5-Ω resistor is: [2008]
a)
4 watt
b)
2 watt
c)
1 watt
d)
5 watt
|
|
Rajeev Sharma answered |
Clearly, 2Ω, 4Ω and ( 1 + 5) Ωresistors are
in parallel. Hence, potential difference is
same across each of them.
∴ I1 × 2 = I2 × 4 = I3 × 6
in parallel. Hence, potential difference is
same across each of them.
∴ I1 × 2 = I2 × 4 = I3 × 6
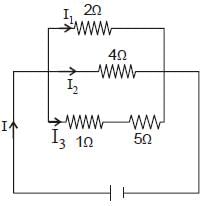
Given I1 = 3A ∴ I1 × 2 = I3 × 6
Given I1 = 3A.
∴ I1 × 2 = I3 × 6 provides
Given I1 = 3A.
∴ I1 × 2 = I3 × 6 provides
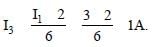
Now, the potential across the 5Ω resistor is
V = I3 × 5 = 1 × 5 = 5V.
∴ the power dissipated in the 5Ωresistor
V = I3 × 5 = 1 × 5 = 5V.
∴ the power dissipated in the 5Ωresistor
The power dissipated in the circuit shown in the figure is 30 Watts. The value of R is: [2012M]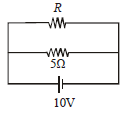
- a)20 Ω
- b)15 Ω
- c)10 Ω
- d)30 Ω
Correct answer is option 'C'. Can you explain this answer?
The power dissipated in the circuit shown in the figure is 30 Watts. The value of R is: [2012M]
a)
20 Ω
b)
15 Ω
c)
10 Ω
d)
30 Ω
|
|
Arya Khanna answered |
The power dissipated in the circuit
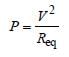
v = 10 volt
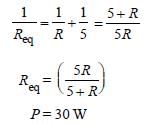
Substituting the values in equation (i)
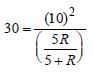
A thermocouple of negligible resistanceproduces an e.m.f. of 40 μV/°C in the linear rangeof temperature. A galvanometer of resistance 10ohm whose sensitivity is 1μA/div, is employedwith the termocouple. The smallest value oftemperature difference that can be detected bythe system will be [2011M]- a)0.5°C
- b)1°C
- c)0.1°C
- d)0.25°C
Correct answer is option 'D'. Can you explain this answer?
A thermocouple of negligible resistanceproduces an e.m.f. of 40 μV/°C in the linear rangeof temperature. A galvanometer of resistance 10ohm whose sensitivity is 1μA/div, is employedwith the termocouple. The smallest value oftemperature difference that can be detected bythe system will be [2011M]
a)
0.5°C
b)
1°C
c)
0.1°C
d)
0.25°C
|
|
Nayanika Reddy answered |
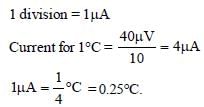
A potentiometer circuit is set up as shown. The potential gradient, across the potentiometer wire, is k volt/cm and the ammeter, present in the circuit, reads 1.0 A when two way key is switched off. The balance points, when the key between the terminals (i) 1 and 2 (ii) 1 and 3, is plugged in, are found to be at lengths ℓ1 cm and ℓ2 cm respectively. The magnitudes, of the resistors R and X, in ohms, are then, equal, respectively, to [2010]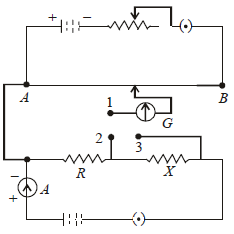
- a)
- b)
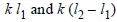
- c)
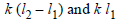
- d)
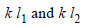
Correct answer is option 'B'. Can you explain this answer?
A potentiometer circuit is set up as shown. The potential gradient, across the potentiometer wire, is k volt/cm and the ammeter, present in the circuit, reads 1.0 A when two way key is switched off. The balance points, when the key between the terminals (i) 1 and 2 (ii) 1 and 3, is plugged in, are found to be at lengths ℓ1 cm and ℓ2 cm respectively. The magnitudes, of the resistors R and X, in ohms, are then, equal, respectively, to [2010]
a)
b)
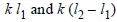
c)
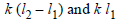
d)
|
|
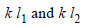
Rohan Unni answered |
(i) When key between the terminals 1
and 2 is plugged in,
P.D. across R = IR = k l1
⇒ R = k l1 as I = 1A
(ii) When key between terminals 1 and 3 is
plugged in,
P.D. across (X + R) = I(X + R) = k l2
⇒ X + R = k l2
∴ X = k (l2 – l1)
∴ R = kl1 and X = k (l2 – l1)
and 2 is plugged in,
P.D. across R = IR = k l1
⇒ R = k l1 as I = 1A
(ii) When key between terminals 1 and 3 is
plugged in,
P.D. across (X + R) = I(X + R) = k l2
⇒ X + R = k l2
∴ X = k (l2 – l1)
∴ R = kl1 and X = k (l2 – l1)
A wire of resistance 4 Ω is stretched to twice itsoriginal length. The resistance of stretched wirewould be [NEET 2013]- a)4 Ω
- b)8 Ω
- c)16 Ω
- d)2 Ω
Correct answer is option 'C'. Can you explain this answer?
A wire of resistance 4 Ω is stretched to twice itsoriginal length. The resistance of stretched wirewould be [NEET 2013]
a)
4 Ω
b)
8 Ω
c)
16 Ω
d)
2 Ω
|
|
Anand Jain answered |
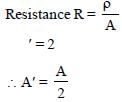
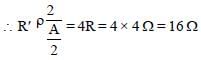
Therefore the resistance of new wire
becomes 16 Ω
becomes 16 Ω
In the circuit shown the cells A and B have negligible resistances. For VA = 12V, R1 = 500Ω and R = 100Ω the galvanometer (G) shows no deflection. The value of VB is : [2012]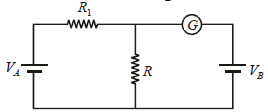
- a)4 V
- b)2 V
- c)12 V
- d)6 V
Correct answer is option 'B'. Can you explain this answer?
In the circuit shown the cells A and B have negligible resistances. For VA = 12V, R1 = 500Ω and R = 100Ω the galvanometer (G) shows no deflection. The value of VB is : [2012]
a)
4 V
b)
2 V
c)
12 V
d)
6 V
|
Soumya Ahuja answered |
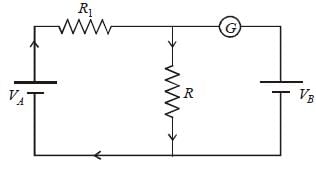
Since deflection in galvanometer is zero so
current will flow as shown in the above
diagram.
current will flow as shown in the above
diagram.
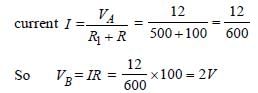
Kirchhoff’s first and second laws for electricalcircuits are consequences of [2006]- a)conservation of electric charge and energyrespectively
- b)conservation of electric charge
- c)conservation of energy and electric chargerespectively
- d)conservation of energy
Correct answer is option 'A'. Can you explain this answer?
Kirchhoff’s first and second laws for electricalcircuits are consequences of [2006]
a)
conservation of electric charge and energyrespectively
b)
conservation of electric charge
c)
conservation of energy and electric chargerespectively
d)
conservation of energy
|
Krish Chakraborty answered |
Kirchhoff ' s first law deals with conservation
of electrical charge & the second law deals
with conservation of electrical energy.
of electrical charge & the second law deals
with conservation of electrical energy.
A current of 2A flows through a 2Ω resistorwhen connected across a battery. The samebattery supplies a current of 0.5 A whenconnected across a 9Ω resistor. The internalresistance of the battery is [2011]- a)0.5 Ω
- b)1/3 Ω
- c)1/4 Ω
- d)1 Ω
Correct answer is option 'B'. Can you explain this answer?
A current of 2A flows through a 2Ω resistorwhen connected across a battery. The samebattery supplies a current of 0.5 A whenconnected across a 9Ω resistor. The internalresistance of the battery is [2011]
a)
0.5 Ω
b)
1/3 Ω
c)
1/4 Ω
d)
1 Ω
|
|
Maheshwar Saini answered |
Let the internal resistance of the battery be
r. Then the current flowing through the
circuit is given by
r. Then the current flowing through the
circuit is given by
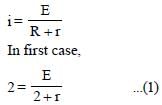
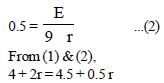
⇒ 1.5 r = 0.5 ⇒ r = 1/3Ω
Two cells, having the same e.m.f., are connected in series through an external resistance R. Cells have internal resistances r1 and r2 (r1 > r2) respectively. When the circuit is closed, the potential difference across the first cell is zero. The value of R is [2006- a)
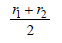
- b)
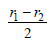
- c)r1 + r2
- d)r1 - r2
Correct answer is option 'D'. Can you explain this answer?
Two cells, having the same e.m.f., are connected in series through an external resistance R. Cells have internal resistances r1 and r2 (r1 > r2) respectively. When the circuit is closed, the potential difference across the first cell is zero. The value of R is [2006
a)
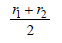
b)
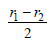
c)
r1 + r2
d)
r1 - r2
|
Swara Desai answered |
Two cells of emf ? are connected in series through external resistance R.
Thus, total resistance is R + r1 + r2
Thus, current across the circuit is total voltage divided by total resistance.
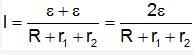
Now, when circuit is closed, the voltage across first cell is zero. Thus, we have
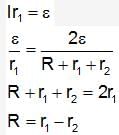
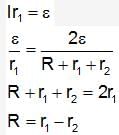
This is the value of R in terms of r1 and r2.
Chapter doubts & questions for Current Electricity - NEET Past Year Papers 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Current Electricity - NEET Past Year Papers in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
NEET Past Year Papers
86 docs|146 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily