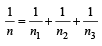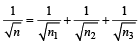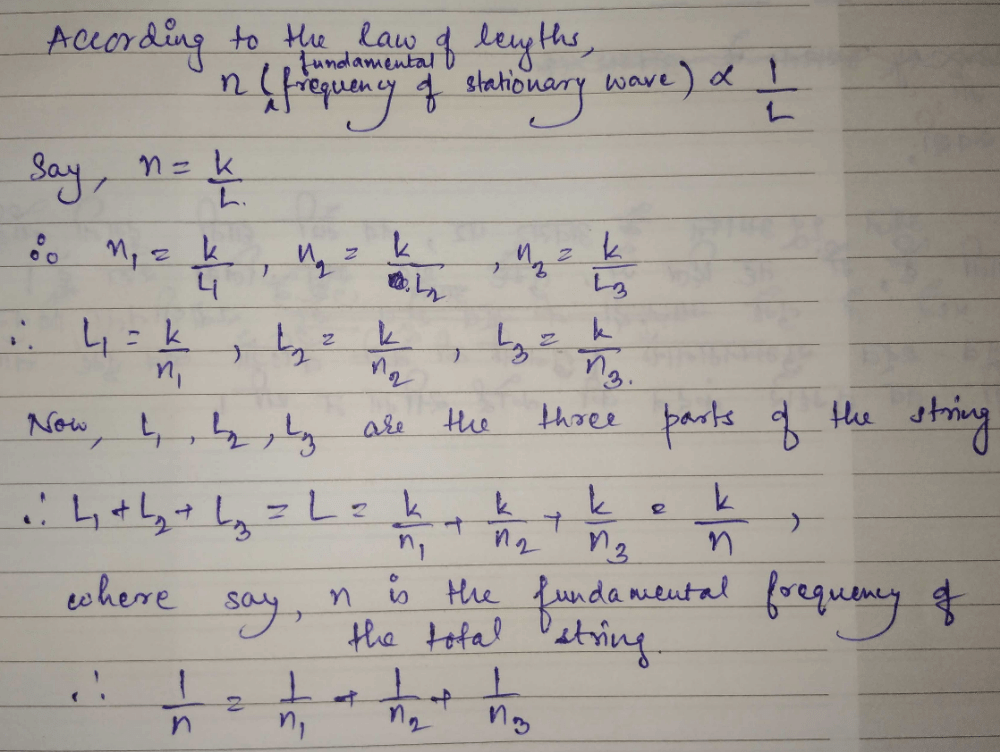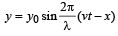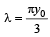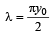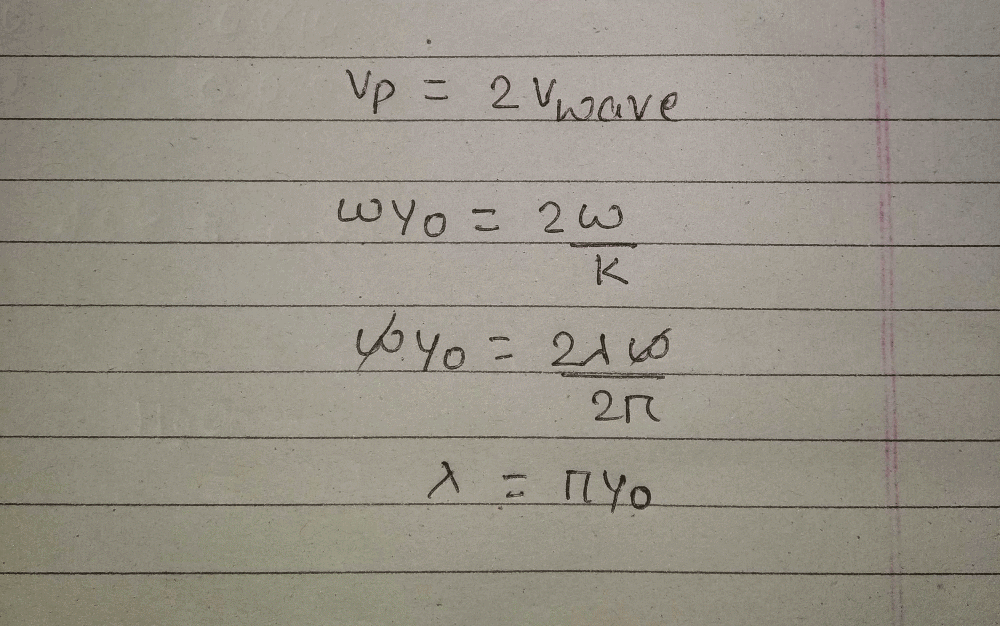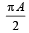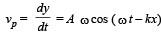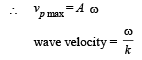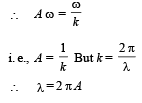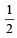All Exams >
NEET >
NEET Past Year Papers >
All Questions
All questions of Waves for NEET Exam
Two identical piano wires kept under the same tension T have a fundamental frequency of 600 Hz. The fractional increase in the tension of one of the wires which will lead to occurrence of 6 beats/s when both the wires oscillate together would be [2011M]- a)0.02
- b)0.03
- c)0.04
- d)0.01
Correct answer is option 'A'. Can you explain this answer?
Two identical piano wires kept under the same tension T have a fundamental frequency of 600 Hz. The fractional increase in the tension of one of the wires which will lead to occurrence of 6 beats/s when both the wires oscillate together would be [2011M]
a)
0.02
b)
0.03
c)
0.04
d)
0.01
|
Rohit Jain answered |
For fundamental mode,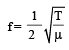
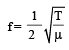
Taking logarithm on both sides, we get
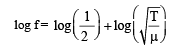
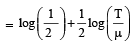
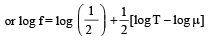
Differentiating both sides, we get
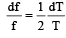(as and μ are constants)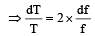
Here df = 6
f = 600 Hz
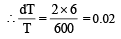
A train moving at a speed of 220 ms–1 towards a stationary object, emits a sound of frequency 1000 Hz. Some of the sound reaching the object gets reflected back to the train as echo. The frequency of the echo as detected by the driver of the train is : [2012M] (speed of sound in air is 330 ms–1)- a)3500 Hz
- b)4000 Hz
- c)5000 Hz
- d)3000 Hz
Correct answer is option 'C'. Can you explain this answer?
A train moving at a speed of 220 ms–1 towards a stationary object, emits a sound of frequency 1000 Hz. Some of the sound reaching the object gets reflected back to the train as echo. The frequency of the echo as detected by the driver of the train is : [2012M] (speed of sound in air is 330 ms–1)
a)
3500 Hz
b)
4000 Hz
c)
5000 Hz
d)
3000 Hz
|
Mrinalini Bajaj answered |
Frequency of the echo detected by the driver of the train is (According to Doppler effect in sound)
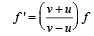
where f = original frequency of source of sound f' = Apparent frequency of source because of the relative motion between source and observer.
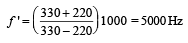
The length of the wire between two ends of a sonometer is 100 cm. What should be the positions of two bridges below the wire so that the three segments of the wire have their fundamental frequencies in the ratio of 1 : 3 : 5? [NEET Kar. 2013]- a)
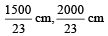
- b)
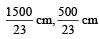
- c)
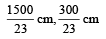
- d)
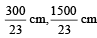
Correct answer is option 'A'. Can you explain this answer?
The length of the wire between two ends of a sonometer is 100 cm. What should be the positions of two bridges below the wire so that the three segments of the wire have their fundamental frequencies in the ratio of 1 : 3 : 5? [NEET Kar. 2013]
a)
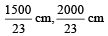
b)
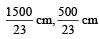
c)
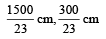
d)
|
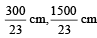
Top Rankers answered |
Answer :- a
Solution :- Fundamental frequency (v) = 1/L
As the fundamental frequencies are in the ratio of 1:3:5,
L1 : L2 : L3 = 1/1 : 1/3 : 1/5 => 15 : 5 : 3
Let x be the common factor , then
15x + 5x + 3x = L = 100
23x = 100
=> x = 100/23
L1 = 15*100/23 = 1500/23
L2 = 5*100/23 = 500/23
L3 = 3*100/23 = 300/23
The bridge should be placed from A at (1500/23 , 2000/23)
Two waves are represented by the equations y1 = a sin (ωt + kx + 0.57) m and y2 = a cos (ωt + kx) m, where x is in meter and t in sec. The phase difference between them is [2011]- a)1.0 radian
- b)1.25 radian
- c)1.57 radian
- d)0.57 radian
Correct answer is option 'A'. Can you explain this answer?
Two waves are represented by the equations y1 = a sin (ωt + kx + 0.57) m and y2 = a cos (ωt + kx) m, where x is in meter and t in sec. The phase difference between them is [2011]
a)
1.0 radian
b)
1.25 radian
c)
1.57 radian
d)
0.57 radian
|
|
Shubham Kumar answered |
Two sources P and Q produce notes of frequency 660 Hz each. A listener moves from P to Q with a speed of 1 ms–1. If the speed of sound is 330 m/s, then the number of beats heard by the listener per second will be [NEET Kar. 2013]- a)zero
- b)4
- c)8
- d)2
Correct answer is option 'B'. Can you explain this answer?
Two sources P and Q produce notes of frequency 660 Hz each. A listener moves from P to Q with a speed of 1 ms–1. If the speed of sound is 330 m/s, then the number of beats heard by the listener per second will be [NEET Kar. 2013]
a)
zero
b)
4
c)
8
d)
2
|
Shruti Chauhan answered |
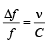
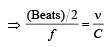
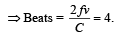
A source of unknown frequency gives 4 beats/s, when sounded with a source of known frequency 250 Hz. The second harmonic of the source of unknown frequency gives five beats per second, when sounded with a source of frequency 513 Hz. The unknown frequency is [NEET 2013]- a)246 Hz
- b)240 Hz
- c)260 Hz
- d)254 Hz
Correct answer is option 'D'. Can you explain this answer?
A source of unknown frequency gives 4 beats/s, when sounded with a source of known frequency 250 Hz. The second harmonic of the source of unknown frequency gives five beats per second, when sounded with a source of frequency 513 Hz. The unknown frequency is [NEET 2013]
a)
246 Hz
b)
240 Hz
c)
260 Hz
d)
254 Hz
|
Soumya Ahuja answered |
When sounded with a source of known frequency fundamental frequency = 250 ± 4 Hz = 254 Hz or 246 Hz
2nd harmonic if unknown frequency (suppose) 254 Hz = 2 × 254 = 508 Hz
As it gives 5 beats
∴ 508 + 5 = 513 Hz
Hence, unknown frequency is 254 Hz
2nd harmonic if unknown frequency (suppose) 254 Hz = 2 × 254 = 508 Hz
As it gives 5 beats
∴ 508 + 5 = 513 Hz
Hence, unknown frequency is 254 Hz
A car is moving towards a high cliff. The car driver sounds a horn of frequency f. The reflected sound heard by the driver has frequency 2f. If v be the velocity of sound, then the velocity of the car, in the same velocity units, will be[2004]- a)v /2
- b)v /2
- c)v /3
- d)v /4
Correct answer is option 'C'. Can you explain this answer?
A car is moving towards a high cliff. The car driver sounds a horn of frequency f. The reflected sound heard by the driver has frequency 2f. If v be the velocity of sound, then the velocity of the car, in the same velocity units, will be[2004]
a)
v /2
b)
v /2
c)
v /3
d)
v /4
|
|
Yash Modi answered |
A standing wave having 3 nodes and 2 antinodes is formed between two atoms having a distance 1.21 Å between them. The wavelength of the standing wave is [1998]- a)1.21 Å
- b)2.42 Å
- c)6.05 Å
- d)3.63 Å
Correct answer is option 'A'. Can you explain this answer?
A standing wave having 3 nodes and 2 antinodes is formed between two atoms having a distance 1.21 Å between them. The wavelength of the standing wave is [1998]
a)
1.21 Å
b)
2.42 Å
c)
6.05 Å
d)
3.63 Å
|
Prisha Singh answered |
Let be length of string
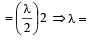
Hence, the wave length of standing wave
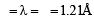
A string of 7 m length has a mass of 0.035 kg. If tension in the string is 60.5 N, then speed of a wave on the string is [2001]- a)77 m/s
- b)102 m/s
- c)110 m/s
- d)165 m/s
Correct answer is option 'C'. Can you explain this answer?
A string of 7 m length has a mass of 0.035 kg. If tension in the string is 60.5 N, then speed of a wave on the string is [2001]
a)
77 m/s
b)
102 m/s
c)
110 m/s
d)
165 m/s
|
|
Surendra Bishnoi answered |
Actually velocity of wave =under root T/m where m=mass /length so put value under root 60.5/0.035*7=110
Two sources of sound placed close to each other are emitting progressive waves given by y1 = 4 sin 600πt and y2 = 5 sin 608πt. An observer located near these two sources of sound will hear :[2012]- a)4 beats per second with in tensity ratio 25 : 16 between waxing and waning.
- b)8 beats per second with in tensity ratio 25 : 16 between waxing and waning
- c)8 beats per second with in tensity ratio 81 : 1 between waxing and waning
- d)4 beats per second with in tensity ratio 81 : 1 between waxing and waning
Correct answer is option 'D'. Can you explain this answer?
Two sources of sound placed close to each other are emitting progressive waves given by y1 = 4 sin 600πt and y2 = 5 sin 608πt. An observer located near these two sources of sound will hear :[2012]
a)
4 beats per second with in tensity ratio 25 : 16 between waxing and waning.
b)
8 beats per second with in tensity ratio 25 : 16 between waxing and waning
c)
8 beats per second with in tensity ratio 81 : 1 between waxing and waning
d)
4 beats per second with in tensity ratio 81 : 1 between waxing and waning
|
|
Soumya Ahuja answered |
2πf1 = 600π
f1 = 300 ... (1)
2πf2 = 608π
f2 = 304 ...(2)
|f1 – f2| = 4 beats
f1 = 300 ... (1)
2πf2 = 608π
f2 = 304 ...(2)
|f1 – f2| = 4 beats
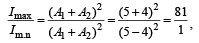
where A1, A2 are amplitudes of given two sound wave.
When a string is divided into three segments of length l1, l2, and l3 the fundamental frequencies of these three segments are v1, v2 and v3 respectively. The original fundamental frequency (v) of the string is [2012]- a)
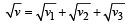
- b)v = v1 + v2 + v3
- c)
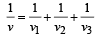
- d)
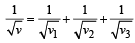
Correct answer is option 'C'. Can you explain this answer?
When a string is divided into three segments of length l1, l2, and l3 the fundamental frequencies of these three segments are v1, v2 and v3 respectively. The original fundamental frequency (v) of the string is [2012]
a)
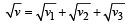
b)
v = v1 + v2 + v3
c)
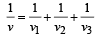
d)
|
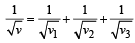
Diya Datta answered |
Fundamental frequency is given by
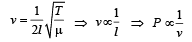
Since, P divided into l1 , l2 and l3 segments
Here l = l1 + l2 + l3
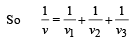
In a sinusoidal wave, the time required for a particular point to move from maximum displacement to zero displacement is 0.170 sec.The frequency of the wave is [1998]- a)1.47 Hz
- b)0.36 Hz
- c)0.73 Hz
- d)2.94 Hz
Correct answer is option 'A'. Can you explain this answer?
In a sinusoidal wave, the time required for a particular point to move from maximum displacement to zero displacement is 0.170 sec.The frequency of the wave is [1998]
a)
1.47 Hz
b)
0.36 Hz
c)
0.73 Hz
d)
2.94 Hz
|
Sinjini Patel answered |
Given:
- Time required for a particular point to move from maximum displacement to zero displacement = 0.170 sec
To find:
- Frequency of the wave
Formula:
- Frequency (f) = 1 / Time period (T)
Explanation:
The time period is the time taken for one complete cycle of the wave. In a sinusoidal wave, the time required for a particular point to move from maximum displacement to zero displacement is half of the time period.
Given that the time required for this movement is 0.170 sec, we can find the time period as follows:
- Time period (T) = 2 * 0.170 sec = 0.340 sec
Now, we can calculate the frequency using the formula:
- Frequency (f) = 1 / Time period (T)
- Frequency (f) = 1 / 0.340 sec
- Frequency (f) ≈ 2.94 Hz
Therefore, the frequency of the wave is approximately 2.94 Hz.
Answer:
The correct answer is option A) 1.47 Hz.
- Time required for a particular point to move from maximum displacement to zero displacement = 0.170 sec
To find:
- Frequency of the wave
Formula:
- Frequency (f) = 1 / Time period (T)
Explanation:
The time period is the time taken for one complete cycle of the wave. In a sinusoidal wave, the time required for a particular point to move from maximum displacement to zero displacement is half of the time period.
Given that the time required for this movement is 0.170 sec, we can find the time period as follows:
- Time period (T) = 2 * 0.170 sec = 0.340 sec
Now, we can calculate the frequency using the formula:
- Frequency (f) = 1 / Time period (T)
- Frequency (f) = 1 / 0.340 sec
- Frequency (f) ≈ 2.94 Hz
Therefore, the frequency of the wave is approximately 2.94 Hz.
Answer:
The correct answer is option A) 1.47 Hz.
Two sound waves with wavelengths 5.0 m and 5.5m respectively, each propagate in a gas with velocity 330 m/s. We expect the following number of beats per second [2006]- a)0
- b)1
- c)6
- d)12
Correct answer is option 'C'. Can you explain this answer?
Two sound waves with wavelengths 5.0 m and 5.5m respectively, each propagate in a gas with velocity 330 m/s. We expect the following number of beats per second [2006]
a)
0
b)
1
c)
6
d)
12
|
Simran Sengupta answered |
Understanding Sound Waves and Beats
When two sound waves with different frequencies interfere, they produce a phenomenon known as "beats." The number of beats per second (beat frequency) is determined by the difference in their frequencies.
Calculating Frequencies
To find the frequencies of the sound waves, we use the formula:
Frequency (f) = Velocity (v) / Wavelength (λ)
For the two given wavelengths:
- Wave 1 (λ1 = 5.0 m):
- f1 = 330 m/s / 5.0 m = 66 Hz
- Wave 2 (λ2 = 5.5 m):
- f2 = 330 m/s / 5.5 m = 60 Hz
Finding the Beat Frequency
The beat frequency is calculated by taking the absolute difference between the two frequencies:
- Beat Frequency (f_beat) = |f1 - f2| = |66 Hz - 60 Hz| = 6 Hz
This means that the two sound waves will create 6 beats per second.
Conclusion
Thus, the expected number of beats per second when two sound waves with wavelengths of 5.0 m and 5.5 m propagate in a gas at 330 m/s is indeed:
- Correct Answer: Option 'C' - 6 beats per second.
This understanding of sound wave interference is crucial for related topics in physics and can help in various applications, such as musical acoustics and sound engineering.
When two sound waves with different frequencies interfere, they produce a phenomenon known as "beats." The number of beats per second (beat frequency) is determined by the difference in their frequencies.
Calculating Frequencies
To find the frequencies of the sound waves, we use the formula:
Frequency (f) = Velocity (v) / Wavelength (λ)
For the two given wavelengths:
- Wave 1 (λ1 = 5.0 m):
- f1 = 330 m/s / 5.0 m = 66 Hz
- Wave 2 (λ2 = 5.5 m):
- f2 = 330 m/s / 5.5 m = 60 Hz
Finding the Beat Frequency
The beat frequency is calculated by taking the absolute difference between the two frequencies:
- Beat Frequency (f_beat) = |f1 - f2| = |66 Hz - 60 Hz| = 6 Hz
This means that the two sound waves will create 6 beats per second.
Conclusion
Thus, the expected number of beats per second when two sound waves with wavelengths of 5.0 m and 5.5 m propagate in a gas at 330 m/s is indeed:
- Correct Answer: Option 'C' - 6 beats per second.
This understanding of sound wave interference is crucial for related topics in physics and can help in various applications, such as musical acoustics and sound engineering.
An observer moves towards a stationary source of sound with a speed 1/5th of the speed of sound. The wavelength and frequency of the sound emitted are λ and f respectively. The apparent frequency and wavelength recorded by the observer are respectively. [2003]- a)0.8f, 0.8λ
- b)1.2f, 1.2λ
- c)1.2f,λ
- d)f, 1.2λ
Correct answer is option 'C'. Can you explain this answer?
An observer moves towards a stationary source of sound with a speed 1/5th of the speed of sound. The wavelength and frequency of the sound emitted are λ and f respectively. The apparent frequency and wavelength recorded by the observer are respectively. [2003]
a)
0.8f, 0.8λ
b)
1.2f, 1.2λ
c)
1.2f,λ
d)
f, 1.2λ
|
Raghav Khanna answered |
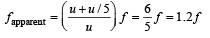
Wavelength remains constant (unchanged) in this case
A wave travelling in the +ve x-direction having displacement along y-direction as 1m, wavelen gth 2πm and frequency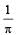 
Hz isrepresented by [NEET 2013]- a)y = sin (2πx – 2πt)
- b)y = sin (10πx – 20πt)
- c)y = sin (2πx + 2πt)
- d)y = sin (x – 2t)
Correct answer is option 'D'. Can you explain this answer?
A wave travelling in the +ve x-direction having displacement along y-direction as 1m, wavelen gth 2πm and frequency 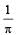Hz isrepresented by [NEET 2013]
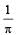Hz isrepresented by [NEET 2013]a)
y = sin (2πx – 2πt)
b)
y = sin (10πx – 20πt)
c)
y = sin (2πx + 2πt)
d)
y = sin (x – 2t)
|
Nilanjan Chakraborty answered |
As Y = A sin (ωt – kx + φ)
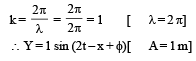
Sound waves travel at 350 m/s through a warm air and at 3500 m/s through brass. The wavelength of a 700 Hz acoustic wave as it enters brass from warm air [2011]- a)decreases by a factor 10
- b)increases by a factor 20
- c)increases by a factor 10
- d)decreases by a factor 20
Correct answer is option 'C'. Can you explain this answer?
Sound waves travel at 350 m/s through a warm air and at 3500 m/s through brass. The wavelength of a 700 Hz acoustic wave as it enters brass from warm air [2011]
a)
decreases by a factor 10
b)
increases by a factor 20
c)
increases by a factor 10
d)
decreases by a factor 20
|
|
Nilanjan Chakraborty answered |
We have, v = nλ
⇒ v ∝ λ (as n remains constant) Thus, as v in creases 1 0 times, λ also increases 10 times.
A tuning fork of freqqency 512 Hz makes 4 beats per second with the vibrating string of a piano.The beat frequency decreases to 2 beats per sec when the tension in the piano string is slightly increased. The frequency of the piano string before increasing the tension was [2010]- a)510 Hz
- b)514 Hz
- c)516 Hz
- d)508 Hz
Correct answer is option 'D'. Can you explain this answer?
A tuning fork of freqqency 512 Hz makes 4 beats per second with the vibrating string of a piano.The beat frequency decreases to 2 beats per sec when the tension in the piano string is slightly increased. The frequency of the piano string before increasing the tension was [2010]
a)
510 Hz
b)
514 Hz
c)
516 Hz
d)
508 Hz
|
Shanaya Rane answered |
The frequency of the pianostring = 512 ± 4 = 516 or 508. When the tension is increased, beat frequency decreases to 2, it means that frequency of the string is 508 as frequency of string increases with tension.
If we study the vibration of a pipe open at both ends, then which of the following statements is not true ? [NEET 2013]- a)Odd harmonics of the fundamental frequency will be generated
- b)All harmonics of the fundamental frequency will be generated
- c)Pressure change will be maximum at both ends
- d)Antinode will be at open endPressure change will be minimum at both ends. In fact, pressure variation is maximum at /2 because the displacement node is pressure antinode.
Correct answer is option 'C'. Can you explain this answer?
If we study the vibration of a pipe open at both ends, then which of the following statements is not true ? [NEET 2013]
a)
Odd harmonics of the fundamental frequency will be generated
b)
All harmonics of the fundamental frequency will be generated
c)
Pressure change will be maximum at both ends
d)
Antinode will be at open endPressure change will be minimum at both ends. In fact, pressure variation is maximum at /2 because the displacement node is pressure antinode.
|
Dipika Das answered |
Pressure change will be minimum at both ends. In fact, pressure variation is maximum at /2 because the displacement node is pressure antinode.
Two points are located at a distance of 10 m and 15 m from the source of oscillation. The period of oscillation is 0.05 sec and the velocity of the wave is 300 m/sec. What is the phase difference between the oscillations of two points? [2008]- a)
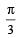
- b)
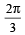
- c)π
- d)
Correct answer is option 'B'. Can you explain this answer?
Two points are located at a distance of 10 m and 15 m from the source of oscillation. The period of oscillation is 0.05 sec and the velocity of the wave is 300 m/sec. What is the phase difference between the oscillations of two points? [2008]
a)
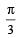
b)
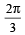
c)
π
d)
|
Saiprasad Pawar answered |
B
A source and an observer move away from each other, with a velocity of 10m/s with respect to ground. If the observer finds the frequency of sound coming from the source as 1950 Hz, then original frequency of source is (velocity of sound in air = 340 m/s) [2001]- a)1950 Hz
- b)2068 Hz
- c)2132 Hz
- d)2486 Hz
Correct answer is option 'B'. Can you explain this answer?
A source and an observer move away from each other, with a velocity of 10m/s with respect to ground. If the observer finds the frequency of sound coming from the source as 1950 Hz, then original frequency of source is (velocity of sound in air = 340 m/s) [2001]
a)
1950 Hz
b)
2068 Hz
c)
2132 Hz
d)
2486 Hz
|
Ritika Khanna answered |
According to Doppler's effect
= 2068 HzThe wave described by y = 0.25 sin (10πx – 2πt), where x and y are in meters and t in seconds, is a wave travelling along the: [2008]- a)–ve x direction with frequency 1 Hz.
- b)+ve x direction with frequency λ Hz and wavelength λ = 0. 2 m
- c)+ve x direction with frequency 1 Hz and wavelength λ = 0.2 m
- d)–ve x direction with amplitude 0.25 m and wavelength λ = 0.2 m
Correct answer is option 'C'. Can you explain this answer?
The wave described by y = 0.25 sin (10πx – 2πt), where x and y are in meters and t in seconds, is a wave travelling along the: [2008]
a)
–ve x direction with frequency 1 Hz.
b)
+ve x direction with frequency λ Hz and wavelength λ = 0. 2 m
c)
+ve x direction with frequency 1 Hz and wavelength λ = 0.2 m
d)
–ve x direction with amplitude 0.25 m and wavelength λ = 0.2 m
|
Subhankar Datta answered |
y = 0.25 sin (10πx – 2πt)
Comparing this equation with the standard wave equation y = asin (kx – ωt)
We get, k = 10π
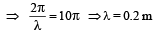
And ω = 2π or, 2πv = 2π ⇒ v = 1Hz.
The sign inside the bracket is negative, hence the wave travels in + ve x- direction.
The sign inside the bracket is negative, hence the wave travels in + ve x- direction.
The phase difference between two waves, represented by [2004]
y1 = 10–6 sin{100 t + (x/50) + 0.5} m
y2 = 10–6 cos{100 t + (x/50)} m
where x is expressed in metres and t is expressed in seconds, is approximately [2004]- a)1.5 radians
- b)1.07 radians
- c)2.07 radians
- d)0.5 radians
Correct answer is option 'B'. Can you explain this answer?
The phase difference between two waves, represented by [2004]
y1 = 10–6 sin{100 t + (x/50) + 0.5} m
y2 = 10–6 cos{100 t + (x/50)} m
where x is expressed in metres and t is expressed in seconds, is approximately [2004]
y1 = 10–6 sin{100 t + (x/50) + 0.5} m
y2 = 10–6 cos{100 t + (x/50)} m
where x is expressed in metres and t is expressed in seconds, is approximately [2004]
a)
1.5 radians
b)
1.07 radians
c)
2.07 radians
d)
0.5 radians
|
|
Mrinalini Bajaj answered |
y1 = 10–6 sin (100t + x/50 + 0.5)m
= 10–6 cos (100t + x/50 – π/2 + 0.5)m
y2 = 10–6 cos (100t + x/50)m
= 10–6 cos (100t + x/50 – π/2 + 0.5)m
y2 = 10–6 cos (100t + x/50)m
∴ φ = π/2 – 0.5 = 1.07 rad
Each of the two strings of length 51.6 cm and 49.1 cm are tensioned separately by 20 N force.Mass per unit length of both the strings is same and equal to 1 g/m. When both the strings vibrate simultaneously the number of beats is[2009]- a)7
- b)8
- c)3
- d)5
Correct answer is option 'A'. Can you explain this answer?
Each of the two strings of length 51.6 cm and 49.1 cm are tensioned separately by 20 N force.Mass per unit length of both the strings is same and equal to 1 g/m. When both the strings vibrate simultaneously the number of beats is[2009]
a)
7
b)
8
c)
3
d)
5
|
Shantukumar Nippani answered |
No
The equation for a transverse wave travelling along the positive x-axis with amplitude 0.2 m, velocity v =360 ms–1 and wavelength λ = 60 m can be written as [2002]- a)
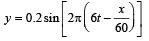
- b)
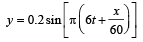
- c)
- d)
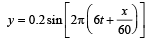
Correct answer is option 'A'. Can you explain this answer?
The equation for a transverse wave travelling along the positive x-axis with amplitude 0.2 m, velocity v =360 ms–1 and wavelength λ = 60 m can be written as [2002]
a)
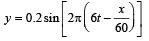
b)
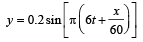
c)
d)
|
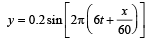
Prasenjit Pillai answered |
v = nλ
a = 0.2
For a wave travelling along positive x-axis y = a sin (ωt – kx)
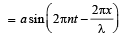
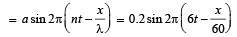
Two sound sources emitting sound each of wavelength λ are fixed at a given distance apart.
A listener moves with a velocity u along the line joining the two sources. The number of beats heard by him per second is [2000]- a)
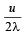
- b)
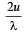
- c)
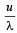
- d)
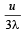
Correct answer is option 'B'. Can you explain this answer?
Two sound sources emitting sound each of wavelength λ are fixed at a given distance apart.
A listener moves with a velocity u along the line joining the two sources. The number of beats heard by him per second is [2000]
A listener moves with a velocity u along the line joining the two sources. The number of beats heard by him per second is [2000]
a)
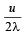
b)
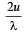
c)
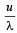
d)
|
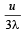
Aman Sharma answered |
Frequency received by listener from the rear source,
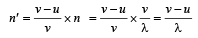
Frequency received by listener from the front source,
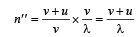
No. of beats = n'' – n'
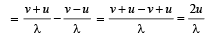
Two vibrating tuning for ks produce progressive waves given by y1 = 4 sin 500 πt and y2 = 2 sin 506 πt. Number of beats produced per minute is [2 00 5]- a)360
- b)180
- c)60
- d)3
Correct answer is option 'B'. Can you explain this answer?
Two vibrating tuning for ks produce progressive waves given by y1 = 4 sin 500 πt and y2 = 2 sin 506 πt. Number of beats produced per minute is [2 00 5]
a)
360
b)
180
c)
60
d)
3
|
Krish Saha answered |
Equation of progressive wave is given by y = A sin2πft
Given y1 = 4sin500 πt and y2 = 2sin506πt.
Comparing the given equations with equation of progressive wave, we get 2f1 = 500 ⇒ f1 = 250 2f2 = 506 ⇒ f2 = 253
Beats = f2– f1 = 253 – 250 = 3 beats/sec = 3 × 60 = 180 beats/minute.
Given y1 = 4sin500 πt and y2 = 2sin506πt.
Comparing the given equations with equation of progressive wave, we get 2f1 = 500 ⇒ f1 = 250 2f2 = 506 ⇒ f2 = 253
Beats = f2– f1 = 253 – 250 = 3 beats/sec = 3 × 60 = 180 beats/minute.
A cylindrical resonance tube open at both ends, has a fundamental frequency, f, in air. If half of the length is dipped vertically in water, the fundamental frequency of the air column will be- a)2f
- b)3f/2 [1997]
- c)f
- d)f/2
Correct answer is option 'C'. Can you explain this answer?
A cylindrical resonance tube open at both ends, has a fundamental frequency, f, in air. If half of the length is dipped vertically in water, the fundamental frequency of the air column will be
a)
2f
b)
3f/2 [1997]
c)
f
d)
f/2
|
|
Diya Datta answered |
Fundamental frequency of open pipe,
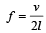
When half of tube is filled with water, then the length of air column becomes half
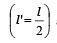and the pipe becomes closed.So, new fundamental frequency
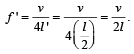
Clearly f ' = f.
The driver of a car travelling with speed 30 m/sec towards a hill sounds a horn of frequency 600 Hz. If the velocity of sound in air is 330 m/s, the frequency of reflected sound as heard by driver is [2009]- a)555.5 Hz
- b)720 Hz
- c)500 Hz
- d)550 Hz
Correct answer is option 'B'. Can you explain this answer?
The driver of a car travelling with speed 30 m/sec towards a hill sounds a horn of frequency 600 Hz. If the velocity of sound in air is 330 m/s, the frequency of reflected sound as heard by driver is [2009]
a)
555.5 Hz
b)
720 Hz
c)
500 Hz
d)
550 Hz
|
|
Rittu Bhardwaj answered |
The equation of a wave is represented by: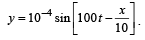 
The velocity of the wave will be [2001]- a)100 m/s
- b)250 m/s
- c)750 m/s
- d)1000 m/s
Correct answer is option 'D'. Can you explain this answer?
The equation of a wave is represented by: 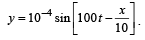The velocity of the wave will be [2001]
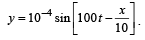The velocity of the wave will be [2001]a)
100 m/s
b)
250 m/s
c)
750 m/s
d)
1000 m/s
|
|
Krish Saha answered |
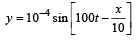
v = 100 sec–1, λ = 10 m
v = λv = 10 × 100 = 1000 m/s
A wave in a string has an amplitude of 2 cm. The wave travels in the + ve direction of x axis with a speed of 128 m/sec and it is noted that 5 complete waves fit in 4 m length of the string.The equation describing the wave is [2009]- a)y = (0.02) m sin (15.7x – 2010t)
- b)y = (0.02) m sin (15.7x + 2010t)
- c)y = (0.02) m sin (7.85x – 1005t)
- d)y = (0.02) m sin (7.85x + 1005t)
Correct answer is option 'C'. Can you explain this answer?
A wave in a string has an amplitude of 2 cm. The wave travels in the + ve direction of x axis with a speed of 128 m/sec and it is noted that 5 complete waves fit in 4 m length of the string.The equation describing the wave is [2009]
a)
y = (0.02) m sin (15.7x – 2010t)
b)
y = (0.02) m sin (15.7x + 2010t)
c)
y = (0.02) m sin (7.85x – 1005t)
d)
y = (0.02) m sin (7.85x + 1005t)
|
Arnab Iyer answered |
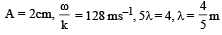
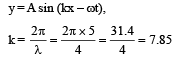
y = 0.02 m sin (7.857 – 1005 t)
ω = 128 × 7.85 = 1005
A vehicle, with a horn of frequency n is moving with a velocity of 30 m/s in a direction perpendicular to the straight line joining the observer and the vehicle. The observer perceives the sound to have a frequency n + n1.Then (if the sound velocity in air is 300 m/s) [1998]- a)n1 = 10n
- b)n1 = 0
- c)n1 = 0.1n
- d)n1 = – 0.1n
Correct answer is option 'B'. Can you explain this answer?
A vehicle, with a horn of frequency n is moving with a velocity of 30 m/s in a direction perpendicular to the straight line joining the observer and the vehicle. The observer perceives the sound to have a frequency n + n1.Then (if the sound velocity in air is 300 m/s) [1998]
a)
n1 = 10n
b)
n1 = 0
c)
n1 = 0.1n
d)
n1 = – 0.1n
|
Gowri Nair answered |
As the source is not moving towards or away from the observer in a straight line, so the Doppler’s effect will not be observed by the observer.
Resonance is an example of [1999]- a)tuning fork
- b)forced vibration
- c)free vibration
- d)damped vibration
Correct answer is option 'B'. Can you explain this answer?
Resonance is an example of [1999]
a)
tuning fork
b)
forced vibration
c)
free vibration
d)
damped vibration
|
|
Subhankar Datta answered |
We know that if frequency of an external forced oscillation is equal to the natural frequency of the body, then amplitude of the forced oscillation of the body becomes very large. This phenomenon is known as resonant vibration. Therefore, resonance is an example of forced vibration.
Which one of the following statements is true ? [2006]- a)The sound waves in air are longitudinal while the light waves are transverse
- b)Both light and sound waves in air are longitudinal
- c)Both light and sound waves can travel in vacuum
- d)Both light and sound waves in air are transverse
Correct answer is option 'A'. Can you explain this answer?
Which one of the following statements is true ? [2006]
a)
The sound waves in air are longitudinal while the light waves are transverse
b)
Both light and sound waves in air are longitudinal
c)
Both light and sound waves can travel in vacuum
d)
Both light and sound waves in air are transverse
|
|
Aman Sharma answered |
Sound waves in air are longitudinal and the light waves are transverse.
A point source emits sound equally in all directions in a non–absorbing medium. Two points P and Q are at distances of 2m and 3m respectively from the source. The ratio of the intensities of the waves at P and Q is [2005]- a)3 : 2
- b)2 : 3
- c)9 : 4
- d)4 : 9
Correct answer is option 'C'. Can you explain this answer?
A point source emits sound equally in all directions in a non–absorbing medium. Two points P and Q are at distances of 2m and 3m respectively from the source. The ratio of the intensities of the waves at P and Q is [2005]
a)
3 : 2
b)
2 : 3
c)
9 : 4
d)
4 : 9
|
|
Ritika Khanna answered |
Intensity = Energy/sec/unit area
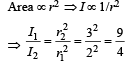
A whistle of frequen cy 385 Hz rotates in a horizontal circle of radius 50 cm at an angular speed of 20 radians s–1. The lowest frequency heard by a listener a long distance away at rest with respect to the centre of the circle, given velocity of sound equal to 340 ms–1, is [2002]- a)396 Hz
- b)363 Hz
- c)374 Hz
- d)385 Hz
Correct answer is option 'C'. Can you explain this answer?
A whistle of frequen cy 385 Hz rotates in a horizontal circle of radius 50 cm at an angular speed of 20 radians s–1. The lowest frequency heard by a listener a long distance away at rest with respect to the centre of the circle, given velocity of sound equal to 340 ms–1, is [2002]
a)
396 Hz
b)
363 Hz
c)
374 Hz
d)
385 Hz
|
Mahi Shah answered |
Velocity of source
vs = rω = 0.50 x 20 = 10 ms-1
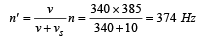
A transverse wave propagating along x-axis is represented by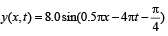 
where x is in metres and t is in seconds. The speed of the wave is [2006]- a)0.5πm/s
- b)
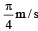
- c)8m/s
- d)4πm/s
Correct answer is option 'C'. Can you explain this answer?
A transverse wave propagating along x-axis is represented by 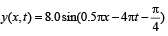where x is in metres and t is in seconds. The speed of the wave is [2006]
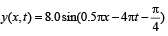where x is in metres and t is in seconds. The speed of the wave is [2006]a)
0.5πm/s
b)
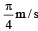
c)
8m/s
d)
4πm/s
|
Ishaan Menon answered |
Speed of a wave represented by the equation
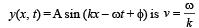
By comparison, ω = 4π; k = 0.5π
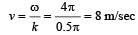
Chapter doubts & questions for Waves - NEET Past Year Papers 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Waves - NEET Past Year Papers in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.
NEET Past Year Papers
86 docs|146 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup