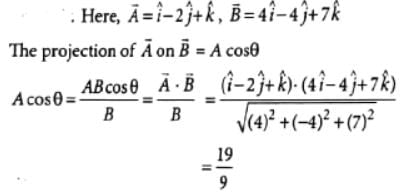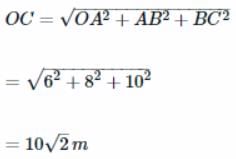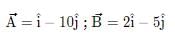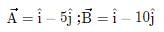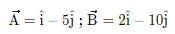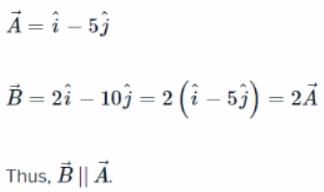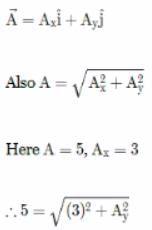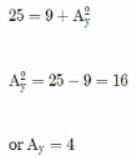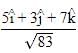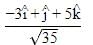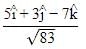All Exams >
NEET >
NCERTs at Fingertips: Textbooks, Tests & Solutions >
All Questions
All questions of Motion in a Plane for NEET Exam
Which of the following is not a scalar quantity?- a)Temperature
- b)Coefficient of friction
- c)Charge
- d)Impulse
Correct answer is option 'D'. Can you explain this answer?
Which of the following is not a scalar quantity?
a)
Temperature
b)
Coefficient of friction
c)
Charge
d)
Impulse
|
|
Vivek Patel answered |
Impulse (I)
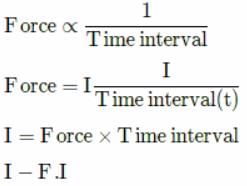
Since force is a vector quantity and impulse is the product of the sudden force applied and the time interval to bring equivalent the system. So Impulse also a vector quantity which have same direction to the force applied.
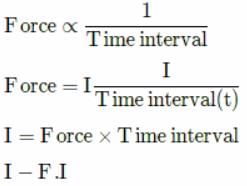
Since force is a vector quantity and impulse is the product of the sudden force applied and the time interval to bring equivalent the system. So Impulse also a vector quantity which have same direction to the force applied.
Two particles are projected simultaneously in the same vertical plane, from the same point, both with different speeds and at different angles with horizontal. The path followed by one, as seen by the other, is- a)A vertical line
- b)A parabola
- c)A hyperbola
- d)A straight line making a constant angle (≠ 90∘) with horizontal
Correct answer is option 'D'. Can you explain this answer?
Two particles are projected simultaneously in the same vertical plane, from the same point, both with different speeds and at different angles with horizontal. The path followed by one, as seen by the other, is
a)
A vertical line
b)
A parabola
c)
A hyperbola
d)
A straight line making a constant angle (≠ 90∘) with horizontal
|
|
Mira Joshi answered |
Let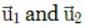 be the initial velocities of the two particles and θ1 and θ2 be their angles of projection with the horizontal.
be the initial velocities of the two particles and θ1 and θ2 be their angles of projection with the horizontal.
The velocities of the two particles after time t are,
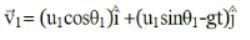
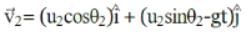
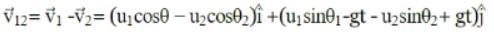

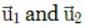 be the initial velocities of the two particles and θ1 and θ2 be their angles of projection with the horizontal.
be the initial velocities of the two particles and θ1 and θ2 be their angles of projection with the horizontal.The velocities of the two particles after time t are,
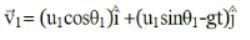
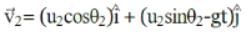
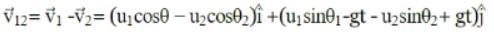

In case of a projectile motion, what is the angle between the velocity and acceleration at the highest point?- a)0°
- b)45°
- c)90°
- d)180°
Correct answer is option 'C'. Can you explain this answer?
In case of a projectile motion, what is the angle between the velocity and acceleration at the highest point?
a)
0°
b)
45°
c)
90°
d)
180°
|
|
Suresh Iyer answered |
At the highest point, velocity is acting horizontally and acceleration ( = acceleration due to gravity) is acting vertically downwards. Therefore, at the highest point the angle between velocity and acceleration is 90∘ .
The driver of a car moving towards a rocket launching pad with a speed of 6 ms−1 observed that the rocket is moving with a speed of 10 ms−1 the upward speed of the rocket as seen by the stationary observer is
- a)4 ms−1
- b)6 ms−1
- c)11 ms−1
- d)8 ms−1
Correct answer is option 'D'. Can you explain this answer?
The driver of a car moving towards a rocket launching pad with a speed of 6 ms−1 observed that the rocket is moving with a speed of 10 ms−1 the upward speed of the rocket as seen by the stationary observer is
a)
4 ms−1
b)
6 ms−1
c)
11 ms−1
d)
8 ms−1
|
|
Jithin Nair answered |
-1 suddenly sees a rocket launching vertically upwards with a velocity of 80ms-1. What is the relative velocity of the car with respect to the rocket?
The relative velocity of the car with respect to the rocket can be found by adding the velocity of the car and the velocity of the rocket.
Relative velocity = velocity of car + velocity of rocket
Relative velocity = 6 ms-1 + 80 ms-1
Relative velocity = 86 ms-1
Therefore, the relative velocity of the car with respect to the rocket is 86 ms-1.
The relative velocity of the car with respect to the rocket can be found by adding the velocity of the car and the velocity of the rocket.
Relative velocity = velocity of car + velocity of rocket
Relative velocity = 6 ms-1 + 80 ms-1
Relative velocity = 86 ms-1
Therefore, the relative velocity of the car with respect to the rocket is 86 ms-1.
For a particle performing uniform circular motion, choose the incorrect statement form the following.- a)Magnitude of particle velocity (speed) remains constant.
- b)Particle velocity remains directed perpendicular to radius vector.
- c)Direction of acceleration keeps changing as particle moves.
- d)Magnitude of acceleration does not remain constant.
Correct answer is option 'D'. Can you explain this answer?
For a particle performing uniform circular motion, choose the incorrect statement form the following.
a)
Magnitude of particle velocity (speed) remains constant.
b)
Particle velocity remains directed perpendicular to radius vector.
c)
Direction of acceleration keeps changing as particle moves.
d)
Magnitude of acceleration does not remain constant.
|
|
Anjali Sharma answered |
For a particle performing uniform circular motion, magnitude of the acceleration remains constant.
A girl riding a bicycle with a speed of 5 ms−1 towards north direction, observes rain falling vertically down. If she increases her speed to 10 ms−1, rain appears to meet her at 45∘ to the vertical. What is the speed of the rain?- a)5√2 ms−1
- b)5 ms−1
- c)10√2 ms−1
- d)10 ms−1
Correct answer is option 'A'. Can you explain this answer?
A girl riding a bicycle with a speed of 5 ms−1 towards north direction, observes rain falling vertically down. If she increases her speed to 10 ms−1, rain appears to meet her at 45∘ to the vertical. What is the speed of the rain?
a)
5√2 ms−1
b)
5 ms−1
c)
10√2 ms−1
d)
10 ms−1
|
|
Riya Banerjee answered |
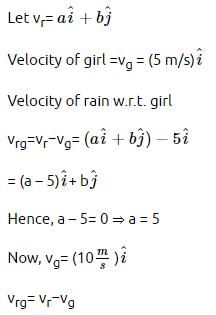
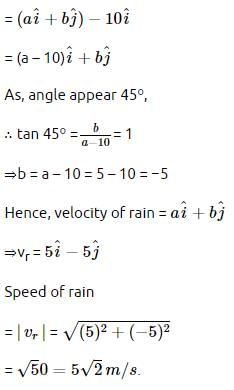
A body executing uniform circular motion has its position vector and acceleration vector- a)Along the same direction
- b)In opposite direction
- c)Normal to each other
- d)Not related to each other
Correct answer is option 'B'. Can you explain this answer?
A body executing uniform circular motion has its position vector and acceleration vector
a)
Along the same direction
b)
In opposite direction
c)
Normal to each other
d)
Not related to each other
|
|
Hansa Sharma answered |
In Circular motion, the Position vector is always outward and passes through the center. whereas the and centripetal acceleration is always toward the center.
∴ Both is the opposite direction.
∴ Both is the opposite direction.
The relation between the time of flight of projectile Tf, and the time to reach the maximum height tm is- a)Tf = 2tm
- b)Tf = tm
- c)Tf = tm/2
- d)Tf = √2 (tm)
Correct answer is option 'A'. Can you explain this answer?
The relation between the time of flight of projectile Tf, and the time to reach the maximum height tm is
a)
Tf = 2tm
b)
Tf = tm
c)
Tf = tm/2
d)
Tf = √2 (tm)
|
|
Raghav Bansal answered |
Time to reach maximum height = tm
Time to reach back to ground = tm
Total time of flight, Tf = tm + tm = 2tm
Time to reach back to ground = tm
Total time of flight, Tf = tm + tm = 2tm
Two particles are projected in air with speed u at angles θ1 and θ2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then which one of the following is correct?
(where T1 and T2 are the time of flight.)- a)θ1 > θ2
- b)θ1 = θ2
- c)T1 < T2
- d)T1 = T2
Correct answer is option 'A'. Can you explain this answer?
Two particles are projected in air with speed u at angles θ1 and θ2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then which one of the following is correct?
(where T1 and T2 are the time of flight.)
(where T1 and T2 are the time of flight.)
a)
θ1 > θ2
b)
θ1 = θ2
c)
T1 < T2
d)
T1 = T2
|
|
Aarya Ahuja answered |
To fully answer your question, I would need you to provide the angles at which the particles are projected and any other relevant information. Additionally, it seems that part of your question is cut off. Could you please provide the complete question?
A hiker stands on the edge of a cliff 490 m above the ground and throws a stone horizontally with a speed of 15 m s-1. The time taken by the stone to reach the ground is- a)5 s
- b)10 s
- c)12 s
- d)15 s
Correct answer is option 'B'. Can you explain this answer?
A hiker stands on the edge of a cliff 490 m above the ground and throws a stone horizontally with a speed of 15 m s-1. The time taken by the stone to reach the ground is
a)
5 s
b)
10 s
c)
12 s
d)
15 s
|
|
Riya Banerjee answered |
Here, u = 15ms−1
h = 490m
Time taken by the stone to reach the ground is
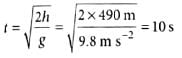
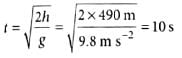
A cricketer can throw a ball to a maximum horizontal distance of 100m. With the same speed how much high above the ground can the cricketer throw the same ball?- a)50 m
- b)100 m
- c)150 m
- d)200 m
Correct answer is option 'A'. Can you explain this answer?
A cricketer can throw a ball to a maximum horizontal distance of 100m. With the same speed how much high above the ground can the cricketer throw the same ball?
a)
50 m
b)
100 m
c)
150 m
d)
200 m
|
|
Meera Singh answered |
Let u be the velocity of projection of the ball. The ball will cover maximum horizontal distance when angle of projection with horizontal, θ = 45∘. Then Rmax = u2/g = 100m
If ball is projected vertically upwards (θ = 90∘) from ground then H attains maximum value.
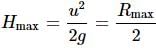
∴ The height to which cricketer can through the ball is = Rmax/2 = 100/2 = 50m.
If ball is projected vertically upwards (θ = 90∘) from ground then H attains maximum value.
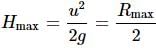
∴ The height to which cricketer can through the ball is = Rmax/2 = 100/2 = 50m.
A particle is moving on a circular path of radius r with uniform speed v. What is the displacement of the particle after it has described an angle of 60°?- a)r√2
- b)r√3
- c)r
- d)2r
Correct answer is option 'C'. Can you explain this answer?
A particle is moving on a circular path of radius r with uniform speed v. What is the displacement of the particle after it has described an angle of 60°?
a)
r√2
b)
r√3
c)
r
d)
2r
|
|
Riya Banerjee answered |
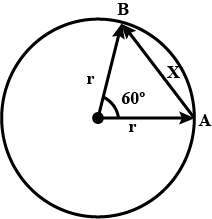
Let the particle is moving from point A to B
Displacement of the particle = AB
According to cosine formula
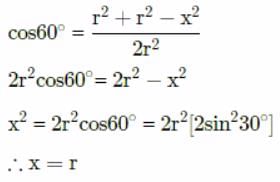
Displacement AB = x = r
Displacement of the particle = AB
According to cosine formula
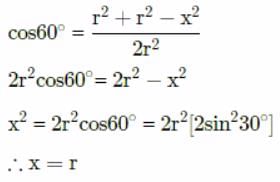
Displacement AB = x = r

The direction cosines of are
are - a)1, 1, 1
- b)2, 2, 2
- c)1/√2, 1/√2, 1/√2
- d)1/√3, 1/√3, 1/√3
Correct answer is option 'D'. Can you explain this answer?
The direction cosines of are
are
 are
are a)
1, 1, 1
b)
2, 2, 2
c)
1/√2, 1/√2, 1/√2
d)
1/√3, 1/√3, 1/√3
|
|
Lavanya Menon answered |
Let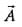 =
= 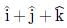 ∴ Ax = 1, Ay = 1, Az = 1
∴ Ax = 1, Ay = 1, Az = 1
and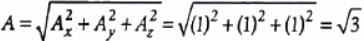
cos α, cos β andcos y are the direction cosines of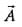 .
.

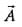 =
= 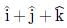 ∴ Ax = 1, Ay = 1, Az = 1
∴ Ax = 1, Ay = 1, Az = 1and
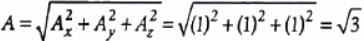
cos α, cos β andcos y are the direction cosines of
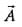 .
.
If x = 5t + 3t2 andy = 4t are the x and y co-ordinates of a particle at any time t second where x and y are in metre, then the acceleration of the particle- a)is zero throughout its motion
- b)is a constant throughout its motion
- c)depends only on its y component
- d)varies along both x and y direction
Correct answer is option 'B'. Can you explain this answer?
If x = 5t + 3t2 andy = 4t are the x and y co-ordinates of a particle at any time t second where x and y are in metre, then the acceleration of the particle
a)
is zero throughout its motion
b)
is a constant throughout its motion
c)
depends only on its y component
d)
varies along both x and y direction
|
|
Harshitha Reddy answered |
Understanding the Motion of the Particle
Given the equations of motion:
- x = 5t + 3t^2
- y = 4t
We need to determine the acceleration of the particle as it moves.
Calculating Velocity
- The velocity in the x-direction (vx) is the derivative of x with respect to time:
vx = dx/dt = 5 + 6t
- The velocity in the y-direction (vy) is the derivative of y with respect to time:
vy = dy/dt = 4
Calculating Acceleration
- The acceleration in the x-direction (ax) is the derivative of vx with respect to time:
ax = dvx/dt = 6
- The acceleration in the y-direction (ay) is the derivative of vy with respect to time:
ay = dy/dt = 0
Analyzing the Results
- The x-component of acceleration (ax) is a constant value of 6 m/s².
- The y-component of acceleration (ay) is 0 m/s².
Thus, the overall acceleration of the particle can be considered constant since it does not vary with time.
Conclusion
- The particle's motion is influenced primarily by the constant acceleration in the x-direction, while the y-direction remains constant without any acceleration (ay = 0).
Hence, the correct answer is option 'B': The acceleration of the particle is a constant throughout its motion.
Given the equations of motion:
- x = 5t + 3t^2
- y = 4t
We need to determine the acceleration of the particle as it moves.
Calculating Velocity
- The velocity in the x-direction (vx) is the derivative of x with respect to time:
vx = dx/dt = 5 + 6t
- The velocity in the y-direction (vy) is the derivative of y with respect to time:
vy = dy/dt = 4
Calculating Acceleration
- The acceleration in the x-direction (ax) is the derivative of vx with respect to time:
ax = dvx/dt = 6
- The acceleration in the y-direction (ay) is the derivative of vy with respect to time:
ay = dy/dt = 0
Analyzing the Results
- The x-component of acceleration (ax) is a constant value of 6 m/s².
- The y-component of acceleration (ay) is 0 m/s².
Thus, the overall acceleration of the particle can be considered constant since it does not vary with time.
Conclusion
- The particle's motion is influenced primarily by the constant acceleration in the x-direction, while the y-direction remains constant without any acceleration (ay = 0).
Hence, the correct answer is option 'B': The acceleration of the particle is a constant throughout its motion.
Which of the following statements is incorrect?- a)In one dimension motion, the velocity and the acceleration of an object are always along the same line
- b)In two or three dimensions, the angle between velocity and acceleration vectors may have any value between 0°and 180°
- c)The kinematic equations for uniform acceleration can be applied in case of a uniform circular motion
- d)The resultant acceleration of an object in circular motion is towards the centre only if the speed is constant
Correct answer is option 'C'. Can you explain this answer?
Which of the following statements is incorrect?
a)
In one dimension motion, the velocity and the acceleration of an object are always along the same line
b)
In two or three dimensions, the angle between velocity and acceleration vectors may have any value between 0°and 180°
c)
The kinematic equations for uniform acceleration can be applied in case of a uniform circular motion
d)
The resultant acceleration of an object in circular motion is towards the centre only if the speed is constant
|
|
Mira Joshi answered |
The kinematic equations for uniform acceleration do not apply in case of uniform circular motion because in this case the magnitude of acceleration is constant but its direction is changing.
A motorboat is racing towards the north at 25 kmh−1 and the water current in that region is 10 kmh−1 in the direction of 60∘ east of south. The resultant velocity of the boat is:- a)11 kmh−1
- b)22 kmh−1
- c)33 kmh−1
- d)44 kmh−1
Correct answer is option 'B'. Can you explain this answer?
A motorboat is racing towards the north at 25 kmh−1 and the water current in that region is 10 kmh−1 in the direction of 60∘ east of south. The resultant velocity of the boat is:
a)
11 kmh−1
b)
22 kmh−1
c)
33 kmh−1
d)
44 kmh−1
|
|
Suresh Iyer answered |
velocity of the water current vc = 10 km/s
velocity of the motorboat vb = 25 km/h
angle between north and south east is 120o
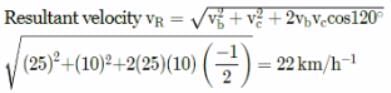
The resultant velocity of the boat is 22km/h−1
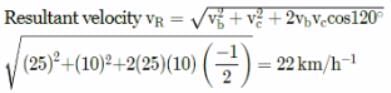
The resultant velocity of the boat is 22km/h−1
When air resistance is taken into account while dealing with the motion of the projectile which of the following properties of the projectile, shows an increase?- a)Range
- b)Maximum height
- c)Speed at which it strikes the ground
- d)The angle at which the projectile strikes the ground
Correct answer is option 'D'. Can you explain this answer?
When air resistance is taken into account while dealing with the motion of the projectile which of the following properties of the projectile, shows an increase?
a)
Range
b)
Maximum height
c)
Speed at which it strikes the ground
d)
The angle at which the projectile strikes the ground
|
|
Gaurav Kumar answered |
In the presence of air resistance, the range, maximum height, speed at which the projectile strikes the ground will decreases whereas the angles at which the projectile strikes the ground will increases.
A person moves 30 m north, then 30 m east, then 30√2 m south-west. His displacement from the original position is:- a)zero
- b)28 m towards south
- c)10 m towards west
- d)15 m towards east
Correct answer is option 'A'. Can you explain this answer?
A person moves 30 m north, then 30 m east, then 30√2 m south-west. His displacement from the original position is:
a)
zero
b)
28 m towards south
c)
10 m towards west
d)
15 m towards east
|
|
Gaurav Kumar answered |
Resolving displacement 30√2 m south-west into two rectangular components, we get
Displacement in south
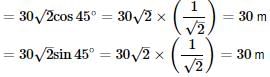
∴ Effective displacement due to 30 m north and 30 m south is zero.
Also effective displacement due to 30 m east and 30 m west in zero.
Displacement in south
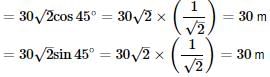
∴ Effective displacement due to 30 m north and 30 m south is zero.
Also effective displacement due to 30 m east and 30 m west in zero.
A football is kicked into the air vertically upwards with velocity u. The velocity of the ball at the highest point is- a)u
- b)2u
- c)zero
- d)4u
Correct answer is option 'C'. Can you explain this answer?
A football is kicked into the air vertically upwards with velocity u. The velocity of the ball at the highest point is
a)
u
b)
2u
c)
zero
d)
4u
|
|
Dev Patel answered |
The velocity of the ball at the highest point is zero.
Two vectors A and B inclined at an angle θ have a resultant R which makes an angle α with A. If the directions of A and B are interchanged, the resultant will have the same- a)Direction
- b)Magnitude
- c)Direction as well as magnitude
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Two vectors A and B inclined at an angle θ have a resultant R which makes an angle α with A. If the directions of A and B are interchanged, the resultant will have the same
a)
Direction
b)
Magnitude
c)
Direction as well as magnitude
d)
None of these
|
|
Gaurav Kumar answered |
Neither the magnitude of vectors nor the angle between the vectors is changed. So, magnitude of the resultant remains unchanged. However, the direction of the resultant will be changed.
In Latin, the word vector means- a)Magnitude
- b)Direction
- c)Carrier
- d)Cap
Correct answer is option 'C'. Can you explain this answer?
In Latin, the word vector means
a)
Magnitude
b)
Direction
c)
Carrier
d)
Cap
|
|
Hansa Sharma answered |
In Latin, the word vector means carrier.
An aeroplane flying horizontally with a speed of 360 km h-1 releases a bomb at a height of 490 m from the ground. If g = 9.8 m s-2, it will strike the ground at- a)10 km
- b)100 km
- c)1 km
- d)16 km
Correct answer is option 'C'. Can you explain this answer?
An aeroplane flying horizontally with a speed of 360 km h-1 releases a bomb at a height of 490 m from the ground. If g = 9.8 m s-2, it will strike the ground at
a)
10 km
b)
100 km
c)
1 km
d)
16 km
|
|
Preeti Iyer answered |
Time taken by the bomb to fall through a height of 490 m
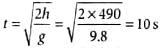
Distance at which the bomb strikes the ground = horizontal velocity x time

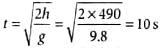
Distance at which the bomb strikes the ground = horizontal velocity x time

Which of the following quantities is dependent of the choice of orientation of the coordinate axes?- a)
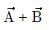
- b)Ax + By
- c)
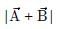
- d)Angle between
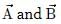
Correct answer is option 'B'. Can you explain this answer?
Which of the following quantities is dependent of the choice of orientation of the coordinate axes?
a)
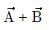
b)
Ax + By
c)
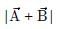
d)
Angle between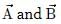
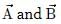
|
|
Dev Patel answered |
A vector, its magnitude and the angle between two vectors do not depend on the choice of the orientation of the coordinate axes. So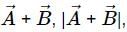 angle between
angle between 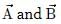 are independent of the orientation of the coordinate axes. But the quantity Ax + By depends upon the magnitude of the components along x and y axes, so it will change with change in coordinate axes.
are independent of the orientation of the coordinate axes. But the quantity Ax + By depends upon the magnitude of the components along x and y axes, so it will change with change in coordinate axes.
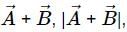 angle between
angle between 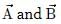 are independent of the orientation of the coordinate axes. But the quantity Ax + By depends upon the magnitude of the components along x and y axes, so it will change with change in coordinate axes.
are independent of the orientation of the coordinate axes. But the quantity Ax + By depends upon the magnitude of the components along x and y axes, so it will change with change in coordinate axes.A bomb is released by a horizontal flying aeroplane. The trajectory of the bomb is- a)a parabola
- b)a straight line
- c)a circle
- d)a hyperbola
Correct answer is option 'A'. Can you explain this answer?
A bomb is released by a horizontal flying aeroplane. The trajectory of the bomb is
a)
a parabola
b)
a straight line
c)
a circle
d)
a hyperbola
|
|
Riya Banerjee answered |
It is an example of projectile motion. Therefore, the trajectory of the bomb is parabola.
Two projectiles are are fired from the same point with the same speed at angles 60° and 30° respectively. Which one of the follwing is true?- a)Their horizontal ranges will be the same
- b)Their maximum heights will be the same
- c)Their landing velocities will be the same
- d)Their times of flight will be the same
Correct answer is option 'A'. Can you explain this answer?
Two projectiles are are fired from the same point with the same speed at angles 60° and 30° respectively. Which one of the follwing is true?
a)
Their horizontal ranges will be the same
b)
Their maximum heights will be the same
c)
Their landing velocities will be the same
d)
Their times of flight will be the same
|
|
Uday Dasgupta answered |
Horizontal Range
- The horizontal range of a projectile is the distance traveled horizontally before hitting the ground.
- The horizontal range of a projectile is given by the formula R = (v^2 * sin(2θ))/g, where v is the initial velocity, θ is the angle of projection, and g is the acceleration due to gravity.
- When both projectiles are fired from the same point with the same speed, the initial velocity v is the same for both.
- Since sin(2*60°) = sin(120°) = sin(2*30°), the horizontal ranges of the projectiles fired at 60° and 30° will be the same.
Therefore, the correct option is:
a) Their horizontal ranges will be the same
- The horizontal range of a projectile is the distance traveled horizontally before hitting the ground.
- The horizontal range of a projectile is given by the formula R = (v^2 * sin(2θ))/g, where v is the initial velocity, θ is the angle of projection, and g is the acceleration due to gravity.
- When both projectiles are fired from the same point with the same speed, the initial velocity v is the same for both.
- Since sin(2*60°) = sin(120°) = sin(2*30°), the horizontal ranges of the projectiles fired at 60° and 30° will be the same.
Therefore, the correct option is:
a) Their horizontal ranges will be the same
The equations of motion of a projectile are given by x = 36t m and 2y = 96t - 9.8t2 m. The angle of projection is- a)sin−1(4/5)
- b)sin−1(3/5)
- c)sin−1(4/3)
- d)sin−1(3/4)
Correct answer is option 'A'. Can you explain this answer?
The equations of motion of a projectile are given by x = 36t m and 2y = 96t - 9.8t2 m. The angle of projection is
a)
sin−1(4/5)
b)
sin−1(3/5)
c)
sin−1(4/3)
d)
sin−1(3/4)
|
|
Vivek Patel answered |
Given x = 36t
and 2y = 96t − 9.8t2
or y = 48t − 4.9t2
Let the initial velocity of projectile be u and angle of projection θ. Then, Initial horizontal component of velocity,
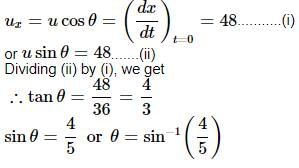
and 2y = 96t − 9.8t2
or y = 48t − 4.9t2
Let the initial velocity of projectile be u and angle of projection θ. Then, Initial horizontal component of velocity,
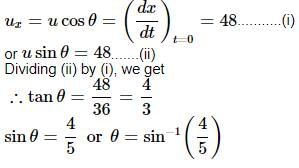
A ball is thrown from the top of a tower with an initial velocity of 10 m s-1 at an angle ot 30° with the horizontal. If it hits the ground at a distance of 17.3 m from the base of the tower, the height of the tower is (Take g = 10 m s-2)- a)5 m
- b)20 m
- c)15 m
- d)10 m
Correct answer is option 'D'. Can you explain this answer?
A ball is thrown from the top of a tower with an initial velocity of 10 m s-1 at an angle ot 30° with the horizontal. If it hits the ground at a distance of 17.3 m from the base of the tower, the height of the tower is (Take g = 10 m s-2)
a)
5 m
b)
20 m
c)
15 m
d)
10 m
|
|
Riya Banerjee answered |
The ball is thrown at an angle, θ = 30o.
Initial velocity of the ball, u = 10 m/s
Horizontal range of the ball, R = 17.3 m
We know that, R = u cosθ t,
where t is the time of flight
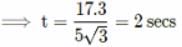
using equation of motion we get:-
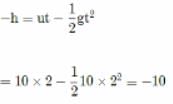
⟹ Height of tower, h = 10 m
We know that, R = u cosθ t,
where t is the time of flight
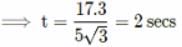
using equation of motion we get:-
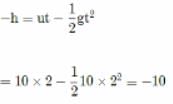
⟹ Height of tower, h = 10 m
Given a + b + c + d = 0, which of the following statements is incorrect?- a)a, b, c, d must each be a null vector.
- b)The magnitude of (a + c) equals the magnitude of (b + d).
- c)The magnitude of a can never be greater than the sum of the magnitudes of b, c and d.
- d)b + c must lie in the plane of a and d if a and d are not collinear, and in the line of a and d if they are collinear.
Correct answer is option 'A'. Can you explain this answer?
Given a + b + c + d = 0, which of the following statements is incorrect?
a)
a, b, c, d must each be a null vector.
b)
The magnitude of (a + c) equals the magnitude of (b + d).
c)
The magnitude of a can never be greater than the sum of the magnitudes of b, c and d.
d)
b + c must lie in the plane of a and d if a and d are not collinear, and in the line of a and d if they are collinear.

|
Top Rankers answered |
(a) Incorrect, because a + b + c + d can be zero in many ways other than each of a, b, c, and d being a null vector.
(b) Correct, as a + b + c + d = 0 implies a + c = -(b + d). Thus, the magnitude of (a + c) is equal to the magnitude of (b + d).
(c) Correct, since a + b + c + d = 0, so a = -(b + c + d). The magnitude of a is equal to the magnitude of (b + c + d). The sum of the magnitudes of b, c, and d will always be greater than or equal to the magnitude of a, so the statement is correct.
(d) Correct, because a + b + c + d = 0 means (b + c) + (a + d) = 0. The resultant sum of three vectors (b + c), a, and d can be zero only if (b + c) is in the plane of a and d. If a and d are collinear, then (b + c) must be along the line of a and d. Hence, the statement is correct.
(b) Correct, as a + b + c + d = 0 implies a + c = -(b + d). Thus, the magnitude of (a + c) is equal to the magnitude of (b + d).
(c) Correct, since a + b + c + d = 0, so a = -(b + c + d). The magnitude of a is equal to the magnitude of (b + c + d). The sum of the magnitudes of b, c, and d will always be greater than or equal to the magnitude of a, so the statement is correct.
(d) Correct, because a + b + c + d = 0 means (b + c) + (a + d) = 0. The resultant sum of three vectors (b + c), a, and d can be zero only if (b + c) is in the plane of a and d. If a and d are collinear, then (b + c) must be along the line of a and d. Hence, the statement is correct.
The speed of a projectile at its maximum height is √3/2 times its initial speed. If the range of the projectile is P times the maximum height attained by it, then P equals- a)4/3
- b)2√3
- c)4√3
- d)3/4
Correct answer is option 'C'. Can you explain this answer?
The speed of a projectile at its maximum height is √3/2 times its initial speed. If the range of the projectile is P times the maximum height attained by it, then P equals
a)
4/3
b)
2√3
c)
4√3
d)
3/4
|
|
Hansa Sharma answered |
Given √3/2 u = u cos θ
speed at maximum height or cos θ = √3/2 or θ = 30o
speed at maximum height or cos θ = √3/2 or θ = 30o
Given that P Hmax = R
We know Hmax = R tan θ/4
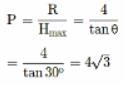
The ceiling of a hall is 40 m high. For maximum horizontal distance, the angle at which the ball may be thrown with a speed of 56 m s-1 without hitting the ceiling of the hall is- a)25°
- b)30°
- c)45°
- d)60°
Correct answer is option 'B'. Can you explain this answer?
The ceiling of a hall is 40 m high. For maximum horizontal distance, the angle at which the ball may be thrown with a speed of 56 m s-1 without hitting the ceiling of the hall is
a)
25°
b)
30°
c)
45°
d)
60°
|
|
Suresh Iyer answered |
Here, u = 56 m s-1 Let θ be the angle of projection with the horizontal to have maximum range, with maximum height = 40 m
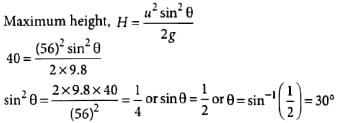
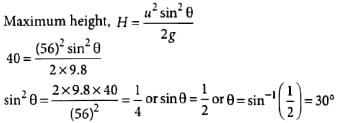
If R and H represent horizontal range and maximum height of the projectile, then the angle of projection with the horizontal is:- a)tan−1 (H/R)
- b)tan−1 (2H/R)
- c)tan−1 (4H/R)
- d)tan−1 (4R/H)
Correct answer is option 'C'. Can you explain this answer?
If R and H represent horizontal range and maximum height of the projectile, then the angle of projection with the horizontal is:
a)
tan−1 (H/R)
b)
tan−1 (2H/R)
c)
tan−1 (4H/R)
d)
tan−1 (4R/H)
|
|
Nandini Sharma answered |
Understanding Projectile Motion
In projectile motion, the angle of projection determines the trajectory of the projectile. When we denote the horizontal range as \( R \) and the maximum height as \( H \), we can derive the angle of projection.
Key Formulas
- The horizontal range \( R \) of a projectile is given by:
\[
R = \frac{v^2 \sin(2\theta)}{g}
\]
- The maximum height \( H \) attained by a projectile is given by:
\[
H = \frac{v^2 \sin^2(\theta)}{2g}
\]
Where:
- \( v \) = initial velocity
- \( g \) = acceleration due to gravity
- \( \theta \) = angle of projection
Relationship Between H and R
To find the angle \( \theta \), we can manipulate these equations.
1. From the maximum height formula:
\[
v^2 = 2gH \cdot \frac{1}{\sin^2(\theta)}
\]
2. Substituting \( v^2 \) in the range formula:
\[
R = \frac{(2gH / \sin^2(\theta)) \cdot \sin(2\theta)}{g}
\]
3. Simplifying gives:
\[
R = \frac{2H \sin(2\theta)}{\sin^2(\theta)}
\]
Using the identity \( \sin(2\theta) = 2\sin(\theta)\cos(\theta) \):
\[
R = \frac{4H \cos(\theta)}{\sin(\theta)}
\]
4. Rearranging leads to:
\[
\tan(\theta) = \frac{4H}{R}
\]
Final Expression for Angle of Projection
Thus, the angle of projection \( \theta \) can be found using:
\[
\theta = \tan^{-1}\left(\frac{4H}{R}\right)
\]
Hence, the correct choice is option **C**: \( \tan^{-1}\left(\frac{4H}{R}\right) \).
In projectile motion, the angle of projection determines the trajectory of the projectile. When we denote the horizontal range as \( R \) and the maximum height as \( H \), we can derive the angle of projection.
Key Formulas
- The horizontal range \( R \) of a projectile is given by:
\[
R = \frac{v^2 \sin(2\theta)}{g}
\]
- The maximum height \( H \) attained by a projectile is given by:
\[
H = \frac{v^2 \sin^2(\theta)}{2g}
\]
Where:
- \( v \) = initial velocity
- \( g \) = acceleration due to gravity
- \( \theta \) = angle of projection
Relationship Between H and R
To find the angle \( \theta \), we can manipulate these equations.
1. From the maximum height formula:
\[
v^2 = 2gH \cdot \frac{1}{\sin^2(\theta)}
\]
2. Substituting \( v^2 \) in the range formula:
\[
R = \frac{(2gH / \sin^2(\theta)) \cdot \sin(2\theta)}{g}
\]
3. Simplifying gives:
\[
R = \frac{2H \sin(2\theta)}{\sin^2(\theta)}
\]
Using the identity \( \sin(2\theta) = 2\sin(\theta)\cos(\theta) \):
\[
R = \frac{4H \cos(\theta)}{\sin(\theta)}
\]
4. Rearranging leads to:
\[
\tan(\theta) = \frac{4H}{R}
\]
Final Expression for Angle of Projection
Thus, the angle of projection \( \theta \) can be found using:
\[
\theta = \tan^{-1}\left(\frac{4H}{R}\right)
\]
Hence, the correct choice is option **C**: \( \tan^{-1}\left(\frac{4H}{R}\right) \).
Which of the following statements.is false regarding the vectors?- a)The magnitude of a vector is always a scalar
- b)Each component of a vector is always a scalar
- c)Two vectors having different magnitudes cannot have their resultant zero
- d)Vectors obey triangle law of addition
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements.is false regarding the vectors?
a)
The magnitude of a vector is always a scalar
b)
Each component of a vector is always a scalar
c)
Two vectors having different magnitudes cannot have their resultant zero
d)
Vectors obey triangle law of addition
|
|
Dev Patel answered |
The magnitude of a vector is a pure number. Each component of a vector is also a vector. The resultant of two vectors can be zero only if they have the same magnitude and opposite directions.
A cyclist is riding with a speed of 27 km h-1. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate of 0.50 m s-1 every second. The net acceleration of the cyclist on the circular turn is- a)0.68 m s-2
- b)0.86 m s-2
- c)0.56 m s-2
- d)0.76 m s-2
Correct answer is option 'B'. Can you explain this answer?
A cyclist is riding with a speed of 27 km h-1. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate of 0.50 m s-1 every second. The net acceleration of the cyclist on the circular turn is
a)
0.68 m s-2
b)
0.86 m s-2
c)
0.56 m s-2
d)
0.76 m s-2
|
|
Preeti Iyer answered |
Given here,
Speed of the cyclist, v = 27 km/h = 7.5m/s
Radius of the circular tun on the road, r = 80 m
Therefore the centripetal acceleration of the cyclist at the moment when velocity is 7.5 m/s is,
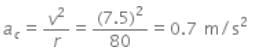
When brakes are applied, the speed is decreased at the rate of 0.5m/s every second.
Speed of the cyclist, v = 27 km/h = 7.5m/s
Radius of the circular tun on the road, r = 80 m
Therefore the centripetal acceleration of the cyclist at the moment when velocity is 7.5 m/s is,
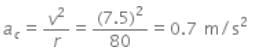
When brakes are applied, the speed is decreased at the rate of 0.5m/s every second.
Therefore the tangential acceleration is,
ar = - 0.5 m/s2
Therefore the total acceleration of the cyclist is,
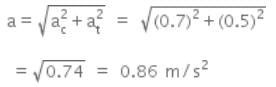
ar = - 0.5 m/s2
Therefore the total acceleration of the cyclist is,
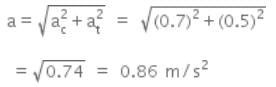
Centripetal acceleration is- a)A constant vector
- b)A constant scalar
- c)A magnitude changing vector
- d)Not a constant vector
Correct answer is option 'D'. Can you explain this answer?
Centripetal acceleration is
a)
A constant vector
b)
A constant scalar
c)
A magnitude changing vector
d)
Not a constant vector
|
|
Geetika Shah answered |
Centripetal acceleration, ac = v2/R
where v is the speed of an object and R is the radius of the circle. It is always directed towards the center of the circle. Since v and R are constants for a given uniform circular motion, therefore the magnitude of centripetal acceleration is also constant. However, the direction of centripetal acceleration changes continuously. Therefore, centripetal acceleration is not a constant vector.
where v is the speed of an object and R is the radius of the circle. It is always directed towards the center of the circle. Since v and R are constants for a given uniform circular motion, therefore the magnitude of centripetal acceleration is also constant. However, the direction of centripetal acceleration changes continuously. Therefore, centripetal acceleration is not a constant vector.
If n is a unit vector in the direction of the vector 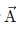 then
then
- a)
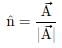
- b)
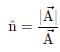
- c)
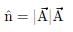
- d)
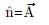
Correct answer is option 'A'. Can you explain this answer?
If n is a unit vector in the direction of the vector 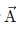 then
then
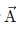 then
thena)
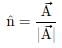
b)
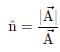
c)
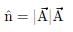
d)
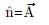
|
|
Mira Joshi answered |
Unit vector is vector with magnitude unity but having specific direction.
Value of unit vector is given by:
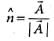
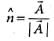
Where,
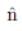 = unit vector
= unit vectorA = vector a
∣A∣ = magnitude of vector a
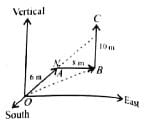
Rain is falling vertically with a speed of 30 ms−1. A woman rides a bicycle with a speed of 12 ms−1 in east to west direction. In which direction she should hold her umbrella?- a)At an angle of tan−1(2/5) with the vertical towards the east.
- b)At angle of tan−1(2/5) with the vertical towards the west.
- c)At angle of tan−1 (5/2) with the vertical towards the east.
- d)At angle of tan−1 (5/2) with the vertical towards the west.
Correct answer is option 'B'. Can you explain this answer?
Rain is falling vertically with a speed of 30 ms−1. A woman rides a bicycle with a speed of 12 ms−1 in east to west direction. In which direction she should hold her umbrella?
a)
At an angle of tan−1(2/5) with the vertical towards the east.
b)
At angle of tan−1(2/5) with the vertical towards the west.
c)
At angle of tan−1 (5/2) with the vertical towards the east.
d)
At angle of tan−1 (5/2) with the vertical towards the west.
|
|
Suresh Iyer answered |
In the figure, 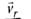 represents the velocity of rain and vb the velocity of the bicycle, the woman is riding. To protect herself from rain, the woman should hold her umbrella in the direction of the relative velocity of rain with respect to the bicycle
represents the velocity of rain and vb the velocity of the bicycle, the woman is riding. To protect herself from rain, the woman should hold her umbrella in the direction of the relative velocity of rain with respect to the bicycle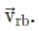 From figure,
From figure,

Therefore, the woman should hold her umbrella at an angle of tan−1(2/5)with the vertical towards the west.
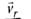 represents the velocity of rain and vb the velocity of the bicycle, the woman is riding. To protect herself from rain, the woman should hold her umbrella in the direction of the relative velocity of rain with respect to the bicycle
represents the velocity of rain and vb the velocity of the bicycle, the woman is riding. To protect herself from rain, the woman should hold her umbrella in the direction of the relative velocity of rain with respect to the bicycle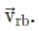 From figure,
From figure,
Therefore, the woman should hold her umbrella at an angle of tan−1(2/5)with the vertical towards the west.
What is approximately the centripetal acceleration (in units of acceleration due to gravity on earth, g = 10 m s-2) of an air-craft flying at a speed of 400 m s-1 through a circular arc of radius 0.6 km?- a)26.7
- b)16.9
- c)13.5
- d)30.2
Correct answer is option 'A'. Can you explain this answer?
What is approximately the centripetal acceleration (in units of acceleration due to gravity on earth, g = 10 m s-2) of an air-craft flying at a speed of 400 m s-1 through a circular arc of radius 0.6 km?
a)
26.7
b)
16.9
c)
13.5
d)
30.2
|
|
Nitya Menon answered |
Centripetal acceleration is the acceleration experienced by an object moving in a circular path. It is always directed towards the center of the circle and its magnitude can be calculated using the formula:
a = v^2 / r
where "a" is the centripetal acceleration, "v" is the velocity of the object, and "r" is the radius of the circular path.
Let's calculate the centripetal acceleration of the aircraft:
Given:
Velocity of the aircraft, v = 400 m/s
Radius of the circular arc, r = 0.6 km = 0.6 × 1000 m = 600 m
Substituting the values into the formula:
a = (400^2) / 600
a = 160000 / 600
a ≈ 266.67 m/s^2
To express the centripetal acceleration in units of acceleration due to gravity on Earth (g = 10 m/s^2), we divide the value by g:
a ≈ 266.67 / 10
a ≈ 26.67 g
Therefore, the approximate centripetal acceleration of the aircraft is 26.67 times the acceleration due to gravity on Earth.
Hence, the correct answer is option A) 26.7.
a = v^2 / r
where "a" is the centripetal acceleration, "v" is the velocity of the object, and "r" is the radius of the circular path.
Let's calculate the centripetal acceleration of the aircraft:
Given:
Velocity of the aircraft, v = 400 m/s
Radius of the circular arc, r = 0.6 km = 0.6 × 1000 m = 600 m
Substituting the values into the formula:
a = (400^2) / 600
a = 160000 / 600
a ≈ 266.67 m/s^2
To express the centripetal acceleration in units of acceleration due to gravity on Earth (g = 10 m/s^2), we divide the value by g:
a ≈ 266.67 / 10
a ≈ 26.67 g
Therefore, the approximate centripetal acceleration of the aircraft is 26.67 times the acceleration due to gravity on Earth.
Hence, the correct answer is option A) 26.7.
A vector is not changed if- a)It is displaced parallel to itself
- b)It is rotated through an arbitrary angle
- c)it is cross-multiplied by a unit vector
- d)It is multiplied by an arbitrary scalar
Correct answer is option 'A'. Can you explain this answer?
A vector is not changed if
a)
It is displaced parallel to itself
b)
It is rotated through an arbitrary angle
c)
it is cross-multiplied by a unit vector
d)
It is multiplied by an arbitrary scalar
|
|
Tejas Chatterjee answered |
Understanding Vector Displacement
Vectors are mathematical entities characterized by both magnitude and direction. The options provided examine different transformations applied to a vector to determine if its essence remains unchanged.
Displacement Parallel to Itself
- When a vector is displaced parallel to its original direction, it retains its characteristics.
- The magnitude and direction remain constant, just shifted in space.
- This transformation does not alter the vector's identity, making it unchanged.
Rotation Through an Arbitrary Angle
- Rotating a vector alters its direction while maintaining the same magnitude.
- This transformation changes the vector's components, hence it is not unchanged.
Cross-Multiplication by a Unit Vector
- Cross-multiplying a vector by a unit vector results in a new vector that is perpendicular to both.
- This operation changes the vector's direction, hence it is not unchanged.
Multiplication by an Arbitrary Scalar
- Multiplying a vector by a scalar changes its magnitude.
- Although the direction may remain the same if the scalar is positive, the vector is still considered changed overall.
Conclusion
- Only option (a), the displacement parallel to itself, ensures that the vector is not changed.
- Understanding these transformations is essential in physics and engineering, particularly in vector analysis.
Vectors are mathematical entities characterized by both magnitude and direction. The options provided examine different transformations applied to a vector to determine if its essence remains unchanged.
Displacement Parallel to Itself
- When a vector is displaced parallel to its original direction, it retains its characteristics.
- The magnitude and direction remain constant, just shifted in space.
- This transformation does not alter the vector's identity, making it unchanged.
Rotation Through an Arbitrary Angle
- Rotating a vector alters its direction while maintaining the same magnitude.
- This transformation changes the vector's components, hence it is not unchanged.
Cross-Multiplication by a Unit Vector
- Cross-multiplying a vector by a unit vector results in a new vector that is perpendicular to both.
- This operation changes the vector's direction, hence it is not unchanged.
Multiplication by an Arbitrary Scalar
- Multiplying a vector by a scalar changes its magnitude.
- Although the direction may remain the same if the scalar is positive, the vector is still considered changed overall.
Conclusion
- Only option (a), the displacement parallel to itself, ensures that the vector is not changed.
- Understanding these transformations is essential in physics and engineering, particularly in vector analysis.
The speed with which the stone hits the ground is- a)15 m s-1
- b)90 m s-1
- c)99 m s-1
- d)49 m s-1
Correct answer is option 'C'. Can you explain this answer?
The speed with which the stone hits the ground is
a)
15 m s-1
b)
90 m s-1
c)
99 m s-1
d)
49 m s-1
|
|
Riya Banerjee answered |
Motion along horizontal direction, ↓+ ve
ux = 15ms−1, ax = 0
vx = ux + axt = 15 + 0 × 10 = 15ms−1
Motion along vertical direction,
uy = 0,ay = g
vy = uy + ayt = 0 + 9.8 × 10 = 98ms−1
∴ Speed of the stone when it hits the ground is
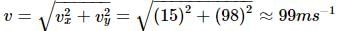
ux = 15ms−1, ax = 0
vx = ux + axt = 15 + 0 × 10 = 15ms−1
Motion along vertical direction,
uy = 0,ay = g
vy = uy + ayt = 0 + 9.8 × 10 = 98ms−1
∴ Speed of the stone when it hits the ground is
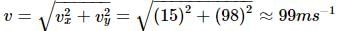

- a)zero
- b)A2B2
- c)AB
- d)√AB
Correct answer is option 'B'. Can you explain this answer?

a)
zero
b)
A2B2
c)
AB
d)
√AB
|
|
Dev Patel answered |
Let θ be angle between vectors 
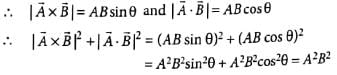
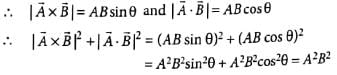
Then the distance from the thrower to the point where the ball returns to the same level is- a)58 m
- b)68 m
- c)78 m
- d)88 m
Correct answer is option 'C'. Can you explain this answer?
Then the distance from the thrower to the point where the ball returns to the same level is
a)
58 m
b)
68 m
c)
78 m
d)
88 m
|
|
Anjali Sharma answered |
Given data,
u = 30ms−1
θ = 300
g = 10ms−2
The distance from the thrower to the point where the ball returns to the same level is


Chapter doubts & questions for Motion in a Plane - NCERTs at Fingertips: Textbooks, Tests & Solutions 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Motion in a Plane - NCERTs at Fingertips: Textbooks, Tests & Solutions in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup


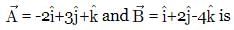

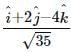
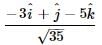
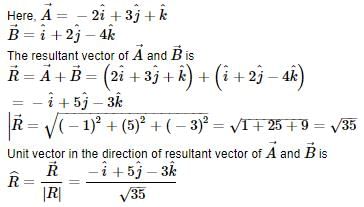
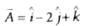 on the vector
on the vector 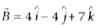 is
is