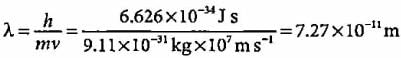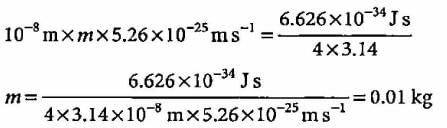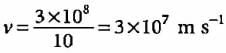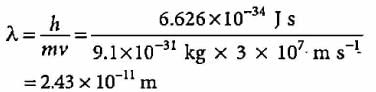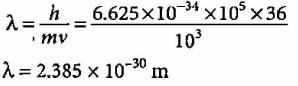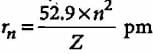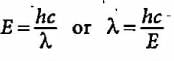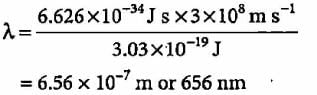All Exams >
NEET >
NCERT Textbooks, Tests & Solutions >
All Questions
All questions of Structure of Atom for NEET Exam
How many subshells and electrons are associated with n = 4?
- a)32, 64
- b)16, 32
- c)4, 16
- d)8, 16
Correct answer is option 'B'. Can you explain this answer?
How many subshells and electrons are associated with n = 4?
a)
32, 64
b)
16, 32
c)
4, 16
d)
8, 16
|
|
Jyoti Sengupta answered |
For nth orbital possible values of azimuthal quantum number (subshell), l are from 0 to (n-1). Total of 'n' values.
In n=4, l=0,1,2,3 thus there are 4 subshells i.e.s,p,d,f respectively.
Magnetic quantum number ml have values from -l to +l and total of 2l+1 values.
For n=4, possible values of l and ml are:
ml=0 for l=0; total ml values =1
ml=−1,0,1 for l=1; total ml values =3
ml=−2,−1,0,1,2 for l=2; total ml values =5
ml=−3,−2,−1,0,1,2,3 for l=3; total ml values =7
Total number of orbitals = total values of ml
for n=4,
∴1+3+5+7=16 orbitals
Each orbital can occupy maximum of two electron
Number of electrons =2×16=32
Therefore in n=4, number of subshells=4, orbitals=16 and number of electrons =32.
Describe the orbital with following quantum numbers:
(i) n = 3, l = 2
(ii) n = 4 , l = 3
- a)(i) 3p, (ii) 4f
- b)(i) 3d, (ii) 4d
- c)(i) 3f, (ii) 4f
- d)(i) 3d, (ii) 4f
Correct answer is option 'D'. Can you explain this answer?
Describe the orbital with following quantum numbers:
(i) n = 3, l = 2
(ii) n = 4 , l = 3
(i) n = 3, l = 2
(ii) n = 4 , l = 3
a)
(i) 3p, (ii) 4f
b)
(i) 3d, (ii) 4d
c)
(i) 3f, (ii) 4f
d)
(i) 3d, (ii) 4f
|
|
Mira Joshi answered |
(i) n = 3, l = 2 ⇒ 3 d
(ii) n = 4 , l = 3 ⇒ 4f
(ii) n = 4 , l = 3 ⇒ 4f
Quantum Numbers Description
i) n = 3, l = 2
- For the quantum numbers n = 3 and l = 2, the orbital is in the 3d subshell.
- The 3d orbital has a complex shape with two angular nodes and can hold a maximum of 10 electrons.
- Electrons in the 3d orbital have higher energy compared to those in the s and p orbitals.
ii) n = 4, l = 3
- For the quantum numbers n = 4 and l = 3, the orbital is in the 4f subshell.
- The 4f orbital has a more complex and intricate shape compared to lower energy orbitals.
- The 4f orbital can hold a maximum of 14 electrons and is located further from the nucleus due to higher energy levels.
i) n = 3, l = 2
- For the quantum numbers n = 3 and l = 2, the orbital is in the 3d subshell.
- The 3d orbital has a complex shape with two angular nodes and can hold a maximum of 10 electrons.
- Electrons in the 3d orbital have higher energy compared to those in the s and p orbitals.
ii) n = 4, l = 3
- For the quantum numbers n = 4 and l = 3, the orbital is in the 4f subshell.
- The 4f orbital has a more complex and intricate shape compared to lower energy orbitals.
- The 4f orbital can hold a maximum of 14 electrons and is located further from the nucleus due to higher energy levels.
How many orbitals in total are associated with 4th energy level?- a)4
- b)9
- c)16
- d)7
Correct answer is option 'C'. Can you explain this answer?
How many orbitals in total are associated with 4th energy level?
a)
4
b)
9
c)
16
d)
7
|
|
Mira Joshi answered |
n = 4, l = 0,1, 2, 3
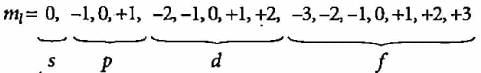
Total number of orbitals 1s + 3p + 5d + 7f = 16
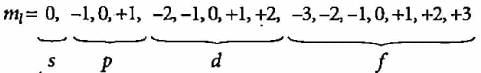
Total number of orbitals 1s + 3p + 5d + 7f = 16
The ratio of charge to mass of an electron in coulombs per gram was determined by J.J. Thomson. He determined this ratio by measuring the deflection of cathode rays in electric and magnetic fields. What value did he find for this ratio?
- a)-1.76 x 108 coulombs/g
- b)1.76 x 10-8 coulombs/g
- c)-1.76 x 1010 coulombs/g
- d)- 1.76 x 10-10 coulombs/g
Correct answer is option 'A'. Can you explain this answer?
The ratio of charge to mass of an electron in coulombs per gram was determined by J.J. Thomson. He determined this ratio by measuring the deflection of cathode rays in electric and magnetic fields. What value did he find for this ratio?
a)
-1.76 x 108 coulombs/g
b)
1.76 x 10-8 coulombs/g
c)
-1.76 x 1010 coulombs/g
d)
- 1.76 x 10-10 coulombs/g
|
|
Riya Banerjee answered |
Charge of an electron is
= −1.6 × 10−19C
Mass of electron is
9.1 × 10−31kg = 9.1 × 10−28g
Thus, Charge/mass ratio is
= −1.6 × 10−19C
Mass of electron is
9.1 × 10−31kg = 9.1 × 10−28g
Thus, Charge/mass ratio is
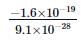
- ve sign is only a convention used by us
= - 1.76 × 108 coulombs/g
Which of the following observations was not correct during Rutherford’s scattering experiment?- a)Most of the α-particles passed through the gold foil undeflected
- b)A small fraction of the α-particles was deflected by small angles
- c)A large number of the α-particles were bounced back
- d)A very few α-particles (~1 in 12,000) were bounced back
Correct answer is option 'C'. Can you explain this answer?
Which of the following observations was not correct during Rutherford’s scattering experiment?
a)
Most of the α-particles passed through the gold foil undeflected
b)
A small fraction of the α-particles was deflected by small angles
c)
A large number of the α-particles were bounced back
d)
A very few α-particles (~1 in 12,000) were bounced back
|
|
Dhruba Choudhury answered |
The question appears to be incomplete as it does not provide any options for the answer choices. Could you please provide the options or complete the question?
Mark the incorrect statement regarding the photoelectric effect.- a)There is no time lag between the striking of light beam and the ejection of electrons from the metal surface
- b)The number of electrons ejected is inversely proportional to the intensity of light
- c)Photoelectric effect is not observed below threshold frequency
- d)The kinetic energy of the electrons increases with increase in frequency of light used
Correct answer is option 'B'. Can you explain this answer?
Mark the incorrect statement regarding the photoelectric effect.
a)
There is no time lag between the striking of light beam and the ejection of electrons from the metal surface
b)
The number of electrons ejected is inversely proportional to the intensity of light
c)
Photoelectric effect is not observed below threshold frequency
d)
The kinetic energy of the electrons increases with increase in frequency of light used

|
Himanshu Das answered |
B) the number of electrons ejected is directly proportional to the intensity of light as a certain amount threshold frequency is required for the photoelectric effect,,,a light with more intesity will contain mor threshold frequency than a low intensity light so the number of electrons ejected will depend upon the intensity of light,,,
The 3d-orbitals having electron density in all the three axes is- a)3dxy
- b)3dz2
- c)3dyz
- d)3dzx
Correct answer is option 'B'. Can you explain this answer?
The 3d-orbitals having electron density in all the three axes is
a)
3dxy
b)
3dz2
c)
3dyz
d)
3dzx
|
|
Gaurav Kumar answered |
dz2 has electron density in all three axes.
What is the colour corresponding to the wavelength of light emitted when the electron in a hydrogen atom undergoes transition from n = 4 to n = 2?- a)Blue
- b)Red
Correct answer is option ''. Can you explain this answer?
What is the colour corresponding to the wavelength of light emitted when the electron in a hydrogen atom undergoes transition from n = 4 to n = 2?
a)
Blue
b)
Red
|
|
Jyoti Sengupta answered |
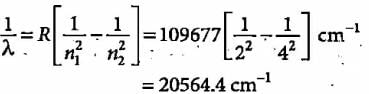
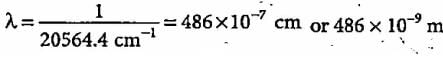
Colour corresponding to this wavelength is blue.
The energy difference between the ground state of an atom and its excited state is 3 x 10-19 J. What is the wavelength of the photon required for this transition?- a)6.6 x 10-34 m
- b)3 x 10-8 m
- c)1.8 x 10-7 m
- d)6.6 x 10-7 m
Correct answer is option 'D'. Can you explain this answer?
The energy difference between the ground state of an atom and its excited state is 3 x 10-19 J. What is the wavelength of the photon required for this transition?
a)
6.6 x 10-34 m
b)
3 x 10-8 m
c)
1.8 x 10-7 m
d)
6.6 x 10-7 m
|
|
Anjali Sharma answered |
ΔE = hc/λ
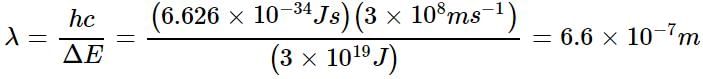
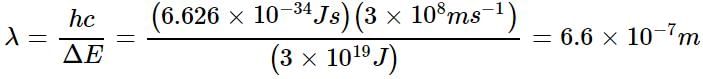
Which of the following is not a correct statement regarding the energies of orbitals?- a)The lower the value of (n + 1) for an orbital, lower is its energy
- b)Electron in the same subshell have equal energy
- c)Energy of s-orbital is lower than the p-orbital and that of p-orbital is lower than the d-orbital
- d)If two orbitals have same value for (n + 1), the orbital with higher value of n will have lower energy
Correct answer is option 'D'. Can you explain this answer?
Which of the following is not a correct statement regarding the energies of orbitals?
a)
The lower the value of (n + 1) for an orbital, lower is its energy
b)
Electron in the same subshell have equal energy
c)
Energy of s-orbital is lower than the p-orbital and that of p-orbital is lower than the d-orbital
d)
If two orbitals have same value for (n + 1), the orbital with higher value of n will have lower energy
|
|
Dev Patel answered |
If two orbitals have same value for (n + l), the orbital with lower value of n will have lower energy.
What will be the energy of one photon of radiation whose frequency is 5 × 1014 Hz?- a)199.51J
- b)3.3 x 10-19J
- c)6.626 x 10-34 J
- d)2.31 x 105 J
Correct answer is option 'B'. Can you explain this answer?
What will be the energy of one photon of radiation whose frequency is 5 × 1014 Hz?
a)
199.51J
b)
3.3 x 10-19J
c)
6.626 x 10-34 J
d)
2.31 x 105 J
|
|
Suresh Iyer answered |
The energy of one photon is given by the expression, E = hν
where, h = 6.626 × 10−34 Js and ν= 5 × 1014 s−1
E = 6.626 × 10−34 × 5 × 1014 = 3.313 × 10−19J
where, h = 6.626 × 10−34 Js and ν= 5 × 1014 s−1
E = 6.626 × 10−34 × 5 × 1014 = 3.313 × 10−19J
What will be the wavenumber of yellow radiation having wavelength 240 nm?
- a)1.724 x 104 cm-1
- b)4.16 x 106 m-1
- c)4 x 1014 Hz
- d)219.3 x 103 cm-1
Correct answer is option 'B'. Can you explain this answer?
What will be the wavenumber of yellow radiation having wavelength 240 nm?
a)
1.724 x 104 cm-1
b)
4.16 x 106 m-1
c)
4 x 1014 Hz
d)
219.3 x 103 cm-1
|
|
Preeti Iyer answered |
Wavelength of yellow light = 240 nm
240 x 10-9 m
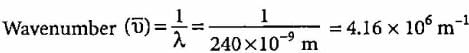
240 x 10-9 m
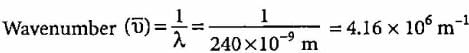
How many electrons in an atom have the following quantum numbers?
n = 4, s = -1/2
- a)32
- b)18
- c)8
- d)16
Correct answer is option 'D'. Can you explain this answer?
How many electrons in an atom have the following quantum numbers?
n = 4, s = -1/2
n = 4, s = -1/2
a)
32
b)
18
c)
8
d)
16
|
|
Ananya Das answered |
n = 4
l = 0, 1 , 2 , 3
ml = 0, (-1, 0, +1), (-2, -1, 0, +1, +2), (-3, -2, -1, 0, +1, +2, +3)
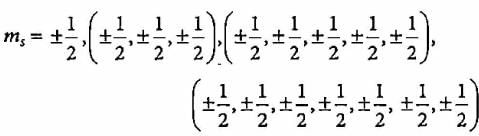
Total number of electrons with ms = - 1/2 will be 16.
l = 0, 1 , 2 , 3
ml = 0, (-1, 0, +1), (-2, -1, 0, +1, +2), (-3, -2, -1, 0, +1, +2, +3)
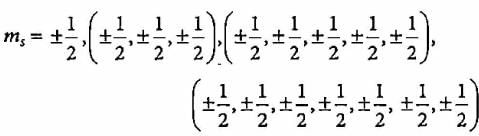
Total number of electrons with ms = - 1/2 will be 16.
Which of the following conclusions regarding the structure of atom is based on Rutherford’s α-particle scattering experiment?- a)The positive charge is concentrated in a very small volume of the atom
- b)The positive charge is scattered with the electrons throughout the atom
- c)The volume occupied by the nucleus is half of the volume of atom
- d)Most of the space in the atom is occupied by the neutrons
Correct answer is option 'A'. Can you explain this answer?
Which of the following conclusions regarding the structure of atom is based on Rutherford’s α-particle scattering experiment?
a)
The positive charge is concentrated in a very small volume of the atom
b)
The positive charge is scattered with the electrons throughout the atom
c)
The volume occupied by the nucleus is half of the volume of atom
d)
Most of the space in the atom is occupied by the neutrons
|
|
Disha Shah answered |
The correct conclusion regarding the structure of the atom based on Rutherford's experiment is that the atom is mostly empty space, with a tiny, dense, positively charged nucleus at the center and negatively charged electrons orbiting around it.
Few electrons have following quantum numbers,
(i) n = 4, l = 1
(ii) n = 4, l = 0
(iii) n = 3, l = 2
(iv) n = 3, l = 1
Arrange them in the order of increasing energy from lowest to highest.- a)(iv) < (ii) < (iii) < (i)
- b)(ii) < (iv) < (i) < (iii)
- c)(i) < (iii) < (ii) < (iv)
- d)(iii) < (i) < (iv) < (ii)
Correct answer is option 'A'. Can you explain this answer?
Few electrons have following quantum numbers,
(i) n = 4, l = 1
(ii) n = 4, l = 0
(iii) n = 3, l = 2
(iv) n = 3, l = 1
Arrange them in the order of increasing energy from lowest to highest.
(i) n = 4, l = 1
(ii) n = 4, l = 0
(iii) n = 3, l = 2
(iv) n = 3, l = 1
Arrange them in the order of increasing energy from lowest to highest.
a)
(iv) < (ii) < (iii) < (i)
b)
(ii) < (iv) < (i) < (iii)
c)
(i) < (iii) < (ii) < (iv)
d)
(iii) < (i) < (iv) < (ii)
|
|
Dev Patel answered |
(i) 4p, (ii) 4s, (iii) 3d, (iv) 3p
The order of increasing energy
(iv) < (ii) < (iii) < (i)
The order of increasing energy
(iv) < (ii) < (iii) < (i)
Electromagnetic radiation of wavelength 242 nm is just sufficient to ionise the sodium atom. What is the ionisation energy of sodium per atom?- a)494.5 x 10-6 J/atom
- b)8169.5 x 10-10 J/atom
- c)5.85 x 10-15 J/atom
- d)8.214 x 10-19 J/atom
Correct answer is option 'D'. Can you explain this answer?
Electromagnetic radiation of wavelength 242 nm is just sufficient to ionise the sodium atom. What is the ionisation energy of sodium per atom?
a)
494.5 x 10-6 J/atom
b)
8169.5 x 10-10 J/atom
c)
5.85 x 10-15 J/atom
d)
8.214 x 10-19 J/atom
|
|
Apoorva Singh answered |

Given below are the spectral lines for an atom of hydrogen. Mark the lines which are not correctly matched with the value of n1 and n2?

- a)(i) and (ii)
- b)(i) arid (hi)
- c)(ii) and (iv)
- d)(i) and (iv)
Correct answer is option 'C'. Can you explain this answer?
Given below are the spectral lines for an atom of hydrogen. Mark the lines which are not correctly matched with the value of n1 and n2?


a)
(i) and (ii)
b)
(i) arid (hi)
c)
(ii) and (iv)
d)
(i) and (iv)
|
|
Preeti Iyer answered |
(ii) Balmer, n1 = 2 ; n2 = 3, 4 ; region - visible
(iv) Pfund, n1 = 5 ; n2 = 6, 7; region - infrared
(iv) Pfund, n1 = 5 ; n2 = 6, 7; region - infrared
What will be the uncertainty in velocity of a bullet with a mass of 10 g whose position is known with ± 0.01 mm?- a)5.275 x 10-33 m s-1
- b)5.275 x 10-25 m s-1
- c)5.275 x 10-5 m s-1
- d)5.275 x 10-28 m s-1
Correct answer is option 'D'. Can you explain this answer?
What will be the uncertainty in velocity of a bullet with a mass of 10 g whose position is known with ± 0.01 mm?
a)
5.275 x 10-33 m s-1
b)
5.275 x 10-25 m s-1
c)
5.275 x 10-5 m s-1
d)
5.275 x 10-28 m s-1
|
|
Suresh Iyer answered |
Δx = ± 0.01 mm = 1 x 10-5 m,
m = 10 g = 1 x 10-2kg
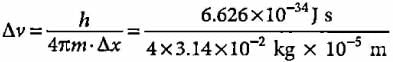
= 5.275 x 10-28m s-1.
m = 10 g = 1 x 10-2kg
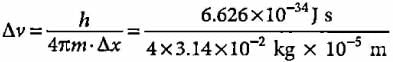
= 5.275 x 10-28m s-1.
Which of the following configurations does not follow Hund’s rule of maximum multiplicity?- a)1s2 2s2 2p6 3s2 3p2
- b)1s2 2s2 2p6 3s2 3p6 4s2 3d6
- c)1s2 2s2 2p6 3s2 3p6 4s1 3d5
- d)1s2 2s2 2p6 3s2 3p4 4s2
Correct answer is option 'D'. Can you explain this answer?
Which of the following configurations does not follow Hund’s rule of maximum multiplicity?
a)
1s2 2s2 2p6 3s2 3p2
b)
1s2 2s2 2p6 3s2 3p6 4s2 3d6
c)
1s2 2s2 2p6 3s2 3p6 4s1 3d5
d)
1s2 2s2 2p6 3s2 3p4 4s2
|
|
Dev Patel answered |
The configuration does not follow Hund’s rule of maximum multiplicity because 3p will be fully filled before the electrons go to 4s.
What is the electronic configuration of O2- ion?- a)1s2 2s2 2p6
- b)1s2 2s2 2p4
- c)1s2 2s2 2p5
- d)1s2 2s2 2p3
Correct answer is option 'A'. Can you explain this answer?
What is the electronic configuration of O2- ion?
a)
1s2 2s2 2p6
b)
1s2 2s2 2p4
c)
1s2 2s2 2p5
d)
1s2 2s2 2p3
|
|
Raghav Bansal answered |
O2- ion contains 2 electrons more than O. Hence its electronic configuration will be 1s2 2s2 2p6.
In how many elements the last electron will have the following set of quantum numbers, n = 3 and l = 1?- a)2
- b)8
- c)6
- d)10
Correct answer is option 'C'. Can you explain this answer?
In how many elements the last electron will have the following set of quantum numbers, n = 3 and l = 1?
a)
2
b)
8
c)
6
d)
10
|
|
Ashwin Saini answered |
Explanation:
The set of quantum numbers given are n=3 and l=1.
The principal quantum number (n) determines the energy level of the electron, while the azimuthal quantum number (l) determines the subshell in which the electron resides.
For l=1, the subshell is the p subshell. In the third energy level (n=3), there are three subshells: s, p, and d.
The maximum number of electrons that can occupy a p subshell is 6, according to the Pauli Exclusion Principle and Hund's Rule.
Therefore, the number of elements that can have the quantum numbers n=3 and l=1 (p subshell) is 6.
Option C is correct.
The set of quantum numbers given are n=3 and l=1.
The principal quantum number (n) determines the energy level of the electron, while the azimuthal quantum number (l) determines the subshell in which the electron resides.
For l=1, the subshell is the p subshell. In the third energy level (n=3), there are three subshells: s, p, and d.
The maximum number of electrons that can occupy a p subshell is 6, according to the Pauli Exclusion Principle and Hund's Rule.
Therefore, the number of elements that can have the quantum numbers n=3 and l=1 (p subshell) is 6.
Option C is correct.
Which of the following quantum numbers are correct for the outermost electron of sodium atom?- a)n = 4, l = 0, m = 0, s = +1/2
- b)n = 3, l = 0, m = 0, s = -1/2
- c)h = 3, l = 1, m = +1, s = +1/2
- d)n = 3, l = 2, m = -1, s = -1/2
Correct answer is option 'B'. Can you explain this answer?
Which of the following quantum numbers are correct for the outermost electron of sodium atom?
a)
n = 4, l = 0, m = 0, s = +1/2
b)
n = 3, l = 0, m = 0, s = -1/2
c)
h = 3, l = 1, m = +1, s = +1/2
d)
n = 3, l = 2, m = -1, s = -1/2
|
|
Suresh Iyer answered |
11Na = 1s2 2s2 2p6 3s1
For 3s1, n = 3, l = 0, ml = 0, s = -1/2
For 3s1, n = 3, l = 0, ml = 0, s = -1/2
A body of mass 10 g is moving with a velocity of 100 m s-1. The wavelength associated with it is- a)6.626 x 10-7 m
- b)6.626 x 10-34 m
- c)6.626 x 10-4 m
- d)6.626 x 10-35 m
Correct answer is option 'B'. Can you explain this answer?
A body of mass 10 g is moving with a velocity of 100 m s-1. The wavelength associated with it is
a)
6.626 x 10-7 m
b)
6.626 x 10-34 m
c)
6.626 x 10-4 m
d)
6.626 x 10-35 m
|
|
Milan Nambiar answered |
Explanation:
The given problem involves calculating the de Broglie wavelength associated with a body of mass and velocity.
De Broglie Wavelength Formula:
The de Broglie wavelength (λ) of a particle is given by the formula:
λ = h / mv
Where:
λ = de Broglie wavelength
h = Planck's constant (6.626 x 10^-34 J s)
m = mass of the particle (10 g = 0.01 kg)
v = velocity of the particle (100 m/s)
Calculation:
Substitute the given values into the formula:
λ = (6.626 x 10^-34) / (0.01 x 100)
λ = 6.626 x 10^-34 / 1
λ = 6.626 x 10^-34 m
Therefore, the de Broglie wavelength associated with the body of mass 10 g moving at 100 m/s is 6.626 x 10^-34 m.
So, the correct answer is option B: 6.626 x 10^-34 m.
The given problem involves calculating the de Broglie wavelength associated with a body of mass and velocity.
De Broglie Wavelength Formula:
The de Broglie wavelength (λ) of a particle is given by the formula:
λ = h / mv
Where:
λ = de Broglie wavelength
h = Planck's constant (6.626 x 10^-34 J s)
m = mass of the particle (10 g = 0.01 kg)
v = velocity of the particle (100 m/s)
Calculation:
Substitute the given values into the formula:
λ = (6.626 x 10^-34) / (0.01 x 100)
λ = 6.626 x 10^-34 / 1
λ = 6.626 x 10^-34 m
Therefore, the de Broglie wavelength associated with the body of mass 10 g moving at 100 m/s is 6.626 x 10^-34 m.
So, the correct answer is option B: 6.626 x 10^-34 m.
What is the lowest value of n that allows g orbital to exist?- a)6
- b)7
- c)4
- d)5
Correct answer is option 'D'. Can you explain this answer?
What is the lowest value of n that allows g orbital to exist?
a)
6
b)
7
c)
4
d)
5
|
|
Saumya Sarkar answered |
The lowest value of n that allows the g orbital to exist is 5.
Explanation:
The g orbital is one of the five d orbitals. It has a complex shape and can hold a maximum of 10 electrons. The d orbitals exist in the energy levels beyond the s and p orbitals.
Energy Levels and Subshells:
- The energy levels in an atom are represented by the principal quantum number (n).
- The value of n determines the size and energy of the orbital.
- The subshells, which are further divided into orbitals, are represented by the azimuthal quantum number (l).
- The value of l determines the shape of the orbital.
Order of Filling Orbitals:
The order of filling orbitals is determined by the Aufbau principle, which states that electrons fill the lowest energy level orbitals first before moving to higher energy level orbitals.
Order of Filling Orbitals:
1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p...
Explanation:
1. The s orbitals (spherical) are filled first, starting with the 1s orbital, followed by 2s, 3s, 4s, and so on.
2. The p orbitals (dumbbell-shaped) are filled after the s orbitals, starting with the 2p orbital, followed by 3p, 4p, and so on.
3. The d orbitals (complex shapes) are filled after the p orbitals, starting with the 3d orbital, followed by 4d, 5d, and so on.
4. The f orbitals (even more complex shapes) are filled after the d orbitals, starting with the 4f orbital, followed by 5f, and so on.
The g Orbital:
- The g orbital is the fifth orbital in the d subshell.
- It is filled after the 4s, 3d, and 4p orbitals.
- Therefore, the lowest value of n that allows the g orbital to exist is 5.
Answer:
The correct answer is option 'D' (5).
Explanation:
The g orbital is one of the five d orbitals. It has a complex shape and can hold a maximum of 10 electrons. The d orbitals exist in the energy levels beyond the s and p orbitals.
Energy Levels and Subshells:
- The energy levels in an atom are represented by the principal quantum number (n).
- The value of n determines the size and energy of the orbital.
- The subshells, which are further divided into orbitals, are represented by the azimuthal quantum number (l).
- The value of l determines the shape of the orbital.
Order of Filling Orbitals:
The order of filling orbitals is determined by the Aufbau principle, which states that electrons fill the lowest energy level orbitals first before moving to higher energy level orbitals.
Order of Filling Orbitals:
1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p...
Explanation:
1. The s orbitals (spherical) are filled first, starting with the 1s orbital, followed by 2s, 3s, 4s, and so on.
2. The p orbitals (dumbbell-shaped) are filled after the s orbitals, starting with the 2p orbital, followed by 3p, 4p, and so on.
3. The d orbitals (complex shapes) are filled after the p orbitals, starting with the 3d orbital, followed by 4d, 5d, and so on.
4. The f orbitals (even more complex shapes) are filled after the d orbitals, starting with the 4f orbital, followed by 5f, and so on.
The g Orbital:
- The g orbital is the fifth orbital in the d subshell.
- It is filled after the 4s, 3d, and 4p orbitals.
- Therefore, the lowest value of n that allows the g orbital to exist is 5.
Answer:
The correct answer is option 'D' (5).
An orbital is described with the help of a wave function. Since many wave functions are possible for an electron, there are many atomic orbitals. When atom is placed in a magnetic field the possible number of orientations for an orbital of azimuthal quantum number 3 is:- a)Three
- b)Two
- c)Five
- d)Seven
Correct answer is option 'D'. Can you explain this answer?
An orbital is described with the help of a wave function. Since many wave functions are possible for an electron, there are many atomic orbitals. When atom is placed in a magnetic field the possible number of orientations for an orbital of azimuthal quantum number 3 is:
a)
Three
b)
Two
c)
Five
d)
Seven
|
|
Mira Joshi answered |
When l = 3, magnetic quantum number has 7 values ml = (2l + 1). These values are represented as -3, -2, -1, 0, +1, +2, +3
The probability of finding out an electron at a point within an atom is proportional to the- a)square of the orbital wave function i.e., ψ2
- b)orbital wave function i.e., ψ
- c)Hamiltonian operator i.e., H
- d)principal quantum number i.e., n
Correct answer is option 'A'. Can you explain this answer?
The probability of finding out an electron at a point within an atom is proportional to the
a)
square of the orbital wave function i.e., ψ2
b)
orbital wave function i.e., ψ
c)
Hamiltonian operator i.e., H
d)
principal quantum number i.e., n
|
|
Preeti Iyer answered |
ψ2 is known as probability density and is always positive. From the value of ψ2 at different points with in an atom it is possible to predict the region around the nucleus where electron will most probably be found.
A 100 watt bulb emits monochromatic light of wavelength 400 nm. Calculate the number of photons emitted per second by the bulb.- a)3 x 1020 s-1
- b)2 x 10-20 s-1
- c)2 x 1020 s-1
- d)1 x 10-20 s-1
Correct answer is option 'C'. Can you explain this answer?
A 100 watt bulb emits monochromatic light of wavelength 400 nm. Calculate the number of photons emitted per second by the bulb.
a)
3 x 1020 s-1
b)
2 x 10-20 s-1
c)
2 x 1020 s-1
d)
1 x 10-20 s-1
|
|
Priya Menon answered |
Power of the bulb = 100 watt = 100 J s-1 Energy of one photon E = hv = hc/λ
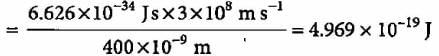
Number of photons emitted
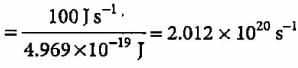
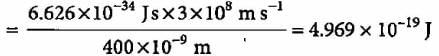
Number of photons emitted
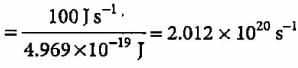
How many number of electrons are present in a particle which carries a charge of 5.5 x 10-16 C?- a)3432
- b)1560
- c)8240
- d)2432
Correct answer is option 'A'. Can you explain this answer?
How many number of electrons are present in a particle which carries a charge of 5.5 x 10-16 C?
a)
3432
b)
1560
c)
8240
d)
2432
|
|
Riya Banerjee answered |
Charge carried by one electron
= 1.6022 x 10-19 C
Electrons presents in 5.5 x 10-16 C
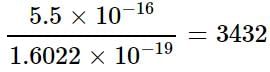
= 1.6022 x 10-19 C
Electrons presents in 5.5 x 10-16 C
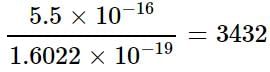
What are the possible values of n, l and ml for an atomic orbital 4f?- a)n = 4, l = 0, 1, 2, 3, ml = -2, -1, 0, +1; +2
- b)n = 4, l = 3, ml = - 3, - 2, - 1, 0, +1, +2, +3
- c)n = 4, l = 2 , ml = - 2 , -1, 0, +1, +2, +3
- d)n = 4, l = 0,1, ml = - 1, 0, +1
Correct answer is option 'B'. Can you explain this answer?
What are the possible values of n, l and ml for an atomic orbital 4f?
a)
n = 4, l = 0, 1, 2, 3, ml = -2, -1, 0, +1; +2
b)
n = 4, l = 3, ml = - 3, - 2, - 1, 0, +1, +2, +3
c)
n = 4, l = 2 , ml = - 2 , -1, 0, +1, +2, +3
d)
n = 4, l = 0,1, ml = - 1, 0, +1
|
|
Jyoti Sengupta answered |
For 4f; n = 4, l = 3,
ml = 7 or -3 , -2, -1 , 0 , +1, +2, +3
ml = 7 or -3 , -2, -1 , 0 , +1, +2, +3
What does the negative electronic energy (negative sign for all values of energy) for hydrogen atom means?
- a)The energy of an electron in the atom is lower than the energy of a free electron at rest which is taken as zero
- b)When the electron is free from the influence of nucleus it has a negative value which becomes more negative
- c)When the electron is attracted by the nucleus the energy is absorbed which means a negative value
- d)Energy is released by hydrogen atom in ground state
Correct answer is option 'A'. Can you explain this answer?
What does the negative electronic energy (negative sign for all values of energy) for hydrogen atom means?
a)
The energy of an electron in the atom is lower than the energy of a free electron at rest which is taken as zero
b)
When the electron is free from the influence of nucleus it has a negative value which becomes more negative
c)
When the electron is attracted by the nucleus the energy is absorbed which means a negative value
d)
Energy is released by hydrogen atom in ground state
|
|
Ujwal Sen answered |
Understanding Negative Electronic Energy in Hydrogen Atom
The concept of negative electronic energy in the hydrogen atom is fundamental to quantum mechanics and atomic theory. Let's explore what this means:
Energy Reference Point
- In atomic physics, the energy of a free electron at rest is considered as the reference point and is assigned a value of zero.
- When an electron is bound to a nucleus (like in a hydrogen atom), its energy is negative, indicating that it is in a lower energy state compared to when it is free.
Lower Energy State
- The negative sign of the energy indicates that the electron is in a more stable configuration when it is bound to the nucleus.
- This means that the electron has less energy than when it is not influenced by the nucleus.
Comparison with Free Electron
- A negative energy value suggests that energy must be added to the system to free the electron from the attractive force of the nucleus.
- Thus, when moving from a bound state to a free state, the energy of the electron transitions from negative to zero, indicating energy absorption.
Conclusion
- Therefore, the correct interpretation is that the energy of an electron in the hydrogen atom is lower than that of a free electron at rest, which is taken as zero. This aligns with option 'A'.
- Understanding this helps in realising the stability of electrons in atoms and their behavior in different energy states.
The concept of negative electronic energy in the hydrogen atom is fundamental to quantum mechanics and atomic theory. Let's explore what this means:
Energy Reference Point
- In atomic physics, the energy of a free electron at rest is considered as the reference point and is assigned a value of zero.
- When an electron is bound to a nucleus (like in a hydrogen atom), its energy is negative, indicating that it is in a lower energy state compared to when it is free.
Lower Energy State
- The negative sign of the energy indicates that the electron is in a more stable configuration when it is bound to the nucleus.
- This means that the electron has less energy than when it is not influenced by the nucleus.
Comparison with Free Electron
- A negative energy value suggests that energy must be added to the system to free the electron from the attractive force of the nucleus.
- Thus, when moving from a bound state to a free state, the energy of the electron transitions from negative to zero, indicating energy absorption.
Conclusion
- Therefore, the correct interpretation is that the energy of an electron in the hydrogen atom is lower than that of a free electron at rest, which is taken as zero. This aligns with option 'A'.
- Understanding this helps in realising the stability of electrons in atoms and their behavior in different energy states.
If uncertainty principle is applied to an object of mass 1 milligram, the uncertainty value of velocity and position will be- a)0.2 x 10-4 m2 s-1
- b)0.52 x 106 m2 s-1
- c)0.52 x 10-28 m2 s-1
- d)2 x 10-34 m2 s-1
Correct answer is option 'C'. Can you explain this answer?
If uncertainty principle is applied to an object of mass 1 milligram, the uncertainty value of velocity and position will be
a)
0.2 x 10-4 m2 s-1
b)
0.52 x 106 m2 s-1
c)
0.52 x 10-28 m2 s-1
d)
2 x 10-34 m2 s-1
|
|
Suresh Iyer answered |

= 0.52 x 10-28 m2 s-1 (1 mg = 10-6 kg)
What will be the orbital angular momentum of an electron in 2s-orbital?- a)Zero
- b)One
- c)Two
- d)Three
Correct answer is option 'A'. Can you explain this answer?
What will be the orbital angular momentum of an electron in 2s-orbital?
a)
Zero
b)
One
c)
Two
d)
Three
|
|
Ameya Bose answered |
Introduction:
The orbital angular momentum of an electron is a property that arises from its motion around the nucleus in an atom. It quantifies the amount of rotational motion an electron has in its orbit. The orbital angular momentum is determined by the principal quantum number (n) and the azimuthal quantum number (l) of the orbital in which the electron resides.
Explanation:
- The principal quantum number, n, describes the energy level of an electron and determines the size of the orbital.
- The azimuthal quantum number, l, describes the shape of the orbital and can take on values from 0 to n-1.
- For an s-orbital, the azimuthal quantum number, l, is equal to 0. Therefore, the orbital angular momentum (L) of an electron in an s-orbital is given by the equation L = √(l(l+1))ħ, where ħ is the reduced Planck's constant.
- Plugging in the value l = 0 into the equation, we get L = √(0(0+1))ħ = √(0)ħ = 0.
- Hence, the orbital angular momentum of an electron in a 2s-orbital is zero.
Conclusion:
The orbital angular momentum of an electron in a 2s-orbital is zero. This is because the azimuthal quantum number, l, for an s-orbital is zero, resulting in a zero value for the orbital angular momentum.
The orbital angular momentum of an electron is a property that arises from its motion around the nucleus in an atom. It quantifies the amount of rotational motion an electron has in its orbit. The orbital angular momentum is determined by the principal quantum number (n) and the azimuthal quantum number (l) of the orbital in which the electron resides.
Explanation:
- The principal quantum number, n, describes the energy level of an electron and determines the size of the orbital.
- The azimuthal quantum number, l, describes the shape of the orbital and can take on values from 0 to n-1.
- For an s-orbital, the azimuthal quantum number, l, is equal to 0. Therefore, the orbital angular momentum (L) of an electron in an s-orbital is given by the equation L = √(l(l+1))ħ, where ħ is the reduced Planck's constant.
- Plugging in the value l = 0 into the equation, we get L = √(0(0+1))ħ = √(0)ħ = 0.
- Hence, the orbital angular momentum of an electron in a 2s-orbital is zero.
Conclusion:
The orbital angular momentum of an electron in a 2s-orbital is zero. This is because the azimuthal quantum number, l, for an s-orbital is zero, resulting in a zero value for the orbital angular momentum.
An element with mass number 81 contains 31.7% more neutrons as compared to protons. Find the symbol of the atom- a)

- b)
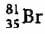
- c)
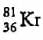
- d)
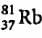
Correct answer is option 'B'. Can you explain this answer?
An element with mass number 81 contains 31.7% more neutrons as compared to protons. Find the symbol of the atom
a)

b)
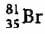
c)
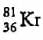
d)
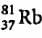
|
|
Mira Joshi answered |
Mass number of the element = 81
i.e., p + n = 81
Let the number of protons be x.
Number of neutrons
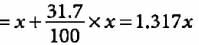
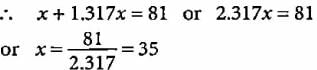
Symbol of the element
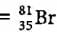
i.e., p + n = 81
Let the number of protons be x.
Number of neutrons
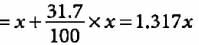
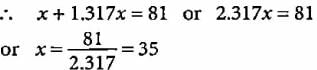
Symbol of the element
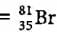
The third line of the Balmer series in the emission spectrum of the hydrogen atom is due to the transition from the- a)Fourth Bohr orbit to the first Bohr orbit
- b)Fifth Bohr orbit to the second Bohr orbit
- c)Sixth Bohr orbit to the third Bohr orbit
- d)Seventh Bohr orbit to the third Bohr orbit
Correct answer is option 'B'. Can you explain this answer?
The third line of the Balmer series in the emission spectrum of the hydrogen atom is due to the transition from the
a)
Fourth Bohr orbit to the first Bohr orbit
b)
Fifth Bohr orbit to the second Bohr orbit
c)
Sixth Bohr orbit to the third Bohr orbit
d)
Seventh Bohr orbit to the third Bohr orbit
|
|
Gaurav Kumar answered |
Rydberg’s formula for calculation of wavenumbers of hues in hydrogen spectrum is
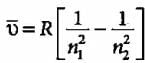
For Balmer series, n1 = 2 and n2 = 3, 4, 5, so third line of the Balmer series is due to transition from fifth Bohr orbit to second Bohr orbit
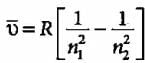
For Balmer series, n1 = 2 and n2 = 3, 4, 5, so third line of the Balmer series is due to transition from fifth Bohr orbit to second Bohr orbit
A certain metal when irradiated by light (v = 3.2 x 1016 Hz) emits photoelectrons with twice K.E. as did photoelectrons when the same metal is irradiated by light (v = 2.0 x 1016 Hz). The v0 of the metal is- a)1.2 x 1014 Hz
- b)8 x 1015 Hz
- c)1.2 x 1016 Hz
- d)4 x 1012 Hz
Correct answer is option 'B'. Can you explain this answer?
A certain metal when irradiated by light (v = 3.2 x 1016 Hz) emits photoelectrons with twice K.E. as did photoelectrons when the same metal is irradiated by light (v = 2.0 x 1016 Hz). The v0 of the metal is
a)
1.2 x 1014 Hz
b)
8 x 1015 Hz
c)
1.2 x 1016 Hz
d)
4 x 1012 Hz
|
|
Riya Banerjee answered |
(K.E.)1 = hv1 - hv0
(K.E)2 = hv2 - hv0
As (K.E)1 = 2 x (K.E.)2
∴ (hv1 - hv0)0) = 2(hv2 - hv0)
or v0 = 2v2 - v1
= 2 x (2 x 1016) - (3.2 x 1016)
= 0.8 x 1016 Hz or 8 x 1015 Hz
(K.E)2 = hv2 - hv0
As (K.E)1 = 2 x (K.E.)2
∴ (hv1 - hv0)0) = 2(hv2 - hv0)
or v0 = 2v2 - v1
= 2 x (2 x 1016) - (3.2 x 1016)
= 0.8 x 1016 Hz or 8 x 1015 Hz
The wavelength of visible light is- a)200 nm - 370 nm
- b)780 nm - 890 nm
- c)380 nm - 760 nm
- d)900 nm - 2000 nm
Correct answer is option 'C'. Can you explain this answer?
The wavelength of visible light is
a)
200 nm - 370 nm
b)
780 nm - 890 nm
c)
380 nm - 760 nm
d)
900 nm - 2000 nm
|
|
Jyoti Sengupta answered |
Visible light wavelength is from 380 nm to 760 nm.
Two electrons present in M shell will differ in- a)Principal quantum number
- b)Azimuthal quantum number
- c)Magnetic quantum number
- d)Spin quantum number.
Correct answer is option 'D'. Can you explain this answer?
Two electrons present in M shell will differ in
a)
Principal quantum number
b)
Azimuthal quantum number
c)
Magnetic quantum number
d)
Spin quantum number.
|
|
Jyoti Sengupta answered |
For electrons present in M shell the value of other quantum numbers are same. But, the value of spin quantum number will be different.
The electron in Bohr’s model of hydrogen atom is pictured as revolving around the nucleus in order for it to- a)Emit protons
- b)Keep from being pulled into the nucleus
- c)Keep from being repelled by the nucleus
- d)Possess energy
Correct answer is option 'D'. Can you explain this answer?
The electron in Bohr’s model of hydrogen atom is pictured as revolving around the nucleus in order for it to
a)
Emit protons
b)
Keep from being pulled into the nucleus
c)
Keep from being repelled by the nucleus
d)
Possess energy
|
|
Meera Singh answered |
Revolving electrons possess energy.
Which of the following configurations represents a noble gas?- a)1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d10 5s2
- b)1s2 2s2 2p6 3s2 3p6 3d10 4s2 4f14 5s2
- c)1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d10 5s2 5p6
- d)1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d10 5s2 5p3
Correct answer is option 'C'. Can you explain this answer?
Which of the following configurations represents a noble gas?
a)
1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d10 5s2
b)
1s2 2s2 2p6 3s2 3p6 3d10 4s2 4f14 5s2
c)
1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d10 5s2 5p6
d)
1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d10 5s2 5p3
|
|
Janhavi Patel answered |
Explanation:
Noble Gas Configuration:
- A noble gas configuration is when an atom has achieved a stable electron configuration similar to that of a noble gas.
- Noble gases have a completely filled outermost energy level, which makes them very stable and unreactive.
Identifying the Noble Gas Configuration:
- The electron configuration given in option 'C' is 1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d10 5s2.
- This configuration represents the noble gas Krypton (Kr), which has the electron configuration of [Ar] 4s2 3d10 4p6.
- By comparing the given configuration with the electron configuration of Krypton, we can see that it matches, indicating a noble gas configuration.
Conclusion:
- Option 'C' (1s2 2s2 2p6 3s2 3p6 3d10 4s2 4p6 4d10 5s2) represents a noble gas configuration similar to that of Krypton, making it the correct answer.
The number of electrons which will together weigh one gram is- a)1.098 x 1027 electrons
- b)9.1096 x 1031 electrons
- c)1 electron
- d)1 x 104 electrons
Correct answer is option 'A'. Can you explain this answer?
The number of electrons which will together weigh one gram is
a)
1.098 x 1027 electrons
b)
9.1096 x 1031 electrons
c)
1 electron
d)
1 x 104 electrons
|
|
Mira Joshi answered |
Mass of electron = 9.1096 x 10-31 kg
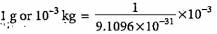
= 1.098 x 1027 electrons
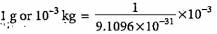
= 1.098 x 1027 electrons
Match the column I with column II and mark the appropriate choice.
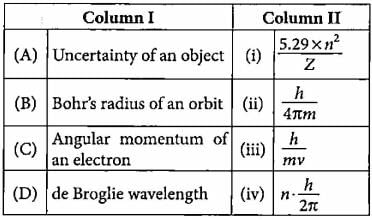
- a)(A) → (iii), (B) → (iv), (C) → (i), (D) → (ii)
- b)(A) → (ii), (B) → (i), (C) → (iv), (D) → (iii)
- c)(A) → (iv), (B) → (iii), (C) → (i), (D) → (ii)
- d)(A) → (i), (B) → (ii), (C) → (iv), (D) → (iii)
Correct answer is option 'B'. Can you explain this answer?
Match the column I with column II and mark the appropriate choice.


a)
(A) → (iii), (B) → (iv), (C) → (i), (D) → (ii)
b)
(A) → (ii), (B) → (i), (C) → (iv), (D) → (iii)
c)
(A) → (iv), (B) → (iii), (C) → (i), (D) → (ii)
d)
(A) → (i), (B) → (ii), (C) → (iv), (D) → (iii)

|
Navina Rajavelu answered |
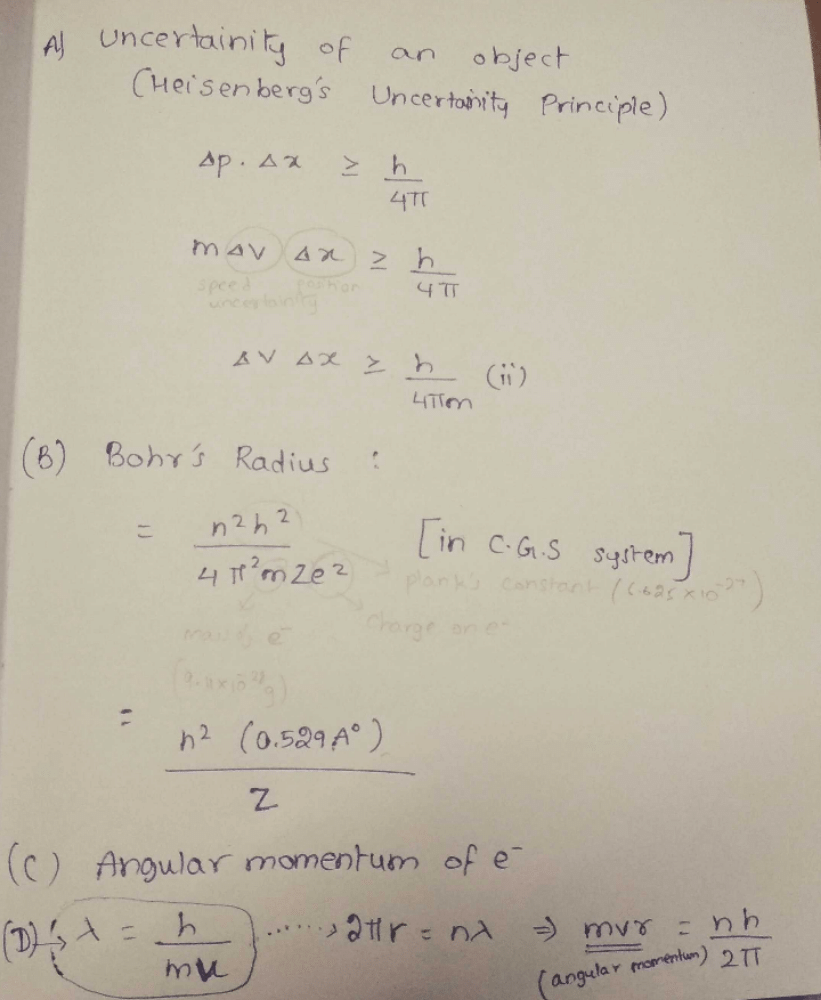
Chapter doubts & questions for Structure of Atom - NCERT Textbooks, Tests & Solutions 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Structure of Atom - NCERT Textbooks, Tests & Solutions in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup