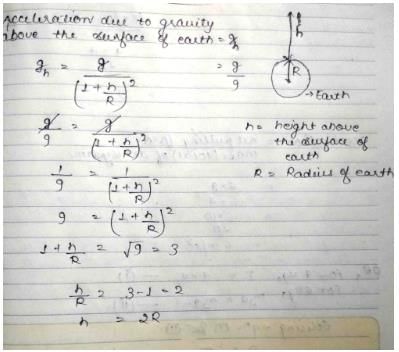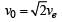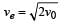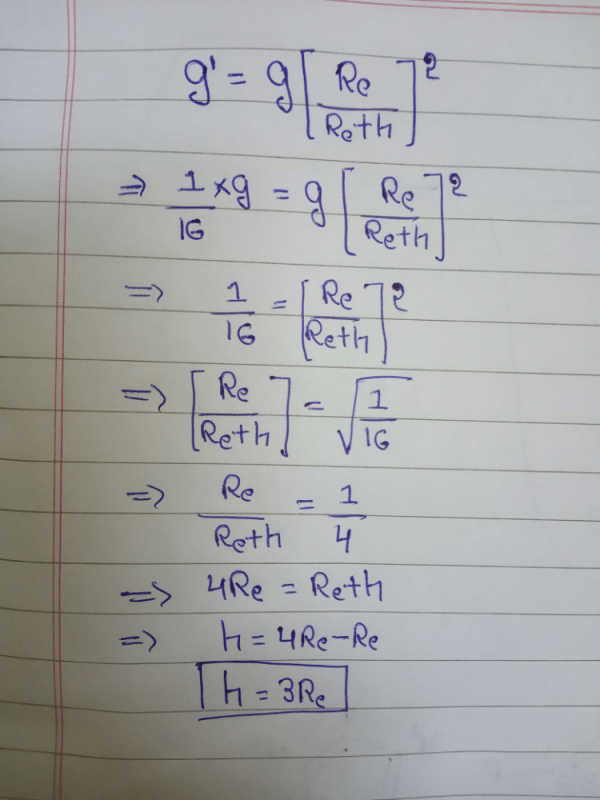All Exams >
NEET >
Topic-wise MCQ Tests for NEET >
All Questions
All questions of Gravitation for NEET Exam
Can you explain the answer of this question below:The value of escape velocity on earth when the body is thrown making an angle of 45o with the horizontal is
- A:
11.2 x 21/4 km/s
- B:
22.4 km/s
- C:
11.2 x 21/2 km/s
- D:
11.2 km/s
The answer is d.
The value of escape velocity on earth when the body is thrown making an angle of 45o with the horizontal is
11.2 x 21/4 km/s
22.4 km/s
11.2 x 21/2 km/s
11.2 km/s
|
|
Neha Joshi answered |
Escape velocity does not depend on the angle of projection. Escape velocity will remain the same.
Hence, escape velocity is 11.2km/s .
Hence, escape velocity is 11.2km/s .
Two bodies with same mass “m” separated by a distance “r” exert a gravitational force of F on each other. Suppose the distance between them is doubled and the force becomes F’. The ratio of two forces is- a)1:4
- b)4:1
- c)1:2
- d)2:1
Correct answer is 'B'. Can you explain this answer?
Two bodies with same mass “m” separated by a distance “r” exert a gravitational force of F on each other. Suppose the distance between them is doubled and the force becomes F’. The ratio of two forces is
a)
1:4
b)
4:1
c)
1:2
d)
2:1
|
|
Niharika Nair answered |
We know that the force of gravitation is inversely proportional to square of the distance between the two bodies,
i.e. F∝ r-2
Hence, when the distance between them will be doubled, the force will be reduced by 4 times
So, the ratio will be 4:1
Two uniform spherical stars made of same material have radii R and 2R. Mass of the smaller planet is m. They start moving from rest towards each other from a large distance under mutual force of gravity. The collision between the stars is inelastic with coefficient of restitution 1/2.Kinetic energy of the system just after the collision is- a)

- b)

- c)

- d)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
Two uniform spherical stars made of same material have radii R and 2R. Mass of the smaller planet is m. They start moving from rest towards each other from a large distance under mutual force of gravity. The collision between the stars is inelastic with coefficient of restitution 1/2.
Kinetic energy of the system just after the collision is
a)
b)
c)
d)
Cannot be determined

|
EduRev JEE answered |


Which is untrue about orbital velocity?
- a)increases with the increase in height of satellite
- b)depends on mass and radius of planet around which it revolves
- c)it is independent of mass of satellite
- d)decreases with an increase in radius of orbit
Correct answer is option 'A'. Can you explain this answer?
Which is untrue about orbital velocity?
a)
increases with the increase in height of satellite
b)
depends on mass and radius of planet around which it revolves
c)
it is independent of mass of satellite
d)
decreases with an increase in radius of orbit
|
|
Om Desai answered |
The untrue statement about orbital velocity is:
1. increases with the increase in height of satellite
Explanation: Orbital velocity is the speed at which an object revolves around a planet or other celestial body in a stable orbit. According to the equation for orbital velocity, v = √(GM/r+h), where G is the gravitational constant, M is the mass of the planet, and r is the radius of the orbit.
As the height of the satellite increases (meaning it gets far to the planet), its h increase , so reasulting in decrease in velocity .
The other statements are true:
2. depends on mass and radius of planet around which it revolves: As mentioned in the equation, orbital velocity depends on both the mass (M) of the planet and the radius (r) of the orbit.
3. it is independent of mass of satellite: The mass of the satellite does not appear in the equation for orbital velocity, so it does not affect the speed at which the satellite orbits the planet.
4. decreases with an increase in radius of orbit: From the equation, we can see that as the radius of the orbit (r) increases, the orbital velocity (v) decreases.
1. increases with the increase in height of satellite
Explanation: Orbital velocity is the speed at which an object revolves around a planet or other celestial body in a stable orbit. According to the equation for orbital velocity, v = √(GM/r+h), where G is the gravitational constant, M is the mass of the planet, and r is the radius of the orbit.
As the height of the satellite increases (meaning it gets far to the planet), its h increase , so reasulting in decrease in velocity .
The other statements are true:
2. depends on mass and radius of planet around which it revolves: As mentioned in the equation, orbital velocity depends on both the mass (M) of the planet and the radius (r) of the orbit.
3. it is independent of mass of satellite: The mass of the satellite does not appear in the equation for orbital velocity, so it does not affect the speed at which the satellite orbits the planet.
4. decreases with an increase in radius of orbit: From the equation, we can see that as the radius of the orbit (r) increases, the orbital velocity (v) decreases.
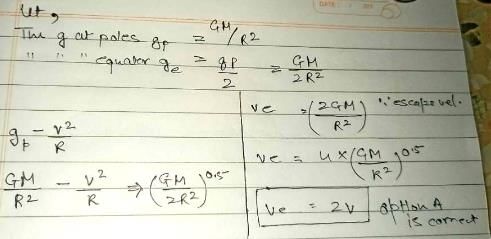
A spherical uniform planet is rotating about its axis. The velocity of a point on its equator is V. Due to the rotation of planet about its axis the acceleration due to gravity g at equator is 1/2 of g at poles. The escape velocity of a particle on the pole of planet in terms of V.- a)Ve = 2V
- b)Ve= V
- c)Ve= V/2
- d)Ve =
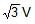
Correct answer is option 'A'. Can you explain this answer?
A spherical uniform planet is rotating about its axis. The velocity of a point on its equator is V. Due to the rotation of planet about its axis the acceleration due to gravity g at equator is 1/2 of g at poles. The escape velocity of a particle on the pole of planet in terms of V.
a)
Ve = 2V
b)
Ve= V
c)
Ve= V/2
d)
Ve = 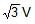

|
Mohit Rajpoot answered |
What does the term escape speed of a planet mean?- a)the minimum speed of an object to reach a height equal to the radius of the planet
- b)cannot be defined
- c)the minimum speed required for an object to reach infinity
- d)the maximum speed required for an object to reach infinity
Correct answer is option 'C'. Can you explain this answer?
What does the term escape speed of a planet mean?
a)
the minimum speed of an object to reach a height equal to the radius of the planet
b)
cannot be defined
c)
the minimum speed required for an object to reach infinity
d)
the maximum speed required for an object to reach infinity
|
|
Om Desai answered |
Escape velocity is the minimum velocity with which the body has to be projected vertically upwards from the surface of the earth so that it crosses the gravitational field of earth and never returns back on its own.
India’s first artificial satellite was:- a)Sputnik
- b)Rohini
- c)Insat
- d)Aryabhatta
Correct answer is option 'D'. Can you explain this answer?
India’s first artificial satellite was:
a)
Sputnik
b)
Rohini
c)
Insat
d)
Aryabhatta
|
|
Geetika Shah answered |
India's first artificial satellite was Aryabhata. Launched by soviet union on 19 April 1975
A particle of mass 10 g is kept on the surface of a uniform sphere of mass 100 kg and radius 10 cm. Find the work to be done against the gravitational force between them, to take the particle far away from the sphere, (you may take G = 6.67 × 10-11 Nm2/kg-2) [AIEEE 2005]- a)13.34 × 10-10 J
- b)3.33 × 10-10 J
- c)6.67 × 10-9J
- d)6.67 × 10-10 J
Correct answer is option 'D'. Can you explain this answer?
A particle of mass 10 g is kept on the surface of a uniform sphere of mass 100 kg and radius 10 cm. Find the work to be done against the gravitational force between them, to take the particle far away from the sphere, (you may take G = 6.67 × 10-11 Nm2/kg-2)
[AIEEE 2005]
a)
13.34 × 10-10 J
b)
3.33 × 10-10 J
c)
6.67 × 10-9J
d)
6.67 × 10-10 J
|
|
Preeti Iyer answered |
ΔW = Workdone = vf − ui
= 0 − [− GMmR]
ΔW = 6.67 × 10−11× 100 / 0.1 x 10/1000 = 6.67×10−10J
= 0 − [− GMmR]
ΔW = 6.67 × 10−11× 100 / 0.1 x 10/1000 = 6.67×10−10J
The escape velocity of a body depends upon mass as [AIEEE 2002]- a)m0
- b)m1
- c)m2
- d)m3
Correct answer is option 'A'. Can you explain this answer?
The escape velocity of a body depends upon mass as [AIEEE 2002]
a)
m0
b)
m1
c)
m2
d)
m3
|
|
Pooja Shah answered |
We know that escape velocity, 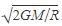
Where M is the mass of the planet and R is the radius of the planet.
Thus we can see that v does not depend upon the mass of the object.
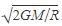
Where M is the mass of the planet and R is the radius of the planet.
Thus we can see that v does not depend upon the mass of the object.
Statement I : For a mass M kept at the centre of a cube of side a, the flux of gravitational field passing through its sides is 4p GM.andStatement II : If the direction of a field due to apoint source is radial and its dependence on the distance r from the source is given as 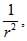 its flux through a closed surface depends only on the strength of the source enclosed by the surface and not on the size or shape of the surface. [AIEEE 2008]
its flux through a closed surface depends only on the strength of the source enclosed by the surface and not on the size or shape of the surface. [AIEEE 2008]- a)Statement I is true; Statement II is true; Statement II is not a correct explanation for Statement I.
- b)Statement I is true; Statement II is false.
- c)Statement I is false; Statement II is true.
- d)Statement I is true; Statement II is true; Statement II is a correct explanation for Statement I
Correct answer is option 'A'. Can you explain this answer?
Statement I : For a mass M kept at the centre of a cube of side a, the flux of gravitational field passing through its sides is 4p GM.
and
Statement II : If the direction of a field due to apoint source is radial and its dependence on the distance r from the source is given as 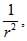 its flux through a closed surface depends only on the strength of the source enclosed by the surface and not on the size or shape of the surface.
its flux through a closed surface depends only on the strength of the source enclosed by the surface and not on the size or shape of the surface.
[AIEEE 2008]
a)
Statement I is true; Statement II is true; Statement II is not a correct explanation for Statement I.
b)
Statement I is true; Statement II is false.
c)
Statement I is false; Statement II is true.
d)
Statement I is true; Statement II is true; Statement II is a correct explanation for Statement I
|
|
Krishna Iyer answered |
Gravity flux:
g × area = 4 π GM
Same as electric flux gravitation flux depends only on the strength of mass hot on shape as in electric flux it depend on the amount of charge not on shape or size of surface.
g × area = 4 π GM
Same as electric flux gravitation flux depends only on the strength of mass hot on shape as in electric flux it depend on the amount of charge not on shape or size of surface.
A satellite which appears to be at a fixed position at a definite height to an observer is called:- a)Geostationary satellite and geosynchronous satellite
- b)Polar satellite
- c)Geostationary satellite
- d)Geosynchronous satellite
Correct answer is option 'A'. Can you explain this answer?
A satellite which appears to be at a fixed position at a definite height to an observer is called:
a)
Geostationary satellite and geosynchronous satellite
b)
Polar satellite
c)
Geostationary satellite
d)
Geosynchronous satellite
|
|
Neha Joshi answered |
As the relative velocity of the satellite with respect to the earth is zero, it appears stationary from the Earth surface and therefore it is called is geostationary satellite or geosynchronous satellite.
An unmanned space probe is to the thrown with such a velocity that it does not return to earth. It should be thrown with- a)velocity ≥ (2GM/ R)1/2
- b)a great velocity but nothing more can be said
- c)velocity >(2GM)1/2/ R necessarily
- d)only the velocity = (2GM)1/2/R
Correct answer is option 'A'. Can you explain this answer?
An unmanned space probe is to the thrown with such a velocity that it does not return to earth. It should be thrown with
a)
velocity ≥ (2GM/ R)1/2
b)
a great velocity but nothing more can be said
c)
velocity >(2GM)1/2/ R necessarily
d)
only the velocity = (2GM)1/2/R
|
|
Riya Banerjee answered |
It should be thrown with a velocity greater than or equal to escape velocity of the planet only then it will not return to Earth
Escape Velocity = √(2GM/R) = (2GM/R)1/2
Hence A is the correct answer.
Escape Velocity = √(2GM/R) = (2GM/R)1/2
Hence A is the correct answer.
Two bodies of masses m and 4 m are placed at a distance r. The gravitational potential at a point on the line joining them where the gravitational field is zero, is [AIEEE 2011]- a)
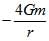
- b)

- c)

- d) zero
Correct answer is option 'C'. Can you explain this answer?
Two bodies of masses m and 4 m are placed at a distance r. The gravitational potential at a point on the line joining them where the gravitational field is zero, is
[AIEEE 2011]
a)
b)
c)
d)
zero
|
|
Preeti Iyer answered |
Let the point be the position when the gravitational field is zero

the point P is at a distance r/3 from mass m and 2r/3 from mass 4m
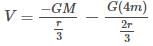
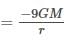
Assuming the earth to be a sphere of uniform density the acceleration due to gravity- a)At a point outside the earth is inversely proportional to the square of its distance from the center
- b) At a point outside the earth is inversely proportional to its distance from the centre
- c)At a point inside is zero
- d)At a point inside is proportional to its distance from the centre
Correct answer is option 'A,D'. Can you explain this answer?
Assuming the earth to be a sphere of uniform density the acceleration due to gravity
a)
At a point outside the earth is inversely proportional to the square of its distance from the center
b)
At a point outside the earth is inversely proportional to its distance from the centre
c)
At a point inside is zero
d)
At a point inside is proportional to its distance from the centre
|
|
Krishna Iyer answered |
As g is inversely proportional to (R+h)2 when we go away from earth's surface g is inversely proportional to square of the distance and g is directly proportional to (R-d) when we go inside the surface of Earth therefore g is directly proportional to distance travelled inside the Earth
g=Gmr/a3=r for r<R
g=Gm/a2 for r<R
g=Gmr/a3=r for r<R
g=Gm/a2 for r<R
When a satellite moves in a circular orbit, the _______acceleration is provided by the gravitational attraction of the earth- a)tangential
- b)centrifugal
- c)centripetal
- d)fictitious
Correct answer is option 'C'. Can you explain this answer?
When a satellite moves in a circular orbit, the _______acceleration is provided by the gravitational attraction of the earth
a)
tangential
b)
centrifugal
c)
centripetal
d)
fictitious
|
|
Hansa Sharma answered |
When any body or particle moves in circular orbit centripetal force acts on it and to move the object centripetal acceleration is necessary. So, when a satellite moves in circular orbit the centripetal acceleration is provided by the gravitational attraction of the earth.
The escape velocity for the moon is nearly- a)11.2km/s
- b)2.4km/s
- c)24km/s
- d)10km/s
Correct answer is option 'B'. Can you explain this answer?
The escape velocity for the moon is nearly
a)
11.2km/s
b)
2.4km/s
c)
24km/s
d)
10km/s
|
|
Rohit Shah answered |
About 11.2 km/s
In common usage, the initial point is on the surface of a planet or moon. On the surface of the Earth, the escape velocity is about 11.2 km/s, which is approximately 33 times the speed of sound (Mach 33) and several times the muzzle velocity of a rifle bullet (up to 1.7 km/s).
What could be the maximum value for gravitational potential energy?- a)1
- b)zero
- c)infinity
- d)1000
Correct answer is option 'B'. Can you explain this answer?
What could be the maximum value for gravitational potential energy?
a)
1
b)
zero
c)
infinity
d)
1000
|
|
Riya Banerjee answered |
As, U=−Gm1m2/r,
it can be used to describe the potential energy in a system of point charges (or radially symmetric spheres) as a function of their separation distance r, then the maximum value is zero at infinite separation.
Hence, its maximum value is zero at infinity.
it can be used to describe the potential energy in a system of point charges (or radially symmetric spheres) as a function of their separation distance r, then the maximum value is zero at infinite separation.
Hence, its maximum value is zero at infinity.
Two spherical bodies of mass M and 5M and radii R and 2R respectively are released in free space with initial separation between their centres equal to 12R. If they attract each other due to gravitational force only. then the distance covered by the smaller body just before collision is [AIEEE 2003]- a)2.5 R
- b)4.5 R
- c)7.5 R
- d)1.5 R
Correct answer is option 'C'. Can you explain this answer?
Two spherical bodies of mass M and 5M and radii R and 2R respectively are released in free space with initial separation between their centres equal to 12R. If they attract each other due to gravitational force only. then the distance covered by the smaller body just before collision is [AIEEE 2003]
a)
2.5 R
b)
4.5 R
c)
7.5 R
d)
1.5 R
|
|
Anjana Sharma answered |
A geostationary satellite is at a height h above the surface of earth. If earth radius is R 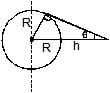
- a)The minimum colatitude on earth upto which the satellite can be used for communication is sin_1 (R/R + h)
- b)The maximum colatitudes on earth upto which the satellite can be used for communication is sin_1 (R/R + h)
- c)The area on earth escaped from this satellite is given as 2pR2(1 + sinq)
- d) The area on earth escaped from this satellite is given as 2pR2(1 + cosq)
Correct answer is option 'A,C'. Can you explain this answer?
A geostationary satellite is at a height h above the surface of earth. If earth radius is R
a)
The minimum colatitude on earth upto which the satellite can be used for communication is sin_1 (R/R + h)
b)
The maximum colatitudes on earth upto which the satellite can be used for communication is sin_1 (R/R + h)
c)
The area on earth escaped from this satellite is given as 2pR2(1 + sinq)
d)
The area on earth escaped from this satellite is given as 2pR2(1 + cosq)

|
Knowledge Hub answered |
Minimum colatitude=sin θ=R/R+h
θ=sin-1(R/R+h)
The curved area AB on earth =2πR2(1−sinθ)
Area on earth escaped from satellite =4πR2−2πR2(1−sinθ)
=2πR2(1+sinθ)
θ=sin-1(R/R+h)
The curved area AB on earth =2πR2(1−sinθ)
Area on earth escaped from satellite =4πR2−2πR2(1−sinθ)
=2πR2(1+sinθ)
A satellite of mass m revolves around the earth of radius R at a height x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is [AIEEE 2004]- a)gx
- b)
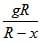
- c)
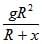
- d)
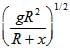
Correct answer is option 'D'. Can you explain this answer?
A satellite of mass m revolves around the earth of radius R at a height x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
[AIEEE 2004]
a)
gx
b)
c)
d)
|
|
Gaurav Kumar answered |
½ mv2 = GMm/2r
r = R + x
g = GM/R2
v = [gR2/R+x]2
r = R + x
g = GM/R2
v = [gR2/R+x]2
A satellite A of mass m is at a distance of r from the surface of the earth. Another satellite B of mass 2m is at a distance of 2r from the earth’s centre. Their time periods are in the ratio of [1993]- a)1 : 2
- b)1 : 16
- c)1 : 32
- d)
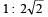
Correct answer is option 'D'. Can you explain this answer?
A satellite A of mass m is at a distance of r from the surface of the earth. Another satellite B of mass 2m is at a distance of 2r from the earth’s centre. Their time periods are in the ratio of [1993]
a)
1 : 2
b)
1 : 16
c)
1 : 32
d)
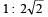

|
Abhishek Desai answered |
Time period does not depend on the mass.
Also, T2 ∝ r3 .
Also, T2 ∝ r3 .
The time period of a satellite of earth is 5 h. If the separation between the earth and the satellite is increased to 4 times the previous value, the new time period will become [AIEEE 2003]- a)10 h
- b)80 h
- c)40 h
- d)20 h
Correct answer is option 'C'. Can you explain this answer?
The time period of a satellite of earth is 5 h. If the separation between the earth and the satellite is increased to 4 times the previous value, the new time period will become [AIEEE 2003]
a)
10 h
b)
80 h
c)
40 h
d)
20 h
|
|
Om Desai answered |
Read more on Sarthaks.com -
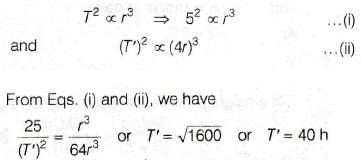
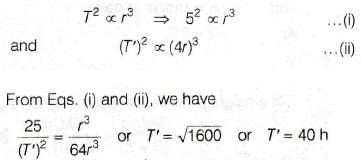
The height at which the acceleration due to gravity becomes g/9 (where g = the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is- a) R/2
- b)2R
- c)R/3
- d)3R
Correct answer is option 'B'. Can you explain this answer?
The height at which the acceleration due to gravity becomes g/9 (where g = the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is
a)
R/2
b)
2R
c)
R/3
d)
3R
|
|
Bhargavi Sen answered |
To find the height at which the acceleration due to gravity becomes g/9, let's analyze the gravitational force equation.
Gravitational force (F) between two objects is given by:
F = (G * m1 * m2) / r^2
where G is the gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between their centers.
The acceleration due to gravity (g) is the force experienced by an object of mass m due to the gravitational attraction of the Earth. It is given by:
g = (G * M) / R^2
where M is the mass of the Earth and R is the radius of the Earth.
Since the acceleration due to gravity is directly proportional to the mass of the Earth and inversely proportional to the square of the radius, we can write:
g' = (G * M') / (R')^2
where g' is the new acceleration due to gravity, M' is the new mass of the Earth, and R' is the new radius of the Earth.
We are given that g' = g/9. Substituting this into the equation above, we get:
g/9 = (G * M') / (R')^2
Simplifying, we find:
(R')^2 = (9 * M' * R^2) / (G * M)
To find the height at which the acceleration due to gravity becomes g/9, we need to find the difference between the new radius (R') and the original radius (R). Let's call this difference ΔR.
ΔR = R' - R
Now, let's substitute the expression for (R')^2 into the equation for ΔR:
ΔR = sqrt((9 * M' * R^2) / (G * M)) - R
Since the new mass M' is the same as the original mass M (since we are still considering the Earth), we can simplify further:
ΔR = sqrt((9 * R^2) / G) - R
To find the height, we need to multiply ΔR by the radius of the Earth, R:
Height = R * ΔR
Substituting the expression for ΔR, we get:
Height = R * (sqrt((9 * R^2) / G) - R)
Simplifying further, we find:
Height = R * (3R / sqrt(G) - R)
Since G is a constant, the height can be written as:
Height = 3R - R^2 / sqrt(G)
Therefore, the height at which the acceleration due to gravity becomes g/9 is given by 3R - R^2 / sqrt(G), which is equivalent to option B, 2R.
Gravitational force (F) between two objects is given by:
F = (G * m1 * m2) / r^2
where G is the gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between their centers.
The acceleration due to gravity (g) is the force experienced by an object of mass m due to the gravitational attraction of the Earth. It is given by:
g = (G * M) / R^2
where M is the mass of the Earth and R is the radius of the Earth.
Since the acceleration due to gravity is directly proportional to the mass of the Earth and inversely proportional to the square of the radius, we can write:
g' = (G * M') / (R')^2
where g' is the new acceleration due to gravity, M' is the new mass of the Earth, and R' is the new radius of the Earth.
We are given that g' = g/9. Substituting this into the equation above, we get:
g/9 = (G * M') / (R')^2
Simplifying, we find:
(R')^2 = (9 * M' * R^2) / (G * M)
To find the height at which the acceleration due to gravity becomes g/9, we need to find the difference between the new radius (R') and the original radius (R). Let's call this difference ΔR.
ΔR = R' - R
Now, let's substitute the expression for (R')^2 into the equation for ΔR:
ΔR = sqrt((9 * M' * R^2) / (G * M)) - R
Since the new mass M' is the same as the original mass M (since we are still considering the Earth), we can simplify further:
ΔR = sqrt((9 * R^2) / G) - R
To find the height, we need to multiply ΔR by the radius of the Earth, R:
Height = R * ΔR
Substituting the expression for ΔR, we get:
Height = R * (sqrt((9 * R^2) / G) - R)
Simplifying further, we find:
Height = R * (3R / sqrt(G) - R)
Since G is a constant, the height can be written as:
Height = 3R - R^2 / sqrt(G)
Therefore, the height at which the acceleration due to gravity becomes g/9 is given by 3R - R^2 / sqrt(G), which is equivalent to option B, 2R.
Satellites A and B are orbiting around the earth in orbits of ratio R and 4R respectively. The ratio of their areal velocities is- a)1 : 2
- b)1 : 4
- c)1 : 8
- d)1 : 16
Correct answer is option 'A'. Can you explain this answer?
Satellites A and B are orbiting around the earth in orbits of ratio R and 4R respectively. The ratio of their areal velocities is
a)
1 : 2
b)
1 : 4
c)
1 : 8
d)
1 : 16
|
|
Gaurav Kumar answered |
Answer :- a
Solution :- L = mvr
⇒L=m√GMr/r
L = m√GMr−−−−.....(1)
L = 2mdA/dt....(2)
From (1) and (2)
dA/dt ∝ (r)^1/2
= √(dA/dt)1/(dA/dt)2
= √4/1 = 2/1
Gravitational Potential is:- a)negative, scalar quantity , unit JKg-1
- b)positive, vector quantity , unit JKg-1
- c)positive, scalar quantity , unit JKg-1
- d)negative, vector quantity , unit JKg-1
Correct answer is option 'A'. Can you explain this answer?
Gravitational Potential is:
a)
negative, scalar quantity , unit JKg-1
b)
positive, vector quantity , unit JKg-1
c)
positive, scalar quantity , unit JKg-1
d)
negative, vector quantity , unit JKg-1

|
Ayush Joshi answered |
Gravitational potential (radial fields) at a point in a radial field is the work done per unit mass against the field, in bringing a small mass from infinite distance to the point. Since gravitational fields are attractive and the potential at infinite distance is zero, all points within the field have negative values of potential. Gravitational potential is a scalar quantity with SI unit J kg^-1. The symbol used is mostly V but sometimes or Vr or V(r). A radial gravitational field is one in which the field strength has the same magnitude at all points at a given distance from the center.
The gravitational potential due to the gravitational force on the earth is defined as the- a)potential energy multiplied by the mass of the object
- b)potential energy of the mass placed at that point
- c)numerically equal to the potential energy
- d)potential energy of a unit mass at that point.
Correct answer is option 'D'. Can you explain this answer?
The gravitational potential due to the gravitational force on the earth is defined as the
a)
potential energy multiplied by the mass of the object
b)
potential energy of the mass placed at that point
c)
numerically equal to the potential energy
d)
potential energy of a unit mass at that point.
|
|
Nandini Patel answered |
Gravitational Potential
Gravitational Potential is dened as the potential energy of a particle of unit mass at that point due to the gravitational force exerted byearth. Gravitational potential energy of a unit mass is known as gravitational potential.
A particle of mass M is situated at the centre of a spherical shell of same mass and radius a. The gravitational potential at a point situated at 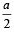 distance from the centre, will be: [2010]
distance from the centre, will be: [2010]- a)
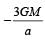
- b)
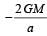
- c)
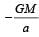
- d)
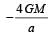
Correct answer is option 'A'. Can you explain this answer?
A particle of mass M is situated at the centre of a spherical shell of same mass and radius a. The gravitational potential at a point situated at 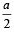 distance from the centre, will be: [2010]
distance from the centre, will be: [2010]
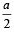 distance from the centre, will be: [2010]
distance from the centre, will be: [2010]a)
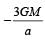
b)
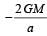
c)
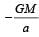
d)
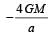

|
Pankaj Kulkarni answered |
Potential at the given point = Potential at the point due to the shell + Potential due to the particle
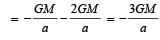
The kinetic energy needed to project a body of mass m from the earth's surface (radius R) to infinity is [AIEEE 2002]- a)
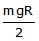
- b)

- c) mgR
- d)
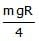
Correct answer is option 'C'. Can you explain this answer?
The kinetic energy needed to project a body of mass m from the earth's surface (radius R) to infinity is [AIEEE 2002]
a)
b)
c)
mgR
d)
|
|
Geetika Shah answered |
If any object through with escaping velocity then the object will never come back at the ground, So we can assume it will reach at infinite distance.
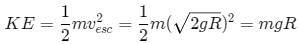
Assuming earth to be a sphere of uniform density, what is the value of ‘g’ in a mine 100 km below the earth’s surface? (Given, R = 6400 km) [2001]- a)9.65 m/s2
- b)7.65 m/s2
- c)5.06 m/s2
- d)3.10 m/s2
Correct answer is option 'A'. Can you explain this answer?
Assuming earth to be a sphere of uniform density, what is the value of ‘g’ in a mine 100 km below the earth’s surface? (Given, R = 6400 km) [2001]
a)
9.65 m/s2
b)
7.65 m/s2
c)
5.06 m/s2
d)
3.10 m/s2

|
Jatin Chakraborty answered |
We know that effective gravity g' at depth below earth surface is given by
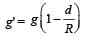
Here, d = 100 km, R = 6400 km,

A satellite of mass 5M orbits the earth in a circular orbit. At one point in its orbit, the satellite explodes into two pieces, one of mass M and the other of mass 4M. After the explosion the mass M ends up travelling in the same circular orbit, but in opposite direction. After explosion the mass 4M is in- a)Bound orbit
- b)Unbound orbit
- c)Partially bound orbit
- d)Data is insufficient to determine the nature of the orbit
Correct answer is option 'B'. Can you explain this answer?
A satellite of mass 5M orbits the earth in a circular orbit. At one point in its orbit, the satellite explodes into two pieces, one of mass M and the other of mass 4M. After the explosion the mass M ends up travelling in the same circular orbit, but in opposite direction. After explosion the mass 4M is in
a)
Bound orbit
b)
Unbound orbit
c)
Partially bound orbit
d)
Data is insufficient to determine the nature of the orbit
|
|
Suresh Reddy answered |
Applying the conservation of momentum, we get:
V = velocity of 5M, V1 = velocity of 4M, V2 = velocity of M and ATQ V2 = -V
5MV = 4MV1 + M(-V)
6MV = 4MV1
V1 = 3/2 V
Now, Vo = orbital velocity and Ve = escape velocity
Ve = √2 Vo
In a bound orbit the object is gravitationally bound to the body that is the source of gravity (like the Earth is bound to the Sun, or the Moon to the Earth). An unbound orbit is typically hyperbolic, and the object will escape from the source of gravity
V = velocity of 5M, V1 = velocity of 4M, V2 = velocity of M and ATQ V2 = -V
5MV = 4MV1 + M(-V)
6MV = 4MV1
V1 = 3/2 V
Now, Vo = orbital velocity and Ve = escape velocity
Ve = √2 Vo
In a bound orbit the object is gravitationally bound to the body that is the source of gravity (like the Earth is bound to the Sun, or the Moon to the Earth). An unbound orbit is typically hyperbolic, and the object will escape from the source of gravity
The orbit of a planet P round the sun S. AB and CD are the minor and major axes of the ellipse. 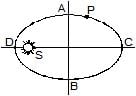 If t1 is the time taken by the planet to travel along ACB and t2 the time along BDA, then
If t1 is the time taken by the planet to travel along ACB and t2 the time along BDA, then- a) t1 = t2
- b)t1 > t2
- c) t1 < t2
- d)Nothing can be concluded
Correct answer is option 'B'. Can you explain this answer?
The orbit of a planet P round the sun S. AB and CD are the minor and major axes of the ellipse.
If t1 is the time taken by the planet to travel along ACB and t2 the time along BDA, then
a)
t1 = t2
b)
t1 > t2
c)
t1 < t2
d)
Nothing can be concluded
|
|
Pooja Shah answered |
Here, the angular momentum is conserved i.e. mvr is constant. Where r is the distance from centre of the sun to centre of the planet.
Now, consider one point each from both the mentioned paths. (Shown in fig.)
Applying conservation of angular momentum for these points we get
mv1r1=mv2r2. Simplifying this, v1/v2=r2/r1<1
Time period are given by
t1=L/ v1, t2= L/ v2
Comparing them by taking the ratio
t1/t2=(L/ v1)×(v2/L)
So, t1/t2=v2/v1>1.Thus t1>t2
Now, consider one point each from both the mentioned paths. (Shown in fig.)
Applying conservation of angular momentum for these points we get
mv1r1=mv2r2. Simplifying this, v1/v2=r2/r1<1
Time period are given by
t1=L/ v1, t2= L/ v2
Comparing them by taking the ratio
t1/t2=(L/ v1)×(v2/L)
So, t1/t2=v2/v1>1.Thus t1>t2
If a tunnel is cut at any orientation through earth, then a ball released from one end will reach the other end in time (neglect earth rotation)- a)84.6 minutes
- b)42.3 minutes
- c)8 minutes
- d)Depends on orientation
Correct answer is option 'B'. Can you explain this answer?
If a tunnel is cut at any orientation through earth, then a ball released from one end will reach the other end in time (neglect earth rotation)
a)
84.6 minutes
b)
42.3 minutes
c)
8 minutes
d)
Depends on orientation
|
|
Neha Joshi answered |
Total time period will be 84.6 min when ball released from one end and it come backs to same point as in oscillation.
When ball is released from one end then time taken to reach other end will be half of total time period then that will be 42.3 min.
When ball is released from one end then time taken to reach other end will be half of total time period then that will be 42.3 min.
The mass of a spaceship is 1000kg. It is to be launched from the earth's surface out into free space. The value of g and R (radius of earth) are 10 m/s2 and 6400 Km respectively. The required energy for this work will be [AIEEE 2012]- a)6.4 x 1011 J
- b)6.4 x 108 J
- c) 6.4 x 109J
- d)6.4 x 1010J
Correct answer is option 'D'. Can you explain this answer?
The mass of a spaceship is 1000kg. It is to be launched from the earth's surface out into free space. The value of g and R (radius of earth) are 10 m/s2 and 6400 Km respectively. The required energy for this work will be
[AIEEE 2012]
a)
6.4 x 1011 J
b)
6.4 x 108 J
c)
6.4 x 109J
d)
6.4 x 1010J
|
|
Jithin Saini answered |
Given,
Mass of spaceship (m) = 1000 kg
Acceleration due to gravity (g) = 10 m/s²
Radius of Earth (R) = 6400 km
We need to find out the required energy to launch the spaceship from Earth's surface to free space.
Potential Energy Calculation
When we lift an object against the gravitational force, the work done is stored as potential energy. The potential energy of an object at a height 'h' above the surface of the Earth is given by:
PE = mgh
where m is the mass of the object, g is the acceleration due to gravity and h is the height.
- Calculate the height attained by the spaceship
The spaceship is launched from the Earth's surface to free space. Therefore, the height attained by the spaceship is equal to the distance between the Earth's surface and the edge of the atmosphere.
- Calculate the radius of the atmosphere
The edge of the atmosphere is not clearly defined. However, the Kármán line is considered to be the boundary between the Earth's atmosphere and outer space. The Kármán line is located at a height of 100 km above the Earth's surface.
- Calculate the height of the spaceship
Height of the spaceship = Height of Kármán line - Radius of the Earth
Height of the spaceship = 100 km - 6400 km
Height of the spaceship = -6300 km (negative sign indicates that the spaceship is below the Earth's surface)
- Calculate the potential energy of the spaceship
PE = mgh
PE = 1000 kg x 10 m/s² x (-6300000 m)
PE = -6.3 x 10¹⁰ J (negative sign indicates that the potential energy is negative since the spaceship is below the Earth's surface)
Kinetic Energy Calculation
The kinetic energy of an object is given by:
KE = ½mv²
where m is the mass of the object and v is its velocity.
- Calculate the escape velocity of the spaceship
The escape velocity is the minimum velocity required to escape the gravitational field of the Earth. It is given by:
Vesc = √(2GM/R)
where G is the gravitational constant, M is the mass of the Earth and R is the distance between the spaceship and the center of the Earth.
- Calculate the distance between the spaceship and the center of the Earth
The distance between the spaceship and the center of the Earth is equal to the sum of the radius of the Earth and the height of the spaceship.
Distance between spaceship and center of Earth = Radius of Earth + Height of spaceship
Distance between spaceship and center of Earth = 6400 km - 6300 km
Distance between spaceship and center of Earth = 100 km
- Calculate the escape velocity of the spaceship
Vesc = √(2GM/R)
Vesc = √(2 x 6.67 x 10⁻¹¹ Nm²/kg² x 5.97 x 10²⁴ kg / 6.38 x 10⁶ m)
Vesc = 11.2 km/s
- Calculate the kinetic energy of the spaceship
KE = ½mv²
KE = ½ x 1000 kg x (11.2 km/s)²
KE = 6.2 x 10¹⁰ J
Total Energy Calculation
The total energy required
Mass of spaceship (m) = 1000 kg
Acceleration due to gravity (g) = 10 m/s²
Radius of Earth (R) = 6400 km
We need to find out the required energy to launch the spaceship from Earth's surface to free space.
Potential Energy Calculation
When we lift an object against the gravitational force, the work done is stored as potential energy. The potential energy of an object at a height 'h' above the surface of the Earth is given by:
PE = mgh
where m is the mass of the object, g is the acceleration due to gravity and h is the height.
- Calculate the height attained by the spaceship
The spaceship is launched from the Earth's surface to free space. Therefore, the height attained by the spaceship is equal to the distance between the Earth's surface and the edge of the atmosphere.
- Calculate the radius of the atmosphere
The edge of the atmosphere is not clearly defined. However, the Kármán line is considered to be the boundary between the Earth's atmosphere and outer space. The Kármán line is located at a height of 100 km above the Earth's surface.
- Calculate the height of the spaceship
Height of the spaceship = Height of Kármán line - Radius of the Earth
Height of the spaceship = 100 km - 6400 km
Height of the spaceship = -6300 km (negative sign indicates that the spaceship is below the Earth's surface)
- Calculate the potential energy of the spaceship
PE = mgh
PE = 1000 kg x 10 m/s² x (-6300000 m)
PE = -6.3 x 10¹⁰ J (negative sign indicates that the potential energy is negative since the spaceship is below the Earth's surface)
Kinetic Energy Calculation
The kinetic energy of an object is given by:
KE = ½mv²
where m is the mass of the object and v is its velocity.
- Calculate the escape velocity of the spaceship
The escape velocity is the minimum velocity required to escape the gravitational field of the Earth. It is given by:
Vesc = √(2GM/R)
where G is the gravitational constant, M is the mass of the Earth and R is the distance between the spaceship and the center of the Earth.
- Calculate the distance between the spaceship and the center of the Earth
The distance between the spaceship and the center of the Earth is equal to the sum of the radius of the Earth and the height of the spaceship.
Distance between spaceship and center of Earth = Radius of Earth + Height of spaceship
Distance between spaceship and center of Earth = 6400 km - 6300 km
Distance between spaceship and center of Earth = 100 km
- Calculate the escape velocity of the spaceship
Vesc = √(2GM/R)
Vesc = √(2 x 6.67 x 10⁻¹¹ Nm²/kg² x 5.97 x 10²⁴ kg / 6.38 x 10⁶ m)
Vesc = 11.2 km/s
- Calculate the kinetic energy of the spaceship
KE = ½mv²
KE = ½ x 1000 kg x (11.2 km/s)²
KE = 6.2 x 10¹⁰ J
Total Energy Calculation
The total energy required
A hollow spherical shell is compressed to half its radius. The gravitational potential at the centre- a)Increases
- b) Decreases
- c) Remains same
- d)Ruring the compression increases then returns at the previous value
Correct answer is option 'B'. Can you explain this answer?
A hollow spherical shell is compressed to half its radius. The gravitational potential at the centre
a)
Increases
b)
Decreases
c)
Remains same
d)
Ruring the compression increases then returns at the previous value
|
|
Suresh Iyer answered |
Gravitational Potential V = -GM/R for hollow spherical shell at the centre. If we replace R by R/2 then we get V = -2GM/R. Therefore it decreases.
A body of mass m rises to height h = R/5 from the earth's surface, where R is earth's radius. If g is acceleration due to gravity at earth's surface, the increase in potential energy is- a)Mg/h
- b)
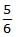 mgh
mgh - c)
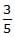 mgh
mgh - d)
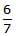 mgh
mgh
Correct answer is option 'B'. Can you explain this answer?
A body of mass m rises to height h = R/5 from the earth's surface, where R is earth's radius. If g is acceleration due to gravity at earth's surface, the increase in potential energy is
a)
Mg/h
b)
c)
d)
|
|
Suresh Iyer answered |
Initial PE = -GMm/R
Final PE = -GMm/R+h, (h=R/5)
Increase in PE = final - initial
= -GMm/R + (R/5) - (-GMm/R)
=GMm(1/R - 5/6R)
=GMm/R * 1/6
= gmR/6 (g= GM/R)
=gm5h/6 (h=R/5)
Final PE = -GMm/R+h, (h=R/5)
Increase in PE = final - initial
= -GMm/R + (R/5) - (-GMm/R)
=GMm(1/R - 5/6R)
=GMm/R * 1/6
= gmR/6 (g= GM/R)
=gm5h/6 (h=R/5)
The mass and diameter of a planet are twice those of earth. What will be the period of oscillation of a pendulum on this planet if it is a seconds pendulum on earth ?- a)
 second
second - b)
 seconds
seconds - c)
 second
second - d)
 second
second
Correct answer is option 'B'. Can you explain this answer?
The mass and diameter of a planet are twice those of earth. What will be the period of oscillation of a pendulum on this planet if it is a seconds pendulum on earth ?
a)
b)
c)
d)
|
|
Pooja Shah answered |
As Mp=2Me and Dp=2De
or Rp=2Re
Hence, gp= GMp/(Rp)2 =G(2Me)/(2Re)2 = GMe/2Re2 =ge/2
Time period of pendulum on the planet Tp=2π√ l/gp
Tp=2π√2l/ge=√2×2π√l/ge=√2×Te
Tp=√2×2=2√2s
or Rp=2Re
Hence, gp= GMp/(Rp)2 =G(2Me)/(2Re)2 = GMe/2Re2 =ge/2
Time period of pendulum on the planet Tp=2π√ l/gp
Tp=2π√2l/ge=√2×2π√l/ge=√2×Te
Tp=√2×2=2√2s
A communications Earth satellite- a)Goes round the earth from east to west
- b)Can be in the equatorial plane only
- c)Can be vertically above any place on the earth
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A communications Earth satellite
a)
Goes round the earth from east to west
b)
Can be in the equatorial plane only
c)
Can be vertically above any place on the earth
d)
none of these
|
|
Pooja Shah answered |
Communication satellites are supposed to be geostationary in nature. So, from the above properties options B is correct.
In side a hollow spherical shell- a)Everywhere gravitational potential is zero
- b)Everywhere gravitational field is zero
- c) Everywhere gravitational potential is same
- d)Everywhere gravitational field is same
Correct answer is option 'B,C,D'. Can you explain this answer?
In side a hollow spherical shell
a)
Everywhere gravitational potential is zero
b)
Everywhere gravitational field is zero
c)
Everywhere gravitational potential is same
d)
Everywhere gravitational field is same
|
|
Lavanya Menon answered |
The gravitational field inside a uniform spherical shell is 0 from gauss law for gravitation since no mass is enclosed in any Gaussian surface.
Since gravitational potential is given by φ=−∫ gdr, hence, φ=constant since g=0.
Since the gravitational field is 0 everywhere, it is apparently the same everywhere.
Answer is B,C,D.
Since gravitational potential is given by φ=−∫ gdr, hence, φ=constant since g=0.
Since the gravitational field is 0 everywhere, it is apparently the same everywhere.
Answer is B,C,D.
Weightlessness is:- a)a situation in which the effective weight of the body becomes zero
- b)a situation in which the effective weight of the body becomes 10N
- c)a situation in which the effective weight of the body becomes 9.8N.
- d)a situation in which the effective mass of the body becomes zero
Correct answer is option 'A'. Can you explain this answer?
Weightlessness is:
a)
a situation in which the effective weight of the body becomes zero
b)
a situation in which the effective weight of the body becomes 10N
c)
a situation in which the effective weight of the body becomes 9.8N.
d)
a situation in which the effective mass of the body becomes zero

|
Akshay Shah answered |
Weight becomes zero in a freefall or when the total force on your body is zero.For example in a freely falling lift the contact force on your body is zero,so the wieghting machine would show zero reading.so you are wieghtless.
The mean radius of earth is R, its angular speed on its own axis is ω and the acceleration due to gravity at earth's surface is g. What will be the radius of the orbit of a geostationary satellite ? [1992]- a)( R2g/ω2)1/3
- b)( Rg/ω2)1/3
- c)( R2ω2/g)1/3
- d)( R 2g /ω)1/3
Correct answer is option 'A'. Can you explain this answer?
The mean radius of earth is R, its angular speed on its own axis is ω and the acceleration due to gravity at earth's surface is g. What will be the radius of the orbit of a geostationary satellite ? [1992]
a)
( R2g/ω2)1/3
b)
( Rg/ω2)1/3
c)
( R2ω2/g)1/3
d)
( R 2g /ω)1/3

|
Sarthak Saini answered |
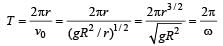
Hence, 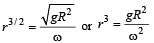
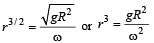
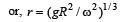
The time period of an earth satellite in circular orbit is independent of [AIEEE 2004]- a) The mass of the satellite
- b)Radius of its orbit
- c)Both the mass and radius of the orbit
- d)Neither the mass of the satellite nor the radius of its orbit
Correct answer is option 'A'. Can you explain this answer?
The time period of an earth satellite in circular orbit is independent of
[AIEEE 2004]
a)
The mass of the satellite
b)
Radius of its orbit
c)
Both the mass and radius of the orbit
d)
Neither the mass of the satellite nor the radius of its orbit
|
|
Raghav Bansal answered |
T = 2π a/v
a = radius of orbit
v = velocity of satellite
It is independent of mass of satellite
a = radius of orbit
v = velocity of satellite
It is independent of mass of satellite
Infinite number of bodies, each of mass 2 kg are situated on x-axis at distances 1m, 2m, 4m, 8m, ..... respectively, from the origin. The resulting gravitational potential due to this system at the origin will be [NEET 2013]- a)
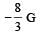
- b)
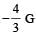
- c)– 4 G
- d)– G
Correct answer is option 'C'. Can you explain this answer?
Infinite number of bodies, each of mass 2 kg are situated on x-axis at distances 1m, 2m, 4m, 8m, ..... respectively, from the origin. The resulting gravitational potential due to this system at the origin will be [NEET 2013]
a)
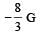
b)
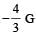
c)
– 4 G
d)
– G

|
Pioneer Academy answered |

Gravitational potential 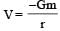
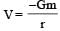
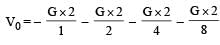
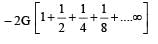
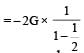
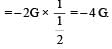
Chapter doubts & questions for Gravitation - Topic-wise MCQ Tests for NEET 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Gravitation - Topic-wise MCQ Tests for NEET in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily