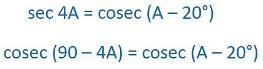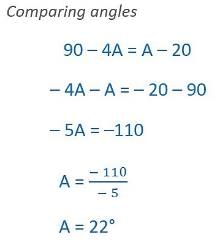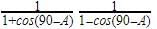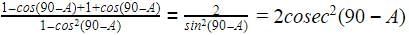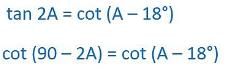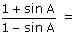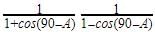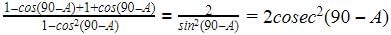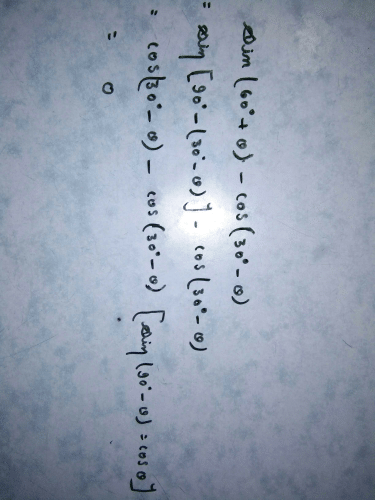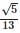All Exams >
Class 10 >
Online MCQ Tests for Class 10 >
All Questions
All questions of Introduction to Trigonometry for Class 10 Exam
If tan A = 3/2, then the value of cos A is- a)
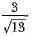
- b)
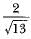
- c)2/3
- d)
Correct answer is option 'B'. Can you explain this answer?
If tan A = 3/2, then the value of cos A is
a)
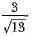
b)
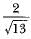
c)
2/3
d)
|
EduRev Class 10 answered |
Tanθ = Perpendicular / Base
We are given that TanA = 3/2
On comparing
Perpendicular = 3
Base = 2
To fing hypotenuse
Hypotenuse2 = Perpendicular2 + Base2
Hypotenuse2 = 32 + 22
Hypotenuse =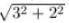
Hypotenuse = 3.6
We are given that TanA = 3/2
On comparing
Perpendicular = 3
Base = 2
To fing hypotenuse
Hypotenuse2 = Perpendicular2 + Base2
Hypotenuse2 = 32 + 22
Hypotenuse =
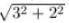
Hypotenuse = 3.6
Cosθ = Base / Hypotenuse
CosA = 2 / 3.6
Hence the value of Cos A is 2/3.6=2/√13
CosA = 2 / 3.6
Hence the value of Cos A is 2/3.6=2/√13
If tan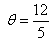 
, then 
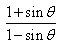is equal to- a)24
- b)12/13
- c)25
- d)9
Correct answer is option 'C'. Can you explain this answer?
If tan 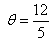, then 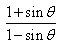is equal to
, then is equal toa)
24
b)
12/13
c)
25
d)
9
|
Vp Classes answered |
tanθ = 12/5
so sinθ = 12/13
so
(1 + 12/13)/(1-12/13)
= 25/1 = 25
The value of (sin 30° + cos 30°) - (sin 60° + cos 60°) is- a)-1
- b)0
- c)1
- d)2
Correct answer is option 'B'. Can you explain this answer?
The value of (sin 30° + cos 30°) - (sin 60° + cos 60°) is
a)
-1
b)
0
c)
1
d)
2
|
Ritu Saxena answered |
sin 30° = 1/2,
cos 30°=√3/2,
sin 60°=√3/2,
cos 60°=1/2,
By putting the value of sin 30°, cos 30°, sin 60° and cos 60° in equation
cos 30°=√3/2,
sin 60°=√3/2,
cos 60°=1/2,
By putting the value of sin 30°, cos 30°, sin 60° and cos 60° in equation
We get=
(sin30°+cos30°)-(sin60°+cos60°)=(1/2+√3/2)-(√3/2+1/2)
=0
(sin30°+cos30°)-(sin60°+cos60°)=(1/2+√3/2)-(√3/2+1/2)
=0
The value of (sin 45° + cos 45°) is- a)1/√2
- b)√2
- c)√3/2
- d)1
Correct answer is option 'B'. Can you explain this answer?
The value of (sin 45° + cos 45°) is
a)
1/√2
b)
√2
c)
√3/2
d)
1
|
Krishna Iyer answered |
sin 45° + cos 45°
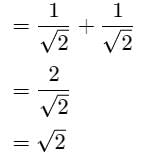
Hence, the answer is = √2
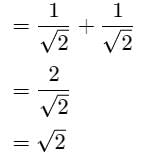
Hence, the answer is = √2
Can you explain the answer of this question below:If 7sin2x + 3cos2x = 4 then , secx + cosecx =- A:
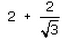
- B:
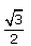
- C:
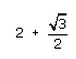
- D:
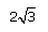
The answer is a.
If 7sin2x + 3cos2x = 4 then , secx + cosecx =
A:
B:
C:
D:
|
Gunjan Lakhani answered |
7sin2x+3cos2 x=4
7sin2x+3(1-sin2x)=4
7sin2x+3-3sin2x=4
4sin2x=4-3
4sin2x=1
sin2x=¼
sinx=½
Cosec x=1/sinx=2
Cos x=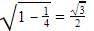
Sec x= 1/cos x=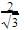
Cosec x + sec x=2+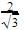
7sin2x+3(1-sin2x)=4
7sin2x+3-3sin2x=4
4sin2x=4-3
4sin2x=1
sin2x=¼
sinx=½
Cosec x=1/sinx=2
Cos x=
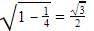
Sec x= 1/cos x=
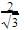
Cosec x + sec x=2+
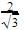
The value of the expression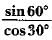 
is- a)√3/2
- b)1/2
- c)1
- d)2
Correct answer is option 'C'. Can you explain this answer?
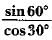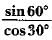The value of the expression is
isa)
√3/2
b)
1/2
c)
1
d)
2
|
|
Krishna Iyer answered |
We know that sin 60 =√3/2 and cos 30 = √3/2.
Therefore , Sin 60/cos 30= (√3/2)/(√3/2) = 1
Therefore , Sin 60/cos 30= (√3/2)/(√3/2) = 1
The value of tan1°.tan2°.tan3°………. tan89° is :- a)2
- b)1
- c)1/2
- d)0
Correct answer is option 'B'. Can you explain this answer?
The value of tan1°.tan2°.tan3°………. tan89° is :
a)
2
b)
1
c)
1/2
d)
0
|
Meera Rana answered |
tan 1.tan 2.tan 3...tan (90 - 3 ).tan ( 90 - 2 ).tan ( 90 - 1)
=tan 1.tan 2 .tan 3...cot 3.cot 2.cot 1
=tan 1.cot 1.tan 2.cot 2.tan 3.cot 3 ... tan 89.cot 89
1 x 1 x 1 x 1 x ... x 1 =1
=tan 1.tan 2 .tan 3...cot 3.cot 2.cot 1
=tan 1.cot 1.tan 2.cot 2.tan 3.cot 3 ... tan 89.cot 89
1 x 1 x 1 x 1 x ... x 1 =1
If tan θ = a/b then the value of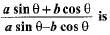 
- a)
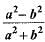
- b)
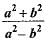
- c)
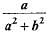
- d)
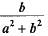
Correct answer is option 'B'. Can you explain this answer?
If tan θ = a/b then the value of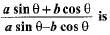
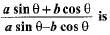
a)
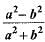
b)
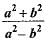
c)
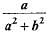
d)
|
|
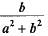
Vp Classes answered |
Let,angle= θ
(asinθ + bcosθ)/(asinθ - bcosθ)
Dividing both numerator and denominator from cosθ
We get,
atanθ +b/atanθ - b
= ( a.a/b + b) /(a.a/b - b) =(a²/b +b)/(a²/b - b)
=(a² + b²/a²- b²)
(asinθ + bcosθ)/(asinθ - bcosθ)
Dividing both numerator and denominator from cosθ
We get,
atanθ +b/atanθ - b
= ( a.a/b + b) /(a.a/b - b) =(a²/b +b)/(a²/b - b)
=(a² + b²/a²- b²)
The value of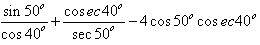 
is- a)2
- b)0
- c)4
- d)-2
Correct answer is option 'D'. Can you explain this answer?
The value of 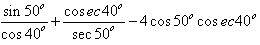is
isa)
2
b)
0
c)
4
d)
-2
|
|
Krishna Iyer answered |
we know sin(90 - a) = cos(a)
cos(90 - a) = sin(a)
sin(a) = 1/cosec(a)
sec(a) = 1/cos(a)
cos40 = cos(90-50) = sin50
cosec40 = cosec(90-50) = sec50
so our expression becomes
sin50/sin50 + sec50/sec50 - 4cos50 / sin40
= 1 + 1 - 4(1) since cos50 = sin40
= -2
If 6cotθ + 2cosecθ = cotθ + 5cosecθ, then cosθ is- a)4/5
- b)5/3
- c)3/5
- d)5/4
Correct answer is option 'C'. Can you explain this answer?
If 6cotθ + 2cosecθ = cotθ + 5cosecθ, then cosθ is
a)
4/5
b)
5/3
c)
3/5
d)
5/4
|
|
Raghav Bansal answered |
6cot+2cosec=cot+5cosec
6cot-cot=5cosec-2cosec
5cot=3cosec
5cos/sin=3/sin
cos=3/5
6cot-cot=5cosec-2cosec
5cot=3cosec
5cos/sin=3/sin
cos=3/5
If ΔABC is right angled at C, then the value of cos (A + B) is- a)0
- b)1
- c)1/2
- d)√3/2
Correct answer is option 'A'. Can you explain this answer?
If ΔABC is right angled at C, then the value of cos (A + B) is
a)
0
b)
1
c)
1/2
d)
√3/2
|
Aniket Chavan answered |
Since ABC is right-angled and angle C is 90degree
therefore,
A+B=180degree - C
A+B=180degree-90degree
A+B= 90degree
Therefore,cos (A+B)=cos90degree
=0
5 cot2 A – 5 cosec2 A =- a)– 5
- b)1
- c)0
- d)5
Correct answer is option 'A'. Can you explain this answer?
5 cot2 A – 5 cosec2 A =
a)
– 5
b)
1
c)
0
d)
5
|
Kalyan Jain answered |
Given: 5cot²A × 5cosec²A
To find: the value of the expression
Solution:
We know that:
cot²A = 1/(tan²A) and cosec²A = 1/(sin²A)
Substituting these values in the given expression, we get:
5cot²A × 5cosec²A = 5(1/(tan²A)) × 5(1/(sin²A))
= 25/(tan²A × sin²A)
But we know that:
tan²A × sin²A = (sinA/cosA)² × sin²A = sin³A/cos²A
Substituting this value in the expression, we get:
25/(tan²A × sin²A) = 25/(sin³A/cos²A)
= 25(cos²A/sin³A)
= 25cot²A × cosec²A
Substituting the values of cot²A and cosec²A, we get:
25cot²A × cosec²A = 25(1/(tan²A)) × 5(1/(sin²A))
= 25/(tan²A × sin²A)
We can see that this is the same expression that we started with.
Therefore, 5cot²A × 5cosec²A = 25/(tan²A × sin²A)
Answer: Option A) 5
To find: the value of the expression
Solution:
We know that:
cot²A = 1/(tan²A) and cosec²A = 1/(sin²A)
Substituting these values in the given expression, we get:
5cot²A × 5cosec²A = 5(1/(tan²A)) × 5(1/(sin²A))
= 25/(tan²A × sin²A)
But we know that:
tan²A × sin²A = (sinA/cosA)² × sin²A = sin³A/cos²A
Substituting this value in the expression, we get:
25/(tan²A × sin²A) = 25/(sin³A/cos²A)
= 25(cos²A/sin³A)
= 25cot²A × cosec²A
Substituting the values of cot²A and cosec²A, we get:
25cot²A × cosec²A = 25(1/(tan²A)) × 5(1/(sin²A))
= 25/(tan²A × sin²A)
We can see that this is the same expression that we started with.
Therefore, 5cot²A × 5cosec²A = 25/(tan²A × sin²A)
Answer: Option A) 5
Match the Columns:
- a)1 - A, 2 - C, 3 - B
- b)1 - B, 2 - C, 3 - A
- c)1 - B, 2 - C, 3 - D
- d)1 - D , 2 - B , 3 - A
Correct answer is option 'B'. Can you explain this answer?
Match the Columns:
a)
1 - A, 2 - C, 3 - B
b)
1 - B, 2 - C, 3 - A
c)
1 - B, 2 - C, 3 - D
d)
1 - D , 2 - B , 3 - A
|
|
Krishna Iyer answered |
Correct Answer :- b
Explanation : If θ is one of the acute angles in a triangle, then the sine of theta is the ratio of the opposite side to the hypotenuse, the cosine is the ratio of the adjacent side to the hypotenuse, and the tangent is the ratio of the opposite side to the adjacent side.
If cos (40° + A) = sin 30°, the value of A is:
- a)60°
- b)20°
- c)40°
- d)30°
Correct answer is option 'B'. Can you explain this answer?
If cos (40° + A) = sin 30°, the value of A is:
a)
60°
b)
20°
c)
40°
d)
30°
|
|
EduRev Class 10 answered |
cos(θ)=sin(90-θ)
so 40+A+30=90
A=20
so 40+A+30=90
A=20
The value of tan 1∘ tan 2∘ tan 3∘………… tan 89∘ is- a)0
- b)1
- c)12
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The value of tan 1∘ tan 2∘ tan 3∘………… tan 89∘ is
a)
0
b)
1
c)
12
d)
none of these
|
|
Krishna Iyer answered |
tan 1° tan2° tan3° ..............tan 89°
= tan(90° - 89°) tan(90° - 88°) tan(90° - 87°) ......... tan 87° tan 88° tan 89°
= cot 89° cot 88° cot 87° .............tan 87° tan 88° tan 89°
= (cot 89° tan 89°) (cot 88° tan 88°) (cot 87° tan 87°) .............(cot 44° tan 44°) tan 45°
= 1x1x1x1x1.........1 = 1
= tan(90° - 89°) tan(90° - 88°) tan(90° - 87°) ......... tan 87° tan 88° tan 89°
= cot 89° cot 88° cot 87° .............tan 87° tan 88° tan 89°
= (cot 89° tan 89°) (cot 88° tan 88°) (cot 87° tan 87°) .............(cot 44° tan 44°) tan 45°
= 1x1x1x1x1.........1 = 1
=
9 sec2 A - 9tan2 A is equal to- a)1
- b)9
- c)8
- d)0
Correct answer is option 'B'. Can you explain this answer?
9 sec2 A - 9tan2 A is equal to
a)
1
b)
9
c)
8
d)
0
|
|
Kiran Mehta answered |
9 sec2 A - 9 tan2 A
= 9( sec2 A - tan2 A)
= 9 × 1
= 9
= 9( sec2 A - tan2 A)
= 9 × 1
= 9
The value of cos θ cos(90° - θ) – sin θ sin (90° - θ) is:
- a)1
- b)0
- c)-1
- d)2
Correct answer is option 'B'. Can you explain this answer?
The value of cos θ cos(90° - θ) – sin θ sin (90° - θ) is:
a)
1
b)
0
c)
-1
d)
2
|
Vikas Kumar answered |
Explanation:
- Given expression: cos θ cos(90° - θ) – sin θ sin (90° - θ)
- We know that cos(90° - θ) = sin θ and sin(90° - θ) = cos θ
- Substitute these values into the expression:
= cos θ * sin θ - sin θ * cos θ
= sin θ cos θ - sin θ cos θ
= 0
- Therefore, the value of the expression is 0.
- Given expression: cos θ cos(90° - θ) – sin θ sin (90° - θ)
- We know that cos(90° - θ) = sin θ and sin(90° - θ) = cos θ
- Substitute these values into the expression:
= cos θ * sin θ - sin θ * cos θ
= sin θ cos θ - sin θ cos θ
= 0
- Therefore, the value of the expression is 0.
If A and B are the angles of a right angled triangle ABC, right angled at C, then 1+cot2A =- a)cot2B
- b)sec2B
- c)cos2B
- d)tan2B
Correct answer is option 'B'. Can you explain this answer?
If A and B are the angles of a right angled triangle ABC, right angled at C, then 1+cot2A =
a)
cot2B
b)
sec2B
c)
cos2B
d)
tan2B
|
Siddharth answered |
ABC is a Δ, right angle at c.
1 +cot^2 =?........
we know that.....
Cosec^2 - cot^2= 1...
So,
=> 1+ cot^2
=> cosec^2 A
=> (AB)^2/( CB)^2
= sec ^2B.
Out of the following options, the two angles that are together classified as complementary angles are- a)120° and 60°
- b)50° and 30°
- c)65° and 25°
- d)70° and 30°
Correct answer is option 'C'. Can you explain this answer?
Out of the following options, the two angles that are together classified as complementary angles are
a)
120° and 60°
b)
50° and 30°
c)
65° and 25°
d)
70° and 30°
|
Namita khanna answered |
B)90
c)45
The two angles that are together classified as complementary angles are b)90 and c)45.
c)45
The two angles that are together classified as complementary angles are b)90 and c)45.
The value of cos2 17° – sin2 73° is- a)0
- b)1
- c)-1
- d)3
Correct answer is 'A'. Can you explain this answer?
The value of cos2 17° – sin2 73° is
a)
0
b)
1
c)
-1
d)
3
|
Amit Sharma answered |
cos217-sin273
=cos217-sin2(90-17)
=cos217-cos217 (because sin(90-x)=cos x)
=0
=cos217-sin2(90-17)
=cos217-cos217 (because sin(90-x)=cos x)
=0
If cosec A - cot A = 4/5, then cosec A = - a)47/40
- b)59/40
- c)51/40
- d)41/40
Correct answer is option 'D'. Can you explain this answer?
If cosec A - cot A = 4/5, then cosec A =
a)
47/40
b)
59/40
c)
51/40
d)
41/40
|
Abhiram Malik answered |
cosecA = 41/40
Explanation :
cosecA - cotA = 4/5 ---( 1 )
=> (cosecA - cotA)(cosecA + cotA)=(4/5) (cosecA + cotA)
=> (cosec�A-cot�A) = (4/5)(cosecA +cotA)
=> 1 = (4/5)(cosecA + cotA)
=> cosecA +cotA = 5/4 ---(2)
Now ,
Add (1) and (2 ), we get
=> 2coseecA = (4/5+5/4)
=> 2cosecA = (16+25)/20
=> cosecA = 41/40
Therefore,
cosecA = 41/40
Ratios of sides of a right triangle with respect to its acute angles are known as- a)trigonometric identities
- b)trigonometry
- c)trigonometric ratios of the angles
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Ratios of sides of a right triangle with respect to its acute angles are known as
a)
trigonometric identities
b)
trigonometry
c)
trigonometric ratios of the angles
d)
none of these
|
Ishan Choudhury answered |
The ratios of sides of a right-angled triangle with respect to any of its acute angles are known as the trigonometric ratios of that particular angle.
7 sin2 θ + 3 cos2 θ = 4 then :- a)tan θ = 1/√2
- b)tan θ = 1/2
- c)tan θ = 1/3
- d)tan θ = 1/√3
Correct answer is option 'D'. Can you explain this answer?
7 sin2 θ + 3 cos2 θ = 4 then :
a)
tan θ = 1/√2
b)
tan θ = 1/2
c)
tan θ = 1/3
d)
tan θ = 1/√3
|
|
Nirmal Kumar answered |
7Sin²A+3Cos²A=4,
3Cos²A+3Sin²A+4Sin²A=4,
3(sin²A+Cos²A)+4sin²A=4,
4Sin²A=1,
sin²A=1/2×1/2,
SinA=1/2=Sin 30,
A=30,
tanA=tan30=1/√3
3Cos²A+3Sin²A+4Sin²A=4,
3(sin²A+Cos²A)+4sin²A=4,
4Sin²A=1,
sin²A=1/2×1/2,
SinA=1/2=Sin 30,
A=30,
tanA=tan30=1/√3
The value of 3/4 tan2 30° – 3 sin2 60° + cosec2 45° is- a)1
- b)8
- c)0
- d)12
Correct answer is option 'C'. Can you explain this answer?
The value of 3/4 tan2 30° – 3 sin2 60° + cosec2 45° is
a)
1
b)
8
c)
0
d)
12
|
|
Malini shah answered |
To solve for the value of 3/4tan230, we need to use a calculator. Here are the steps:
1. Press the "tan" button on your calculator.
2. Type in "230".
3. Press the "equals" button.
4. Take note of the value shown on the screen.
5. Divide the value by 4.
6. Multiply the result by 3.
The final answer will depend on the degree of accuracy you need. Rounded to two decimal places, the value of 3/4tan230 is approximately -1.42.
In sin 3θ = cos (θ – 26°), where 3θ and (θ – 26°) are acute angles, then value of θ is :- a)30°
- b)29°
- c)27°
- d)26°
Correct answer is option 'B'. Can you explain this answer?
In sin 3θ = cos (θ – 26°), where 3θ and (θ – 26°) are acute angles, then value of θ is :
a)
30°
b)
29°
c)
27°
d)
26°
|
|
Krishna Iyer answered |
sin3θ = cos(θ - 26°)
=> cos(90° - 3θ) = cos(θ - 26°)
=> 90° - 3θ = θ - 26°
=> 3θ + θ = 90° + 26°
=> 4θ = 116°
=> θ = 116°/4
=> θ = 29°
=> cos(90° - 3θ) = cos(θ - 26°)
=> 90° - 3θ = θ - 26°
=> 3θ + θ = 90° + 26°
=> 4θ = 116°
=> θ = 116°/4
=> θ = 29°
The value of sin2 15° + sin2 30° + sin2 45° + sin2 60° + sin2 75° is :- a)1
- b)3/2
- c)5/2
- d)3
Correct answer is option 'C'. Can you explain this answer?
The value of sin2 15° + sin2 30° + sin2 45° + sin2 60° + sin2 75° is :
a)
1
b)
3/2
c)
5/2
d)
3
|
|
Avi Saini answered |
The value of sin(215) in degrees is approximately -0.574.
If angle A is acute and cos A = 8/17 then cot A is :- a)8/15
- b)17/8
- c)15/8
- d)17/15
Correct answer is option 'A'. Can you explain this answer?
If angle A is acute and cos A = 8/17 then cot A is :
a)
8/15
b)
17/8
c)
15/8
d)
17/15
|
Pooja Shah answered |
Cos A=8/17=B/H
base=8x, hypotenuse=17x
By pythagoras theorem,
H2 =P2 + B2
289x2 = P2 + 64x2
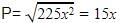
Cot A=B/P=8x/15x=8/15
base=8x, hypotenuse=17x
By pythagoras theorem,
H2 =P2 + B2
289x2 = P2 + 64x2
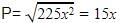
Cot A=B/P=8x/15x=8/15
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. The height of the tower is:- a)√5 m
- b)√15 m
- c)6 m
- d)2.25 m.
Correct answer is option 'C'. Can you explain this answer?
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. The height of the tower is:
a)
√5 m
b)
√15 m
c)
6 m
d)
2.25 m.
|
|
Pooja Shah answered |
Given AB is the tower.
P and Q are the points at distance of 4m and 9m respectively.
From fig, PB = 4m, QB = 9m.
Let angle of elevation from P be α and angle of elevation from Q be β.
Given that α and β are supplementary. Thus, α + β = 90
In triangle ABP,
tan α = AB/BP – (i)
In triangle ABQ,
tan β = AB/BQ
tan (90 – α) = AB/BQ (Since, α + β = 90)
cot α = AB/BQ
1/tan α = AB/BQ
So, tan α = BQ/AB – (ii)
From (i) and (ii)
AB/BP = BQ/AB
AB^2 = BQ x BP
AB^2 = 4 x 9
AB^2 = 36
Therefore, AB = 6.
Hence, height of tower is 6m.
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angles of elevation from his eyes to the top of the building increases from 30 to 60° as he walks towards the building. The distance he walked towards the building is :- a)19 √3 m
- b)57(√3)3 m
- c)38 √3 m
- d)18 √3 m
Correct answer is option 'A'. Can you explain this answer?
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angles of elevation from his eyes to the top of the building increases from 30 to 60° as he walks towards the building. The distance he walked towards the building is :
a)
19 √3 m
b)
57(√3)3 m
c)
38 √3 m
d)
18 √3 m
|
|
Rising Star answered |
If 3 cot θ = 2, then the value of tan θ- a)2/3
- b)3/2
- c)
- d)
Correct answer is option 'B'. Can you explain this answer?
If 3 cot θ = 2, then the value of tan θ
a)
2/3
b)
3/2
c)
d)
|
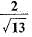
Hrishikesh Choudhary answered |
3cot theta =2
=> cot theta = 2/3
=> 1/tan theta =2/3
=>. tan theta = 3/2
hence, the answer is tan theta =3/2
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks then the width of the river is :- a)3 (√3 –1)m
- b)3 (√3 +1)m
- c)(3 + √3)m
- d)(3 – √3 )m.
Correct answer is option 'B'. Can you explain this answer?
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks then the width of the river is :
a)
3 (√3 –1)m
b)
3 (√3 +1)m
c)
(3 + √3)m
d)
(3 – √3 )m.
|
|
Subham Ghosh answered |
° and 45°. If the bridge is 80 meters long, how wide is the river?
Let's label the diagram:
We want to find the width of the river, which is represented by the distance between points A and B.
To solve this problem, we need to use trigonometry. Specifically, we can use the tangent function:
tan(angle) = opposite/adjacent
We can use this formula for both angles of depression:
tan(30°) = AB/80
tan(45°) = AC/80
Simplifying these equations, we get:
AB = 80 tan(30°) ≈ 46.4 meters
AC = 80 tan(45°) ≈ 80 meters
Now we can use the Pythagorean theorem to find the length of BC:
BC^2 = AC^2 - AB^2
BC^2 = (80)^2 - (46.4)^2
BC ≈ 64.1 meters
Therefore, the width of the river (AB) is approximately 46.4 meters, and the length of the bridge (BC) is approximately 64.1 meters.
Let's label the diagram:
We want to find the width of the river, which is represented by the distance between points A and B.
To solve this problem, we need to use trigonometry. Specifically, we can use the tangent function:
tan(angle) = opposite/adjacent
We can use this formula for both angles of depression:
tan(30°) = AB/80
tan(45°) = AC/80
Simplifying these equations, we get:
AB = 80 tan(30°) ≈ 46.4 meters
AC = 80 tan(45°) ≈ 80 meters
Now we can use the Pythagorean theorem to find the length of BC:
BC^2 = AC^2 - AB^2
BC^2 = (80)^2 - (46.4)^2
BC ≈ 64.1 meters
Therefore, the width of the river (AB) is approximately 46.4 meters, and the length of the bridge (BC) is approximately 64.1 meters.
Chapter doubts & questions for Introduction to Trigonometry - Online MCQ Tests for Class 10 2025 is part of Class 10 exam preparation. The chapters have been prepared according to the Class 10 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 10 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Introduction to Trigonometry - Online MCQ Tests for Class 10 in English & Hindi are available as part of Class 10 exam.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup