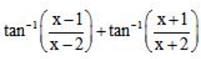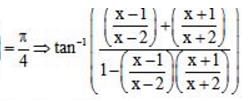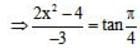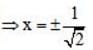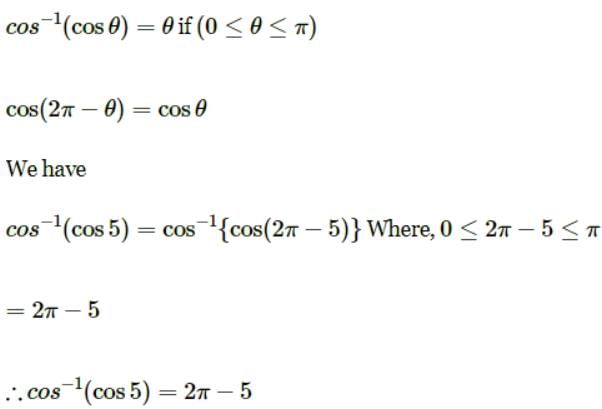All Exams >
JEE >
Mathematics CUET UG Mock Test Series 2026 >
All Questions
All questions of Chapter 2 - Inverse Trigonometric Functions for JEE Exam
Can you explain the answer of this question below: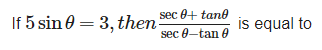
- A:
4
- B:
1/4
- C:
2
- D:
none of these.
The answer is a.
4
1/4
2
none of these.

|
Divey Sethi answered |
sin θ is 3/5.
on simplifying:
(secθ + tanθ)/(secθ - tanθ)
We get, (1+sin θ)/(1-sin θ)
=(1+3/5)/(1-3/5)
=(8/2)
=4
on simplifying:
(secθ + tanθ)/(secθ - tanθ)
We get, (1+sin θ)/(1-sin θ)
=(1+3/5)/(1-3/5)
=(8/2)
=4
Value of 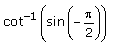
- a)
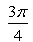
- b)
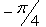
- c)-1
- d)
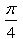
Correct answer is option 'A'. Can you explain this answer?
Value of 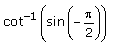
a)
b)
c)
-1
d)
|
|
Aravind Rane answered |
Cot-1[sin(-90)] =cot-1(-1) =π-cot-1(1) =π-π/4 =3π/4
The simplest form of 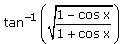 for x > 0 is …
for x > 0 is …- a)x
- b)-x/2
- c)2x
- d)x/2
Correct answer is option 'D'. Can you explain this answer?
The simplest form of 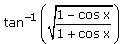 for x > 0 is …
for x > 0 is …
a)
x
b)
-x/2
c)
2x
d)
x/2
|
|
Mira Joshi answered |
tan-1(1-cosx/1+cosx)½
= tan-1{(2sin2 x/2) / (2cos2 x/2)}½
= tan-1{(2sin2 x/2) / (2cos2 x/2)}
= tan-1(tan x/2)
= x/2
= tan-1{(2sin2 x/2) / (2cos2 x/2)}½
= tan-1{(2sin2 x/2) / (2cos2 x/2)}
= tan-1(tan x/2)
= x/2
Evaluate sin(3 sin–10.4)a)0.56b)0.31c)0.64d)0.9Correct answer is 'D'. Can you explain this answer?
|
|
Subhankar Choudhary answered |
3sin^-1(x) = sin^-1(3x - 4x^3) when -1/2<=x<=1/2
Definitely 0.4 comes in this range of x and so
Definitely 0.4 comes in this range of x and so
3sin^-1(0.4) = sin^-1[3*0.4 - 4*0.4^3]
3sin^-1(0.4) = sin^-1[1.2 - 4*0.064]
3sin^-1(0.4) = sin^-1[1.2 - 0.256]
3sin^-1(0.4) = sin^-1[0.944]
3sin^-1(0.4) = sin^-1[1.2 - 4*0.064]
3sin^-1(0.4) = sin^-1[1.2 - 0.256]
3sin^-1(0.4) = sin^-1[0.944]
Finally , sin(3sin^-1(0.4)) = sin{sin^-1(0.944)} = 0.944
The maximum value of sin x + cos x is- a)1
- b)2
- c)√2
- d)
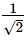
Correct answer is option 'C'. Can you explain this answer?
The maximum value of sin x + cos x is
a)
1
b)
2
c)
√2
d)
|
|
Shreya Gupta answered |
sinx + cosx=sinx + sin(90-x)=2sin{(x+90-x)/2}cos{(... morex-90+x)/2}using the formula
Can you explain the answer of this question below:Value of 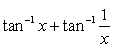 is
is
- A:
π/2
- B:
1/x
- C:
x
- D:
π
The answer is a.
Value of is
π/2
1/x
x
π

|
Case Studies answered |
Tan-1(1/x) = cot-1(x) and tan-1(x) + cot-1(x) =90degree
The value ofcos150−sin150 is- a)

- b)

- c)0
- d)

Correct answer is option 'D'. Can you explain this answer?
The value ofcos150−sin150 is
a)
b)
c)
0
d)

|
Poojan Angiras answered |
Heyy!!! write cos 15 and sin 15 as cos(60-45) and sin(60-45) respectively.And then apply formula of cos(a+b) and sin(a+b).Proceed as the question u will get correct answer :-):-)^_^
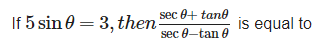
- a)4
- b)1/4
- c)2
- d)none of these.
Correct answer is option 'A'. Can you explain this answer?
a)
4
b)
1/4
c)
2
d)
none of these.
|
|
Krishna Iyer answered |
sin θ is 3/5.
on simplifying:
(secθ + tanθ)/(secθ - tanθ)
We get, (1+sin θ)/(1-sin θ)
=(1+3/5)/(1-3/5)
=(8/2)
=4
on simplifying:
(secθ + tanθ)/(secθ - tanθ)
We get, (1+sin θ)/(1-sin θ)
=(1+3/5)/(1-3/5)
=(8/2)
=4
Evaluate :cos (tan–1 x)- a)
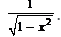
- b)
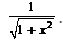
- c)
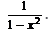
- d)
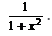
Correct answer is option 'B'. Can you explain this answer?
Evaluate :cos (tan–1 x)
a)
b)
c)
d)
|
|
Preeti Iyer answered |
tan−1 x = θ , so that x=tanθ . We need to determine cosθ .
sec2θ = 1 + tan2θ = 1 + x2
∴s ecθ = ±√(1+x2)
Then, cos(tan−1x) = cosθ=1/secθ = ±1/√(1+x2)
sec2θ = 1 + tan2θ = 1 + x2
∴s ecθ = ±√(1+x2)
Then, cos(tan−1x) = cosθ=1/secθ = ±1/√(1+x2)
If ab + bc + ca = 0, then find 1/a2-bc + 1/b2 – ca + 1/c2- ab- a)π
- b)0
- c)-1
- d)2π
Correct answer is option 'B'. Can you explain this answer?
If ab + bc + ca = 0, then find 1/a2-bc + 1/b2 – ca + 1/c2- ab
a)
π
b)
0
c)
-1
d)
2π
|
|
Preeti Iyer answered |
Given ab+bc+ca=0 and asked to find value 1/(a2-bc ... more) + 1/(c2-ab) + 1/(a2-bc)Put -ac = ab + bc ; -ab = ac+ bc and -bc =ab +
If sin A + cos A = 1, then sin 2A is equal to- a)2
- b)1/2
- c)0
- d)1
Correct answer is option 'C'. Can you explain this answer?
If sin A + cos A = 1, then sin 2A is equal to
a)
2
b)
1/2
c)
0
d)
1
|
|
Suresh Iyer answered |
(Sin A + Cos A)2 = sin2A + cos2A + 2 sinAcosA
1 = 1 + Sin 2A
so, Sin 2A = 0
Hence A = 0
The number of solutions of the equation sin-1 x - cos-1 x = sin-1(1/2) is
a) 3
b) 1
c) 2
d) infinite.
Correct answer is option 'B'. Can you explain this answer?
|
|
Raghavendra Ghoshal answered |
Solution:
Given equation is sin^-1(x) - cos^-1(x) = sin^-1(1/2)
We know that sin(x) + cos(x) = √2 cos(x - π/4)
So, sin^-1(x) - cos^-1(x) = π/2 - sin^-1(√2x)
Therefore, the given equation becomes π/2 - sin^-1(√2x) = sin^-1(1/2)
sin(sin^-1(x)) = xsin(π/2 - sin^-1(√2x)) = √[1 - 2x^2]
√[1 - 2x^2] = 1/2
2x^2 = 3/4
x = ±√3/2
Therefore, the given equation has only 1 solution, which is x = √3/2 or x = -√3/2.
Hence, the correct answer is option B.
Given equation is sin^-1(x) - cos^-1(x) = sin^-1(1/2)
We know that sin(x) + cos(x) = √2 cos(x - π/4)
So, sin^-1(x) - cos^-1(x) = π/2 - sin^-1(√2x)
Therefore, the given equation becomes π/2 - sin^-1(√2x) = sin^-1(1/2)
sin(sin^-1(x)) = xsin(π/2 - sin^-1(√2x)) = √[1 - 2x^2]
√[1 - 2x^2] = 1/2
2x^2 = 3/4
x = ±√3/2
Therefore, the given equation has only 1 solution, which is x = √3/2 or x = -√3/2.
Hence, the correct answer is option B.
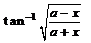 is equal to
is equal to- a)
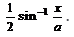
- b)
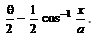
- c)
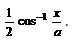
- d)
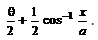
Correct answer is 'C'. Can you explain this answer?
a)
b)
c)
d)
|
|
Nikita Singh answered |
Let y = tan−1[(a−x)/(a+x)]1/2
put x = a cos θ
Now, y = tan−1[(a − a cos θ)/(a + a cos θ)]1/2
⇒ y = tan−1((1 − cos θ)/(1 + cos θ))1/2
⇒ y = tan−1[[(1−cos θ)(1−cos θ)]/(1+cos θ)(1−cos θ)]1/2
⇒ y = tan−1[(1−cos θ)2/1 − cos2θ]1/2
⇒ y = tan−1[(1 − cos θ)/sin θ]
⇒ y = tan−1[2 sin2(θ/2)/2 sin(θ/2) . cos(θ/2)]
⇒ y = tan−1[tan(θ/2)]
⇒ y = θ/2
⇒ y = 1/2 cos−1(x/a)
put x = a cos θ
Now, y = tan−1[(a − a cos θ)/(a + a cos θ)]1/2
⇒ y = tan−1((1 − cos θ)/(1 + cos θ))1/2
⇒ y = tan−1[[(1−cos θ)(1−cos θ)]/(1+cos θ)(1−cos θ)]1/2
⇒ y = tan−1[(1−cos θ)2/1 − cos2θ]1/2
⇒ y = tan−1[(1 − cos θ)/sin θ]
⇒ y = tan−1[2 sin2(θ/2)/2 sin(θ/2) . cos(θ/2)]
⇒ y = tan−1[tan(θ/2)]
⇒ y = θ/2
⇒ y = 1/2 cos−1(x/a)
cos2θ is not equal to- a)1−2sin2θ
- b)2cos2θ−1
- c)
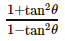
- d)
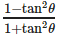
Correct answer is option 'C'. Can you explain this answer?
cos2θ is not equal to
a)
1−2sin2θ
b)
2cos2θ−1
c)
d)
|
|
Priyanka Sharma answered |
cos 2θ is equal to cos2θ - sin2θ = 2cos2θ - 1
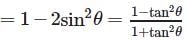
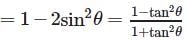
Evaluate sin(3 sin–1 0.4)- a)0.9
- b)0.31
- c)0.64
- d)0.56
Correct answer is option 'D'. Can you explain this answer?
Evaluate sin(3 sin–1 0.4)
a)
0.9
b)
0.31
c)
0.64
d)
0.56

|
Mohit Rajpoot answered |
3sin^-1(x) = sin^-1(3x - 4x^3) when -1/2<=x<=1/2
Definitely 0.4 comes in this range of x and so
Definitely 0.4 comes in this range of x and so
3sin^-1(0.4) = sin^-1[3*0.4 - 4*0.4^3]
3sin^-1(0.4) = sin^-1[1.2 - 4*0.064]
3sin^-1(0.4) = sin^-1[1.2 - 0.256]
3sin^-1(0.4) = sin^-1[0.944]
3sin^-1(0.4) = sin^-1[1.2 - 4*0.064]
3sin^-1(0.4) = sin^-1[1.2 - 0.256]
3sin^-1(0.4) = sin^-1[0.944]
Finally , sin(3sin^-1(0.4)) = sin{sin^-1(0.944)} = 0.944
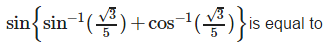
- a)

- b)1
- c)0
- d)none of these.
Correct answer is option 'B'. Can you explain this answer?
a)
b)
1
c)
0
d)
none of these.
|
|
Nikita Singh answered |
sin-1√3/5 = A
Sin A = √3/5 , cos A = √22/5
Therefore Cos-1√3/5 = B
Cos B = √3/5 , sin B = √22/5
sin(A+B) = sinA cosB + cosA sinB
= √3/5 * √3/5 + √22/5 * √22/5
= 3/25 * 22/25
= 25/25
= 1
Sin A = √3/5 , cos A = √22/5
Therefore Cos-1√3/5 = B
Cos B = √3/5 , sin B = √22/5
sin(A+B) = sinA cosB + cosA sinB
= √3/5 * √3/5 + √22/5 * √22/5
= 3/25 * 22/25
= 25/25
= 1
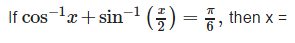
- a)±√3.
- b)0
- c)
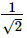
- d)1
Correct answer is option 'D'. Can you explain this answer?
a)
±√3.
b)
0
c)
d)
1

|
Devendra Singh answered |
Apply apply formula of Sin inverse X + Cos inverse X and the question will be solved
When x = π/2, then tan x, is- a)∞ or −∞
- b)−∞−∞
- c)∞
- d)not defined.
Correct answer is option 'D'. Can you explain this answer?
When x = π/2, then tan x, is
a)
∞ or −∞
b)
−∞−∞
c)
∞
d)
not defined.

|
Poulomi Datta answered |
tan π/2 = n.d.i.e. not defined.
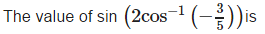
- a)7/25
- b)-24/25
- c)24/25
- d)none of these.
Correct answer is option 'B'. Can you explain this answer?
a)
7/25
b)
-24/25
c)
24/25
d)
none of these.

|
Seblewongel Girma answered |
Sin(2(0.705π))=-24/25
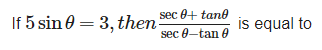
- a)4
- b)1/4
- c)2
- d)none of these.
Correct answer is 'A'. Can you explain this answer?
a)
4
b)
1/4
c)
2
d)
none of these.

|
Ishita Deshpande answered |
SinQ is 3/5.
on simplifying:
(secQ+tanQ)/(secQ-tanQ)
We get...(1+sinQ)/(1-sinQ)
=(1+3/5)/(1-3/5)
=(8/2)
=4
on simplifying:
(secQ+tanQ)/(secQ-tanQ)
We get...(1+sinQ)/(1-sinQ)
=(1+3/5)/(1-3/5)
=(8/2)
=4
If ƒ(x) = tan(x), then f-1(1/√(3)) =- a)π/6
- b)π/4
- c)π/3
- d)π
Correct answer is option 'A'. Can you explain this answer?
If ƒ(x) = tan(x), then f-1(1/√(3)) =
a)
π/6
b)
π/4
c)
π/3
d)
π
|
|
Sanjana Mishra answered |
Please provide more context or ask a specific question.
Evaluate: sin (2 sin–10.6)- a)0.6
- b)0.66
- c)0.36
- d)0.96
Correct answer is option 'D'. Can you explain this answer?
Evaluate: sin (2 sin–10.6)
a)
0.6
b)
0.66
c)
0.36
d)
0.96
|
|
Nikita Singh answered |
Let, sin-1(0.6) = A…………(1)
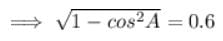 ( Since, sin² A + cos² A = 1 ⇒ sin² A = 1 - cos² A ⇒ sin A = √(1-cos² A) )
( Since, sin² A + cos² A = 1 ⇒ sin² A = 1 - cos² A ⇒ sin A = √(1-cos² A) )
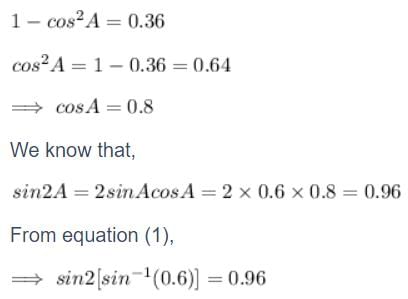
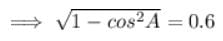 ( Since, sin² A + cos² A = 1 ⇒ sin² A = 1 - cos² A ⇒ sin A = √(1-cos² A) )
( Since, sin² A + cos² A = 1 ⇒ sin² A = 1 - cos² A ⇒ sin A = √(1-cos² A) )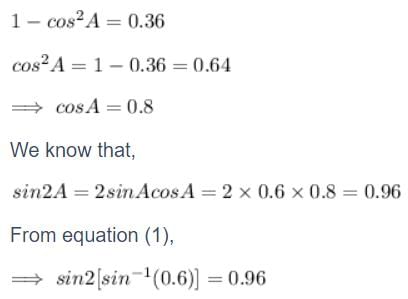
The simplest form of 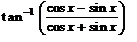
- a)
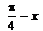
- b)
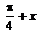
- c)2x
- d)
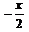
Correct answer is option 'A'. Can you explain this answer?
The simplest form of 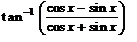
a)
b)
c)
2x
d)

|
Top Rankers answered |
(cosx−sinx)/(cosx+sinx) = (1−tanx)/(1+tanx)
tan(A−B) = (tanA−tanB)/(1 + tanAtanB)
= tan(π/4−x)
putting this value in question.
tan−1tan(π/4−x)
π/4−x.
tan(A−B) = (tanA−tanB)/(1 + tanAtanB)
= tan(π/4−x)
putting this value in question.
tan−1tan(π/4−x)
π/4−x.
If ƒ(x) = √(2tan(x)),then f-1(√(2)) =- a)0
- b)1
- c)√(2)
- d)2
Correct answer is option 'B'. Can you explain this answer?
If ƒ(x) = √(2tan(x)),then f-1(√(2)) =
a)
0
b)
1
c)
√(2)
d)
2
|
|
Siddharth Chakraborty answered |
If what? Please provide more information for me to assist you better.
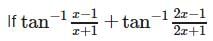
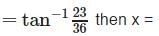
- a)4/3
- b)-3/8
- c)4/3 or -3/8
- d)none of these.
Correct answer is option 'B'. Can you explain this answer?
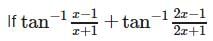
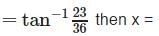
a)
4/3
b)
-3/8
c)
4/3 or -3/8
d)
none of these.
|
|
Chirag Verma answered |
The correct option is B.
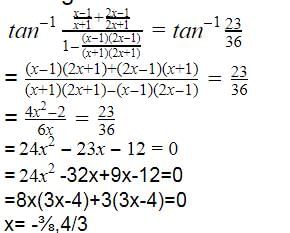
Evaluate 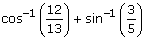
- a)
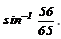
- b)
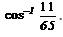
- c)
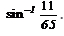
- d)
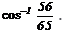
Correct answer is 'A'. Can you explain this answer?
Evaluate 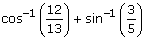
a)
b)
c)
d)
|
|
Ritu Singh answered |
Correct Answer :- a
Explanation : cos-1(12/13) + sin-1 (3/5)
⇒ sin-1 5/13 + sin-1 3/5
Using the formula, sin-1x + sin-1y = sin-1( x√1-y² + y√1-x² )
⇒ sin-1 ( 5/13√1-9/25 + 3√1-25/169)
⇒ sin-1 ( 5/13 × 4/5 + 3/5 × 12/13)
⇒ sin-1 (30 + 36 / 65)
⇒ sin-1 (56/ 65)
The principal value of cos–1 (cos 5) is- a)5
- b)π – 5
- c)5 – π
- d)2π – 5
Correct answer is option 'D'. Can you explain this answer?
The principal value of cos–1 (cos 5) is
a)
5
b)
π – 5
c)
5 – π
d)
2π – 5
|
|
Madhurima Patel answered |
Sorry, your question is incomplete. Please provide more information.
If and x + y + z = xyz, then a value of tan−1x+tan−1y+tan−1z is- a)3π/2
- b)π/2
- c)π
- d)none of these.
Correct answer is option 'C'. Can you explain this answer?
If and x + y + z = xyz, then a value of tan−1x+tan−1y+tan−1z is
a)
3π/2
b)
π/2
c)
π
d)
none of these.
|
|
Ruchi Kumar answered |
This question is incomplete and cannot be answered. Please provide more information.
What is the maximum and minimum value of sin x +cos x?- a)0, -1
- b)1, 0
- c)-1, -√2
- d)√2, –√2
Correct answer is option 'D'. Can you explain this answer?
What is the maximum and minimum value of sin x +cos x?
a)
0, -1
b)
1, 0
c)
-1, -√2
d)
√2, –√2
|
|
Nilanjan Mehra answered |
Maximum and Minimum Value of sin x + cos x
Sin x + cos x can be expressed as a single trigonometric function using the identities sin x = cos(90° - x) and cos x = sin(90° - x). Therefore, sin x + cos x can be written as √2 sin(x + 45°).
Maximum Value:
- The maximum value of sin x + cos x occurs when the value of sin(x + 45°) is at its maximum.
- The maximum value of sin(x + 45°) is 1.
- Therefore, the maximum value of sin x + cos x is √2.
Minimum Value:
- The minimum value of sin x + cos x occurs when the value of sin(x + 45°) is at its minimum.
- The minimum value of sin(x + 45°) is -1.
- Therefore, the minimum value of sin x + cos x is -√2.
Therefore, the maximum value of sin x + cos x is √2 and the minimum value is -√2. Hence, option 'D' is the correct answer.
Sin x + cos x can be expressed as a single trigonometric function using the identities sin x = cos(90° - x) and cos x = sin(90° - x). Therefore, sin x + cos x can be written as √2 sin(x + 45°).
Maximum Value:
- The maximum value of sin x + cos x occurs when the value of sin(x + 45°) is at its maximum.
- The maximum value of sin(x + 45°) is 1.
- Therefore, the maximum value of sin x + cos x is √2.
Minimum Value:
- The minimum value of sin x + cos x occurs when the value of sin(x + 45°) is at its minimum.
- The minimum value of sin(x + 45°) is -1.
- Therefore, the minimum value of sin x + cos x is -√2.
Therefore, the maximum value of sin x + cos x is √2 and the minimum value is -√2. Hence, option 'D' is the correct answer.
cot (cos−1x) is equal to- a)
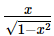
- b)
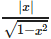
- c)
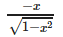
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
cot (cos−1x) is equal to
a)
b)
c)
d)
none of these

|
Athul Patel answered |
Put,
cos-1x = θ ⇒ x = cos θ ⇒ cos θ
cos-1x = θ ⇒ x = cos θ ⇒ cos θ
Direction: Read the following text and answer the following questions on the basis of the same:The value of an inverse trigonometric functions which lies in the range of Principal branch is called the principal value of that inverse trigonometric functions.Principal value of cot-1(√3) is :- a)π/3
- b)π
- c)π/6
- d)π/2
Correct answer is option 'C'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
The value of an inverse trigonometric functions which lies in the range of Principal branch is called the principal value of that inverse trigonometric functions.
Principal value of cot-1(√3) is :
a)
π/3
b)
π
c)
π/6
d)
π/2
|
|
Tanuja Kapoor answered |
Cot -1(√3) =cot-1 (cot (π/6) = π/6
If cos(-1)x + cos(-1)y = 2π, then the value of sin(-1)x + sin(-1)y is - a)−π
- b)π
- c)0
- d)none of these.
Correct answer is option 'A'. Can you explain this answer?
If cos(-1)x + cos(-1)y = 2π, then the value of sin(-1)x + sin(-1)y is
a)
−π
b)
π
c)
0
d)
none of these.

|
Rishika Mishra answered |
If cos(-1)x + cos(-1) y = 2π, then the value of sin(-1)x + sin(-1)y = π−2π = −π.
sin (200)0 + cos (200)0 is- a)Zero
- b)Positive
- c)Zero or positive.
- d)Negative
Correct answer is option 'D'. Can you explain this answer?
sin (200)0 + cos (200)0 is
a)
Zero
b)
Positive
c)
Zero or positive.
d)
Negative
|
|
Dipika Dey answered |
To determine the sign of sin(200)0 and cos(200)0, we need to recall the unit circle and the values of sine and cosine for angles in the different quadrants.
The unit circle is a circle with a radius of 1 unit, centered at the origin (0,0) on a coordinate plane. It helps us understand the relationship between angles and the coordinates on the circle.
The circle is divided into four quadrants: Quadrant I (0°-90°), Quadrant II (90°-180°), Quadrant III (180°-270°), and Quadrant IV (270°-360°).
In Quadrant I, both the x-coordinate (cosine) and the y-coordinate (sine) are positive. In Quadrant II, the x-coordinate (cosine) is negative, but the y-coordinate (sine) is positive. In Quadrant III, both the x-coordinate (cosine) and the y-coordinate (sine) are negative. In Quadrant IV, the x-coordinate (cosine) is positive, but the y-coordinate (sine) is negative.
Now let's consider the given angle, 200°.
Since 200° is greater than 180°, it lies in Quadrant III.
- The cosine of 200° will be negative because it is in Quadrant III.
- The sine of 200° will also be negative because it is in Quadrant III.
Hence, sin(200)0 and cos(200)0 are both negative.
Therefore, the correct answer is option 'D' - Negative.
The unit circle is a circle with a radius of 1 unit, centered at the origin (0,0) on a coordinate plane. It helps us understand the relationship between angles and the coordinates on the circle.
The circle is divided into four quadrants: Quadrant I (0°-90°), Quadrant II (90°-180°), Quadrant III (180°-270°), and Quadrant IV (270°-360°).
In Quadrant I, both the x-coordinate (cosine) and the y-coordinate (sine) are positive. In Quadrant II, the x-coordinate (cosine) is negative, but the y-coordinate (sine) is positive. In Quadrant III, both the x-coordinate (cosine) and the y-coordinate (sine) are negative. In Quadrant IV, the x-coordinate (cosine) is positive, but the y-coordinate (sine) is negative.
Now let's consider the given angle, 200°.
Since 200° is greater than 180°, it lies in Quadrant III.
- The cosine of 200° will be negative because it is in Quadrant III.
- The sine of 200° will also be negative because it is in Quadrant III.
Hence, sin(200)0 and cos(200)0 are both negative.
Therefore, the correct answer is option 'D' - Negative.
Direction: Read the following text and answer the following questions on the basis of the same:The value of an inverse trigonometric functions which lies in the range of Principal branch is called the principal value of that inverse trigonometric functions.Principal value of sin -1(1) + sin-1(1/√2) is- a)2π
- b)π
- c)3π/4
- d)π/3
Correct answer is option 'C'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
The value of an inverse trigonometric functions which lies in the range of Principal branch is called the principal value of that inverse trigonometric functions.
Principal value of sin -1(1) + sin-1(1/√2) is
a)
2π
b)
π
c)
3π/4
d)
π/3
|
|
Sonal Chauhan answered |
Principal Value of Inverse Trigonometric Functions
Introduction:
Inverse trigonometric functions are the inverse functions of trigonometric functions. They are used to find the angle measures corresponding to given trigonometric ratios. The principal branch refers to the values of the inverse trigonometric functions that lie within a specific range.
Principal Value:
The principal value of an inverse trigonometric function is the value that lies within the range of the principal branch. In other words, it is the value of the inverse trigonometric function that is considered as the primary or principal value. For example, the principal value of sin^(-1)(1) is denoted as sin^(-1)(1) and represents the angle whose sine is 1.
Finding the Principal Value of sin^(-1)(1):
To find the principal value of sin^(-1)(1), we need to determine the angle whose sine is 1. The sine function takes values between -1 and 1, inclusive. Therefore, we need to find the angle in the principal branch whose sine is 1.
Determining the Angle:
We know that the sine function is positive in the first and second quadrants. In the first quadrant, the sine function is positive and equal to 1 at π/2 radians or 90 degrees. Therefore, sin^(-1)(1) = π/2.
Finding the Principal Value of sin^(-1)(1/√2):
To find the principal value of sin^(-1)(1/√2), we need to determine the angle whose sine is 1/√2. The sine function takes values between -1 and 1, inclusive. Therefore, we need to find the angle in the principal branch whose sine is 1/√2.
Determining the Angle:
We know that the sine function is positive in the first and second quadrants. In the first quadrant, the sine function is positive and equal to 1/√2 at π/4 radians or 45 degrees. Therefore, sin^(-1)(1/√2) = π/4.
Conclusion:
The principal value of sin^(-1)(1) is π/2 and the principal value of sin^(-1)(1/√2) is π/4. Therefore, the correct answer is option C) 3π/4.
Introduction:
Inverse trigonometric functions are the inverse functions of trigonometric functions. They are used to find the angle measures corresponding to given trigonometric ratios. The principal branch refers to the values of the inverse trigonometric functions that lie within a specific range.
Principal Value:
The principal value of an inverse trigonometric function is the value that lies within the range of the principal branch. In other words, it is the value of the inverse trigonometric function that is considered as the primary or principal value. For example, the principal value of sin^(-1)(1) is denoted as sin^(-1)(1) and represents the angle whose sine is 1.
Finding the Principal Value of sin^(-1)(1):
To find the principal value of sin^(-1)(1), we need to determine the angle whose sine is 1. The sine function takes values between -1 and 1, inclusive. Therefore, we need to find the angle in the principal branch whose sine is 1.
Determining the Angle:
We know that the sine function is positive in the first and second quadrants. In the first quadrant, the sine function is positive and equal to 1 at π/2 radians or 90 degrees. Therefore, sin^(-1)(1) = π/2.
Finding the Principal Value of sin^(-1)(1/√2):
To find the principal value of sin^(-1)(1/√2), we need to determine the angle whose sine is 1/√2. The sine function takes values between -1 and 1, inclusive. Therefore, we need to find the angle in the principal branch whose sine is 1/√2.
Determining the Angle:
We know that the sine function is positive in the first and second quadrants. In the first quadrant, the sine function is positive and equal to 1/√2 at π/4 radians or 45 degrees. Therefore, sin^(-1)(1/√2) = π/4.
Conclusion:
The principal value of sin^(-1)(1) is π/2 and the principal value of sin^(-1)(1/√2) is π/4. Therefore, the correct answer is option C) 3π/4.
If 2tan−1(cos x) = tan−1(2cosecx) , then x =- a)
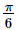
- b)
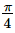
- c)
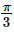
- d)none of these.
Correct answer is option 'B'. Can you explain this answer?
If 2tan−1(cos x) = tan−1(2cosecx) , then x =
a)
b)
c)
d)
none of these.

|
Sagar Mukherjee answered |
If 2 tan-1 (cos x) = tan -1(2 cosec x),
2tan-1(cos x) = tan-1 (2 cosec x)

= tan-1(2 cosec x)
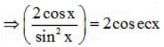
= cot x cosec x = cosec x = x = π/4
Direction: Read the following text and answer the following questions on the basis of the same:The value of an inverse trigonometric functions which lies in the range of Principal branch is called the principal value of that inverse trigonometric functions.Principal value of sin–1 (½) is- a)π/6
- b)π/3
- c)π/4
- d)π/2
Correct answer is option 'A'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
The value of an inverse trigonometric functions which lies in the range of Principal branch is called the principal value of that inverse trigonometric functions.
Principal value of sin–1 (½) is
a)
π/6
b)
π/3
c)
π/4
d)
π/2
|
|
Preeti Iyer answered |
Sin-1(½) = y
sin y = ½
Principal value branch of sin–1 is (-π/2, π/2)
and sin(π/6) = ½
⇒ Principal value of sin-1(½) is π/6.
The number of solutions of the equation 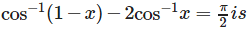
- a)One
- b)two
- c)more than one
- d)none of these.
Correct answer is option 'A'. Can you explain this answer?
The number of solutions of the equation 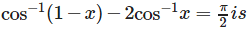
a)
One
b)
two
c)
more than one
d)
none of these.

|
Nilesh Goyal answered |
As no value of x in (0, 1) can satisfy the given equation.Thus, the given equation has only one solution.
Chapter doubts & questions for Chapter 2 - Inverse Trigonometric Functions - Mathematics CUET UG Mock Test Series 2026 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chapter 2 - Inverse Trigonometric Functions - Mathematics CUET UG Mock Test Series 2026 in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Related JEE Content

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup

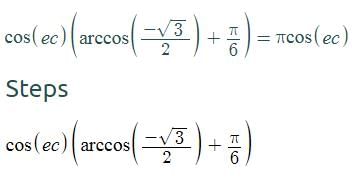

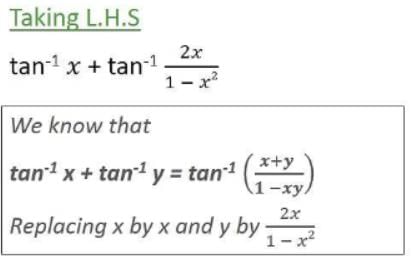
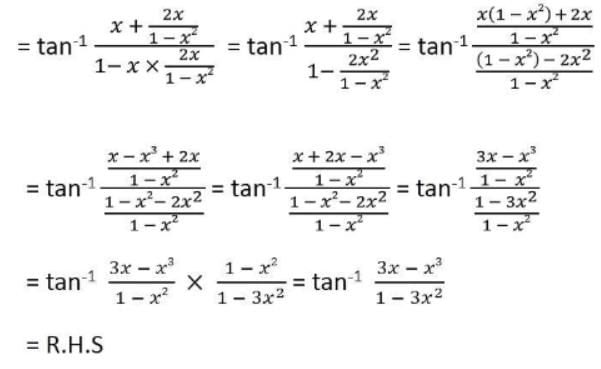
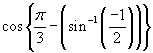 is given by
is given by