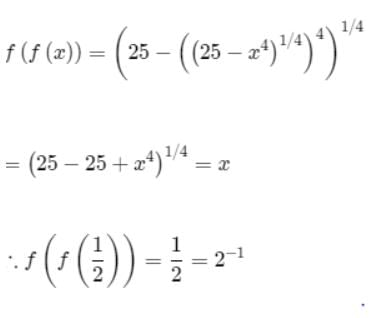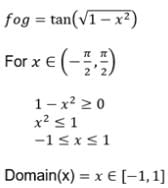All Exams >
Commerce >
Online MCQ Tests for Commerce >
All Questions
All questions of Relations and Functions for Commerce Exam
If f(x) = x2 and g(x) = cosx, which of the following is true?- a)f + g is even function
- b)f – g is an odd function
- c)f + g is not defined
- d)f + g is an odd function
Correct answer is option 'A'. Can you explain this answer?
If f(x) = x2 and g(x) = cosx, which of the following is true?
a)
f + g is even function
b)
f – g is an odd function
c)
f + g is not defined
d)
f + g is an odd function
|
|
Raghav Bansal answered |
if f(x) is an odd function
So, f(−x)=−f(x)
F(−x)=cos(f(−x))
=cos(−f(x))
=cos(f(x))
=F(x)
So cos(f(x)) is an even function
So, f(x) and g(x) is an even function
If A = {1, 2, 3 }, B = {4, 5, 6 }, which of the following is not a relation from A to Ba) R1 = {(1, 4), (1, 5),(1, 6)}b) R2 = {(1, 5), (2, 4), (3, 6)}c) R3 = {(4, 2), (2, 6), (5, 1), (2, 4)}d) R4 = {(1, 4), (1, 5), (3, 6), (2, 6), (3, 4)}Correct answer is option 'C'. Can you explain this answer?
|
|
Poonam Reddy answered |
A × B = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
If n(A) = p and n(B) = q, then how many relations are there from A to B.- a)pq
- b)3pq
- c)2pq
- d)(pq)2
Correct answer is option 'C'. Can you explain this answer?
If n(A) = p and n(B) = q, then how many relations are there from A to B.
a)
pq
b)
3pq
c)
2pq
d)
(pq)2
|
|
Preeti Khanna answered |
Number of relation from A to B = 2n(A)×n(B)
n(A) = p, n(B) = q
⇒ Number of relation from A to B = 2pq
⇒ Number of relation from A to B = 2pq
If A = {1, 2, 3}, and B = {3, 6} then the number of relations from A to B is
- a)32
- b)23
- c)23
- d)26
Correct answer is option 'D'. Can you explain this answer?
If A = {1, 2, 3}, and B = {3, 6} then the number of relations from A to B is
a)
32
b)
23
c)
23
d)
26
|
|
Preeti Iyer answered |
The number of relations between sets can be calculated using 2mn where m and n represent the number of members in each set.
So, number of relations from A to B is 26.
So, number of relations from A to B is 26.
Let R be a relation defined on the set of N natural numbers as R = {(x, y): y is a factor of x, x, y∈ N} then,- a)(2, 4) ∈ R
- b)(9, 5) ∈ R
- c)(4, 2) ∈ R
- d)(3, 9) ∈ R
Correct answer is option 'C'. Can you explain this answer?
Let R be a relation defined on the set of N natural numbers as R = {(x, y): y is a factor of x, x, y∈ N} then,
a)
(2, 4) ∈ R
b)
(9, 5) ∈ R
c)
(4, 2) ∈ R
d)
(3, 9) ∈ R
|
|
Om Desai answered |
R = {(x, y): y is a factor of x, x, y∈ N}
As we know that 2 is a factor of 4
So, according to the options (4, 2) ϵ R
As we know that 2 is a factor of 4
So, according to the options (4, 2) ϵ R
Let A = {1, 2, 3, …, 50} and R be the relation “is square of” on A. Then R as a subset of A x A is written as:
- a){(1, 1), (2, 2), (3, 3), (4, 4) (5, 5), (6, 6), (7, 7)}
- b){(1, 1), (2, 5), (3, 9), (4, 15) (5, 25), (6, 36), (7, 49)}
- c){(1, 1), (4, 4), (9, 9), (16, 16) (25, 25), (36, 36), (49, 49)}
- d){(1, 1), (4, 2), (9, 3), (16, 4) (25, 5), (36, 6), (49, 7)}
Correct answer is option 'D'. Can you explain this answer?
Let A = {1, 2, 3, …, 50} and R be the relation “is square of” on A. Then R as a subset of A x A is written as:
a)
{(1, 1), (2, 2), (3, 3), (4, 4) (5, 5), (6, 6), (7, 7)}
b)
{(1, 1), (2, 5), (3, 9), (4, 15) (5, 25), (6, 36), (7, 49)}
c)
{(1, 1), (4, 4), (9, 9), (16, 16) (25, 25), (36, 36), (49, 49)}
d)
{(1, 1), (4, 2), (9, 3), (16, 4) (25, 5), (36, 6), (49, 7)}
|
|
Tejas Verma answered |
Since x is the square of y in relation R.
i.e. option D is correct.
i.e. option D is correct.
Which of the following statement is false?- a)If R is a relation from A to B, then domain of R is a subset of A and range of R is a subset of B.
- b)If A = {1, 2, 3, 4} and B = {5, 6}, then the number of relations from A to B is 256.
- c)A subset of A × B is called a relation from the set A to set B.
- d)If A = {x, y, z} and B = {1, 2} then the number of relations from A to B is 22.
Correct answer is option 'D'. Can you explain this answer?
Which of the following statement is false?
a)
If R is a relation from A to B, then domain of R is a subset of A and range of R is a subset of B.
b)
If A = {1, 2, 3, 4} and B = {5, 6}, then the number of relations from A to B is 256.
c)
A subset of A × B is called a relation from the set A to set B.
d)
If A = {x, y, z} and B = {1, 2} then the number of relations from A to B is 22.
|
|
Riya Banerjee answered |
Option D: The number of relations from A to B is 23*2= 26
Let R be a relation defined as
R = {(x, y): y = 2x, x is natural number < 5} then Range of R is given as ,- a){2, 4, 6, 8}
- b){2, 4, 6, 8, 10}
- c){1, 2, 3, 4}
- d)N
Correct answer is option 'A'. Can you explain this answer?
Let R be a relation defined as
R = {(x, y): y = 2x, x is natural number < 5} then Range of R is given as ,
R = {(x, y): y = 2x, x is natural number < 5} then Range of R is given as ,
a)
{2, 4, 6, 8}
b)
{2, 4, 6, 8, 10}
c)
{1, 2, 3, 4}
d)
N
|
|
Gaurav Kumar answered |
X is a natural number and x < 5, the number is 1, 2, 3, 4
y = 2x
y = 2x
► x(1), y = 2 × 1 = 2
► x(2), y = 2 × 2 = 4
► x(3), y = 2 × 3 = 6
► x(4), y = 2 × 4 = 8
► x(2), y = 2 × 2 = 4
► x(3), y = 2 × 3 = 6
► x(4), y = 2 × 4 = 8
Range = {2, 4, 6, 8}
Which of the following is not an example of polynomial function ?- a)g(x) = 8x2 + 5x – 2
- b)p(x) =5x3 + 3x2 + x – 2
- c)h(x) =3 root of x minus 1 over x
- d)f(x) = 3x2 + x – 2
Correct answer is option 'C'. Can you explain this answer?
Which of the following is not an example of polynomial function ?
a)
g(x) = 8x2 + 5x – 2
b)
p(x) =5x3 + 3x2 + x – 2
c)
h(x) =3 root of x minus 1 over x
d)
f(x) = 3x2 + x – 2
|
|
Lavanya Menon answered |
A polynomial function is a function which involves only non-negative integer powers or only positive integer exponents of a variable in an equation.
In option C, powers of x are negative and fractional.
In option C, powers of x are negative and fractional.
If X = {1, 2, 3, 4}, Y = {1, 2, 3,…., 20}, and f: X –> Y be the correspondence which assigns each element in X the value equal to its square, then the domain, co-domain and range of f is- a)Domain = {1, 2, …, 20}, Range = {1, 2, 3, 4}, Co domain = {1, 2, 3, 4}
- b)Domain = {1, 4, 9, 16}, Range = {1, 2, 3, 4}, Co domain = {1, 2, 3, …, 16}
- c)Domain = {1, 2, 3, 4}, Range = {1, 4, 9, 16}, Co domain = {1, 2, 3, …, 20}
- d)Domain = {1, 2, 3, 4}, Range = {1, 4, 9, 16}, Co domain = {1, 2, 3, …, 16}
Correct answer is option 'B'. Can you explain this answer?
If X = {1, 2, 3, 4}, Y = {1, 2, 3,…., 20}, and f: X –> Y be the correspondence which assigns each element in X the value equal to its square, then the domain, co-domain and range of f is
a)
Domain = {1, 2, …, 20}, Range = {1, 2, 3, 4}, Co domain = {1, 2, 3, 4}
b)
Domain = {1, 4, 9, 16}, Range = {1, 2, 3, 4}, Co domain = {1, 2, 3, …, 16}
c)
Domain = {1, 2, 3, 4}, Range = {1, 4, 9, 16}, Co domain = {1, 2, 3, …, 20}
d)
Domain = {1, 2, 3, 4}, Range = {1, 4, 9, 16}, Co domain = {1, 2, 3, …, 16}
|
|
Raghav Bansal answered |
The correct option is B
Since the function is defined from
XY.So the domain will be the set X which is {1,2,3,4}. Codomain is what may possibly come out of a function. So codomain is the whole set Y which is {1,2,3,...,20}. Range is The range is the set of possible output values which will be the values in the set of Y which have a pre-image. That is, the value of squares. So the range is {1,4,,9,16}.
Let X = {1, 2, 3, 4}, Y = {1, 2, …, 10} and f : X –> Y be defined by f(x) = 2x + 1, x ∈ X. Then the range of f is- a){1, 2,…., 10}
- b){5, 6, 7, 8, 9, 10}
- c){3, 5, 7, 9}
- d){1, 2, 3, 4}
Correct answer is option 'C'. Can you explain this answer?
Let X = {1, 2, 3, 4}, Y = {1, 2, …, 10} and f : X –> Y be defined by f(x) = 2x + 1, x ∈ X. Then the range of f is
a)
{1, 2,…., 10}
b)
{5, 6, 7, 8, 9, 10}
c)
{3, 5, 7, 9}
d)
{1, 2, 3, 4}
|
|
Krishna Iyer answered |
X = {1, 2, 3, 4}
Y = {1, 2, …, 10}
f: X→ Y be defined by
f(x) = 2x + 1
f (1) = 3
f (2) = 5
f (3) = 7
f (4) = 9
Range(f) = {3, 5, 7, 9}
Y = {1, 2, …, 10}
f: X→ Y be defined by
f(x) = 2x + 1
f (1) = 3
f (2) = 5
f (3) = 7
f (4) = 9
Range(f) = {3, 5, 7, 9}
Which of the following relations is not a function?- a)R= {(1,2), (3,4),(2,1),(5,1)}
- b)R={(1,2), (1,4)(3,1),(5,1)}
- c)R= {(1,2), (3,4)(2,1),(5,2)}
- d)R= {(2,1), (4,4)(3,1),(5,1)}
Correct answer is option 'B'. Can you explain this answer?
Which of the following relations is not a function?
a)
R= {(1,2), (3,4),(2,1),(5,1)}
b)
R={(1,2), (1,4)(3,1),(5,1)}
c)
R= {(1,2), (3,4)(2,1),(5,2)}
d)
R= {(2,1), (4,4)(3,1),(5,1)}
|
|
Gaurav Kumar answered |
A function is a relation in which no two ordered pairs have the same first element. A function associates each element in its domain with one and only one element in its range. R={(1,2), (1,4)(3,1),(5,1)} is not a function because all the first elements are not different.
The function f (x) = x + cos x- a)is defined for all reals
- b)assumes only negative values
- c)assumes only positive values
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The function f (x) = x + cos x
a)
is defined for all reals
b)
assumes only negative values
c)
assumes only positive values
d)
none of these
|
|
Om Desai answered |
f(x) = x
g(x) = cosx
D(f) = R
D(g) = R
D(f+g) = D(f) ⋂ D(g)
So , D(f+g) = R
Therefore, given function is defined for real numbers.
g(x) = cosx
D(f) = R
D(g) = R
D(f+g) = D(f) ⋂ D(g)
So , D(f+g) = R
Therefore, given function is defined for real numbers.
The range of the function 
- a)[1/3,3]
- b)[3, ∞)
- c)R
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The range of the function 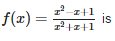
a)
[1/3,3]
b)
[3, ∞)
c)
R
d)
none of these

|
Amrit Raj answered |
It think option c is correct
If f(x) = x2 and g(x) = x are two functions from R to R then f(g(2)) is
- a)8
- b)4
- c)1
- d)2
Correct answer is option 'B'. Can you explain this answer?
If f(x) = x2 and g(x) = x are two functions from R to R then f(g(2)) is
a)
8
b)
4
c)
1
d)
2
|
|
Raghav Bansal answered |
f(g(2)) compare f(gx) x=2
on comparing g(x)=x, g(2)=2
f(g(x)) = f(2) = x2 = 22= 4
on comparing g(x)=x, g(2)=2
f(g(x)) = f(2) = x2 = 22= 4
The function f : R → R defined by y = f(x) = 5 for each x ∈ R is- a)Modulus function
- b)Signum function
- c)Identity function
- d)Constant function
Correct answer is option 'D'. Can you explain this answer?
The function f : R → R defined by y = f(x) = 5 for each x ∈ R is
a)
Modulus function
b)
Signum function
c)
Identity function
d)
Constant function

|
Pioneer Academy answered |
Constant Function is defined as the real valued function.
f: R→R, y = f(x) = c for each x∈R and c is a constant.
So ,this function basically associate each real number to a constant value.
It is a linear function where f(x1) = f(x2) for all x1,x2 ∈R
f: R→R, y = f(x) = c for each x∈R and c is a constant.
So ,this function basically associate each real number to a constant value.
It is a linear function where f(x1) = f(x2) for all x1,x2 ∈R
If A = [a, b], B = [c,d], C = [d, e] then {(a, c), (a, d), (a,e), (b,c), (b, d), (b, e)} is equal to- a)A∪(B∩C)
- b)A∩(B∪C)
- c)A×(B∩C)
- d)A×(B∪C)
Correct answer is option 'D'. Can you explain this answer?
If A = [a, b], B = [c,d], C = [d, e] then {(a, c), (a, d), (a,e), (b,c), (b, d), (b, e)} is equal to
a)
A∪(B∩C)
b)
A∩(B∪C)
c)
A×(B∩C)
d)
A×(B∪C)
|
|
Jatin Sen answered |
Understanding the Sets
To analyze the sets A, B, and C:
- A = [a, b]
- B = [c, d]
- C = [d, e]
Defining Operations
1. Union (U): Combines elements from both sets.
2. Intersection (∩): Contains elements common to both sets.
3. Cartesian Product (×): Forms pairs from elements of two sets.
Calculating B ∩ C
- B = [c, d]
- C = [d, e]
Common Element:
- The only common element is d.
- Therefore, B ∩ C = [d].
Calculating B U C
- B = [c, d]
- C = [d, e]
Combined Elements:
- B U C = [c, d, e].
Forming the Cartesian Product
- Now, we will find A × (B U C):
A = [a, b] and B U C = [c, d, e]
Pairs:
- From A and B U C, we get:
- (a, c)
- (a, d)
- (a, e)
- (b, c)
- (b, d)
- (b, e)
Final Cartesian Product:
- A × (B U C) = {(a, c), (a, d), (a, e), (b, c), (b, d), (b, e)}.
Conclusion
The set {(a, c), (a, d), (a, e), (b, c), (b, d), (b, e)} is indeed equal to A × (B U C), confirming that option 'D' is the correct answer.
To analyze the sets A, B, and C:
- A = [a, b]
- B = [c, d]
- C = [d, e]
Defining Operations
1. Union (U): Combines elements from both sets.
2. Intersection (∩): Contains elements common to both sets.
3. Cartesian Product (×): Forms pairs from elements of two sets.
Calculating B ∩ C
- B = [c, d]
- C = [d, e]
Common Element:
- The only common element is d.
- Therefore, B ∩ C = [d].
Calculating B U C
- B = [c, d]
- C = [d, e]
Combined Elements:
- B U C = [c, d, e].
Forming the Cartesian Product
- Now, we will find A × (B U C):
A = [a, b] and B U C = [c, d, e]
Pairs:
- From A and B U C, we get:
- (a, c)
- (a, d)
- (a, e)
- (b, c)
- (b, d)
- (b, e)
Final Cartesian Product:
- A × (B U C) = {(a, c), (a, d), (a, e), (b, c), (b, d), (b, e)}.
Conclusion
The set {(a, c), (a, d), (a, e), (b, c), (b, d), (b, e)} is indeed equal to A × (B U C), confirming that option 'D' is the correct answer.
If f and g are two functions over real numbers defined as f(x) = 3x + 1, g(x) = x2 + 2, then find f-g- a)x2+1
- b)3x + x2
- c)3x – x2-1
- d)x2+1-3x
Correct answer is option 'C'. Can you explain this answer?
If f and g are two functions over real numbers defined as f(x) = 3x + 1, g(x) = x2 + 2, then find f-g
a)
x2+1
b)
3x + x2
c)
3x – x2-1
d)
x2+1-3x
|
|
Karthikeyeni Baskaran answered |
It is just a simple subtraction...subtract g from f
Which of the following is incorrect?- a)Modulus function, Domain: R; Range: [0, infinity)
- b)Signum function, Domain: R; Range: {-1, 0,1}
- c)Constant function, Domain: R; Range: R
- d)Identity function, Domain: R; Range: R
Correct answer is option 'C'. Can you explain this answer?
Which of the following is incorrect?
a)
Modulus function, Domain: R; Range: [0, infinity)
b)
Signum function, Domain: R; Range: {-1, 0,1}
c)
Constant function, Domain: R; Range: R
d)
Identity function, Domain: R; Range: R
|
|
Preeti Khanna answered |
Constant Function is defined as the real valued function.
f : R→R, y = f(x) = c for each x∈R and c is a constant.
f : R→R, y = f(x) = c for each x∈R and c is a constant.
So, this function basically associate each real number to a constant value.
It is a linear function where f(x1) = f(x2) for all x1,x2 ∈ R
For f : R→R, y = f(x) = c for each x ∈ R
Domain = R
Range = {c}
The value of c can be any real number.
Domain = R
Range = {c}
The value of c can be any real number.
Number of subsets of a set of order three is- a)2
- b)4
- c)6
- d)8
Correct answer is option 'D'. Can you explain this answer?
Number of subsets of a set of order three is
a)
2
b)
4
c)
6
d)
8
|
|
Raj Ghoshal answered |
Number of Subsets of a Set of Order Three
To find the number of subsets of a set of order three, we need to consider all possible combinations of elements in the set.
Let's say we have a set S = {a, b, c}. We can represent each element of the set as a binary digit, where 0 represents the absence of the element and 1 represents the presence of the element.
- Empty Set: The empty set is a subset of every set, so it is included.
- Single Element Subsets: There are three single element subsets - {a}, {b}, and {c}.
- Two Element Subsets: There are three possible two-element subsets - {a, b}, {a, c}, and {b, c}.
- Three Element Subset: There is only one three-element subset - {a, b, c}.
Therefore, the total number of subsets of the set S = {a, b, c} is 1 (empty set) + 3 (single element subsets) + 3 (two-element subsets) + 1 (three-element subset) = 8.
Hence, the correct answer is option 'D' - 8.
In summary, to find the number of subsets of a set of order three, we consider all possible combinations of elements, including the empty set and subsets of different sizes. By applying this approach to the given set S = {a, b, c}, we find that there are 8 subsets in total.
To find the number of subsets of a set of order three, we need to consider all possible combinations of elements in the set.
Let's say we have a set S = {a, b, c}. We can represent each element of the set as a binary digit, where 0 represents the absence of the element and 1 represents the presence of the element.
- Empty Set: The empty set is a subset of every set, so it is included.
- Single Element Subsets: There are three single element subsets - {a}, {b}, and {c}.
- Two Element Subsets: There are three possible two-element subsets - {a, b}, {a, c}, and {b, c}.
- Three Element Subset: There is only one three-element subset - {a, b, c}.
Therefore, the total number of subsets of the set S = {a, b, c} is 1 (empty set) + 3 (single element subsets) + 3 (two-element subsets) + 1 (three-element subset) = 8.
Hence, the correct answer is option 'D' - 8.
In summary, to find the number of subsets of a set of order three, we consider all possible combinations of elements, including the empty set and subsets of different sizes. By applying this approach to the given set S = {a, b, c}, we find that there are 8 subsets in total.
The domain and range of the function f: R → R defined by: f = {(x+1, x+5): x ∈ {0, 1, 2, 3, 4, 5}}
- a)Domain = {2, 3, 4, 5, 6}; Range = {6, 7, 8, 9, 10}
- b)Domain = R ; Range = R
- c)Domain = {1, 2, 3, 4, 5, 6}; Range = {5, 6, 7, 8, 9, 10}
- d)Domain = {1, 2, 3, 4, 5}; Range = {5, 6, 7, 8, 9}
Correct answer is option 'C'. Can you explain this answer?
The domain and range of the function f: R → R defined by: f = {(x+1, x+5): x ∈ {0, 1, 2, 3, 4, 5}}
a)
Domain = {2, 3, 4, 5, 6}; Range = {6, 7, 8, 9, 10}
b)
Domain = R ; Range = R
c)
Domain = {1, 2, 3, 4, 5, 6}; Range = {5, 6, 7, 8, 9, 10}
d)
Domain = {1, 2, 3, 4, 5}; Range = {5, 6, 7, 8, 9}

|
Tejas Chawla answered |

Correct answer is C.
The domain of the function f(x)= 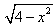 is all real x such that
is all real x such that- a)x<2
- b)-2
- c)-2 ≤ x ≤ 2
- d)x>-2
Correct answer is option 'C'. Can you explain this answer?
The domain of the function f(x)= 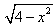 is all real x such that
is all real x such that
a)
x<2
b)
-2
c)
-2 ≤ x ≤ 2
d)
x>-2
|
|
Geetika Shah answered |
4 - x2 = 0
=> (2+x)(2-x) = 0
x = +-2
Now select a test point, let it be x = 0. Then y = (4 - (0)2)1/2 = 2, so the function is defined on [-2,2]
Thus, the graph of y = (4 - x2)1/2 is a semicircle with radius 2 and domain is [-2,2]
=> (2+x)(2-x) = 0
x = +-2
Now select a test point, let it be x = 0. Then y = (4 - (0)2)1/2 = 2, so the function is defined on [-2,2]
Thus, the graph of y = (4 - x2)1/2 is a semicircle with radius 2 and domain is [-2,2]
If f (x) 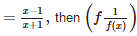 equals
equals- a)1/x
- b)0
- c)1
- d)x
Correct answer is option 'A'. Can you explain this answer?
If f (x) 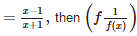 equals
equals
a)
1/x
b)
0
c)
1
d)
x
|
|
Pooja Shah answered |
f(x) = (x−1)/(x+1)
1/f(x) = (x+1)/(x-1)
f(1/f(x)) = [(x+1)/(x-1) - 1]/[(x+1)/(x-1) + 1]
⇒ (x+1-x+1)/(x+1+x-1)
= 2/2x
= 1/x
1/f(x) = (x+1)/(x-1)
f(1/f(x)) = [(x+1)/(x-1) - 1]/[(x+1)/(x-1) + 1]
⇒ (x+1-x+1)/(x+1+x-1)
= 2/2x
= 1/x
Let f : R → R be defined by f (x) = 3x – 4, then 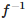 (x) is equal to
(x) is equal to- a)3x + 4
- b)
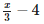
- c)x+4/3
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
Let f : R → R be defined by f (x) = 3x – 4, then 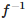 (x) is equal to
(x) is equal to
a)
3x + 4
b)
c)
x+4/3
d)
none of these
|
|
Hansa Sharma answered |
f(x) = 3x - 4
Let f(x) = y
y = 3x - 4
y + 4 = 3x
x = (y+4)/3
x → f-1(x) and y → x
f-1(x) = (x+4)/3
Let f(x) = y
y = 3x - 4
y + 4 = 3x
x = (y+4)/3
x → f-1(x) and y → x
f-1(x) = (x+4)/3
f(x) = x is called- a)an identity function
- b)a constant function
- c)inverse function
- d)step function
Correct answer is option 'A'. Can you explain this answer?
f(x) = x is called
a)
an identity function
b)
a constant function
c)
inverse function
d)
step function
|
|
Mira Sharma answered |
In mathematics, an identity function, also called an identity relation or identity map or identity transformation, is a function that always returns the same value that was used as its argument. In equations, the function is given by f(x) = x.
The domain of the real-valued function 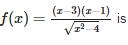
- a)(-∞, - 1) ∪ (1, ∞).
- b)(-∞, - 2) ∪ (1, ∞)
- c)(-∞, - 2) ∪ (2, ∞)
- d)(1, 2)
Correct answer is option 'C'. Can you explain this answer?
The domain of the real-valued function 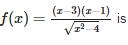
a)
(-∞, - 1) ∪ (1, ∞).
b)
(-∞, - 2) ∪ (1, ∞)
c)
(-∞, - 2) ∪ (2, ∞)
d)
(1, 2)
|
|
Lavanya Menon answered |
f(x) = (x-3)(x-1)/[(x2 -4)^1/2]
= x2 - 4 = 0
(x-2)(x+2) = 0
x = 2 and -2
(-∞, -2 ) U (2,∞)
= x2 - 4 = 0
(x-2)(x+2) = 0
x = 2 and -2
(-∞, -2 ) U (2,∞)
Which of the following is not true?- a)Every relation from the set A to the set B is a function from the set A to the set B.
- b)If f is a function from A to B and (a, b) ∈ f, then f(a) = b, where a is called the pre-image of b under f.
- c)Every function from the set A to the set B is a relation from the set A to the set B
- d)If f is a function from A to B and (a, b) ∈ f, then f(a) = b, where b is called the image of a under f.
Correct answer is option 'A'. Can you explain this answer?
Which of the following is not true?
a)
Every relation from the set A to the set B is a function from the set A to the set B.
b)
If f is a function from A to B and (a, b) ∈ f, then f(a) = b, where a is called the pre-image of b under f.
c)
Every function from the set A to the set B is a relation from the set A to the set B
d)
If f is a function from A to B and (a, b) ∈ f, then f(a) = b, where b is called the image of a under f.
|
|
Pooja Shah answered |
A relation f from a set A to a set B is said to be function if every element of set A has one and only one image in set B. In other words, a function f is a relation such that no two pairs in the relation has the same first element. The notation f : X →Y means that f is a function from X to Y.
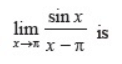
- a)1
- b)2
- c)-1
- d)-2
Correct answer is option 'C'. Can you explain this answer?
a)
1
b)
2
c)
-1
d)
-2

|
Mohit Rajpoot answered |
lim(x → π) sinx/x-π
lim(h → 0) sin(π-h)/π-h-π
lim(h → 0) -sinh/h
⇒ -1
lim(h → 0) sin(π-h)/π-h-π
lim(h → 0) -sinh/h
⇒ -1
If f(x) = x2 – x + 1; g(x) = 7x – 3, be two real functions then (f + g)(3) is- a)25
- b)3
- c)7
- d)18
Correct answer is option 'A'. Can you explain this answer?
If f(x) = x2 – x + 1; g(x) = 7x – 3, be two real functions then (f + g)(3) is
a)
25
b)
3
c)
7
d)
18
|
|
Riya Banerjee answered |
f(x) = x2 – x + 1; g(x) = 7x – 3
(f+g)(x) = (x2 - x + 1 + 7x - 3)
=(x2 - x + 7x + 1 - 3)
= x2 + 6x - 2
(f+g)(3) = x2 + 6x - 2
= (3)2 + 6(3) - 2
= 9 + 18 - 2
= 25
(f+g)(x) = (x2 - x + 1 + 7x - 3)
=(x2 - x + 7x + 1 - 3)
= x2 + 6x - 2
(f+g)(3) = x2 + 6x - 2
= (3)2 + 6(3) - 2
= 9 + 18 - 2
= 25
The function sin 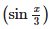 is periodic with period
is periodic with period- a)2π
- b)8π
- c)4π
- d)6π
Correct answer is option 'D'. Can you explain this answer?
The function sin 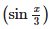 is periodic with period
is periodic with period
a)
2π
b)
8π
c)
4π
d)
6π
|
|
Preeti Iyer answered |
sin(sinx/3)
As we know that {T : 2π}
T = (sinx/3)
2π = (sinx/3)
Period = 6π
As we know that {T : 2π}
T = (sinx/3)
2π = (sinx/3)
Period = 6π
The interval in which the values of f (x) lie where f (x) = 3 sin 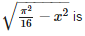
- a)[0,
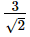 ]
] - b)[-3, 3]
- c)
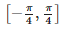
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The interval in which the values of f (x) lie where f (x) = 3 sin 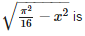
a)
[0, 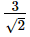 ]
]
b)
[-3, 3]
c)
d)
none of these
|
|
Om Desai answered |
f(x) = 3.sin(√π2/16 − x2)
since the quantity within the square root can not be negative.
therefore
π2/16 − x2 ≥ 0
x2 ≤ π2/16
−π/4 ≤ x ≤ π/4
the minimum value of the function is 3.sin0=0
and the maximum value of the function is 3sinπ/4 = 3/√2
therefore range is [0, 3/√2]
since the quantity within the square root can not be negative.
therefore
π2/16 − x2 ≥ 0
x2 ≤ π2/16
−π/4 ≤ x ≤ π/4
the minimum value of the function is 3.sin0=0
and the maximum value of the function is 3sinπ/4 = 3/√2
therefore range is [0, 3/√2]
A condition for a function y = f (x) to have an inverse is that it should be- a)an even function
- b)defined for all x
- c)strictly monotone and continuous in the domain
- d)continuous every where
Correct answer is option 'C'. Can you explain this answer?
A condition for a function y = f (x) to have an inverse is that it should be
a)
an even function
b)
defined for all x
c)
strictly monotone and continuous in the domain
d)
continuous every where
|
|
Krishna Iyer answered |
For a function to have its inverse in a given domain, it should be continuous in that domain and should be a one-one function in that domain.
If the function is one-one in the domain, then it has to be strictly monotonic.
For example y=sin(x) has its domain in xϵ[−π/2,π/2] since it is strictly monotonic and continuous in that domain.
If the function is one-one in the domain, then it has to be strictly monotonic.
For example y=sin(x) has its domain in xϵ[−π/2,π/2] since it is strictly monotonic and continuous in that domain.
Let x be any real, then [x + y] = [x] + [y] holds for- a)y∈ R, y ∈ Q.
- b)y ∈ R
- c)y ∈ Q
- d)y ∈ I
Correct answer is option 'D'. Can you explain this answer?
Let x be any real, then [x + y] = [x] + [y] holds for
a)
y∈ R, y ∈ Q.
b)
y ∈ R
c)
y ∈ Q
d)
y ∈ I
|
|
Neha Joshi answered |
Let y has some fractional part
x = 6.5
y = 0.9
[x] = 6, [y] = 0, [x]+[y] = 6
[x + y] = [7.4] = 7
[x + y] ≠ [x]+[y]
Let x, y be integers
x = 6.5
y = 1
[x] = 6, [y] = 1, [x]+[y] = 7
[x + y] = [7.5] = 7
[x + y] = [x]+[y]
So, [x + y] = [x]+[y] holds for y ϵ I
x = 6.5
y = 0.9
[x] = 6, [y] = 0, [x]+[y] = 6
[x + y] = [7.4] = 7
[x + y] ≠ [x]+[y]
Let x, y be integers
x = 6.5
y = 1
[x] = 6, [y] = 1, [x]+[y] = 7
[x + y] = [7.5] = 7
[x + y] = [x]+[y]
So, [x + y] = [x]+[y] holds for y ϵ I
Find the domain of the function f(x) = 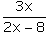
- a)R – {-4}
- b)R
- c)R – {4}
- d)R+
Correct answer is option 'C'. Can you explain this answer?
Find the domain of the function f(x) = 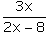
a)
R – {-4}
b)
R
c)
R – {4}
d)
R+
|
|
Lavanya Menon answered |
f(x) = 3x/2x-8
denominator can't be zero so
2x - 8 not equal to 0
x should not equal to 4
we have domain R - {4}
denominator can't be zero so
2x - 8 not equal to 0
x should not equal to 4
we have domain R - {4}
On the set Z of all integers define f ; Z → Z as follows : f (x) = {x/2 if x is even, and f (x) = 0 if x is odd , then f is
- a)onto but not one-one
- b)into
- c)one-one but not onto
- d)one-one and onto
Correct answer is option 'A'. Can you explain this answer?
On the set Z of all integers define f ; Z → Z as follows : f (x) = {x/2 if x is even, and f (x) = 0 if x is odd , then f is
a)
onto but not one-one
b)
into
c)
one-one but not onto
d)
one-one and onto
|
|
Sneha Sarkar answered |
To define a function f on the set Z of all integers, we need to specify how the function maps each integer to another value.
For example, we can define a function f as follows:
- f(n) = n + 1, where n is any integer in Z.
This function takes an integer n and returns the next integer in the sequence. For example, f(1) = 2, f(0) = 1, f(-1) = 0, and so on.
Another example of a function on Z could be:
- f(n) = n^2, where n is any integer in Z.
This function takes an integer n and returns its square. For example, f(2) = 4, f(-3) = 9, and so on.
There are infinite possible functions that can be defined on the set Z, depending on how we want to map the integers to other values. The specific definition of the function would depend on the desired outcome or purpose of the function.
For example, we can define a function f as follows:
- f(n) = n + 1, where n is any integer in Z.
This function takes an integer n and returns the next integer in the sequence. For example, f(1) = 2, f(0) = 1, f(-1) = 0, and so on.
Another example of a function on Z could be:
- f(n) = n^2, where n is any integer in Z.
This function takes an integer n and returns its square. For example, f(2) = 4, f(-3) = 9, and so on.
There are infinite possible functions that can be defined on the set Z, depending on how we want to map the integers to other values. The specific definition of the function would depend on the desired outcome or purpose of the function.
Which is not true for the graph of the real function y = x2:- a)The least value of x2 is one and will be so when x = 1.
- b)For this function domain = Real numbers
- c)The parabola will open upward.
- d)The graph of the given function is a parabola.
Correct answer is option 'A'. Can you explain this answer?
Which is not true for the graph of the real function y = x2:
a)
The least value of x2 is one and will be so when x = 1.
b)
For this function domain = Real numbers
c)
The parabola will open upward.
d)
The graph of the given function is a parabola.
|
|
Om Desai answered |
For the graph y=x2
The least value of x2 is zero and square of any number will also be zero.
The least value of x2 is zero and square of any number will also be zero.
The domain of the function 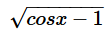 is
is- a){2 n π: n ∈ I}
- b){ }
- c)R
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The domain of the function 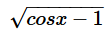 is
is
a)
{2 n π: n ∈ I}
b)
{ }
c)
R
d)
none of these
|
|
Geetika Shah answered |
For f to be defined term under square root has to be greater than zero.
⇒ cosx − 1 ≥ 0
⇒ cosx ≥ 1
Only possible if cosx = 1
⇒ x = 2nπ ∀ n∈Z
⇒ cosx − 1 ≥ 0
⇒ cosx ≥ 1
Only possible if cosx = 1
⇒ x = 2nπ ∀ n∈Z
If f(x) =  is equal to
is equal to- a)f (x)
- b)2 f (x)
- c)4 f(x)
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
If f(x) =  is equal to
is equal to
a)
f (x)
b)
2 f (x)
c)
4 f(x)
d)
none of these
|
|
Om Desai answered |
f(x) = log[(1+x)/(1-x)] ……….(1)
Substitute 2x/1+x2 in place of x in equation(1)
f(2x1+x2)=log(1+2x1+x2)(1−2x1+x2)
⟹f(2x/(1+x2))=log[1+(2x/(1+x2))/(1-(2x/1+x2))]
⟹f(2x/(1+x2))=log((1+x2+2x)/(1+x2−2x))
⟹f(2x/(1+x2))=log((1+x)2 / (1−x))2
⟹f(2x/ (1+x2))=log(1+x / 1−x)2
We know that logmn=nlogm
⟹f(2x/(1+x2))=2log(1+x / 1−x)
From equation (1):
f(2x/(1+x2))=2f(x)
Substitute 2x/1+x2 in place of x in equation(1)
f(2x1+x2)=log(1+2x1+x2)(1−2x1+x2)
⟹f(2x/(1+x2))=log[1+(2x/(1+x2))/(1-(2x/1+x2))]
⟹f(2x/(1+x2))=log((1+x2+2x)/(1+x2−2x))
⟹f(2x/(1+x2))=log((1+x)2 / (1−x))2
⟹f(2x/ (1+x2))=log(1+x / 1−x)2
We know that logmn=nlogm
⟹f(2x/(1+x2))=2log(1+x / 1−x)
From equation (1):
f(2x/(1+x2))=2f(x)
Chapter doubts & questions for Relations and Functions - Online MCQ Tests for Commerce 2025 is part of Commerce exam preparation. The chapters have been prepared according to the Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Relations and Functions - Online MCQ Tests for Commerce in English & Hindi are available as part of Commerce exam.
Download more important topics, notes, lectures and mock test series for Commerce Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup